Introduction

Two-dimensional (2D) magnetic van der Waals (vdW) materials have seen rising attention since their recent introduction into the field of spintronics and beyond1. Many of these materials show promising properties for future applications, such as the semiconducting 2D ferromagnet CrI32, the metallic 2D ferromagnet Fe3GeTe23 and the very recently discovered metallic 2D ferromagnet Fe5GeTe2 that orders even at relatively high temperatures4,5. Not only has its magnetic order exhibited significant complexity6, the closely related material (Fe0.5Co0.5)5GeTe2, whose magnetic order exists at room temperature7,8, has already been shown to host skyrmions9. The operation of a spintronic device requires ferromagnetic materials with room-temperature magnetic ordering, but most of the 2D vdW magnetic materials are either not ferromagnetic or do not possess a high magnetic ordering temperature. Here, Fe5GeTe2 is unique in that it has attracted specific scientific attention due to its room-temperature ferromagnetism with an ordering temperature of TC ≈ 310 K. To make use of a magnetic system for applications, spin structures are often required as information carriers. Interest in the dynamics of spin structures accordingly motivated recent studies on domain walls in vdW magnets10,11. A particularly promising and exciting spin structure is the magnetic skyrmion12,13,14, which has also been observed in the related material Fe3GeTe215,16. Hence, for 2D magnet applications, the required next step is the observation of topological magnetic spin structures near room temperature in Fe5GeTe2. Recently, meron spin structures have been observed in domain walls of Fe5GeTe2, but they could only be stabilized well below room temperature17. Fe5GeTe2 is additionally intriguing as it exhibits an irreversible magneto-structural phase transition upon cooling below ≈ 100 K for the first time after synthesization of quenched Fe5GeTe2 crystals18. This means that Fe5GeTe2 crystals, which have been quenched to room temperature in the synthesization process remain in a metastable phase at room temperature before reaching a stable phase after cooling below ≈ 100 K for the first time. Upon heating back up to higher temperatures even above room temperature, Fe5GeTe2 remains in this magneto-structural phase, thus indicating the thermal stability of this phase. There is particular interest in the spin structures in a Fe5GeTe2 crystal, before and after going through the irreversible phase transition upon cooling below T≈100 K. These phases are termed the metastable pre-cooling and the stable post-cooling phases. Real space probing of the crystal lattice and spin structure in both of these phases is still a major open question.

In the present work, bulk magnetic properties in the phases of 2D Fe5GeTe2 are characterized using a superconducting quantum interference device (SQUID), in combination with magnetic domain images using Lorentz transmission electron microscopy (L-TEM), which reveals stable topological spin structures up to room temperature. Further, the crystallographic space groups previously suggested for Fe5GeTe2 are investigated and we resolve open questions about their symmetry by presenting a spin chirality analysis. The spin chirality analysis involves careful considerations of the chirality of observed spin structures in Fe5GeTe2, in order to deduce if the chiral Dzyaloshinskii-Moriya interaction (DMI) is present in the sample. Finally, the complex magnetic ordering of Fe5GeTe2 is closely examined and we determine that the system is not in a spin glassy state. This is done via a careful comparison of the effective anisotropy obtained on a macroscopic scale with the effective anisotropy obtained on a microscopic scale.

Results and discussion

Structural and composition analysis

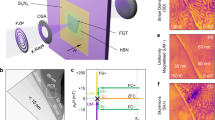
Figure 1(a) shows a cross-section atomic resolution high angle annular dark-field detector (HAADF) scanning transmission electron microscopy (STEM) image of the quenched single-crystal Fe5GeTe2 used in the present work. Figure 1(b) is a color-coded composition map obtained using energy dispersive X-ray (EDX) spectroscopy, which shows the periodic distribution of iron, germanium and tellurium. 2D layers consist of a sandwich of two planes of Te (brightest columns) with Ge and Fe planes located in-between. The layers are stacked along the c-axis and are approximately 1 nm thick including the vdW gap (dark area between two neighboring Te planes). A schematic model of the atomic structure is overlaid in the middle of Fig. 1(a) with the same color code as in Fig. 1(b). Following the notation used by May et al.4, the Fe(2) and Fe(3) columns can be identified but the Fe(1) columns are not visible. Since STEM images show a projection of the crystal structure over the thickness of the lamella, this iron site is not easily visible because of its split-site nature4. Figure 1(c) is another HAADF STEM that shows the presence of a stacking fault as indicated by red lines and an arrow, which has been previously reported in Fe5GeTe219. Here, stacking faults were observed primarily near the surface of the crystal (down to 200 nm below the surface). They are scarce deeper in the bulk of the sample, which has essentially a regular crystal structure, as shown in Fig. 1(a). Figure 1(d) is a plan-view image where the c-axis is perpendicular to the image, which shows the hexagonal shape of the lattice.

Fig. 1: High resolution analyses of the crystal structure of Fe5GeTe2.
figure 1

a High resolution high angle annular dark-field detector (HAADF) scanning transmission electron microscopy (STEM) image of the structure with the c-axis along the vertical direction in the image plane. b Color-coded energy dispersive X-ray (EDX) composition map showing the distribution of iron, germanium and tellurium. A schematic model of the atomic structure is overlaid on image (a) with the same color code as in panel b. c HAADF STEM image showing a stacking fault as indicated by red lines and an arrow. d HAADF STEM image of the structure with the c-axis perpendicular to the image plane.

Full size image

Magnetic imaging of skyrmionic spin structures

We first observe the magnetization configuration at room temperature in our sample in the pre-cooling phase, as the types of spin structures also entail information about the underlying crystal structure of Fe5GeTe2. The space group of Fe5GeTe2 has not so far been identified unambiguously. Li et al. and May et al. report the centrosymmetric space group \(R\bar{3}m\) (No. 166)4,20, whereas Stahl et al. reported the non-centrosymmetric space group R3m (No. 160)19. Here we consider the skyrmionic spin structures in Fe5GeTe2 to resolve this space group issue. A prerequisite for chiral spin structures, such as skyrmions and chiral domain walls, is the DMI, which occurs in systems with broken inversion symmetry21. In this regard, chiral spin structures would not be stabilized in bulk Fe5GeTe2 if its space group is \(R\bar{3}m\), whereas they could be stabilized in bulk Fe5GeTe2 with the non-centrosymmetric space group R3m.

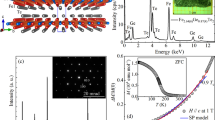
Figure 2(a, b) show an in-focus phase shift image and the corresponding magnetic induction map reconstructed from an off-axis electron hologram obtained in a lamella cut perpendicular to the c-axis. The sample is magnetized along the crystallographic c-axis, which can also be deduced from SQUID measurements, as discussed in section Supplementary Note 1 and shown in Supplementary Fig. S1 of the supplementary information. Two different types of circular spin structures can be observed. These bubbles with a black or white electron phase contrast correspond to type-I bubbles with a clockwise or counter-clockwise field rotation22. These two possible chiralities were found to occur with equal probabilities. Bubbles that show a black to white phase gradient correspond to topologically trivial type-II bubbles in which the rotation of the field changes22. Figure 2(c) shows schematically the magnetic field in type-I and type-II bubbles. The presence of both type-II and type-I bubbles with two possible chiralities indicate that they are not stabilized by bulk DMI23, but likely by dipolar interactions. We give further reasoning for our conclusion that these bubbles are likely stabilized by dipolar interactions in the supplementary section Supplementary Note 6 and Supplementary Fig. S5. Furthermore, all observed bubbles are Bloch-type bubbles, as can be seen in Fig. 2b, which is an indication that no significant interfacial DMI is present in our Fe5GeTe2 sample either24. These observations are indicative of underlying centrosymmetry and thus support the results of Li et al. and May et al. regarding the centrosymmetric space group \(R\bar{3}m\) for Fe5GeTe24,20. It is worth noting that the L-TEM samples used here have been cut such that the stacking faults observed near the surface of bulk samples are not present. While additional stacking faults can occur during the phase transition, as shown in supplementary section Supplementary Note 8, Supplementary Fig. S7 and Supplementary Fig. S8, the images in Fig. 2 are recorded in the pre-cooling phase, such that symmetry breaking due to stacking faults is expected to be negligible.

Fig. 2: Magnetic imaging of Fe5GeTe2 in the pre-cooling phase, revealing skyrmionic spin structures.
figure 2

a Phase shift image obtained using off-axis electron holography at T = 200 K and B = 0 mT in Fe5GeTe2 with the c-axis perpendicular to the image plane after previously applying out-of-plane fields up to B = 566 mT. b Corresponding color-coded magnetic induction map where the direction of the magnetic field is given by the color wheel. Type-II as well as type-I bubbles with opposite winding numbers are present. c Schematic illustration of type-I and type-II bubbles. d Series of Fresnel images taken at various temperatures and external out-of-plane fields (parallel to the c-axis) with a defocus of −1 mm, in a ≈ 100 nm thick plan-view lamella (c-axis is perpendicular to the image plane). The magnetization within the magnetic bubbles opposes the external field, whereas the areas the magnetization between the bubbles are parallel to the field. Bubbles begin to form at higher external fields for lower temperatures.

Full size image

A series of Fresnel defocus images taken at different temperatures and external fields, as shown in Fig. 2(d), reveals that the formation of bubbles is favorable over labyrinth domains at larger applied fields, and that the bubbles form at fields slightly smaller than the saturating fields at any temperature. This is in line with previous results on other systems, where it was shown that skyrmion formation can be favorable at sufficiently strong external fields25. Furthermore, we observe that the sizes of the magnetic bubbles shrink as the opposing net magnetization grows with external field, which is also in line with previous reports for chiral skyrmions and non-chiral skyrmions22,26. In the individual field sweeps shown in Fig. 2(d), the sample is previously saturated along the positive field direction, then the external field is turned off and finally the field sweep is done from zero field until the sample saturates again at a high positive field. In this case, bubbles are stabilized even at zero external field, since the external field gradually ramps down from the saturation field, nucleating bubbles slightly below the saturation field. With this history, even when zero external field is reached, a transformation to e.g., stripe domains is not observed.

Pre-cooling and post-cooling magnetic properties

In order to explore the bulk magnetic properties of quenched Fe5GeTe2 in both the metastable pre-cooling and stable post-cooling phases, we have taken SQUID measurements of our sample while it is going through the phase transition. With SQUID the magnetization of bulk Fe5GeTe2 can be measured quantitatively and quickly, which is not possible with L-TEM. The temperature dependence of the magnetization for two magnetic field directions, B parallel to the ab-plane (Bab-plane) and B parallel to the c-axis (Bc-axis) in an external field of 0.1 T for Fe5GeTe2 is shown in Fig. 3(a) and (b), respectively. For Bab-plane, the first Field Cooled Cooling (FCC1) curve reveals three magnetic anomalies. The anomaly at 271 K corresponds to the magnetic ordering temperature (TC). The anomaly related to decreasing magnetization at 136 K (TC2) may correspond to a transition to a spin glassy phase27. Another possible explanation is that Fe5GeTe2 may be in a ferrimagnetic order under these conditions, as previously suggested for a similar temperature range by Ohta et al. and Alahmed et al., respectively28,29. However, as soon as our sample reaches the stable post-cooling phase, it is found to be in a ferromagnetic state. Finally, the anomaly of a sudden increase in magnetization at T = 87 K corresponds to an irreversible magneto-structural phase transition (TS) from a metastable pre-cooling phase to a stable post-cooling phase, consistent with previous results4,19. In the Field Cooled Warming (FCW) curve and the FCC2 curve, no such anomaly is evident at ≈100 K, thus confirming the 87 K anomaly of FCC1 data was due to the non-reversible nature of this magneto-structural phase transition. While a weak anomaly with an increase in magnetization is evident at 118 K in FCW followed by a narrow hysteresis between FCW and FCC2, it may be due to some spin reoriented phase transition. Further, the critical temperature TC has shifted from 270 K to 310 K. Such a shift in TC is consistent with previous reports18. The difference in the net magnetization between 100 K to 300 K for FCW and FCC1 curves may be partially caused by the two different spin textures that Fe5GeTe2 exhibits between the stable post-cooling and the metastable pre-cooling phases, which will be discussed later in more detail.

Fig. 3: Magnetization vs. temperature of Fe5GeTe2.
figure 3

The external field B is applied along the c-axis and in the ab-plane with a field strength of 0.1 T, while the temperature T is varied and the magnetization M is measured. Zero field cooled (ZFC) indicates that the sample was cooled without application of an external field and then the field of 0.1 T was applied at the lowest temperature followed by measurements performed during warming. Field cooled cooling (FCC) and field cooled warming (FCW) indicates measurements performed subsequently during cooling and warming with the field kept on, respectively. The numbers 1, 2, 3 define the measurement sequence. When the external magnetic field is in the ab-plane (a), the sequence is FCC1, followed by FCW and finally FCC2, while for B along the c-axis (b), the sequence is FCC followed by FCW and finally ZFC. TC denotes the critical temperature associated with the phase transition to the paramagnetic phase and at TC2 the magnetization starts to exhibit its characteristic behavior. The standard deviation of each data point is smaller than 100 A/m and as such smaller than the displayed markers.

Full size image

Due to the irreversibility of the phase transition that occurs at 87 K, newly synthesized crystal pieces were chosen for the Bc-axis measurements. The Bc-axis data curves show similar magnetic behavior to that of the Bab-plane configuration. The slightly different values of TC2 and TS for the Bab-plane and Bc-axis FCC curves may be due to the magneto-crystalline anisotropy. That TC is almost the same value in both configurations further indicates that the magneto-crystalline anisotropy is a possible origin of the observed difference in TC2 and TS for the two measurement configurations. The third and final curve is a zero-field cooled (ZFC) curve, which also shows a TC of 310 K with low net magnetization. The large difference between the ZFC and FCW curves may have resulted from the occurrence of different domain configurations due to the external magnetic field-induced reorientation of ferromagnetic components. Consequently, the characteristic properties of the M-T curve are observed in two independent samples, once when a field is applied along the c-axis, and once when the field is applied perpendicular to the c-axis.

In Fig. 4, one can quantitatively see an increase in magnetization in the post-cooling phase compared to the pre-cooling phase under otherwise equivalent conditions. This is true for the wide range of measured temperatures and external fields, in both the Bc-axis and Bab-plane configurations. For example, at 150 K and 100 mT in the Bab-plane configuration:

$${M}_{{{{{{{\rm{pre}}}}}}{\mbox{-}}{{{{{\rm{cooling}}}}}}}}^{{{{{{{{\rm{150K}}}}}}}}}(B=100\,{{{{{{{\rm{mT}}}}}}}})=(5.75\pm 0.12)\cdot 1{0}^{5}{{{{{{{\rm{A}}}}}}}}\,{{{{{{{{\rm{m}}}}}}}}}^{-1},$$
(1)
$${M}_{{{{{{\rm{post}}}}}}{\mbox{-}}{{{{{\rm{cooling}}}}}}}^{{{{{{{{\rm{150K}}}}}}}}}(B=100\,{{{{{{{\rm{mT}}}}}}}})=(6.54\pm 0.13)\cdot 1{0}^{5}{{{{{{{\rm{A}}}}}}}}\,{{{{{{{{\rm{m}}}}}}}}}^{-1}.$$
(2)

The SQUID measurements yielded a saturation magnetization of

$${M}_{{{{{{{{\rm{s}}}}}}}}}=(8.12\pm 0.16)\cdot 1{0}^{5}{{{{{{{\rm{A}}}}}}}}\,{{{{{{{{\rm{m}}}}}}}}}^{-1}.$$
(3)
Fig. 4: Magnetic field dependent magnetization curves.
figure 4

The external field B is applied along the c-axis and in the ab-plane at different temperatures, while the magnetization M is measured. a, b for the pre-cooling and c, d for the post-cooling phase. The standard deviation of each data point is smaller than 100 A/m and as such smaller than the displayed markers.

Full size image

To confirm the validity of this saturation magnetization value, an independent method to determine the saturation magnetization via analysis of the stripe domain patterns is used30. The resulting value is Ms = (2.56 ± 1.40)⋅106 A m−1. This value has a relatively large uncertainty, and the method neglects e.g., shape anisotropy and surface defects. However, it is sufficiently close to the saturation magnetization measured with the SQUID and thus confirms its validity. The details of the method and calculation can be found in section Supplementary Note 2 and Supplementary Fig. S2 of the supplementary information.

At this point, it is worth noting that the M-H curve at 120 K in the pre-cooling phase shown in Fig. 4(a) is in line with the other recorded curves. This suggests that the decreasing magnetization with decreasing temperature observed in this regime in Fig. 3 is not due to a spin glassy state31. This is in line with results discussed later in this paper, where the magnetic ordering of Fe5GeTe2 is discussed and it is found that Fe5GeTe2 is not in a spin glassy state using an independent method.

Finally, we have taken a series of Fresnel defocus images of our sample at temperatures ranging from 95 K to 290 K and at a constant external field of B = 100 mT along the c-axis, both in the pre-cooling and post-cooling phases. The phase transition from the metastable pre-cooling to the stable post-cooling phase in the TEM lamellae was achieved by cooling the sample down to ≈77 K, leaving it in liquid nitrogen for one hour. The images for these temperature sweeps are shown in Fig. 5. Furthermore, a direct comparison of field sweeps at 95 K for both phases is shown in the supplementary section Supplementary Note 7 and Supplementary Fig. S6. A striking difference between the two sets of images in Fig. 5 is that skyrmionic bubbles are formed in the pre-cooling phase, but stripe domains form in the post-cooling phase, under otherwise equivalent circumstances. Since magnetic skyrmions predominantly form when an external field close to the saturation field is applied, this suggests that the saturation field of our sample has increased during the phase transition to the post-cooling phase. This could be explained by an increase in the magnetization in the post-cooling state, as this would mean that the dipolar energy is still large relative to the external field contribution. Magnetometry measurements of a bulk sample using a SQUID support this idea, and yield larger magnetizations at moderate fields in the post-cooling phase compared to the pre-cooling phase, as discussed earlier in this subsection.

Fig. 5: Fresnel images of Fe5GeTe2 at various temperatures.
figure 5

The temperature is indicated in the figure and a constant external field of B = 100 mT is applied. A defocus of −1 mm was used in a plan-view lamella (c-axis is perpendicular to the image plane), recorded before a and after b leaving the sample in liquid nitrogen for one hour.

Full size image

Magnetic ordering

It was shown in the previous subsection that Fe5GeTe2 shows a decrease in magnetization upon cooling from TC2 down to TS while the sample is in the metastable pre-cooling phase (see Fig. 3), which indicates that Fe5GeTe2 might exhibit ferrimagnetic order or is in a spin glassy state. To distinguish these effects, we study next whether or not Fe5GeTe2 is in a glassy spin state. To this end, the micromagnetic anisotropy constant K is experimentally determined in two independent ways and compared. One method is to consider the hard-axis saturation field \({B}_{{{{{{{{\rm{sat}}}}}}}}}^{{{{{{{{\rm{IP}}}}}}}}}\), which is simply related to the exchange constant via the Stoner-Wohlfarth model32. By finding the total energy minimum with a given field applied along the hard-axis, and including Zeeman and anisotropy interactions, one finds that the expression for in-plane saturation is:

$${K}_{{{{{{{{\rm{IP}}}}}}}}}={B}_{{{{{{{{\rm{sat}}}}}}}}}^{{{{{{{{\rm{IP}}}}}}}}}\frac{{M}_{{{{{{{{\rm{s}}}}}}}}}}{2}.$$
(4)

A complementary approach to determine K is via the domain wall width δ33:

$$\delta =\pi \Delta =\pi \sqrt{\frac{A}{{K}_{\delta }}},$$
(5)

where A is the micromagnetic exchange constant and Δ is a fit parameter used in the determination of the domain wall width δ from the measured domain wall profile. Note that when measuring KIP, the quantities involved are determined on a macroscopic scale, whereas the determination of Kδ will require knowledge of the exchange interaction, which is short-ranged and dominates on the nanoscale. Thus, local disorder present in spin glasses34 would manifest itself by affecting Kδ and KIP differently and leading to different values. Consequently, if Kδ and KIP are consistent with each other, Fe5GeTe2 is not in a spin glassy state.

To obtain Kδ, the micromagnetic exchange coupling constants were calculated using the JuKKR density functional theory (DFT) code35 (see the Methods section). This code employs the method of infinitesimal rotations36,37,38 to map the interactions among spins \({\vec{S}}_{i}={\vec{M}}_{i}/{\mu }_{i}\) (\({\mu }_{i}=| {\vec{M}}_{i}|\)) at lattice sites i onto the extended classical Heisenberg Hamiltonian

$$H=-\mathop{\sum}\limits_{i\ne j}{J}_{ij}\left({\vec{S}}_{i}\cdot {\vec{S}}_{j}\right)-\mathop{\sum}\limits_{i\ne j}{\vec{D}}_{ij}\cdot \left({\vec{S}}_{i}\times {\vec{S}}_{j}\right)-\mathop{\sum}\limits_{i}K{({\vec{S}}_{i}\cdot {\hat{e}}_{z})}^{2},$$
(6)

where the first term describes the exchange interaction, the second term represents DMI, and the final term describes the uniaxial out-of-plane anisotropy. The micromagnetic spin stiffness is

$$A=\frac{1}{2V}\mathop{\sum}\limits_{i\ne j}{J}_{ij}{\vec{r}}_{ij}^{2},$$
(7)

where V is the volume per Fe atom, which can be calculated from the exchange coupling constants37. These parameters define the micromagnetic energy functional

$$E[\vec{m}]=\int d{\vec{r}}\left[A{(\nabla \vec{m})}^{2}+K{m}_{z}^{2}\right],$$
(8)

where the contribution of the spiralization that is related to the DMI vectors is neglected because it is found to vanish. The micromagnetic exchange constant obtained from this method is

$${A}_{{{{{{{{\rm{DFT}}}}}}}}}=0.1508\,{{{{{{{\rm{eV}}}}}}}}\,{{{{{{{{\rm{nm}}}}}}}}}^{-1}.$$
(9)

An alternative, independent method to approximate the micromagnetic exchange constant A by considering the magnetic ordering temperature and crystal structure, is presented and executed in section Supplementary Note 3 of the supplementary information. The result is AH = (0.060 ± 0.007) eV nm−1 and it is fairly close to the DFT value considering that many assumptions are made in this alternative method. Further calculations and comparisons to experiment, which support the DFT models and calculations are presented in the supplementary sections Supplementary Note 4 and Supplementary Note 5.

To determine the effective anisotropy Kδ using the spin stiffness A, we next need to determine the domain wall width δ. The domain wall parameter Δ can in principle be determined from phase shift images obtained using off-axis electron holography by fitting the magnetic phase gradient profile perpendicular to a domain wall. Whereas Fresnel images would introduce problems in the accurate determination of the domain wall profiles due to their necessary defocus, off-axis electron holography images are in-focus and as such allow one to extract the domain wall profiles directly. The profile can then immediately be fit to the well-known theoretical domain wall profile \({M}_{{{{{{{{\rm{z}}}}}}}}}^{{{{{{{{\rm{theo}}}}}}}}}(x)={M}_{0}\cdot \tanh (x/\Delta )\). In reality the profiles will not be perfectly centered, so we use a fit function which allows for shifts:

$${M}_{{{{{{{{\rm{z}}}}}}}}}^{{{{{{{{\rm{fit}}}}}}}}}(x)={M}_{0}\cdot \tanh ((x-{x}_{{{{{{{{\rm{shift}}}}}}}}})/\Delta )+{M}_{{{{{{{{\rm{shift}}}}}}}}},$$
(10)

where M0 is the amplitude of the magnetization, x is the position perpendicular to the domain wall, and xshift and Mshift are the free fit parameters accounting for imperfect centering. To obtain reliable results, each line drawn perpendicular to the domain walls has a width of 277.5 nm (300 pixels) to average across. An example of such a line is shown in Fig. 6(a), and the corresponding magnetic profile and fit is shown in panel (b). Overall, the domain wall width has been determined via four independent lines at 95 K and five different lines at 200 K. The resulting domain wall widths are δ95K = (24.2 ± 5.2) nm and δ200K = (36.3 ± 3.5) nm. The uncertainties are estimated via the standard deviation of the domain wall widths obtained from all lines used at each temperature. Accordingly, the fit parameters are Δ = δ/π. These experimental domain wall widths are in line with results from a DFT calculation evaluated in the supplementary section Supplementary Note 5. The corresponding results are shown in Supplementary Fig. S3 and Supplementary Fig. S4. Thus, all required parameters to find Kδ via equation (5) are known, and we find using ADFT and the parameters Δ:

$${K}_{\delta }^{{{{{{{{\rm{95K}}}}}}}}}=(2.55\pm 0.55)\cdot 1{0}^{-3}\,{{{{{{{\rm{eV}}}}}}}}\,{{{{{{{{\rm{nm}}}}}}}}}^{-3},$$
(11)
$${K}_{\delta }^{{{{{{{{\rm{200K}}}}}}}}}=(1.13\pm 0.11)\cdot 1{0}^{-3}\,{{{{{{{\rm{eV}}}}}}}}\,{{{{{{{{\rm{nm}}}}}}}}}^{-3}.$$
(12)
Fig. 6: Analysis of the magnetic contrast of a magnetic domain wall, with the aim to determine the domain wall width.
figure 6

a Magnetic phase gradient image obtained using off-axis electron holography. A profile was extracted in the direction perpendicular to a 180∘ domain wall along the wide line. b Phase gradient profile (blue) and corresponding fit (orange). This example shows one magnetic profile across a domain wall at 95 K. Error bars are omitted for readability; the standard deviation of each measured gray value is 0.009.

Full size image

For the alternative determination of the anisotropy via the saturation field along the hard-axis KIP, images of the cross-section lamella sample are recorded at various field strengths at 95 K and 200 K (examples of images at 95 K are shown in Supplementary Fig. S1(c–e) in the supplementary information). The point at which the magnetic contrast completely vanishes as a function of magnetic field is approximated by splining the data for which there is magnetic contrast, and interpolating to the point where the minority domain has a width of zero. It should be noted that, since the field may not be applied perfectly perpendicular to the c-axis, this field is the monodomainization field, and serves as a lower bound for the hard-axis saturation field. However, it can be used as an estimation for the hard-axis saturation field. In this case, the saturation fields are estimated to be \({B}_{{{{{{{{\rm{sat}}}}}}}}}^{{{{{{{{\rm{IP,95K}}}}}}}}}=(285\pm 85)\,{{{{{{{\rm{mT}}}}}}}}\) and \({B}_{{{{{{{{\rm{sat}}}}}}}}}^{{{{{{{{\rm{IP,200K}}}}}}}}}=(143\pm 43)\,{{{{{{{\rm{mT}}}}}}}}\). Accordingly, in conjunction with the saturation magnetization Ms from the SQUID measurements and inserting into equation (4), the micromagnetic anisotropy constants from this method are evaluated to be

$${K}_{{{{{{{{\rm{IP}}}}}}}}}^{{{{{{{{\rm{95K}}}}}}}}}=(0.72\pm 0.22)\cdot 1{0}^{-3}\,{{{{{{{\rm{eV}}}}}}}}\,{{{{{{{{\rm{nm}}}}}}}}}^{-3},$$
(13)
$${K}_{{{{{{{{\rm{IP}}}}}}}}}^{{{{{{{{\rm{200K}}}}}}}}}=(0.36\pm 0.11)\cdot 1{0}^{-3}\,{{{{{{{\rm{eV}}}}}}}}\,{{{{{{{{\rm{nm}}}}}}}}}^{-3}.$$
(14)

Finally, the anisotropy constants obtained via both the domain wall and hard-axis saturation method can be compared. At 95 K the ratio between the effective anisotropy constants is \({K}_{\delta }^{{{{{{{{\rm{95K}}}}}}}}}/{K}_{{{{{{{{\rm{IP}}}}}}}}}^{{{{{{{{\rm{95K}}}}}}}}}=3.53\pm 1.30\), and at 200 K it is \({K}_{\delta }^{{{{{{{{\rm{200K}}}}}}}}}/{K}_{{{{{{{{\rm{IP}}}}}}}}}^{{{{{{{{\rm{200K}}}}}}}}}=3.11\pm 0.98\). Thus, the two methods to determine K used in this work, although they are completely independent and cover vastly different length scales, yield results which are on the same order of magnitude. The fact that the ratio Kδ/KIP may systematically be larger than 1 could be attributed to the fundamental approximations used. Namely, since the hard-axis saturation field will be slightly larger than the monodomainization field, which we used to estimate the saturation field, KIP should in reality be systematically slightly larger than the values we obtained. If the obtained anisotropy constants would differ by a large margin one could suggest that the material might be in a spin glassy state. But since they do not differ greatly, this analysis implies that the material is not in a spin glassy state. As such, this analysis in conjunction with the SQUID results indicates that Fe5GeTe2 might not be in a spin glassy state, but in a ferrimagnetic state while it is in the pre-cooling phase, as previously claimed28,29.

Conclusions

In conclusion, we have presented experimental observations of spin structures and determined magnetic properties in the promising 2D vdW magnet Fe5GeTe2, to understand the magnetic ordering of this material. Non-chiral magnetic skyrmions form in the material near room temperature when magnetic fields close to the saturation field are applied. The achirality of these magnetic bubbles suggests that there is no considerable bulk DMI present in Fe5GeTe2, which in turn supports the conclusion that Fe5GeTe2 exhibits an underlying centrosymmetry, in line with the reported \(R\bar{3}m\) crystal structure, rather than the otherwise proposed non-centrosymmetric R3m crystal structure. Furthermore, the observed magnetic bubbles are Bloch-type bubbles, which suggests that there is no significant interfacial DMI in our samples either. Future studies on Fe5GeTe2 heterostructures, which induce the formation of Néel-type bubbles due to interfacial DMI are feasible16. Since Fe5GeTe2 exhibits a lower magnetization in the pre-cooling phase than in the post-cooling phase, we were able to observe bubbles at lower fields and down to zero external field in the pre-cooling phase compared to the post-cooling phase. Furthermore, by considering the anisotropy constants obtained via two independent methods, namely via the hard-axis saturation field and via the domain wall profile and predicted exchange constants, we conclude that Fe5GeTe2 is not in a spin glassy state. However, a significant drop of the magnetization with decreasing temperature observed in SQUID measurements suggests that Fe5GeTe2 is a ferrimagnet instead of a simple ferromagnet whilst in the pre-cooling phase. Future neutron diffraction experiments are required to fully ascertain the spin structure of Fe5GeTe2. We have thus completed the necessary steps toward room temperature spintronics devices based on skyrmion type spin structures, which are of significant interest for novel information storage and non-conventional computing concepts using 2D magnets.

Methods

A. Crystal synthesis

Single crystals of Fe5GeTe2 with an average size of 2 × 2 × 0.5 mm3 were synthesized in quartz glass ampoules from the elements Fe, Ge, and Te in a 6 : 1 : 2 ratio in the presence of iodine as mineralizer. Similar to reference4, Ge was supplied as a powder on the bottom of the quartz glass tube. Fe and Te were pressed to separate pellets of 1 mm diameter and positioned on top of the Ge powder without direct contact between the pellets. The reaction thus predominantly occurs through the gas phase and increases the single crystal size to several millimeters. The vacuum-sealed ampules were heated up to 750 ∘C with 120 K/h and kept at this temperature for about 2 weeks before quenching them in room temperature water. The composition of the single crystals was confirmed by energy dispersive X-ray spectroscopy (Tescan SEM Vega TS 5130 MM equipped with a silicon drift detector, Oxford) with a ratio of Fe : Ge : Te of 4.72(5) : 1 : 1.94(4).

B. Lamella preparation

Electron transparent cross-section and plan-view lamellae were prepared using a 30 kV Ga+ focused ion beam and scanning electron microscope (FIB-SEM) FEI Helios platform. The energy of the ion beam was decreased to 5 kV in the last steps of the thinning to minimize surface damage.

C. Transmission electron microscopy

Scanning transmission electron microscopy (STEM) and energy dispersive X-ray (EDX) spectroscopy were carried out using an FEI Titan TEM equipped with a Schottky field emission gun operated at 200 kV, a CEOS probe aberration corrector, a high angle annular dark-field detector (HAADF) and a Super-X EDX detection system39. Composition maps were obtained using the Thermo Fisher Scientific Velox software.

Magnetic imaging was carried out using Fresnel defocus and off-axis electron holography in an FEI Titan TEM equipped with a Schottky field emission gun, a CEOS image aberration corrector, a post-specimen electron biprism and a 4k × 4k Gatan K2-IS direct detection camera40. A liquid-nitrogen-cooled specimen holder (Gatan model 636) was used to vary the sample temperature. The microscope was operated at 300 kV in magnetic field-free conditions (Lorentz mode) by using the first transfer lens of the aberration corrector as the primary imaging lens. The conventional objective lens was used to apply the chosen magnetic fields to the sample, which were pre-calibrated using a Hall probe. The field is applied along the electron beam direction i.e., perpendicular to the sample plane. For off-axis electron holography, the electron biprism was used to overlap a reference wave travelling in vacuum with an object wave passing through the sample. An elliptical illumination was used to optimize the coherence of the beam in the direction perpendicular to the biprism. The hologram width was 2.7 μm and the fringe spacing was 2.5 nm. Magnetic induction maps were reconstructed using Fourier transforms with the Holoworks plugin in the Digital Micrograph software (Gatan)41. The contribution of the mean inner potential to the phase was removed by subtracting the phase of an hologram acquired above the Curie temperature.

D. DFT atomistic exchange tensor calculations

We performed density functional theory (DFT) calculations for bulk Fe5GeTe2 using the experimental lattice constants, a = 4.04(2)Å, c = 29.19(3) Å, from May et al.4. In order to account for the two Fe atoms at 50% occupancy we employed the use of the coherent potential approximation (CPA)42. We perform our calculations with the JuKKR code35 which implements the full potential Korringa Kohn Rostoker (KKR) Green’s Function method42 with an exact description of the shape of the atomic cell43,44. We use an angular momentum cutoff lmax = 3 and a generalised gradient approximation (GGA) to obtain the exchange-correlation potential45. Our calculations of the exchange coupling constants for the determination of the atomistic spin stiffness are based on the model of infinitesimal rotations36,37. The domain wall widths calculated in the supplementary section Supplementary Note 5 are determined using the Spirit code46. The calculations are orchestrated through the AiiDA framework47 via the AiiDA-KKR48 and AiiDA-Spirit49 plugins.