Abstract
Topological signals defined on nodes, links and higher dimensional simplices define the dynamical state of a network or of a simplicial complex. As such, topological signals are attracting increasing attention in network theory, dynamical systems, signal processing and machine learning. Topological signals defined on the nodes are typically studied in network dynamics, while topological signals defined on links are much less explored. Here we investigate Dirac synchronization, describing locally coupled topological signals defined on the nodes and on the links of a network, and treated using the topological Dirac operator. The dynamics of signals defined on the nodes is affected by a phase lag depending on the dynamical state of nearby links and vice versa. We show that Dirac synchronization on a fully connected network is explosive with a hysteresis loop characterized by a discontinuous forward transition and a continuous backward transition. The analytical investigation of the phase diagram provides a theoretical understanding of this topological explosive synchronization. The model also displays an exotic coherent synchronized phase, also called rhythmic phase, characterized by non-stationary order parameters which can shed light on topological mechanisms for the emergence of brain rhythms.
Similar content being viewed by others
Introduction
Synchronization1,2,3,4,5,6,7 pervades physical and biological systems8,9. It is key to characterize physiological10 and brain rhythms11, to understand collective animal behavior12, and is also observed in non biological systems such as coupled Josephson junctions13, lasers14 and ultracold atoms15,16.
While topology is recognized to play a fundamental role in theoretical physics17,18, statistical mechanics19 and condensed matter20,21,22,23, its role in determining the properties of synchronization phenomena24,25,26,27 has only started to be unveiled.
Recently, sparked by the growing interest in higher-order networks and simplicial complexes28,29,30,31, the study of topology32,33,34,35,36,37,38,39,40,41 and topological signals24,25,26,42,43,44,45,46,47,48,49,50 is gaining increasing attention in network theory, dynamical systems and machine learning. In a network, topological signals are dynamical variables that can be associated to both nodes and links. While in dynamical systems it is common to consider dynamical variables associated to the nodes of a network and affected by interactions described by the links of the network, the investigation of the dynamics of higher order topological signals is only at its infancy24,25,26,42,43,44,50.
Topological signals associated to the links of a network are of relevance for a variety of complex systems. For instance, topological signals associated to links, also called edge signals, are attracting increased interest in the context of brain research51,52 and can be relevant to understand the behaviour of actual neural systems. Indeed, they can be associated to synaptic oscillatory signals related to intracellular calcium dynamics53, involved in synaptic communication among neurons54, which could influence the processing of information through the synapses and memory storage and recall. Furthermore, edge signals can be used to model fluxes in biological transportation networks and even in power-grids55,56,57,58.
It has recently been shown25 that the topological signals associated to simplices of a given dimension in a simplicial complex can be treated with a higher-order Kuramoto model that uses boundary operators to show how the irrotational and solenoidal components of the signal synchronize. When these two components of the dynamics are coupled by a global adaptive coupling25, the synchronization transition then becomes abrupt. These results open the perspective to investigate the coupled dynamics of signals of different dimension both on networks and on simplicial complexes. Thus, in26 it has been shown that a global adaptive coupling can give rise to a discontinuous synchronization transition. However the global adaptive mechanism adopted in Ref. 26 is not topological and on a fully connected network, the synchronization dynamics proposed in26 does not display a stable hysteresis loop. Therefore, important open theoretical questions are whether a discontinuous synchronization transition can be observed when topological signals are coupled locally, and whether a topological coupling of the signals can lead to a stable hysteresis loop even for fully connected networks.
Here, we propose a dynamical model called Dirac synchronization that uses topology and, in particular, the topological Dirac operator43,59 to couple locally the dynamics of topological signals defined on the nodes and links of a network. Dirac synchronization describes a Kuramoto-like dynamics for phases associated to the nodes and the links, where for the synchronization dynamics defined on the nodes, we introduce a time-dependent phase lag depending on the dynamics of the topological signals associated to the nearby links, and vice-versa. This adaptive and local coupling mechanism induces a non-trivial feedback mechanism between the two types of topological signals leading to a rich phenomenology. The main phenomena observed include a discontinuous forward transition and a rhythmic phase where a complex order parameter oscillates at constant frequency also in the frame in which the intrinsic frequencies are zero in average.
Results and discussion
Motivation and main results
Dirac synchronization adopts a coupling mechanism of node and link topological signals dictated by topology that makes use of the topological Dirac operator43,59 and the higher-order Laplacians41,42,45. A crucial element of Dirac synchronization is the introduction of adaptive phase lags both for phases associated to nodes and phases associated to links. Constant phase lags have been traditionally studied in the framework of the Sakaguchi and Kuramoto model60,61, which in the presence of a careful fine tuning of the internal frequencies62,63, time delays64 or non trivial network structure65 can lead to non-trivial phase transitions and chimera states. Recently, space-dependent phase lags have been considered as pivotal elements to describe cortical oscillations66. Here, we show that time-dependent phase-lags are a natural way to couple dynamical topological signals of nodes and links, leading to a very rich phenomenology and a non-trivial phase diagram, including discontinuous synchronization transitions even for a Gaussian distribution of the internal frequencies.
The properties of Dirac synchronization are very rich and differ significantly from the properties of the higher-order Kuramoto26. Most importantly the order parameters of the two models are not the same, as Dirac synchronization has order parameters which are linear combinations of the signal of nodes and links revealing a very interdependent dynamics of the two topological signals. On the contrary, the order parameters of the higher-order Kuramoto model are associated exclusively to one type of topological signals: there is one order parameter depending on node signals and one depending on link signals. Moreover, the phase diagram of Dirac synchronization on a fully connected network includes a discontinuous forward transition and a continuous backward transition with a thermodynamically stable hysteresis loop. Finally, the coherent phase of Dirac synchronization also called rhythmic phase, is non-stationary. In this phase the nodes are not just distinguished in two classes (frozen and drifting) like in the Kuramoto model but they might display a non-stationary dynamics in which one of the two phases associated to the node is drifting and the other is oscillating with a relatively small amplitude while still contributing to the corresponding order parameter.
In this work, we investigate the phase diagram of Dirac synchronization numerically and analytically capturing both the stationary and the non-stationary phases of Dirac synchronization. The theoretical results are in excellent agreement with extensive numerical simulations.
Interestingly, we can predict analytically the critical coupling constant for the discontinuous forward transition and capture the salient features of the observed rhythmic phase.
Large attention has been recently devoted to investigate which mechanisms are able to induce discontinuous, explosive synchronization transitions67,68 in simple networks69,70,71,72,73, adaptive networks74, multiplex networks65,71,75,76,77,78 and simplicial complexes25,79,80,81. The discontinuous transition of Dirac synchronization is driven by the onset of instability of the incoherent phase, similarly to what happens in other synchronization models treating exclusively nodes signals73,76. Moreover, Dirac synchronization is driven by a topologically induced mechanism resulting in an abrupt, discontinuous synchronization transition that cannot be reduced to the recently proposed framework82 intended to unify the different approaches to explosive transitions.
The emergent rhythmic phase of Dirac synchronization extends to a wide range of values of the coupling constant and is actually the only coherent phase that can be observed in the infinite network limit. The rhythmic phase, characterized by non-stationary order parameters, might shed light on the mechanisms involved in the appearance of brain rhythms and cortical oscillations11,66,83 since Kuramoto-like dynamics has been reported to be a very suitable theoretical framework to investigate such brain oscillatory behaviour66. Oscillations of the order parameters occur, for example, in the presence of stochastic noise and time delays84, in networks with neighbour frequency correlations85, and in the context of the D-dimensional Kuramoto model86 in87. However, while in87 the magnitude of the order parameter displays large fluctuations, in Dirac synchronization we have a wide region of the phase diagram in which one of the two complex order parameters (the complex order parameter Xα) oscillates at a low frequency without large fluctuations in its absolute value, while the other (the complex order parameter Xβ) has non-trivial phase and amplitude dynamics. In addition to the explosive forward synchronization transition and the complex rhythmic phase described above, the bifurcation diagram of the system features a continuous backward transition, resulting in a very rich phenomenology that could potentially give insight into new mechanisms for the generation of brain rhythms66.
Note that Dirac synchronization is fully grounded in discrete topology but it is rather distinct from the synchronization model proposed in Ref. 88, the most notable differences being (i) that Dirac synchronization treats topological signals defined on nodes and links of a network while Ref. 88 only treats node signals, (ii) that Dirac synchronization makes use of the topological Dirac operator which Ref. 88 does not, and (iii) that Dirac synchronization treats non-identical oscillators while Ref. 88 focuses on identical ones.
Dirac Synchronization with local coupling
Uncoupled synchronization of topological signals
We consider a network G = (V, E) formed by a set of N nodes V and a set of L links E. The generic link ℓ has a positive orientation induced by the node labels, i.e. ℓ = [i, j] is positively oriented if i < j. The topology of the network is captured by the incidence matrix B mapping any positively oriented link ℓ of the network to its two end-nodes. Specifically, the incidence matrix B is a rectangular matrix of size N × L with elements
The standard Kuramoto dynamics1 describes the synchronization of the phases \({{{{{{{\boldsymbol{\theta }}}}}}}}={({\theta }_{1},{\theta }_{2}\ldots ,{\theta }_{N})}^{\top }\) associated to the nodes of the network. In absence of interactions, each phase θi oscillates at some intrinsic frequency ωi, typically drawn from a unimodal random distribution. Here, we consider the normal distribution \({\omega }_{i} \sim {{{{{{{\mathcal{N}}}}}}}}({{{\Omega }}}_{0},1/{\tau }_{0})\). However, the phases of next nearest neighbours are coupled to each other by an interaction term that tends to align phases. This term is modulated by a coupling constant \(\hat{\sigma }\), which is the control parameter of the dynamics. In terms of the incidence matrix B, the standard Kuramoto model can be expressed as
where \({{{{{{{\boldsymbol{\omega }}}}}}}}={({\omega }_{1},{\omega }_{2},\ldots ,{\omega }_{N})}^{\top }\) indicates the vector of intrinsic frequencies. Note that in Eq. (2) and in the following by \(\sin ({{{{{{{\bf{x}}}}}}}})\), we indicate the vector where the sine function is taken elementwise. As a function of the coupling constant, the Kuramoto model is known to display a synchronization transition with order parameter
The higher-order Kuramoto model25 captures synchronization of topological signals (phases) defined on the n-dimensional faces of a simplicial complex, with n > 0. Let us consider the topological signals defined on the links, denoted by the vector of phases \({{{{{{{\boldsymbol{\phi }}}}}}}}={({\phi }_{{\ell }_{1}},{\phi }_{{\ell }_{2}},\ldots ,{\phi }_{{\ell }_{L}})}^{\top }\). On a network, formed exclusively by nodes and links, the higher-order Kuramoto dynamics for these phases can be written as
where \(\tilde{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) indicates the vector of internal frequencies of the links, \(\tilde{{{{{{{{\boldsymbol{\omega }}}}}}}}}={({\tilde{\omega }}_{{\ell }_{1}},{\tilde{\omega }}_{{\ell }_{2}},\ldots ,{\tilde{\omega }}_{{\ell }_{L}})}^{\top }\), with \({\tilde{\omega }}_{\ell } \sim {{{{{{{\mathcal{N}}}}}}}}({{{\Omega }}}_{1},1/{\tau }_{1})\). The phases associated to the links can be projected to the nodes by applying the incidence matrix that acts like a discrete divergence of the signal defined on the links. The projection of the phases of the links onto the nodes, indicated by ψ, is given by
As a function of the coupling constant, the higher-order Kuramoto model has been recently shown in Ref. 25 to display a synchronization transition with order parameter
Let us define the Dirac operator43 of the network as the (N + L) × (N + L) matrix with block structure
whose square is given by the Laplacian operator
Here L[0] = BB⊤ is the graph Laplacian describing node to node diffusion occurring through links, and L[1] = B⊤B is the 1-(down)-Laplacian describing the diffusion from link to link through nodes42,45.
Using the Dirac operator, the uncoupled dynamics of nodes and links of a network can simply be written as
where Φ and Ω are N + L dimensional column vectors given by
The dynamics of the phases associated to the nodes is identical to the standard Kuramoto dynamics, and for the vast majority of network topologies, it displays a continuous phase transition at a non-zero value of the coupling constant4. However, the dynamics of the phases associated to the links, for the higher-order Kuramoto model, displays a continuous phase transition at zero coupling constant25.
Dirac synchronization
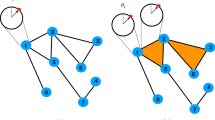
Having defined the uncoupled dynamics of topological signals associated to nodes and links, given by Eqs. (9), an important theoretical question that arises is how these equations can be modified to couple topological signals defined on nodes and links in non-trivial ways (see Fig. 1). In Ref. 26, a global adaptive coupling modulating the coupling constant with the order parameters Rθ and Rψ was shown to lead to a discontinuous explosive transition of the coupled topological signals. However, the adaptive coupling proposed in26 is not local: it does not admit a generalization that locally couples the different topological signals, a desirable feature since it might be argued that physical systems are typically driven by local dynamics. For instance, if the dynamics of nodes and links is assumed to treat brain dynamics, it would be easier to justify a local coupling mechanism rather than a global adaptive dynamics. Here we formulate the equations for the Dirac synchronization of locally coupled signals defined on nodes and links. We start from the uncoupled Eq. (9) and introduce a local adaptive term in the form of a phase lag. More precisely, we introduce a phase lag for the node dynamics that depends on the topological signal associated to the nearby links, and vice versa, we consider a phase lag for the link dynamics that depends on the signal on the nodes at its two endpoints. The natural way to introduce these phase lags is by using the Laplacian matrix \({{{{{{{\bf{{{{{{{{\mathcal{L}}}}}}}}}}}}}}}}\), with an appropriate normalization to take into consideration the fact that nodes might have very heterogeneous degrees, while links are always only connected to the two nodes at their endpoints. While the model can be easily applied to any network, we consider the case of a fully connected network to develop a thorough theoretical treatment of the dynamics. As we will show, even in this case, the model displays a rich phenomenology. Therefore, we propose the Dirac synchronization model driven by the dynamical equations
where the matrix \({{{{{{{\bf{{{{{{{{\mathcal{K}}}}}}}}}}}}}}}}\) is given by
i.e., \({{{{{{{\bf{{{{{{{{\mathcal{K}}}}}}}}}}}}}}}}\) is a block-diagonal matrix whose non-zero blocks are formed by the diagonal matrix of node degrees K[0] and by the diagonal matrix K[1] of link generalized degrees, encoding the number of nodes connected to each link. Therefore K[1] has all diagonal elements given by 2 in any network while K[0] has all diagonal elements given by N − 1 in the case of a fully connected network. Moreover, in Eq. (11) and in the following we will make use of the matrices γ and \({{{{{{{\bf{{{{{{{{\mathcal{I}}}}}}}}}}}}}}}}\) given by
where IX indicates the identity matrix of dimension X × X. On a sparse network, Dirac synchronization obeying Eq.(11) involves a local coupling of the phases on the nodes with a topological signal defined on nearby links and a coupling of the phases of the links with a topological signal defined on nearby nodes. In particular we substitute the argument of the \(\sin (x)\) function in Eq.(9) with
Indeed, to have a meaningful model, one must require that the interaction term (in the linearized system) is positive definite which for us implies that the first order term to couple the signal of nodes and links includes a phase-lag proportional to the Laplacian, i.e, proportional to the square of the Dirac operator \({{{{{{{{\bf{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}}^{2}={{{{{{{\bf{{{{{{{{\mathcal{L}}}}}}}}}}}}}}}}\). However one could also envision more general models where higher powers of the Dirac operator could be included. It is to be mentioned that the introduction of the matrix γ is necessary to get a non-trivial phase diagram, while \({{{{{{{{\mathcal{K}}}}}}}}}^{-1}\) is important to have a linearized coupling term that is semidefinite positive. Finally, we note that the introduction of quadratic terms in Eq. (14) is in line with the analogous generalization of the Dirac equation for topological insulators proposed in Ref. 21 which also includes an additional term proportional to the square of the momentum (analogous to our Laplacian).
In Dirac synchronization topological signals associated to the nodes and the links of a network are coupled locally thanks to the Dirac operator. The considered topological signals are the phases of oscillators associated to nodes (blue oscillator symbols placed on nodes) or to links (non-filled oscillator symbols placed on links) of a network. The two insets show schematically the time-series of node [1] and link [1, 2] signals respectively.
For our analysis on fully connected networks, we draw the intrinsic frequencies of the nodes and of the links, respectively, from the distributions \({\omega }_{i} \sim {{{{{{{\mathcal{N}}}}}}}}({{{\Omega }}}_{0},1)\) and \({\tilde{\omega }}_{\ell } \sim {{{{{{{\mathcal{N}}}}}}}}(0,1/\sqrt{N-1})\). This rescaling of the frequencies on the links ensures that the induced frequencies on the nodes defined shortly in Eq. (18) are themselves normally distributed, with zero mean and unit-variance. It is instructive to write Eq. (11) separately as a dynamical system of equations for the phases θ associated to the nodes and the phases ϕ associated to the links of the network, giving
This expression reveals explicitly that the coupling between topological signals defined on nodes and links consists of adaptive phase lags determined by the local diffusion properties of the coupled dynamical signals.
Using Eq. (8), we observe that the linearized version of the proposed dynamics in Eq. (11) still couples nodes and links according to the dynamics
Note that one can interpret this linearized dynamics as a coupling between node phases and phases of nearby nodes (which is described by the Laplacian operator \({{{{{{{\bf{{{{{{{{\mathcal{L}}}}}}}}}}}}}}}}\)). Additionally, the phases of the nodes are coupled with the phases of their incident links and of the links connected to their neighbour nodes (which is mediated by the term proportional to \({{{{{{{\bf{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}{{{{{{{{\bf{{{{{{{{\mathcal{K}}}}}}}}}}}}}}}}}^{-1}{{{{{{{\bf{{{{{{{{\mathcal{L}}}}}}}}}}}}}}}}\)). A similar interpretation is in place for the dynamics of the links.
Dynamics projected on the nodes
Let us now investigate the dynamical equations that describe the coupled dynamics of the phases θ associated to the nodes and the projection ψ of the phases associated to the links, with ψ given by Eq. (5). Since K[1] and B⊤ commute, in terms of the phases θ and ψ, the equations dictating the dynamics of Dirac synchronization read
where
(see Methods for details on the distribution of \(\hat{{{{{{{{\boldsymbol{\omega }}}}}}}}}\)), and where we have used the definition of L[1] = B⊤B. The Eqs. (17) can be written elementwise as
where the variables αi and βi are defined as
with \(\hat{{{\Theta }}}\) given by
and \(\bar{c}=N/(N-1)\). We observe that \(\hat{{{\Theta }}}\) is the average phase of the nodes of the network that evolves in time at a constant frequency \(\hat{{{\Omega }}}\), determined only by the intrinsic frequencies of the nodes. In fact, using Eqs. (19), we can easily show that
Here and in the following, we indicate with G0(ω) the distribution of the intrinsic frequency ω of each node, and with \({G}_{1}(\hat{\omega })\) the marginal distribution of the frequency \(\hat{\omega }\) for any generic node of the fully connected network (for the explicit expression of \({G}_{1}(\hat{\omega })\), see Methods).
In order to study the dynamical Eqs. (19), entirely capturing the topological synchronization on a fully connected network, we introduce the complex order parameters Xα and Xβ associated to the phases αi and βi of the nodes of the network, i.e.
where Rξ and ηξ are real, and ξ ∈ {α, β}. Using this notation, Eqs. (19) can also be written as
Since Eqs. (25) are invariant under translation of the αi variables, we consider the transformation
where α0 is independent of time. Interestingly, this invariance guarantees that if Xα is stationary then we can always choose α0 such that Xα is also real, i.e., Xα = Rα. Independently of the existence or not of a stationary solution, this invariance can be used to also simplify Eqs. (25) to
where we indicate with αi and \({e}^{{{{{{{{\rm{-i}}}}}}}}{{{{{{{{\boldsymbol{\alpha }}}}}}}}}_{i}}\) the vectors
and where the vector \({{{{{{{{\boldsymbol{\kappa }}}}}}}}}_{i}={({\kappa }_{i,\alpha },{\kappa }_{i,\beta })}^{\top }\) and the matrix \(\hat{{{{{{{{\bf{X}}}}}}}}}\) in Eq. (27) are given by
Phase diagram of Dirac synchronization
In Dirac synchronization, the dynamics of the phases associated to the nodes is a modification of the standard Kuramoto model1,3,5, and includes a phase-lag that depends on the phases associated to the links. It is therefore instructive to compare the phase diagram of Dirac synchronization with the phase diagram of the standard Kuramoto model. The standard Kuramoto model with normally distributed internal frequencies with unitary variance, has a continuous phase transition at the coupling constant \(\sigma ={\sigma }_{c}^{{{\mbox{std}}}}\) given by
with the order parameter Rθ becoming positive for \(\sigma \; > \; {\sigma }_{c}^{{{\mbox{std}}}}\). The synchronization threshold \({\sigma }_{c}^{{{\mbox{std}}}}\) coincides with the onset of the instability of the incoherent phase where Rθ = 0. Consequently, the forward and backward synchronization transitions coincide. The phase diagram for Dirac synchronization is much richer. Let us here summarize the main properties of this phase diagram as predicted by our theoretical derivations detailed in the Methods section.
The major differences between Dirac synchronization and the standard Kuramoto model are featured in the very rich phase diagram of Dirac synchronization (see schematic representation in Fig. 2) which includes discontinuous transitions, a stable hysteresis loop, and a non-stationary coherent phase (which we call rhythmic phase), in which the complex order parameters Xα and Xβ are not stationary. In order to capture the phase diagram of the explosive Dirac synchronization, we need to theoretically investigate the rhythmic phase where the density distribution of the node’s phases is non-stationary.
The schematic representation of the phase diagram of the standard Kuramoto model with order parameter Rθ depending on the coupling constant σ (a) is compared with the phase diagram of Dirac synchronization characterized by the two order parameters Rα and Rβ depending on the coupling constant σ (b, c). The synchronization transition of the standard Kuramoto model occurs continuously at the synchronization threshold \({\sigma }_{c}^{\,{{\mbox{std}}}}\) and the forward and backward transitions coincide. For Dirac synchronization, the forward transition observed for increasing values of σ starting from σ = 0, is discontinuous at \({\sigma }_{c}^{\star }\) where we observe an abrupt transition from an incoherent state where Rα = 0 (but Rβ > 0) to a non-stationary coherent state of the complex order parameters with Rα > 0 (and Rβ > 0). This non-stationary coherent phase, also called rhythmic phase, is characterized by non-trivial oscillations of the order parameter Xα in the complex plane which are observed at essentially constant absolute value ∣Xα∣. This phenomenon occurs in the region indicated here by dashed-lines. For \(\sigma \; > \; {\sigma }_{S}^{\star }\), where \({\sigma }_{S}^{\star }\) diverges in the limit of infinite network size, the coherent state becomes stationary. The backward transition of Dirac synchronization, observed for decreasing values of σ, first displays a transition from a stationary coherent state to a non-stationary coherent state at \({\sigma }_{S}^{\star }\), then displays a continuous phase transition from the non-stationary coherent phase to the incoherent phase at σc.
Moreover, our theoretical predictions indicate that the onset of the instability of the incoherent state does not coincide with the bifurcation point at which the coherent phase can be first observed. This leads to a hysteresis loop characterized by a discontinuous forward transition, and a continuous backward transition. In the context of the standard Kuramoto model, the study of the stability of the incoherent phase puzzled the scientific community for a long time89,90, until Strogatz and Mirollo proved in Ref. 91 that σc corresponds to the onset of instability of the incoherent phase, and later Ott and Antonsen92 revealed the underlying one-dimensional dynamics of the order parameter in the limit N → ∞. Here we conduct a stability analysis of the incoherent phase (see Methods for the analytical derivations), and we find that the incoherent phase becomes unstable only for \(\sigma ={\sigma }_{c}^{\star }\), with \({\sigma }_{c}^{\star }\) given by
Interestingly, the bifurcation point where the synchronized branch merges with the incoherent solution in the backward transition, is expected for a smaller value of the coupling constant \({\sigma }_{c} \; < \; {\sigma }_{c}^{\star }\) that we estimate with an approximate analytical derivation, (which will be detailed below), to be equal to
It follows that Dirac synchronization displays a discontinuous forward transition at \({\sigma }_{c}^{\star }\), and a continuous backward transition at σc.
The forward transition displays a discontinuity at \({\sigma }_{c}^{\star }\), where we observe the onset of a rhythmic phase, the non-stationary coherent phase of Dirac synchronization, characterized by oscillations of the complex order parameters Xα and Xβ. This phase persists up to a value \({\sigma }_{S}^{\star }\) where the coherent phase becomes stationary. The backward transition is instead continuous. One observes first a transition between the stationary coherent phase and the non-stationary coherent phase at \({\sigma }_{S}^{\star }\), and subsequently a continuous transition at σc.
From our theoretical analysis, we predict the phase diagram sketched in Fig. 2, consisting of a thermodynamically stable hysteresis loop, with a discontinuous forward transition at \({\sigma }_{c}^{\star }\) and a continuous backward transition at σc. The coherent rhythmic phase disappears at \({\sigma }_{S}^{\star }\), where \({\sigma }_{S}^{\star }\) diverges in the large network limit. Therefore, for N → ∞, the system always remains in the rhythmic phase.
These theoretical predictions are confirmed by extensive numerical simulations (see Fig. 3) of the model defined on a fully connected network of N = 20,000 nodes (although we can observe some minor instance-to-instance differences). These results are obtained by integrating Eqs. (19) using the 4th order Runge-Kutta method with time step Δt = 0.005. The coupling constant σ is first increased and then decreased adiabatically in steps of Δσ = 0.03. From this numerically obtained bifurcation diagram, we see that our theoretical prediction of the phase diagram (solid and dashed lines) matches very well the numerical results (red and blue triangles). However, the discontinuous phase transition, driven by deviations from the incoherent phase, is observed at \({\sigma }_{c}^{\star }(N) \; < \; 2.14623...\) in finite networks. We study this effect quantitatively by measuring the transition threshold on systems of varying size N, averaging 100 independent iterations for each N (see Fig. 4). We find that the observed distance from the theoretical critical point given in Eq. (31) decreases consistently with a power-law in N, with scaling exponent 0.177 (computed with integration time \({T}_{\max }=5\)), confirming further our theoretical prediction of \({\sigma }_{c}^{\star }\). The observed behavior is consistent with the earlier transition being caused by finite N effects. For finite N, the system will have fluctuations about the incoherent state which may bring the system to the basin of attraction of the rhythmic phase and cause a transition even when the incoherent state is stable. Thus, the observed transition point depends on N (larger N implies smaller fluctuations), and \({T}_{\max }\) (larger \({T}_{\max }\) implies larger probability of transition before reaching \({\sigma }_{c}^{* }\)).
The forward and backward Dirac synchronization transitions of the real order parameters Rα (a) and Rβ (b) are plotted as a function of the coupling constant σ. The numerical results are obtained for a network of N = 20,000 nodes, by integrating the dynamical equations with a 4th order Runge-Kutta method with time step Δt = 0.005 where, for each value of σ the dynamics is equilibrated up to time \({T}_{\max }=10\). The coupling constant σ is adiabatically increased and then decreased with steps of size Δσ = 0.03. For each step in σ, the plotted values of the real order parameters are averaged over the last fifth of the time series. Black lines indicate the theoretical predictions as developed in Eqs. (67). Solid lines indicate steady state solutions of the continuity equations and dashed lines represent theoretical predictions in the non-stationary coherent phase. The discontinuous transition point occurs at a coupling strength below the theoretical estimate due to finite-size effects. We show with the dotted line the location of the onset of the instability as extracted from finite size scaling corresponding to the network size N = 20000.
a Shows the absolute value of the difference between the synchronization threshold \({\sigma }_{c}^{\star }(N)\) in a network of N nodes and the theoretical prediction \({\sigma }_{c}^{\star }\) of the synchronization threshold in an infinite network. The value of \({\sigma }_{c}^{\star }(N)\) shown are averaged over 100 independent realizations of the forward transition. We find that these finite size effects depend on the equilibration time \({T}_{\max }\) (here shown for \({T}_{\max }=5\) and 10). Indeed, for larger integration times, the probability that finite-size fluctuations about the incoherent size bring the system to the basin of attraction of the rhythmic phase increases. Thus, the observed transition point depends on N (larger N implies smaller fluctuations), and \({T}_{\max }\) (larger \({T}_{\max }\) implies larger probability of transition before reaching \({\sigma }_{c}^{* }\)). This process has negligible effect on the rest of the phase diagram. The finite size effects are fitted by a power-law scaling function \(| {\sigma }_{c}^{\star }(N)-{\sigma }_{c}^{\star }| =c{N}^{-\xi }\) with c = 1.208, ξ = 0.177 and c = 0.7906, ξ = 0.1065 respectively for \({T}_{\max }=5\) (dashed line) and \({T}_{\max }=10\) (dotted line). The standard deviation (over the 100 iterations, \({T}_{\max }=5\)) of the order parameters Rα and Rβ are shown in the forward transition in panels (b) and (c) respectively. This is highest closest to the transition point, and tends to the theoretical estimate as N increases.
Finally, we find that this rich phase diagram is only observable by considering the correct order parameters for Dirac synchronization, Rα and Rβ, which characterize the synchronization of the coupled topological signals as predicted by the analytical solution of the model. This is due to the local coupling introduced in Dirac synchronization, which couples together the phases of nodes and adjacent links locally and topologically. Interestingly this is a phenomenon that does not have an equivalent in the model26 in which the signals of nodes and links are coupled by a global order parameter. Therefore as we will show with our theoretical derivation of the phase diagram of the model, the phases α and β become the relevant variables to consider instead of the original phases associated exclusively to the nodes θ and to the projected signal of the links into the nodes ψ. Indeed, in agreement with our theoretical expectations, numerical results clearly show that the transition cannot be detected if one considers the naïve uncoupled order parameters Rθ and Rψ, which remain close to 0 for all values of σ.
Numerical investigation of the rhythmic phase
In this section we investigate numerically the rhythmic phase, observed for \({\sigma }_{c} \; < \; \sigma \; < \; {\sigma }_{S}^{\star }\) in the backward transition, and for \({\sigma }_{c}^{\star } \; < \; \sigma \; < \; {\sigma }_{S}^{\star }\) in the forward transition. In this region of the phase space, the system is in a non-stationary state where we can no longer assume that Xα and Xβ are stationary.
In order to study the dynamical behaviour of the complex order parameters characterized by slow fluctuations, we consider a fully connected network of size N = 500, where we are able to follow the non-stationary dynamics for a long equilibration time \({T}_{\max }\).
For \(\sigma \; > \; {\sigma }_{S}^{\star }\), the order parameters are stationary as shown in Fig. 5a, b. However, in the rhythmic phase, the order parameters do not reach a stable fixed point and their real and imaginary parts undergo fluctuations as shown in Fig. 5c–h. In particular, close to the onset of the rhythmic phase \({\sigma }_{S}^{\star }\), the order parameter Xα displays a slow rotation in the complex plane with constant emergent frequency ΩE, and constant absolute value ∣Xα∣ = Rα as shown in Fig. 5c. In this region, Xβ performs a periodic motion along a closed limit cycle (see Fig. 5d). If the value of the coupling constant is decreased, first the order parameter Xβ displays a more complex dynamics (Fig. 5f) while Xα continues to oscillate at essentially constant absolute value Rα (Fig. 5e). As σ approaches σc, higher frequency oscillations of the magnitude of Xα also set in, see Fig. 5g. The phase space portraits corresponding to the dynamics of the complex order parameters presented in Fig. 5 are shown in Fig. 6, revealing the nature of the fluctuations of the order parameters.
The trajectories of the real and imaginary parts of the complex order parameters Xα and Xβ are displayed for different values of the coupling constant σ in the backward transition. These results are obtained by neglecting the transient, in a network of N = 500 nodes with σ = 3.4 (a, b), with σ = 3.37 (c, d) and with σ = 1.69 (e, f).
The dynamics of the complex order parameter Xα is particularly interesting in relation to the study of brain rhythms and cortical oscillations, which have their origin in the level of synchronization within neuronal populations or cortical areas. In order to describe the non-trivial dynamical behaviour of Xα during the backward transition, we show in Fig. 7 the phase portrait of Xα when the coupling constant σ is decreased in time in a fully connected network of size N = 500, where at each value of the coupling constant the dynamics is equilibrated for a time \({T}_{\max }=10\). From Fig. 7a, it is apparent that for \({\sigma }_{c} \; < \; \sigma \; < \; {\sigma }_{S}^{\star }\), the order parameter Xα displays slow frequency oscillations with an amplitude that decreases as the coupling constant σ is decreased. Moreover, this complex time series reveals that the amplitude is also affected on very short time scales by fluctuations of small amplitude and much faster frequencies. These are seen to become increasingly significant as the coupling constant approaches σc. In Fig. 7b, we highlight the region close to the transition between stationarity and rhythmic phase. We confirm excellent agreement with the theoretical estimate of the onset of the steady state Eq. (50) and compare this to the measured frequency of oscillation ΩE. As expected, the onset of non-stationarity coincides with the emergence of oscillations, as seen in the phase space evolution and direct measurement of ΩE.
The evolution of the complex order parameter Xα during the backward synchronization transition is plotted in panel (a) as the coupling constant decreases (each σ step is indicated by the colors of different lines). These results have been obtained for a network of N = 500, \({T}_{\max }=10\), and Δσ = 0.03. During this backward transition, the onset of the rhythmic phase at \({\sigma }_{S}^{\star }\) and the onset of the incoherent phase at σc are indicated. The onset of the rhythmic phase corresponds exactly to the emergence of a non-zero oscillation frequency ΩE, as shown in panel (b).
Finally, we numerically observe that the angular frequency of oscillations of Xα in the rhythmic phase depends on the network size, as well as the coupling strength. In order to evaluate this effect, we have conducted simulations of Dirac synchronization with varying system size. For each network size, we performed 100 independent iterations of the phase diagram. We show in Fig. 8 the average of the oscillation frequency ΩE measured at each σ step in the rhythmic phase along the forward transition for varying N. These simulations were obtained with equilibration time \({T}_{\max }=10\), and the individual frequencies measured for each iteration are averaged over the last fifth of the time series.
The absolute value of the emergent frequency ∣ΩE∣ characterizing the rhythmic phase is shown as a function of σ, for networks of different network sizes N. The data is averaged over 100 realizations of the intrinsic frequencies along the forward transition. The equilibration time taken is \({T}_{\max }=10\).
These results confirm that the oscillation frequency of the order parameter Xα decreases with stronger coupling strength and reaches 0 at the onset of steady state for all finite system sizes. These extended numerical simulations also confirm that this corresponds precisely to the predicted onset of the steady state, as shown for a single iteration with N = 500 in Fig. 7. As expected, we also confirm that the rhythmic phase extends further for larger systems. Moreover, Fig. 8 clearly reveals that the oscillation frequency of the coherent phase decreases as the systems considered increase in size.
Theoretical treatment of Dirac synchronization
The continuity equation
We can obtain analytical stationary solutions to the dynamics of Dirac synchronization in Eqs. (27) by using a continuity equation approach91. This approach is meant to capture the dynamics of the distribution of the phases αi and βi. To this end let us define the density distribution \({\rho }^{(i)}(\alpha ,\beta | {\omega }_{i},{\hat{\omega }}_{i})\) of the phases αi and βi given the frequencies ωi and \({\hat{\omega }}_{i}\). Since the phases obey the deterministic Eq. (27), it follows that the time evolution of this density distribution is dictated by the continuity equation
where the current Ji is defined as
and ∇ = (∂α, ∂β). Here the velocity vector vi is given by
In order to solve the continuity equation, we extend the Ott-Antonsen92 approach to this 2-dimensional case, making the ansatz that the Fourier expansion of \({\rho }^{(i)}(\alpha ,\beta | {\omega }_{i},{\hat{\omega }}_{i})\) can be expressed as
where c. c. denotes the complex conjugate of the preceding quantity. The expansion coefficients are given by
for n > 0, m > 0. The series in Eq. (36) converges for ∣ai∣ ≤ 1 and ∣bi∣ ≤ 1 provided that we attribute to α and β an infinitesimally small imaginary part.
For Xα ≠ 0, ai ≠ 0 and bi ≠ 0, the continuity equation is satisfied if and only if (see Methods for details) ai and bi are complex variables with absolute value one, i.e., ∣ai∣ = ∣bi∣ = 1, that satisfy the system of differential equations
where here and in the following we indicate with \({X}_{\alpha }^{\star }\) the complex conjugate of Xα, and with \({a}_{i}^{-1}={a}_{i}^{\star }\) and \({b}_{i}^{-1}={b}_{i}^{\star }\) the complex conjugate of ai and bi respectively. We note that the only stationary solutions of these equations are
with di,α, di,β defined as
and having absolute value ∣di,α∣ ≤ 1 and ∣di,β∣ ≤ 1. This last constraint is necessary to ensure ∣ai∣ = ∣bi∣ = 1. This result is very different from the corresponding result for the standard Kuramoto model because it implies that the coherent phase with Rα > 0 cannot be a stationary solution in the infinite network limit as long as ω and \(\hat{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) are drawn from an unbounded distribution. Indeed, a necessary condition to have all the phases in a stationary state implies that ∣di,α∣ ≤ 1 and ∣di,β∣ ≤ 1 for every node of the network. This implies in turn that the frequencies ω and \(\hat{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) are bounded as we will discuss in the next sections.
In the case in which Xα = 0, instead, the continuity equation is satisfied if and only if (see Methods for details) ai and bi, with ∣ai∣ ≠ 0 and ∣bi∣ = 1, follow the system of differential equations
For ∣ai∣ = 0, the equation for bi is unchanged, but bi can have an arbitrary large absolute value. In this last case, the steady state solution of Eqs. (41) reads
with
Let us now derive the equations that determine the order parameters Xα and Xβ for any possible value of the coupling constant σ. Let us assume that the frequencies ωi and \({\hat{\omega }}_{i}\) associated to each node i are known. With this hypothesis, the complex order parameters can be expressed in terms of the density \({\rho }^{(i)}(\alpha ,\beta | {\omega }_{i},{\hat{\omega }}_{i})\) as
When \({\rho }^{(i)}(\alpha ,\beta | \omega ,\hat{\omega })\) satisfies the generalized Ott-Antonsen ansatz given by Eq. (36) and Eq. (37), these complex order parameters can be expressed in terms of the functions \({a}_{i}({\omega }_{i},{\hat{\omega }}_{i})\) and \({b}_{i}({\omega }_{i},{\hat{\omega }}_{i})\) as
where \({a}_{i}^{\star }\) and \({b}_{i}^{\star }\) are the complex conjugates of ai and bi, respectively.
If the internal frequencies ωi and \({\hat{\omega }}_{i}\) are not known, we can express these complex order parameters in terms of the marginal distributions G0(ω) and \({G}_{1}(\hat{\omega })\) as
This derivation shows that \(a(\omega ,\hat{\omega })\) and \(b(\omega ,\hat{\omega })\) can be obtained from the integration of (Eqs. (38) and (41)). In particular, as we discuss in the next paragraph (paragraph II E 2) these equations will be used to investigate the steady state solution of this dynamics and the range of frequencies on which this stationary solution can be observed. However for Dirac synchronization we observe a phenomenon that does not have an equivalent in the standard Kuramoto model. Indeed Eqs. (38) and (41) do not always admit a coherent stationary solution, and actually the non-stationary phase, also called rhythmic phase, is the stable one in the large network limit. In this case we observe that Eqs. (38) and (41) are equivalent to Eqs. (27) and therefore even their numerical integration is not advantageous with respect to the numerical integration of the original dynamics. Therefore the Ott-Antonsen approach is important to demonstrate the emergence of a rhythmic phase but cannot be used to derive the phase diagram of Dirac syncrhonization, which will be derived in the following using other theoretical approaches.
The stationary phases of Dirac synchronization
In the previous section we have shown that Dirac synchronization admits a stationary state in the following two scenarios:
-
Incoherent Phase - This is the incoherent phase where for each node i, ai and bi are given by Eqs. (42). In this phase, Rα = 0 and the order parameter \({X}_{\beta }={R}_{\beta }{e}^{i{\eta }_{\beta }}\) is determined by the equations
$${R}_{\beta }\cos {\eta }_{\beta } = \; \frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}\sqrt{1-{\hat{d}}_{i,\beta }^{2}}H(1-{\hat{d}}_{i,\beta }^{2}),\\ {R}_{\beta }\sin {\eta }_{\beta } = \; \frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}{\hat{d}}_{i,\beta }H(1-{\hat{d}}_{i,\beta }^{2}),$$(47)where \({\hat{d}}_{i,\beta }\) is given by Eq. (43) and H(⋅) is the Heaviside step function. Finally, if the intrinsic frequencies ω and projected frequencies \(\hat{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) are not known, we can average \({a}_{i}^{\star }(\omega ,\hat{\omega })\) and \({b}_{i}^{\star }(\omega ,\hat{\omega })\) appearing in Eqs. (45) over the marginal distributions G0(ω) and \({G}_{1}(\hat{\omega })\). We observe that the steady state Eqs. (47) always has a solution compatible with ηβ = 0, indicating that the contribution from the phases βi that are drifting is null. Therefore, Rβ in the incoherent phase is given by
$${R}_{\beta }=\int d\omega {\int}_{| {\hat{d}}_{i,\beta }| \le 1}d\hat{\omega }{G}_{0}(\omega ){G}_{1}(\hat{\omega })\sqrt{1-{\hat{d}}_{i,\beta }^{2}}.$$(48) -
Stationary Coherent Phase - This is the coherent phase where for each node i, ai and bi are given by Eqs. (39), respectively. Note that this phase differs significantly from the coherent phase of the standard Kuramoto model where drifting phases can also give rise to a stationary continuity equation. Indeed the constraints ∣ai∣ = ∣bi∣ = 1 imply that this phase can only be observed when there are no drifting phases, and for each node i the phases αi, βi are frozen. This can only occur in finite size networks, provided that the coupling constant σ is sufficiently large. Indeed, ∣ai∣ = ∣bi∣ = 1 implies that ∣di,α∣ ≤ 1 and ∣di,β∣ ≤ 1 for all nodes i of the network. By using the explicit expression of di,α and di,β given by the Eqs. (40), this implies that the stationary coherent phase can only be achieved if
$$\sigma \ge \frac{1}{{R}_{\alpha }}\mathop{\max }\limits_{i}| {\omega }_{i}-\hat{{{\Omega }}}| ,\sigma \ge \mathop{\max }\limits_{i}| {\hat{\omega }}_{i}-\,{{\mbox{Im}}}\,{X}_{\beta }| ,$$(49)are simultaneously satisfied, which gives
$${\sigma }_{S}^{\star }=\max \left(\mathop{\max }\limits_{i}\frac{| {\omega }_{i}-\hat{{{\Omega }}}| }{{R}_{\alpha }},\mathop{\max }\limits_{i}| {\hat{\omega }}_{i}-\,{{\mbox{Im}}}\,{X}_{\beta }| \right).$$(50)We numerically find excellent agreement with this estimate, as discussed previously.
Using a similar derivation as the one outlined for the incoherent phase, we can derive the expression for Rα and Rβ in the stationary coherent phase, which can be expressed as
$${R}_{\alpha } =\; \frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}\sqrt{1-{d}_{i,\alpha }^{2}},\\ {R}_{\beta } =\; \frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}\sqrt{1-{d}_{i,\beta }^{2}},$$(51)where di,αdi,β are both smaller than one in absolute value and given by Eqs. (40). If the frequencies of the individual nodes are not known, averaging over the distributions G0(ω) and \({G}_{1}(\hat{\omega })\) one finds that ImXβ = 0 and the order parameters Rα and Rβ can be expressed as
$${R}_{\alpha } = \; \int d\omega {G}_{0}(\omega )\sqrt{1-{d}_{i,\alpha }^{2}},\\ {R}_{\beta }= \; \int d\hat{\omega }{G}_{1}(\hat{\omega })\sqrt{1-{d}_{i,\beta }^{2}}.$$(52)From this discussion, and since this phase can only be observed for a coupling constant σ satisfying Eqs. (49), it follows that this stationary coherent phase can only be achieved if the internal frequencies ω and \(\hat{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) are bounded. Since the internal frequencies are Gaussian distributed, this implies that the stationary coherent phase is only observed in finite size networks at a value of the coupling constant that increases with the network size N. We were able to verify this effect numerically, finding that \({\sigma }_{S}^{\star }\) clearly increases with N.
The theoretical interpretation of the non-stationary rhythmic phase
From the theoretical treatment of the stationary phases of Dirac synchronization performed in the previous paragraph, we draw the important conclusion that the coherent phase of Dirac synchronization is non-stationary in the thermodynamic limit. Indeed, in this phase, the continuity equation is characterized by a non-vanishing current. This is very different phenomenology in comparison with the standard Kuramoto model, where the drifting phases can still coexist with a stationary continuity equation.
In order to treat the coherent non-stationary phase (the rhythmic phase), we provide here an approximate theoretical framework that captures the essential physics of this dynamics. Our starting point is the dynamical equation (Eq. (27)) obeyed by the vector \({{{{{{{{\boldsymbol{\alpha }}}}}}}}}_{i}={({\alpha }_{i},{\beta }_{i})}^{\top }\) of phases associated to each node i. We also make the important numerical observation that in the non-stationary coherent phase, the order parameter \({X}_{\alpha }={R}_{\alpha }{e}^{{{{{{{{\rm{i}}}}}}}}{\eta }_{\alpha }}\) acquires a phase velocity even if \(\hat{{{\Omega }}}=0\). We characterize this phase as a rhythmic phase with
where we note, however, that numerical simulations reveal that the observed emergent frequency ΩE decreases with increasing network size (see Fig. 8).
While in the standard Kuramoto model the phases are either frozen in the rotating moving frame of the order parameter or drifting, in Dirac synchronization the scenario is richer, because some phases are allowed to oscillate but still contribute to the order parameters. Indeed, by studying Eq. (27) with the hypothesis that ηα obeys Eq. (53), we can classify the phases αi associated to each node i of the network into four classes (whose typical trajectories are shown in Fig. 9):
The trajectory of the (αi, βi) phases is shown in the plane \(({{\mbox{Im}}}\,({X}_{\alpha }{e}^{-{{{{{{{\rm{i}}}}}}}}\alpha }),\sin \beta )\) for nodes with frozen phases (green and purple trajectories), for nodes with α-oscillating phases (blue trajectory) and nodes with β oscillating phases (red and yellow trajectories). Data are obtained from numerical simulation of Dirac synchronization in their backward transition for a value of the coupling constant σ = 1.77 and network size N = 500.
-
(a)
Nodes with frozen phases- These are nodes i that for large times have both αi and βi phases frozen in the rotating frame. A typical streamplot of the phases of these nodes is represented in Fig. 10a. Under the simplifying assumption that only the order parameter Xα rotates with frequency ΩE, these phases obey
$${\dot{\alpha }}_{i}={{{\Omega }}}_{E},\quad {\dot{\beta }}_{i}=0.$$(54)Therefore, in the rotating frame of the order parameters these phases are frozen on the values
$$\sin ({\alpha }_{i}-{\eta }_{\alpha })={d}_{i,\alpha },\sin {\beta }_{i}={d}_{i,\beta }.$$(55)with
$${d}_{i,\alpha } = \; \frac{{\omega }_{i}-\hat{{{\Omega }}}-{{{\Omega }}}_{E}/(1+\bar{c}/2)}{\sigma {R}_{\alpha }}\\ {d}_{i,\beta } = \; \frac{-{\hat{\omega }}_{i}+\bar{c}{{{\Omega }}}_{E}/(1+\bar{c}/2)}{\sigma }+\,{{\mbox{Im}}}\,{X}_{\beta }.$$(56)A necessary condition for the nodes to be frozen is that
$$| {d}_{i,\alpha }| \,\le \,1,\quad | {d}_{i,\beta }| \,\le \,1,$$(57)so that Eqs. (55) are well defined. Therefore in the plane \((\,{{\mbox{Im}}}\,({X}_{\alpha }{e}^{-{{{{{{{\rm{i}}}}}}}}\alpha }),\sin \beta )\), these phases in theory should appear as a single dot. Since in the real simulations the order parameter Xβ has a non-zero phase, these phases appear in Fig. 9 as little localized clouds instead of single dots.
-
(b)
Nodes with α-oscillating phases- These are nodes i that for large times have the phase βi drifting, while the phase αi oscillates in a non-trivial way contributing to the order parameter Xα. A typical streamplot of the phases of these nodes is represented in Fig. 10b. Asymptotically in time, these phases obey
$${\dot{\alpha }}_{i}={{{\Omega }}}_{E},\quad \overline{\sin {\beta }_{i}}\simeq 0,$$(58)where we denote a late-time average with an overbar. By inserting these conditions in the dynamical Eq. (27), it follows that
$$\overline{{{{{{{{\rm{Im}}}}}}}}({X}_{\alpha }{e}^{-{{{{{{{\rm{i}}}}}}}}{\alpha }_{i}})}\simeq \frac{1}{\sigma }({{{\Omega }}}_{E}-{\kappa }_{\alpha ,i}).$$(59)Approximating \(\overline{{{{{{{{\rm{Im}}}}}}}}({X}_{\alpha }{e}^{-{{{{{{{\rm{i}}}}}}}}{\alpha }_{i}})}\simeq {R}_{\alpha }\sin \overline{({\eta }_{\alpha }-{\alpha }_{i})}\), we get
$$\sin \overline{({\alpha }_{i}-{\eta }_{\alpha })}\simeq {\hat{d}}_{i,\alpha }\equiv \frac{1}{\sigma {R}_{\alpha }}({\kappa }_{\alpha ,i}-{{{\Omega }}}_{E}).$$(60)From these arguments, it follows that these αi oscillating phases are encountered when
$$| {\hat{d}}_{i,\alpha }| \,\le \,1,\quad | {d}_{i,\beta }| \ge 1.$$(61)In the plane \((\,{{\mbox{Im}}}\,({X}_{\alpha }{e}^{-{{{{{{{\rm{i}}}}}}}}\alpha }),\sin \beta )\), these phases have a trajectory that spans only a limited range of the values of Im(Xαe−iα) while the βi phases are drifting (see the blue trajectory in Fig. 9).
-
(c)
Nodes with β-oscillating phases- These are nodes i that at large times have the phase αi drifting, while the phase βi oscillates in a non-trivial way, contributing to the order parameter Xβ. A typical streamplot of the phases of these nodes is represented in Fig. 10c. Therefore, asymptotically in time, the phases of these nodes obey
$$\overline{{{{{{{{\rm{Im}}}}}}}}({X}_{\alpha }{e}^{-{{{{{{{\rm{i}}}}}}}}{\alpha }_{i}})}\simeq 0,\quad {\dot{\beta }}_{i}=0.$$(62)By inserting these conditions in the dynamical Eq. (27), we conclude that
$$\overline{\sin {\beta }_{i}}\simeq -{\hat{d}}_{i,\beta }\equiv \frac{-{\kappa }_{\beta ,i}}{\sigma }.$$(63)By approximating \(\overline{\sin {\beta }_{i}}\simeq \sin {\overline{\beta }}_{i}\), we obtain the following estimation of \(\sin \overline{{\beta }_{i}}\)
$$\sin \overline{{\beta }_{i}}\simeq -{\hat{d}}_{i,\beta }=\frac{-{\kappa }_{\beta ,i}}{\sigma }.$$(64)It follows that these nodes are encountered when the following conditions are satisfied:
$$| {\hat{d}}_{i,\beta }| \,\le \,1,\quad | {d}_{i,\alpha }| \ge 1.$$(65)In the plane \((\,{{\mbox{Im}}}\,({X}_{\alpha }{e}^{-{{{{{{{\rm{i}}}}}}}}\alpha }),\sin \beta )\), these phases have a trajectory that spans only a limited range of the values of \(\sin {\beta }_{i}\) while the αi phases are drifting (see the red and yellow trajectories in Fig. 9).
-
(d)
Nodes with drifting phases- These are nodes whose phases do not satisfy any of the previous conditions, where one observes
$$\overline{{{{{{{{\rm{Im}}}}}}}}}({X}_{\alpha }{e}^{-{{{{{{{\rm{i}}}}}}}}{\alpha }_{i}})\simeq 0,\quad \overline{\sin {\beta }_{i}}\simeq 0.$$(66)
A typical streamplot of the phases of these nodes is represented in Fig. 10d. The phases of these nodes do not contribute to any of the order parameters.
Streamplots of Eq. (27), for Xα = Rα = 0.8 (\(\tilde{{{\Omega }}}=0\)) and σ = 2. The four different streamplots corresponds to nodes with frozen phases (a) ω = 1, \(\hat{\omega }=0.5\), to nodes with α-oscillating phases (b) ω = 1, \(\hat{\omega }=-3.5\), to nodes with β-oscillating phases (c) ω = 8, \(\hat{\omega }=8\), to nodes with drifting phases (d) ω = 7, \(\hat{\omega }=3\).
The frozen phases and the α-oscillating phases both contribute to the order parameter Rα while the frozen phases and the β-oscillating phases both contribute to Rβ. Therefore, the order parameters Rα and Rβ can be approximated by
where di,α, di,β are given by Eq. (40) and \({\hat{d}}_{i,\alpha }\), \({\hat{d}}_{i,\beta }\) are given by
If the frequencies of the individual nodes are not known, in the approximation in which ImXβ ≃ 0, the order parameters Rα and Rβ can be expressed as
We now make use of the numerical observation that ΩE decreases with the network size, implying that the period of the oscillations of the order parameter Xα becomes increasingly long with increasing network sizes. By substituting ΩE = 0, these equations can be used to determine the order parameters Rα and Rβ as a function of the coupling constant σ in the limit N → ∞. Indeed, these are the equations that provide the theoretical expectation of the phase diagram in Fig. 3. Moreover, these equations can be used to estimate the critical value σc by substituting ΩE = 0 and expanding the self-consistent expression of Rα for small values of Rα. To this end, we write the self-consistent equation for Rα as
For Rα ≪ 1, we make the following approximations
Inserting these expressions into the self-consistent equation for Rα, we can derive the equation determining the value of the coupling constant σ = σc at which we observe the continuous phase transition,
where erf(x) is the error function and erfc(x) is the complementary error function. This equation can be solved numerically, providing the value of σc given by
Similarly, we can consider the classification of the different phases of oscillators to study the onset of the instability of the incoherent phase. We obtain the estimate for \({\sigma }_{c}^{\star }\) given by (see Methods for details)
Conclusions
In this work, we have formulated and discussed the explosive Dirac synchronization of locally coupled topological signals associated to the nodes and to the links of a network. Topological signals associated to nodes are traditionally studied in models of non-linear dynamics of a network. However, the dynamics of topological signals associated to the links of the network is so far much less explored.
In brain and neuronal networks, the topological signals of the links can be associated to a dynamical state of synapses (for example oscillatory signals associated to intracellular calcium dynamics involved in synaptic communication among neurons54), and more generally they can be associated to dynamical weights or fluxes associated to the links of the considered network. The considered coupling mechanism between topological signals of nodes and links is local, meaning that every node and every link is only affected by the dynamics of nearby nodes and links. In particular, the dynamics of the nodes is dictated by a Kuramoto-like system of equations where we introduce a phase lag that depends on the dynamical state of nearby links. Similarly, the dynamics of the links is dictated by a higher-order Kuramoto-like system of equations25 where we introduce a phase lag dependent on the dynamical state of nearby nodes.
On a fully connected network, Dirac synchronization is explosive as it leads to a discontinuous forward synchronization transition and a continuous backward synchronization transition. Therefore, Dirac synchronization determines a topological mechanism to achieve abrupt discontinuous synchronization transitions. The theoretical investigation of the model predicts that the discontinuous transition occurs at a theoretically predicted value of the coupling constant \({\sigma }_{c}^{\star }\) when the incoherent phase loses stability. However, for smaller value of the coupling constant, the incoherent phase can coexist with the coherent one.
The coherent phase can be observed for σ > σc. However, for \({\sigma }_{c} \; < \; \sigma \; < \; {\sigma }_{S}^{\star }\), the system is in a rhythmic phase characterized by non-stationary order parameters. Here, we theoretically predict the numerical value of \({\sigma }_{S}^{\star }\) and we investigate numerically the dynamics of the order parameters in the rhythmic phase.
This work shows how topology can be combined with dynamical systems leading to a new framework to capture abrupt synchronization transitions and the emergence of non trivial rhythmic phases.
This work can be extended in different directions. First of all, the model can be applied to more complex network topologies including not only random graphs and scale-free networks but also real network topologies such as experimentally obtained brain networks. Secondly, using the higher-order Dirac operator43,59, Dirac synchronization can be extended to simplicial complexes where topological signals can be defined also on higher-order simplices such as triangles, tetrahedra and so on. We hope that this work will stimulate further theoretical and applied research along these lines.
Methods
Internal frequencies of the projected dynamics
The frequencies \(\hat{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) characterising the uncoupled dynamics of the projected variables ψ can be determined using Eq. (18) from the internal frequencies of the links \(\tilde{{{{{{{{\boldsymbol{\omega }}}}}}}}}\). In particular, since the frequencies \(\tilde{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) are normally distributed, the frequencies \(\hat{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) will also be normally distributed. However, Eq. (18) implies that the frequencies \(\hat{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) are correlated. Let us recall that the internal frequencies of the links \(\tilde{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) are taken to be independent Gaussian variables with zero average and standard deviation \(1/\sqrt{N-1}\), i.e.
for each link ℓ of the network. Using the definition of the incidence matrix B, it is easy to show that the expectation of \({\hat{\omega }}_{i}\) is given by
Given that in a fully connected network each node has degree ki = N − 1, the covariance matrix C is given by the graph Laplacian L[0] of the network, i.e.
where we have indicated with \({\left\langle \ldots \right\rangle }_{c}\) the connected correlation. Therefore, the covariance matrix has elements given by
Moreover we note that the average of \(\hat{{{{{{{{\boldsymbol{\omega }}}}}}}}}\) over all the nodes of the network is zero. In fact
where we indicate with 1 the N-dimensional column vector of elements 1i = 1.
With these hypotheses, the marginal probability \({G}_{1}(\hat{\omega })\) that the internal frequency \({\hat{\omega }}_{i}\) of a generic node i is given by \({\hat{\omega }}_{i}=\hat{\omega }\) can be expressed as (see26 for the derivation),
where we have put
Derivation of the stationary state expression for a i and b i
Let us now consider a given node i and its continuity equation, Eq. (33). By using the ansatz defined in Eq. (37) and omitting the index i as long as Xα ≠ 0, we can observe that the continuity Eq. (33) is satisfied if the following equations are satisfied for m = 0, n ≠ 0 and for n = 0, m ≠ 0,
Moreover, for every m > 0, n > 0 the following equation needs to be satisfied
As long as a ≠ 0 and Xα ≠ 0, all these equations are satisfied if and only if ∣a∣ = ∣b∣ = 1 and
For Xα = 0, instead, by proceeding in a similar way, we get that for ∣a∣ ≠ 0, ∣b∣ = 1, the equations for a and b are given by
while for ∣a∣ = 0, the equation for b is unchanged but b can have an arbitrary large absolute value.
The onset of the instability of the incoherent phase
In this section we use stability considerations to derive the synchronization threshold \({\sigma }_{c}^{\star }\). This approach is analogous to similar approaches used to study the onset of instability of the incoherent phase in models focusing solely on signals defined on the nodes of a network73,76. Let us now consider the first of Eqs. (38) for every \({a}_{i}({\omega }_{i},{\hat{\omega }}_{i})\), and study the stability of the trivial solution in which \({a}_{i}({\omega }_{i},{\hat{\omega }}_{i})=0\) for every node i and every choice of the frequencies \((\omega ,\hat{\omega })\), also implying that Rα = 0. The stationary solutions for ai and bi describe a discontinuous transition from steady state solutions with ai = 0 to ∣ai∣ = 1. Studying the stability of the incoherent phase is therefore non-trivial. In order to do so, we study the continuity equations using the generalized Ott-Antonsen ansatz and we consider non zero values of ai with absolute value ∣ai∣ ≪ 1 while keeping ∣bi∣ = 1 so that \({b}_{i}^{-1}={b}_{i}^{\star }\). With these hypotheses, we notice that Eq. (84) describing the dynamics of the high frequency α modes of ρ(α, β) are negligible and we can just focus on Eq. (82) obtained for m = 0, n = 1. Since \({a}_{i}(\omega ,\hat{\omega })\) is only a function of \((\omega ,\hat{\omega })\), in this section we simplify the notation by omitting the index i. This entails for instance considering the function \(a(\omega ,\hat{\omega })\) instead of \({a}_{i}({\omega }_{i},{\hat{\omega }}_{i})\). A similar convention is used for other variables only depending on the node i through the internal frequencies ω = ωi and \(\hat{\omega }={\hat{\omega }}_{i}\). To this end, we write Eq. (82) as
with F(a, b, Xα) given by
where \({\kappa }_{\alpha }={\kappa }_{\alpha }(\omega ,\hat{\omega })\). In this equation Xα is intended to be a function of all the variables a according to Eqs. (46). By linearizing Eq. (87) for \(a(\omega ,\hat{\omega })={{\Delta }}a(\omega ,\hat{\omega })\ll 1\) for every value of \((\omega ,\hat{\omega })\), and neglecting fluctuations in the variables \(b(\omega ,\hat{\omega })\), we obtain
where we have defined B as
with \(\bar{b}=\bar{b}(\omega ,\hat{\omega })\) being the stationary solution of Eq. (38) in the limit Xα → 0 and aj → 0, ∀ j and where \({{{{{{{\mathcal{S}}}}}}}}\) indicates
In order to predict the onset of the instability of the incoherent phase, i.e., in order to predict the value of \({\sigma }_{c}^{\star }\), we study the discrete spectrum of Eq. (88). Assuming that Eq. (88) has Lyapunov exponent λ, we find that \({{\Delta }}a(\omega ,\hat{\omega })\) obeys
where \(\hat{{{\Delta }}}(\omega ,\hat{\omega })\) is given by
By inserting Eq. (91) in the definition of \({{{{{{{\mathcal{S}}}}}}}}\) given by Eq. (90), we obtain a self-consistent equation that reads
Therefore, this equation provides the value of the Lyapunov exponent λ for any given value of the coupling constant σ. We look for the onset of the instability \(\sigma ={\sigma }_{c}^{\star }\) of the incoherent solution Rα = 0 by imposing that its Lyapunov exponent vanishes, i.e., λ = 0.
In order to solve this equation, we need to find the explicit form for B in the limit Xα → 0. By considering the stationary solution in the incoherent phase, we obtain that the variable B is given by
as long as ∣bi∣ = 1, i.e. as long as ∣κβ/σ∣ ≤ 1. We can now insert this expression in \(\hat{{{\Delta }}}\) finding
for ∣κβ/σ∣ ≤ 1. Otherwise, since we assume ai ≠ 0, bi does not have a stationary value and in expectation over time we have
This leads to
for ∣κβ/σ∣ ≥ 1.
In the limit N → ∞, we have that \(\bar{c}\to 1\) and \(\hat{{{\Omega }}}\to {{{\Omega }}}_{0}.\) Therefore in this limit, we obtain
By using this explicit expression for \(\hat{{{\Delta }}}\) in terms of the frequency of the nodes, it is straightforward to see that \(\hat{I}\) can be evaluated with the method of residues leading to
By inserting the values of these integrals in Eq. (93) and solving for σ, we get that the synchronization threshold occurs at
Data availability
This manuscript does not use any data with mandated deposition.
Code availability
All codes are available upon request to the Corresponding Author.
References
Kuramoto, Y. Self-entrainment of a population of coupled non-linear oscillators. In Araki, H. (ed.) International Symposium on Mathematical Problems in Theoretical Physics, 420–422 (Springer Berlin Heidelberg, Berlin, Heidelberg, 1975).
Strogatz, S. H. Nonlinear dynamics and chaos with student solutions manual: With applications to physics, biology, chemistry, and engineering (CRC Press, 2018).
Strogatz, S. H. From kuramoto to crawford: Exploring the onset of synchronization in populations of coupled oscillators. Physica D: Nonlinear Phenomena 143, 1–20 (2000).
Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y. & Zhou, C. Synchronization in complex networks. Phys. Rep. 469, 93–153 (2008).
Boccaletti, S., Pisarchik, A. N., Del Genio, C. I. & Amann, A. Synchronization: from coupled systems to complex networks. (Cambridge University Press, 2018).
Pikovsky, A., Kurths, J., Rosenblum, M. & Kurths, J. Synchronization: a universal concept in nonlinear sciences. 12 (Cambridge University Press, 2003).
Schaub, M. T. et al. Graph partitions and cluster synchronization in networks of oscillators. Chaos: An Interdisciplinary J. Nonlinear Sci. 26, 094821 (2016).
Strogatz, S. H. Sync: How order emerges from chaos in the universe, nature, and daily life (Hachette UK, 2012).
Gross, T. Not one, but many critical states: A dynamical systems perspective. Front. Neural Circuits 15, 7 (2021).
Glass, L. & Mackey, M. C. From clocks to chaos (Princeton University Press, 2020).
Buzsaki, G. Rhythms of the Brain (Oxford University Press, 2006).
Couzin, I. D. Synchronization: the key to effective communication in animal collectives. Trends Cognitive Sci. 22, 844–846 (2018).
Wiesenfeld, K., Colet, P. & Strogatz, S. H. Frequency locking in josephson arrays: Connection with the kuramoto model. Phys. Rev. E 57, 1563 (1998).
Soriano, M. C., García-Ojalvo, J., Mirasso, C. R. & Fischer, I. Complex photonics: Dynamics and applications of delay-coupled semiconductors lasers. Rev. Modern Phys. 85, 421 (2013).
Zhu, B. et al. Synchronization of interacting quantum dipoles. New J. Phys. 17, 083063 (2015).
Witthaut, D., Wimberger, S., Burioni, R. & Timme, M. Classical synchronization indicates persistent entanglement in isolated quantum systems. Nat. Commun. 8, 1–7 (2017).
Nakahara, M. Geometry, topology and physics (CRC Press, 2003).
Yang, C. N., Ge, M.-L. & He, Y.-H. Topology and Physics(World Scientific, 2019).
Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C: Solid State Phys. 6, 1181 (1973).
Shankar, S., Souslov, A., Bowick, M. J., Marchetti, M. C. & Vitelli, V. Topological active matter. Nat. Rev. Phys. 4, 380–398 (2022).
Shen, S.-Q. Topological insulators, vol. 174 (Springer, 2012).
Fruchart, M. & Carpentier, D. An introduction to topological insulators. Comptes Rendus Physique 14, 779–815 (2013).
Tang, E., Agudo-Canalejo, J. & Golestanian, R. Topology protects chiral edge currents in stochastic systems. Phys. Rev. X 11, 031015 (2021).
Millán, A. P., Restrepo, J. G., Torres, J. J. & Bianconi, G. In: Battiston, F., Petri, G. (eds) Higher-Order Systems. Understanding Complex Systems, 269–299 (Springer International Publishing, Cham, 2022).
Millán, A. P., Torres, J. J. & Bianconi, G. Explosive higher-order kuramoto dynamics on simplicial complexes. Phys. Rev. Lett. 124, 218301 (2020).
Ghorbanchian, R., Restrepo, J. G., Torres, J. J. & Bianconi, G. Higher-order simplicial synchronization of coupled topological signals. Commun. Phys. 4, 120 (2021).
Hart, J. D., Zhang, Y., Roy, R. & Motter, A. E. Topological control of synchronization patterns: Trading symmetry for stability. Phys. Rev. Lett. 122, 058301 (2019).
Bianconi, G. Higher-order networks: An introduction to simplicial complexes. (Cambridge University Press, Cambridge, 2021).
Battiston, F. et al. The physics of higher-order interactions in complex systems. Nat. Phys. 17, 1093–1098 (2021).
Battiston, F. et al. Networks beyond pairwise interactions: Structure and dynamics. Phys. Rep. 874, 1–92 (2020).
Bick, C., Gross, E., Harrington, H. A. & Schaub, M. T. What are higher-order networks? arXiv preprint arXiv:2104.11329 (2021).
Giusti, C., Ghrist, R. & Bassett, D. S. Two’s company, three (or more) is a simplex. J. Comput. Neurosci. 41, 1–14 (2016).
Otter, N., Porter, M. A., Tillmann, U., Grindrod, P. & Harrington, H. A. A roadmap for the computation of persistent homology. EPJ Data Sci. 6, 1–38 (2017).
Ziegler, C., Skardal, P. S., Dutta, H. & Taylor, D. Balanced hodge laplacians optimize consensus dynamics over simplicial complexes. Chaos: An Interdisciplinary J. Nonlinear Sci. 32, 023128 (2022).
Krishnagopal, S. & Bianconi, G. Spectral detection of simplicial communities via hodge laplacians. Phys. Rev. E 104, 064303 (2021).
Jost, J. Mathematical concepts (Springer, 2015).
Taylor, D. et al. Topological data analysis of contagion maps for examining spreading processes on networks. Nat. Commun. 6, 1–11 (2015).
Mulas, R., Kuehn, C. & Jost, J. Coupled dynamics on hypergraphs: Master stability of steady states and synchronization. Phys. Rev. E 101, 062313 (2020).
Patania, A., Vaccarino, F. & Petri, G. Topological analysis of data. EPJ Data Sci. 6, 1–6 (2017).
Petri, G. et al. Homological scaffolds of brain functional networks. J. Royal Soc. Interface 11, 20140873 (2014).
Horak, D. & Jost, J. Spectra of combinatorial laplace operators on simplicial complexes. Adv. Math. 244, 303–336 (2013).
Torres, J. J. & Bianconi, G. Simplicial complexes: Higher-order spectral dimension and dynamics. J. Phys. Complex. 1, 015002 (2020).
Bianconi, G. The topological dirac equation of networks and simplicial complexes. J. Phys. Complex. 2, 035022 (2021).
Arnaudon, A., Peach, R. L., Petri, G. & Expert, P. Connecting hodge and sakaguchi-kuramoto: a mathematical framework for coupled oscillators on simplicial complexes. arXiv preprint arXiv:2111.11073 (2021).
Barbarossa, S. & Sardellitti, S. Topological signal processing over simplicial complexes. IEEE Transac. Signal Process. 68, 2992–3007 (2020).
Schaub, M. T., Benson, A. R., Horn, P., Lippner, G. & Jadbabaie, A. Random walks on simplicial complexes and the normalized Hodge 1-Laplacian. SIAM Rev. 62, 353–391 (2020).
Schaub, M. T., Zhu, Y., Seby, J.-B., Roddenberry, T. M. & Segarra, S. Signal processing on higher-order networks: Livin’ on the edge… and beyond. Signal Proc. 187, 108149 (2021).
Ebli, S., Defferrard, M. & Spreemann, G. Simplicial neural networks. arXiv preprint arXiv:2010.03633 (2020).
Bodnar, C. et al. Weisfeiler and lehman go topological: Message passing simplicial networks. In Meila, M. & Zhang, T. (eds.) Proceedings of the 38th International Conference on Machine Learning, vol. 139 of Proceedings of Machine Learning Research, 1026–1037 (PMLR, 2021).
DeVille, L. Consensus on simplicial complexes: Results on stability and synchronization. Chaos: An Interdiscip. J. Nonlinear Sci. 31, 023137 (2021).
Faskowitz, J., Betzel, R. F. & Sporns, O. Edges in brain networks: Contributions to models of structure and function. Netw. Neurosci. 6, 1–28 (2022).
Sporns, O., Faskowitz, J., Teixeira, A. S., Cutts, S. A. & Betzel, R. F. Dynamic expression of brain functional systems disclosed by fine-scale analysis of edge time series. Netw. Neurosci. 5, 405–433 (2021).
Dupont, G., Combettes, L., Bird, G. S. & Putney, J. W. Calcium oscillations. Cold Spring Harbor Pers. Biol. 3, a004226 (2011).
Pasti, L., Volterra, A., Pozzan, T. & Carmignoto, G. Intracellular calcium oscillations in astrocytes: A highly plastic, bidirectional form of communication between neurons and astrocytes in situ. J. Neurosci. 17, 7817–7830 (1997).
Huang, W. et al. A graph signal processing perspective on functional brain imaging. Proc. IEEE 106, 868–885 (2018).
Rocks, J. W., Liu, A. J. & Katifori, E. Hidden topological structure of flow network functionality. Phys. Rev. Lett. 126, 028102 (2021).
Katifori, E., Szöllősi, G. J. & Magnasco, M. O. Damage and fluctuations induce loops in optimal transport networks. Phys. Rev. Lett. 104, 048704 (2010).
Kaiser, F., Ronellenfitsch, H. & Witthaut, D. Discontinuous transition to loop formation in optimal supply networks. Nat. Commun. 11, 1–11 (2020).
Lloyd, S., Garnerone, S. & Zanardi, P. Quantum algorithms for topological and geometric analysis of data. Nat. Commun. 7, 1–7 (2016).
Sakaguchi, H. & Kuramoto, Y. A soluble active rotater model showing phase transitions via mutual entertainment. Prog. Theoretical Phys. 76, 576–581 (1986).
English, L. Q., Zeng, Z. & Mertens, D. Experimental study of synchronization of coupled electrical self-oscillators and comparison to the sakaguchi-kuramoto model. Phys. Rev. E 92, 052912 (2015).
Omel’chenko, E. & Wolfrum, M. Nonuniversal transitions to synchrony in the sakaguchi-kuramoto model. Phys. Rev. Lett. 109, 164101 (2012).
Omel’chenko, E. & Wolfrum, M. Bifurcations in the sakaguchi–kuramoto model. Physica D: Nonlinear Phenom. 263, 74–85 (2013).
Yeung, M. S. & Strogatz, S. H. Time delay in the kuramoto model of coupled oscillators. Phys. Rev. Lett. 82, 648 (1999).
Eldering, J., Lamb, J. S., Pereira, T. & dos Santos, E. R. Chimera states through invariant manifold theory. Nonlinearity 34, 5344 (2021).
Breakspear, M., Heitmann, S. & Daffertshofer, A. Generative models of cortical oscillations: Neurobiological implications of the kuramoto model. Front. Human NeuroSci. 4, 190 (2010).
Boccaletti, S. et al. Explosive transitions in complex networks’ structure and dynamics: Percolation and synchronization. Phys. Rep. 660, 1–94 (2016).
D’Souza, R. M., Gómez-Gardeñes, J., Nagler, J. & Arenas, A. Explosive phenomena in complex networks. Adv. Phys. 68, 123–223 (2019).
Gómez-Gardenes, J., Gómez, S., Arenas, A. & Moreno, Y. Explosive synchronization transitions in scale-free networks. Phys. Rev. Lett. 106, 128701 (2011).
Coutinho, B., Goltsev, A., Dorogovtsev, S. & Mendes, J. Kuramoto model with frequency-degree correlations on complex networks. Phys. Rev. E 87, 032106 (2013).
Zhang, X., Boccaletti, S., Guan, S. & Liu, Z. Explosive synchronization in adaptive and multilayer networks. Phys. Rev. Lett. 114, 038701 (2015).
Zhang, X., Hu, X., Kurths, J. & Liu, Z. Explosive synchronization in a general complex network. Phys. Rev. E 88, 010802 (2013).
Arola-Fernández, L. et al. Self-organized explosive synchronization in complex networks: Emergence of synchronization bombs. arXiv preprint arXiv:2203.03728 (2022).
Avalos-Gaytán, V. et al. Emergent explosive synchronization in adaptive complex networks. Phys. Rev. E 97, 042301 (2018).
Nicosia, V., Skardal, P. S., Arenas, A. & Latora, V. Collective phenomena emerging from the interactions between dynamical processes in multiplex networks. Phys. Rev. Lett. 118, 138302 (2017).
Peron, T., Eroglu, D., Rodrigues, F. A. & Moreno, Y. Collective dynamics of random janus oscillator networks. Phys. Rev. Res. 2, 013255 (2020).
Kachhvah, A. D. & Jalan, S. Delay regulated explosive synchronization in multiplex networks. New J. Phys. 21, 015006 (2019).
Jalan, S., Rathore, V., Kachhvah, A. D. & Yadav, A. Inhibition-induced explosive synchronization in multiplex networks. Phys. Rev. E 99, 062305 (2019).
Skardal, P. S. & Arenas, A. Abrupt desynchronization and extensive multistability in globally coupled oscillator simplexes. Phys. Rev. Lett. 122, 248301 (2019).
Skardal, P. S. & Arenas, A. Higher order interactions in complex networks of phase oscillators promote abrupt synchronization switching. Commun. Phys. 3, 1–6 (2020).
Lucas, M., Cencetti, G. & Battiston, F. Multiorder laplacian for synchronization in higher-order networks. Phys. Rev. Res. 2, 033410 (2020).
Kuehn, C. & Bick, C. A universal route to explosive phenomena. Sci. Adv. 7, eabe3824 (2021).
Cabral, J., Hugues, E., Sporns, O. & Deco, G. Role of local network oscillations in resting-state functional connectivity. Neuroimage 57, 130–139 (2011).
Yeung, M. S. & Strogatz, S. H. Time delay in the kuramoto model of coupled oscillators. Phys. Rev. Lett. 82, 648 (1999).
Restrepo, J. G. & Ott, E. Mean-field theory of assortative networks of phase oscillators. EPL (Europhysics Letters) 107, 60006 (2014).
Chandra, S., Girvan, M. & Ott, E. Continuous versus discontinuous transitions in the d-dimensional generalized kuramoto model: Odd d is different. Phys. Rev. X 9, 011002 (2019).
Dai, X. et al. Discontinuous transitions and rhythmic states in the d-dimensional kuramoto model induced by a positive feedback with the global order parameter. Phys. Rev. Lett. 125, 194101 (2020).
Sone, K., Ashida, Y. & Sagawa, T. Topological synchronization of coupled nonlinear oscillators. Phys. Rev. Res. 4, 023211 (2022).
Kuramoto, Y. & Nishikawa, I. Statistical macrodynamics of large dynamical systems. case of a phase transition in oscillator communities. J. Stat. Phys. 49, 569–605 (1987).
Kuramoto, F. & Nishikawa, I. Onset of collective rhythms in large populations of coupled oscillators. In Cooperative Dynamics in Complex Physical Systems, 300–306 (Springer, 1989).
Strogatz, S. H. & Mirollo, R. E. Stability of incoherence in a population of coupled oscillators. J. Stat. Phys. 63, 613–635 (1991).
Ott, E. & Antonsen, T. M. Low dimensional behavior of large systems of globally coupled oscillators. Chaos: An Interdiscip. J. Nonlinear Sci. 18, 037113 (2008).
Acknowledgements
G.B. acknowledges funding from the Alan Turing Institute and from Royal Society IEC\NSFC\191147. J.J.T. acknowledges financial support from the Consejería de Transformación Económica, Industria, Conocimiento y Universidades, Junta de Andalucía and European Regional Development Funds, Ref. P20_00173. This work is also part of the Project of I+D+i Ref. PID2020-113681GB-I00, financed by MICIN/AEI/10.13039/501100011033 and FEDER “A way to make Europe". This research utilized Queen Mary’s Apocrita HPC facility, supported by QMUL Research-IT. https://doi.org/10.5281/zenodo.438045.
Author information
Authors and Affiliations
Contributions
G.B. designed the research; L.C., J.G.R., J.J.T., and G.B. performed the research; L.C., J.G.R., G.B. contributed to the numerical implementations of the algorithm; L.C., J.G.R., G.B. have contributed to the theoretical derivations; L.C., J.G.R., J.J.T., and G.B. have contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests. G.B. is a Guest Editor of the Collection “Higher-order interaction networks” for Communications Physics, but was not involved in the editorial review of, or the decision to publish this article.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Calmon, L., Restrepo, J.G., Torres, J.J. et al. Dirac synchronization is rhythmic and explosive. Commun Phys 5, 253 (2022). https://doi.org/10.1038/s42005-022-01024-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01024-9
This article is cited by
-
Persistent Dirac for molecular representation
Scientific Reports (2023)
-
Simplicial cascades are orchestrated by the multidimensional geometry of neuronal complexes
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.