Abstract
Laser communications from small satellite platforms empowers the establishment of quantum key distribution (QKD), relying on quantum superposition states of single photons to realize unconditional security between distant parties at a global scale. Although recent breakthrough experiments have demonstrated the feasibility of satellite-to-ground QKD links, the underlying statistical characteristics of quantum atmospheric channels have not been well-understood and experimentally verified in the literature. In this paper, we highlight that classical atmospheric statistical models can be applied for describing random fluctuations of the quantum channels. To verify this fact, we report a statistical verification study of quantum atmospheric channels from the world’s first low-Earth orbit (LEO) 50-kg-class microsatellite-to-ground quantum-limited communication experiment. The verified statistical model is then applied to numerically investigate the quantum bit-error rate (QBER) and secret-key length (SKL) of a decoy-state efficient Bennett-Brassard 1984 (BB84) QKD protocol with optimized parameters considering finite-key effects, implemented over a LEO 6-unit (6U)-CubeSat-to-ground link. Important insights of the physical channel effects including pointing errors and atmospheric turbulence on the QBER and SKL are then revealed. Finally, we present a study using a deep-learning-based long short-term memory (LSTM) recurrent neural network (RNN) for predicting photon-count fluctuations over quantum atmospheric channels.
Similar content being viewed by others
Introduction
The space sector has witnessed an unprecedented growth in recent years, expected to become the next trillion-dollar industry, due to the declining launch costs by reusable rockets and advances in miniaturized satellites that significantly reduce the size, weight, and costs. These transformative technologies have sparked a paradigm shift to providing the Internet access from space and establishing a globally connected cyber-physical system. This can be realized via a satellite constellation consisting of thousands of small satellites orbiting in low-Earth orbit (LEO) that are seamlessly connected with each other and their coordinated ground networks, thereby delivering low-latency and high-capacity worldwide communication services. Over the past decade, laser communications have emerged as an alternative solution to radio frequency bands for high-capacity data links from space, especially for miniaturized platforms such as microsatellites and CubeSats where stringent requirements of limited size, weight, and power consumption are applied1,2.
In parallel with the evolution of satellite broadband Internet services, the Internet providers will have to face far more cybersecurity risks as the global networks become highly complex and eavesdroppers become more powerful by harnessing the computing power of soon-to-be-available quantum computers, which could possibly perform trillions of floating-point operations per second. This poses a serious security threat to current confidential communication mechanisms which rely solely on computational complexities. In this regard, quantum key distribution (QKD) stands out as a viable countermeasure against adversary with unbounded computing power, due to its intrinsic information-theoretic security by exploiting quantum superposition states of single photons to exchange secure keys between distant parties3. These secure keys are then used for encrypting and decrypting the confidential messages sent over the Internet. As a matter of fact, an eavesdropper is imposed by the quantum no-cloning theorem, thus preventing it from perfectly eavesdropping the secure keys distributed by means of QKD4. A satellite QKD network can be implemented with satellites playing the roles as trusted nodes or untrusted nodes. More specifically, in the trusted-node approach, each satellite establishes two separate QKD links with two distant ground stations to distil the secure key5, whereas in the untrusted node approach the satellite prepares entangled photons and sends to the two ground stations for which the secure key can be subsequently shared6. Other methods to utilize untrusted satellite nodes include measurement-device-independent (MDI)7,8 and twin-field9 QKD protocols. In MDI QKD, two distant ground stations prepare phase-randomized weak-coherent pulses and send to the satellite, where an untrusted Bell-state measurement is performed to project the incoming signals into a Bell state. The detection results are then publicly announced to the OGSs for the key distillation process. The recently proposed twin-field QKD also resembles MDI QKD, however, optical fields imparted with the same random phase, i.e., twins, are used to generate a quantum key. Although a number of experimental studies have been devoted to investigate the feasibility of QKD links from space10,11,12,13,14,15, only until 2017 several remarkable milestones of practical satellite quantum communications were successfully achieved16,17,18,19,20. These groundbreaking achievements have marked the blooming of a new era of globally-secured satellite-based quantum Internet.
Nevertheless, the beauty of satellite QKD does not come without challenges. A satellite-to-ground QKD link suffers from the signal degradation and random fluctuations. Particularly, the atmosphere existing in the last 20-km range above the ground surface causes scattering and absorption effects that degrade the signal intensity. In addition, the optical beam is geometrically broadened when propagating over hundreds to thousands of kilometers, which results in a big beam footprint ranging from a few to hundreds of meters when reaching the OGS. This causes severe geometrical losses when receiving by telescopes with limited sizes. The optical signal also experiences amplitude and phase fluctuations due to atmospheric turbulence, which results from random variations of the refractive index of multiple air packets smaller than the beam size that interact with the propagating beam in the atmosphere. Moreover, mechanical vibrations on the satellite platform lead to pointing errors that cause random displacements of the optical beam received at the ground station, which contribute to the signal fluctuations. To characterize all these effects, the quantum atmospheric channel is usually studied by statistical means, where the probability distribution of transmittance (PDT) plays the central role in describing the fluctuating loss over the quantum channel.
In this paper, we propose the use of a classical PDT model that has never been applied to characterize the satellite-to-ground quantum atmospheric channels. The proposed PDT model is statistically verified with experimental data for quantum atmospheric channels by using the photon-count data received at NICT’s optical ground station (OGS) during the world’s first LEO-to-ground quantum-limited communication experiment with a 50-kg-class microsatellite. The verified PDT model is subsequently applied to numerically investigate the quantum bit-error rate (QBER) and secret-key length (SKL) of a decoy-state efficient Bennett-Brassard 1984 (BB84) QKD protocol with optimized system parameters, considering the finite-key analysis to account for statistical fluctuations between the measurement rates and underlying probabilities of the data collected during a finite time interval of the LEO-to-ground communications window. Our numerical results reveal useful insights into the effects of pointing errors and atmospheric turbulence on the QBER and SKL during a practical quantum communications window for a satellite pass. Finally, we present a study on the prediction of received photon counts by means of deep learning, using the long short-term memory (LSTM) recurrent neural network (RNN). Then, the potential application of deep learning in exploiting quantum channel characteristics for real-time autonomous estimation and optimization of the future satellite-based QKD networks is further discussed.
Results
Statistical channel models
Conventionally, the description of pure losses in linear quantum optics can be expressed by the input–output relation
where \({\hat{a}}_{{{{{{{{\rm{in}}}}}}}}}\) and \({\hat{a}}_{{{{{{{{\rm{out}}}}}}}}}\) denote the input and output field annihilation operators, respectively, and \(\hat{c}\) is an environmental mode operator being in the vacuum state. η is the transmittance that characterizes the linear losses of the channel, i.e., the fraction of input photons that makes it to the output on average21, as well as the channel capacity for quantum communications22. For preserving the canonical commutation relations for the quantized optical field operators in the input-output relation, η is restricted to the domain \(\left[0,1\right]\). When the quantum signal is transmitted through the atmospheric channel, η characterizes the fluctuating loss and is a random variable. The operator input-output relation in Eq. (1) can then be transformed into the Schrödinger picture of motion to obtain the corresponding density operators. Using the Glauber-Sudarshan P representation, the connection between sent and received quantum states through the atmosphere can be described as23
where \({P}_{{{{{{{{\rm{in}}}}}}}}}\left(\alpha \right)\) and \({P}_{{{{{{{{\rm{out}}}}}}}}}\left(\alpha \right)\) denote the input and output P functions, respectively24,25. \(f\,\left(\eta \right)\) is the PDT of the atmospheric channel transmittance, and η is mathematically defined as26,27,28,29
where \({\mathbb{A}}\) is the area of the receiving aperture, \({I}_{{{{{{{{\rm{beam}}}}}}}}}\,\left({{{{{{{\mathbf{\varrho }}}}}}}},L\right)\) is the normalized intensity of a classical beam in a given spatial point at the receiving aperture plane, with L the beam propagation distance and ϱ the transverse spatial coordinate chosen that ϱ = 0 coincides with the center of the receiving aperture. It should be noted that the output \({P}_{{{{{{{{\rm{out}}}}}}}}}\left(\alpha \right)\) is obtained by averaging the input-output relation between the corresponding P functions over the PDT of η. Therefore, the characterization of quantum signals over the atmosphere reduces merely to identify a consistent and accurate model of \(f\,\left(\eta \right)\). It should be emphasized that the restriction range \(\left[0,1\right]\) to preserve the commutation relations in Eq. (1) refers to the pure-loss channel transmittance on average. Thus, for the fluctuating channel in Eq. (2), this restriction is applied on the statistical mean, i.e., \({\mathbb{E}}\left[\eta \right]\in \left[0,1\right]\), where \({\mathbb{E}}\left[\cdot \right]\) denotes the expectation operator.
It is evident from Eq. (3) that the PDT of η is governed by the probability density function (PDF) of \({I}_{{{{{{{{\rm{beam}}}}}}}}}\,\left({{{{{{{\boldsymbol{\varrho }}}}}}}},L\right)\), where the intensity can attain arbitrary high values due to the atmospheric turbulence-induced intensity fluctuations, i.e., \({I}_{{{{{{{{\rm{beam}}}}}}}}}\,\left({{{{{{{\boldsymbol{\varrho }}}}}}}},L\right)\in [0,\infty )\). The PDF of \({I}_{{{{{{{{\rm{beam}}}}}}}}}\,\left({{{{{{{\boldsymbol{\varrho }}}}}}}},L\right)\) is well-developed in classical communications considering all physical channel effects that include the deterministic loss due to absorption and scattering, the random beam misalignments, and the turbulence-induced random intensity fluctuations. Nevertheless, for low-loss atmospheric channels over short communication distances, the classical channel PDF, e.g., log-normal model, results in a non-zero probability of the instantaneous η being larger than 127, which is physically unrealistic over quantum channels. To deal with this issue, previous studies have suggested that the classical channel PDF characterizing the channel fluctuations must be vanishing at η = 1 and hence forced to truncate the log-normal model for the domain η > 126,27,28,29. Due to this truncation, a closed-form expression for the PDT of η considering both atmospheric turbulence and beam misalignments does not exist and complex numerical estimations are required28. For a LEO satellite-to-ground quantum channel where the total losses are very high, the typical values of η are however far less than 1, i.e., η → 0. Due to this fact, the instantaneous values of turbulence-induced intensity fluctuations could obtain high values without violating the physical limit η = 1 as long as the instantaneous intensity increases are below an appropriate finite value larger than 1. This is indeed true for intensity fluctuations under practical operation conditions. Thus, it could be a good approximation to the physically valid region η → 1 by taking the upper limit of the integration over instantaneous intensity fluctuations to infinity, which further allows the adoption of well-known and tractable classical channel PDFs. This would provide very useful theoretical tools to conveniently investigate the impact of LEO-to-ground channel effects on the quantum channel transmittance as well as the QKD system performance. On the other hand, we will subsequently prove that the statistical mean of η that describes the fluctuating losses governed by a classical channel PDT is always within the domain \(\left[0,1\right]\), thus preserving the commutation relations.
Following mathematical descriptions as in classical channels, over a LEO satellite-to-ground link, the quantum channel transmittance η consists of three degradation factors including the deterministic loss due to absorption and scattering ηl, the random intensity fluctuations due to atmospheric turbulence Ia, and the random fraction of received power captured by a finite-size telescope considering pointing errors-induced fluctuations and beam broadening-induced geometrical loss ηp. Since Ia and ηp are statistically independent processes30, η can be formulated as
For zenith angles below 60° where the elongation effect is negligible and a practical quantum communications window can be carried out, ηl can be simply scaled as31
where ξ denotes the zenith angle and \({\tau }_{{{{{{{{\rm{zen}}}}}}}}}\in \left[0,1\right]\) is the deterministic transmission efficiency at zenith, which can be conveniently estimated by the popular MODTRAN code. In describing the random atmospheric turbulence Ia in the weak regime, the log-normal (LN) probability distribution is adopted, written as32
where \({\sigma }_{{{{{{{{\rm{R}}}}}}}}}^{2}\) denotes the Rytov variance for the satellite downlink path over the atmosphere, given as32
where λ denotes the wavelength of the optical beam, HOGS is the altitude of the OGS above sea level, Hatm is the maximum altitude where the atmosphere exists, \({C}_{{{{{{{{\rm{n}}}}}}}}}^{2}\,\left(h\right)\) is the altitude-dependent refractive index structure parameter profile. It is noted that the Rytov variance could be used as a figure of merit for the strength of turbulence, with \({\sigma }_{{{{{{{{\rm{R}}}}}}}}}^{2} < 1\) referring to weak turbulent media while \({\sigma }_{{{{{{{{\rm{R}}}}}}}}}^{2}=1\) and \({\sigma }_{{{{{{{{\rm{R}}}}}}}}}^{2} > 1\) indicating moderate and strong turbulence conditions, respectively33. From Eq. (6), the n-th statistical moment for the LN random variable is respectively expressed as30
The mean value of Ia can be derived from the first statistical moment by replacing n = 1 in Eq. (8), leading to \({\mathbb{E}}\left[{I}_{{{{{{{{\rm{a}}}}}}}}}\right]=1\).
In satellite-to-ground links, the optical beam is geometrically broadened when propagating over hundreds to thousands of kilometers, which results in a big beam footprint ranging from a few to hundreds of meters when reaching the OGS. The smaller the beam size, the more accuracy of pointing and tracking mechanisms is required. For quantum communications, this is very important as smaller beam footprints significantly reduce the losses when receiving through a finite-aperture telescope. However, mechanical errors in the tracking and pointing system and vibrations of the satellite and OGS platforms will cause the random beam jitters at the OGS, contributing to the fluctuating losses. It has been confirmed that beam wandering is not an issue since it is caused mostly by large-scale turbulence near the transmitter, which is not the case in satellite-to-ground downlinks32. Assuming a Gaussian beam, the normalized spatial distribution of the transmitted intensity at distance L from the transmitter is given as
where ρ denotes the radial vector from the beam center with \(\left\Vert \cdot \right\Vert\) the norm of a vector, and wL is the beam waist calculated at \(\exp \left(-2\right)\) at a distance L. Taking into account the beam diffraction and atmospheric turbulence-induced broadening, wL for a downlink path can be written as \({w}_{L}=W\sqrt{1+T}\), where W represents the beam waist due to pure diffraction for a collimated beam and T is the broadening coefficient due to turbulence, expressed as32
where k = 2π/λ, w0 = λ(πθ)−1 is the beam radius at the transmitter output aperture with θ the transmitted beam’s divergence half-angle, T is readily given as32
Assuming a circular receiving telescope aperture with opening area \({\mathbb{A}}\) and radius a, ηp can be written as34
where r denotes the radial vector representing random beam displacements. To this end, it is noteworthy that the definition of ηp in Eq. (12) is similar to the definition of channel transmittance in Eq. (3), representing the fraction of power collected when coupling the received beam to a finite receiving aperture. Due to the symmetry of the beam shape and receiver area, the characterization of ηp depends only on the radial jitter distance \(r=\left\Vert {{{{{{{\boldsymbol{r}}}}}}}}\right\Vert\). An accurate and widely-used approximation of ηp is readily given as34
where \({A}_{0}={\left[{{{{{{{\rm{erf}}}}}}}}\left(\nu \right)\right]}^{2}\) is the maximum fraction of collected power over the receiving aperture when there are no pointing errors (i.e., r = 0) that represents the deterministic geometrical loss, \(\nu =\frac{\sqrt{\pi }a}{\sqrt{2}{w}_{L}}\), \(\,{{\mbox{erf}}}\,\,\left(x\right)\,=\,\frac{2}{\sqrt{\pi }}\int\nolimits_{0}^{x}\exp \left(-{t}^{2}\right)\,{{\mbox{d}}}\,t\) is the Gauss error function, and wLeq is the equivalent beam-width calculated as
with wL calculated from Eqs. (10) and (11). This approximation is valid when wL > 6a, which is practically true for free-space laser communication systems. To derive a PDT for ηp, we need to find the distribution of r considering the random jitters in both the horizontal x and elevation y axes. Previous studies on quantum atmospheric channels have assumed that r follows a Gaussian distribution28,29, a Rayleigh distribution27,31, and a Rician distribution26. However, for the most general case, r should follow a four-parameter Beckmann distribution where the jitters in both x and y axes are two independent Gaussian random variables with different means (μx, μy) and variances (σx, σy)30. In fact, the four-parameter Beckmann is a versatile model that includes all special cases of pointing errors30, yet has never been applied in the quantum atmospheric channel. The distribution model of r following Beckmann distribution then reads as
It is noted that Eq. (15) is not only capable of characterizing the random displacements of the receiving optical beam but also that of the OGS due to tracking errors, since the random displacements in both the horizontal and vertical axes of the OGS telescope can also be considered as independent Gaussian random variables. From Eqs. (13) and (15), the first statistical moment of ηp is given as30
where \({\varphi }_{x}=\frac{{w}_{L{{{{{{{\rm{eq}}}}}}}}}}{2{\sigma }_{x}}\) and \({\varphi }_{y}=\frac{{w}_{L{{{{{{{\rm{eq}}}}}}}}}}{2{\sigma }_{y}}\) are the ratios between the equivalent beam-width and the beam-jitter variances for the horizontal x and vertical y directions, respectively. For strong pointing errors, i.e., σx, σy → ∞, we then have φx, φy → 0, and vice versa for weak pointing errors. From this relationship and Eq. (16), we can easily derive that
Since \({A}_{0}\in \left[0,1\right]\), from Eq. (17) we always have \({\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\in \left[0,1\right]\). From Eq. (4), the first statistical moment of η can be written as \({\mathbb{E}}\,[\eta ]={\eta }_{{{{{{{{\rm{l}}}}}}}}}{\mathbb{E}}\,[{I}_{{{{{{{{\rm{a}}}}}}}}}]{\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\)30. With \({\eta }_{{{{{{{{\rm{l}}}}}}}}}\in \left[0,1\right]\), \({\mathbb{E}}\,[{I}_{{{{{{{{\rm{a}}}}}}}}}]=1\), and \({\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\in \left[0,1\right]\), it is straightforward to confirm that \({\mathbb{E}}\,[\eta ] \in \left[0,1\right]\), which satisfies the commutation relations between sent and received quantum states.
Utilizing an accurate approximation of the Beckmann distribution by a Rayleigh distribution with a modified variance, Eq. (15) can be rewritten as35,
where \({\sigma }_{{{{{{{{\rm{mod}}}}}}}}}={\left(\frac{3{\mu }_{x}^{2}{\sigma }_{x}^{4}+3{\mu }_{y}^{2}{\sigma }_{y}^{4}+{\sigma }_{x}^{6}+{\sigma }_{y}^{6}}{2}\right)}^{1/3}\) is the modified beam-jitter variance approximation. Combining Eqs. (13) and (18), the probability distribution of ηp can be derived as35
where \({\varphi }_{{{{{{{{\rm{mod}}}}}}}}}=\frac{{w}_{L{{{{{{{\rm{eq}}}}}}}}}}{2{\sigma }_{{{{{{{{\rm{mod}}}}}}}}}}\) is the ratio between the equivalent beam width and the modified beam-jitter variance, \({A}_{{{{{{{{\rm{mod}}}}}}}}}\,\,=\,\,{A}_{0}G\) with \(G\,=\,\exp \left(\frac{1}{{\varphi }_{{{{{{{{\rm{mod}}}}}}}}}^{2}}\,-\,\frac{1}{2{\varphi }_{x}^{2}}\,-\,\frac{1}{2{\varphi }_{y}^{2}}\,-\,\frac{{\mu }_{x}^{2}}{2{\sigma }_{x}^{2}{\varphi }_{x}^{2}}\,-\,\frac{{\mu }_{y}^{2}}{2{\sigma }_{y}^{2}{\varphi }_{y}^{2}}\right)\). The probability distribution of η = ηlIaηp with Ia and ηp being statistically independent can be expressed as34
where \({f}_{{I}_{{{{{{{{\rm{a}}}}}}}}}}\left({I}_{{{{{{{{\rm{a}}}}}}}}}\right)\) follows Eq. (6) and \({f}_{{I}_{{{{{{{{\rm{a}}}}}}}}}}\left(\eta | {I}_{{{{{{{{\rm{a}}}}}}}}}\right)\) is the conditional probability given a turbulence state Ia, written as
where \({f}_{{\eta }_{{{{{{{{\rm{p}}}}}}}}}}\left(\cdot \right)\) follows Eq. (19). With the help of Eqs. (6) and (19), substituting Eq. (21) into Eq. (20), we arrive at
Applying (3.322.1) in36 to solve the integration in Eq. (22), the composite PDT model of η considering approximated Beckmann pointing errors with the LN turbulence can be respectively expressed in a closed-form expression as34
where \({{{{{{{\rm{erfc}}}}}}}}\,\left(x\right)\,=\,\frac{2}{\sqrt{\pi }}\,\int\nolimits_{x}^{\infty }\,\exp \left(-{t}^{2}\right)\,{{{{{{{\rm{d}}}}}}}}t\) is the complementary error function and \(\mu \,=\,\frac{{\sigma }_{{{{{{{{\rm{R}}}}}}}}}^{2}}{2}\,\left(1\,+\,2{\varphi }_{{{{{{{{\rm{mod}}}}}}}}}^{2}\right)\).
LEO satellite-to-ground atmospheric turbulence channel with receiver aperture-averaging effect
To quantify the strength of atmospheric turbulence-induced fluctuations on the received signal, the turbulence scintillation index (SI) denoted as \({\sigma }_{{{{{{{{\rm{SI}}}}}}}}}^{2}\) is usually utilized, which is the normalized variance of the turbulence channel coefficient Ia, expressed as32
Since space-to-ground communications experiences very high losses, a big telescope is often used at the OGS to increase the amount of captured power level. When the size of the OGS telescope is larger than the transverse correlation width, i.e., a parameter associated with the irradiance of a Gaussian-beam wave in the plane of the receiver, the aperture-averaging effect of scintillation can occur, where the SI is reduced with increasing aperture sizes32. For a typical satellite downlink propagation path below 60° zenith angle, the implied transverse correlation width is on the order of 7 ~ 10 cm, depending on wavelengths32. Our OGS telescope at NICT headquarters in Tokyo, Japan has a diameter D = 1 m, which is significantly larger than the typical downlink transverse correlation width, thus aperture-averaging effect is certainly applied. The SI for a satellite downlink with aperture-averaging is readily derived as32
where D (m) is the OGS telescope diameter, \({C}_{{{{{{{{\rm{n}}}}}}}}}^{2}\,\left(h\right)\) is defined in Eq. (7) and determined from the modified Hufnagel-Valley model for our OGS site as37
where MT = 0.2 is the modification factor, v (m/s) denotes the high-altitude root-mean-squared (rms) transverse wind speed in m/s, h is the altitude, A is the nominal refractive index structure parameter estimated near the ground varying from 10−17 to 10−13. The rms transverse wind speed v can be simply expressed for altitude above 5 km as32
where \(V\left(h\right)\) is the vertical altitude-dependent wind profile commonly described by the Greenwood model, which assumes a Gaussian profile with the peak at the tropopause layer, and the addition of a pseudo-wind component due to the LEO satellite motion for a zenith viewing angle, written as32
where ws (rad/s) is the slew rate at zenith of the optical beam associated with a satellite moving with respect to an observer on the ground, vg (m/s) is the ground wind speed, vT is the wind speed at tropopause, hT is the altitude of the tropopause, and LT is the thickness of the tropopause layer. Although Bufton’s work38 is often cited as the source for the wind profile in Eq. (28), there was no explicit wind model proposed by Bufton while the basic form of the model was evidently presented by Greenwood39. It is also important to note that hT = 9400 m, LT = 4800 m, and vT = 30 m/s in the Greenwood model, given that the zero altitude corresponds to a mean sea level altitude of 3048 m for the experiment site in Hawaii. When the model is applied to other experiment sites, the altitude of the tropopause should be revised as hT = 9400 + 3048 − HOGS. Another important point is that the altitude-dependent Greenwood wind profile in Eq. (28) implies that the optical system is pointed at zenith (ξ = 0°), however, actual zenith angles are usually higher for many practical satellite passes, thus the vertical altitude in the wind model should be rewritten for an arbitrary minimum zenith angle as
where \(h\,=\,{h}_{{{{{{{{\rm{slant}}}}}}}}}\cos \left({\xi }_{\min }\right)\) is the vertical altitude calculated from a varying slant distance hslant over the atmosphere and scaled at \({\xi }_{\min }\), with \({\xi }_{\min }\) the minimum zenith angle of the satellite pass. In Eq. (29), the slew rate ws is often calculated from the magnitude of the change in azimuth and elevation angles of the OGS telescope for a zenith over flight of the satellite. Nevertheless, this approach may contain OGS telescope tracking errors which results in an overestimation of the slew rate of the optical beam. We therefore propose to approximate the slew rate based on the satellite velocity and slant communication distance at \({\xi }_{\min }\) scaled to vertical distance at zenith, written as \({w}_{{{{{{{{\rm{s}}}}}}}}}\approx {v}_{{{{{{{{\rm{sat}}}}}}}}}/\left({L}_{\min }\cos \left({\xi }_{\min }\right)\right)\), where vsat is the satellite velocity and \({L}_{\min }\) is the satellite-OGS slant distance at \({\xi }_{\min }\). Finally, Eq. (27) can be rewritten as
where Hatm is re-defined as the maximum vertical altitude of the atmosphere scaled from the maximum slant path \({h}_{{{{{{{{\rm{slant,max}}}}}}}}}\) over the atmosphere at \({\xi }_{\min }\), which is assumed as \({h}_{{{{{{{{\rm{slant,max}}}}}}}}}=20000\) m in general for simplicity. As a result, \({H}_{{{{{{{{\rm{atm}}}}}}}}}=20000\cos \left({\xi }_{\min }\right)\). This implies that the vertical altitude-dependent wind profile in Eq. (30) is characterized for the altitudes between \(5000\cos \left({\xi }_{\min }\right)\) and \({H}_{{{{{{{{\rm{atm}}}}}}}}}=20000\cos \left({\xi }_{\min }\right)\). When \({\xi }_{\min }=0\), Eqs. (29) and (30) reduce to Eqs. (28) and (27), respectively, indicating the characterized altitudes between 5000 m and 20,000 m. It is noted that for the weak turbulence regime, the Rytov variance in Eq. (23) is approximately equivalent to the SI of the signal received at our 1-m OGS with the aperture-averaging effect, thus Eq. (23) is rewritten as
where \(\mu \,=\,\frac{{\sigma }_{{{{{{{{\rm{SI}}}}}}}}}^{2}\,\left(D\right)}{2}\,\left(1\,+\,2{\varphi }_{{{{{{{{\rm{mod}}}}}}}}}^{2}\right)\). Other parameters are the same as defined in Eq. (23).
On 5 August 2016, we performed the world’s first LEO-to-ground quantum-limited communication experiment using a 50-kg-class microsatellite, namely SOCRATES (Space Optical Communications Research Advanced Technology Satellite), and the 1-m OGS in Tokyo16. Figure 1a shows the zenith angle and satellite-OGS distance of the SOCRATES pass, during which the quantum-limited communication link was established for about 140 s as highlighted in red. In this section, we utilize the zenith angle and satellite-OGS distance data in Fig. 1a and Eq. (25) to theoretically investigate how the turbulence SI changes during a LEO satellite pass for our 1-m OGS. The zenith angle is limited to 60° for a practical quantum communications window with negligible elongation effects29,40. Figure 1b investigates the turbulence SI for two distinct levels of ground wind speeds, e.g., 1.5 m/s and 25 m/s respectively corresponding to light air and strong gale conditions in Beaufort wind force scale. In general, it is observed that the slew rate-induced pseudo-wind results in high rms transverse wind speeds, e.g., 127.18 m/s and 149.4 m/s for the two considered cases. These transverse wind speeds apparently affect the refractive structure index profile in Eq. (26), showing significant differences of SI values when the rms wind speed changes from 127.18 m/s to 149.4 m/s. In all cases, the SI attains higher values at high zenith angles (i.e., long satellite-OGS distances) and vice versa, and the SI values are always below 1 during the considered satellite pass, thus enabling the adoption of Eq. (31) in modeling the fluctuations due to the weak atmospheric turbulence and pointing errors. In Fig. 1c, we further investigate the impact of different values of ground turbulence refractive structure index A for the same zenith angle, e.g., at the smallest zenith angle of 31.45°. It is seen that the turbulence SI values nearly do not change when varying A, due to the aperture-averaging effect suppressing stronger fluctuations at higher A. In contrast, the rms transverse wind speed is the dominant factor that significantly affects the turbulence SI values, especially for LEO satellite downlinks due to the high slew rate of the optical beam, which is often neglected in many previous studies.
In a, zenith angle (solid navy-blue curve) and satellite-to-ground distance (dashed orange curve) are shown from the orbital data of SOCRATES satellite. The SOCRATES satellite was inserted in a Sun-synchronous near-circular sub-recurrent orbit at an altitude of 628 km with an inclination of 97.9° and a period of 97.4 min. Duration of established link is highlighted in red. In b, using the orbital data in a, the turbulence scintillation index (SI) for two different ground wind speeds (navy blue curves) and zenith angle (orange dotted curve) are plotted with ground turbulence refractive index A = 10−14 m−2/3. The solid navy-blue curve shows the turbulence SI when the ground wind speed vg = 1.5 m/s and root-mean-squared (rms) transverse wind speed v = 127.18 m/s, and the dashed navy-blue curve shows the turbulence SI when the ground wind speed vg = 25 m/s and rms transverse wind speed v = 149.4 m/s. In c, turbulence SI versus ground turbulence refractive index for two different wind speeds are plotted. The solid blue curve and the dashed red curve respectively depict the turbulence SI when the ground wind speeds vg = 1.5 m/s (i.e., rms transverse wind speed v = 127.18 m/s) and vg = 25 m/s (i.e., rms transverse wind speed v = 149.4 m/s). In b and c, given parameters include wavelength λ = 0.85 μm, optical ground station (OGS) altitude HOGS = 122 m, minimum zenith angle \({\xi }_{\min }=31.45\)°, minimum satellite-OGS distance \({L}_{\min }=744.5\) km, slew rate ws = 0.011 rad/s, and satellite velocity vsat = 7000 m/s.
Statistics of photon counting at the receiver
Assuming a photon counting interval T, the probability of counting n photons in a time interval [t0, t0 + T] can be expressed as a Poisson distribution, written as41
where q is the mean photon count given as41
where I(t) is the received intensity at the photodetector and s represents the detection efficiency. The mean photon count q in a counting interval at the receiver will experience fluctuations due to atmospheric turbulence and pointing errors in the physical channel. In our statistical analysis, we choose a counting interval T = 1 ms, which is assumed to be within the coherence time of channel fluctuations, thus the channel state can be considered constant and uncorrelated with the previous value. Now, Eq. (33) can be written as q = sIT, where I = I0η with I0 the intensity at the transmitter and η defined in Eq. (4). As a result, the PDT of q follows the mathematical form of the PDT of η, which is derived in Eq. (31). Since q is the mean photon count at the receiver after suffering from the total channel loss, we need to normalize the PDT to the statistical mean of the channel transmittance to characterize the fluctuations of q, which is derived as Eq. (48) in Methods, “Normalized PDT for statistical verifications”. With the help of Eq. (48), the PDT of the mean photon count q can be formulated as
where \(\langle q \rangle\) denotes the measured mean photon number in a counting interval T = 1 ms at the receiver41,42. Since q fluctuates according to Eq. (34), the probability of counting n photons in Eq. (32) can be replaced by the Mandel formula41,42, written as
and we define Eq. (35) with \(f\,\left(q\right)\) in Eq. (34) as Mandel with LN and approximated Beckmann to differentiate with previously verified photon-counting statistics with \(f\,\left(q\right)\) described as a LN model41,42, i.e., Mandel with LN. It is clearly seen from Eq. (35) that the fluctuations in p(n) come from both the Poisson-count distribution and the channel distribution governed by Eq. (34). The Poisson-count distribution can be considered as the photon-count shot noise, which always exists even in channels with no fluctuations. To verify the PDT of channel fluctuations, we aim to verify the photon-counting probability in Eq. (35), i.e., Mandel with LN and approximated Beckmann, with the histogram of photon-count data in each interval of T = 1 ms. The integral in Eq. (35) can be evaluated by using a Gauss–Laguerre quadrature approximation43, i.e., \(\int\nolimits_{0}^{\infty }\exp (-x)f(x)\,{{\mbox{d}}}\,x\approx \mathop{\sum }\nolimits_{j = 1}^{J}{\omega }_{j}f({x}_{j})\) with ωj and xj the weight factors and the abscissas of Laguerre polynomials, and J the number of Laguerre polynomials. Finally, Eq. (35) can be expressed as
It should be noted that the photon-counting probability in previous studies41,42, i.e., Mandel with LN, can be similarly evaluated using the Gauss–Laguerre quadrature approximation as in Eq. (36). Details of the derivation are presented in Supplementary Note 1.
Experimental system descriptions and data preparations
In our quantum-limited communication experiment, a small 5.9-kg optical terminal, namely SOTA (Small Optical TrAnsponder), was installed onboard SOCRATES, transmitting pseudo-random binary sequences (PRBSs) of non-orthogonal linearly polarized states using a wavelength of 0.8 μm at a repetition rate of 10 MHz to the 1-m OGS in Tokyo, Japan16. The polarized weak-coherent states were then received by the single-photon detectors with a minimum QBER of less than 5% in a quantum-limited communication experiment that emulates the B92 QKD protocol44. Figure 2a shows a picture of SOTA housing two linearly polarized laser diodes (Tx2 and Tx3) used for the quantum-limited communication experiment at 0.8 μm and a circularly polarized laser diode at 1.549 μm used for satellite tracking and classical measurements. Figure 2b illustrates the actual separation angle at −44∘ of Tx2 and Tx3. Tx2 emits a horizontal polarized pulse (H) and Tx3 emits a −45∘ polarized pulse, which constitute the sequences of H- and −45∘-polarization states. The divergence angles of optical beams transmitted through Tx2 and Tx3 are 970 μrad and 880 μrad measured at −3 dB full width, respectively. Figure 2c, d respectively describe the structure and components of the 1-m OGS’s telescope and quantum receiver for detecting the photons transmitted from Tx2 and Tx3. The SPCMs used in the quantum receiver are Si avalanche photodiodes, where the received photon counts were time-tagged at a resolution of 1 picosecond (ps). Finally, Fig. 2e shows a 5-cm aperture telescope focusing the receiving light onto a 1-mm InGaAs-PIN photodetector for classical light measurements, coaxially installed on the 1-m aperture telescope. The 1.549 μm classical beam is transmitted from Tx4 with a divergence angle of ~223 μrad and received through the 5-cm aperture detector resulting in voltage signals, which were recorded at 20 kHz to cover all high-frequency components of fluctuations.
a SOTA terminal (18 cm width × 11 cm depth × 27 cm height). b Configuration of the two linearly polarized laser diodes Tx2 and Tx3 equipped in SOTA. c OGS' 1-m aperture telescope. d Quantum receiver for detecting 0.8 μm quantum signals transmitted from Tx2 and Tx3. The 1.549 μm circularly polarized beam path after the 1-m telescope was for satellite tracking and separated from the 0.8 μm path by using a dichroic mirror. e 5-cm aperture detector coaxially installed on the telescope to detect 1.549 μm classical signals transmitted from Tx4 for classical measurements. DM: dichroic mirror, PD: photodetector; IR: infrared; BS: beam splitter; PBS: polarizing beam splitter; HWP: half-wave plate; SPCM: single-photon counter module. The four SPCMs are Si avalanche photodiodes with a detection timing resolution of 250 ps, and the total noise count rate (dark counts and background) from all SPCMs is 0.9 count/ms. Detector's afterpulse probability is 0.5%. Received photon counts were time-tagged by a time-interval analyzer with a timing resolution of 1 ps, generating a time-tagged photon-count sequence for each SPCM. Each detected bit from the received photon-count sequence is time-tagged with a resolution of 1 ns, including the timing jitter of the SPCM and other electronics.
For pointing, tracking and acquisition process, the OGS emitted a high-power (20 W) wide-beam (300-μrad divergence angle) beacon at 1.064 μm wavelength towards the predicted position of the satellite according to its orbital information. When the satellite acquires the beacon signal, the downlink starts while the satellite keeps tracking the beacon. A schematic of the path of the received beacon beam in the SOTA optics is depicted in Supplementary Fig. 1. It is seen from Supplementary Fig. 1 that the pointing accuracy of Tx2 and Tx3 in our quantum-limited experiment was solely based on a coarse quadrant detector (QD) serving as a coarse pointing sensor (CPS) that controls the pointing direction of SOTA’s 2-axis gimbal, while that of Tx4 relied on both the coarse-pointing 2-axis gimbal and a closed-loop system using a fine QD as a fine-pointing sensor (FPS) and a fine-pointing mirror (FPM) to stabilize and finely control the pointing direction of the beam through Tx4. For Tx2 and Tx3, pointing errors may come from the residual error of the coarse pointing due to gimbal and satellite platform vibrations and detection noise of the coarse QD. For Tx4, pointing errors may arise from both the FPS and CPS noises, and satellite platform vibrations. It should be emphasized that these sources of pointing errors are generated from the electronic and mechanical parts with the fundamental frequency response of about 60 Hz for SOTA’s pointing and tracking system. As a reference, vibration frequency was mainly below 30 Hz in Micius satellite45.
During the SOCRATES pass on 5 August 2016, we select a 12-s duration, 22:59:21–22:59:33 (JST), from the total 140 s of the established link for further statistical analyses, since during this period the pointing systems on the satellite and the OGS are most stable after the link acquisition process for both classical and quantum links received by the 5-cm detector and 1-m OGS, respectively. In addition, the movements of the position and orientation of SOTA gimbal and OGS reference frame were best aligned for the quantum link, which gives a valid estimation of the QBER16. For the physical channel analyses, we first investigate the spectrogram of the received voltage at the 5-cm aperture detector to discern the frequency responses of atmospheric turbulence- and pointing errors-induced fluctuations over time, while the PDT in Eq. (31) will be used to statistically verify the quantum channels in LEO satellite-to-ground links, using photon-count data measured at the 1-m OGS. Supplementary Fig. 2 first depicts the SOCRATES pass information including the zenith angle and satellite-OGS distance for the selected 12-s data (22:59:21-22:59:33 JST on 5 August 2016), and Supplementary Fig. 3 and Fig. 3 show 12-s data of the received voltage from the 5-cm aperture detector and the photon counts from all four SPCMs in the quantum receiver after the 1-m aperture telescope, respectively.
Since the data in Supplementary Fig. 3 were sampled at 20 kHz (20,000 samples per second), we were able to investigate the frequency response up to 10 kHz for the spectrogram, which is defined as an intensity plot of the short-time Fourier transform magnitude, i.e., a sequence of fast Fourier transforms of windowed data segments with the windows overlapped in time46. Supplementary Fig. 4 depicts the spectrogram of the received voltage data over 12 s with windowed sections of 128 samples and 120 samples of overlap between adjoining sections for frequency up to 4 kHz, as the energy contained in higher frequencies becomes very small, indicating negligible effects. As seen in Supplementary Fig. 4, there are clearly two ranges of frequency responses, including one up to 60 Hz and one ranging from 60 to 200 Hz to around 1 kHz. It is evident that the energy concentrated mainly in the frequencies below 60 Hz, matching the frequency response of SOTA’s pointing-and-tracking system and indicating dominant effect on the signal fluctuations. Concurrently, higher frequencies indicate the existence of turbulence-induced fluctuations, with energy contained mostly in the frequencies up to 200 Hz with some parts intermittently appear around 1 kHz at smaller magnitudes, indicating weak fluctuations due to turbulence. Due to the difference in frequency responses of fluctuations from pointing-and-tracking system and atmospheric turbulence, random variables describing these effects can be considered independence, leading to the final form of the PDT as in Eq. (31).
As the LEO satellite is constantly moving along its orbit with varying zenith angles and distances towards the OGS, we will divide the raw photon-count data in Fig. 3 into twelve 1-s datasets so that for each second the channel conditions (depending on zenith angles and distances) can be assumed to be approximately unchanged. The probability distribution in Eq. (36) is then applied to fit with the histogram data of photon counts from all twelve datasets. The photon-count data in Fig. 3 were grouped at a counting interval T = 1 ms time bin42, making 1000 samples per a 1-s dataset. This implies that all fluctuations up to 1 kHz that change the number of counts every ms could be taken into account. It is important to note that the background and detector’s noise counts are not removed from the total photon counts in our datasets. However, as specified in the caption of Fig. 2, the average noise count contribution is very small, thus we could reasonably assume that it does not considerably affect the statistical characteristics of photon-count fluctuations due to turbulence and pointing errors. It should be further highlighted that there has been no previous study verifying a statistical PDT with actual experimental LEO satellite-to-ground photon-count data. In the literature, the statistical analysis of photon counts over quantum channels has only been verified with data from horizontal links41,42, certifying the accuracy of the LN turbulence model. However, previous statistical studies41,42 did not take into account the inevitable contribution from pointing errors, thus omitting the actual behaviors of the composite channels. Our statistical verification study in this paper fills in this gap and contributes to the designs and modeling of satellite-to-ground quantum communication systems.
Photon-count statistical verifications
For statistical verifications of the theoretical PDT, we utilize the goodness of fit (GoF) R2 statistical metric commonly used to test the distribution’s fitness, which is mathematically expressed as
where N denotes the number of bins of the histogram data, fm,i and fp,i are respectively the measured and predicted occurence of the i-th bin, and \(\bar{f}=\frac{\mathop{\sum }\nolimits_{i = 1}^{N}{f}_{{{{{{{{\rm{m}}}}}}}},i}}{N}\) is the mean of the measured data. R2 → 1 determines that the probability distribution model is considered to better fit the experimental data and vice versa. To quantify the strength of the random fluctuations of the experimental data, the same definition of SI as in Eq. (24) is adopted, which is the normalized variance of the measured data, mathematically expressed as
where M is the number of data samples and dm,i is the value of the i-th sample of the measured data.
Figure 4 illustrates the histograms of twelve 1-second photon-count datasets and their corresponding fitted probability distribution. It is noted that the number of histogram bins N is chosen by an automatic binning algorithm that returns bins with a specific uniform width, which cover the range of elements in each dataset and reveal the underlying shape of the distribution. The bin width in each dataset is specified in the caption of Fig. 4. Table 1 is provided for the examination of GoF and fitting parameters of the channel PDT. Since the SI of all datasets is well below 1 as seen in Table 1, the atmospheric turbulence is apparently in weak conditions, thus we aim to verify the Mandel with LN & approximated Beckmann model, in comparison with the Mandel with LN model validated in previous studies41,42, for the satellite-to-ground quantum channels under weak turbulence regimes. It is also noticed that there is a considerable discrepancy between \({\sigma }_{{{{{{{{\rm{SI}}}}}}}},\exp }^{2}\) and \({\sigma }_{{{{{{{{\rm{SI}}}}}}}}}^{2}\,\left(D\right)\). This is because \({\sigma }_{{{{{{{{\rm{SI}}}}}}}}}^{2}\,\left(D\right)\) merely quantifies the strength of the atmospheric turbulence-induced fluctuations, while \({\sigma }_{{{{{{{{\rm{SI}}}}}}}},\exp }^{2}\) further includes Poisson fluctuations in the photon detection process. This also highlights the significant contribution of Poisson shot noise due to the quantized nature of the photon detection process, especially for small numbers of photon counts in our datasets. More specifically, Supplementary Fig. 5 quantifies the Poisson noise percentage, which is calculated as a ratio of the standard deviation of Poisson distribution to that of the measured photon counts in each dataset. The standard deviation of Poisson distribution is equal to the square root of the mean number of photon counts. It is seen that the Poisson noise percentage is more than 40% for datasets with mean photon counts below 55. It is also observed that the Poisson noise percentage is inversely proportional to the mean number of photon counts. Interestingly, while the mean counts are similar in datasets 1 and 6, their Poisson noise percentages are still different. This is due to the distinct influences of channel-induced fluctuations with \({\sigma }_{{{{{{{{\rm{SI}}}}}}}}}^{2}\,\left(D\right)\) and \({\varphi }_{{{{{{{{\rm{mod}}}}}}}}}\) in dataset 1 being more severe than that in dataset 6, leading to a lower Poisson noise percentage in dataset 1. This confirms that the Poisson noise percentage is lower in the dataset with stronger channel-induced fluctuations and vice versa, given a similar mean number of photon counts.
Each dataset contains the photon-count data during 1 s with a counting interval of 1 millisecond. From a to l, the gray bars represent histograms of the photon-count data, where the number of histogram bins is chosen by an automatic binning algorithm that returns bins with a specific uniform width, which cover the range of elements in each dataset and reveal the underlying shape of the distribution. The dashed-dotted blue curve with triangle markers depicts the fitted Mandel with log-normal (LN) distribution, and the solid red curve with square markers shows the fitted Mandel with LN and approximated Beckmann distribution. Eq. (S3) in Supplementary Note 1 and Eq. (36) with the number of Laguerre polynomials J = 30 are respectively used to plot the Mandel with LN and the Mandel with LN and approximated Beckmann distributions. a dataset 1, bin width = 1. b dataset 2, bin width = 1. c dataset 3, bin width = 5. d dataset 4, bin width = 3. e dataset 5, bin width = 1. f dataset 6, bin width = 1. g dataset 7, bin width = 1. h dataset 8, bin width = 3. i dataset 9, bin width = 1. j dataset 10, bin width = 3. k dataset 11, bin width = 5. l dataset 12, bin width = 5.
In accordance with results from previous studies41,42, the Mandel with LN model, in general, shows a good fit with the histogram data, giving GoF R2 in the range from 0.93922 to 0.99276 across all datasets. Nevertheless, the Mandel with LN model can only be considered as a good approximation, and does not fully describe the true physical effects of the fluctuating channel, which also constitutes the random fluctuations from pointing errors. This fact has been demonstrated further from the GoF of the Mandel with LN & approximated Beckmann model, which fully describes the true nature of the random fluctuations. The Mandel with LN & approximated Beckmann model generally provides a GoF R2 with a higher accuracy or at least approximately the same accuracy compared to the Mandel with LN model. Although the accuracy improvement seems small, e.g., less than 1%, it helps to better describe the statistical mean of channel fluctuations and separately estimate the impacts of turbulence and pointing errors, which is crucial for security analyses of quantum communication systems. Regarding the fitting parameter of pointing errors, it is seen that \({\varphi }_{{{{{{{{\rm{mod}}}}}}}}}\) varies from 4.0422 to 5.4079. The pointing errors represent geometrical losses due to the wide beam footprints associated with the random beam jitters, resulting in the random fluctuating losses, which significantly affect the fractions of photons arrived at the OGS. The variety of \({\varphi }_{{{{{{{{\rm{mod}}}}}}}}}\) logically explains additional random contributions to the abrupt changes of the received photon counts in Fig. 3, which could be the consequences of different pointing-error levels during 12 s due to the coarse tracking and pointing from SOTA Tx2 and Tx3. Thanks to the high GoF metric and the versatility in characterizing various pointing-error levels, the Mandel with LN & approximated Beckmann model in Eq. (36) becomes a validated statistical model for characterizing the received photon-count fluctuations. Consequently, the LN & approximated Beckmann model in Eq. (31) is therefore verified for characterizing quantum atmospheric channels, taking into account deterministic losses and random fluctuations due to both atmospheric turbulence and pointing errors.
Application in decoy-state efficient BB84 QKD systems
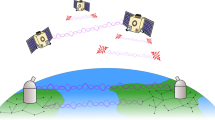
Over the past few years, small satellite platforms, i.e., CubeSats in particular, have attracted much attention for operations in LEO as an alternative to traditional, large satellite platforms due to the relatively low cost and recent synergistic advances in the miniaturization of both satellite and quantum communication systems. Various projects have been planned to realize quantum communications using CubeSats, including 3U-CubeSats’ uplink47 and downlink48, 6U-CubeSats’ downlinks49,50, and 12U-CubeSat’s uplink51. With the realization of quantum communications in both uplink and downlink, a future of space quantum networks relying on LEO constellations of CubeSats could become feasible, serving as a secure communication backbone for ground networks with increased coverage and link availability at a global scale. To further assist the quantum system design and mission planning, we aim to investigate the performance of a space QKD link using the verified PDT model that characterizes physical effects of quantum atmospheric channels and CubeSat’s generalized pointing errors, which have not been considered in previous studies47,48,49,50,51.
Capitalizing on the verified LN & approximated Beckmann channel model, in this section, we will proceed to apply this model on the performance investigation of a decoy-state efficient BB84 QKD protocol with optimized parameters considering finite-key effects52 over a LEO-to-ground downlink using a 6U-CubeSat platform. The decoy-state efficient BB84 protocol is preferred since it is able to detect photon-number-splitting eavesdropping and enables high-key-rate QKD using weak-coherent pulses over large distances53. Due to different design constraints, SOTA terminal was limited to very small transmitting apertures, ranging from 0.6 to 5 cm, thus resulting in a big divergence angle in the order of hundreds of μrad. For example, at 744-km distance and with Tx2 divergence angle of 970 μrad measured at −3 dB full width, the beam footprint at the OGS is about 721.68 m. This causes a huge geometrical loss when receiving through our 1-m OGS, e.g., ~−57.167 dB loss. With the experience from SOTA, we will make several improvements in future satellite QKD experiments. Particularly, for the future QKD realization from a 6U-CubeSat, we opt to develop a miniaturized lasercom terminal, namely CubeSOTA, which is capable of emitting laser beams with a small divergence angle and supported by a fine-pointing mechanism. Figure 5 illustrates a 6U-CubeSat platform carrying the CubeSOTA terminal for LEO-to-ground quantum communications with NICT’s OGS. The CubeSOTA terminal54 hosts a 9-cm aperture Cassegrain telescope with a central obscuration of 2.7 cm that produces a diffraction-limited full-angle divergence of 33 μrad at \(\exp \left(-2\right)\) of the Gaussian beam profile (i.e., 20 μrad at −3 dB full width). Assuming the same 744-km distance and divergence angle of 20 μrad at −3 dB full width, CubeSOTA could produce a beam footprint as small as ~14.88 m in diameter, which should significantly reduce the geometrical loss by ~33.7 dB compared to SOTA when receiving through the 1-m OGS. With such a narrow beam, a fine-pointing system consisting of FPS and FPM is required to enhance the pointing accuracy. Nevertheless, unexpected mechanical errors from the fine-pointing system and excessive vibrations from the satellite platform will still cause random beam jitters at the OGS. It is also noteworthy that when the Gaussian beam with a central obscuration in the near field is transmitted, it still results in a Gaussian diffraction-limited irradiance profile in the far field, which has been verified by experiment and wave-optics simulation55.
Table 2, unless otherwise noted, summarizes main link and system parameters of the considered decoy-state efficient BB84 QKD protocol. The beam-jitters’ means and variances at the OGS due to pointing errors, i.e., (μx, μy, σx, σy) in Eq. (31), are related to the corresponding parameters of angle-jitters, i.e., (\({\mu }_{{\theta }_{x}},{\mu }_{{\theta }_{y}},{\sigma }_{{\theta }_{x}},{\sigma }_{{\theta }_{y}}\)), at CubeSOTA transmitting aperture by \({\mu }_{x}\,=\,{\mu }_{{\theta }_{x}}L,{\mu }_{y}\,=\,{\mu }_{{\theta }_{y}}L,{\sigma }_{x}\,=\,{\sigma }_{{\theta }_{x}}L,{\sigma }_{y}\,=\,{\sigma }_{{\theta }_{y}}L\) with θ defined in Table 2. We also define three levels of pointing errors, including weak (\({\mu }_{{\theta }_{x}}\,=\,{\mu }_{{\theta }_{y}}\,=\,0\), \({\sigma }_{{\theta }_{x}}\,=\,{\sigma }_{{\theta }_{y}}\,=\,\theta /5\)), moderate (\({\mu }_{{\theta }_{x}}\,=\,\theta /5\), \({\mu }_{{\theta }_{y}}\,=\,\theta /3\), \({\sigma }_{{\theta }_{x}}\,=\,{\sigma }_{{\theta }_{y}}=\theta /2\)), and strong (\({\mu }_{{\theta }_{x}}\,=\,\theta /5\), \({\mu }_{{\theta }_{y}}\,=\,\theta /3\), \({\sigma }_{{\theta }_{x}}\,=\,\theta /1.5\), \({\sigma }_{{\theta }_{y}}\,=\,\theta /2\)) conditions. The equivalent beam-width (i.e., beam radius) at the OGS can be calculated as in Eq. (14). Figure 6a illustrates the pointing-error beam-jitter variance, i.e., \({\sigma }_{{{{{{{{\rm{mod}}}}}}}}}\) in Eq. (18), for the three defined pointing-error levels versus the beam-footprint diameter at the OGS for the LEO satellite pass in Fig. 1a. It is observed that both the beam-footprint diameter and beam-jitter variance are larger at high zenith angles due to the longer propagation distances from the satellite to the OGS. The ratio between the equivalent beam-width and the beam-jitter variance, i.e., \({\varphi }_{{{{{{{{\rm{mod}}}}}}}}}\) defined in Eq. (19), is however almost unchanged, due to the proportional increasing and decreasing of beam sizes and jitters. In addition, when increasing the ground wind speed from 1.5 to 25 m/s (i.e., increasing turbulence SI), the beam-footprint diameter is almost unaltered. This is because the turbulence-induced beam broadening coefficient T in Eq. (11) is very small over the downlink atmosphere, thus the long-term spot size for the downlink beam is essentially the same as its diffractive spot size32, given the zenith angles in our satellite pass. To this end, we could conclude that turbulence has a negligible influence on the channel transmittance, and the mean channel loss merely depends on the severity of the satellite’s pointing errors. Figure 6b, c then reveals the mean channel loss \({\mathbb{E}}\,[\eta ]={\eta }_{{{{{{{{\rm{l}}}}}}}}}{\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\) and total system loss equivalent to \({\eta }_{{{{{{{{\rm{TX}}}}}}}}}{\eta }_{\det }{\eta }_{{{{{{{{\rm{l}}}}}}}}}{\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\) with ηTX and \({\eta }_{\det }\) defined in Table 2, for different pointing-error levels. For the sake of comparisons, we also show the case of no fluctuations (i.e., no turbulence and pointing errors), where the channel and system losses can be similarly derived with \({\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\) replaced by ηp = A0, with A0 defined in Eq. (13).
Using data from the satellite pass in Fig. 1a, we theoretically investigate the pointing-error beam jitters and losses. In a, we plot the beam-jitter variances with different pointing-error levels versus the received beam-footprint diameter under different ground wind speeds. The footprint diameter is two times the equivalent beam-width (i.e., beam radius) at the ground station calculated as in Eq. (14), with the radius of the receiving telescope aperture a = 0.5 m. The beam-jitter variance, i.e., \({\sigma }_{{{{{{{{\rm{mod}}}}}}}}}\), is calculated by Eq. (18). The solid, dashed-dotted, and dashed navy-blue curves indicate the weak, moderate, and strong pointing errors, respectively. The dotted orange curve and the orange curve with round markers represent the footprint diameters when the ground wind speeds vg = 1.5 m/s and vg = 25 m/s, respectively. In b, c, the mean channel loss and total system loss are respectively investigated versus zenith angle under different pointing-error levels and compared with the case of no fluctuations. The solid, dashed, dashed-dotted, and dotted navy-blue curves indicate losses under no fluctuations, weak, moderate, and strong pointing errors, respectively. The solid orange curve shows the zenith angle during the satellite pass. From a to c, the three levels of pointing errors are defined as weak (\({\mu }_{{\theta }_{x}}\,=\,{\mu }_{{\theta }_{y}}\,=\,0\), \({\sigma }_{{\theta }_{x}}\,=\,{\sigma }_{{\theta }_{y}}\,=\,\theta /5\)), moderate (\({\mu }_{{\theta }_{x}}\,=\,\theta /5\), \({\mu }_{{\theta }_{y}}\,=\,\theta /3\), \({\sigma }_{{\theta }_{x}}\,=\,{\sigma }_{{\theta }_{y}}=\theta /2\)), and strong (\({\mu }_{{\theta }_{x}}\,=\,\theta /5\), \({\mu }_{{\theta }_{y}}\,=\,\theta /3\), \({\sigma }_{{\theta }_{x}}\,=\,\theta /1.5\), \({\sigma }_{{\theta }_{y}}\,=\,\theta /2\)). For the case of no fluctuations (i.e., no turbulence and pointing errors), the channel and system losses can be derived with \({\mathbb{E}}\,\left[{\eta }_{{{{{{{{\rm{p}}}}}}}}}\right]\) replaced by ηp = A0, with A0 defined in Eq. (13).
Taking into account all the physical effects, we will numerically investigate the QBER and SKL of a decoy-state efficient BB84 QKD system with practical finite-key analyses implemented over the CubeSOTA-OGS link, following the theoretical framework and simulation software provided by Sidhu et al. 52 (for details, please see Methods, “QBER and SKL with finite-key effects”). We first fix the transmission duration of 365 s and optimize the protocol parameters to use during the pass, then iterate over the window duration to find the highest resulting SKL. The time window duration denoted as Δt is defined as the transmission half-window duration t0 + Δt where t0 = 0 represents the time instant corresponding to the lowest zenith angle. For each Δt, the optimal protocol parameters that maximize the SKL extractable from the data block are generated by the simulation software. To compare systems with different losses, the system loss metric \({\eta }_{{{{{{{{\rm{loss}}}}}}}}}^{{{{{{{{\rm{sys}}}}}}}}}\) is used and defined as the loss value achieved at the lowest zenith angle, i.e., the minimum system loss in the satellite pass. Figure 7a re-presents the total system loss given in Fig. 6c versus the time window duration Δt of 182 s and the \({\eta }_{{{{{{{{\rm{loss}}}}}}}}}^{{{{{{{{\rm{sys}}}}}}}}}\) values corresponding to systems affected by different physical conditions are also added. In Fig. 7b, c, we show the SKL and QBER as a function of Δt for different \({\eta }_{{{{{{{{\rm{loss}}}}}}}}}^{{{{{{{{\rm{sys}}}}}}}}}\) values, respectively. For each value of Δt, the SKL extractable from received data within the full-window duration of 2Δt is optimized over protocol parameters defined in Table 2. It is observed that increasing Δt beyond 150 s leads to a minor SKL improvement for all considered systems, however, it is still desirable to construct keys from the maximum achievable data up to the maximum zenith angle of 60° for a practical communications window. It is noted that including data from higher zenith angles is detrimental to the SKL if \({\eta }_{{{{{{{{\rm{loss}}}}}}}}}^{{{{{{{{\rm{sys}}}}}}}}}\) is as large as −40 dB52, thus careful considerations of Δt for collecting data should be given depending on the \({\eta }_{{{{{{{{\rm{loss}}}}}}}}}^{{{{{{{{\rm{sys}}}}}}}}}\) value of the system. As expected in Fig. 7c, the QBER is gradually increased at higher values of Δt, as more data are collected over higher losses at large zenith angles. The non-smooth QBER appears because it is not the objective function of the optimization52. Optimized parameters as a function of Δt for different physical link conditions are finally shown in Fig. 7d–g. It is observed that PX decreases with increasing \({\eta }_{{{{{{{{\rm{loss}}}}}}}}}^{{{{{{{{\rm{sys}}}}}}}}}\) from Fig. 7d to Fig. 7g. This is because we need to collect more Z-basis events by increasing the probability (1 − PX) to compensate for greater statistical fluctuations that cause worse estimations of the X-basis vacuum and single-photon yields and phase error rate, as fewer photons are detected with increasing system loss. This leads to an important conclusion that better bounds on the parameter estimations from finite statistics dominate the SKL compared with the raw key length when \({\eta }_{{{{{{{{\rm{loss}}}}}}}}}^{{{{{{{{\rm{sys}}}}}}}}}\) is large52.
The quantum bit error rate (QBER) and secret-key length (SKL) are investigated for a decoy-state efficient BB84 QKD protocol with finite-key analyses. The time window duration denoted as Δt is defined as the transmission half-window duration t0 + Δt where t0 = 0 represents the time instant corresponding to the lowest zenith angle. In a, the total system loss given in Fig. 6c is re-presented versus the time window duration Δt of 182 s, and the \({\eta }_{{{{{{{{\rm{loss}}}}}}}}}^{{{{{{{{\rm{sys}}}}}}}}}\) values corresponding to systems affected by different physical conditions are also added. The solid, dashed, dashed-dotted, and dotted navy-blue curves indicate losses under no fluctuations, weak, moderate, and strong pointing errors, respectively. In b-c, SKL and QBER are shown as a function of Δt for different \({\eta }_{{{{{{{{\rm{loss}}}}}}}}}^{{{{{{{{\rm{sys}}}}}}}}}\) values, respectively. For each value of Δt, the SKL extractable from received data within the full-window duration of 2Δt is optimized over protocol parameters defined in Table 2. The solid, dashed, dashed-dotted, and dotted navy-blue and orange curves indicate the SKL and QBER under no fluctuations, weak, moderate, and strong pointing errors, respectively. In d–g, we respectively show the optimized parameters as a function of Δt for different physical link conditions including no fluctuations, weak, moderate, and strong pointing errors. The solid, dashed, dotted, and dashed-dotted navy-blue curves indicate parameters PX, \({P}_{{\mu }_{1}}\), \({P}_{{\mu }_{2}}\), \({P}_{{\mu }_{3}}\), respectively. The solid and dashed orange curves indicate parameters μ1 and μ2, respectively. All parameters are defined in Table 2.
Photon-count predictions using an LSTM RNN
For quantum communications, it is of critical importance to attain a high signal-to-noise ratio (SNR), since the probability of detecting the correct state, i.e., the fidelity denoted as F, depends on the SNR as42
where the SNR is defined as
with Ns the average number of detected photons and Nn the average amount of noise from dark counts and background radiation. Due to this fact, an idea of exploiting channel fluctuations by acquiring the single photons only at the particular moments when the fluctuations increase the channel transmission above a threshold was proposed42. This technique is particularly helpful in cases of strong fluctuations and high noise, however, at the cost of decreasing the overall photon counts in a given time. This is because some threshold selections above the average photon counts are imposed, thus considering only the duration of events with over-threshold counting. To exploit information of the instantaneous transmission of the quantum channel, a probing channel by means of a classical signal is required42. To avoid the need of a dedicated classical channel and accelerate real-time data processing, we propose the application of deep learning for predicting the quantum atmospheric channel fluctuations through the received photon counts, thus avoiding the need of classical-channel probing and post-processing. In the future space QKD networks where many small satellites and ground stations are interconnected by QKD links, the amount of data for post-processing becomes extremely large, causing significant delays in the networks for the estimation and optimization of quantum links. Deep learning-based algorithms, therefore, stand out as promising solutions to realize a real-time autonomous operation of the QKD networks. One of the direct applications is to predict the instantaneous channel transmittance, then the predicted channel transmittance could be automatically inputted to an operating software to perform real-time system optimizations and configurations.
In this paper, an LSTM RNN will be used to train a portion of the received photon counts over a period of time and predict the future received data, thereby revealing the channel transmittance fluctuations. We will present results to show the potential performance of the LSTM RNN using the photon-count data from the SOTA experiment campaign on 5 August 2016. In particular, we choose a 1-minute duration of photon counts ~22:59:00−23:00:00 (JST) with counting interval of 1 ms. The reason for not using the whole dataset during the complete pass is due to the fact that photon counts at the beginning of the pass were affected by the unstable tracking during the link acquisition process, not the physical channel conditions. In addition, because we did not track the polarization angle of SOTA, but established the polarization reference frame by post-processing, the polarizations were best aligned during the chosen 1-min duration16.
A standard neural network consists of an input layer describing the input features, a number of hidden layers each containing a number of hidden units for combining and weighting the input values by activation functions to produce new values, and an output layer for making a prediction decision using the values computed in the hidden layers. An RNN is a type of neural network where the outputs from previous time steps are taken as the inputs for the current time step at a hidden unit. However, basic RNNs suffer from the vanishing gradient problem, i.e., as the weight receives an update proportional to the partial derivative of the error function with respect to the current weight in each iteration of training, the gradient decreases as the number of layers increases and becomes vanishingly small, thus preventing the learning of the network. Fortunately, LSTM RNNs have emerged to solve this problem56, enabling a wide range of applications in various fields57,58,59. Recently, an LSTM network has been applied to predict the variations of phase voltage in a Faraday-Michelson interferometer-based BB84 QKD system60. However, the effectiveness of the LSTM RNN in predicting the received photon counts over a LEO satellite-to-ground quantum atmospheric channel has never been explored in the literature and our results aim to fill in this gap. Supplementary Fig. 6 illustrates an unfolding RNN with an LSTM hidden unit architecture, which includes a memory cell, an input gate, an output gate, and a forget gate, where the memory cell remembers values over arbitrary time intervals and the three gates regulate the flow of information into and out of the cell. With this architecture, the LSTM unit could maintain long-standing relevant information and discard irrelevant information in a time series.
Let \({{{{{{{\mathbf{x}}}}}}}}={\left[{x}_{1},{x}_{2},\ldots ,{x}_{T}\right]}^{{{{{{{{\rm{T}}}}}}}}}\) denote the univariate time series of the photon counts. The input xt \(({x}_{t}\in {\mathbb{R}},1\le t\le T)\) is connected to its corresponding hidden state ht, i.e., the output vector of the LSTM hidden units, via the operation of the three gates, which can be expressed by the following equations.
where ⊙ is the Hadamard product, σg(⋅) and σc(⋅) denote the sigmoid and hyperbolic tangent activation functions, respectively. it, ft, ot, and ct are the output vectors of the input gate, the forget gate, the output gate, and the memory cell, respectively at time step t. More specifically, it decides whether or not to add new information from the current inputs \({\tilde{{{{{{{{\mathbf{c}}}}}}}}}}_{t}\), i.e., the cell input activation vector, to the memory cell C that yields ct. The forget gate ft selects and removes old information ct−1 from the memory cell. The output gate ot selects the useful information ct from the memory cell to update the hidden state vector ht. \(\left\{{{{{{\mathbf{i}}}}}}_{t},{{{{{\mathbf{f}}}}}}_{t},{{{{{\mathbf{o}}}}}}_{t},{{{{{\mathbf{c}}}}}}_{t},{\tilde{{{{{\mathbf{c}}}}}}}_{t}, {{{{{\mathbf{h}}}}}}_{t}\right\} \in {\mathbb{R}}^{d}\) with d the number of LSTM hidden units in a hidden layer. \({{{{{\mathbf{W}}}}}} \in {\mathbb{R}}^{d}\), \({{{{{\mathbf{U}}}}}} \in {\mathbb{R}}^{d \times d}\), and \({{{{{{{\mathbf{b}}}}}}}}\in {{\mathbb{R}}}^{d}\) are respectively the weight matrices and bias vector parameters learned during the training process and shared across LSTM hidden units. Finally, the output layer of the LSTM network predicts the received photon count P from the hidden state ht through a linear regression module, expressed as P = wrht + br, where wr and br are the weight vectors and bias to be learned during the training stage. The goal is to make the predicted output value as close as possible to the target output by minimizing a loss function of the predicted and target values in the training process.
Figure 8a shows the photon-count data over 1-min duration with the counting interval of 1 ms. The total data are divided into two datasets, where the first 30-s data (containing 29,944 samples) are used in the training stage and the last 30-s data (containing 30,025 samples) are used as the test data to validate the photon-count predictions of the LSTM network during 22:59:30–23:00:00 (JST). In the training process, the root mean square error (RMSE) metric is chosen as the loss function, which measures the quadratic mean of the differences between the predicted output values and the target output values, with a lower RMSE indicating a better prediction performance. This loss function is minimized by employing the batch gradient descent method based on the Adam optimization algorithm61, with parameters chosen as α = 0.01, β1 = 0.9, β2 = 0.999, and ϵ = 10−8. The number of epochs is set at 200. Regarding the LSTM network configuration, a hidden layer consisting of d = 5 LSTM hidden units is selected. The numbers of epochs and hidden units are chosen after a careful investigation of different values in order to achieve a stable prediction performance. The LSTM network was run on a desktop computer equipped with an Intel Core i7-10700 8-core central processing unit with 32 GB random access memory (RAM) and an Nvidia GeForce RTX 2070 SUPER graphics processing unit.
In a, we show the total photon-count data in 1 min (22:59:00–23:00:00 JST) on 5 August 2016, with the counting interval of 1 ms. The total data are divided into two datasets, where the first 30-s data are used in the training stage and the last 30-s data are used as the test data to validate the photon-count predictions. In b, the predicted photon counts during 30 s (22:59:30–23:00:00 JST), averaged over 10 runs together with 95% confidence interval, are plotted. In c, the average prediction result in b is compared with the test data in a.
LSTM RNNs are essentially stochastic, as they rely on randomness such as random initial weights in each training epoch during stochastic gradient descent. This results in different predictions each time the same model is fit on the same data. Therefore, it is useful to repeat the diagnostic run multiple times to evaluate the stability of the prediction performance. Figure 8b depicts the predicted photon counts during 30 s (22:59:30–23:00:00 JST), averaged over 10 runs together with 95% confidence interval. It is seen that the prediction performance is stable during the first 5 s and gradually varying with larger confidence bounds in the rest of the predicted data. The average prediction is also compared with the test data in Fig. 8c, which shows a relatively good match in the first 5 s, whereas the predicted photon counts are considerably lower than the actual data in the rest 25 s. The reason behind the performance observed in Fig. 8b,c is due to the fact that the training dataset in Fig. 8a contains data of less than 100 photon counts, while the test dataset contains multiple sudden spikes with photon counts up to ten times higher than that in the training dataset. This means the test data are more difficult to predict given the amount of data used in the training process. Nevertheless, the predicted data are still able to follow the fluctuating patterns in the test data, which give hints about the future instantaneous fluctuating loss of the quantum atmospheric channels.
Finally, the convergence of the loss function RMSE averaged over 10 runs is shown in Supplementary Fig. 7 for the training and test datasets. It should be noted that the data were preprocessed by first converting to the log scale and then applying the min-max scaler to rescale all variables into the range \(\left[0,1\right]\). The RMSE values in Supplementary Fig. 7 were calculated from the rescaled values of the data used within the LSTM network. It is noticed that the training and test RMSEs quickly decrease in the first 50 epochs and converged at approximately the same value at 80 epochs. When the number of epochs increases further, the improvement in the test RMSE becomes very small and slowly converged to the same value with the training RMSE at 200 epochs. From this, it can be confirmed that our developed LSTM network provides a good fit with the training and test datasets. Otherwise, it can be considered under-fitted or over-fitted if the training and test loss functions do not converge and stabilize around the same value.
Discussion
In this paper, we have confirmed the validity of a classical channel model in describing the statistical fluctuations of satellite-to-ground quantum atmospheric channels under weak atmospheric turbulence conditions and generalized pointing errors, which is applicable for a practical quantum communications window below a 60° zenith angle. We have further applied the verified channel model for the numerical investigation of QBER and SKL with finite-key analyses of the decoy-state efficient BB84 QKD protocol implemented over the LEO 6U-CubeSat-to-ground link. Our numerical results revealed that pointing errors exert a significant impact on both the QBER and SKL of the QKD link, while the atmospheric turbulence has a negligible influence on the QKD performance given the practical communications window below 60° zenith angle. In conclusion, for achieving a reliable satellite-to-ground QKD link with the highest SKL, it is of utmost importance to generate a narrow beam with a stable pointing accuracy against tracking errors and platform vibrations. Under our considered CubeSat-to-ground system, a practical total key length of ~1.98 × 106 bits can be achieved over a 365-s communications window with the source rate of 100 MHz, given that satellite pointing-angle jitter variances in both axes are 3.3 μrad and the transmitted beam divergence half-angle at \(\exp (-2)\) is 16.5 μrad. Indeed, other system configurations and channel conditions can be also investigated for the engineering designs of CubeSat-based QKD missions using our analysis.
In addition, we presented a study on the deep-learning-based prediction of received photon counts over quantum atmospheric channels. By using the LSTM RNN and 1-min photon-count data, we were able to predict the fluctuating patterns of the received photon counts over 30 s, which indicates the feasibility to predict the channel transmittance fluctuations during a satellite pass. This promises a couple of advantages such as exploiting the instantaneous channel fluctuations by real-time adaptive thresholds to improve the fidelity of weak-coherent states and evaluating in advance the QKD link performance. Although our prediction results did not catch up with the actual number of photon counts in the test data, there are several points of improvement that could be considered. Firstly, if a satellite-to-ground QKD link with a stable pointing accuracy can be established, it is expected that the data would not exhibit abrupt changes with ten times difference in the number of photon counts as in our datasets. This helps to reduce the abnormal discrepancy between the training and test datasets, thereby promising a better prediction performance. Secondly, for improving the prediction performance, a combination of offline and online training mechanisms may be applied, where the offline training step is to learn the sequential patterns of the historical data from different satellite passes and the online training step is to train on a fraction of real-time data and then update the trained network to perform predictions. Finally, for real-time predictions during the practical quantum communications window of a LEO satellite pass (typically 5–6 min), the training and prediction time must be shortened as much as possible. The training time is the time to train the neural network after receiving a fraction of real-time data, and the prediction time is the duration for the network to complete all predictions for the rest of the satellite pass. After the training and prediction periods, all the data in the remaining time of the satellite pass have already been predicted ahead of time. As a reference, the training and prediction time of our developed LSTM RNN, averaged over ten runs, is shown in Supplementary Fig. 8, where the total training and prediction time over 200 epochs is 59.204 s and 13.756 s, respectively. This is still not fast enough for real-time predictions considering our 1-min dataset and further improvements should be made in the future. It is noted that the training and prediction time depends greatly on the amount of data, the available computational power, and the configurations of the neural network.
METHODS
Normalized PDT for statistical verifications
The PDT in Eq. (31) is normalized to the statistical mean of the channel transmittance, i.e., \({\mathbb{E}}\,[\eta ]={\eta }_{{{{{{{{\rm{l}}}}}}}}}{\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\) with \({\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\) defined in Eq. (16). This reduces to the normalization of ηp to \({\eta }_{{{{{{{{\rm{l}}}}}}}}}{\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\), denoted as ηp,norm, and deriving the normalized PDT of η = ηlIaηp,norm. From Eq. (13) and using a Rayleigh approximation for the Beckmann random variable r35, the normalized ηp can be rewritten as
where \({{\Psi }}=\frac{{A}_{{{{{{{{\rm{mod}}}}}}}}}}{{\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]}\). The normalized PDT of η = ηlIaηp,norm with Ia characterized by a LN distribution can now be written as34
where \({\varphi }_{{{{{{{{\rm{mod}}}}}}}}}\) is defined in Eq. (19) and μ is defined in Eq. (31). For statistical verifications with the histogram data, Ψ is one of the fitting parameters of the PDT that contains the characteristics of the random beam movements in both horizontal and elevation directions described in the Beckmann distribution. Since it is difficult to estimate the four parameters of the non-zero means and variances in both directions from the mathematical expressions of \({A}_{{{{{{{{\rm{mod}}}}}}}}}\) and \({\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\), the value of Ψ is fitted to the histogram data as an estimation of the ratio \({A}_{{{{{{{{\rm{mod}}}}}}}}}/{\mathbb{E}}\,[{\eta }_{{{{{{{{\rm{p}}}}}}}}}]\).
QBER and SKL with finite key effects
A BB84 QKD system is often based on attenuated laser pulses, i.e., weak coherent states, as perfect single-photon sources are difficult to attain in practice. However, the attenuated laser source occasionally generates more than one photon per pulse, which causes a security loophole for an eavesdropper, namely Eve, to perform the photon-number-splitting attack where Eve stops all single-photon signals and splits multi-photon signals transmitted from the transmitter, namely Alice, then keeps one copy for herself and resends the rest to the receiver, namely Bob. Fortunately, to cope with this attack, Alice and Bob could prepare and test the transmission properties of the channel via some decoy states, through which the presence of Eve could be revealed. This method, when applied to the conventional BB84 protocol, is known as the decoy-state BB84 QKD scheme53. The security of this decoy-state BB84 QKD was initially developed with the asymptotic-key regime assumption. However, in real-world scenarios, the security of the QKD system critically depends on the number of data points that the system can collect during a finite time interval, which requires finite-key analyses to account for the statistical fluctuations between the measurement rates and underlying probabilities. This is typically the case for LEO satellite-based QKD systems, where the communications window for each overpass is short29,52,62. In this paper, we, therefore, aim to utilize the PDT model in Eq. (31) to derive the mean channel transmittance and total system loss over a single satellite pass for investigating the decoy-state efficient BB84 QKD performance with finite-key analyses. Specifically, we follow Sidhu et al. 52 for presenting the finite-key analyses of a LEO satellite-to-ground QKD link, which adopts the statistical fluctuation analysis using the multiplicative Chernoff bound63, which is tighter than the Chernoff bound originally proposed by Zhang et al. 64. For a further read on active attacks of the decoy-state method, a formal security proof for all possible attacks has been recently reported65.
We consider the efficient BB84 protocol with weak coherent pulses using two decoy states. The two-decoy state protocol parameters and the amount of data used in a block are optimized. Alice first encodes signals in X and Z bases with unequal probabilities, respectively denoted as PX and 1 − PX. The X basis is used for key generation and the Z basis is utilized only for parameter estimations. The error rate of the announced sifted Z basis is used to bound the leaked information from the sifted X basis raw key. Alice then randomly transmits one of three intensities μj with j ∈ {1, 2, 3} and corresponding probabilities \({P}_{{\mu }_{j}}\), where 1, 2, and 3 respectively refer to the signal, weak-decoy, and vacuum pulses. We assume the intensities satisfy the condition μ1 > μ2 > (μ3 = 0). It is noted that the data collected over the satellite pass are processed as a single block without segmentation, incorporating finite statistics and uncertainties to maintain high levels of composable security52. After Bob receives the signals and the reconciliation process, error correction, and post-processing steps have been completed, we can define some measurement statistics from the sifted key. Specifically, we define the number of events for each basis and each intensity as \({n}_{{{{{{{{\rm{X}}}}}}}},{\mu }_{j}}\) and \({n}_{{{{{{{{\rm{Z}}}}}}}},{\mu }_{j}}\), respectively. Similarly, we define the number of bit errors for each basis and for each intensity as \({m}_{{{{{{{{\rm{X}}}}}}}},{\mu }_{j}}\) and \({m}_{{{{{{{{\rm{Z}}}}}}}},{\mu }_{j}}\). The finite-block SKL is readily given by66
where \(\left\lfloor \cdot \right\rfloor\) is the floor function, sX,0, sX,1, and ϕX respectively denote the X-basis vacuum yield, single-photon yield, and phase error rate in the sifted X basis. The parameter λEC provides an estimate, i.e., a bound, on the number of bits required for error correction. \(h(x)=-x{\log }_{2}(x)-(1-x){\log }_{2}(1-x)\) denotes the binary Shannon entropy function. The reliability and security of the protocol are characterized by the correctness and secrecy parameters, respectively denoted as εc (i.e., the shared secret keys are identical except with a small probability εc) and εs66. The protocol is ε = εc + εs-secure if it is εc-correct and εs-secret. A refined estimate of λEC taking into account the error correction depending on the data block size is given as67
where nX is the data block size, F−1 is the inverse of the cumulative distribution function of the binomial distribution, and the QBER in the X basis is calculated as
From Eq. (49), the SKL is thus a function of the X-basis encoding probability PX, the source intensities μj and corresponding probabilities \({P}_{{\mu }_{j}}\), and the transmission time window Δt used to construct block data over a satellite pass. The optimized SKL is generated by optimizing over the parameter space of six variables \(\{{P}_{{{{{{{{\rm{X}}}}}}}}},{\mu }_{1},{\mu }_{2},{P}_{{\mu }_{1}},{P}_{{\mu }_{2}},{{\Delta }}t\}\). Details about the optimization algorithm and analytical expressions of the optimized parameters can be found in Sidhu et al. 52.
Data availability
The data that support the plots within this paper and other findings of this study may be available from the corresponding author upon reasonable request, given the permission of the Japanese National Institute of Information and Communications Technology (NICT). The raw data are not publicly available and subject to export control.
Code availability
The code used in this study may be available from the corresponding author upon reasonable request, given the permission of the Japanese National Institute of Information and Communications Technology (NICT).
References
Toyoshima, M. Recent trends in space laser communications for small satellites and constellations. IEEE/OSA J. Lightw. Technol. 39, 693–699 (2021).
Carrasco-Casado, A. et al. Optical communication on CubeSats—enabling the next era in space science. In Proc. International Conference on Space Optical Systems and Applications (ICSOS) 46–52 (IEEE, 2017).
Trinh, P. V., Pham, A. T., Carrasco-Casado, A. & Toyoshima, M. Quantum key distribution over FSO: current development and future perspectives. In Proc. Progress in Electromagnetics Research Symposium (PIERS-Toyama) (2018).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Carrasco-Casado, A. et al. QKD from a microsatellite: the SOTA experience. In Proc. SPIE 10660, Quantum Information Science, Sensing, and Computation X, 106600B (2018).
Sidhu, J. S. et al. Advances in space quantum communications. IET Quant. Commun. 2, 182–217 (2021).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Braunstein, S. L. & Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 108, 130502 (2012).
Lucamarini, M., Yuan, Z. L., Dynes, J. F. & Shields, A. J. Overcoming the rate-distance limit of quantum key distribution without quantum repeaters. Nature 557, 400–403 (2018).
Villoresi, P. et al. Experimental verification of the feasibility of a quantum channel between space and earth. N. J. Phys. 10, 033038 (2008).
Toyoshima, M. et al. Polarization measurements through space-to-ground atmospheric propagation paths by using a highly polarized laser source in space. Opt. Express 17, 22333–22340 (2009).
Yin, J. et al. Experimental quasi-single-photon transmission from satellite to earth. Opt. Express 21, 20032 (2013).
Vallone, G. et al. Experimental satellite quantum communications. Phys. Rev. Lett. 115, 040502 (2015).
Dequal, D. et al. Experimental single-photon exchange along a space link of 7000 km. Phys. Rev. A 93, 010301(R) (2016).
Carrasco-Casado, A. et al. LEO-to-ground polarization measurements aiming for space QKD using small optical trAnsponder (SOTA). Opt. Express 24, 12254 (2016).
Takenaka, H. et al. Satellite-to-ground quantum-limited communication using a 50-kg-class microsatellite. Nat. Photonics 11, 502–508 (2017).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Yin, J. et al. Satellite-to-ground entanglement-based quantum key distribution. Phys. Rev. Lett. 119, 200501 (2017).
Liao, S.-K. et al. Space-to-ground quantum key distribution using a small-sized payload on tiangong-2 space lab. Chin. Phys. Lett. 34, 090302 (2017).
Liao, S. K. et al. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 120, 030501 (2018).
Braunstein, S. L. & van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513 (2005).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017).
Semenov, A. A. & Vogel, W. Quantum light in the turbulent atmosphere. Phys. Rev. A 80, 021802(R) (2009).
Sudarshan, E. C. G. Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Phys. Rev. Lett. 10, 277 (1963).
Glauber, R. J. Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766 (1963).
Vasylyev, D. Y., Sememov, A. A. & Vogel, W. Toward global quantum communication: beam wandering preserves nonclassicality. Phys. Rev. Lett. 108, 220501 (2012).
Vasylyev, D., Sememov, A. A. & Vogel, W. Atmospheric quantum channels with weak and strong turbulence. Phys. Rev. Lett. 117, 090501 (2016).
Vasylyev, D., Vogel, W. & Sememov, A. A. Theory of atmospheric quantum channels based on the law of total probability. Phys. Rev. A 97, 063852 (2018).
Vasylyev, D. & Vogel, W. Satellite-mediated quantum atmospheric links. Phys. Rev. A 99, 053830 (2019).
AlQuwaiee, H., Yang, H. & Alouini, M. On the asymptotic capacity of dual-aperture FSO systems with generalized pointing error model. IEEE Trans. Wirel. Commun. 15, 6502–6512 (2016).
Dequal, D. et al. Feasibility of satellite-to-ground continuous-variable quantum key distribution. npj Quantum Inform. 7, 3 (2021).
Andrews, L. C. & Phillips, R. L. Laser Beam Propagation Through Random Media (Bellingham, WA, USA: SPIE Press, 2005).
Ghalaii, M. & Pirandola, S. Quantum communications in a moderate-to-strong turbulent space. Commun. Phys. 5, 38 (2022).
Farid, A. A. & Hranilovic, S. Outage capacity optimization for free-space optical links with pointing errors. IEEE/OSA J. Lightw. Technol. 25, 1702–1710 (2007).
Boluda-Ruiz, R., Garcia-Zambrana, A., Castillo-Vazquez, C. & Castillo-Vazquez, B. Novel approximation of misalignment fading modeled by Beckmann distribution on free-space optical links. OSA Opt. Express, 24, 22635–22649 (2016).
Gradshteyn, I. S. & Ryzhik, I. M. Table of Integrals, Series and Products 7th edn (New York, NY, USA: Academic, 2007).
Toyoshima, M., Takenaka, H. & Takayama, Y. Atmospheric turbulence-induced fading channel model for space-to-ground laser communications links. Opt. Express 19, 15965–15975 (2011).
Bufton, J. L. Comparison of vertical profile turbulence structure with stellar observations. Appl. Opt. 12, 1785–1793 (1973).
Greenwood, D. P. Bandwidth specification for adaptive optics systems. J. Opt. Soc. Am. 67, 390–393 (1977).
Pirandola, S. Satellite quantum communications: fundamental bounds and practical security. Phys. Rev. Res. 3, 023130 (2021).
Milonni, P. W., Carter, J. H., Peterson, C. G. & Hughes, R. J. Effects of propagation through atmospheric turbulence on photon statistics. J. Opt. B: Quantum Semiclass. Opt. 6, S742–S745 (2004).
Capraro, I. et al. Impact of turbulence in long range quantum and classical communications. Phys. Rev. Lett. 109, 200502 (2012).
Abramowitz, M. & Stegun, I. A. Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables, 9th edn (New York, NY: Dover 1972).
Bennett, C. H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 68, 3121–3124 (1992).
Wang, X. et al. Angular micro-vibration of the Micius satellite measured by an optical sensor and the method for its suppression. Appl. Opt. 60, 1881–1887 (2021).
Trinh, P. V. et al. Experimental channel statistics of drone-to-ground retro-reflected FSO links with fine-tracking systems. IEEE Access 9, 137148–137164 (2021).
Neumann, S. P. et al. Q3Sat: quantum communications uplink to a 3U CubeSat—feasibility & design. EPJ Quantum Technol. 5, 4 (2018).
Haber, R., Garbe, D., Schilling, K. & Rosenfeld, W. QUBE—a CubeSat for quantum key distribution experiments. In Proc. AIAA/USU Conference on Small Satellites (2018).
Oi, D. K. et al. CubeSat quantum communications mission. EPJ Quantum Technol. 4, 6 (2017).
Mazzarella, L. et al. QUARC: quantum research CubeSat–a constellation for quantum communication. Cryptography 4, 7 (2020).
Kerstel, E. et al. Nanobob: a CubeSat mission concept for quantum communication experiments in an uplink configuration. EPJ Quantum Technol. 5, 6 (2018).
Sidhu, J. S. et al. Finite key effects in satellite quantum key distribution. (2021). npj Quantum Inform. 8, 18 (2022).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Carrasco-Casado, A. et al. Intersatellite-link demonstration mission between CubeSOTA (LEO CubeSat) and ETS9-HICALI (GEO satellite). In Proc. International Conference on Space Optical Systems and Applications (ICSOS) 1–5 (IEEE, 2019).
Dolash, T. M., Cooper, M. A., Spencer, M. F. & Shakir, S. A. Demonstration of a general scaling law for far-field propagation. Appl. Opt. 60, G1–G9 (2021).
Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735–1780 (1997).
Yan, H. & Ouyang, H. Financial time series prediction based on deep learning. Wirel. Pers. Commun. 102, 683–700 (2018).
Rashid, K. M. & Louis, J. Times-series data augmentation and deep learning for construction equipment activity recognition. Adv. Eng. Inform. 42, 100944 (2019).
Tran, H. T. T., Nguyen, D. V., Ngoc, N. P. & Thang, T. C. Overall quality prediction for HTTP adaptive streaming using LSTM network. IEEE Trans. Circuits Syst. Video Technol. 31, 3212–3226 (2021).
Liu, J.-Y., Ding, H.-J., Zhang, C.-M., Xie, S.-P. & Wang, Q. Practical phase-modulation stabilization in quantum key distribution via machine learning. Phys. Rev. Appl. 12, 014059 (2019).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. In Proc. 3rd International Conference on Learning Representations (ICLR) 1–15 (2015).
Lim, C. C.-W., Xu, F., Pan, J.-W. & Ekert, A. Security analysis of quantum key distribution with small block length and its application to quantum space communications. Phys. Rev. Lett. 126, 100501 (2021).
Yin, H.-L. et al. Tight security bounds for decoy-state quantum key distribution. Sci. Rep. 10, 14312 (2020).
Zhang, Z., Zhao, Q., Razavi, M. & Ma, X. Improved key-rate bounds for practical decoy-state quantum-key-distribution systems. Phys. Rev. A 95, 012333 (2017).
Trushechkin, A. S., Kiktenko, E. O., Kronberg, D. A. & Fedorov, A. K. Security of the decoy state method for quantum key distribution. Phys.-Usp. 64, 88 (2021).
Lim, C. C. W., Curty, M., Walenta, N., Xxu, F. & Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 89, 022307 (2014).
Tomamichel, M. et al. Fundamental finite key limits for one-way information reconciliation in quantum key distribution. Quantum Inform. Process. 16, 280 (2017).
Acknowledgements
The authors thank M. Akioka, T. Kubooka, and H. Endo from NICT for their technical support of SOCRATES operation. P.V.T. and A.C.-C. thank Prof. Konrad Banaszek from University of Warsaw and Prof. Veronica Fernandez from Spanish National Research Council for fruitful discussions. The authors thank the anonymous reviewers for insightful comments and suggestions.
Author information
Authors and Affiliations
Contributions
M.T., H.T., M.F., and M.S. conceived and designed the experiments. H.T., M.K., and M.F. conducted the experiments. M.T. and M.S. supervised the experiments. P.V.T. performed the statistical analyses and implemented the neural network. P.V.T. and A.C.-C. analyzed the results and wrote the paper with discussions and input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Trinh, P.V., Carrasco-Casado, A., Takenaka, H. et al. Statistical verifications and deep-learning predictions for satellite-to-ground quantum atmospheric channels. Commun Phys 5, 225 (2022). https://doi.org/10.1038/s42005-022-01002-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01002-1
This article is cited by
-
Quantum communication based cyber security analysis using artificial intelligence with IoMT
Optical and Quantum Electronics (2024)
-
Finite key performance of satellite quantum key distribution under practical constraints
Communications Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.