Introduction

There is an enormous need for faster and more efficient information processing. Quantum computing is widely discussed as a future computing technology, especially with regard to computing power and the very favorable scaling properties1,2,3,4,5,6,7,8,9. However, current quantum computing technologies are still far from ubiquitous. In particular, the need to operate in the milli-Kelvin temperature range is a significant obstacle.

In the field of quantum information technology, the basic unit of information is defined as a quantum bit or qubit for short8,9,10,11,12. The qubit is most often represented by a superposition of two wavefunctions, which describe the two orthonormal basis states of the system. Thus, from the information content point of view, a qubit is a multi-valued object characterized by two independent continuous parameters, such as the ratio of wave function amplitudes and their relative phase. Qubits are regularly represented as states on the surface of a Bloch sphere, see Fig. 1a.

Fig. 1: System of two magnon Bose–Einstein condensates (BECs).
figure 1

a The green and blue dots at the north and south poles of the Bloch sphere represent pure \(\left|+\right\rangle\) and \(\left|-\right\rangle\) states of the double magnon condensate BEC± formed in two different global energy minima of the magnon system, while the red dot shows the position of a mixed state of BEC+ and BEC−. b Schematic spectrum of magnons and BEC generation via parametric pumping using microwave photons of frequency ωp with small wavenumbers qp ≈ 0. The green and blue thick lines schematically depict the dispersion branches of the lowest-frequency magnon mode for the positive and negative wavevectors qz along the magnetization direction z. The red dashed arrows indicate the process of decaying the pump photon into two magnons of half the pump frequency and opposite wavevectors. The green and blue dots mark the spectral positions of the BEC+ and BEC− formed in the two global energy minima at \({q}_{z}=+{q}_{{}_{{{{{{{{\rm{BEC}}}}}}}}}}\) and \({q}_{z}=-{q}_{{}_{{{{{{{{\rm{BEC}}}}}}}}}}\). The green and blue shaded areas symbolize the corresponding magnon gaseous states. c Numerical simulation of the condensation process of parametrically populated magnon gas in an yttrium-iron-garnet (YIG) ferrimagnetic film. The fine structure of the magnon gas population corresponds to the thickness magnon modes of this film. The YIG film-thickness is 5 μm. The pumping frequency ωp/(2π) is 7.5 GHz with a pump duration of 50 ns. The bias magnetic field is 100 mT. d Spatial interference pattern formed by the superposition of the BEC+ and BEC− states along the magnetization direction z. The magnon density stripes along the perpendicular direction y correspond to the BEC wave fronts. The color code indicates the normalized magnon density in c and d. The quite regular structure of the interference pattern corresponds to a relatively high degree of spatial coherence of the magnon BEC.

Full size image

In quantum optics, applying the Bloch sphere to describe coherent atomic states13 as well as coherent and squeezed spin states14 has a long history. Moreover, a powerful platform for demonstrating quantum correlations in the context of the Bloch sphere is provided by atomic Bose–Einstein condensates (BECs)15. The BEC is a collective object, in which particles or quasiparticles represented by a coherent wavefunction populate the lowest energy level of a system16,17,18,19,20,21,22,23. In the search for physical systems suitable for representing a set of qubits, macroscopic quantum states of matter, such as BECs, are promising candidates, in particular because of their inherent coherence and resistance to noise (see, for example, papers24,25,26,27,28,29,30,31, reviews5,6 and references therein). Coherent control of BECs at the level of one qubit has already been achieved on atom chips32,33. Recently, essential steps were made toward demonstrating entanglement between two BECs34,35, which is crucial for implementing multi-qubit systems. Also, the long-lived entanglement of two macroscopic atomic ensembles has been demonstrated36 as an example of a non-maximally entangled state suitable for a particular purpose, such as atomic teleportation37,38.

It is noteworthy that a Bose–Einstein condensate can be created using magnons in ferrimagnetic crystals even at room temperature39,40,41,42,43,44,45,46,47,48,49,50,51. Moreover, such a condensate is two-component, with components formed in two energetically degenerate minima of the magnon spectrum. As was shown earlier, in the general case a two-component Bose–Einstein condensate naturally represents a qubit suitable for quantum calculations26.

In our paper, based on the idea of Byrnes et al.26, we present the possibilities of manipulating the room-temperature two-component magnon BEC for at least partial implementation of magnon-BEC-based qubit calculus. However, the BEC in our paper belongs to a different parameter range. Byrnes et al.26 analyze a low-temperature BEC with a large but finite number N of condensed bosons, drawing attention, for instance, to the decrease in the evolution time of a two-qubit system by a factor of 1/N. In our analysis, we took from the very beginning the limit N → ∞, considering a classical analog of the qubit logic. At room temperature, magnon BECs operate in the classical regime, and some effects that exist only in the quantum mechanical regime, such as entanglement of states, are not accessible. However, a rather large subset of architectural aspects, algorithms, and modi operandi used in quantum computing can be adapted and made operational. Many algorithms do not rely on quantum mechanical entanglement52,53 and could be implemented with the classical qubit functionality discussed here. This approach removes the technical obstacles that exist in quantum calculations, such as the need to operate at milli-Kelvin temperatures, and allows potentially the operation in a room-temperature solid-state device with standard microwave interface technology. An important issue in this context is scaling. Quantum computing claims polynomial scaling of computation time with system size, which is very advantageous over the merely exponential scaling properties of conventional, classical Boolean logic. Recently, it has been shown that polynomial scaling holds for a number of algorithms that use wave-based computing in a non-quantum mechanical implementation (see, e.g., refs. 54,55). Thus, in terms of computation time, there is a fairly favorable gap between classical Boolean and true quantum-mechanical computing concepts, which can be filled by the magnon BEC concept presented here.

Results

Magnon BEC as classical analog of a qubit

The magnon BEC phenomenon addresses the spontaneous formation of a coherent state or wave—a macroscopic quantum state—in an otherwise disordered magnonic system. At room temperature, a magnon BEC can form in a weakly interacting magnon gas if the chemical potential of the system is increased to the minimum magnon energy, for example by increasing the magnon density via external injection39,40,41,43,44. The most prominent method to inject magnons is parallel parametric pumping56,57, in which external microwave photons of frequency ωp and wavenumber qp ≃ 0 split into two magnons with the frequency ωm = ωp/2 and wavevectors ± qm58. The overpopulated magnon gas near the bottom of the magnon spectrum relaxes to the two lowest energy states via multi-magnon scattering processes, forming a double-BEC state with the two BECs located in the two global minima of the system as shown in Fig. 1b. The observed exciting dynamics of such a double-BEC, such as the inherent coherency51,59, density patterns45,46,60, quantized vorticity45, supercurrents47,48, Bogoliubov waves49, and Josephson oscillations47,50, all at room temperature, are further encouraging to consider magnon BECs for performing a classical subset of qubit computing operations.

We take into account the fact that for an in-plane magnetized film, in the two-dimensional in-plane wavevector landscape, the magnon frequency spectrum ω = ω(q) has two minima at symmetric values of the wavevectors ± qBEC pointing along and against the direction of magnetization z, see Fig. 1b. Consequently, the condensate consists of two components, BEC+ and BEC−, forming the double-BEC and described by the wavefunctions \({{{\Psi }}}^{+}\left(z,t\right)\exp [{{{{{{{\rm{i}}}}}}}}({q}_{{{{{{{{\rm{BEC}}}}}}}}}z-{\omega }_{{{{{{{{\rm{BEC}}}}}}}}}t)]\) and \({{{\Psi }}}^{-}(z,t){{{{{{{\rm{\\,exp }}}}}}}}[{{{{{{{\rm{i}}}}}}}}({-q}_{{{{{{{{\rm{BEC}}}}}}}}}z-{\omega }_{{{{{{{{\rm{BEC}}}}}}}}}t)]\), respectively. The fundamental basis for the description of the phenomena in this semi-classical limit is the nonlinear Schrödinger equation, also known as Gross–Pitaevskii equation61. In the one-dimensional version, which is fully applicable here, it reads

$$ \left[{{{{{{{\rm{i}}}}}}}}\frac{\partial }{\partial t}+{D}_{zz}\frac{{\partial }^{2}}{\partial {z}^{2}}-T{|{{{\Psi }}}^{+}|}^{2}-S{\left|{{{\Psi }}}^{-}\right|}^{2}-{P}^{+}\left(z,t\right) +{{{{{{{\rm{i}}}}}}}}{{\Gamma }}\right]\cdot {{{\Psi }}}^{+}\left(z,t\right) \\ ={{{{{{{\rm{i}}}}}}}}{F}^{+}\left(z,t\right),$$
(1a)
$$ \left[{{{{{{{\rm{i}}}}}}}}\frac{\partial }{\partial t}+{D}_{zz}\frac{{\partial }^{2}}{\partial {z}^{2}}-T{\left|{{{\Psi }}}^{-}\right|}^{2}-S{|{{{\Psi }}}^{+}|}^{2}-{P}^{-}\left(z,t\right)+{{{{{{{\rm{i}}}}}}}}{{\Gamma }}\right]\cdot {{{\Psi }}}^{-}\left(z,t\right) \\ ={{{{{{{\rm{i}}}}}}}}{F}^{-}\left(z,t\right).$$
(1b)

Here, \({D}_{zz}={\partial }^{2}\omega ({{{{{{{\bf{q}}}}}}}})/2\partial {q}_{z}^{2}\) is the dispersion coefficient in the z-direction, and T and S are the amplitudes of self- and cross-interactions between BEC+ and BEC−, respectively. \({P}^{\pm }\left(z,t\right)\) are the external potentials caused, for instance, by variations of longitudinal magnetizing fields and \({F}^{\pm }\left(z,t\right)\) are the external forces caused, e.g., by transversal microwave magnetic fields. The magnon relaxation rate, originating, for example, from the interaction with the phonon bath, is denoted by Γ. For Γ = 0, Eq. (1) has stationary solutions, which describe the two magnon BECs at the bottom of the spin-wave spectrum in the + qBEC and − qBEC positions. If Γ ≠ 0, the wavefunctions \({{{\Psi }}}^{\pm }\left(z,t\right)\) decay as \(\exp \left(-{{\Gamma }}t\right)\).

In the space-homogeneous case, there is, apart from the oscillating factor \(\exp [{{{{{{{\rm{i}}}}}}}}({q}_{{{{{{{{\rm{BEC}}}}}}}}}z)]\), no z-dependence, and Eq. (1) becomes identical to the general form of a degenerate two-level system. An example of such a system is a quantum particle with spin S = 1/2, which has a wavefunction consisting of a spin-up \({\psi }_{1/2}^{+}\) and a spin-down \({\psi }_{1/2}^{-}\) component. To stress this analogy, we introduce the normalized BEC wavefunctions

$${\psi }^{\pm }\left(z,t\right)={{{\Psi }}}^{\pm }\left(z,t\right)/\sqrt{{\left|{{{\Psi }}}^{+}\left(z,t\right)\right|}^{2}+{\left|{{{\Psi }}}^{-}\left(z,t\right)\right|}^{2}},$$
(2a)
$${\left|{\psi }^{+}\left(z,t\right)\right|}^{2}+{\left|{\psi }^{-}\left(z,t\right)\right|}^{2}=1.$$
(2b)

The qubit state position on the Bloch sphere [see Fig. 1a] is given by the polar angle θ and azimuthal angle φ. In our case, they are defined by the normalized densities of the two BECs, \({N}^{\pm }={\left|{\psi }^{\pm }\left(z,t\right)\right|}^{2}\) with

$${N}^{+}\left(z,t\right)+{N}^{-}\left(z,t\right)=1\,,$$
(3a)
$$\theta ={{{{{{{\rm{Arccos}}}}}}}}\left\{\left[{N}^{+}\left(z,t\right)-{N}^{-}\left(z,t\right)\right]/2\right\}\,,$$
(3b)
$$\varphi ={{{{{{{\rm{Arg}}}}}}}}\left\{{\psi }^{+}\left(z,t\right)\cdot {\psi }^{-* }\left(z,t\right)\right\}\,.$$
(3c)

Thus, to address any position on the Bloch sphere, we need to control (i) the number of magnons in each of the two BECs and (ii) their relative phase. The implementation of this control will be demonstrated below by means of numerical micromagnetic simulations62,63.

Initialization of magnon double-BEC state at the equator of the Bloch sphere

A convenient way to generate a magnon BEC is to use the parametric excitation mechanism by a space-homogeneous electromagnetic field for generation of magnons in the gaseous magnon regime and to let these magnons condense into the two BEC states via dominating four-magnon-scattering events39,40. Due to the momentum conservation during the magnon termalization processes, the resulting numbers of magnons in the BEC+ and BEC− states also remain the same, N+ = N−, as it has been evidenced by numerous magnon BEC experiments45,48,49,50 and by results of numerical modeling shown in Fig. 1c. It means that such a prepared initial double-BEC state lies somewhere on the equator of the Bloch sphere, \(\cos \theta =0\), and the azimuthal angle ϕ has an arbitrary value (further below we will address how to control ϕ). We note that the coherency of the generated BECs is evidenced by the spatial interference pattern of the two condensates as observed experimentally45, and shown by our micromagnetic simulations displayed in Fig. 1d. Despite the presence of small non-uniformities in the spatial interference pattern evidencing the existence of quantized vorticities, the coherency of the two BECs on the larger scale is preserved45,51,64.

Initialization of magnon double-BEC state at the poles and any latitude of the Bloch sphere

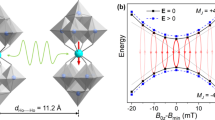
We propose to use a moving periodic pattern of a microwave magnetic field in order to pump magnon pairs dominantly to the positive or negative half of the wavevector space. It acts like an artificial propagating microwave field with controlled wavevector and frequency. This moving pattern can be created by an array of L parallel wires separated by a distance a and connected to a set of phase-locked microwave generators operating at the pumping frequency ωp, see Fig. 2a. They work analogous to a phased array65,66: The phases of the signals applied to the wires are chosen such that the phase difference \({{{\Delta }}}_{{{{{{{{\rm{wire}}}}}}}}}\) between neighbored wires is fixed to \({{{\Delta }}}_{{{{{{{{\rm{wire}}}}}}}}}=2\pi /K\) with K being an integer number. Thus, moving magnetic field patterns are generated, which oscillate with ωp and propagate with wavevector ∣qp∣ = 2π/(Ka). For K > 2 the field pattern has a well-defined unique direction of propagation, which is indicated by the sign of \({{{\Delta }}}_{{{{{{{{\rm{wire}}}}}}}}}\).

Fig. 2: Wavevector-selective parametric pumping and formation of an asymmetric magnon Bose–Einstein condensate (BEC).
figure 2

a Phased-array magnetic field excitation mechanism. The red bars represent microstrip antennas placed on the surface of an yttrium-iron-garnet (YIG) film. The wavevector \(+{q}_{{}_{{{{{{{{\rm{BEC}}}}}}}}}}\) of the BEC+ component of the double BEC is directed along the magnetization direction z. b Schematic view of wavevector-selective parametric pumping scheme using microwave photons of frequency ωp with large wavenumbers \({q}_{z}={q}_{{{{{{{{\rm{p}}}}}}}}}\gtrsim +2{q}_{{}_{{{{{{{{\rm{BEC}}}}}}}}}}\). The red dashed arrows illustrate the process of decaying the pump photon into two magnons with co-directional wavevectors. In this case, the density of magnon gas and the magnon condensate BEC+ in the area of positive wavenumbers qz (the green shaded area and large green dot, respectively) significantly exceeds the density of magnon gas and the magnon condensate BEC− in the area of negative wavenumbers qz (the blue shaded area and small blue dot, respectively). c Micromagnetic modeling of BEC formation using such wavevector-selective parametric pumping. The color code indicates the normalized magnon density.

Full size image

Such a field pattern, which is characterized by a reciprocal lattice vector \(|{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{p}}}}}}}}}|\) pointing into the direction of motion and the microwave frequency ωp, will pump pairs of co-propagating magnons with frequencies ωp/2 and wavevectors qpm ≤ qp/2, qpm∥qp, see Fig. 2b. In this scenario, the thermalization of the parametric magnons will result in the population of either BEC− or BEC+ states. This means that the prepared initial state of the magnon double-BEC is either at the north or south pole of the Bloch sphere. By proper choice of qp, it is possible to populate BEC+ and BEC− states with predefined densities N+ and N−, i.e., to adjust the polar angle of the magnon system. The validity of this approach is demonstrated by the results of our micromagnetic simulations as shown in Fig. 2c.

Semi-classical qubit protocols using Rabi-like oscillations

Achieving a controlled change in the state of the previously initialized double-BEC system, e.g., a transformation of BEC+ into BEC− and vice versa, and addressing any intermediate state, is essential for computing. Indeed, our objective is to implement unitary transformations on the Bloch sphere to resemble logic state operations.

The following tools and approaches serve as key ingredients for implementing the functionalities of the Pauli-X and -Z gates and the Hadamard gate. For this purpose, we use the concept of Rabi-oscillations, which refers to a cyclic energy exchange in a two-level quantum system in the presence of a driving field67,68,69. The system of the two magnon BECs represents the analogy of a two-level system in the wavevector domain, and thus, we translate the Rabi cycle into this domain as discussed in the following.

Let us consider the double-BEC system initialized in the north pole state, i.e., at BEC+ as shown in Fig. 2c. Instead of a time-dependent field, here we use a space-dependent stationary magnetic field to induce a Rabi cycle between the two BEC wavevector components. This field is generated using a dynamic magnonic crystal (MC)70 similar to the setup that is shown in Fig. 2a. However, instead of a phased array driven by microwave currents, we insert pulsed DC currents into the wires to control the bias magnetic field. Consequently, this changes the energy landscape of the system. Once this MC is turned on, it creates a gap in the magnon dispersion relation at the wavevector corresponding to the periodicity of the crystal. This leads to a Bragg reflection of the incoming magnons at that particular wavevector, which in our case is \({q}_{{}_{{{{{{{{\rm{BEC}}}}}}}}}}\)70. However, if the magnons already exist in the system and the MC is switched on, geometrically-induced coupling between the existing magnons and the MC leads to the oscillations of the magnons between the opposite wavevector-states given their equivalent frequencies71.

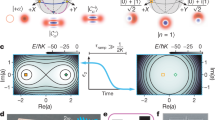
In a numerical simulation experiment, we activate the MC once the pure BEC+ state is established. Figure 3a shows the distribution of the condensed magnon density at the wavevector space in two given time spans. During the course of time from, e.g., t1 = 25 ns to t2 = 175 ns, the magnons are transferred from BEC+ to BEC−. The oscillation cycle is more visible in Fig. 3b, which represents the normalized magnon densities at BEC− and BEC+ as a function of time. Interestingly, the oscillations between the two condensates continue until the condensed magnons dissipate due to the magnetic damping. Moreover, the oscillation cycle can be tuned using the MC modulation amplitude, i.e., by the amplitude of the spatially periodic magnetic field produced by the MC. As shown in Fig. 3c, increasing the MC amplitude leads to shorter oscillation cycles, and consequently higher oscillations frequencies. This can be understood by a stronger coupling of the magnons and the MC71. Indeed, the repetition of this action turns the double-BEC back into its initial state, thus representing the bit-flip operation described by the Pauli-X matrix, \(X=\left[{{0}\atop{1}}\; {{1}\atop{0}}\right]\). By changing the oscillation cycles, it is also possible to transfer the system to a superposition of BEC+ and BEC−, characterized by finite densities of both BECs. The proposed and demonstrated mechanism not only further suggests the coherency of the generated condensates, but also provides a strong tool to manipulate the magnon BEC states on the Bloch sphere even as a function of time, which is an additional degree of freedom for this purpose.

Fig. 3: Rabi oscillations in magnon Bose–Einstein condensate (BEC) within a magnonic crystal.
figure 3

a Wavenumber-dependent distribution of the magnon density at the bottom of spin-wave spectrum for two moments of time t1 = 25 ns and t2 = 175 ns. b Normalized peak magnon BEC densities \({I}_{{{{{{{{\rm{BEC}}}}}}}}}^{+}\) and \({I}_{{{{{{{{\rm{BEC}}}}}}}}}^{-}\) at wavenumbers \({q}_{z}=+{q}_{{}_{{{{{{{{\rm{BEC}}}}}}}}}}\) and \({q}_{z}=-{q}_{{}_{{{{{{{{\rm{BEC}}}}}}}}}}\), respectively, as functions of time. c Periodicity of the Rabi oscillations as a function of the magnitude of a spatially-periodic magnetic field induced by the dynamic magnonic crystal.

Full size image

Furthermore, controlling the azimuthal angle of the double-BEC system is essential as well. This is possible by controlling the relative phase between the two BECs. By inserting a microwave RF field with a frequency smaller than the linewidth of the BEC into a structure similar to the one used to realize the dynamic MC, it is possible to change the relative BEC phase (see Fig. 4) and consequently the position of the double-BEC system on the Bloch sphere. We emphasize that patterning such structures is a task that can be accomplished with today’s nanostructuring techniques.

Fig. 4: Control of the azimuthal angle of the double magnon Bose–Einstein condensate (BEC).
figure 4

The black dotted curve represents the reference realization of the spatial distribution of the spontaneously formed double-BEC along the magnetization field direction. The magnetic density is integrated along the y-axis perpendicular to the magnetization field, see Fig. 1d. The solid red curve shows the change in this distribution when an external radio-frequency signal with a frequency of 0.1 MHz and an amplitude of 0.5 mT is applied to the structure of the dynamic magnon crystal during 50 ns. The shown spatial shift of the double-BEC's interference pattern by about a quarter of the BEC wavelength λBEC corresponds to a change in the azimuthal angle φ of about π/2.

Full size image

The dynamic MC can be optimized for simultaneous work with phase-adjusted RF and pulsed DC-signals. This allows one to manipulate both the polar and azimuthal angles of a double-BEC state, and, by extension, to pave the way towards implementation of various phase-shift gates. For example, as an outlook, we expect the implementation of the Pauli-Z gate, represented by the Pauli-Z matrix, \(Z=\left[{{1}\atop{0}}\; {{0}\atop{-1}}\right]\). By having the possibility of controlled rotation in relation to the different axes of the Bloch’s sphere, the functionality of the Hadamard gate, \(H=\frac{1}{\sqrt{2}}\left[{{1}\atop{1}}\; {{1}\atop{-1}}\right]\)can be achieved.

DISCUSSION

The aim of the presented study is to demonstrate that several qubit calculus functionalities are feasible to implement using a magnon double-BEC at room temperature. Our work might initiate a new direction in the field of magnonics by bridging the field of macroscopic quantum states of magnons and quantum computing functionalities72,73,74. We have used two spatially overlapping and interfering stationary magnon BECs with opposite wavevectors as a classical analog of a qubit. We presented the wavevector-selective parallel pumping mechanism for initialization of this double-BEC system at the north or south pole of the Bloch sphere. Moreover, we have shown that Rabi-like oscillations can be translated into the wavevector domain to manipulate the magnon double-BEC state on the Bloch sphere. Realistic numerical simulations close to the experimental conditions provide evidence for the feasibility of this approach and they also shed light on the proposed mechanisms.

Generally speaking, one can imagine that some other system of two coherent waves can also be considered to implement the classical analog of qubit logic—for example, two coherently exited spin-wave modes. However, we believe that an essential difference between a two-component magnon BEC and a system of two arbitrary magnon modes is the spontaneous nature of BEC formation. It opens up wide opportunities for manipulating BECs parameters by external influences, as we have shown here, or in the process of inter-qubit interaction, which is crucial for computations. Moreover, it is expected that this spontaneously formed coherent double-BEC state can be maintained for a long interval of time if constant magnon injection is implemented by gentle methods that do not lead to a strong disturbance of the magnon system. This can be achieved by relatively weak parametric pumping near the BEC threshold59,75, incoherent parametric pumping76, and the use of spintronic methods of magnon injection in nanoscale magnetic samples41,44. In addition, arbitrarily chosen spin-wave modes will have nonzero group velocities, making them highly inconvenient to manipulate. Besides the fact that they will propagate in space, requiring a large sample size, the two coupled modes will efficiently interact if they have the same group velocities only, which can make them indistinguishable. A natural way out of this set of problems is to couple modes having zero group velocities. It is exactly the case of the double BEC we have considered.

As an outlook, the next steps to be taken are obvious: It is the realization of coupling of two and more double-BEC magnon systems. The coupling of spatially separate magnon BECs has already been demonstrated, leading to the phenomenon of magnon Josephson oscillations50,77,78. Microwave antenna structures for the phase coherent detection and generation of magnon BECs can be used to coherently couple double-BEC systems over larger spatial distances. It should be noted that the determination of the full set of possible operations and their actual implementation in the double-BEC system is a topic for further research.

In summary, our study provides a significant momentum in the frontier between the functionality of a quantum bit (qubit) that make substantial use of entanglement, and systems consisting of an interacting set of classic BECs implementing a subset of qubit-based algorithms for which entanglement is not required.

Methods

Micromagnetic modeling

Solving the equation of the magnetization motion have been carried out numerically using the open source MuMax 3.0 package. It uses the Dormand–Prince method62 for the integration of the Landau–Lifshitz–Gilbert equation:

$$\frac{d{{{{{{{\bf{M}}}}}}}}}{dt}=-| g| {{{{{{{\bf{M}}}}}}}}\times \frac{\delta W}{\delta {{{{{{{\bf{M}}}}}}}}({{{{{{{\bf{r}}}}}}}},t)}+\frac{\alpha }{{M}_{{{{{{{{\rm{s}}}}}}}}}}\left({{{{{{{\bf{M}}}}}}}}\times \frac{d{{{{{{{\bf{M}}}}}}}}}{dt}\right)\,.$$
(4a)

Here, M is the magnetization vector, Ms is the saturation magnetization, δW/δM(r, t) is the variational derivative of the energy density of the ferromagnetic material, which is equal to the effective magnetic field Beff, g is the gyromagnetic ratio, and α is the damping constant. The effective magnetic field reads

$${{{{{{{{\bf{B}}}}}}}}}_{{{{{{{{\rm{eff}}}}}}}}}={{{{{{{{\bf{B}}}}}}}}}_{{{{{{{{\rm{demag}}}}}}}}}+{{{{{{{{\bf{B}}}}}}}}}_{{{{{{{{\rm{exch}}}}}}}}}+{{{{{{{{\bf{B}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}+{{{{{{{{\bf{B}}}}}}}}}_{{{{{{{{\rm{thermal}}}}}}}}}\,,$$
(4b)

which includes the standard contributions of the demagnetizing field due to the magnetostatic energy, exchange interactions, the external bias field, and the thermal field. The latter is represented by stochastic fluctuations62. Further information about the numerical method to compute these terms can be found in the paper of Vansteenkiste et al.62

The system under investigation is a film with dimensions of 51.2 μm  ×  25.6 μm  ×  5 μm that is divided into 1024 × 512 × 16 cells. An external magnetic field is applied in the plane with an amplitude of 100 mT. Realistic magnetic parameters of the YIG film are used: Ms = 140 kA m−1, α = 0.0002, the exchange constant Aexch = 3.5 pJ m−163,64,79. Magnons are injected using parallel parametric pumping, in which, microwave photons of frequency of ωp = 2π·7.5 GHz generate magnons with the frequency ωp/2 = 2π·3.75 GHz. To this end, a high amplitude uniform oscillating field, which is parallel to the external magnetization field, is applied to the system to pump magnons to the lower branch of the spin-wave spectrum. For the wavevector-selective parametric pumping, this has been done using a set of parallel wires as described in the main text. The duration of the pumping pulse is fixed to tpump = 50 ns in all simulations, and the system is then relaxed toward its equilibrium state to permit the BEC to establish at the bottom of the magnon spectrum. All simulations have been carried out assuming room temperature T = 300 K. The used setup in this study resembles typical conditions of real experiments39,40.

The micromagnetic simulations were carried out in two steps. First, the external field is applied in the film plane to establish the relaxed magnetization state. This state is consequently used as the ground state in the dynamic simulations, in which parallel parametric pumped magnons are generated using an oscillating field that is applied parallel to the static field. The dynamic components of the magnetization, M(x, y, z, t) of each cell are collected over a period of time. To process the raw data, one and two-dimensional fast Fourier transformation has been carried out on the collected data set63.

Landau–Lifshitz–Gilbert and Gross–Pitaevskii equations

In the actual numerical simulations of the magnon system, we used the classical Landau–Lifshitz–Gilbert equation (4) for the magnetic moment M, while the analytical discussion of the magnon Bose–Einstein condensate was conducted mainly in the framework of the Gross–Pitaevskii equations (1), traditionally used in this problem. These two approaches are closely related.

In order to derive the Gross–Pitaevskii equation (1) from the Landau–Lifshitz–Gilbert equation (4), we recall the Holstein–Primakoff transformation in quantum mechanics80

$${S}_{+} \equiv \; {S}_{x}+{{{{{{{\rm{i}}}}}}}}{S}_{y}=\hslash \sqrt{2s-{a}^{{{{\dagger}}} }a}\,a\,,\\ {S}_{-} \equiv \; {S}_{x}-{{{{{{{\rm{i}}}}}}}}{S}_{y}=\hslash {a}^{{{{\dagger}}} }\sqrt{2s-{a}^{{{{\dagger}}} }a}\,,\\ {S}_{z} \equiv \; \hslash (s-{a}^{{{{\dagger}}} }a),$$
(5)

which defines the spin operators S±, Sz in terms of the boson creation and annihilation operators, a† and a, effectively truncating their infinite-dimensional Fock space to the finite-dimensional subspaces. Its classical analog

$${M}_{+}({{{{{{{\bf{r}}}}}}}},t) \equiv \; {M}_{x}+{{{{{{{\rm{i}}}}}}}}{M}_{y}=b\sqrt{2g\left({M}_{{{{{{{{\rm{s}}}}}}}}}-g{b}^{* }b\right)}\,,\\ {M}_{-}({{{{{{{\bf{r}}}}}}}},t) \equiv \; {M}_{x}-{{{{{{{\rm{i}}}}}}}}{M}_{y}={M}_{+}^{* }\,,\\ {M}_{z}({{{{{{{\bf{r}}}}}}}},t) \equiv \; {M}_{{{{{{{{\rm{s}}}}}}}}}-g{b}^{* }b,$$
(6)

represents the magnetization vector M(r, t) in terms of the canonical variables, the complex spin-wave amplitudes b(r, t) and b*(r, t), which are the classical analogs of a and a†, see, e.g., Eq. (3.4.8) in the book of L’vov57. Here, * denotes the complex conjugation.

When substituting representation (6) into the Landau–Lifshitz–Gilbert equation (4) with α = 0, it transforms into the canonical Hamiltonian form81:

$${{{{{{{\rm{i}}}}}}}}\frac{\partial b({{{{{{{\bf{r}}}}}}}},t)}{\partial t}=\frac{\delta {{{{{{{\mathcal{H}}}}}}}}}{\delta {b}^{* }({{{{{{{\bf{r}}}}}}}},t)}\,.$$
(7a)

Here, the Hamiltonian functional \({{{{{{{\mathcal{H}}}}}}}}\) (often called for shortness Hamiltonian), is the energy density W expressed in terms of canonical veriables (6). For future purposes it is convenient to consider Eq. (7a) in the Fourier representation introducing bq(t), the Fourier transform of b(r, t):

$${{{{{{{\rm{i}}}}}}}}\frac{d{b}_{{{{{{{{\bf{q}}}}}}}}}(t)}{dt}=\big[{\omega }_{{{{{{{{\bf{q}}}}}}}}}-{{{{{{{\rm{i}}}}}}}}{\gamma }_{{{{{{{{\bf{q}}}}}}}}}\big]{b}_{{{{{{{{\bf{q}}}}}}}}}(t)+\,{{\mbox{interaction terms}}}\,\,.$$
(7b)

We have added here a damping term γq = α ωq originating from the last term on the right-hand side of Eq. (4a).

In order to obtain a simplified description of two narrow packages of magnons around q = ± q0 and \({\omega }_{{{{{{{{\bf{q}}}}}}}}}={\omega }_{\min }\), we consider for simplicity only one spatial dimension z and introduce so-called slow-envelope variables

$${{{\Psi }}}^{\pm }(z,t)=\exp ({{{{{{{\rm{i}}}}}}}}{\omega }_{\min }t)\,\,\int \,{b}_{q}(t)\exp \left[{{{{{{{\rm{i}}}}}}}}(q\pm {q}_{0})\cdot z\right]\frac{dq}{2\pi }\,,$$
(8)

where bq(t) is the Fourier transform of b(z, t). Then, using the standard procedure (see, e.g., Sec. 1.5.1. in the book of Zakharov et al.82), one derives from the canonical equations of motion (7b) for bq(t) two coupled one-dimensional Gross-Pitaevskii equations (1).