Abstract
As ferroelectric Hf0.5Zr0.5O2 (HZO) thickness scales below 10 nm, the switching characteristics are severely distorted typically showing an antiferroelectric-like behavior (pinched hysteresis) with reduced remanent polarization. Using Landau-Ginsburg-Devonshire (LGD) theory for the analysis of the experimental results, it is shown here that, in thin (5 nm) HZO, depolarization fields drive the system in a stable paraelectric phase coexisting with a metastable ferroelectric one, which explains the pinched hysteresis. This state of matter resembles a first order ferroelectric above the Curie temperature which is known to result in similar double-loop behavior. Here, based on the analysis of experimental data in the framework of LGD theory, it is reported that charge injection and trapping at pre-existing interface defects during field cycling (“wake-up”) screens the depolarization field stabilizing ferroelectricity. It is found in particular that a sufficiently large energy density of interface states is beneficial for the recovery of fully open ferroelectric loops.
Similar content being viewed by others
Introduction
Scaling of ferroelectricity both vertically and laterally has scientific and technological interest. In most known ferroelectrics (FE), ferroelectricity tends to vanish as thickness is reduced. The technologically important, Si-compatible doped HfO2 FE in general follows this trend so films below 10 nm show weakened ferroelectricity while reports on ferroelectric films thinner than 5 nm are rare. Interestingly though, in Zr-doped HfO2, scaled down to 1 nm, ferroelectricity is enhanced due to confinement strain1. In addition, it is theoretically predicted that ferroelectricity in HfO2 can be scaled laterally to about 3 Å (half unit cell width)2. These works imply that Hafnia based and more specifically Hf0.5Zr0.5O2 (HZO) FE can be scaled down to the ultimate limit both vertically and laterally. Nevertheless, experiments reveal that extrinsic factors such as dead layers at FE/electrode interfaces or finite screening lengths in the electrodes result in incomplete screening of polarization charges building up depolarization fields (DFs)3. The latter become important in thin films and destabilize ferroelectricity. Although incomplete screening is generally harmful for ferroelectricity, it is also considered to be essential for the operation of ferroelectric tunnel junction (FTJ) memories4,5. Therefore, it is a big challenge to reconcile ferroelectric stability with the presence of DFs (due to uncompensated polarization charges) in ultrathin ferroelectric FTJs.
Polarization switching characteristics such as ferroelectric hysteresis loops, remanent polarization (Pr) and coercive fields (Ec) are adversely affected by thickness scaling6,7. It is generally observed that HZO often shows either a constricted (pinched) P-V loop or an antiferroelectric (AFE)-like loop in the pristine state with drastically reduced Pr6,8,9. Typically, the pinched loops recover to fully open FE hysteresis accompanied with a significant enhancement of Pr after field cycling, a behavior often quoted as “wake-up” effect10. While pinched loops and wake-up effects are present in thick (>10 nm) films, they occur more often and become pronounced as thickness scales down to 5 nm6,8,9,11. As a consequence, a larger number of field cycling is required in thin films to open up the FE loops. It should be noted though that pinched loops and wake-up effects may appear more often when certain growth techniques are used or certain electrode combinations are chosen.
The factors that could be responsible for the pinched characteristics and the wake-up effect have been discussed to some extent in the literature10,11,12,13,14,15. Although several explanations have been proposed, accumulated evidence points to the DF as the most probable cause of loop pinching and wake-up behavior10,13. The DF could be expressed as a bulk effect14 in relatively thick films due to the presence of non-polar phases coexisting with ferroelectric domains. It is widely accepted though that the DF mainly originates from interfacial dead layers and/or finite screening lengths in the electrodes. The DF of this origin increases as the FE thickness is reduced and can be a serious destabilizing factor of ferroelectricity in ultrathin films. The exact mechanism of ferroelectricity suppression in scaled FE films as well as its recovery by field cycling are not fully understood at present.
Inspired by recent studies16, here we use phenomenological Landau-Ginsburg-Devonshire (LGD) theory for 1st order FE to model the effect of the DF and describe in semiquantitative terms the switching behavior of thin HZO FE. We show that the effect of the DF is to introduce in the LGD Gibbs free energy a quadratic (P2) positive energy term, which counteracts the negative P4 term yielding a triple potential well. The latter potential describes a stable paraelectric phase (P = 0) coexisting with a metastable ferroelectric state leading to the degradation of ferroelectric switching (pinching) in ultrathin films. We also show that LGD theory describes satisfactorily the wake-up mechanism by considering charge injection at pre-existing interface defects which mitigates the DF resulting in the opening of the hysteresis loop.
Results
We first present the scaling trends of HZO capacitors and the main switching characteristics of the thinnest (5 nm) ferroelectric HZO obtained. Thickness scaling and proper choice of electrode materials are both important for operation of single layer FTJ. Semiconductor bottom electrodes such as Ge or Nb-doped SrTiO3 (NSTO) are used because of their lower carrier densities compared to metals which allow for uncompensated polarization charges, the latter being very important for the FTJ functionality. Ge produces sharp, crystalline interfaces with HZO17 therefore, it is preferred over Si which typically forms low-k interfacial oxides or silicates. On the other hand, NSTO has been used successfully for the fabrication of BaTiO3 (BTO)/NSTO FTJs4, where the giant tunneling electroresistance effect was obtained by modulating the Schottky barrier thickness at the interface, for various Nb concentration18, therefore it could be a good candidate also for HZO/NSTO FTJs. HZO is deposited by plasma assisted molecular beam deposition17,19,20 and crystallization annealing is performed via Rapid Thermal Annealing (RTA)20 or Flash Lamp Annealing (FLA)17 as described elsewhere17,19,20,21 and in Methods.
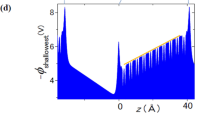
The main structural characteristics of the thinnest TiN/HZO/Ge capacitor structures are shown in Fig. 1 and Supplementary Note 1. Grazing Incidence X-ray Diffraction (GIXRD) scans before (gray line, amorphous) and after annealing (blue line) are shown in Fig. 1a. The latter shows no evidence of the non-polar monoclinic phase (green lines at 28.4 and 31.7 deg22) while the main peak at 30.7 deg (Fig. 1a) is attributed to a combination of the ferroelectric orthorhombic phase Pca2123) and the tetragonal phase P42/nmc22.
a Grazing Incidence X-Ray Diffraction (GIXRD) spectra before (gray line, amorphous) and after annealing (blue line), gaussian fit (cyan line) and reference powder diffraction patterns of tetragonal t-ZrO2, monoclinic m-HZO and orthorhombic o-HZO. b X-Ray Reflectometry (XRR) and Fast Fourier Transform (FFT) scan. c High-resolution Transmission Electron Microscopy (HRTEM) image of the Ge/ HZO /TiN heterostructure. d FFT pattern of the crystallite marked by the square in (c). e simulation of the FFT in (d) assuming Pca21 orthorhombic ferroelectric structure along the [-23-1] zone axis. f, g Show the crystallite in detail and an HRTEM simulation with the orthorhombic ferroelectric phase Pca21 embedded in the real image in (g). A defocus of −20 was assumed, which is the same as the one used to obtain the experimental real image in (f).
From the Scherrer fit of the peak at 30.7 deg, with k-factor ranging from 0.7 to 1, the average crystalline grain size along the direction ω−2θ/2 = 15 deg (approximately in-plane) is estimated to be between 4 and 5.6 nm. A HZO thickness of 5 nm is accurately measured by X ray reflectivity (Fig. 1b) and cross-sectional Transmission Electron Microscopy (TEM) (Fig. 1c and Supplementary Fig. 1). No interfacial layers at the top and bottom surface of HZO are detected by TEM (Fig. 1c and Supplementary Fig. 1), although a non-discernible amorphous TiOxNy layer at the top interface cannot be excluded. Based on filtering of the Fast Fourier Transform (FFT) pattern (Fig. 1d)), the grain size of the HZO polycrystalline film is estimated between 5 nm and 20 nm (Supplementary Fig. 1), noting that the lower limit is compatible with the GIXRD results discussed above. Based on FFT (Fig. 1d, e) and real image (Fig. 1g) simulations, the observed nanocrystallites (Fig. 1f) are compatible with the ferroelectric orthorhombic phase Pac21. However, the distinction between orthorhombic and tetragonal at the macroscale based on GIXRD (Fig. 1a) is difficult. It is anticipated that possible tetragonal phase will be present in rather small quantities since, after wake-up, the remanent polarization Pr is high (>20 μC cm−2) (see Supplementary Note 2 and discussion below) indicating the dominance of the ferroelectric orthorhombic phase.
Figure 2 shows the evolution of the switching characteristics as a function of decreasing HZO thickness for Ge and NSTO Metal Ferroelectric Semiconductor (MFS) capacitors. The general trend is that thick HZO capacitors show full ferroelectric hysteresis loops in the pristine state, while as the thickness is reduced, the hysteresis loops become distorted and at 5 nm, they are pinched (AFE-like) yielding low remanent polarization. Full hysteresis loops are recovered (“waked-up”) after field cycling while the two switching peaks in the displacement current nearly merge.
For thick HZO films (Fig. 2a and b), only few cycles are needed but for thinner films, larger number of cycles are required to wake-up the devices. In some cases (as in Fig. 2c, g), the devices are not affected by cycling at all and remain pinched. It should be noted that for 4 nm HZO and thinner (Fig. 2d, h, l, p), ferroelectricity becomes obsolete and HZO behaves like a normal dielectric.
The waked up devices down to the thinnest 5 nm HZO show high remanent polarization Pr > 20 μC cm−2 after correction, with only small parasitic (non-switchable) polarization (see PUND measurements in Supplementary Fig. 2) and a low coercive voltage Vc ~ 1 V. These performance characteristics are very promising for low voltage/low power FTJ memory devices. Moreover, the high Pr indicates the predominance of the ferroelectric orthorhombic phase as already mentioned above.
The capacitance-voltage measurements on p-Ge/HZO/TiN capacitors at 1 kHz are shown in Fig. 3 featuring the characteristic “butterfly” structure due to ferroelectricity in HZO. Due to the “butterfly” structure which masks the capacitance variations with bias, and the low energy gap of Ge (consequently the high minority carrier concentration) the C-V at room temperature looks more like an MFM capacitor rather than MFS. Note however, that at lower temperatures where the minority carrier concentration is dramatically reduced, a more typical MOS-like behavior is recovered with a clear distinction between accumulation and depletion17. The accumulation capacitance Cacc (measured at > −2V) of the 5 and 15 nm capacitors are measured to be 3.1 and 1.7 μF cm−2, respectively. If a single layer HZO is assumed, the measured Cacc yields a value of HZO relative dielectric constant εF = 18 which is not compatible with the orthorhombic ferroelectric phase, since the latter has an expected value of εF in the range between 30 and 40 [refs. 20,24,25,26,27,28]. It is therefore necessary to consider an interfacial capacitance Cint in series with the FE capacitance CF in order to account for the measured Cacc. Taking into account both 5 nm and 15 nm capacitors and by assuming the same Cint and εF, values of Cint ~ 6 μF cm−2 and εF ~ 39 are extracted. This value of Cint is considerably smaller than the values of 30–110 μF cm−2 reported for Metal-Ferroelectric-Metal (MFM) capacitors27,29 with very thin or no interfacial layers.
In our case, Cint could be dominated from the semiconductor region near the interface due to the finite screening length l. Using an expression3 for \(l=\frac{{{{{{\rm{h}}}}}}}{q}* \sqrt{\frac{{\varepsilon }_{0}{\varepsilon }_{{Ge}}}{3{m}^{* }}}* {\left(\frac{3}{8\pi }\right)}^{\frac{1}{3}}* {\left(\frac{1}{{n}_{h}}\right)}^{\frac{1}{6}}\) (h is the Planck constant and q is the electron charge), derived for metallic systems and assuming a hole concentration nh = 1.6*1017 cm−3, effective mass m* = 0.29me30 and εs (Ge) = 16, a value of l ~ 3.5 nm and a corresponding capacitance Cs~ε0εs/l~3.6 μF cm−2 are estimated. Although Cs is only a rough estimate of the semiconductor capacitance, it does not differ much from the Cint derived from capacitance measurements. In fact, a capacitance Cit due to interface defect charging could be added in parallel to Cs so the total capacitance Cint = Cs + Cit could better match the measured value of 6 μF cm−2 (see above). In conclusion, the semiconductor capacitance, including possible contribution from interface defects, could account for the rather small value of measured Cint even in the absence of interfacial (dead) dielectric layers.
Metastable ferroelectricity and pinched pristine hysteresis curves
To analyze the switching characteristics of the thin HZO MFS capacitors,
we assume a 1st order ferroelectric with Gibbs free energy [Eq. 1].
where P is the polarization order parameter and α < 0, β < 0 and γ > 0 are the Landau coefficients. From simple electrostatics (see Supplementary Note 3, for details and refs. 31,32), the electric field EF in the ferroelectric is given by
Where V is the applied bias on the MFS, and CF, Cint are the capacitances of the ferroelectric and interfacial layers, respectively and tF is the FE thickness. The first term in the right-hand side of the equation accounts for the reduction of the volage in the ferroelectric by a factor \({\left[1+\frac{{C}_{F}}{{C}_{{int}}}\right]}^{-1}\), since part of the voltage drops on interfacial (dead layers), or, on the semiconductor near the interface. The second term in the right-hand side of Eq. (2) is the electric field built as a result of uncompensated charge. The surface charge σ is the charge trapped at pre-existing defects at the interface; it has a sign opposite to that of P and assists in the compensation of polarization charges thus stabilizing P. Charge σ becomes important only during field cycling (wake-up) when charge injection and trapping occur and it will be discussed in subsequent sections. Here in this section, we study the pristine case where σ ≈ 0. It should be noted that when V = 0, then P = Ps (spontaneous polarization) and EF = Edep= \(-\frac{{P}_{s}}{{\varepsilon }_{0}{\varepsilon }_{F}}{\left[1+\frac{{C}_{{int}}}{{C}_{F}}\right]}^{-1}\), that is the DF.
Using (1) and (2) with σ ≈ 0, the FE thickness dependent expression for G becomes
In the last equation, CF has been expressed as CF = ε0εF/tF, where tF is the FE thickness. A corresponding expression for Cint cannot be given due to the lack of knowledge about the interfacial (dead) layer characteristics. Instead, experimental Cint values are deduced from C-V analysis (see Fig. 3 and related discussion above) which yield Cint.
The polarization switching dynamics under the influence of a time varying bias V are described by the Landau-Khalatnikov (L-K) equation \(\delta \frac{{dP}}{{dt}}=-\frac{{dG}}{{dP}}\) 33,34 where δ is the kinetic (or viscosity) coefficient. Using Gibbs free energy from Eq. (3), the L-K equation becomes:
The L-K Eq. (4) is solved by applying time-varying, triangular waveforms for V (see Supplementary Note 4, Supplementary Note 5) to simulate the experimental P-V curve while equation \(J=\frac{{dD}}{{dt}}={\varepsilon }_{0}\frac{d{\rm E}}{{dt}}+\frac{{dP}}{{dt}}\) is complementarily used to calculate the displacement current J-V curves. The simulated curves (Fig. 4a and b) using a kinetic coefficient δ = 2.5*106 s cm F−1 and Landau parameters α = −23*1010 cm F−1, β = −21.4*1019 cm5 F−1 Cb−2 and γ = 15.5*1028 cm9 F−1 Cb−4, are in semiquantitative agreement with the experiment.
a,b Experimental data (dotted) and simulation (red line) of Polarization (P) and Displacement current (I) respectively, as a function of Voltage (V) at 1KHz for 5 nm Hf0.5Zr0.5O2 (HZO) films. c Gibbs free energy landscape drawn using the Landau coefficients which are determined from the simulated P-V and I-V.
The deviations are partly due to non-idealities of the experimental curves. A small offset in the voltage (~0.15 V) was set in the calculations in order to account for rigid shifts to higher bias due to small workfuncion differences between top TiN and bottom Ge electrodes. The simplified phenomenological LGD model which ignores extrinsic factors affecting switching dynamics (see discussion section) also accounts for the discrepancies between for the experimental and simulated curves.
At a fixed FE thickness of tF = 5 nm, Cint and εF are the two parameters which control the depolarization ~P2 term in Eq. (3), hence the pinching of the hysteresis curve. It should be emphasized that the pinching characteristics (reduced Pr) are best simulated with Cint = 5.5 μF cm−2 and εF = 39 which compare well with the values of Cint and εF obtained from the analysis of the C-V measurements (Fig. 3). Our modeling indicates that the positive depolarization term (~P2) in the Gibbs free energy counteracts the negative ¼ βP4 (and the negative ½ αP2) term and results in the triple potential well (Fig. 4c) which describes a metastable HZO ferroelectric. The stable paraelectric phase (P = 0) is then responsible for the pinching of the P-V hysteresis reducing the remanent polarization to near zero values. More insights are given in the discussion and conclusions section below.
To better illustrate the influence of Cint on the ferroelectric stability and the switching characteristics, the Gibbs free energy landscapes and the P-V curves for two different Cint values of 10 and 20 μF/cm2 are given in Fig. 5. When Cint is has an intermediate value ~10 μF cm−2, the 6 nm film shows metastable ferroelectricity (pink curve) and a weakly pinched loop with reduced Pr. The 4 and 2 nm HZO show very small remanent polarization and an ordinary dielectric behavior. When Cint becomes larger (20 μF cm−2), the situation is improved since the 6 nm HZO has stable ferroelectricity and a fully open hysteresis loop with high Pr.
The 4 nm HZO is marginally stable ferroelectric (blue curve), with a nearly open ferroelectric loop and only the very thin 2 nm film shows metastable ferroelectricity resembling an ordinary dielectric behavior. Therefore, it can be concluded that by increasing the Cint above 20 μF cm−2 it is possible to drive the system to a stable ferroelectric state even for very thin films <4 nm.
In MFM capacitors, an infinitely high Cint corresponds to perfect metal electrodes forming sharp interfaces27,29 with the HZO (without dead layers). However as already briefly mentioned in the introduction, at least one of the electrodes should be less than perfect to allow for incomplete compensation of the polarization charge, which is essential for the operation of ultrathin FTJs. Therefore, in most cases of interest related to FTJs, Cint is expected to be small resulting in loop pinching. Nevertheless, severely pinched loops at small thickness <6 nm can be recovered by injecting charge during field cycling, as described in the following section.
Field cycling (“wake-up”) in the framework of Landau-Ginzburg-Devonshire theory
Charge injection35 can occur during field cycling since pre-existing defect states are filled with trapped electrons which could tunnel through interfacial layer barriers, if such barriers exist. This mechanism (Fig. 6) provides efficient screening of polarization charges mitigating Edep thus stabilizing polarization. Both, polarization P and applied bias V, control the states available for trapping and consequently the total trapped charge.
a Unpolarized MIFIM with charge neutral interfaces showing flat bands in equilibrium. b Polarized MIFIM in equilibrium (V = 0) showing depolarization and interfacial fields Edep and Eint respectively. P is the polarization and Φ is the electron potential lowering at the interface due to the positive polarization charges at the interface on the right. c The MIFIM at a finite bias V establishing a field parallel to the polarization. Vint is the voltage drop at the interfacial layers resulting in a total Φ+Vint electron potential lowering at the interface on the right. The potential lowering creates a trapped charge −|σ | and +|σ | at the opposite interfaces due to the set of trap levels, indicated by red (green) squares, moving below (above) the Fermi energy level EF.
Although the analysis presented below is made for the case of identical I and M-layers on either side (Fig. 6a), with appropriate adaptations it could be valid more generally for a structure with different insulator (I) and metal (M) layers on the opposite sides including the cases where one I-layer is missing or one M-layer is a semiconductor. As a first approximation, a constant energy density of states is considered here.
Once established (Fig. 6b), the polarization lowers the potential for electrons at the interface by an amount Φ proportional to P according to Φ = (tF/2)|Edep | = tFP/2ε0εF(1 + Cint/CF). As a consequence, a portion of interface states within an energy ΔEΦ = eΦ moves below EF and becomes accessible to electrons for trapping.
An applied external bias V further lowers the potential (Fig. 6c) at the interface by an amount Vint = V/2(1 + Cint/CF) making more states accessible to electrons in an energy interval ΔEV = eVint. The total states accessible for charge trapping are within the energy interval ΔΕ = e(Φ + Vint) therefore, the total trapped charge, in absolute value, is
In Eq. (5), ntr is the trapped electrons density per unit energy which is determined by solving the Shockley Read Hall36,37 rate equation ∂ntr/∂t = cn(Dit −ntr) −enntr. Dit is the density of interface states per unit energy and cn, en are the capture and emission rates38.
In Fig. 7a the trapped carrier density per unit energy is plotted as a function of field cycles and for two different Dit, while the details near the origin are shown in Fig. 7b. The carriers are captured in the first half of the cycle, while a smaller portion is emitted back to the electrodes during the second half of the cycle. A positive balance of carriers remains captured after each complete cycle so gradually the trapped density increases and finally saturates at a value that depends on the Dit: a larger Dit allows for more trapped charge density as can be seen from the comparison between the green and red curves in Fig. 7a.
a The carrier density per unit energy ntr as determined from the Shockley Read Hall (SRH) rate equation. Density of interface traps Dit is the interface energy density of states. b Detail near the origin (marked by the square in (a)), showing the trapping and de-trapping in each cycle. c The total charge σ trapped in all interface energy states which are made available by polarization P and bias V for Dit = 1.4 × 1013 eV−1 cm−2. d Detail at the origin (marked by square in (c)) showing separately the contribution of polarization (red) and voltage (blue) to the total trapped charge.
The corresponding total charge density σ captured in all energy levels made available by P and V is calculated using Eq. (5) and is plotted in Fig. 7c. The detail at the origin in Fig. 7d shows the different contributions from the polarization P (red) and the bias V (blue) according to Eq. (5) as well as the total σ (black). It should be noted that σ has always opposite sign to both, the polarization charges and the bias therefore it changes sign in each half period when P and V also change sign. The two interfaces have charges of opposite sign which alternates in each half period. Setting a relatively high value of Dit ~ 1.4 × 1013 eV−1 cm−2, the calculated charge is accumulated to both interfaces increasing in amplitude and saturating after about 160 cycles at a value of about 10 μC cm−2 which is a substantial fraction of the polarization charge (~20 μC cm−2) (Fig. 7c).
This indicates that after cycling, the polarization charge is sufficiently screened, thus minimizing the DF and stabilizing ferroelectricity.
A large Dit determines the screening efficiency of the polarization charges and ensures the opening of the ferroelectric loop. On the other hand, en (consequently cn) determine how fast the traps are filled up to the saturation value. Higher en (and cn) ensures faster filling so wake-up and loop opening is easier occurring only after a small number of cycles.
Introducing the contribution of trapped charge σ (Eq. (5) and Fig. 7c)) in the expression for the electric field EF (Eq. (2)), additional P2 and P terms appear in the Gibbs free energy (Eq. (3)) and L-K equations (Eq. (4), and Supplementary Fig. 5)), respectively, that counteract the depolarization terms and make ferroelectricity stable again alleviating the pinched characteristics after cycling is completed. The results are summarized in Fig. 8 above.
Although a direct fitting of the experimental curves is not possible due to non-idealities in the experimental data, a qualitative agreement between experimental data (Fig. 8a) and simulation (Fig. 8b) is observed. Using Dit = 1.4 × 1013 eV−1 cm−2 and en = 20 sec−1 the simulation reproduces the trend of the P-V curves which shows a progressive opening of the hysteresis loop as the number of cycles increases. The loop opening is accompanied by a corresponding transition from a metastable ferroelectric state (pristine, black curve) to a stable ferroelectric state (160 cycles, pink curve) as seen from the Gibbs free energy plots in Fig. 8c.
It should be noted that both Dit and en are compatible with experimental observations in the literature and in the present work. Briefly, we refer to our electrical admittance spectroscopy (Supplementary Note 6): the Dit value at Ge/HZO interface is estimated from ac conductance losses to be 0.93–3.5 × 1013 eV−1 cm−2 (Table S1), which is very similar to the Dit value deduced from the simulation results in Fig. 8. It should be noted that a Dit which is an order of magnitude smaller (see Supplementary Note 7), is insufficient to open the loop inducing only marginal changes to the pristine curves. The low Dit could explain the behavior of some of the thinnest samples where the pristine, pinched characteristics do not recover after extensive cycling (See Fig. 2, and Supplementary Fig. 7).
Discussion
The phenomenological LGD mean field theory and the associated L-K equation assume an idealized homogeneous FE with a single order parameter P, which switches between two stable states under the influence of an electric field. However, in practical cases, analysis is complicated due to extrinsic effects that are typically involved during ferroelectric polarization switching. Nucleation of reverse polarization domains at defects, growth and propagation of domain walls, inhomogeneous field distribution as described by Nucleation Limited Switching (NLS)39, Kolmogorov-Avrami-Ishibashi (KAI)40,41,42 and Inhomogeneous Field Mechanism (IFM)43 models, respectively, all result to extrinsic switching which deviates from the intrinsic one. One notable deviation is the coercive field Ec which in conventional (perovskite) FEs is typically 10 times lower44 than the intrinsic Ec expected from LGD/K-L theory45. KAI could account for the low Ec value in conventional (e.g., perovskite) FE since Ec is expected to be reduced by a factor proportional to the thickness of the domain wall. Interestingly though, HfO2-based FE show experimental Ec values which are large (~1 MV/cm) and comparable to the intrinsic ones. This could be explained by the negligible domain wall thickness predicted in HfO2 FE2, essentially excluding KAI as a possible mechanism that plays a major role in switching. Recent comparative study has shown that NLS and IFM provide a microscopic description of switching and they are not in contradiction with LGD/L-K theory, but they offer versatility and complementarity for the description of ferroelectric switching in HZO7. Finally, a nanoscopic study based on negative capacitance HZO structures supports the intrinsic switching scenario against nucleation-driven switching (NLS)46.
Based on the aforementioned, it is concluded that the LGD/L-K theory employed here in this work is in principle a good framework to semi-quantitatively study the behavior of ferroelectricity and the intrinsic switching dynamics at small thickness of HfO2-based FE. Adaptations using more realistic multidomain models47 could improve the analysis without contradicting the main conclusions drawn here. In this work we show that LGD/L-K theory describes satisfactorily both the AFE-like characteristics of pristine loops as well as the recovery into full ferroelectric loop by field cycling.
The discussion about the possible cause of the AFE-like behavior in (thin) HZO FE is ongoing given that an AFE phase has never been observed in HZO in an unambiguous way. It is intriguing that the double-loop or AFE-like behavior does not necessarily imply the presence of an AFE phase. It is known that the double-loop typically appears in 1st order FE above the Curie temperature Tc48. This has inspired us to propose an explanation as illustrated schematically in Fig. 9.
a Double potential well showing a stable ferroelectric state (blue solid line). The presence of depolarization adds a quadratic (~P2) energy term represented by the red dashed parabola. b The convolution of a double potential well with a parabolic term coming from depolarization yields the triple potential well, which resembles a 1st order ferroelectric above Tc. c The temperature (T) dependence of Gibbs free energy for a 1st order ferroelectric. T0 and Tc are the Curie–Weiss and Curie temperatures, respectively. For T < T0 (blue curve) the material is a stable ferroelectric. For T0 < T < Tc (gray curve), the material has a stable ferroelectric state coexisting with a metastable paraelectric one (P = 0). For T > Tc (magenta curve), the material shows a stable paraelectric (P = 0) phase coexisting with a metastable ferroelectric one yielding a triple potential well similar to that in (b).
In an ideal HZO ferroelectric with perfect screening of polarization charges by the electrodes, the Gibbs free energy landscape shows a double potential well (blue solid curve in Fig. 9a)49 so the material is in a stable ferroelectric state with only two minima. However, in a real HZO ferroelectric with uncompensated polarization charge and associated finite DF (particularly important in thin HZO), a positive quadratic (~P2) energy term is added (broken red line in Fig. 9a) which raises the polarization minima above zero energy forming a triple potential well with stable paraelectric (P = 0) and a metastable ferroelectric state (Fig. 9b). This situation resembles the triple potential well (magenta line) which is known to be formed in a 1st order ferroelectric above Tc (Fig. 9c) associated with an AFE-like double hysteresis loop48. Therefore, a thin HZO with enhanced depolarization behaves like a 1st order ferroelectric above Tc. In other words, scaling down HZO, reduces the effective Tc of the material which falls into a metastable ferroelectric state. This could be the origin of ferroelectric loop pinching and degradation of ferroelectric switching marked by a severe reduction of remanent polarization in the pristine state. The pinching of the pristine loops can be viewed as a spontaneous reaction of the material to reduce Pr, therefore to reduce Edep and the associated electrostatic energy built in the FE.
During field cycling (wake-up), the injected charge at pre-existing defect traps mitigates the effect of DF which is equivalent to say that the broken red parabola in Fig. 9a is reduced, so the Gibbs free energy recovers toward a double potential well again, stabilizing ferroelectricity as evidenced by a fully opened hysteresis loop. It is important to note that the degree of hysteresis loop recovery is controlled by the density Dit of the interface traps. By appropriate interface defect engineering it would be possible to inject a controlled amount of charge and reduce the DF as much as required to ensure ferroelectric stability without completely screening Ed to allow for functional FTJ devices.
Apart from LGD/L-K described here, other explanations for the AFE-like pristine loops and the wake-up behavior have been proposed in the literature including defect redistribution that either assists domain wall depinning, or stabilizes the orthorhombic phase12,50,51, field-induced phase transformation from non-polar to ferroelectric phase12,50, field-induced crystallization and ferroelastic switching15 to name a few. However, the issue has remained controversial since quantification, especially of the cycling response, is lacking. In addition, the tetragonal phase which was initially thought to be responsible for the pinched loops, was found later to be non-polar, so it cannot be considered responsible for the AFE-like characteristics. While several of the aforementioned explanations could be in effect for thick films, the increasing importance of DFs as thickness is reduced cannot be ignored. Our work takes full account of the DF effects and describes semi-quantitatively the thickness dependence of switching characteristics and the AFE-like behavior of very thin HZO. Also, our work captures the trend during cycling elucidating the importance of interface defect density in loop opening and ferroelectricity recovery (wake-up).
Our analysis of degradation in the framework of LGD/L-K is based on the assumption that HZO is a 1st order ferroelectric. If a 2nd order FE HZO model was used instead, a depolarization term, if strong enough, could only lead to a destabilization of ferroelectricity resembling an ordinary dielectric. This is because in 2nd order FE, β is always positive and α is negative, so the positive depolarization term competes only with the negative term proportional to α which are both quadratic. If the latter term dominates, the potential landscape is always a double potential well yielding stable ferroelectric state (see Supplementary Note 8). If the former (depolarization) term dominates instead, the potential landscape is a single upward varying parabola characteristic of a normal dielectric (see Supplementary Fig. 8). A triple potential well with metastable ferroelectricity can never be obtained in a 2nd order ferroelectric under the influence of depolarization. Therefore, the observation of metastable ferroelectricity with pinched P-V hysteresis is an indication that the ferroelectric (HZO in our case) is a 1st order ferroelectric as has also been recently proposed52 based on large thermal hysteresis observed during heating/cooling cycle.
The influence of depolarization leading to pinched loops and wake up effects is more pronounced in HZO compared to other more conventional FE (e.g., perovskites) mainly because of the following two reasons. First, some of the perovskites are second order FE and according to the analysis in the preceding paragraph and in supplementary (Supplementary Fig. 8), as second order FE they are not expected to exhibit triple potential wells and pinched loops unlike HZO which is first order ferroelectric. Second, for the perovskites with a first order ferroelectric transition, the relevant depolarization term \(\frac{1}{{\varepsilon }_{0}{\varepsilon }_{F}}{\left[1+\frac{{t}_{F}{C}_{{int}}}{{\varepsilon }_{0}{\varepsilon }_{F}}\right]}^{-1}{P}^{2}\) entering the expression for G (Eq. 3) is inversely proportional to the dielectric constant εF. The latter has a high value (εF > 100 in most perovskites) therefore the depolarization term plays a minor role yielding no triple well, consequently no pinched loops. In contrast, HZO having a small εF(~30–39), contributes a larger depolarization term in G, yielding more pronounce pinched loops in the pristine state.
Methods
Ge substrates used here are considered as good candidates for FeFET with better reliability compared to Si counterparts and with easier “gate first” transistor processing due to lower dopant activation temperature in the same range as HZO crystallization annealing temperature.
Hf0.5Zr0.5O2 films were prepared by atomic oxygen beam deposition on p-type (001) Ge substrates with resistivity of 0.03–0.07 Ω cm. Ge substrates were annealed at 450 °C for several minutes prior to deposition until a clean, 2 × 1 reconstructed, Ge surface appeared. Subsequently, 5 nm-thick Hf0.5Zr0.5O2 amorphous oxide layers were deposited at 100 °C followed by 10 nm thick TiN metal growth at the same temperature. Hf and Zr metals metal were evaporated with a rate of ~0.1 Å s−1 from the e-guns, in the presence of atomic oxygen beam generated by a remote radio frequency plasma source at 350 watt while Ti was evaporated with a rate of ~0.2 Å s−1 from the e-gun in the presence of atomic nitrogen beam at the same power. To fabricate the MFS capacitors, Ti(5 nm)/Pt(40 nm) metal contacts were deposited on the Ge/HZO/TiN device layer structures by photolithography producing 50 μm dots. Subsequently, the samples received either rapid thermal annealing (RTA) at 550 °C for 30 s in N2 atmosphere and a ramp-up rate of 150 °C s−1 or millisecond flash annealing (FLA) which consists of the following steps: a 120 s preheat at 375 °C followed by an energy flash of 70 J cm−2. Finally, the TiN layer is selectively etched by NH4OH/H2O2/H2O solution to finalize the Ge MFS capacitor. Polarization and displacement current of the ferroelectric capacitors at 1 kHz were measured using an aixAcct Systems TF Analyzer 1000.
Grazing-Incidence X-Ray Diffraction (GIXRD) and X-Rays Reflectivity measurements were performed on a Bruker D8 Discover diffractometer equipped with a rotating anode generator.
The cross-section specimens for TEM investigations have been prepared using a dual beam (scanning electron microscope-focused ion beam, SEM-FIB) system from Tescan (model Lyra 3XMU). TEM observations were performed using a probe-corrected analytical high-resolution JEMARM 200 F electron microscope operated at 200 kV. The crystalline phases in HZO were identified using several TEM techniques, including conventional and high-resolution imaging (TEM/HRTEM), but also FFT. The HRTEM patterns and atomic structural models were simulated using the multislice technique, with the use of Crystal Kit and Mac TempasX software kits. In each case, series of simulated images were generated according to the sample thickness t and the defocus of the objective lens Δf.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Cheema, S. S. et al. Enhanced ferroelectricity in ultrathin films grown directly on silicon. Nature 580, 478–482 (2020).
Lee, H.-J. et al. Scale-free ferroelectricity induced by flat phonon bands in HfO2. Science 369, 1343–1347 (2020).
Mehta, R. R., Silverman, B. D. & Jacobs, J. T. Depolarization fields in thin ferroelectric films. J. Appl. Phys. 44, 3379 (1973).
Di, Z. W. Ferroelectric Tunnel Junctions: Modulations on the Potential Barrier. Adv. Mater. 32, 1904123 (2020).
Covi, E., Mulaosmanovic, H., Max, B., Slesazeck, S. & Mikolajick, T. Ferroelectric based Synapses and Neurons for Neuromorhic Computing. Neuromorph. Comput. Eng. in press, https://doi.org/10.1088/2634-4386/ac4918 (2022).
Park, J. Y. et al. A perspective on semiconductor devices based on fluorite-structured ferroelectrics from the materials–device integration perspective. J. Appl. Phys. 128, 240904 (2020).
Materano, M. et al. Polarization switching in thin doped HfO2 ferroelectric layers. Appl. Phys. Lett. 117, 262904 (2020).
Park, M. H. et al. Study on the size effect in Hf0.5Zr0.5O2 films thinner than 8 nm before and after wake-up field cycling. Appl. Phys. Lett. 107, 192907 (2015).
Park, M. H. et al. Morphotropic Phase Boundary of Hf1–xZrxO2 Thin Films for Dynamic Random Access Memories. ACS Appl. Mater. Interf. 10, 42666 (2018).
Mehmood, F., Mikolajick, T. & Schroeder, U. Wake-Up Mechanisms in Ferroelectric Lanthanum-Doped Hf0.5Zr0.5O2 Thin Films. Phys. Status Solidi A 217, 2000281 (2020).
Tahara, K. et al. Strategy Toward HZO BEOL-FeRAM with Low-Voltage Operation (≤1.2V), Low Process Temperature, and High Endurance by Thickness Scaling. 2021 Symposium VLSI Technol. 17, 1–2 (2021)
Grimley, E. D. et al. Structural Changes Underlying Field-Cycling Phenomena in Ferroelectric HfO2 Thin Films. Adv. Electron. Mater. 2, 1600173 (2016).
Lomenzo, P. D., Richter, C., Mikolajick, T. & Schroeder, U. Depolarization as Driving Force in Antiferroelectric Hafnia and Ferroelectric Wake-Up. ACS Appl. Electron. Mater. 2, 1583–1595 (2020).
Mehmood, F. et al. Bulk Depolarization Fields as a Major Contributor to the Ferroelectric Reliability Performance in Lanthanum Doped Hf0.5Zr0.5O2 Capacitors. Adv. Mater. Interf. 6, 1901180 (2019).
Lederer, M. et al. On the Origin of Wake-Up and Antiferroelectric-Like Behavior in Ferroelectric Hafnium Oxide. Phys. Status Solidi RRL 15, 2100086 (2021).
Lomenzo, P. D. et al. A Gibbs energy view of double hysteresis in ZrO2 and Si-doped HfO2. Appl. Phys. Lett. 117, 142904 (2020).
Zacharaki, C. et al. Very large remanent polarization in ferroelectric Hf1-xZrxO2 grown on Ge substrates by plasma assisted atomic oxygen deposition. Appl. Phys. Lett. 114, 112901 (2019).
Xi, Z. et al. Giant tunnelling electroresistance in metal/ferroelectric/semiconductor tunnel junctions by engineering the Schottky barrier. Nat. Commun. 8, 15217 (2017).
Zacharaki, C. et al. Reliability aspects of ferroelectric TiN/Hf1-xZrxO2/Ge capacitors grown by plasma assisted atomic oxygen deposition. Appl. Phys. Lett. 117, 212905 (2020).
Zacharaki, C. et al. Depletion induced depolarization field in Hf1-xZrxO2 metal-ferroelectric-semiconductor capacitors on germanium. Appl. Phys. Lett. 116, 182904 (2020).
O’Connor, E. et al. Stabilization of ferroelectric HfxZr1−xO2 films using a millisecond flash lamp annealing technique. APL Mater. 6, 121103 (2018).
Materlik, R., Künneth, C. & Kersch, A. The origin of ferroelectricity in Hf1−xZrxO2: a computational investigation and a surface energy model. J. Appl. Phys. 117, 134109 (2015).
Müller, J. et al. Ferroelectricity in Simple Binary ZrO2 and HfO2. Nano Lett. 12, 4318–4323 (2012).
Park, M. H. et al. Ferroelectricity and Antiferroelectricity of Doped Thin HfO2-Based Films. Adv. Mater. 27, 1811–1831 (2015).
Park, M. H. et al. Evolution of phases and ferroelectric properties of thin Hf0.5Zr0.5O2 films according to the thickness and annealing temperature. Appl. Phys. Lett. 102, 242905 (2013).
Mittmann, T. et al. Optimizing process conditions for improved Hf1-xZrxO2 ferroelectric capacitor performance. Microelectron. Eng. 178, 48–51 (2017).
Kim, H. J. et al. A study of the wake-up effect of ferroelectric Hf0.5Zr0.5O2 films by pulse switching mechanism. Nanoscale 8, 1383 (2016).
Lyu, J., Song, T., Fina, I. & Sanchez, F. High polarization, endurance and retention in sub 5 nm Ηf0.5Ζr 0.5Ο2 films. Nanoscale 12, 11280 (2020).
Oh, S., Kim, H., Kashir, A. & Hwang, H. Effect of dead layers on the ferroelectric property of ultrathin HfZrOx film. Appl. Phys. Lett. 117, 252906 (2020).
Sze, S. M. & Ng, K. K. Physics of Semiconductor Devices - Third Edition, p. 789 (John Wiley and Sons, 2007).
Kim, Y. J. et al. Interfacial charge-induced polarization switching in Al2O3/Pb(Zr,Ti)O3 bi-layer. J. Appl. Phys. 118, 224105 (2015).
Kim, Y. J. et al. Frustration of Negative Capacitance in Al2O3/BaTiO3 Bilayer Structure. Sci. Rep. 6, 19039 (2016).
Landau, L. D. & Khalatnikov, I. M. On the anomalous absorption of a sound near to points of phasetransition of the second kind. Dokl. Akad. Nauk. SSSR 96, 469 (1954) in “Collected Papers of L. D. Landau edited by D. ter Haar, 1st Edition, Pergamon Press (1965).
Blinc, R. & Zeks, B. Soft Modes in Ferroelectrics and Antiferroelectrics. p. 21 (American Elsevier New York, North-Holland, Amsterdam, 1974).
Park, H. W. et al. Polarizing and depolarizing charge injection through a thin dielectric layer in a ferroelectric – dielectric bilayer. Nanoscale 13, 2556–2572 (2021).
Shockley, W. & Read, W. T. Statistics of the recombinations of holes and electrons. Phys. Rev. 87, 835–842 (1952).
Hall, R. N. Electron-hole recombination in Germanium. Phys. Rev. 87, 387 (1952).
Rollo, T., Blanchini, F., Giordano, G., Specogna, R. & Esseni, D. Stabilization of negative capacitance in ferroelectric capacitors with and without a metal interlayer. Nanoscale 12, 6121 (2020).
Tagantsev, A. K., Stolichnov, I., Setter, N., Cross, J. S. & Tsukada, M. Non-Kolmogorov-Avrami switching kinetics in ferroelectric thin films. Phys. Rev. B 66, 214109 (2002).
Kolmogorov A. N. On the Statistical Theory of Crystallization of Metals. Izv. Akad. Nauk SSSR Ser. Mater. 3, 355 (1937).
Avrami, M. Kinetics of phase change. I general theory. J. Chem. Phys. 7, 1103 (1939).
Ishibashi, Y. & Takagi, Y. Note on ferroelectric domain switching. J. Phys. Soc. Jpn. 31, 506 (1971).
Zhukov, S. et al. Dynamics of polarization reversal in virgin and fatigued ferroelectric ceramics by inhomogeneous field mechanism. Phys. Rev. B 82, 014109 (2010).
Zhao, D. et al. Depolarization of multidomain ferroelectric materials. Nat. Commun. 10, 2547 (2019).
Fridkin, V. M. & Ducharme, S. General features of the intrinsic ferroelectric coercive field. Phys. Solid State 43, 1320–1324 (2001).
Stolichnov, I. et al. Intrinsic or nucleation-driven switching: an insight from nanoscopic analysis of negative capacitance Hf1−xZrxO2-based structures. Appl. Phys. Lett. 117, 172902 (2020).
Pešić, M. et al. A computational study of hafnia-based ferroelectric memories: from ab initio via physical modeling to circuit models of ferroelectric device. J. Comput. Electron. 16, 1236–1256 (2017).
See e.g., G. Burns “Solid State Physics”. 536–542 (Academic Press Inc, 1985) edition.
Hoffmann, M. et al. Unveiling the double-well energy landscape in a ferroelectric layer. Nature 565, 464–467 (2019).
Pešic, M. et al. Physical mechanisms behind the field-cycling behavior of HfO2-based ferroelectric capacitors. Adv. Funct. Mater. 26, 25 (2016).
Lomenzo, P. D. et al. TaN interface properties and electric field cycling effects on ferroelectric Si-doped HfO2 thin films. J. Appl. Phys. 117, 134105 (2015).
Mimura, T., Shimizu, T., Sakata, O. & Funakubo, H. Large thermal hysteresis of ferroelectric transition in HfO2-based ferroelectric films. Appl. Phys. Lett. 118, 112903 (2021).
Acknowledgements
Funding from the EU H2020 projects BeFerroSynaptic-871737 and 3eFERRO-780302 is gratefully acknowledged. L.P. and C.M.I. acknowledge partial funding through project CEPROFER/PN-III-P4-ID-PCCF-2016-0047 (contract 16/2018, funded by UEFISCDI).
Author information
Authors and Affiliations
Contributions
N.S. was involved in the growth of HZO layers and performed the electrical characterization. P.T. contributed to the growth and device modeling. C.Z. was involved in the device processing and electrical characterization. S.C. was involved in RTA crystallization annealing. L.B.-L. performed Flash Lamp Annealing of the samples, Grazing Incidence X-ray diffraction scans and X ray reflectometry scans in order to extract the film thickness and phase composition. C.I. and L.P. performed High Resolution Transmission Electron Microscopy in order to image the domain configuration of the films and confirm film thickness. A.D. was involved in the electrical characterization and data analysis.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Pavan Nukala and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Siannas, N., Zacharaki, C., Tsipas, P. et al. Metastable ferroelectricity driven by depolarization fields in ultrathin Hf0.5Zr0.5O2. Commun Phys 5, 178 (2022). https://doi.org/10.1038/s42005-022-00951-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00951-x
This article is cited by
-
Ferroelectricity in hafnia controlled via surface electrochemical state
Nature Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.