Introduction

The non-Abelian braiding statistics of Majorana zero modes (MZMs) is a key component in realizing topological quantum computing1. Evidence for the existence of these modes has been observed in one-2,3,4,5,6,7,8 and two-dimensional (2D)9,10,11 topological superconductors, however, their unambiguous identification has been experimentally hampered by the small superconducting gaps in these systems, which are often only of the order of a few hundred μeV. The recent report of topological superconductivity in the iron-based superconductor FeSe0.45Te0.55, as evidenced by the observation of a surface Dirac cone12,13,14,15, of MZMs in the vortex core16,17,18,19 and at the end of line defects in monolayer FeSe0.5Te0.5 deposited on a SrTiO3 substrate20, and of a Majorana edge mode at a domain wall21, has therefore been greeted with much enthusiasm as this system possesses a significantly larger superconducting gap of a few meV. The origin of topological surface superconductivity was proposed to arise from a band-inversion involving the bulk pz and dxz-bands12,22,23,24—rendering FeSe0.45Te0.55 a 3D topological insulator—and the gapping of the ensuing surface Dirac cone by proximity induced superconductivity (we refer to this as the 3DTI mechanism). This topological surface state is described by a Z2 invariant and protected by time-reversal symmetry. However, a series of recent angle-resolved photoemission spectroscopy (ARPES) experiments13,14,15 on FeSe1−xTex with Te concentrations ranging from x = 0.55 to x = 0.7 have reported that the Dirac cone becomes gapped below Tc not only at the Fermi energy, EF, as expected for proximity induced superconductivity, but also at the Dirac point which lies approximately 8 meV below EF. The latter gapping is a direct consequence of a broken time-reversal symmetry, and was interpreted as arising from the emergence of surface ferromagnetism14, a conclusion has received further support from the observation of such magnetism in quantum sensing experiments on FeSe0.3Te0.725. As topological surface superconductivity arising from the 3DTI mechanism is destroyed by already rather weak surface ferromagnetism26,27, the question naturally arises of whether a different mechanism might be responsible for the emergence of topological surface superconductivity and the ensuing Majorana modes16,17,18,19,20,21 in FeSe0.45Te0.55.

In this article, we address this question by proposing that the ferromagnetism observed experimentally13,14,15,25 is a key element in the emergence of topological superconductivity in the α-, β- and γ-bands of FeSe0.45Te0.55, when combined with two other essential properties of FeSe0.45Te0.55: its superconducting gap of s±-wave symmetry and strong Rashba spin–orbit (RSO) interaction28,29 arising from the broken inversion symmetry at the surface. This proposed mechanism for topological superconductivity in FeSe0.45Te0.55 is qualitatively different from the 3DTI mechanism, in that its starting point is the 2D nature of superconductivity in FeSe0.45Te0.5530,31,32,33. While it is well established that the interplay of ferromagnetism, RSO interaction and an s±-wave superconducting gap can in general lead to topological superconductivity34,35,36,37,38,39,40,41, we demonstrate here, using a material-specific 5-band model42 that the proposed mechanism does not only give rise to robust topological superconducting phases on the surface of FeSe0.45Te0.55, characterized by a Z topological invariant, the Chern number, but also explains the observation of Majorana zero modes in vortex cores16,17,18,19 and at the end of line defects20 in monolayer FeSe0.5Te0.5/SrTiO320, as well as the emergence of dispersive Majorana edge modes along domain walls21. In addition, we propose an experimental signature, the presence or absence of supercurrents along domain walls, which can distinguish topological Majorana modes from trivial in-gap states and can be imaged via a scanning superconducting quantum interference device (SQUID)43. Our model predicts that topological superconductivity can also emerge in other iron-based superconductors, if surface ferromagnetism either occurs naturally, or can be induced, for example, through doping with magnetic defects or the addition of magnetic surface layers.

Results

Theoretical model

Our starting point for the investigation of topological superconductivity on the surface of FeSe0.45Te0.55 is the experimental observation that superconductivity in the iron-based superconductors emerges form the pairing of electrons in the α-, β-, and γ-bands33. ARPES experiments on the parent compound FeSe have shown that these bands are quasi two-dimensional, exhibiting only a weak dispersion along kz31,32,33. The smooth (and weak) dependence of Tc with Te-doping provides strong evidence that these bands remain quasi two-dimensional with Te-doping in FeSe1−xTex44. We, therefore, employ a 2D 5-orbital model45 that has previously been employed to successfully describe the 2D superconducting properties of the iron-based superconductors. The hopping parameters for this model were extracted from a fit to ARPES experiments on FeSe0.42Te0.5846 and scanning tunneling spectroscopy (STS) experiments on FeSe0.45Te0.5542. To describe the emergence of topological superconductivity on the surface of FeSe0.45Te0.55, we include in this model (a) the experimentally observed surface ferromagnetism13,14,15,25 through an exchange field, and (b) a RSO interaction that arises from the breaking of the inversion symmetry on the surface (for detail, see Supplementary Note 1). The resulting Hamiltonian in real space is given by

$${H}_{0}= -\mathop{\sum }\limits_{a,b=1}^{5}\mathop{\sum}\limits_{{{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{{r}}}}}}}^{\prime}}},\sigma }{t}_{{{{{{{{\bf{r,{r}}}}}}}^{\prime}}}}^{ab}{c}_{{{{{{{{\bf{r}}}}}}}},a,\sigma }^{{{{\dagger}}} }{c}_{{{{{{{{\bf{{r}}}}}}}^{\prime}}},b,\sigma }-\mathop{\sum }\limits_{a=1}^{5}\mathop{\sum}\limits_{{{{{{{{\bf{r}}}}}}}},\sigma }{\mu }_{a}{c}_{{{{{{{{\bf{r}}}}}}}},a,\sigma }^{{{{\dagger}}} }{c}_{{{{{{{{\bf{r}}}}}}}},a,\sigma }\\ +i\alpha \mathop{\sum }\limits_{a=1}^{5}\mathop{\sum}\limits_{{{{{{{{\bf{r}}}}}}}},{{{{{{{\boldsymbol{\delta }}}}}}}},\sigma ,\sigma ^{\prime} }{c}_{{{{{{{{\bf{r}}}}}}}},a,\sigma }^{{{{\dagger}}} }{\left({{{{{{{\boldsymbol{\delta }}}}}}}}\times {{{{{{{\boldsymbol{\sigma }}}}}}}}\right)}_{\sigma \sigma ^{\prime} }^{z}{c}_{{{{{{{{\bf{r}}}}}}}}+{{{{{{{\boldsymbol{\delta }}}}}}}},a,\sigma ^{\prime} }^{}+J\mathop{\sum }\limits_{a=1}^{5}\mathop{\sum}\limits_{{{{{{{{\bf{r}}}}}}}},\sigma ,{\sigma }^{\prime}}{{{{{{{{\bf{S}}}}}}}}}_{{{{{{{{\bf{r}}}}}}}}}\cdot {c}_{{{{{{{{\bf{r}}}}}}}},a,\sigma }^{{{{\dagger}}} }{{{{{{{{\boldsymbol{\sigma }}}}}}}}}_{\sigma {\sigma }^{\prime}}{c}_{{{{{{{{\bf{r}}}}}}}},a,{\sigma }^{\prime}}^{}\\ +\mathop{\sum }\limits_{a=1}^{5}\mathop{\sum}\limits_{\langle \langle {{{{{{{\bf{r}}}}}}}},{{{{{{{\bf{{r}}}}}}}^{\prime}}}\rangle \rangle }{{{\Delta }}}_{{{{{{{{\bf{r}}}}}}}}{{{{{{{{\bf{r}}}}}}}}}^{\prime}}^{a}{c}_{{{{{{{{\bf{r}}}}}}}},a,\uparrow }^{{{{\dagger}}} }{c}_{{{{{{{{\bf{{r}}}}}}}^{\prime}}},a,\downarrow }^{{{{\dagger}}} }+{{{{{{{\rm{H.c.}}}}}}}}$$
(1)

Here a, b = 1, . . . , 5 are the orbital indices corresponding to the dxz-, dyz-, \({d}_{{x}^{2}-{y}^{2}}\)-, dxy-, and \({d}_{3{z}^{2}-{r}^{2}}\)-orbitals, respectively, \(-{t}_{{{{{{{{\bf{r{r}}}}}}}^{\prime}}}}^{ab}\) represents the electronic hopping amplitude between orbital a at site r and orbital b at site \({{{{{{{\bf{{r}}}}}}}^{\prime}}}\) on a 2D square lattice, μa is the on-site energy in orbital a, \({c}_{{{{{{{{\bf{r}}}}}}}},a,\sigma }^{{{{\dagger}}} }({c}_{{{{{{{{\bf{r}}}}}}}},a,\sigma })\) creates (annihilates) an electron with spin σ at site r in orbital a, and σ is the vector of spin Pauli matrices. The superconducting order parameter \({{{\Delta }}}_{{{{{{{{\bf{r}}}}}}}}{{{{{{{\bf{r}}}}}}}}^{\prime} }^{a}\) represents intra-orbital pairing between next-nearest neighbor Fe sites r and \({{{{{{{\bf{r}}}}}}}}^{\prime}\) (in the 1 Fe unit cell), yielding a superconducting s±-wave symmetry42. Moreover, α denotes the RSO interaction arising from the breaking of the inversion symmetry at the surface3 with δ being the vector connecting nearest neighbor sites. Due to the full superconducting gap, which suppresses Kondo screening, we consider the magnetic moments to be static in nature, such that Sr is a classical vector representing the direction of a surface atom’s spin located at r, and J is its exchange coupling with the conduction electron spin. We here assume that the magnetic moment couples with equal strength to all 5 orbitals. The experimentally observed opening of a gap at the Dirac point13,14,15 implies an ordering of the magnetic moments perpendicular to the surface, as also confirmed by quantum sensing experiments25, such that \(\langle {{{{{{{{\bf{S}}}}}}}}}_{{{{{{{{\bf{r}}}}}}}}}\rangle =S\hat{{{{{{{{\bf{z}}}}}}}}}\) with S being the ordered spin moment on the surface. In the normal state, the above Hamiltonian yields Fermi surfaces42 that are consistent with those reported by ARPES experiments on FeSe0.42Te0.5846 (see Supplementary Note 1 and Supplementary Fig. 1). Due to the orbital character of the Fermi surfaces, the superconducting order parameter is only non-zero in the dxz-, dyz-, and dxy-orbitals42. The local density of states (LDOS) resulting form the above Hamiltonian in the superconducting state reproduces all salient features of the differential conductance, dI/dV, measured via STS (see Supplementary Note 1 and Supplementary Fig. 1), and in particular shows the existence of several superconducting gaps ranging from 1.6 meV to 2.4 meV. As noted in ref. 15, the electronic structure of FeSe0.45Te0.55 obtained from DFT calculations22 shows significant differences to those observed via ARPES experiments46, such that the former cannot be used as a reliable starting point for our calculations. Below, we assume that the topological superconducting state arising from the 3DTI mechanism is destroyed26,27 by the experimentally observed surface ferromagnetism13,14,15,25—a destruction which is achieved already for rather weak exchange coupling JS (see “Discussion” below)—and thus neglect the bulk bands and Dirac cone associated with the 3DTI mechanism.

We note that due to the particle-hole symmetry of the superconducting state, and the broken time-reversal symmetry arising from the presence of magnetic moments, FeSe0.45Te0.55 belongs to the topological class D47,48. For a 2D system, the topological invariant is therefore given by the Chern number, which can be computed via49

$$C = \frac{1}{2\pi i}\int_{{{{{{{{\rm{BZ}}}}}}}}}{{{{{{\rm{d}}}}}}}^{2}k{{{{{{{\rm{Tr}}}}}}}}({P}_{{{{{{{{\bf{k}}}}}}}}}[{\partial }_{{k}_{x}}{P}_{{{{{{{{\bf{k}}}}}}}}},{\partial }_{{k}_{y}}{P}_{{{{{{{{\bf{k}}}}}}}}}])\\ {P}_{{{{{{{{\bf{k}}}}}}}}} = \mathop{\sum}\limits_{{E}_{n}({{{{{{{\bf{k}}}}}}}}) < 0}\left|{{{\Psi }}}_{n}({{{{{{{\bf{k}}}}}}}})\right\rangle \left\langle {{{\Psi }}}_{n}({{{{{{{\bf{k}}}}}}}})\right|$$
(2)

where En(k) and \(\left|{{{\Psi }}}_{n}({{{{{{{\bf{k}}}}}}}})\right\rangle\) are the eigenenergies and the eigenvectors of the Hamiltonian in Eq. (1), with n being a band index, and the trace is taken over Nambu and spin space.

Topological phase diagram

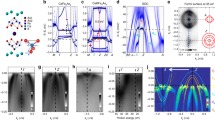
The existence of a hard superconducting gap, a RSO interaction, and an out-of-plane ferromagnetic order are in general sufficient requirements for the emergence of topological surface superconductivity34,35,36,37,38,39,40,41. To demonstrate that this emergence is a robust phenomenon in FeSe0.45Te0.55 within the proposed model, we present in Fig. 1 the topological phase diagram—in terms of the Chern number C—computed from Eq. (2) as a function of the effective magnetic exchange strength JS, and of a shift of the chemical potential, Δμ, from its value extracted in ref. 42. We find that already for rather weak magnetism, as reflected in a magnetic exchange coupling JS of the order of a few meV, the system undergoes transitions into topological superconducting phases.

Fig. 1: Topological phase diagram.
figure 1

Topological phase diagram of FeSe0.45Te0.55 in the (Δμ, JS)-plane with α = 7 meV. Here, α is the Rashba spin–orbit coupling, and JS is the magnetic exchange strength. Δμa is a shift in the chemical potential of orbital a from the value used in Eq. 1), i.e., μa → μa + Δμa. Here, Δμa = Δμ for all orbitals a. The solid, dashed, and dotted black lines indicate gap closings at the Γ-, X/Y-, and M-points, respectively, which accompany the topological phase transitions. ΔC is the change in the Chern number across a topological phase transition. The gray area denotes the gapless region.

Full size image

We note that the positions of the topological phase transitions are independent of the strength of the RSO interaction α (as long as α does not vanish), only the topological gap increases with increasing α. While the presence of topological phases is robust against shifts in the chemical potential, varying Δμ induces transitions between topological phases characterized by different Chern numbers. With increasing JS (keeping all other band parameters fixed), the Fermi surfaces eventually cross the nodal lines of the superconducting s±-wave order parameter, and the system becomes gapless (as denoted by the gray area in Fig. 1), and hence topologically trivial. We note, however, that this gapless region of the phase diagram can be shifted to larger values of JS by appropriately adjusting the band parameters in Eq. (1). The points in the (Δμ, JS)-plane, where the topological phase transitions occur, are determined by the closing of the superconducting gap. Analytical expressions for these phase transition lines can be obtained (see Supplementary Note 2) and are plotted as solid, dashed, and dotted lines in Fig. 1) representing the closing of the gap at the Γ-, X/Y-, and M-points in the Brillouin zone, respectively. The X/Y-, and M-points possess a multiplicity of m = 2 and m = 1, leading to a change in the Chern number by ΔC = +2 and ΔC = −1, respectively. In contrast, while the Γ-point possesses a multiplicity of m = 1, the vanishing of the RSO interaction at the Γ-point yields a simultaneous gap closing in two bands, leading to a change in the Chern number by ΔC = −2. We note that the inclusion of a conventional L ⋅ S spin–orbit coupling28,29 in the Hamiltonian does not qualitatively change the topological phase diagram shown in Fig. 1, but rather increases the parameter space in which topological superconducting phases can be found (see Supplementary Note 3 for a more detailed discussion).

Having established the presence of topological superconducting phases in FeSe0.45Te0.55 arising from the proposed mechanism, we next turn to a discussion of their unique physical properties that have been observed experimentally.

MZM in a vortex core

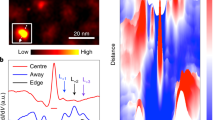
The experimental observation of MZMs localized in vortex cores16,17,18,19 represents a salient signature of the topological nature34,50,51,52,53 of the superconducting surface in FeSe0.45Te0.55. To investigate the emergence of a vortex core MZM within our model, we implement the magnetic field via the Peierls substitution and compute the spatial dependence of the superconducting order parameters in the dxz-, dyz-, and dxy-orbitals self-consistently (for details, see Supplementary Note 4). The resulting spatial structure of the superconducting order parameter in the dxz-orbital, which vanishes at the center of the vortex, in the topological C = −1 phase is shown in Fig. 2a (the analogous plots for the dyz-, and dxy-orbitals are shown in Supplementary Note 4). We find that all three superconducting order parameters possess the same spatial symmetry as the orbitals they arise from, i.e., a C2-symmetry in the dxz-, and dyz-orbitals, and a C4-symmetry in the dxy-orbital. A linecut of the energy-resolved LDOS for the dxz- (Fig. 2b) and dxy-orbitals (Fig. 2c) through the vortex core reveals the existence of a MZM in the topological C = −1 phase, which is absent in the trivial C = 0 phase (Fig. 2d) (results for other orbitals are shown in Supplementary Note 4).

Fig. 2: Majorana zero mode in a vortex core.
figure 2

a Spatial dependence of the superconducting order parameter in the dxz-orbital near a vortex core for a magnetic field of B = 2T. Color bar represents the normalized superconducting order parameter. Linecut of the orbitally-resolved local density of states, Na(r, E), through the center of the vortex core along the x-axis for the b dxz-, and c dxy-orbital in the topological phase with Chern number C = −1 and (JS, α, Δμxz, Δμyz, Δμxy) = (7.5, 7, 4, 4, 1) meV (the Majorana zero mode is indicated by a yellow arrow). Here, α is the Rashba spin–orbit coupling, and JS is the magnetic exchange strength. Color bar represents the normalized local density of states. d Linecut of the orbitally-resolved local density of states, Na(r, E), through the center of the vortex core along the x-axis for the dxz-orbital in the trivial C = 0 phase with (JS, α, Δμxz, Δμyz, Δμxy) = (3, 7, 4, 4, 1) meV. For the C = −1 topological phase (same parameters as in b, c): e Radially integrated local density of states for the dxz-orbital. f Energy position of the of the low energy states, as revealed by the peaks in the local density of states in (e).

Full size image

In addition to the MZM, the LDOS for all orbitals reveals topologically trivial Caroli-de Gennes-Matricorn (CdGM) states54, similar to results obtained in other iron-based superconductors55. The radially integrated LDOS for the dxz-orbital (see Fig. 2e) shows an equal energy spacing of the low-energy CdGM states described by En = nE0 (see Fig. 2f). This integer spacing of the low-energy CdGM states was also observed in refs. 18,19. Moreover, certain CdGM states possess a large spatial extent, exhibiting significant spectral weight up to a distance of r ≈ 20a0 from the vortex core (see red arrows in Fig. 2b). These spatially extended CdGM states, in turn, also exhibit an equal energy spacing \({E}_{p}^{\prime}=p{E}_{0}^{\prime}\), with \({E}_{0}^{\prime} > {E}_{0}\) (see filled red circles in Fig. 2f). While the existence of an MZM is topologically protected, we find that the spatial and energy structure of the trivial CdGM states can vary significantly within a given topological phase (see Supplementary Note 4). Indeed, the spatial structure of the CdGM states even varies significantly between orbitals (cf. the LDOS for the dxz- and dxy-orbitals shown in Fig. 2b and c, respectively) for a given point in the phase diagram. This might explain the observation that while different STS experiments have observed the existence of zero-energy vortex core bound states in FeSe0.45Te0.55, the observed spatial and energy structure of the trivial CdGM states varies greatly between experiments16,17,18,19. While it will be of interest in the future to develop a more detailed understanding of how the spatial and energy structure of the CdGM states emerges from the multi-band electronic structure of FeSe0.45Te0.55, and how the observed differential conductance  emerges from co-tunneling effects, our results demonstrate that the spatial and energy structure of the CdGM states bears no relevance for the existence of a topological phase, in agreement with the experimental observations16,17,18,19.

Moreover, the experimental observation that only a fraction of vortices on the surface of FeSe0.45Te0.55 possesses MZMs16,17 has remained an important unsolved problem. One possible explanation for this finding could arise from the experimental observation of strong disorder on the surface of FeSe0.45Te0.5556,57, which is particular evident in the spatial variation of the chemical potential57. Indeed, within the scenario proposed here, spatial variations in the chemical potential, as reflected in Δμ in Fig. 1, could lead to topological or trivial domains on the surface of FeSe0.45Te0.55, in which case only those vortices located in the topological domains would exhibit a MZM. As trivial and topological domains need to be separated by a domain wall, which necessarily harbors a chiral Majorana mode (see “Discussion” below) the observation of such a mode in LDOS linecuts connecting trivial and topological vortices would be an important signature of this scenario26.

MZM at the end of line defects

The recent observation of MZMs at the end of line defects in monolayer FeSe0.5Te0.5 deposited on a SrTiO3 substrate20 has raised the question of whether these MZMs are a characteristic feature of an underlying topological phase, similar to line defect MZMs predicted to occur in topological px + ipy-wave superconductors58, or are independent of it, simply utilizing the monolayer’s complex electronic structure to form a 1D topological superconductor as proposed in refs. 20,59,60. While it is currently unknown whether the FeSe0.5Te0.5/SrTiO3 system is a topological superconductor, we note that the mechanism proposed here can in general give rise to topological superconductivity in monolayer systems (if ferromagnetism is present), while the 3DTI mechanism12,22,23,24 cannot. We therefore want to address two important questions: (i) can line defect MZMs emerge within the model of Eq. (1), and (ii) if so, are these MZMs directly tied to the existence of topological surface superconductivity, thus representing a sufficient condition for its existence.

To address these questions we represent the line defect for simplicity as a line of potential scatterers (though magnetic scatterers could also be realized59,60) described by the Hamiltonian

$${H}_{def}={U}_{0}\mathop{\sum }\limits_{a=1}^{5}\mathop{\sum}\limits_{{{{{{{{\bf{R}}}}}}}},\sigma }{c}_{{{{{{{{\bf{R}}}}}}}},a,\sigma }^{{{{\dagger}}} }{c}_{{{{{{{{\bf{R}}}}}}}},a,\sigma },$$
(3)

where U0 is the potential scattering strength, and the sum runs over all sites R of the line defect. In Fig. 3a, we present the energies of the three lowest energy states for a line defect of length L = 119 in the C = −1 phase as a function of U0. One can clearly discern three regions of U0 (shown with a gray background in Fig. 3a) where the lowest energy state is essentially located at zero energy (with the LDOS exhibiting a full gap of 1.6 meV, see Supplementary Note 1), suggesting the existence of a MZM. At the boundary of the white and gray regions in Fig. 3a, the superconducting gap of an infinitely long line defect closes, consistent with the occurrence of a topological phase transition. Further evidence for the existence of Majorana modes is revealed by line-cuts of the LDOS along the line defect with U0 = 71 meV, located in the rightmost gray region in Fig. 3a, for the lowest and second lowest energy states with energies E1 and E2, respectively (see Fig. 3b). The spectral weight of the lowest energy state at E1 is confined to the end of the line defect—with essentially no spectral weight located inside the defect line—consistent with the localized nature of an MZM. In contrast, the state at E2 exhibits considerable spectral weight along the entire length of the line defect. This result is also confirmed by a spatial plot of the LDOS at energies E1 and E2, shown in Fig. 3c and d, respectively. These findings provide strong evidence that the zero energy states localized at the end of the line defects in Fig. 3c are MZMs. Line defect MZMs also exist in the C = −3 phase, but no zero-energy states occur at the end of a line defect when FeSe0.45Te0.55 is in the topological trivial (C = 0) phase (see Supplementary Note 5). Within our model, the existence of line defect MZMs is therefore directly tied to and a sufficient condition for the existence of an underlying topological superconducting phase, while a failure to observe MZMs at line defects does not necessarily imply a trivial nature of the underlying superconducting phase. We thus predict that in addition to FeSe0.5Te0.5/SrTiO3, MZMs should emerge when line defects are placed on the surface of bulk FeSe0.45Te0.55. Finally, we note that while topological superconductivity on the surface of FeSe0.45Te0.55 is characterized by a Z topological invariant, the line defect as a one-dimensional system possesses a topological Z2 classification, similar to the Kitaev chain61.

Fig. 3: Majorana zero mode at the end of line defects.
figure 3

a Energies of the three lowest energy states, E1, E2, E3 as a function of scattering strength U0 for a line defect of length L = 119 sites in the topological phase with Chern number C = −1 and (JS, α, Δμ) = (7.5, 7, 0) meV. Here, α is the Rashba spin–orbit coupling, and JS is the magnetic exchange strength. The regions of U0 where the line defect exhibits a zero-energy state at its ends are shown using a gray background. b Linecut of the local density of states along the line defect for the two lowest energy states at E1, E2, and U0 = 71 meV. The plot of the local density of states at energies c E1 and d E2 for U0 = 71 meV. Filled black circles in c indicate the positions of the defects. The color bar represents the normalized local density of states.

Full size image

Chiral Majorana modes along domain walls

The bulk-boundary correspondence dictates that Majorana edge modes need to arise along domain walls that separate regions of different Chern numbers61. Indeed, the observation of a nearly constant LDOS at a domain wall in FeSe0.45Te0.5521 was recently interpreted as a signature of a Majorana edge mode (whether the observed mode is helical in nature as would arise from the 3DTI mechanism12,22,23,24,50, or chiral, as in our model, is experimentally currently unclear).

This raises the intriguing question not only as to which types of physical domain walls can give rise to the emergence of Majorana modes, but also of how to distinguish Majorana modes from trivial, in-gap states. To address this question, we calculate the electronic structure near two different types of domain walls: a spin domain wall at which the magnetic moment is inverted, i.e., S → −S, and a π-phase domain wall, where the superconducting order parameter undergoes a π-phase shift, i.e., Δ → −Δ, for all electronic bands. As the spin domain wall separates regions with different Chern numbers (since S → −S implies C → −C), the bulk boundary correspondence requires the emergence of dispersive Majorana edge modes that traverse the superconducting gap, as shown in Fig. 4a where we present the system’s electronic band structure as a function of momentum k∥ along the domain wall (Majorana modes are shown as red lines). In addition, the system also exhibits trivial in-gap modes, which do not connect the upper and lower bands. Similar results also hold for a domain wall separating a topological from a trivial domain. In contrast, regions separated by a π-phase domain wall possess the same Chern number, and the electronic band structure therefore only exhibits trivial in-gap states, as shown in Fig. 4b. In Fig. 4c, d, we present the LDOS as a function of energy along a linecut perpendicular to the domain wall. In both cases, we find that the LDOS near the domain wall exhibits considerable spectral weight inside the superconducting gap, with the LDOS being nearly energy independent for the spin domain wall, but exhibiting a pronounced peak at zero-energy for the π-phase domain wall. A linecut of the zero-energy LDOS, shown in Fig. 4e, f, however, reveals that the zero-energy state is localized close to the domain wall in both cases. Thus, the differences in the LDOS between these two types of domain walls is quantitative rather than qualitative in nature, and STS measurements might therefore not be able to distinguish between topological Majorana edge modes, and trivial in-gap states. However, a qualitative difference between these domain walls can be identified when considering the spatial structure of the induced supercurrents (see Supplementary Note 6). For a spin domain wall, the chirality of the induced supercurrent, which is determined by the sign of the Chern number, changes between the two separated regions, implying that the supercurrents associated with each region flow in the same direction along the domain wall40, as shown in Fig. 4g, yielding a non-vanishing net supercurrent. In contrast, for the π-phase domain wall, the chirality of the supercurrents in both regions is the same, implying that they flow in opposite directions along the domain wall (see Fig. 4h), yielding a vanishing net supercurrent. This qualitative difference, a non-zero net supercurrent for a spin domain wall and a vanishing net supercurrent for the π-phase domain wall, can be imaged using a SQUID, thus providing an unambiguous experimental signature to distinguish the existence of topological Majorana modes for a spin domain wall, from that of trivial in-gap states for a π-phase domain wall.

Fig. 4: Chiral Majorana modes along domain walls.
figure 4

Electronic band structure as a function of momentum k∥ along the domain wall for a a spin, and b a π-phase domain wall. Energy-resolved local density of states for c the spin, and d the π-phase domain wall along a linecut perpendicular to the domain wall. The position of the domain wall is indicated by a dashed gray line. Spatial plot of the zero-energy local density of states for e a spin, and f a π-phase domain wall. Spatial distribution of supercurrents near g the spin, and h the π-phase domain wall. For both domain walls, (α, Δμ) = (7, 0) meV, with JS = ±7.5 meV corresponding to domains with Chern number C = ±1 separated by the spin domain wall. Here, α is the Rashba spin–orbit coupling, and JS is the magnetic exchange strength.

Full size image

Discussion

We proposed a microscopic mechanism for the emergence of topological surface superconductivity in FeSe0.45Te0.55 arising from the interplay of surface magnetism, a RSO interaction, and a hard superconducting gap with s±-wave symmetry. This mechanism explains not only the emergence of robust topological phases already for weak surface magnetism, with effective magnetic exchange couplings of a few meV, but also the experimental observations of (i) MZMs in vortex cores, (ii) MZMs at the end of line defects in monolayer systems, and (iii) chiral Majorana edge modes at domain walls. In addition, we demonstrated that by measuring supercurrents along domain walls using a SQUID it is possible to distinguish topological Majorana modes from trivial in-gap states. Within our scenario, the existence of Majorana modes is driven by the topological nature of the α-, β- and γ-bands, in contrast to the previously proposed 3DTI mechanism12,22,23,24. Our proposal is motivated by a series of recent ARPES experiments on FeSe1−xTex with 0.55 ≤ x ≤ 0.713,14,15 which interpreted the opening of a gap at the Dirac point below Tc as arising from the onset of surface ferromagnetism (though other explanations invoking time-reversal symmetry breaking have also been proposed62), an interpretation that received further support from the direct observation of ferromagnetism in quantum sensing experiments on FeSe0.3Te0.725. However, such surface ferromagnetism26,27 destroys the topological superconducting phase arising from the 3DTI mechanism via a topological phase transition into a trivial half quantum anomalous Hall (hQAH) state26 when JS exceeds a critical value of \({(JS)}_{cr}=\sqrt{{E}_{D}^{2}+{{{\Delta }}}^{2}}\), where ED is the energy of the Dirac point, and Δ is the superconducting gap. In FeSe0.45Te0.55, where ED ≈ −8 meV, and Δ ≈ 2 meV42, this implies a destruction of the topological phase at (JS)cr ≈ 8–9 meV, which is quite weak as typical values of JS are of the order of eV, rather than meV10. On the other hand, for such values of JS, the mechanism we proposed renders stable topological superconducting phases, as shown in Fig. 1. The question naturally arises of whether the available ARPES data13,14,15 provide evidence for a topological phase transition and a concomitant gap closing at the Γ-point taking place below Tc when JS exceeds (JS)cr. While the ARPES data14 clearly show a temperature evolution below Tc in which the spectral function of the Dirac point located at Γ shifts towards the Fermi energy (as expected when approaching a gap closing), the small superconducting gap of Δ ≈ 2 meV in combination with an energy resolution of the ARPES experiments of ΔE ≈ 2.5 meV14 make it difficult to ascertain whether the gap indeed closes. Clearly, future high resolution ARPES experiments are required to answer this important question. Another interesting topic in this regard for future research will be to identify new approaches to either manipulate the observed surface ferromagnetism (and identify its microscopic origin) or artificially create it through the use of magnetic adatoms.

There are two intriguing consequences arising from the scenario we proposed. First, as follows from Fig. 1 and the above discussion, there exists a range of JS < (JS)cr in which both our model and the 3DTI mechanism give rise to topological superconducting phases, opening the exciting possibility for their coexistence in FeSe0.45Te0.55. Indeed, the first experimental evidence for the coexistence of topological phases in the iron-based superconductors was recently reported63. Identifying the physical properties of such coexisting topological phases could provide new paths to the engineering of Majorana modes. Second, a key element for the emergence of topological surface superconductivity within our scenario is the presence of surface ferromagnetism. This opens the enthralling possibility to find topological phases in other iron-based superconductors exhibiting surface ferromagnetism, or to quantum engineer topological superconductivity in heterostructures consisting of iron-based superconductors and magnetic layers. Both possibilities provide exciting prospects for the future discovery and quantum engineering of topological superconductivity.

Methods

To compute the Chern number of FeSe0.45Te0.55, yielding the topological phase diagram of Fig. 1, we employ Eq. (2). To calculate the electronic structure of a vortex, we implement the magnetic field via the Peierls substitution and compute the spatial dependence of the superconducting order parameters in the dxz-, dyz-, and dxy-orbitals self-consistently, as described in Supplementary Note 4. The LDOS is computed by rewriting the Hamiltonian of Eq. (1) in terms of a Hamiltonian matrix, \(\hat{H}\), in real and Nambu space, and calculating the retarded Greens function matrix \({\hat{g}}^{{{{{{{{\rm{r}}}}}}}}}\) using \({\hat{g}}^{{{{{{{{\rm{r}}}}}}}}}(\omega )={\left[(\omega +{{{{{\rm{i}}}}}}\delta )\hat{1}-\hat{H}\right]}^{-1}\). The local, spin-resolved density of states, N(r, ω, σ) at site r is then obtained via \(N({{{{{{{\bf{r}}}}}}}},\sigma ,\omega )=-{{{{{{{\rm{Im}}}}}}}}\left[{\hat{g}}^{{{{{{{{\rm{r}}}}}}}}}({{{{{{{\bf{r}}}}}}}},\sigma ;{{{{{{{\bf{r}}}}}}}},\sigma ;\omega )\right]/\pi\). The supercurrent is calculated using the Keldysh formalism, as described in Supplementary Note 6.