Introduction

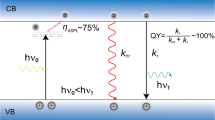
Over the past few years, micro/nanostructured all-inorganic semiconductor perovskites hold great promises as microscale light source for potential application in photonic integrated systems due to their extraordinary optoelectronic properties1,2,3,4,5. Substantial research on lasing emission from cesium lead halide perovskites with diverse morphologies, including nanowires6, nanosheets7, microspheres8, microdisks9 and quantum dots10, has been conducted under optical pumping. Related photophysics involved in the stimulated emission has also been explored in Fabry‒Pérot cavity11,12,13,14 and whispering-gallery-mode cavity15,16,17,18. Among the CsPbX3 (X=Cl, Br, and I) perovskites, the superior stability and better quantum efficiency render the bromide counterparts very promising in the next generation green-emitting devices. Particularly, the short green laser pulses with high peak energies are always highly required for medical treatment and underwater communication19,20. To date, despite a plethora of publications on lasing action in CsPbBr3 perovskites, it remains rare to establish concern on how to achieve the short pulse from such material system.

At present, three major techniques have been employed to generate short laser pulses from semiconductor lasers, including mode-locking, Q-switching and gain-switching techniques. Gain-switching technique is a very simple method for short-pulse generation via directly modulating optical gain in semiconductor lasers. It requires neither complicated laser systems, delicate alignment, nor elaborate device structures21,22, and the output pulse frequency can be modulated freely by an external pump source with tunable frequency. The gain-switched pulse width can be compressed to a few picoseconds (ps) by applying post-processing techniques, such as pulse shaping23, spectral filtering24, and pulse compression25,26. Gain-switched pulses with duration from several to hundreds of ps have been obtained in various semiconductor lasers using above techniques or even without any post-processing27,28,29,30,31, and even sub-picosecond pulses have been obtained recently via gain-switching and spectral-filtering techniques32. Compared to the conventional II‒VI and III‒V semiconductor compounds systems, lead halide perovskite microcavity lasers exhibit higher optical gain and shorter photon lifetime, making it more fascinating for the ultrashort pulses generation through gain-switching. However, investigation on gain-switching characteristics in a perovskite laser is still lacking in spite of its great value in practical applications. Generally, a kinetic rate equations model is utilized to study the fundamental electrical and photophysical kinetics in gain-switched process, where the optical gain is usually assumed to be linearly related to the carrier density33. The recent studies, however, have revealed strong gain-saturation nonlinearity, especially under strong pumping conditions33,34. Moreover, it has been demonstrated that carrier recombination processes play an important role during gain-switching35. The carrier recombination rate R can be characterized by a function of carrier densities n with ABC coefficients, the so called ABC model, i.e., R(n) = An + Bn2 + Cn3, where A, B, and C are Shockley‒Read‒Hall (SRH), radiative, and Auger coefficients, respectively. Consequently, the gain-saturation nonlinearity and the ABC model should be introduced into the rate equation model to comprehensively understand the carrier kinetics and short pulse generation mechanism during gain-switching processes.

In this work, we reported single-mode laser operations in CsPbBr3 microwires under femtosecond (fs) optical pumping. The short pulses of dozen ps were experimentally obtained by excitation-fluence dependent time-resolved photoluminescence (TRPL). Clear gain-switching mechanism for the short pulses generation were revealed. With taking the gain nonlinearities and the carrier recombination ABC model into account, the gain-switching characteristics and dynamics of short pulses from the CsPbBr3 microwires were semi-quantitively simulated at elevated pump levels based on a modified rate equation model. It was found that the low transient saturated gain of CsPbBr3 microwires under gain-switching operations greatly affected the generation of shorter optical pulse, and the carrier heating could be a possible reason accounting for the low saturated gain. Our study opens the door of gain switching for perovskite lasers and provides a significant guidance for understanding generation dynamics and limit factors of short pulses, which are very important for real-world applications, such as optical storage36, ultrafast optical communication30, bioimaging31, and time-resolved spectroscopy37.

Results and discussion

Synthesis and characterization of CsPbBr3 microwires

The CsPbBr3 perovskite microwires were synthetized by a liquid-phase self-assembled growth method on a sapphire (Al2O3) substrate. The top-view scanning electron microscopy (SEM) images in Fig. 1a, b show that the microstructures of as-grown CsPbBr3 perovskite are dominated by microwires with smooth, clean surface and edge, indicating the excellent crystalline quality of the CsPbBr3 microwires. The lengths of the wires range from ten to several tens of microns, and the widths are a few microns. From the elemental mapping shown in Fig. 1c–f, it can be observed that the three elements of Cs, Pb, Br are evenly distributed in the individual CsPbBr3 perovskite microwire. And the energy dispersive X-ray spectroscopy (EDS) analysis presented in Fig. 1g reveals that the atomic ratios of Cs, Pb and Br are 18.49:20.84:60.67, which performs a good agreement with the ideal 1:1:3 stoichiometry of CsPbBr3. The X-ray diffraction (XRD) measurement has also been carried out for the CsPbBr3 microwires, as shown in Fig. 1h. It is found that the CsPbBr3 possesses the orthorhombic crystal phase which can be identified by the clear diffraction peak splitting. Figure 1i shows typical absorption and room-temperature photoluminescence (PL) spectra of the CsPbBr3 microwires. A clear absorption edge around 530 nm and a strong PL emission centered at 536 nm are revealed, which are consistent with previous studies38.

Fig. 1: Characterizations of the synthesized CsPbBr3 perovskite microwires.
figure 1

a, b Scanning electron microscopy images of CsPbBr3 microwires. Scale bars in a and b are 20 and 5 μm, respectively. Element mapping of Cs (d), Pb (e) and Br (f) for the corresponding individual CsPbBr3 microwire in c. Scale bars in c–f are 5 μm. Here, the background of the element mapping signals is black in color, while the element signals of Cs, Pb, and Br are blue, green, and red, respectively. Because of the similar detection energies for Br and Al, which comes from the Al2O3 substrate, the signal intensity of Br for CsPbBr3 microwire seems to be lower than that for substrate area. While the energy dispersive X-ray spectroscopy analysis shows that the atomic ratios of Cs, Pb and Br within the investigated microwires are in good agreement with the ideal 1:1:3 stoichiometry of CsPbBr3. g Energy dispersive X-ray spectroscopy analysis of the CsPbBr3 microwire. The red rectangular region of the inset shows the measured area. h X-ray diffraction pattern of the CsPbBr3 microwires. i Absorption and photoluminescence (PL) spectra of the CsPbBr3 microwires.

Full size image

Single-mode laser emissions from CsPbBr3 microwires

To explore the potential of CsPbBr3 microwires for laser application, an individual CsPbBr3 microwire was optically pumped by 400-nm fs pulse at room temperature. Figure 2a presents the dark-field optical image of the individual microwire at a low excitation intensity below the lasing threshold. The corresponding images at threshold and above threshold are respectively shown in Fig. 2b, c. It can be seen that the emission intensity below threshold was almost uniform for the whole individual microwire while above threshold the coherent green light was emitted from the two end-facets, indicating the transition from spontaneous emission to Fabry‒Pérot mode stimulated radiation. Figure 2d displays the emission spectra evolution for the investigated CsPbBr3 microwire at various excitation intensities. The spectra are vertically offset for clarity. Under low excitation intensity, only a predominant broad luminescence, characteristic of spontaneously emitted light centered at near 536 nm can be observed. As excitation energy increased to 37.2 μJ cm−2, a distinctive narrow peak at about 544 nm emerges at the low energy side of the spectrum, and grows rapidly with the continued increase of pumping fluence. Moreover, the single narrow peak still persisted even at elevated excitation intensity. Usually, most of microscale wires are subject to random fluctuations and instabilities, showing typical multimode lasing. Here, an unambiguous single-mode lasing was achieved owing to the high-quality laser cavity formed by the smooth crystal end-facets. The plots of integrated emission intensity and the full width at half maximum (FWHM) versus excitation density are shown in Fig. 2e. The log-log “S-shaped” curve and linewidth narrowing clearly confirm the lasing action very well. The lasing threshold (Pth) is accordingly derived to be 37.2 μJ cm−2, and the FWHM below and above the threshold are around 30 and 0.21 nm, respectively. Meanwhile, the spontaneous emission coupling factor β can be extracted from the “S” curve to be about 0.09. The enlarged spectra in Fig. 2f disclose that blueshift and spectral broadening occur as the pump intensity increases. Generally, there are many origins may result in the peak shift, such as electron/hole many-body interactions, band filling, thermally induced refractive index change and optical density fluctuations39,40, which will be discussed in more details in the latter section. Based on the relationship of Q = λ/δλ, where Q, λ and δλ are cavity quality factor, peak wavelength and FWHM, respectively, we calculated the Q factors at various excitation fluences. As shown in Fig. 2g, with increasing the excitation level, the Q factor gradually increases and finally saturates to a maximum value of ~2500. For example, the inset of Fig. 2g illustrates the FWHM of ~0.23 nm for the lasing mode at 543.8 nm at a pump fluence of 72.3 μJ cm−2, corresponding to a relatively high Q factor of ~2367. The maximum value of Q factor is higher than those recently reported in some CsPbBr3 microstructures41,42, which can be ascribed to the excellent crystal quality of the as-synthesized CsPbBr3 perovskites. Here, the spontaneous emission coupling factor β is relavant to the photon radiation process as decribed in our rate equation model. The Q factor can also be described by \(Q=\frac{2\pi }{\lambda }\frac{{n}_{g}}{{g}_{th}}\)43, where ng is the group index of refraction and gth is the threshold gain. Theoretical simulations show that with decreasing differential gain g0 and/or saturated gain gs or increasing the transparent carrier density n0 while fixing other material parameters, the lasing threshold value increases monotonously, resulting in the change in Q-value according to the expression. That is to say, the lasing threshold and the Q factor are physically determined by the material parameters as well as the cavity structure under gain-switching operations.

Fig. 2: Lasing characteristics of individual CsPbBr3 microwire.
figure 2

Optical images of luminescence signal below threshold (a), at threshold (b) and above threshold (c) under 400-nm fs excitation. Scale bars in a–c are 5 μm. d Emission spectra of CsPbBr3 microwires at different pump fluences. For clarity, the curves have been vertically shifted and some of them are magnified. e Integrated emission intensity (red circles) and full width at half maximum (FWHM, cyan squares) versus excitation energy density. The error bars that represent the standard deviation from the mean are too small to be visible. The representative kink behavior is exhibited and the lasing threshold is derived to be about 37.2 μJ cm−2. The spontaneous emission coupling factor β is estimated to be ~0.09 from the “S-shaped” curve. f Enlarged spectra with various excitation energy from 1.2 to 2.4 Pth. g The Q factors at various excitation fluences above the lasing threshold. The error bars here are too small to be visible. Inset is the lasing spectrum at a pump fluence of 72.3 μJ cm−2 with a emission peak at 543.8 nm and a FWHM (δλ) of about 0.23 nm, corresponding to a Q factor of ~2367.

Full size image

Gain-switching dynamics in CsPbBr3 microwires

The gain of a semiconductor laser can be switched from a state below threshold into inversion by directly modulating the pump pulse intensity, and then the laser produces stimulated emission. Generally, a larger lasing threshold means more difficult to establish the population inversion and the consequent stimulated emission with ultrashor pulse width. Thus, if the threshold value increases, the difficulty in establishing gain-switching is then dramatically increased, and an additional bias voltage is necessary to help to establish the population inversion quickly. On the other hand, a higher threshold means a higher operating temperature, which could deteriorate the pulse stability under gain-switching. To gain insight into the gain-switched lasing characteristics and dynamics of CsPbBr3 microwires, the excitation-intensity-dependent TRPL were performed using a streak-camera system. Figure 3a–d shows the single-mode TRPL images and the corresponding linear plots of the spectrally integrated pulse waveforms of the CsPbBr3 microwires at various excitation intensities above the lasing threshold (additional images are provided in Supplementary Note 1, Supplementary Figs. 1 and 2). All the output pulse started after the excitation pulse has ended, indicating the efficient gain switching. It can be obviously seen that time interval between the excitation and emission pulses, called delay time, gradually decreases as the excitation intensity increases. This phenomenon is one of the emblematic gain-switching properties, which have been widely demonstrated experimentally and theoretically in various gain-switched semiconductor lasers27,36,44,45,46. Here, it is worth noting that the measured 4.95-ps pulse width of the fs pump pulse shown in Fig. 3e is due to setup-resolution limit of the streak camera. In our scenarios, the pulse widths of the output emissions are all shorter than 19 ps with delay times smaller than 40 ps. The generation of short pulse without any post-processing indicates the superior potentiality of CsPbBr3 microstructures as ultrafast light sources. Besides, the spectral broadening and peak blue-shift with increasing pump density are unambiguously observed, which coincides with the time-integrated spectroscopy shown in Fig. 2. The blue-shift at higher excitation fluence can be interpreted by the transient reduction of refractive index with the increase of carrier density in the ultrafast pump case. It can also be seen from the streak camera that the wavelength of the emission pulses presents almost linearly dependence on time decay, that is, the entire gain-switched pulses were linearly down-chirped.

Fig. 3: Excitation-intensity-dependent time-resolved photoluminescence.
figure 3

a–d Temporally- and spectrally-resolved streak-camera images, and the corresponding spectral-integrated waveforms of output gain-switched lasing pulses from CsPbBr3 microwires for various excitation fluences above the lasing threshold. The excitation fluences are respectively displayed in the top-right of the graphs, varying from 43.5 to 60.0 μJ cm−2. e Streak-camera image of the fs pump pulses. The measured 4.95-ps pulse width of the fs pulse is due to the limit of setup-resolution. The plotted time window of each single streak-camera image is 75 ps.

Full size image

The chirp renders the spectral and pulse width broadening, hindering the generation of shorter pulse. Figure 4a performs the spectral property of the gain-switched pulse at 60 μJ cm−2 and the corresponding streak-camera image in the inset. The delay time increases almost linearly with the increase of wavelength (linear down chirp) with a slope of 41.5 ps nm−1. In gain switching process, the chirp is inevitable due to the gain-switching operation principle. Gain switching must include a sudden change in carrier density and the carrier-induced refractive index changes in a resonator during pulse generation23. In the main part of the optical pulse, strong stimulated radiation leads to a decrease in carrier density and hence an increase in refractive index, resulting in a decrease of the oscillation frequency. The fast change of transient frequency in time domain significantly limits the pulse width. As shown in Fig. 4a, the pulse widths are only approximately 10 ps below 543.4 nm but they rapidly increase at wavelengths above 543.4 nm. Such complex spectral dynamics makes it very difficult to obtain short pulses from gain-switched semiconductor lasers. Thus, it is highly desirable to understand the dynamic characteristics of gain-switched pulses from perovskite lasers for ultrashort pulse generation. Figure 4b presents the log-log plots of the normalized output pulse waveforms at elevated pump fluences, showing typical gain-switching characteristics, i.e., clear exponential rise and decay of the output pulses. The delay times (squares), rise times (circles) and pulse widths/FWHMs (diamonds) of these gain-switched short pulses extracted from the experimental data are summarized in Fig. 4c, d. It can be seen that they gradually decreased under progressively higher excitation fluences and eventually saturated to a lower minimum with further increasing the pump density. The shortest delay time and pulse width were limited to 26 and 13.6 ps, respectively. Such excitation fluence dependences of output laser pulses have been widely observed in other gain-switched semiconductor lasers44,45,46, providing clear signatures of gain-switched lasing behaviors in CsPbBr3 microwires.

Fig. 4: Gain-switching characteristics of output pulses in CsPbBr3 microwires.
figure 4

a Delay time and pulse width of optical pulse at 60 μJ cm−2 with respect to wavelength. The error bars that represent the standard deviation from the mean are too small to be visible. The inset shows the streak camera image at 60 μJ cm−2. b Normalized log-log plots of gain-switched pulse waveforms in Fig. 3. An exponential model (gray solid lines) fits well to the experimental data. The excitation energy-dependent delay time (red squares), rise time (circles), pulse width (diamonds) (c) and decay time (black squares) (d) of gain-switched pulses. The error bars here are too small to be visible. Dashed curves show the simulation results.

Full size image

Rate equation analysis of gain-switched laser outputs

The interaction between carrier and photon determines the properties of output pulse in stimulated emission process. For better understanding the gain-switched lasing behavior in the transient pumping regime and clarifying the factors in the pulse width limitations of the CsPbBr3 microwires, a modified single-mode laser rate equation analysis35 was carried out with taking gain nonlinearities and carrier recombination ABC model into account. The rate equation model can be described as following,

$$\frac{dn}{dt}=\frac{p(t)}{\hslash \upsilon \sigma }-{\it{\varGamma}}{v}_{g}g\frac{s}{1+\varepsilon s}-An-B{n}^{2}-C{n}^{3}$$
(1)
$$\frac{ds}{dt}=\it{\varGamma }{v}_{g}g\frac{s}{1+\varepsilon s}-\frac{s}{{\tau }_{p}}+\beta B{n}^{2}$$
(2)
$$g={g}_{0}(n-{n}_{0}){\left[1+\frac{{g}_{0}(n-{n}_{0})}{{g}_{s}}\right]}^{-1}$$
(3)

where n is the carrier density, p(t) is the transient optical pumping power given by a Gaussian distribution with a pulse duration of 0.5 ps, \(\hslash \upsilon\) and σ are respectively the pump photon energy and pump area in the CsPbBr3 microwires, Γ is the confinement factor, vg is the group velocity, g is the carrier-density-dependent nonlinear material gain defined by a function of gs (saturated gain), g0 (differential gain) and n0 (transparent carrier density), s is the photon density, ε is the gain compression factor, β is the spontaneous emission coupling factor, and τp denotes the photon lifetime.

Here, we use semi-quantitive numerical simulations to fit the experimental results because there still exist some unknown parameters in these rate equations. The pump area σ is about 1.03 × 10−5 cm2 and the vg is 6.02 × 10−3 cm ps−1 47. The spontaneous emission coupling factor β was 0.09 as estimated from Fig. 2e. We plausibly assumed Γ = 1, because the CsPbBr3 microwires act as not only gain materials but also high-quality resonators. For the simulations, the saturated gain gs, differential gain g0, and gain compression factor ε are three primary variations that were continuously modulated to match the simulation results with the experimental data shown in Fig. 4c, d. Generally, the saturated gain gs significantly affects the delay time and rise time but has almost no effect on decay time of the output laser pulses. When gs is fixed, the pulse shape hardly changes with varying the differential gain g0, while the gain compression factor ɛ suppresses the pulse peak but has almost no obvious effect on the rise time34. The numerical calculation process was performed iteratively until the simulation converges to self-consistent results.

As is known, the complicated intrinsic gain nonlinearities have a strong influence on the dynamical characteristics of semiconductor lasers, including dynamic frequency chirping, stability and pulse shaping of lasers33, especially under high-density pulsed injection. And the carrier recombination plays an important role during gain-switching35. Consequently, the gain saturation and gain compression that reflect the gain nonlinearities, and the carrier recombination ABC model are ingeniously introduced into the rate equation model in our case to analyze the gain-switching characteristics of a perovskite microwire laser. In the simulations, the saturated gain gs, differential gain g0, and gain compression factor ε are continuously adjusted within a reasonable range under gain-switching operations. The best fitting results (dashed curves) can be obtained with gs = 88 cm−1, g0 = 0.6 × 10−9 cm, and ε = 0.92 × 10−12 cm, as exhibited in Fig. 4c, d.

The photon lifetime τp within the cavity was calculated to be about 0.7 ps using the relationship of τp = Q/ω, where Q is the cavity quality factor and ω is angular frequency48. However, such theoretical value usually deviates from the experimental one. According to the previous report45, the decay time of output pulse is almost determined by the photon lifetime τp, which means that the more appropriate value of τp in the simulations should derived from the experimental decay curve with slight adjustment. Resultly, the emplyed τp in the simulations are chosen to be very close to the experimental decay time but not the theoretical one by τp = Q/ω. It was found that only when gs is around 88 cm−1, the simulation results of rise time and delay time can be consistent with the experimental data, implying that gs plays a crucial role in determining the rise time and delay time, which is in good agreements with our previous study45. All parameters used in the calculation are summarized in Table 1.

Table 1 Definitions and values of simulation parameters.
Full size table

It’s worth noting that such a saturated gain of gs = 88 cm−1 is far less than the gain values (350–1200 cm−1) from CsPbBr3 perovskite by a variable stripe-length method49,50. When we assumed that gs is larger than 300, consistency between experimental and simulation results cannot be achieved for any choice of other parameters. The small value of saturated gain is considered to be caused by some nonlinear properties under gain-switching operations. In previous studies, some possible origins responsible for the nonlinearities have been discussed, and the most possible physical mechanisms focus on spectral hole burning and carrier heating33. In our condition, the carrier density rise sharply in an ultra-short time interval during gain-switching process under fs laser pumping, which may eventually result in an elevation of transient carrier temperature in the CsPbBr3 microwire. The dynamical carrier temperature can be estimated by fitting the exponential high-energy tail of temporally and spectrally-resolved PL spectrum described by the relationship of emission intensity \(I(\hslash \upsilon ) \propto \exp (-\hslash \upsilon /kT)\)46,51, where \(I(\hslash \upsilon )\) denotes emission intensity, k is Boltzmann factor, and T is the carrier temperature. The estimated carrier temperatures were 380 and 460 K under excitation energy of 0.4 Pth and 0.9 Pth, respectively (see Supplementary Note 2, Supplementary Fig. 3). Therefore, the carrier heating should be the most possibly additional dynamical gain-suppression parameter that gives rise to the reduction of saturated gain in the present work. Since the low saturated gain can significantly increase the pulse width of gain-switched pulses, we can reasonably conclude that the carrier heating may be another possible reason for limiting the generation of shorter pulse in the CsPbBr3 microwires laser.

Conclusions

In summary, a single-mode lasing behavior is observed from CsPbBr3 microwires under fs optical pumping. The output laser pulses are investigated with streak camera measurements at various excitation intensities, and clear gain-switching mechanism for the short pulse generation are revealed. The shortest green pulse is obtained as short as 13.6 ps without any post-processing. To insight into the gain-switching dynamics of the CsPbBr3 perovskite, we use a rate equation model combining with gain nonlinearities and carrier recombination ABC model to semi-quantitatively simulate the excitation intensity dependencies of the delay time, pulse width, and rise time of the output laser pulses. A close consistency is obtained between the experimental and simulation results by continuously adjusting the three parameters of saturated gain gs, differential gain g0, and gain compression factor ε. Moreover, it is found that the carrier heating is a possible reason for the low saturated gain during gain-switching and hence limits the pulse width of the output pulses from the perovskite microwires. These results open the door of gain switching for perovskite lasers and provide a significant guidance for understanding generation dynamics and limit factors of short pulses.

Methods

Synthesis of CsPbBr3 perovskite microwires

The compounds CsPbBr3 perovskite microwires were synthesized using a liquid-phase recrystallization method in an ambient environment. The 40 mmol L−1 N,N’-dimethylformamide (DMF)-CsPbBr3 precursor solution was prepared by mixing PbBr2 (0.4 mmol) and CsBr (0.4 mmol) powders in 10 mL DMF solution. Then, the mixed solution was magnetically stirred for 4 h at a temperature of 70 °C. Next, 30 μL DMF-CsPbBr3 solution was dip-cast onto a sapphire (Al2O3) substrate, which was preheated to a high temperature of 60 °C by a heater and keep the temperature unchanged to evaporate the solvent until the DMF solvent completely evaporated. The all-inorganic CsPbBr3 microwires were successfully synthesized.

Material characterization

The morphology of synthesized CsPbBr3 perovskite microstructures and luminescence signals were characterized respectively using scanning electron microscopy (SEM, XL30FEG, Philips, the Netherlands) and a charge-coupled device (CCD) camera. The elemental composition of the microwires was determined by energy dispersive X-ray spectroscopy (EDS, AMETEK EDAX). The crystal phase of the microwires was investigated using an X-ray diffraction (XRD) spectrometer (German Brook AXS D8 Discove). The UV–visible absorption spectra were measured using a Varian Cary 5000 spectrophotometer with an integrating sphere attachment in the range of 300–1000 nm.

Optical measurements

All the PL and TRPL experiments were performed with the home-built confocal μ-PL system at room temperature (20 °C) by impulsive fs optical pumping at 400 nm. The 400-nm pulses were generated by frequency doubling the 800-nm fs pulses from a mode-locked Ti:sapphire regenerative amplifier (Verdi G8, Coherent, America) with 35-fs pulse duration and 1 kHz repetition rate. The pump beam was focalized to a diameter of 36 μm. The PL signals were detected by a triple-grating spectrometer (SR303, Andor) with an electrically-cooled CCD. The limited resolution of the spectrometer is 0.05 nm for the PL measurements. The TRPL was detected via a streak camera system (Hamamatsu, C10910) with a temporal resolution of ~5 ps. The 800 nm pulses with 80 MHz repetition rate, which emitted from the mode-locked Ti:sapphire laser, is converted into electrical signal as trigger signal of delay unit (C12270-01) by a PIN diode (C1808-03). The excitation-fluence-dependent PL signals in the TRPL measurements were detected by a spectrometer (HRS-300) and then collected by a streak camera with a digital CMOS camera through scanning of electric and magnetic fields.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.