Introduction

Nuclear spins around a nitrogen-vacancy (NV) center1,2,3 in diamond (Fig. 1a) have long coherence times: over 10 seconds for nitrogen and carbon nuclear spins4,5 and ~1.9 min for carbon nuclear spin pairs6. Thus, such spins are promising as quantum memories for quantum repeaters7 and quantum computers8. However, changes in magnetic fields such as external noise fields or hyperfine fields by the electron spin due to optical excitation cause either a bit-flip or phase-flip error. To avoid such errors, various kinds of quantum error correction (QEC)9 have been demonstrated10,11,12. Waldherr et al.10 demonstrated QEC with nitrogen and two carbon nuclear spins, Taminiau et al. demonstrated QEC with an NV electron and two carbon nuclear spins11, and Cramer et al. demonstrated a stabilizer code with three carbon isotopes12. However, these demonstrations were carried out under relatively strong magnetic fields such as 6200 Gauss with individual error corrections10 or 403 Gauss with repetitive error corrections based on dynamical decoupling11,12. Under the magnetic fields, an increase in the fidelity of the controlled-phase (C-Z) gate by increasing the external magnetic field strongly depends on the carbon position relative to the NV center unless the field is well aligned to the hyperfine field (see discussion section and Supplementary Note 1) (Fig. 1b, c). In contrast, the fidelity can be increased independent of the carbon position under a zero magnetic field, where the hyperfine field uniquely defines the quantization axis, which allows time-reversal operation in any timing, resulting in high fidelity single nuclear spin manipulation conditioned by the NV electron, as discussed later. The application of an external magnetic field also limits the integration with other physical qubits. For example, superconducting qubits, which we believe are the most promising candidates for quantum computers, become unstable by the application of a magnetic field due to the penetration of magnetic flux into the superconductor or the Josephson junction. The accessible magnetic field is ~100 Gauss even in the plane of the superconducting loop13,14,15,16,17 unless using exotic junctions such as semiconductor nanowires. Although a flux qubit relies on applying external magnetic fields, it is usually <1 Gauss to introduce a half flux in the loop to stabilize the qubit, and the application of higher magnetic fields beyond a half-flux field reduces the supercurrent in the junction18. A zero magnetic field is also advantageous for qubit integration because a spatially uniform magnetic field can be easily obtained compared to individually tuned magnetic fields. A flux qubit working under a completely zero magnetic field with a ferromagnetic π-shifted Josephson junction, which does not require any precise tuning of the flux in a qubit loop by individual coil currents, is under development toward large-scale integration of quantum computers with flexible layout19,20. To further extend the scale of quantum computers in size and that of quantum communications21 in distance, it is desirable to use spins in diamond, which serve as quantum interfaces22,23,24,25 with long-time memory and excellent optical accessibility for connecting quantum computers to optical quantum networks26. Li et al.27 recently demonstrated coherent coupling of a single NV center spin to a superconducting flux qubit via a nanomechanical resonator and Scarlino et al. demonstrated coherent coupling of a semiconductor double quantum dot charge qubit to a superconducting transmon qubit via a microwave photon28, which also operate under a zero magnetic field. Furthermore, it is essential to provide error tolerance not only to the NISQ (noisy intermediate-scale quantum)29 based on stabilizer codes such as surface codes30,31,32,33,34,35 but also to the quantum interface, which should also work under a zero magnetic field for stable and reliable operations with flexible layout. In this report, we first demonstrate the quantum operation of the electron and nuclear spins and their correlated operations based on the geometric phase in the absence of a magnetic field. We then demonstrate the most fundamental three-qubit QEC36 for either a bit-flip or phase-flip error using three nuclear spins on nitrogen and two carbon isotopes in the vicinity of an NV center.

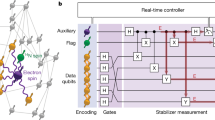
Fig. 1: Carbon spin manipulation with and without magnetic field.
figure 1

a Schematic structure of a nitrogen-vacancy center in diamond, where carbon (C) adjacent to a vacancy (e) is replaced by impurity nitrogen (N), whose spin error is protected by two carbon isotope spins serving as ancilla qubits for quantum error correction. The green-colored 13C atoms’ placement is just an artistic choice. b Quantization axis of carbon nuclear spins, which is determined by the hyperfine field by the electron spin as well as the external magnetic field if applied. c Simulated Rabi frequency dependence of the fidelity (F) of the holonomic controlled-phase gate based on the geometric phase between two carbon nuclear spins (13C1, 1.14 MHz; 13C2, 0.33 MHz) under a zero magnetic field (blue line), 100 Gauss (green line), 1000 gauss (red line), and 10000 Gauss (orange line). The angle between the external and hyperfine magnetic fields is set at 45 degrees for both carbon nuclear spins. Under a magnetic field, the fidelity is limited by the influence of the two quantum axes, but under a zero magnetic field, the fidelity improves by decreasing the Rabi frequency. The nitrogen nuclear spin is not considered here because the quantization axis does not change with the presence of a magnetic field. d Energy level diagram of the relevant spin system containing one nitrogen and two carbon isotopes together with an optically detected magnetic resonance spectrum relating to the |0⟩s−|±1⟩s transition. PL denotes photoluminescence. \({D}_{0}=2.877\) MHz is the zero-field splitting. Hyperfine splittings are observed (14N,2.2 MHz;13C1,1.14 MHz;13C2,0.33 MHz). The energy levels inside the blue rectangles are used in this study.

Full size image

Results

Physical system

The ground state electrons in a negatively charged NV center constitute a spin-1 triplet system represented by ms = 0, ±1, and form a V-type three-level system under a zero magnetic field. The degenerate ms = ±1 levels are used as a processor qubit (this is called a geometric qubit37,38,39,40,41,42,43,44,45) and ms = 0 as an ancilla. Although a degenerate qubit based on ms = ±1 cannot be manipulated by a microwave field, it can be manipulated by a polarized microwave field via the ancilla state ms = 043. A nuclear spin of nitrogen impurity, which is a component of the NV center, also constitutes a spin-1 system, where the mI = ± 1 levels are degenerate, as is the electron spin under a zero magnetic field. The mI = 0, −1 levels are used as a memory qubit represented by |0⟩ (mI = 0) and |1⟩ (mI = −1) in this demonstration. Carbon isotopes (13C) with a spin-half nuclear spin are quantized along the hyperfine field by the electron spin to form eigenstates represented by |0⟩ \(({m}_{{{{{{\rm{I}}}}}}}=-1/2)\) and |1⟩ \(({m}_{{{{{{\rm{I}}}}}}}=1/2)\). We use two carbon nuclear spins coupled to the processor electron spin as auxiliary memory qubits. All nuclear spins can be individually manipulated with the help of hyperfine interactions with the electron spin, as indicated by the ODMR (optically detected magnetic resonance) measurement (Fig. 1d).

Entanglement generation of three qubits

We first evaluate the microwave intensity and the angle between microwaves irradiating through two crossed wires placed on the sample to perform universal quantum operations of a degenerate two-level subsystem of spin-1 triplet electrons called a geometric qubit43. During nuclear spin manipulation, we set the electron spin state into |+1⟩S by using a microwave with a right-circular polarization, which eases individual manipulation of the nitrogen and carbon nuclear spins. Figure 1c shows that the fidelity is increased by decreasing the Rabi frequency, although it is limited in practice since the manipulation time cannot exceed T2*. In this demonstration, however, we obtained higher fidelity by extending the manipulation time to the effective T2* induced by weakly coupled carbons with hyperfine couplings below 0.1 MHz by using the GRAPE (gradient ascent pulse engineering)-optimized waveform46 considering two strongly coupled carbons.

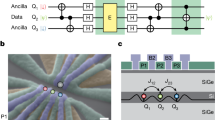
Figure 2a shows the quantum circuit that generates entanglement between three nuclear spins (one nitrogen and two carbons) known as the GHZ state \(\frac{1}{\sqrt{2}}\) \(({|000\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}+{|111\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}})\). The necessary operational elements for the demonstration are state initialization, universal quantum gate, and state measurement of nuclear spins. The three nuclear spins are first initialized into \({|000\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\) (see Supplementary Note 2). Carbon nuclear spins are initialized by probabilistic projection by conditional electron rotation (so-called measurement-based initialization) with a high fidelity of more than 99%. On the other hand, the nitrogen nuclear spin is deterministically initialized with about 95% fidelity since the measurement-based initialization allows only about 90% fidelity (see Supplementary Note 3, 4) due to the depolarization during the optical excitation for the electron spin measurement. The Hadamard gate, which makes a superposition of the basis states, of the nuclear spins is implemented by applying a π/2 pulse of a radio wave that resonates with the hyperfine splitting of the corresponding carbon nuclear spin (Fig. 2b). The correlated operation between the three nuclear spins is implemented by applying the holonomic C-Z gate based on the geometric phase43,47,48,49 with the help of the electron spin because the direct interaction between nuclear spins is too weak. This is achieved by a 2π rotation in the Bloch sphere spanned by |+1⟩S and |0⟩S of the electron spin conditioned by the nuclear spin state, adding a π phase only for \({|110\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\) and \({|101\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\) (e.g., \(({|110\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\rightarrow -{|110\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}})\) (Fig. 2c). Finally, after the generation of the GHZ state, the joint states of the three nuclear spins are measured by a single-shot measurement (Fig. 2d), confirming the classical correlation of entanglement with 78% fidelity. Although the quantum correlation is not measured since the measurement time is unrealistic, it should have about the same fidelity as the classical correlation since we confirmed that the two-spin entangled state has about the same fidelity as the classically correlated state (see Supplementary Note 6). The probability of \({|111\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\) is smaller than that of \({|000\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\) because the nitrogen nuclear spin is likely depolarized into |0⟩N during the optical excitation to read out the electron spin state.

Quantum error correction

The QEC codes implemented in this demonstration are fundamental building blocks of Shor’s QEC code36. Although complete QEC is achieved by a nine-qubit code, we demonstrate a three-qubit code that can correct either a bit-flip error (Fig. 3a) or a phase-flip error (Fig. 3b), which are otherwise identical except for the Hadamard gates inserted immediately after encoding and before decoding. In this experiment, the error that occurs on the nitrogen nuclear spin is protected by two carbon nuclear spins. Although an error occurring on any single qubit after encoding is corrected, errors occurring on multiple qubits cannot be corrected.

Figure 3 shows whether the bit-flip and phase-flip errors can be corrected by intentionally inserting an error in the encoded nitrogen nuclear spin. The carbon nuclear spins are prepared into \({|00\rangle }_{{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\) and the nitrogen nuclear spin is prepared into one of |ψ⟩ = |0⟩, |1⟩, |+⟩, |−⟩, |+i⟩, |−i⟩. The encoding and decoding are configured with the same gates as the three-qubit entanglement shown in Fig. 2. The quantum Toffoli gate for the QEC is also configured with the combination of Hadamard gates and the holonomic C-Z gate that adds the π phase only for \({|111\rangle }_{{{{{{{\rm{N}}}}}},{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\). Quantum tomography measurements on the nitrogen nuclear spin state after the QEC showed that the state fidelities against bit-flip and phase-flip errors are, respectively, 75.4% and 74.6% on average (see Supplementary Note 5) (Fig. 3c, d).

Fig. 2: Three-qubit entanglement generation.
figure 2

a Quantum circuit for entanglement generation between three nuclear spins, one nitrogen, and two carbon isotopes. This is equivalent to the quantum circuit of encoding in three-qubit quantum error correction in Fig. 3. H, X, and Y, respectively, denote Hadamard, Pauli-X, and Pauli-Y gates. b Pulse sequence in the experiment. Nuclear spin manipulation is performed by radiofrequency (RF), and the geometric phase manipulation between the electron (e), nitrogen (N), and carbon (C) is performed by microwaves (MW) using the GRAPE algorithm. RO, Init, Ey, and A1, respectively, denote readout, initialize and two orbital excited states. c Conceptual diagram of the holonomic controlled-phase gate in the encoding. The π phase is given to \({|110\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\) and \({|101\rangle }_{{{{{{\rm{N}}}}}},{{{{{{\rm{C}}}}}}}_{1},{{{{{{\rm{C}}}}}}}_{2}}\). D0 is the zero-field splitting and HFN is the hyperfine (HF) splitting between the electron and the nitrogen. d Classical evaluation of the GHZ entanglement generation for three qubits. Correlations are confirmed by measuring the z axis for all nitrogen and carbon nuclear spins. Since the quantum correlation of three qubits can be measured with the same technique as the quantum correlation of two qubits, it was not measured in consideration of the experimental time.

Full size image
Fig. 3: QEC with three qubits.
figure 3

a, b Quantum circuit of three-qubit quantum error correction (QEC) for bit-flip (a) and phase-flip (b) errors. The phase-flip code (b) is the same as the bit-flip code (a) except for the Hadamard (H) gates inserted immediately after encoding and before decoding. X, Y, and Z, respectively, denote Pauli-X, Pauli-Y, and Pauli-Z gates. c, d Bloch sphere representation of nitrogen nuclear spin state by state tomography after the quantum error correction (QEC) against bit-flip (c) and phase-flip (d) errors (left) and the state fidelity of the nitrogen nuclear spin for six initialized states (right). The dotted lines represent the estimated fidelity when state preparation and measurement (SPAM) errors are included. Blue (red) bars represent experimental results with (without: w/o) QEC. Since the error does not affect the fidelity in the corresponding bases ({+,−} in c and {0,1} in d), there is no difference between with or without error and those fidelities are even higher without QEC. Error bars are defined as the standard deviation of the photon shot noise.

Full size image

Discussion

To evaluate the usefulness of the QEC, we measure the state fidelity of the nitrogen nuclear spin when the probability of a single intentionally generated error is varied, both with and without the QEC (Fig. 4a). The initial state of the nitrogen nuclear spin is fixed at |+⟩N, and only the nitrogen nuclear spin is subjected to phase errors. Without QEC, the fidelity degrades in proportion to the error probability. The 10% deviation from the ideally obtained fidelities with error probabilities of both 0 and 1 should be due to state preparation and measurement (SPAM) errors. On the other hand, with QEC, the fidelity is constant regardless of the error probability. Although the fidelity is inferior to that without QEC due to operational errors for an error probability below 0.15, it exceeds that without QEC as expected for an error probability over 0.15.

Fig. 4: Fidelity of QEC.
figure 4

a Dependence of the state fidelity of the nitrogen spin initialized to |+⟩N on the error probability. The blue (red) solid line is the experimental result of the fidelity obtained with (without: w/o) quantum error correction (QEC). The dotted line is the simulated fidelity without QEC. Because of the manipulation error in addition to the state preparation and measurement error, the fidelity without QEC is higher for p < 0.15, while the fidelity with QEC is higher for p > 0.15. Error bars are defined as the standard deviation of the photon shot noise. b Estimated fidelity degradation of quantum encoding (decoding) operations as a function of the hyperfine coupling with another carbon that cannot be detected by optically detected magnetic resonance. The holonomic controlled-phase (C-Z) gate with the GRAPE-optimized pulse in the coding (decoding) operation is applied to a certain state, and the operational fidelity is simulated by the trace inner product between the generated state and the ideal state. Since the holonomic C-Z gate is optimized in the Hamiltonian with two carbons (13C1, 1.14 MHz;13C2, 0.33 MHz), the presence of the third carbon degrades the operational fidelity.

Full size image

The operational error should be caused mainly by environmental carbons whose hyperfine couplings are smaller than 0.1 MHz, which cannot be distinguished by ODMR measurement (Fig. 1d). Figure 4b shows the dependence of the fidelity of the encoding (decoding) operation on the hyperfine coupling in the presence of another carbon in addition to the two carbons used in the experiment. From the results of the experiment such as ODMR measurement and Rabi oscillation (see Supplementary Note 7), the hyperfine coupling is estimated to be in the range of 0.06–0.12, resulting in fidelity degradation of ~10% in addition to a SPAM error of 10%. The fidelity can be improved by initializing undetected carbons using dynamical decoupling with radio frequency (DDRF)5,50,51. Even higher fidelity can be obtained by optimizing the waveform of the microwaves to be robust against unknown hyperfine coupling in a specific range.

Finally, we compare our results with previous related experiments10,11,12. The most relevant experiment was given by Waldherr et al.10, which demonstrated QEC with nitrogen and two carbon nuclear spins as in our demonstration but at 6200 Gauss. The situation in Fig. 4a in our demonstration exactly corresponds to that in Fig. 3b in ref. 10, and the obtained fidelities are about the same within error bars. This means that we successfully excluded magnetic fields to achieve the same level of QEC without the necessity of a precise field alignment along the NV axis. Other relevant experiments were given by Taminiau et al.10, which demonstrated QEC with an NV electron and two carbon nuclear spins, and Cramer et al.12, which demonstrated stabilizer code with three carbon isotopes, both with dynamical decoupling schemes at 403 Gauss. Although these experiments cannot be directly compared with our experiments since they protect different spins from ours, their fidelities are relatively lower than ours possibly because the carbon isotopes used in their experiments were not properly oriented along the external magnetic field. It is shown in Fig. 2a in Methods of ref. 10 that usable carbon isotopes are limited to around six at 403 Gauss and to ~9 at 10 T with hyperfine of over 20 kHz11,52. To overcome this limitation, Bradley et al.5 developed a more elaborate DDRF method5,50,51. Although this method enables the detection of carbon isotope spins with a weak or negligible perpendicular hyperfine component as shown in Fig. S3 in this reference, the angle between the external and hyperfine fields must be within around 10−2 (0.6 degrees) to achieve infidelity of 10−4 at 403 Gauss5, which is still consistent with our simulation shown in Fig.1c and Fig. 1 in SI. On the other hand, although we can only manipulate strongly coupled carbons due to the limitation from T2* in the current scheme, we can also manipulate weakly coupled carbons limited by T2 instead of T2*. The combination of robust dynamical decoupling in three-level systems under low magnetic fields developed by Vetter et al.53 and nuclear spin manipulation with radiofrequency synchronized with the decoupling developed by Bradley et al.5, enables the implementation of two-qubit gates between an electron and a weakly coupled carbon under a zero magnetic field. With the increase in operatable carbon isotopes, we expect to realize Shor’s nine-qubit QEC code even under a zero magnetic field.

In conclusion, we demonstrated a three-qubit QEC against either a bit-flip or phase-flip error by introducing the holonomic C-Z gate of three nuclear spins around an NV center in diamond under a zero magnetic field. This demonstration is applicable to the construction of a large-scale distributed quantum computer and a long-haul quantum communication network by connecting quantum systems vulnerable to a magnetic field, such as superconducting qubits with spin-based quantum memories.

Methods

We use a single naturally occurring NV center in a high-purity type IIa chemical-vapor deposition-grown diamond with crystal orientation of <100> produced by Element Six. The diamond is cooled to 5 K to prolong the electron spin coherence. To achieve a zero magnetic field, the residual magnetic field including the geomagnetic field is canceled out by a three-dimensional coil. The currents of the three coils are adjusted by monitoring the spin-echo coherence time, which reaches its maximum at a zero magnetic field. Two orthogonal copper wires are attached to the sample surface to apply microwaves with arbitrary polarization. The optical system consists of a homemade confocal microscope system. A green laser (515 nm) is used for charge and electron spin initialization by nonresonant excitation, and two red lasers (637 nm) are used for further electron spin initialization with the |A1⟩ state and spin measurement using the |Ey⟩ state by resonant excitation.