Cross-scale analysis of temperature compensation in the cyanobacterial circadian clock system

Abstract

Circadian clock proteins often reveal temperature-compensatory responses that counteract temperature influences to keep their enzymatic activities constant over a physiological range of temperature. This temperature-compensating ability at the reaction level is likely crucial for circadian clock systems, to which the clock proteins are incorporated, to achieve the system-level temperature compensation of the oscillation frequency. Nevertheless, temperature compensation is yet a puzzling phenomenon, since side chains that make up the clock proteins fluctuate more frequently due to greater thermal energy at higher temperature. Here, we investigated temperature influences on the dynamics of KaiC, a temperature-compensated enzyme (ATPase) that hydrolyzes ATP into ADP in the cyanobacterial circadian clock system, using quasielastic neutron scattering. The frequency of picosecond to sub-nanosecond incoherent local motions in KaiC was accelerated by a factor of only 1.2 by increasing the temperature by 10 °C. This temperature insensitivity of the local motions was not necessarily unique to KaiC, but confirmed also for a series of temperature-sensitive mutants of KaiC and proteins other than clock-related proteins. Rather, the dynamics associated with the temperature-compensatory nature of the reaction- and system-level was found in global diffusional motions, which was suggested to regulate the temperature dependence of ATPase activity and dephosphorylation process presumably through changes in the hexamer conformation of KaiC. The spatiotemporal scale at which cross-scale causality of the temperature sensitivity is established is finite, and extends down to picosecond to sub-nanosecond dynamics only in a very limited part of KaiC, not in its entire part.

Introduction

Circadian clocks are endogenous timing systems that rhythmically control various biological processes with an ~24-h period¹. This rhythm persists stably even without any external cues, and the period length is kept constant even when ambient temperature changes (temperature compensation). The phase of the clock system can be shifted upon receiving external stimuli such as light and temperature and then synchronized to the phase of the outer world. These unique characteristics enable organisms to optimize their fitness during day/night environmental cycles^2,3,4,5.

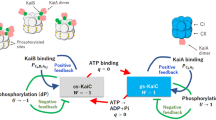
Temperature compensation is a remarkable characteristic of the circadian clock systems. Q10 values, the factor by which reaction speed or cycle frequency is accelerated by increasing the ambient temperature by 10 °C, are mostly in the range of 0.9–1.1 for circadian clock systems, whereas those of most biochemical reactions⁶ and the Belousov–Zhabotinsky oscillator^7,8,9,10 range from 2 to 3. As schematically shown in Fig. 1a, circadian clocks exhibiting system-level temperature compensation often comprise unique clock proteins with temperature-compensated biochemical activities such as adenosine triphosphate (ATP) hydrolysis (ATPase)^11,12,13, and protein phosphorylation (kinase)^14,15,16 and dephosphorylation (phosphatase)^14,15. A simple but attractive idea that emerged from studies^{12,13,15,17,18} of these biochemical activities is that the reaction-level temperature compensability is somehow correlated to system- or even higher cell-level temperature compensability (Fig. 1a). A great deal of effort has been devoted to elucidating the mechanism of this connectivity via experimental^{12,13,15,16,18} and modeling^{19,20,21,22,23} approaches.

Fig. 1: Potential cross-scale causal relationship in the circadian clock system of cyanobacteria.

a Spatiotemporal hierarchy spanning from atomic-scale dynamics, molecular-scale reaction, molecular system-scale frequency, and cellular-scale frequency. When the ATPase activity of KaiC doubles as a result of amino acid substitutions (orange arrow), both the in vitro system- and cell-level frequencies also double^12,17,25. In cyanobacteria, the temperature (T) sensitivity of ATPase is correlated with those of the system and cell levels. (Inset) Three extreme cases of temperature influence on clock-protein dynamics. Thermal fluctuations are sensitively accelerated, insensitively compensated, or sensitively compensated through a balance of opposing contributions. b Temperature-dependent ATPase mutation sites mapped onto the crystal structure of KaiC^32,33. Zoomed-in-views of c S258, d F247, e Q361, f N390, g F470, and h phosphorylated S431 and T432 in KaiC. Hydrogen bonds are highlighted by green dotted lines.

Nevertheless, temperature compensation remains a puzzling phenomenon in terms of protein dynamics, as atoms and side chains in proteins should fluctuate more frequently at higher temperature due to their greater thermal energy. Three extreme cases can be considered (inset in Fig. 1a). First, thermal fluctuation in these key clock proteins is accelerated in a temperature-dependent manner, as observed for ordinary proteins. Second, the atoms and side chains in temperature-compensated clock proteins fluctuate in a temperature-insensitive manner via unknown mechanisms. Third, some opposing but balancing contributions act at the level of protein dynamics level, i.e., one contribution accelerates but the other decelerates so that they differentially affect the elementary reaction steps to achieve overall compensation. Experimental investigations of the dynamics of temperature-compensated clock proteins are needed to distinguish among these cases.

KaiC, a temperature-compensated clock protein in cyanobacterium Synechococcus elongatus PCC 7942^11,12,13, acts as a circadian oscillator with other two clock proteins, KaiA and KaiB²⁴. Its most striking feature is that its temperature-compensated circadian rhythm can be reconstructed even in vitro by mixing KaiA, KaiB, and KaiC in the presence of ATP²⁵ (Fig. 1a). An ATP molecule binds a Walker motif in each of the tandemly duplicated domains called the N-terminal C1 and C-terminal C2 domains (Fig. 1b). These ATP binding events trigger oligomerization of KaiC into a double-ring hexamer. The ATP molecule bound to the C2 domain (C2-ATP) is used mostly as the source of phosphoryl group that is transferred to (auto-kinase) and then removed from (auto-phosphatase) S431 and T432 in KaiC. In the presence of KaiA and KaiB, the status of the dual phosphorylation site alters in a cyclic manner: ST → SpT → pSpT → pST → ST, where S, T, pS, and pT represent S431, T432, phosphorylated S431, and phosphorylated T432, respectively^26,27. The frequency of this phosphorylation cycle (P-cycle) is proportional to the rate of hydrolysis of C1-bound ATP (C1-ATP) into adenosine diphosphate (ADP) in the absence of KaiA and KaiB (Fig. 1a)^12,13,17. More importantly, the ATPase activity of KaiC is perfectly temperature-compensated (Q10_ATP = 1.0)¹². The in vitro Kai oscillator that consists of temperature-compensated KaiC provides a practical means for studying cross-scale properties of temperature-compensation phenomena at the system, reaction, and dynamics levels (Fig. 1a).

Quasielastic neutron scattering (QENS) is a powerful and direct technique for accessing protein dynamics at the picosecond to nanosecond time scales²⁸. Because hydrogen atoms, which constitute up to half of all atoms in proteins, are distributed near uniformly in the three-dimensional structures of proteins, an averaged view of protein dynamics can be extracted from QENS spectra²⁹. In this study, we designed a series of KaiC mutants (Fig. 1b) with temperature-dependent periods (Fig. 1c–e), inverse temperature-dependent period (Fig. 1f), temperature-compensated but shortened-period (Fig. 1g), or arrhythmicity (Fig. 1h), and measured the temperature sensitivity of their protein dynamics using the neutron spectrometer BL02 (DNA: Biomolecular Dynamics Spectrometer) in the Material and Life Science Experimental Facility of Japan Proton Accelerator Research Complex (MLF/J-PARC)³⁰. Our QENS data revealed that the frequency of picosecond to sub-nanosecond incoherent motions is essentially temperature-insensitive in KaiC, regardless of the presence or absence of the temperature-sensitive mutations. The spatiotemporal scale at which cross-scale causality of the temperature sensitivity is established is finite, and extends down to picosecond to sub-nanosecond dynamics only in a very limited part of KaiC, not in its entire part.

Results

Screening and characterization of temperature-sensitive mutants of KaiC

As confirmed by the positions along the horizontal axis in Fig. 2a, the ATPase activity of KaiC^WT is as low as 11 d⁻¹ and almost temperature-insensitive (Q10_ATP^WT = 0.89 ± 0.10), as previously reported¹². Consistently with previous studies^11,15,25, the P-cycle frequency (f_P = 24/period) of KaiC^WT in the presence of KaiA and KaiB was also temperature-compensated (Fig. 2b) (Q10_fp^WT = 1.08 ± 0.04). Consequently, data points taken at different temperatures for KaiC^WT nearly overlapped in the ATPase–f_P plot (Fig. 2a). Taking advantage of potential reaction–system correlations, we screened the temperature-sensitive mutants of KaiC using an in vitro ATPase-based screening system³¹. Among a number of KaiC mutants screened for temperature-dependent ATPase activity, four candidates were characterized in detail as they revealed stable but temperature-dependent system-level oscillation (Fig. 2c–f).

Fig. 2: Screening and characterization of temperature-sensitive mutants of KaiC.

a Temperature dependence of the relationship between the ATPase activity of KaiC alone and in vitro KaiC phosphorylation-cycle (P-cycle) frequency (f_P = 24/period) in the presence of KaiA and KaiB. P-cycles of b KaiC^WT, c KaiC^S258A, d KaiC^F247A, e KaiC^Q361E, f KaiC^N390A, g KaiC^F470Y at four different temperatures: 303 (blue), 308 (green), 313 (orange), and 318 K (red). Dark-colored circles correspond to the mean from independent preparations and measurements (pale-colored squares, triangles, and diamonds). Light blue circles plotted in panel b correspond to the P-cycle of KaiC^WT in a D₂O buffer. h Correlation of Q10 values between ATPase (Q10_ATP) and P-cycle (Q10_fp). Error bars correspond to one standard deviation obtained from three independent experiments, except that they are shown as three standard deviations for Q10_fp.

The first was the S258A mutant of KaiC (KaiC^S258A). According to the X-ray crystal structure of KaiC^WT32,33, S258 is located in the C2 domain (Fig. 1b and c). The ATPase activity of KaiC^S258A at 303 K (6.3 ± 1.1 d⁻¹) was lower than that of KaiC^WT (11.8 ± 1.1 d⁻¹) but increased in a temperature-dependent manner up to 14.1 ± 1.8 d⁻¹ at 318 K (Q10_ATP^S258A = 1.73 ± 0.22) (Fig. 2a). Consistent with this, the f_P value for KaiC^S258A increased from 0.78 to 1.40 d⁻¹ as the temperature increased (Fig. 2c) (Q10_fp^S258A = 1.56 ± 0.01). Because of this correlation, the data trace for KaiC^S258A extends almost diagonally from low- to high-temperature conditions in the ATPase–f_P plot (Fig. 2a). The second and third mutants (KaiC^F247A, KaiC^Q361E), which replaced residues that neighbored in the C1–C2 interface (Figs. 1b, 2d, and e), are also traced diagonally (Fig. 2a). The f_P value for KaiC^F247A increased from 1.12 to 1.97 d⁻¹ as temperature increased (Fig. 2d) (Q10_fp^F247A = 1.63 ± 0.01), as observed for the mutant’s ATPase activity (Fig. 2a) (Q10_ATP^F247A = 1.47 ± 0.05), whereas KaiC^Q361E exhibited a slightly weakened correlation between Q10_ATP^Q361E (1.70 ± 0.15) and Q10_fp^Q361E (1.23 ± 0.02) (Fig. 2e and h). The fourth is an inverse temperature-dependent mutant that harbors the N390A substitution in the C2–C2 interface (KaiC^N390A, Fig. 1f) nearby the C1 domain (Fig. 1b). The ATPase activity and f_P value of KaiC^N390A became smaller at higher temperatures (Fig. 2f) in a correlated manner, as evidenced by its diagonal trace (Fig. 2a) with inversed temperature sensitivities (Q10_ATP^N390A = 0.47 ± 0.07, Q10_fp^N390A = 0.69 ± 0.02). However, KaiC^N390A became arrhythmic at the highest temperature of 318 K (Fig. 2f).

Taking into consideration the limited persistence of the P-cycle for KaiC^F247A and KaiC^N390A at 318 K (Fig. 2d and f), we dissolved KaiC^WT and the four KaiC mutants exhibiting reaction–system correlation in a D₂O buffer (Supplementary Note 1) and subjected them to QENS experiments at different temperatures: 283, 293, 302, 313, and 317 K for KaiC^WT, 302 (low) and 310 or 313 K (high) for KaiC^S258A, KaiC^F247A, KaiC^Q361E, and KaiC^N390A. For comparison purposes, we conducted further QENS experiments using two other KaiC mutants^12,25; a temperature-compensated but period-shortened F470Y mutant of KaiC (KaiC^F470Y: Q10_ATP^F470Y = 1.07 ± 0.06 and Q10_fp^F470Y = 1.09 ± 0.05) (Figs. 1b, 1g, 2a, 2g, and 2h) and a temperature-compensated but arrhythmic S431D/T432E double mutant (KaiC^DE: Q10_ATP^DE = 0.98 ± 0.07) mimicking the fully phosphorylated KaiC-pSpT (Figs. 1b, 1h, 2a, and 2h). Noted that the circadian rhythm of KaiC^WT was barely influenced by the D₂O buffer used in this study (light blue circles in Fig. 2b).

KaiC dynamics detected by QENS

To investigate the temperature dependence of KaiC dynamics, we conducted QENS experiments of KaiC^WT at five different temperatures from 283 to 317 K. It must be noted that 293 K is approximately the critical temperature of the in vitro oscillator³⁴, below which the P-cycle becomes arrhythmic (zero amplitude). As shown in Fig. 3a, a difference QENS spectrum S(Q, E) of KaiC^WT, where Q is the momentum transfer and E is the energy transfer of neutrons, could be obtained at each temperature by subtracting the background spectrum of the D₂O solvent from the sample spectrum, on the basis of scaling factors calculated from neutron scattering cross-sections. The resultant S(Q, E) for KaiC^WT at all the temperatures shared a common feature of temperature-dependent broadening of a narrow elastic peak and a wide quasielastic component derived from global and local motions, respectively (Fig. 3a). To analyze the Q- and temperature dependencies of these two components quantitatively, we attempted to fit the following equation²⁸ to each S(Q,E) in Fig. 3b–f:

$$S(Q,E)=\, [{A}_{0}(Q)\delta (E)+\{1-{A}_{0}(Q)\}{L}_{{{{{{\rm{local}}}}}}}(Q,E)]\times {L}_{{{{{{\rm{global}}}}}}}(Q,E)\\ \times RF(Q,E)+BG(Q)$$

(1)

where A₀(Q) is the elastic incoherent structure factor (EISF); δ(E) is Dirac delta function; RF(Q,E) is the instrumental resolution function obtained from the spectrum of vanadium; BG(Q) is the background; and L_local(Q,E) and L_global(Q,E) are Lorentzian functions, (Γ(Q)/π) (E² + Γ(Q)²)⁻¹, describing local internal motion and global diffusive motion of the protein, respectively, where Γ(Q) is the half-width at half maximum. Q-averaged χ² values resulting from fitting of Eq. (1) to the experimental data of KaiC^WT was ~0.93 ± 0.07 (Fig. 3b–f), assuring optimum quality of the curve-fitting procedure.

Fig. 3: Representative quasielastic neutron scattering (QENS) spectra, S(Q,E), of KaiC^WT at Q = 1.05 Å⁻¹.

a S(Q,E) measured at five different temperatures from 283 to 317 K. Experimental spectra, S_exp(Q,E), at b 283 K, c 293 K, d 302 K, e 313 K, and f 317 K are fitted using S_fit(Q,E), which includes contributions of two Lorentzian functions, LZ1(Q,E) = L_global(Q,E) and LZ2(Q,E) = L_global(Q,E)$\times$L_local(Q,E), background BG(Q), and resolution function RF(Q,E) as defined in Eq. (1). The error bars come from the propagation of the standard deviation of the Poisson distribution in creating Q–E maps.

For the KaiC mutants, QENS experiments were conducted at low (302 K) and high (310 or 313 K) temperatures that were within the physiologically functional range of temperature as the circadian clock. Although most of the KaiC mutants showed similar S(Q,E) to KaiC^WT (Fig. 4a, 4c, 4e, and 4f), visually distinguishable differences were observed for KaiC^F247A and KaiC^N390A (Fig. 4b and d). In order to make more detailed and quantitative comparisons, each S(Q,E) of the KaiC mutants was analyzed using Eq. (1) in the same way as KaiC^WT (panels g–r in Fig. 4). In the following, we describe the global and local motions of KaiC on the basis of temperature dependencies of Γ_global(Q) and Γ_local(Q), respectively.

Fig. 4: Representative quasielastic neutron scattering (QENS) spectra, S(Q,E), of KaiC mutants at Q = 1.05 Å⁻¹.

Comparison of QENS spectra acquired at low and high temperatures for a KaiC^S258A, b KaiC^F247A, c KaiC^Q361E, d KaiC^N390A, e KaiC^F470Y, and f KaiC^DE. Blue, orange, and pink lines correspond to the spectra at 302, 313, and 310 K, respectively. For comparison, the QENS spectra of KaiC^WT at 313 K (black thick line) are normalized to match the top-peak intensity of the mutants. g–l At the low temperature of 302 K. m–r At a high temperature of 310 or 313 K. Experimental spectra, S_exp(Q,E), are fitted using S_fit(Q,E), which includes contributions of two Lorentzian functions, LZ1(Q,E) = L_global(Q,E) and LZ2(Q,E) = L_global(Q,E)$\times$L_local(Q,E), background BG(Q), and resolution function RF(Q,E) as defined in Eq. (1). The error bars come from the propagation of the standard deviation of the Poisson distribution in creating Q–E maps.

Global motions of KaiC

Γ_global(Q) provides information on the frequency of the global motions, whose properties are most straightforwardly inspected using the plot of Γ_global(Q) vs Q². Linear Q²-dependencies of Γ_global(Q) were confirmed for KaiC^WT at every temperature (Fig. 5a), indicating its boundary-free diffusions including translational and rotational diffusions. Thus, the linear slope in Fig. 5a relates to an apparent boundary-free diffusion coefficient (D_global). The D_global for KaiC^WT at 302 and 313 K were 3.54 ± 0.09 and 4.48 ± 0.10 × 10⁻⁷ cm² s⁻¹, respectively (Fig. 5h), which were similar to those (3.75 and 4.97 × 10⁻⁷ cm² s⁻¹) calculated using the known crystal structure of the KaiC hexamer (Supplementary Note 2).

Fig. 5: Temperature- and Q²-dependences of global motions (Γ_global(Q)) in KaiC.

a KaiC^WT, b KaiC^S258A, c KaiC^F247A, d KaiC^Q361E, e KaiC^N390A, f KaiC^F470Y, and g KaiC^DE. The slope of each linear fit corresponds to the apparent diffusion coefficient, D_global. Error bars correspond to the errors resulted from the curve-fitting analysis using Eq. (1) as shown in Figs. 3 and 4. h D_global and its temperature dependence, Q10_global. White bars for KaiC^S258A, KaiC^F247A, and KaiC^Q361E correspond to the D_global values at 313 K, which were estimated by linear extrapolation of the D_global values determined at 302 and 310 K. A hatched bar represents Q10_global^WT estimated from the slope of Arrhenius plot using five different temperatures (283, 293, 302, 313, and 317 K) (Supplementary Fig. 2a), as previously reported⁶⁵. A shaded bar represents Q10_global^WT estimated from the slope of Arrhenius plot using three different temperatures (302, 313, and 317 K) within the physiologically functional range of temperature (Supplementary Fig. 2a). Other Q10_global presented as black bars were estimated as the ratio of measurement results (R_Low and R_High) at two temperatures (T_Low and T_High) using Q10 = (R_High/R_Low)^{10/(THigh-TLow)}; T_Low = 302 K, T_High = 313 or 310 K. Error bars correspond to the errors associated with the linear regression analysis (a–g).

The temperature dependencies of the D_global (Q10_global) for KaiC^WT and the KaiC mutants (Fig. 5b–g) were ~1.2 (Fig. 5h), similar to other examples: ~1.2 (300–310 K) in human hemoglobin (Hb)³⁵ and ~1.2 (290–300 K) in α-synuclein (αSyn)³⁶. These observations are essentially consistent with the Stokes-Einstein diffusion that predicts D_global $\propto$ T/η(T), where T and η(T) are the temperature and solvent viscosity at T, respectively. Assuming η(302) = 1.016 cP and η(313) = 0.799 cP for the present D₂O solvent (Supplementary Note 2), the term of T/η(T) increases 1.3-fold by raising the temperature form 302 to 313 K. This agreement between Q10_global and the increase ratio of T/η(T) indicates that the temperature dependence of the hydrodynamic radius is rather small. Thus, we suggest that KaiC^WT and the KaiC mutants are maintained as intact hexamers during the QENS measurements in the observed temperature range.

In contrast to Q10_global, the absolute D_global values of the temperature-sensitive mutants shared a common feature. The D_global values estimated at high temperature for KaiC^S258A, KaiC^F247A, KaiC^Q361E, and KaiC^N390A were systematically smaller than those of KaiC^WT, KaiC^F470Y, and KaiC^DE (Fig. 5h). In order to make a fair comparison, it is necessary to take into account that the measured temperature of KaiC^S258A, KaiC^F247A, KaiC^Q361E is lower by 3 K than the others. On the basis of the pseudo-linear temperature dependence of the D_global values for KaiC^WT (Fig. 5h), the D_global values at 313 K for KaiC^S258A, KaiC^F247A, KaiC^Q361E were estimated by linear extrapolation of the D_global values determined at 302 and 310 K (white bars in Fig. 5h). Even after applying these corrections, the D_global values tended to be smaller in the temperature-sensitive mutants. These results suggest that the global hexamer structure of the temperature-sensitive mutants may be slightly different from those of KaiC^WT and the temperature-compensated KaiC mutants (KaiC^F470Y, KaiC^DE).

Local motions of KaiC

In contrast to Γ_global(Q), Γ_local(Q) reflects picosecond to sub-nanosecond incoherent local fluctuations of side-chain and main-chain in KaiC. Γ_local(Q) of KaiC^WT increased asymptotically to approach a plateau at high Q² (Fig. 6a). As at high Q, the motions over short distances predominate, the plateau values correspond to the elementary displacements of the local motions. Slight but temperature-dependent increase in the high-Q plateau of KaiC^WT suggests that the side-chain and main-chain motions in KaiC^WT are accelerated by thermal fluctuations (Fig. 6a).

Fig. 6: Temperature- and Q²-dependences of local motions (Γ_local(Q)) in KaiC.

a KaiC^WT, b KaiC^S258A, c KaiC^F247A, d KaiC^Q361E, e KaiC^N390A, f KaiC^F470Y, and g KaiC^DE. Solid lines represent resultant fits using a jump-diffusion model that predicts the jump-diffusion coefficient, D_local, as the curvature of the saturating curves and the reciprocal of residence time, τ⁻¹, as Γ_local(Q) converged at infinite Q. Error bars correspond to the errors resulted from the curve-fitting analysis using Eq. (1) as shown in Figs. 3 and 4. h τ⁻¹ and its temperature dependence, Q10_local. i D_local and its temperature dependence, Q10_D-local. A hatched bar represents Q10_local^WT or Q10_D-local^WT estimated from the slope of Arrhenius plot using five different temperatures (283, 293, 302, 313, and 317 K) (Supplementary Fig. 2b and 2c), as previously reported⁶⁵. A shaded bar represents Q10_local^WT or Q10_D-local^WT estimated from the slope of Arrhenius plot using three different temperatures (302, 313, and 317 K) within the physiologically functional range of temperature (Supplementary Fig. 2b and 2c). Other Q10_local presented as black bars were estimated as the ratio of measurement results (R_Low and R_High) at two temperatures (T_Low and T_High) using Q10 = (R_High/R_Low)^{10/(THigh-TLow)}; T_Low = 302 K, T_High = 313 or 310 K. Error bars correspond to the errors associated with the analysis using jump-diffusion model²⁸ (a–g).

To determine the temperature sensitivity of the local motions quantitatively, Q²-dependencies of Γ_local(Q) were analyzed by using a jump-diffusion model²⁸: Γ_local(Q) = D_localQ² (1 + D_localQ²τ)⁻¹, where D_local is the jump-diffusion coefficient and τ is the residence time spent on one site before jumping to others. The model gave reasonable fits to temperature- and Q²-dependent Γ_local(Q) of KaiC^WT (lines in Fig. 6a). The resultant τ⁻¹ values for KaiC^WT were slightly temperature-dependent (Fig. 6h). Arrhenius plot analyses using five different temperatures (283, 293, 302, 313, and 317 K) resulted in the activation energy of 4.0 ± 0.6 kcal mol⁻¹ (Supplementary Note 3), which corresponded to the Q10 value of 1.23 ± 0.04 for the internal motions (Q10_local, hatched bar in Fig. 6h). The estimation of the Q10_local^WT value was not seriously affected by limiting the physiologically functional range of temperature (302, 313, and 317 K: Q10_local^WT = 1.15 ± 0.11, shaded bar in Fig. 6h, Supplementary Note 3) and by taking a ratio of τ⁻¹ at low (302 K) and high (313 K) temperatures (Q10_local^WT = 1.10 ± 0.14, black bar in Fig. 6h). The Q10 values of D_local (Q10_D-local) for KaiC^WT varied in the range from 1.16 to 1.36 depending on the analysis method (Fig. 6i), probably due to the larger associated errors compared to the τ⁻¹ values.

Γ_local(Q) of the KaiC mutants, which revealed the same high-Q saturation as KaiC^WT (Fig. 6b–g), could be analyzed reasonably with the jump-diffusion model. Regardless of whether they are temperature-compensated or temperature-dependent, the Q10_local values of the KaiC mutants ranged from 0.97 to 1.20 and were comparable to KaiC^WT within error (Fig. 6h). A similar trend was confirmed for Q10_D-local (Fig. 6i). These results suggest that the average behavior of the local fluctuations occurring throughout KaiC, at least on picosecond to sub-nanosecond time scales, is not clearly correlated with the reaction and system levels in terms of temperature dependence.

While the mutations had small effects on the temperature dependence of the local dynamics, the absolute values of τ⁻¹ were markedly different from KaiC^WT in several temperature-sensitive mutants. The τ⁻¹ values for KaiC^F247A were 0.14 ± 0.01 ps⁻¹ at low and high temperatures and were reduced ~50–70% relative to KaiC^WT (Fig. 6h). Conversely, the local motions in KaiC^N390A were 30–40% faster (0.29 ± 0.01–0.33 ± 0.02 ps⁻¹) than KaiC^WT (Fig. 6h). D_local was essentially unaffected by temperature change or mutations (Fig. 6i), except in the case of KaiC^F247A, where a large error prevented us from identifying clear increase in D_local.

Fractional change in apparently immobile atoms in the temperature-dependent ATPase mutants of KaiC

EISF is defined as the ratio of the elastic peak intensity to the sum of elastic and quasielastic scattering intensities as in Eq. (1), providing information on the geometry of molecular motions and the fraction of mobile and immobile atoms on the time scale (~55 ps) of the spectrometer. As shown in Fig. 7a–g, EISF of KaiC^WT and the mutants were plotted against Q and then fitted using the following equation, assuming diffusion in an ensemble of spheres whose radii (a) follow a lognormal distribution³⁷:

$${{{{{\rm{EISF}}}}}}(Q)=p+(1-p){\int }_{0}^{\infty }\frac{1}{s\sqrt{2\pi }a}{e}^{-\frac{{({{{{\mathrm{ln}}}}}(a/c))}^{2}}{2{s}^{2}}}{\left[\frac{3{j}_{1}(Qa)}{Qa}\right]}^{2}da$$

(2)

where p is the fraction of atoms whose motions are outside the current instrumental energy window and therefore appear immobile; (1 − p) correspond to the fraction of atoms diffusing within the sphere ensemble; c is the median of the distribution; s is the variance in the natural logarithmic space; and j₁ denotes the spherical Bessel function of the first kind of order.

Fig. 7: Elastic incoherent structure factor (EISF) analyses under the assumption of sphere-ensemble model.

a KaiC^WT, b KaiC^S258A, c KaiC^F247A, d KaiC^Q361E, e KaiC^N390A, f KaiC^F470Y, and g KaiC^DE. Solid lines represent the resultant fits of Eq. (2). Error bars correspond to the errors resulted from the curve-fitting analysis using Eq. (1) as shown in Figs. 3 and 4. h Immobile fraction, p. i Radial distribution functions of mobile fraction. Black, purple, blue, pink, orange, and red lines correspond to the distributions at 283, 293, 302, 310, 313, and 317 K, respectively. Error bars correspond to the errors associated with the EISF analysis³⁷ using Eq. (2) (a–g).

The results of EISF analysis support the current observations on the local dynamics. Consistent with the Q10_local^WT value of 1.15 ± 0.11, the immobile fraction of KaiC^WT was maintained at ~0.6 in the physiologically functional range of temperature (Fig. 7h). In KaiC^F470Y and KaiC^DE, the immobile fractions were nearly unaffected by temperature change or mutations within the experimental error. On the other hand, the immobile fraction of KaiC^F247A increased 25% as the temperature increased, despite its nearly temperature-compensated τ⁻¹ value (Q10_local^F247A = 0.97 ± 0.16). Interestingly, a reverse trend was confirmed in KaiC^N390A. At the same time, all the temperature-sensitive mutants of KaiC exhibited smaller immobile fractions than KaiC^WT at 302 K. This result that the temperature-dependent mutations shifted certain motions from immobile to mobile fractions (Fig. 7h) is directly or indirectly related to the systematic decrease in the D_global values (Fig. 5h).

In KaiC^WT and KaiC^F470Y, atoms diffusing within a radius of 3–6 Å (Fig. 7i) constituted a major mobile component. By contrast, the mobile fractions of the temperature-sensitive mutants and KaiC^DE were distributed mainly in reduced radii of 1–2 Å relative to KaiC^WT. Thus, KaiC^S258A, KaiC^F247A, KaiC^Q361E, and KaiC^N390A are the temperature-dependent ATPase mutants with the reductions in D_global (Fig. 5h), immobile fraction p (Fig. 7h), and amplitudes of local motions (Fig. 7i).

Discussion

Over the past decades, chronobiologists have sought a reasonable model that explains the three physiological properties of the circadian clock systems: self-sustained oscillation, temperature compensation, and synchronization^2,3,4. The circadian clock of cyanobacteria is an ideal experimental system for this purpose, as its physiological properties can be studied in relation to the physicochemical properties of clock-related components at the molecular and atomic scales.

Among the three Kai proteins, KaiC is the core of the cyanobacterial clock system. In the presence of both KaiA and KaiB, KaiC exhibits a phosphorylation rhythm (Fig. 2b) whose frequency (f_P) is correlated with the ATPase activity of KaiC alone (Fig. 2a). For example, when the ATPase activity of KaiC doubles as a result of amino acid substitutions, the frequencies of both the in vitro system-scale and the cellular-scale rhythms also double (Fig. 1a)^12,17,25.

This causal relationship, in which properties are transferred through upward causation from bottom to top in the spatiotemporal hierarchy, was also confirmed for temperature compensation from the reaction to the cellular scale (Fig. 1a). The ATPase activity of KaiC^WT is temperature-compensated; probably because of this, both the in vitro and in vivo rhythms¹³ are also temperature-independent. This phenomenological interpretation is further supported by the four examples of temperature-sensitive mutants of KaiC. In contrast to KaiC^WT (Q10_ATP^WT = 0.89 ± 0.10), the f_P values for KaiC^S258A (Q10_ATP^S258A = 1.73 ± 0.22), KaiC^F247A (Q10_ATP^F247A = 1.47 ± 0.05), and KaiC^Q361E (Q10_ATP^Q361E = 1.70 ± 0.15) increased in a temperature-dependent manner (Fig. 2c–e), and the f_P value for KaiC^N390A (Q10_ATP^N390A = 0.47 ± 0.07) obeyed the inverse temperature dependence (Fig. 2f). The well correlated Q10 values between the ATPase activity and f_P values in the four mutants (Fig. 2h) clearly demonstrate that the reaction-to-system scale causal relationship arises from the temperature-compensated ATPase activity of KaiC.

In the present study, we utilized QENS technique to test how far down the microscopic spatiotemporal scale the causality of the temperature sensitivity can be established. The Q10_global values were estimated to be ~1.2 for KaiC^WT and the mutants (Fig. 5h), confirming that the global motions of KaiC are accelerated by the temperature dependence of T/η(T) according to the Stokes-Einstein diffusion law. The limited temperature dependence was also observed for the parameters, such as τ⁻¹ and D_local, which characterize the local dynamics of KaiC. Even though the P-cycle and ATPase activity were accelerated in a temperature-dependent manner (Q10_ATP and Q10_fp as high as 1.7) in the three mutants (KaiC^S258A, KaiC^F247A, KaiC^Q361E) and decelerated in the inverse temperature-dependent manner (Q10_ATP and Q10_fp as low as 0.5) in one mutant (KaiC^N390A) (Fig. 2h), the Q10_local and Q10_D-local values for all the four temperature-sensitive mutants monotonously resulted in 1.0–1.2 (Fig. 6h and i). The similar temperature dependence was also confirmed for the local dynamics of the temperature-compensated but short-period (KaiC^F470Y) and arrhythmic (KaiC^DE) mutants. Our current QENS observations indicate that the spatiotemporal scale at which causality of the temperature sensitivity is established is finite. Given that QENS detects the average image of the fluctuations of all the hydrogen atoms scattered in the protein molecule, we can conclude that causality is established down to the local dynamics only in a very limited part of KaiC (inset in Fig. 1a).

It is worth discussing our observations in the light of previous QENS studies on proteins other than clock-related proteins. To date, the QENS method has been used in many studies to characterize protein dynamics of small single-domain proteins^38,39 to larger and more complex molecular systems^40,41,42,43, as well as to large-scale conformational changes such as those that occur upon ligand binding^35,44,45, pressurization^46,47,48, unfolding^{37,49,50,51,52,53}, and fibrillization^36,54. The results reported to date for various protein samples indicate that the τ values are mostly distributed in the range of 1–20 ps (τ⁻¹ = 0.05–1.0 ps⁻¹) (see Grimaldo et al²⁹. and references therein), although attention must be paid to the differences in measurement temperature, energy resolution, and analysis methods. The τ value for KaiC^WT, 3.7–8.0 ps (τ⁻¹ = 0.13–0.27 ps⁻¹), is included in the above range, indicating that the internal motion of KaiC^WT is neither exceptionally slow nor too fast.

More detailed comparisons of internal motions are possible by making reference for QENS data for Hb³⁵ and αSyn³⁶, which were acquired at the same beamline with the same energy resolution (12 μeV/55 ps). As shown in Fig. 8, the temperature dependence of the jump-diffusion frequency of KaiC^WT (Q10_local^WT = 1.1–1.2) is not substantially different from the four examples (Q10_local = 1.1–1.3) for deoxygenated Hb (deoxy-Hb), CO-bound Hb (CO-Hb), a fibril state of αSyn (fib-αSyn), and a monomeric but intrinsically disordered form of αSyn (mon-αSyn). This result points to the intrinsically low energy barrier for the local motions independent of protein folds or functions, supporting the present interpretation that the temperature sensitivity of the Kai oscillator does not correlate well with that of the picosecond to sub-nanosecond local dynamics. In the measured range of temperature, however, the τ⁻¹ values for KaiC^WT are 30–50% smaller than those of the four examples. Considering the insensitivity of the internal dynamics even upon an R(CO)-to-T(deoxy) allosteric transition of Hb (Fig. 8), we speculate that the slower jump-diffusion frequency of KaiC^WT may be related to its function and structure as the circadian pacemaker. In fact, the τ⁻¹ values for KaiC^F247A and KaiC^N390A were 50–70% reduced and 30–40% enhanced, respectively, relative to KaiC^WT (Figs. 6h and 8), although not for all temperature-sensitive mutants.

Fig. 8: Temperature dependences of jump-diffusion frequency (τ⁻¹) for KaiC, human hemoglobin (Hb), and α-synuclein (αSyn).

Dashed and solid red lines represent the linear fits of the Arrhenius plot for KaiC^WT using entire (283–317 K) and physiologically functional range (302–317 K) of temperature, respectively. Quasielastic neutron scattering (QENS) data of Hb and αSyn are taken from previous studies^35,36; activation energies of deoxygenated Hb (deoxy-Hb), CO-bound Hb (CO-Hb), fibrillized αSyn (fib-αSyn), and monomeric αSyn (mon-αSyn) are 5.2 ± 0.3, 5.2 ± 0.3, 3.7 ± 0.7, and 2.6 ± 1.9 kcal mol⁻¹, respectively. Values given near fitting lines represent the Q10_local values estimated for 303 K.

In contrast to the featureless temperature dependence of the local motions, all the temperature-sensitive mutants shared the reduced global motions including the translational and rotational diffusions relative to KaiC^WT and temperature-insensitive mutants (KaiC^F470Y and KaiC^DE) (Fig. 5h). Two possibilities can be considered for the reduced D_global.

The first is the deformation into less compact hexamers by the temperature-sensitive mutations. According to the crystallographic structure of KaiC^32,33, every temperature-sensitive mutation is mapped onto its domain-domain interfaces. S258 is located in the outer radius side of the C2 ring (Fig. 1b); the side chain is hydrogen bonded to that of R326 in the neighboring C2 domain (Fig. 1c). This inter–C2-domain hydrogen bond is thus disrupted in KaiC^S258A. F247 and Q361 neighbor each other in the C1–C2 interface (Fig. 1b), which is stabilized by a limited number of inter-domain contacts with lower packing density than the C1–C1 and C2–C2 interfaces (Supplementary Note 4), exemplified by the non-bonded interactions associated with F247 and Q361 (Fig. 1b). The plane of the phenyl ring of F247 in the C1 domain lies nearly parallel to the C1–C2 interface (Fig. 1d), filling the loosely packed boundary through a hydrophobic interaction with L360 in the C2 domain. The F247A substitution is thus interpreted as the mutation that makes the intrinsically low-density interface even looser. Although the C1–C2 packing density will be little affected by the replacement of glutamine to glutamate in KaiC^Q361E (Fig. 1b), a potential hydrogen bond between Q361 and either T238 or N245 in the C1 domain should be modulated or even disrupted (Fig. 1e). The N390A substitution disrupts an inter–C2-domain hydrogen bond between the side chain of N390 and the main-chain carbonyl oxygen atom of G386 (Fig. 1f). Considering these structural features common to the temperature-sensitive mutations, we speculate that the looser inter-domain interactions have resulted in the loss of compactness of the hexamer structure.

The second is the reduction of an additional contribution from internal large-scale motions. Previous QENS study on the R(CO)-to-T(deoxy) allosteric transition of Hb shows a certain similarity to our results³⁵; D_global is notably increased upon the T(deoxy)-to-R(CO) transition while keeping τ⁻¹ nearly unaffected. Authors of that study suggested that internal large-scale relative motions of two αβ dimers could partially contribute to D_global in CO-Hb³⁵. If this is the case, the decrease in D_global is interpreted as a result of the suppression of domains movements within the KaiC hexamer by the temperature-sensitive mutations. In fact, several lines of evidence have pointed out the dynamic properties of inter-ring stacking of KaiC during the circadian cycle⁵⁵.

Since the current temperature-sensitive mutations will not make the inter-domain interactions within the KaiC hexamer more stable, we believe that the contribution of the first case is greater than that of the second. This interpretation is also consistent with the decrease in the immobile fraction of the temperature-sensitive mutations (Fig. 7h). As shown in Fig. 2c–f, the temperature-sensitive mutations resulted in a preferential shortening and elongation of the dephosphorylation process in the P-cycle. The dephosphorylation process is also the timing of the ATPase activation in KaiC¹². Taken together, these results suggest that delicate but close inter-domain interactions are important in regulating the temperature dependence of ATPase and dephosphorylation reactions in KaiC. This view is also supported by the fact that the KaiC hexamer undergoes a quaternary structure change in concert with ATPase and dephosphorylation events³³.

Several studies have suggested that fluctuations and structural polymorphs of the clock proteins play important roles in the circadian clock systems. In mammalian systems, CKIδ-dependent phosphorylation is one of the key reactions that regulates period length and its temperature sensitivity¹⁶. In CKIδ, the temperature dependence of substrate affinity is compensated by the opposing temperature dependence of product affinity¹⁸. On the basis of molecular dynamics (MD) simulation, the authors of that study proposed that the temperature dependence of the amplitude of particular local fluctuations is reversed in the substrate- and product-bound forms, and that this reversal is one of the origins of the biochemical opposition. Structural polymorphs of the clock proteins, which have been confirmed by crystallography, NMR, and MD simulation, also play important roles in the substrate selectivity of CKIδ⁵⁶ and the interaction between CRY1/2 and the CLOCK-BMAL1 complex⁵⁷. In the cyanobacterial system, the rhythmic stacking/unstacking of C1- and C2-rings is coupled to the P-cycle of KaiC⁵⁵. The MD simulation of KaiC suggests a large-scale conformational change during ADP release from the C2 domain⁵⁸. These previous observations are mainly based on the MD simulations and experiments on nanosecond to microsecond time scales, which are much slower than the time scales targeted by the current QENS study.

The mechanism by which a single amino acid substitution can exert a notable effect on reaction- or even system-level temperature compensation deserves further investigation. There is growing experimental evidence that ordinary enzymes actively utilize internal motions, thereby increasing the efficiency of overall catalytic reactions^59,60,61. Because functionally relevant fluctuations often refer to collective motions of atoms on slower time scales (μs to ms), care must be taken in discussing those motions in relation to the incoherent and fast (ps) dynamics detected in this study. However, several studies have demonstrated a linkage between ps–ns fluctuations and slower motions associated with catalytic reactions^62,63,64. Thus, it is necessary to experimentally verify the possibility that the causality of temperature sensitivity in KaiC is still established on limited time scales longer than nanoseconds.

Methods

Expression and purification of Kai proteins

Glutathione S-transferase (GST)-tagged versions of Kai proteins were constructed in pGEX-6P-1. Each Kai GST-fusion protein was expressed in E. coli BL21(DE3) and purified as reported previously^11,26.

ATPase assay

ATPase activities of KaiC^WT and its mutants, dissolved in an H₂O buffer (H1-buffer) including 20 mM Tris/HCl (pH 8.0), 150 mM NaCl, 5 mM MgCl₂, 1 mM DTT, 1 mM EDTA, and 1 mM ATP, were measured at 303, 308, 313, and 318 K as previously reported^11,15.

In vitro rhythm assay

P-cycles of KaiC^WT and its mutants (0.2 mg/ml) were initiated by addition of KaiA (0.04 mg/ml) and KaiB (0.04 mg/ml) in H1-buffer at 303, 308, 313, and 318 K²⁵. For KaiC^F247A and KaiC^Q361E, whose P-cycle were unstable or unobvious at the normal amount of KaiA, KaiA was added at a 2-fold higher concentration (0.08 mg/ml). Aliquots taken from the incubated samples were subjected to SDS-PAGE analysis. The relative abundances of four phosphorylation states of KaiC were quantified by densitometric image analysis of gel bands using the LOUPE software⁶⁵.

Sample preparation for QENS

Every sample was prepared on site immediately before QENS measurements. KaiC^WT and its mutants were purified on a gel-filtration column (Superdex 200 15/30, Cytiva) equilibrated with an H₂O buffer (H2-buffer) containing 50 mM Tris/HCl (pH 8.0), 150 mM NaCl, 5 mM MgCl₂, 3 mM DTT, 1 mM EDTA, and 20 mM ATP. Collected fractions were subjected to rapid buffer exchange in a D₂O buffer (D2-buffer) containing 50 mM Tris/HCl (pD 7.6), 150 mM NaCl, 5 mM MgCl₂, 3 mM DTT, 1 mM EDTA, and 20 mM ATP using a desalting column (HiPrep 50, Cytiva). KaiC^WT, KaiC^S258A, KaiC^F247A, KaiC^Q361E, KaiC^N390A, KaiC^F470Y, and KaiC^DE were concentrated up to 15.0, 12.3, 14.6, 14.3, 16.9, 8.5, and 9.7 mg/mL, respectively. Each 1-mL sample was placed in a double-cylindrical aluminum cell with a sample thickness of 0.5 mm and sealed tightly with indium wire.

QENS experiments

QENS data were recorded using the near-backscattering spectrometer installed at beamline BL02 (DNA) in the Material and Life Science Experimental Facility of Japan Proton Accelerator Research Complex (MLF/J-PARC), Tokai, Ibaraki, Japan³⁰. QENS spectra were recorded over an energy transfer range from −0.5 to 1.5 meV with energy resolution (12 μeV) enabling us to access motions faster than ~55 ps. QENS data were collected at 283, 293, 302, 310, 313, and 317 K with exposure times of 6–10 h for each condition (520−615 kW). The obtained S(Q,E) were corrected for detector efficiency using a vanadium standard, and intensities were normalized as relative intensities using the standard after subtracting the contributions of the empty cell. The background spectrum of the D2-buffer was subtracted from each sample spectrum on the basis of scaling factors calculated from neutron scattering cross-sections, as reported previously^35,36. The temperature was controlled by an LS350 (Lakeshore) with He conductance gas through a GM refrigerator and heat transfer from a cartridge heater installed in a copper block at the top of a sample cell, while monitoring the temperature at the bottom of the cell.

Estimation of the Q10 values

Datasets with more than two temperature points were subjected to Arrhenius plot analysis, and the resulted activation energy (E_a) was converted to the Q10 value at 303 K using exp{(E_a/R)(10/T/(T + 10))}, where T and R represent temperature and the gas constant, respectively⁶⁵. Other Q10 values were presented as the ratio of measurement results (R₁ and R₂) at two temperatures (T₁ and T₂) using Q10 = (R₂/R₁)^10/(T2-T1).

Calculation of D _global

The D_global values of KaiC^WT were simulated at 302 and 313 K using a previously reported method³⁹, the crystal structure (2GBL)³², and HYDROPRO⁶⁶ (Supplementary Note 2).

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.