Abstract
The precision of matter-wave sensors benefits from interrogating large-particle-number atomic ensembles at high cycle rates. Quantum-degenerate gases with their low effective temperatures allow for constraining systematic errors towards highest accuracy, but their production by evaporative cooling is costly with regard to both atom number and cycle rate. In this work, we report on the creation of cold matter-waves using a crossed optical dipole trap and shaping them by means of an all-optical matter-wave lens. We demonstrate the trade off between lowering the residual kinetic energy and increasing the atom number by reducing the duration of evaporative cooling and estimate the corresponding performance gain in matter-wave sensors. Our method is implemented using time-averaged optical potentials and hence easily applicable in optical dipole trapping setups.
Similar content being viewed by others
Introduction
Ever since their first realization, atom interferometers1,2,3,4 have become indispensable tools in fundamental physics5,6,7,8,9,10,11,12,13,14,15,16,17 and inertial sensing18,19,20,21,22,23,24,25,26,27,28,29,30. The sensitivity of such matter-wave sensors scales with the enclosed space-time area which depends on the momentum transferred by the beam splitters as well as the time the atoms spend in the interferometer.
The expansion of the atomic clouds, used in interferometers, needs to be minimized and well controlled to reach long pulse separation times, control systematic shifts, and create ensembles dense enough to detect them after long time-of-flights. Nevertheless, colder ensembles with lower expansion rates typically need longer preparation times. Therefore, matter-wave sensors require sources with a high flux of large cold atomic ensembles to obtain fast repetition rates.
Bose-Einstein condensates (BECs) are well suited to perform interferometric measurements. They are investigated to control systematic effects related to residual motion at a level lower than a few parts in 109 of Earth’s gravitational acceleration20,31,32,33,34. In addition, due to their narrower velocity distribution35, BECs offer higher beam splitting efficiencies and thus enhanced contrast23,36,37, especially for large momentum transfer36,38,39,40,41,42,43. Finally, the inherent atomic collisions present in BECs can enhance matter-wave interferometry by enabling (i) ultra-low expansion rates through collective mode dynamics with a recent demonstration of a 3D expansion energy of \({k}_{B}\cdot 3{8}_{-7}^{+6}\) pK44, and (ii) ultimately the generation of mode entanglement through spin-squeezing dynamics to significantly surpass the standard-quantum limit45,46,47,48.
Today’s fastest BEC sources rely on atom-chip technology, where near-surface magnetic traps allow for rapid evaporation using radio frequency or microwave transitions. This approach benefits from constant high trapping frequencies during the evaporative cooling process, thus leading to repetition rates on the order of 1 Hz with BECs comprising 105 atoms49.
Anyway, since magnetic traps are not suitable in certain situations optical dipole traps become the tool of choice50. Examples are trapping of atomic species with low magnetic susceptibility51,52, or molecules53,54 and composite particles55,56. In optical dipole traps external magnetic field allow tuning parameters, e.g., when using Feshbach resonances57.
Here, the intrinsic link between trap depth and trap frequencies in dipole traps58 inhibits runaway evaporation. Cold ensembles can be only produced in shallow traps, leading to drastically increased preparation time tP. This long standing problem has been recently overcome through the use of time-averaged potentials, where trap depth and trap frequencies can be controlled independently, thus allowing for more efficient and faster evaporation while maintaining high atom numbers52,59.
In this work, we use dynamic time-averaged potentials for efficient BEC generation and demonstrate an all-optical matter-wave lens capable of further reducing the ensemble’s residual kinetic energy. Contrary to pulsed schemes of matter-wave lensing44,60,61,62,63,64,65, we keep the atoms trapped over the entire duration of the matter-wave lens37, which eases implementation in ground-based sensors. Moreover, we show that with this technique one can short-cut the evaporation sequence prior to the matter-wave lens, which increases the atomic flux by enhancing atom number and reducing cycle time while simultaneously reducing the effective temperature. Our method can largely improve the matter-wave sensor’s stability in various application scenarios.
Results
Evaporative cooling
We operate a crossed optical dipole trap at a wavelength of 1960 nm loaded from a 87Rb magneto-optical trap (details in the “Methods” section). The time-averaged potentials are generated by simultaneuos center-position modulation of the crossed laser beams in the horizontal plane. Controlling the amplitude of this modulation and the intensity of the trapping beams enables the dynamic control and decoupling of the trapping frequencies and depth. We chose the waveform of the center-position modulation to generate a parabolic potential52.
Up to 2 × 107 rubidium atoms are loaded into the trap with trapping frequencies ω/2π ≈ {140; 200; 780} Hz in \(\{{x}^{\prime};\,{y}^{\prime};\,z\}\) direction (definition of coordinate systems in the “Methods” section) with a trap depth of 170 μK. For this we operate the trap at the maximum achievable laser intensity of 12 W and the center-position modulation at an amplitude of h0 = 140 μm.
We perform evaporative cooling by reducing the trap depth exponentially in time while keeping the trapping frequencies at a high level by reducing the amplitude of the center-position modulation. This method allows us to generate BECs with up to 4 × 105 atoms within 5 s of evaporative cooling. By shortening the time constant of the exponential reduction we generate BECs with 5 × 104 (2 × 105) particles within 2 s (3 s) of evaporative cooling. At the end of the evaporation sequence the trap has frequencies of ω/2π ≈ {105; 140; 160} Hz and a depth of about 200 nK. The expansion velocity of the condensate released from the final evaporation trap is 2 mm s−1, which corresponds to an effective temperature of 40 nK.
All-optical matter-wave lens
Our matter-wave lens can be applied in any temperature regime explorable in our optical trap. We investigate the creation of collimated atomic ensembles for different initial temperatures of the matter-waves. To this aim, the evaporation sequence is stopped prematurely at different times to generate input atomic ensembles at rest with initial trap frequency ω0 and initial temperature T0. We then initiate the matter-wave lens by a rapid decompression66 of the trap frequency in the horizontal directions from ω0 to ωl. Here we denote by ωl the lensing potential in analogy with the Delta-kick collimation technique. The reduction of the trapping frequencies from the initial ω0 to ωl depends on experimental feasibility, such as the maximum achievable amplitude of the center-position modulation and the modulation amplitude right before the rapid decompression. With ongoing evaporative cooling this amplitude is reduced and thus the trap can be relaxed much further for more continued sequences. However, we need to maintain the confinement in the vertical direction by adjusting the dipole trap’s intensity to suppress heating or loss of atoms.
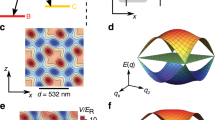
Subsequent oscillations in the trap result in a manipulation in phase space (Fig. 1a, b) for focusing, diffusion, and, importantly collimation of the matter-wave (Fig. 1c). Figure 1c depicts the expansion of a thermal ensemble in 1D for three different holding times (thold) to highlight the importance of a well chosen timing for the lens. Figure 2 shows exemplary expansion velocities (colored circles) depending on the holding time thold. The colored curves in this graph display the simulated behavior following the scaling ansatz (details in the “Methods” section) with an error estimation displayed by shaded areas. Only for the final measurement (also shown in the inset in Fig. 2) we create a BEC with a condensed fraction of 92.5% of the total atom number and apply the matter-wave lens to it.
The drawing in a shows the three trap configurations and the distribution of the atomic ensemble during the matter-wave lens. At the beginning the trap frequency (ωtrap) corresponds to the initial trap frequency (ω0), which is then decompressed to the lens trap frequency (ωl). After the holding time (thold) the trap is switched off (ωtrap = 0). The phase-space (p − x) diagrams in b show the atomic distributions at different timings during the matter-wave lens. Panel c shows the behavior of the time dependency of the trapping frequency. After the holding time in the initial trap the trapping frequency is rapidly decreased at time t = 0. Panel d shows the time evolution of the atomic ensemble’s size (σr), which starts to oscillate (solid and dotted black line) after the trap is relaxed. At time thold = (n + 0.5) × π/ωl, with \(n\in {\mathbb{N}}\), this oscillation reaches an upper turning point (teal curve). The atomic ensemble is released at its maximum size to minimize its later expansion rate. The labeled points (I-VIII) correspond to the phase-space diagrams in b. If the release time (thold) does not match this condition the expansion rate is not minimized (red and blue curve). The dashed-dotted black curve displays the size of a free falling ensemble without lensing, released at time t = 0.
Expansion velocity (σv) after 30 ms of time of flight in dependence of the holding time. The graph shows the expansion velocity for thermal ensembles with different initial temperatures T0 and the Bose-Einstein condensate (BEC) with an initial expansion temperature of T0 = 41 nK and a condensed fraction of Nc/N0 = 92.5%. The markers show the measurements, the dashed-dotted lines the expansion rate from the initial traps (cf. black dashed-dotted line in Fig. 1). The simulations use the scaling ansatz and are depicted as lines with a shaded 1-sigma error estimation for the used trap parameters. The inset displays the size oscillation of the Bose-Einstein condensate on an enlarged scale for better readability.
With the presented method we observe oscillations of the expansion rate, which are in good agreement with the simulations for different ensemble temperatures. For all investigated temperatures an optimal holding time exists for which the final expansion rate is minimized (Fig. 3a). The ratios of σv,l/σv,0 and ωl/ω0 for each measurement is shown in Fig. 3b.
Panel a shows the atom number depending on the expansion velocity (σv) for the resulting expansion velocity (blue circles) after the matter-wave lens and starting points (red circles). The lines connect the corresponding data points. The error bars arise from the time of flight measurements used to determine the expansion velocity. We use the 1-sigma fitting error of the ballistic expansion for σv and the statistical error of measured atom numbers. The two grayed out data points associated with the starting expansion velocities 60 mm s−1 and 6 mm s−1 are not displayed in Fig. 2 while all the others are included. Panel b shows the ratio of the lensed and the initial ensembles expansion velocity (σv,l/σv,0) as well as the trapping frequencies (ωl/ω0) depending on the starting expansion velocity.
The change in atom number from the initial to the lensing trap (Fig. 3a) lies within the error bars and arises mainly due to pointing instabilities of the crossed optical dipole trap beams. The lowest expansion rate is achieved with 553(49) μm s−1 with a related effective temperature of 3.2(0.6) nK and an atom number of 4.24(0.02) × 105. With this method we achieve a more than one order of magnitude lower effective temperature while maintaining a comparable atom number compared to evaporative cooling.
Discussion
In this paper, we demonstrate a technique to reduce the expansion velocity of an atomic ensemble by rapid decompression and subsequent release from an dipole trap at a well-controlled time. The efficiency of the matter-wave lens for higher temperatures is mainly limited experimentally by the limited ratio between the initial and the lensing trap frequency ωl/ω0 (Fig. 3b) which is constrained by the maximum possible spatial modulation amplitude of the trapping beams. In general, according to the Liouville theorem, the expansion speed reduction of the matter-wave is proportional to \({({\omega }_{0}/{\omega }_{l})}^{2}\) where a large aspect ratio enables a better collimated ensemble. The atoms are loaded into the time-average potential with an optimized center-position modulation amplitude of 140 μm, while the maximum is 200 μm. During the evaporation sequence this amplitude is decreased. Consequently, the relaxation of the trap is less efficient at the beginning of the evaporative sequence or directly after the loading of the trap.
Another constraint is that the trap’s confinement in the unpainted vertical direction is required to remain constant. If the vertical trap frequency is increased we observe heating effects and suffer from atom loss when it is decreased. To compensate for the trap depth reduction during the switch from the initial to the lensing trap we increase the dipole trap laser’s intensity accordingly.
An additional modulation in the vertical direction, e.g., by means of a two-dimensional acousto-optical deflector, as well as an intersection angle of 90° would enable the generation of isotropic traps. In such a configuration, the determination of the optimal holding time will benefit from the in-phase oscillations of the atomic ensemble’s size67. When applying our matter-wave lens in a dual-species experiment, isotropy of the trap will also improve the miscibility of the two ensembles68.
To illustrate the relevance for atom interferometers, we discuss the impact of our source in different regimes (details in the “Methods” section) operated at the standard quantum limit for an acceleration measurement. In a Mach-Zehnder-like atom interferometer1,18, the instability reads
after an averaging time τ, neglecting the impact of finite pulse durations on the scale factor69,70,71. Eq. (1) scales with the interferometer contrast C, the atom number per cycle N, the effective wave number nℏkeff indicating a momentum transfer during the atom-light interaction corresponding to 2n photons, and the separation time between the interferometer light pulses TI. The cycle time of the experiment tcycle = tP + 2TI + tD includes the time for preparing the ensemble tP, the interferometer 2TI, and the detection tD. In Eq. (1), the contrast depends on the beam splitting efficiency. This, in turn, is affected by the velocity acceptance and intensity profile of the beam splitting light, both implying inhomogeneous Rabi frequencies, and consequently a reduced mean excitation efficiency35,72,73. Due to expansion of the atomic ensemble and inhomogeneous excitation, a constrained beam diameter implicitly leads to a dependency of the contrast C on the pulse separation time TI, which we chose as a boundary for our discussion. We keep the effective wave-number fixed and evaluate σa(1 s) for different source parameters when varying TI.
Figure 4 shows the result for collimated (solid lines) and uncollimated (dotted lines) ensembles in our model (details in the “Methods” section) and compares them to the instability under use of a molasses-cooled ensemble (dash-dotted line). Up to TI = 100 ms and σa(1 s) = 10−8 m s−2, the molasses outperforms evaporatively cooled atoms or BECs due the duration of the evaporation adding to the cycle time and associated losses. In this time regime, the latter can still be beneficial for implementing large momentum transfer beam splitters36,38,39,40,42,43 reducing σa(τ) or suppressing systematic errors20,31,32,33,34,74 which is not represented in our model and beyond the scope of this paper. According to the curves, exploiting higher TI for increased performance requires evaporatively cooled atoms or BECs. This shows the relevance for experiments on large baselines23,37,74,75,76,77 or in microgravity78,79. We highlight the extrapolation for the Very Long Baseline Atom Interferometer (VLBAI)76,80, targeting a pulse separation time of TI = 1.2 s81. Here, the model describing our source gives the perspective of reaching picokelvin expansion temperatures of matter-wave lensed large atomic ensembles.
Behavior of the instability for shot-noise limited atom interferometers after an integration time of τ = 1 s for different sources (Tab. 1) over the pulse separation time TI. The instability is estimated for molasses cooled ensembles, thermal ensembles released from the optical dipole trap (ODT), and Bose-Einstein condensates (BEC and Advanced) also released from the optical dipole trap. The colors of the curves, except for the molasses and advanced case, agree with the measurements displayed in Fig. 2. The different source parameters are described in more detail in the “Methods” section.
Methods
Experimental realization
The experimental apparatus is designed to operate simultaneous atom interferometers using rubidium and potassium and is described in detail in references9,10,82.
For the experiments presented in this article only rubidium atoms were loaded from a two dimensional to a three dimensional magneto-optical trap (2D/3D-MOT) situated in our main chamber. After 2 s we turn off the 2D-MOT and compress the atomic ensemble by ramping up the magnetic field gradient as well as the detuning of the cooling laser in the 3D-MOT. Subsequent to compression, the atoms are loaded into the crossed dipole trap by switching off the magnetic fields and increasing the detuning of the cooling laser to about − 30Γ, with Γ being the natural linewidth of the D2 transition.
Figure 5 depicts the setup of our crossed optical dipole trap. The center-position modulation of the trapping beams is achieved by modulating the frequency driving the acousto-optical modulator (AOM) (Polytec, ATM-1002FA53.24). A voltage-controlled oscillator (Mini-Circuits, ZOS-150+) generates the signal for this, which is driven by a programmable arbitrary-waveform generator (Rigol, DG1022Z). We chose the waveform to generate a large-volume parabolic potential based on the derivation shown by Roy et al.52. The amplitude of the displacement of the center-position of the dipole trap beam, h0, is controlled by regulating the amplitude of the AOM’s frequency modulation. This yields a maximum beam displacement of h0 = 200 μm (300 μm) at the position of the atoms for the initial (recycled) beam.
Optical setup of the dipole trap and alignment through the vacuum chamber. Vertical arrows point towards the 2D magneto-optical trap (2D-MOT) and the vacuum pumps. The acousto-optical modulator (AOM) is used for modulating the center-position of the laser beams and intensity control. A λ/2 wave plate rotates the polarization of the beam for best diffraction efficiency of the AOM. Lenses L1 (f1 = 100 mm) and L2 (f2 = 300 mm) magnify the beam radius to about 3 mm, 4 mm (vertical, horizontal). Downstream lenses L3, L4, and L5 (f3,4,5 = 150 mm) focus, re-collimate and re-focus the beam into the center of the chamber. The λ/2 and the λ/4 wave plates set the polarization for maximum transmission at the orthogonal oriented polarization beam splitters (PBS). The mirrors (M) are used to guide the beam through the chamber. The purple arrow indicates the direction of absorption detection along the y-direction.
Data acquisition and analysis
We apply our matter-wave lens subsequent to loading the dipole trap and evaporative cooling. The duration of the complete evaporative sequence is 5 s for the measurements presented here we interrupt this sequence after 0 s, 0.2 s, 1 s, 2 s, 3.5 s, 4.3 s and 5 s. Before the step-wise change of the trap frequency (ω0 → ωl) we hold the ensemble in the trap given by the respective evaporation step configuration for 50 ms.
During the matter-wave lens, the rapid decompression of the trap causes oscillations of the ensemble’s radius in the lensing trap. Depending on the release time we observe oscillations by performing absorption imaging with iterating thold for different times after the release from the trap. For each holding time the expansion velocity is extracted by fitting a ballistic expansion. This expansion can be transformed into an effective temperature using:
along each direction. The measurement is performed for different starting temperatures in the thermal regime as well as the BEC.
The simulations shown in Fig. 2 use the scaling ansatz as described in the “Scaling Ansatz” section. Here, the trapping frequencies of the lens potential in x- and y-direction have been extracted by fitting two damped oscillations to the measured data. The starting expansion velocity was set by choosing a reasonable initial radius of the ensemble (Table 1). The other parameters arise from the measurements or simulations of the trapping potentials. The shaded areas in fig. 2 depict an error estimation of the expansion velocity oscillations obtained from performing the simulation by randomly choosing input parameters from within the error bars for 1000 simulation runs and calculating the mean value as well as the standard deviation for each thold.
Scaling Ansatz
In the case of a thermal ensemble in the collision-less regime, the dynamics of a classical gas can be described using the scaling ansatz83,84, which we briefly recall here for sake of simplicity. Here, the size of the ensemble scales with the time dependent dimensionless factor bi(t).
where θi acts as an effective temperature in the directions i ∈ x, y, z. Here ω0,i denotes the initial angular trap frequency and ωi(t) denotes the time-dependent angular trap frequency defined such as: ωi(t) = ωl,i for 0 < t < thold, with ωl,i being the lensing potential, and ωi(t) = 0 after the release (see Fig. 1). This system of coupled differential equations contains the mean field interaction, given by the factor:
with
where as is the s-wave scattering length, n0 the peak density and m the mass of a single particle. Collision effects are also taken into account through
with the relaxation time
and84
In the special case of a BEC, the mean field energy is large compared to the thermal ensemble’s energy (ξ ≈ 1) and the time scale on which collisions appear goes to zero (τ ≈ 0). In this case the time dependent evolution of the matter-wave can be described following Castin & Dum85. Here, the evolution of the BEC’s Thomas-Fermi radius, Ri(t) = bi(t)Ri(0), is described by the time-dependent evolution of the scaling parameter:
and Ri(0) is the initial Thomas-Fermi radius of the BEC along the i-th direction. It is worth to notice that recent studies86,87 extend the analysis of Guéry-Odelin83 and Pedri et al.84 to the BEC regime described by Castin & Dum85.
With this set of equations the time evolution of the ensemble’s size (\({\sigma }_{{r}_{i}}\)) and velocity distribution (\({\sigma }_{{v}_{i}}\)) is determined during the entire sequence of our matter-wave lensing sequence by
and
The scaling parameter bi can be applied either on the radius of a gaussian distributed thermal ensemble or the Thomas-Fermi radius of a BEC.
Estimation of instability in matter-wave sensors
The instability of a matter-wave sensor operating at the standard quantum limit can be estimated using Eq. (1). Here we assume Raman beam splitters (n = 1) with a 1/e2-radius of 1.2 cm and a pulse duration of tπ = 15 μs. The contrast (C) is taken into account as the product of the excitation probabilities of the atom-light interactions during the Mach-Zehnder type interferometer following Loriani et al.72. Table 1 shows the source parameters used for the estimation of the instability. We chose three parameter sets from the here presented measurements of two thermal ensembles released from the optical dipole trap with starting temperatures of T0 = 41μK and 4 μK and the BEC. Besides that we simulated the performance of the interferometer operated with a molasses cooled ensemble combined with a velocity selective Raman pulse of 30 μs73, based on typical parameters in our experiment, and an advanced scenario. For this we assume a BEC with 1 × 106 atoms after a preparation time tP = 1 s with a starting expansion velocity of 2 mm s−1, as anticipated for the VLBAI setup76,80. We extrapolate the performance of our matter-wave lens for this experiment, resulting in expansion velocities of 0.135 mm s−1 corresponding to an equivalent 3D temperature of 200 pK.
Data availability
The data used in this manuscript are available from the corresponding author upon reasonable request.
References
Kasevich, M. & Chu, S. Atomic interferometry using stimulated raman transitions. Phys. Rev. Lett. 67, 181–184 (1991).
Kasevich, M. & Chu, S. Measurement of the gravitational acceleration of an atom with a light-pulse atom interferometer. Appl. Phys. B 54, 321–332 (1992).
Riehle, F., Kisters, T., Witte, A., Helmcke, J. & Bordé, C. J. Optical ramsey spectroscopy in a rotating frame: Sagnac effect in a matter-wave interferometer. Phys. Rev. Lett. 67, 177–180 (1991).
Cronin, A. D., Schmiedmayer, J. & Pritchard, D. E. Optics and interferometry with atoms and molecules. Rev. Mod. Phys. 81, 1051–1129 (2009).
Biedermann, G. W. et al. Testing gravity with cold-atom interferometers. Phys. Rev. A 91, 033629 (2015).
Bouchendira, R., Cladé, P., Guellati-Khélifa, S., Nez, F. & Biraben, F. New determination of the fine structure constant and test of the quantum electrodynamics. Phys. Rev. Lett. 106, 080801 (2011).
Parker, R. H., Yu, C., Zhong, W., Estey, B. & Müller, H. Measurement of the fine-structure constant as a test of the standard model. Science 360, 191–195 (2018).
Damour, T. Testing the equivalence principle: why and how? Classical Quantum Gravity 13, A33–A41 (1996).
Schlippert, D. et al. Quantum test of the universality of free fall. Phys. Rev. Lett. 112, 203002 (2014).
Albers, H. et al. Quantum test of the universality of free fall using rubidium and potassium. The European Physical Journal D 74 (2020).
Fray, S., Diez, C. A., Haensch, T. & Weitz, M. Atomic interferometer with amplitude gratings of light and its applications to atom based tests of the equivalence principle. Phys. Rev. Lett. 93, 240404 (2004).
Bonnin, A., Zahzam, N., Bidel, Y. & Bresson, A. Simultaneous dual-species matter-wave accelerometer. Phys. Rev. A 88, 043615 (2013).
Kuhn, C. et al. A bose-condensed, simultaneous dual-species mach–zehnder atom interferometer. N. J. Phys. 16, 073035 (2014).
Tarallo, M. et al. Test of einstein equivalence principle for 0-spin and half-integer-spin atoms: Search for spin-gravity coupling effects. Phys. Rev. Lett. 113, 023005– (2014).
Zhou, L. et al. Test of equivalence principle at 10−8 level by a dual-species double-diffraction raman atom interferometer. Phys. Rev. Lett. 115, 013004 (2015).
Asenbaum, P., Overstreet, C., Kim, M., Curti, J. & Kasevich, M. A. Atom-interferometric test of the equivalence principle at the 10-12 level. Phys. Rev. Lett. 125, 191101 (2020).
Tino, G. M. Testing gravity with cold atom interferometry: results and prospects. Quantum Sci. Technol. 6, 024014 (2021).
Peters, A., Chung, K. Y. & Chu, S. Measurement of gravitational acceleration by dropping atoms. Nature 400, 849–852 (1999).
Peters, A., Chung, K.-Y. & Chu, S. High-precision gravity measurements using atom interferometry. Metrologia 38, 25– (2001).
Louchet-Chauvet, A. et al. The influence of transverse motion within an atomic gravimeter. N. J. Phys. 13, 065025 (2011).
Freier, C. et al. Mobile quantum gravity sensor with unprecedented stability. J. Phys.: Conf. Ser. 723, 012050 (2016).
Barrett, B. et al. Dual matter-wave inertial sensors in weightlessness. Nature Communications 7 (2016).
Hardman, K. et al. Simultaneous precision gravimetry and magnetic gradiometry with a bose-einstein condensate: A high precision, quantum sensor. Phys. Rev. Lett. 117, 138501 (2016).
Gersemann, M., Gebbe, M., Abend, S., Schubert, C. & Rasel, E. M. Differential interferometry using a Bose-Einstein condensate. Eur. Phys. J. D. 74, 203 (2020).
Savoie, D. et al. Interleaved atom interferometry for high-sensitivity inertial measurements. Science Advances 4 (2018).
Berg, P. et al. Composite-light-pulse technique for high-precision atom interferometry. Phys. Rev. Lett. 114, 063002 (2015).
Stockton, J., Takase, K. & Kasevich, M. Absolute geodetic rotation measurement using atom interferometry. Phys. Rev. Lett. 107, 133001 (2011).
Gauguet, A., Canuel, B., Lévèque, T., Chaibi, W. & Landragin, A. Characterization and limits of a cold-atom sagnac interferometer. Phys. Rev. A 80, 063604 (2009).
Canuel, B. et al. Six-axis inertial sensor using cold-atom interferometry. Phys. Rev. Lett. 97, 010402 (2006).
Geiger, R., Landragin, A., Merlet, S. & Santos, F. P. D. High-accuracy inertial measurements with cold-atom sensors. AVS Quantum Sci. 2, 024702 (2020).
Hensel, T. et al. Inertial sensing with quantum gases: a comparative performance study of condensed versus thermal sources for atom interferometry. Eur. Phys. J. D. 75, 108 (2021).
Heine, N. et al. A transportable quantum gravimeter employing delta-kick collimated bose-einstein condensates. Eur. Phys. J. D. 74, 174 (2020).
Karcher, R., Imanaliev, A., Merlet, S. & Pereira Dos Santos, F. Improving the accuracy of atom interferometers with ultracold sources. N. J. Phys. 20, 113041 (2018).
Schkolnik, V., Leykauf, B., Hauth, M., Freier, C. & Peters, A. The effect of wavefront aberrations in atom interferometry. Appl. Phys. B 120, 311–316 (2015).
Szigeti, S. S., Debs, J. E., Hope, J. J., Robins, N. P. & Close, J. D. Why momentum width matters for atom interferometry with bragg pulses. N. J. Phys. 14, 023009 (2012).
Abend, S. et al. Atom-chip fountain gravimeter. Phys. Rev. Lett. 117, 203003 (2016).
Dickerson, S. M., Hogan, J. M., Sugarbaker, A., Johnson, D. M. S. & Kasevich, M. A. Multiaxis inertial sensing with long-time point source atom interferometry. Phys. Rev. Lett. 111, 083001 (2013).
Gebbe, M. et al. Twin-lattice atom interferometry. Nat. Commun. 12, 2544 (2021).
McDonald, G. D. et al. 80ℏk momentum separation with bloch oscillations in an optically guided atom interferometer. Phys. Rev. A. 88, 053620 (2013).
Chiow, S.-w, Kovachy, T., Chien, H.-C. & Kasevich, M. 102ℏk Large Area Atom Interferometers. Phys. Rev. Lett. 107, 130403 (2011).
Debs, J. E. et al. Cold-atom gravimetry with a bose-einstein condensate. Phys. Rev. A 84, 033610 (2011).
Chiow, S.-w, Herrmann, S., Chu, S. & Müller, H. Noise-immune conjugate large-area atom interferometers. Phys. Rev. Lett. 103, 050402 (2009).
Cladé, P., Guellati-Khélifa, S., Nez, F. & Biraben, F. Large momentum beam splitter using bloch oscillations. Phys. Rev. Lett. 102, 240402– (2009).
Deppner, C. et al. Collective-mode enhanced matter-wave optics. Phys. Rev. Lett. 127, 100401 (2021).
Kruse, I. et al. Improvement of an atomic clock using squeezed vacuum. Phys. Rev. Lett. 117, 143004 (2016).
Szigeti, S. S., Nolan, S. P., Close, J. D. & Haine, S. A. High-precision quantum-enhanced gravimetry with a bose-einstein condensate. Phys. Rev. Lett. 125, 100402 (2020).
Anders, F. et al. Momentum entanglement for atom interferometry. Phys. Rev. Lett. 127, 140402 (2021).
Corgier, R., Gaaloul, N., Smerzi, A. & Pezzè, L. Delta-kick squeezing. Phys. Rev. Lett. 127, 183401 (2021).
Rudolph, J. et al. A high-flux bec source for mobile atom interferometers. N. J. Phys. 17, 065001 (2015).
Chu, S., Bjorkholm, J. E., Ashkin, A. & Cable, A. Experimental observation of optically trapped atoms. Phys. Rev. Lett. 57, 314–317 (1986).
Stellmer, S., Grimm, R. & Schreck, F. Production of quantum-degenerate strontium gases. Phys. Rev. A 87, 013611 (2013).
Roy, R., Green, A., Bowler, R. & Gupta, S. Rapid cooling to quantum degeneracy in dynamically shaped atom traps. Phys. Rev. A 93, 043403 (2016).
Anderegg, L. et al. Laser cooling of optically trapped molecules. Nat. Phys. 14, 890–893 (2018).
Carr, L. D., DeMille, D., Krems, R. V. & Ye, J. Cold and ultracold molecules: science, technology and applications. N. J. Phys. 11, 055049 (2009).
Grimm, R., Weidemüller, M. & Ovchinnikov, Y. B. Optical dipole traps for neutral atoms. In Advances In Atomic, Molecular, and Optical Physics, vol. 42, 95-170 (Elsevier, 2000).
Martínez, I. A., Petrosyan, A., Guéry-Odelin, D., Trizac, E. & Ciliberto, S. Engineered swift equilibration of a brownian particle. Nat. Phys. 12, 843–846 (2016).
Salomon, G., Fouché, L., Lepoutre, S., Aspect, A. & Bourdel, T. All-optical cooling of 39K to Bose-Einstein condensation. Phys. Rev. A. 90, 033405 (2014).
O’Hara, K. M., Gehm, M. E., Granade, S. R. & Thomas, J. E. Scaling laws for evaporative cooling in time-dependent optical traps. Phys. Rev. A 64, 051403 (2001).
Condon, G. et al. All-optical bose-einstein condensates in microgravity. Phys. Rev. Lett. 123, 240402 (2019).
Ammann, H. & Christensen, N. Delta kick cooling: A new method for cooling atoms. Phys. Rev. Lett. 78, 2088–2091 (1997).
Morinaga, M., Bouchoule, I., Karam, J.-C. & Salomon, C. Manipulation of motional quantum states of neutral atoms. Phys. Rev. Lett. 83, 4037–4040 (1999).
Myrskog, S. H., Fox, J. K., Moon, H. S., Kim, J. B. & Steinberg, A. M. Modified “δ-kick cooling” using magnetic field gradients. Phys. Rev. A. 61, 053412 (2000).
Luan, T., Li, Y., Zhang, X. & Chen, X. Realization of two-stage crossed beam cooling and the comparison with delta-kick cooling in experiment. Rev. Sci. Instrum. 89, 123110 (2018).
Kanthak, S. et al. Time-domain optics for atomic quantum matter. N. J. Phys. 23, 093002 (2021).
Gochnauer, D., Rahman, T., Wirth-Singh, A. & Gupta, S. Interferometry in an atomic fountain with ytterbium bose-einstein condensates. Atoms. 9, 58 (2021).
Chu, S., Bjorkholm, J. E., Ashkin, A., Gordon, J. P. & Hollberg, L. W. Proposal for optically cooling atoms to temperatures of the order of 10−6 k. Opt. Lett. 11, 73 (1986).
Li, R.-Z. et al. Expansion dynamics of a spherical bose–einstein condensate. Chin. Phys. B 28, 106701 (2019).
Corgier, R. et al. Interacting quantum mixtures for precision atom interferometry. N. J. Phys. 22, 123008 (2020).
Bertoldi, A., Minardi, F. & Prevedelli, M. Phase shift in atom interferometers: Corrections for nonquadratic potentials and finite-duration laser pulses. Phys. Rev. A 99, 033619 (2019).
Antoine, C. Rotating matter-wave beam splitters and consequences for atom gyrometers. Phys. Rev. A 76, 033609 (2007).
Cheinet, P. et al. Measurement of the sensitivity function in a time-domain atomic interferometer. IEEE Trans. Instrum. Meas. 57, 1141–1148 (2008).
Loriani, S. et al. Atomic source selection in space-borne gravitational wave detection. N. J. Phys. 21, 063030 (2019).
Kasevich, M. et al. Atomic velocity selection using stimulated raman transitions. Phys. Rev. Lett. 66, 2297–2300 (1991).
Abe, M. et al. Matter-wave Atomic Gradiometer Interferometric Sensor (MAGIS-100). Quantum Sci. Technol. 6, 044003 (2021).
Badurina, L. et al. AION: an atom interferometer observatory and network. J. Cosmol. Astropart. Phys. 2020, 011–011 (2020).
Hartwig, J. et al. Testing the universality of free fall with rubidium and ytterbium in a very large baseline atom interferometer. N. J. Phys. 17, 035011 (2015).
Zhou, L. et al. Development of an atom gravimeter and status of the 10-meter atom interferometer for precision gravity measurement. Gen. Rel. Gravit. 43, 1931–1942 (2011).
Kulas, S. et al. Miniaturized lab system for future cold atom experiments in microgravity. Microgravity Sci. Technol. 29, 37–48 (2016).
Vogt, C. et al. Evaporative cooling from an optical dipole trap in microgravity. Phys. Rev. A 101, 013634 (2020).
Schlippert, D. et al. Matter-wave interferometry for inertial sensing and tests of fundamental physics. In CPT and Lorentz Symmetry (WORLD SCIENTIFIC, 2020).
Schilling, M. et al. Gravity field modelling for the hannover 10 m atom interferometer. J. Geodesy. 94, 122 (2020).
Zaiser, M. et al. Simple method for generating bose-einstein condensates in a weak hybrid trap. Phys. Rev. A 83, 035601 (2011).
Guéry-Odelin, D. Mean-field effects in a trapped gas. Phys. Rev. A. 66, 033613 (2002).
Pedri, P., Guéry-Odelin, D. & Stringari, S. Dynamics of a classical gas including dissipative and mean-field effects. Phys. Rev. A. 68, 043608 (2003).
Castin, Y. & Dum, R. Bose-einstein condensates in time dependent traps. Phys. Rev. Lett. 77, 5315–5319 (1996).
Modugno, M., Pagnini, G. & Valle-Basagoiti, M. A. Effective self-similar expansion for the gross-pitaevskii equation. Phys. Rev. A 97, 043604 (2018).
Viedma, D. & Modugno, M. Effective self-similar expansion of a bose-einstein condensate: Free space versus confined geometries. Phys. Rev. Res. 2, 033478 (2020).
Acknowledgements
This work is funded by the German Space Agency (DLR) with funds provided by the Federal Ministry of Economic Affairs and Energy (BMWi) due to an enactment of the German Bundestag under Grant Nos. DLR 50WM1641 (PRIMUS-III), DLR 50WM2041 (PRIMUS-IV), DLR 50WM2245A (CAL-II), DLR 50WM2060 (CARIOQA), and DLR 50RK1957 (QGYRO). We acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)-Project-ID 274200144-SFB 1227 DQ-mat within the projects A05, B07, and B09, and -Project-ID 434617780-SFB 1464 TerraQ within the projects A02 and A03 and Germany’s Excellence Strategy—EXC-2123 QuantumFrontiers—Project-ID 390837967 and from “Niedersächsisches Vorab” through the “Quantum- and Nano-Metrology (QUANOMET)” initiative within the Project QT3. A.H. and D.S. acknowledge support by the Federal Ministry of Education and Research (BMBF) through the funding program Photonics Research Germany under contract number 13N14875.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
W.E., E.M.R., and D.S. designed the experimental setup and the dipole trapping laser system. H.A., A.H., A.R., and D.S. contributed to the design, operation, and maintenance of the laser system and the overall setup. R.C., E.C. and N.G. set the theoretical framework of this work. H.A., R.C., C.S., and D.S. drafted the initial manuscript. H.A., and R.C. performed the analysis of the data presented in this manuscript. H.A., and R.C. under lead of N.G. and C.S. performed the instability study. C.V., M.W., C.L., S.H. together with the other authors discussed and evaluated the results and contributed to, reviewed, and approved of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Albers, H., Corgier, R., Herbst, A. et al. All-optical matter-wave lens using time-averaged potentials. Commun Phys 5, 60 (2022). https://doi.org/10.1038/s42005-022-00825-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00825-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.