Higher order interactions destroy phase transitions in Deffuant opinion dynamics model

Abstract

Most opinion dynamics models are based on pairwise interactions. However in many real situations, discussions take place within groups of people. Here, we define a higher order Deffuant model by generalizing the original pairwise interaction model for bounded-confidence opinion-dynamics to interactions involving a group of agents of size k. The generalized model is naturally encoded in a hypergraph. We study this dynamics in different hypergraph topologies, from random hypergraph ensembles, to spatially embedded hyper-lattices. We show that including higher order interactions induces a drastic change in the onset of consensus for random hypergraphs; instead of the sharp phase transition, characteristic of the dyadic Deffuant model, the system undergoes a smooth size independent crossover to consensus, as the confidence value increases. This phenomenon is absent from regular hypergraphs, which conserve a phase transition.

Introduction

The formation and diffusion of opinion in societies have largely been studied from the point of view of Physics, modelling the society in terms of a dynamical system of interacting agents, by the means of stylized agent-based models, aimed at understanding the role played by different aspects of social interaction in the observed patterns in real life. Different models have been proposed which may be classified according to the representation of the agents’ opinions (scalar or vector, continuous or discrete variables), or by the structure of their interactions (mixed population, or networked systems), or even by the detailed aspects of the dynamics which are in generally grounded on disciplinary knowledge issued from social sciences, like for example, the Social Influence Theory^1,2.

The most popular aspects of social interactions, widely considered by previous studies are homophily, agents interact preferably with similar agents, and social influence, agents which interact become more similar. One influential class of opinion dynamics models are bounded confidence models, which implement homophily by a threshold rule: only agents whose opinions lie within a confidence range may interact. Two outstanding models of this class are the Deffuant–Weisbuch (DW) model³ and the Hegselmann–Krause (HK) model⁴. Both model the opinion of the N agents in the population as a continuous variable x_i ∈ [0, 1], ∀ i = 1, N and their main difference is that while the DW considers pairwise interactions and asynchronous updates, in the HK model, at each step, all the agents synchronously update their opinion by taking the average of each agent’s current opinion and those of their neighbours.

All these models consider pairwise relations between agents which can naturally be modelled by networks¹. However, pairwise interactions do not describe all possible ways of discussion in real life, and the particularities of group discussion and decision making are still a matter of discussion in Social Psychology^5,6,7. This necessity of going beyond pairwise interactions has been first addressed by generalizing previous models to the case of group interactions mainly in the form of a majority rule, as in the voter model⁸ or in the form of an aggregation rule that averages the opinion of the neighbours of the active agent, as in the Hegselmann–Krause model⁴.

Recently, the interest in multi-agent interactions⁹ to model group dynamics at a large scale did rise sharply and several studies were published in the context of opinion dynamics^{10,11,12,13,14,15,16}, (social) contagion^17,18,19 and other dynamical processes^20,21, which modelled the topology of interactions by hypergraphs.

It has been shown that if the multi-agent interaction is non-linear—higher order interaction (HOI)—the system cannot be modelled by any inherently pairwise graph¹². Regarding opinion dynamics, multi-agent interactions need to be considered to address problems where individuals discuss in groups, like professional meetings or private instant messenger groups.

Here we study a generalization of the DW to the case where the interactions involve a group of agents and not only a pair of them. This naturally implies changing the network description into a hypergraph, where each hyperedge represents an interacting group of agents. Our results show that considering hyperedges of size k = 3 is already enough to modify qualitatively the way consensus is reached with respect to the outcomes of the pairwise DW dynamics. This modification is enhanced with the introduction of larger hyperedges to the extent that the phase transition from polarization to consensus is replaced by a smooth crossover. We also show that, as for networks, the outcomes of the dynamics strongly depend on whether the hypergraph is regular or random and we explore the interplay of the dynamical rules and the interaction structure, paying particular attention to the finite-size effects that have been shown to be dominant in bounded confidence models in networks²².

Results

The model

The original DW model is defined for a set of N agents, each with a continuous opinion x_i ∈ [0, 1]. The agents can interact pairwise, provided that the difference of their opinions lies within a confidence interval given by an external parameter ε, and they can also be restricted by an underlying network (e.g., a lattice or a random graph). The asynchronous dynamics takes place in discrete time and at every time step, a pair of neighbouring agents i and j attempts to interact and update their opinion according to

$${x}_{i}(t+1)=\left\{\begin{array}{ll}({x}_{i}(t)+{x}_{j}(t))/2, & {{{{{{\rm{if}}}}}}}\,| {x}_{i}-{x}_{j}| \; < \; \varepsilon \\ {x}_{i}(t), \hfill &\hskip-1.5pc{{{{{\rm{otherwise}}}}}}\end{array}\right.$$

(1)

Note that this dynamics is a particular case of the original model, where the amplitude of opinion change towards the mean opinion is given by a parameter, μ. Here, this parameter is set to its maximal value, such that both agents assume their average opinion after one successful interaction. For homogeneous confidences, this should result in a higher convergence speed to the final state. This update rule means that either two neighbours discuss and arrive at a compromise opinion or do not discuss at all, depending on the confidence parameter ε.

To account for the fact that discussions are not exclusively happening between two persons, but may involve a group of agents, we need to replace graphs encoding pairwise relations, with hypergraphs. A hypergraph ${{{{{{{\mathcal{H}}}}}}}}=(V,E)$ is defined by a set of nodes or vertices V representing the agents and a set of hyperedges E, which is a subset of the powerset of V, i.e., can contain any subset of V. This way a hyperedge e ∈ E establishes a relation between its members, which encodes the group interaction. The number of nodes N = ∣V∣ is called the size of the hypergraph or the system size. The degree d_i of a node i is the number of hyperedges the node is a member of, and we call connectivity of the hypergraph, c, the average of all the degrees. A hypergraph is called uniform or k-uniform, if all hyperedges e ∈ E have the same size k = ∣e∣. For clarity, we refer to conventional graphs as dyadic graphs or 2-uniform hypergraphs.

In this framework, we modify the dynamical rule such that at each time step a random hyperedge e is selected and every member i ∈ e is updated according to

$${x}_{i}(t+1)=\left\{\begin{array}{ll}\overline{{x}_{e}}, &{{\mbox{if}}}\,{\max }_{j\in e}{x}_{j}(t)-{\min }_{j\in e}{x}_{j}(t) \; < \; \varepsilon \\ {x}_{i}(t), &{{\mbox{otherwise}}},\hfill\end{array}\right.$$

(2)

where $\overline{{x}_{e}}=\frac{1}{| e| }{\sum }_{j\in e}{x}_{j}$ is the average opinion of all members of the hyperedge. So interaction only happens if all members are within the confidence range of each other. This rule addresses the situation where an individual holding a very different opinion from the rest of the group, by blocking the discussion, prevents an otherwise possible compromise to reach consensus.

For small confidence ranges ε this means that the probability of a successful interaction for a hyperedge (provided that the opinions of the members are random and independent, which is the case for the initial conditions of our model) decays exponentially in the size k of the hyperedge, and therefore, large groups have a low probability to reach a compromise opinion.

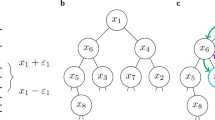
It is worthwhile noticing that the group interaction proposed here is different from the interaction between an agent and its group of neighbours that rules the dynamics of the Hegselmann–Krause (HK) model⁴. This becomes apparent when considering the projection of an example hypergraph onto a dyadic graph shown in Fig. 1.

Fig. 1: Graphs and hypergraphs.

Example of a hypergraph (a) and its projection to a dyadic graph (b). Coloured areas represent different hyperedges. In the hypergraph, the degree of node 4 is d₄ = 1, since it is the only member of one hyperedge, the degree of node 2 is d₂ = 3 since it is a member of three hyperedges.

In the HK model, each agent checks every neighbour synchronously and updates its own opinion by taking into account the opinion of all its neighbours whose opinion differs from its own in less than the confidence, ε, regardless of the differences between the opinions of those neighbours among themselves (which could be larger than the confidence). The HOID model, on the other hand, updates one hyperedge at a time. This means that in the example of Fig. 1, the state of vertex 3 might be updated three times (when updating hyperedges green, violet and orange) provided that all the nodes of each hyperedge have their opinions within the confidence range. As a consequence, a dissenter can block the interaction of all other agents in the hyperedge, a mechanism absent from the HK model. Indeed, if the update rule is non-linear, like the threshold value for the HOID, hypergraph interactions cannot be mapped to a dyadic graph. Also, note that for a 2-uniform hypergraph this model reduces directly to the well studied DW case.

Unless stated otherwise we perform simulations for 1000 independent realizations of the system for each of 300 equidistant values of ε ∈ [0, 0.6], i.e., a resolution in ε space of 0.002. For a better visibility, we present the results as lines instead of symbols. The statistical uncertainty is generally of the order of the width of the line. The raw data of the final states consisting of the locations and sizes of all clusters and convergence times are openly available at²³ for the k > 2 cases.

Note that the HOID on k-uniform hypergraphs reduces to the DW model on the corresponding topology for k = 2, therefore a look back at the DW helps to identify the patterns that are directly related to the higher-order interactions. We include, for comparison, the results of the dyadic DW model for each hypergraph topology.

As explained before, we do not intend to explore the HOID model in the mixed population, due to the high proportion of blocked hyperedges, however, a careful study of the dyadic DW model in the complete graph is useful to identify which observed phenomena are already present in the DW model in the complete graph, which is induced by the interplay between the dyadic DW model and the underlying topology, and finally, which are associated with the introduction of HOID. Such study is included in Supplementary note 1, where we revisit the results of the DW model for the complete network presented in ref. ²², including an extensive finite-size study that goes well beyond the sizes considered so far. The corresponding raw data is openly available at ref. ²⁴.

Random hypergraph ensembles

Homogeneous Erdős–Rényi hypergraphs

In this section, we compare the behaviour of the HOID model on k-uniform ER-hypergraphs, for different values of k. We are interested in relatively sparse hypergraphs so unless stated otherwise, we consider c = 10.

The first striking effect of the HOID model in the region of total fragmentation observed at low ε values in Fig. 2, where the normalized average size of the largest opinion cluster is $\langle S \rangle \approx 0$, and which grows with k. This phenomenon can be understood by recalling that, for fixed low values of ε, the probability for the agents connected by a hyperedge to interact shrinks exponentially in the number of members of the hyperedge, k, since the k random initial opinions must lie within a range of ε. So the amount of blocked hyperedges grows with k and inhibits the dynamics of the system for low values of ε.

Fig. 2: Behaviour of the mean relative size of the largest cluster, for the Erdős–Rényi hypergraph.

Mean relative size of the largest cluster $\langle S \rangle$ as a function of the confidence ε for the HOID model on k-uniform ER hypergraphs with edge sizes k = 2 (a), k = 3 (b), k = 4 (c), k = 5 (d), k = 6 (e), and an expected mean degree of c = 10 for different system sizes (N), each. The insets show the variance Var(S), which is sharpening for k ≤ 3 and vanishing for k ≥ 5, supporting the change from a sharp transition to a crossover.

More interestingly the very existence of a phase transition, for sparse hypergraphs, also depends on k. Figure 2 shows that for k = 2, 3 (k = 4 behaving as a limit case) there is a transition from polarization to consensus which gets sharper with increasing system size, however for k > 4 the transition disappears letting place to a crossover behaviour that becomes independent from the system size. The variances at the inset of the panels confirm this: while they are sharpening with system size for k ≤ 3 (in the manner of a diverging susceptibility) they vanish with system size, for k ≥ 5.

However, this behaviour is a characteristic of sparse hypergraphs. For very large values of the average connectivity c, a sharp transition reappears for the 6-uniform ER-hypergraphs as shown in Fig. 3.

Fig. 3: Behaviour of the mean relative size of the largest cluster for the Erdős–Rényi hypergraph with high connectivity c.

Mean relative size of the largest cluster $\langle S \rangle$ as a function of the confidence ε for the HOID model on six-uniform ER hypergraphs with an expected mean degree of c = 150 for different system sizes.

Here we can observe once again, the importance of the size effects in the study of bounded confidence models, which require extensive simulations in order to reveal important qualitative aspects of their behaviour, as seen in refs. ^22,25. Note that the curves for N = 256, 512 look very similar to the bottom panels of Fig. 2 even at the very high connectivity of c = 150, it is necessary to go to larger sizes to observe the qualitatively different behaviour.

Finally, as consensus is setting in with increasing ε, an extremely shallow minimum appears in the $\langle S \rangle$ curves, in the cases k = 2, 3, for ε ≳ ε_c. This effect is neither related to the HOI, nor to the networked structure, but is a consequence of the asynchronous DW dynamics and is present in the DW model in the mixed population (see Supplementary note 1). For larger k this shallow valley is replaced by an almost perfectly linear increase in $\langle S \rangle$, before the onset of unanimity, for ε = 0.5. This behaviour results from the interplay of the DW dynamics and the hypergraph and is absent from DW on networks. A heuristic argument allows us to explain this behaviour: at these relatively high values of the confidence the majority of agents have converged to the consensus opinion and those who have not, are blocked by at least one blocking agent in all the hyperedges to which they belong (notice that the other agents in the hyperedges could have already converged). Since each agent is part, on average, of c = 10 hyperedges, it is probable that the agents who have not converged are themselves the blocking ones. This means that their opinion differs in at least ε from the consensus opinion, where most of their neighbours are. Assuming that those blocking agents did not allow their edges to interact (or just a few times) they are still very close to their uniformly distributed initial opinion, and therefore their number will decrease linearly in ε, which induces the linear growth in $\langle S \rangle$.

We will see later that this phenomenon also exists for other hypergraph topologies.

Homogeneous Barabási–Albert hypergraphs

It is known that behaviour of the standard DW dynamics is qualitatively similar on the ER, and the BA networks.^26,27. Its generalization to HOI introduces, nevertheless, some differences. While as for the ER hypergraph, the behaviour of the HIOD in the BA hypergraph differs more and more from the corresponding dyadic model as k increases, this differentiation is stronger than for the ER case: Fig. 4b shows that the polarization plateau completely disappears already for k = 3. The size dependence of the order parameter $\langle S \rangle$ and the variance, still suggest a phase transition, however, the difference between the values of $\langle S \rangle$ before and after the transition point is much smaller, than for the ER case.

Fig. 4: Behaviour of the mean relative size of the largest cluster for the Barabasi–Albert hypergraph.

Mean relative size of the largest cluster $\langle S \rangle$ as a function of the confidence ε for the HOID model on k-uniform BA hypergraph with k = 2 (a), k = 3 (b), k = 5 (c), and expected mean degree of c = 10 for different system sizes. The insets show the variance Var(S), which is sharpening for k ≤ 3 and vanishing for k = 5; the same behaviour as for the ER-hypergraph.

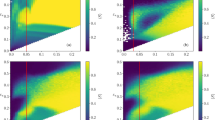
In order to understand the mechanisms that lead to these different behaviours of the order parameter, we examine the trajectories for both systems near the corresponding critical confidences ε_c. Figure 5 shows that while the trajectories for the ER case evolve to consensus by joining two symmetric strands (Fig. 5a), those of the BA case are asymmetric, with one majoritarian strand that contains a much larger share of agents (Fig. 5b).

Fig. 5: Comparison of single sample trajectories near the transition, for Erdős–Rényi and Barabasi–Albert hypergraphs.

Examples of the trajectory of a single realizations of the HOID model of size N = 16,384 and edge size k = 3, close to their transition to consensus. a ER hypergraph with connectivity c = 10. b BA hypergraph with c = 9. The horizontal axis is time in units of sweeps, i.e., N attempted updates. The dark colours show regions where agents are highly concentrated, light colour show regions with only very few agents and white signifies the absence of any agents. The colourmap is truncated at S = 0.2, to better visualize the small clusters, therefore the darkest shade represents all values 0.2 ≤ S ≤ 1.0.

As for the ER case, the sharp transition turns into a smooth crossover for larger values of k.

Figure 6 illustrates the same phenomenon at the final state, where one can observe that the cluster size distributions before and after the transition are very different for ER and BA hypergraphs. The almost isolated peak at S = 0.5 of the ER hypergraph before the transition shows that polarization involves two equally populated strands that join into a single one after the transition (ε = 0.3). On the contrary for the BA hypergraph, the distribution is broad, around S ≈ 0.4, before the transition. Moreover, letting aside the very small clusters (S ≤ 0.1), it looks quite symmetrical around the peak which still indicates polarization although with the existence of branches that could be unequally populated. At the transition, this distribution presents a sharper peak at S ≈ 0.7 showing that one of the two strands has gathered more agents than the other.

Fig. 6: Comparison of cluster size distribution for hypergraphs of different topology.

Cluster size distribution of systems of size N = 65,536, below and above the corresponding critical confidence value, ε_c. a, b ER 3-uniform hypergraph, ε_c = 0.277(1). c, d BA 3-uniform hypergraph, ε_c = 0.257(1).

A heuristic argument to explain these differences could be related to the very high degree nodes (hubs) that are found, by construction, in the BA hypergraph. As a hub belongs to many hyperedges, it is likely to get unblocked in some of the hyperedges it belongs to. As it interacts in one of those hyperedges, its opinion evolves, allowing for the unblocking of the other hyperedges it also belongs to, and therefore, attracting all the nodes belonging to those hyperedges to a common opinion. Other nodes, with less connectivity and not directly connected to the hub, are less likely to grow a large cluster. In the ER, on the other hand, there are no hubs, and it is possible to observe several nodes of relatively high connectivity distributed around the network and not directly connected. They can grow clusters independently around different opinions before joining into a single strand at higher confidence values.

Heterogenoeus hypergraphs

As shown in the previous sections, the behaviour of the system for given connectivity strongly depends on the size of the hyperedges. Therefore it is interesting to study what happens when the system contains hyperedges of different sizes. As we have seen that large hyperedges are more prone to remain blocked one could expect that the dynamics are lead by the smaller, non-blocked ones. To further investigate this point we study an ER-hypergraph that combines hyperedges of k = 3 and k = 5 which have revealed different behaviours in the uniform hypergraphs. We study two different ways of combining these hyperedges of different sizes: (a) same average connectivity for edges of different sizes and (b) same average number of hyperedges of both kinds.

From Eq. (4) (see the “Methods” section) and, knowing that the average number of hyperedges of size k is ${M}_{k}=\left(\genfrac{}{}{0.0pt}{}{N}{k}\right){p}_{k}$, one obtains the ratio of hyperedges of each kind M₃ = 5/3M₅ for the case (a), where we have fixed, c₃ = c₅ = 5 such that c = c₃ + c₅ = 10, for comparison with previous results. For case (b), fixing again c = 10 one obtains the mean degrees of the hyperedges of both sizes as c₃ = 30/8 and c₅ = 50/8, which are on the order of the sparse hypergraphs previously considered.

Figure 7 shows that in case (a) the shape of the curve is a slightly smoothed version of the 3-uniform case without a hint for fundamentally new behaviour, indicating that the k = 3 hyperedges dominate the behaviour. This is not surprising as they are more numerous and less susceptible to being blocked. On the other hand, when the system contains the same number of hyperedges of both kinds, shown in Fig. 7b, one does not observe the predominance of the k = 3 behaviour, instead, the curves look similar to those of the ’intermediate’ 4-uniform case. The same qualitative behaviour is observed when mixing dyadic edges with k = 4 hyperedges, both randomly distributed.

Fig. 7: Behaviour of the mean relative size of the largest cluster for heterogeneous Erdős–Rényi hypergraph.

Mean relative size of the largest cluster $\langle S \rangle$ as a function of the confidence ε for the HOID model on heterogeneous hyper-ER graphs with connectivity of c = 10 = c₃ + c₅, where the connectivity c₃ is caused by k = 3 hyperedges and c₅ by k = 5 hyperedges. In case (a) both types of hyperedges cause the same connectivity c₃ = c₅ = 5. In case (b) there are on average equal numbers of both hyperedges, i.e., c₃ = 30/8 and c₅ = 50/8.

We, therefore, conjecture that when the average number of hyperedges of different sizes is the same, non-uniform hypergraphs do not behave too differently from the uniform hypergraphs with k in the same range, with a behaviour that ‘interpolates’ between the two considered uniform cases. In particular, we do not observe as could have been expected, the smaller k dominating the behaviour in this case, in spite of the property of smaller hyperedges to be much less susceptible to blocking. This is an interesting finding because it gives a hint of the behaviour of heterogeneous hypergraphs: hyperedges of size k may dominate the behaviour when they are many more than the others, however when the average number of hyperedges is similar for all sizes, the expected behaviour would be similar to a uniform hypergraph with an intermediate value of k.

Regular, spatial hypergraphs

We present here the results for the HOID model on hypergraphs built in such a way that they keep the regularities and spatial symmetries of a square lattice, with hyperedges including first, second and third nearest neighbours. In Fig. 8 the results on hypergraphs with hyperedges of sizes k = 3 (panel (b)) and k = 5 (panel (c)) are compared with the corresponding dyadic DW model in the square lattice with only nearest neighbours (panel (a)) and with third nearest neighbours (panel (c)). Notice that the three cases have similar connectivity, c ≈ 12, 15, which is also of the order of the sparse random hypergraphs studied in the section “Random hypergraph ensembles”

Fig. 8: Behaviour of the mean relative size of the largest cluster for hypergraphs on lattices.

Mean relative size of the largest cluster $\langle S \rangle$ as a function of the confidence ε for the HOID model on different lattice-like topologies for different system sizes. Case a nearest-neighbour square lattice with hyperedge size k = 2 and connectivity c = 4, cases b and c spatial hypergraphs defined in the “Methods” section, with k = 3, c = 12 and k = 5, c = 15, and case d square lattice with k = 2 and up to third nearest-neighbour interactions, i.e., c = 12.

Figure 8 shows that the behaviour of regular hypergraphs is completely different from the random case: no polarization is observed for both k values, and there is a sharp transition from complete fragmentation to consensus, that seems continuous (panels (b) and (c)). Moreover, unlike for random hypergraphs, no crossover to a smooth size independent behaviour for k = 5 is found.

It should be noticed that, while a longer reach of the interactions in a dyadic lattice favours consensus, lowering the value of ε_c (panel (d)), it does not for hypergraphs, because reaching further neighbours implies involving larger group sizes which are easier to get blocked.

As for continuous phase transitions in thermodynamics, we observe a scale free distribution of cluster sizes. This is the indication of a divergent correlation length in the thermodynamic limit (see Fig. 9). However, we were not able to scale the order parameter, $\langle {S}_{N} \rangle (\varepsilon )=\widetilde{S}\left((\varepsilon -{\varepsilon }_{{{{{{{{\rm{c}}}}}}}}}){N}^{\nu }\right)$ with a unique exponent above and below the transition.

Fig. 9: Cluster size distribution for hypergraph on a lattice.

Distribution of the cluster sizes, S, for system of size N = 16,384, at confidence value ε = 0.2, for the HOID model on a lattice with edge size k = 3 and connectivity c = 12.

Discussion

We generalized the Deffuant model to higher-order interactions, where the discussions take place in small groups that cannot be reduced to combinations of pairwise interactions. This generalization involves some hypothesis on how the interaction will take place inside the group. While preparing this manuscript, we noticed the work of Hickok et al. ¹⁶, published at the moment in a preprint server, which reports a study of a different extension of the DW model to include HOI. In that work, the authors assume a discordance function that facilitates the interaction of large groups. Here, on the contrary, we just follow the original DW premises by considering that in order to interact, all members of the group must hold opinions inside the confidence interval. This working hypothesis describes the situation where some agents in the group, by holding an opinion that is very far from the others’ may block an otherwise possible compromise. As a consequence, it is more difficult to reach a common opinion as the group becomes larger. Therefore, these works address two possible alternative situations: while Hickok et al. ¹⁶ assume the existence of nodes that could reduce discordance in the group, here we focus on the role of a blocking minority.

At this point it should be noticed that we have generalized the Deffuant model in the case where the interacting agents end up having the same opinion after the interaction. In other words, the parameter μ of the original model is set to its maximum value μ = 1/2. This is a very common choice (see for e.g. ref. ¹⁶) for computational reasons, because this parameter controls the speed of convergence of the model³. However, care should be taken in the case of a heterogeneous model, with the agents characterized by different confidences, as it has been shown that, in this case the characteristic time scales are different for different confidences and modify the outcomes of the dynamics²⁵.

The natural tool to model group interactions are hypergraphs. We therefore perform large-scale simulations of this HOID model in sparse hypergraphs with different hyperedge distributions. We observe that the fact of introducing hyperedges completely changes the dynamics with respect to the DW model in the corresponding network topology. One reason for this is the blocking effect of the hyperedges, which requires higher confidences to overcome fragmentation (the domain of ε values where $\langle S \rangle (\varepsilon )=0$ increases with k).

The most interesting result of the inclusion of hyperedges, is that above a certain size of the groups the sharp transition to consensus, well known from the original Deffuant model, changes to a smooth crossover. In other words, when discussions take place in groups, a small decrease in the confidence will not trigger a sharp disruption of the society from consensus to polarization but a slow decrease of the amount of individuals sharing the same opinion. Since such crossovers are generally preferable to sharp transitions for the stability of real societies, this fundamental mechanism could be of further interest. The counterpart is that, in order to unblock larger hyperedges, larger confidences are required to leave the fragmentation region. When the hypergraph becomes dense the phase transition still holds for hyperedges of k = 6, but it is nevertheless less sharp than for smaller hyperedges.

Furthermore, the introduced model shows a richer behaviour on different hypergraph ensembles: while the dyadic Deffuant model behaves qualitatively in the same way on ER or BA networks, its generalization to hypergraphs shows different agents’ opinion trajectories for ER and BA hypergraph.

Once again, here we see the importance of studying finite size effects for those systems. As system size increases, new phenomena, absent for the smaller ones, often appear. In other cases the independence of the order parameter with the size allows to distinguish a phase transition from a smooth crossover. We note that many studies on opinion dynamics do not look at the size dependence at all or study only fairly small sizes, such that similar fundamental differences for other systems might have been overlooked in the past.

We also show that if the hypergraph is not homogeneous, the expected dominance of small hyperedges (due to the fact that larger ones are more likely to be blocked) does not occur, unless they are significantly majoritarian. If the average number of hyperedges of different sizes is the same, the system behaves similar to a uniform hypergraph case with an intermediate k value. As a consequence, heterogeneous hypergraphs, which are nearer to real societies, will mostly lead to a smooth crossover rather than to a sharp transition.

Spatially structured hypergraphs, unlike random ones, seem to show the same behaviour as dyadic lattices. However, increasing the reach of the interaction in the hypergraphs shows the opposite behaviour than doing so in lattices. While there are no qualitative changes in hypergraphs, besides the expected increase of ε_c, a higher reach in dyadic lattices promotes consensus. This is a consequence of the competing effects on including further neighbours in the hypergraph: on the one hand, it increases the reach but on the other, by increasing the size of the group, it enhances the possibility of blocking hyperedges.

In this work, we study the case where the groups that can potentially interact do not change in time as they are constrained by the underlying topology. It is therefore pertinent to question whether the effects observed here would still hold if we release this constraint by randomly choosing the potentially interacting group among all the agents, at each time step. This setup may seem unrealistic if we interpret each hyperedge as a social group. However, a model that introduces a realistic modification of the interacting groups with time would consist of granting the agents the ability to leave groups and join another group. The departure could be triggered by some measure of the frustration of not being able to reach a consensus within a group. This way of unblocking larger edges and allowing for some renewal of the groups, which models the behaviour in real systems, is the subject of forthcoming work.

Methods

As usual, we start the dynamics with initial opinions drawn from a uniform distribution U[0, 1]. The dynamics eventually leads the system, after a long transient, to a final state²⁸, where the opinions of the agents do not change anymore. As convergence criterion, we require that after performing a sweep, i.e., N attempted updates, we have:

$$\mathop{\sum }\limits_{i=0}^{N}| {x}_{i}(t)-{x}_{i}(t-1)| \; < \; 1{0}^{-3}$$

(3)

This criterion, which has already been tested in different studies of the HK model^22,25,29 does become sharper for larger systems and is especially suited to ensure that regions of very dense agents are static. Since our main observable is the relative size of the largest cluster, S, i.e., the fraction of agents having the majoritarian opinion within a tolerance of 10⁻³, we expect this criterion to lead to accurate results while saving a lot of computations on converged systems.

Random hypergraph ensembles

Although the original DW model was also studied on a complete graph, its generalization to HOI in this configuration is less interesting. In fact, the interaction rule applied here induces a very low probability for the large hyperedges to interact. As the complete hypergraph contains far more large hyperedges than small ones, this will lead to blocking the evolution of the system, making the complete hypergraph non-interesting. Instead, we focus on a selection of ensembles of sparse hypergraphs, i.e., ensembles whose mean degree is independent of the number of nodes. For the sake of comparison, we generalize the HOID model to lattices and random graph ensembles, on which the DW^26,27,30 and related models²² were studied before.

Erdős–Renyí

First, we consider a generalization of the Erdős–Renyí (ER) ensemble to hypergraphs. The dyadic ER consists of graphs where every edge exists with probability p. In the limit of large graphs, p = c/N, where c is the finite expected degree the graphs are sparse.

To construct hyperedges in the same way, let us call p_k, the probability that k nodes taken at random, constitute a hyperedge. Therefore

$${c}_{k}={p}_{k}\frac{k}{N}\left(\begin{array}{l}{N}\\ {k}\end{array}\right)$$

(4)

is the expected degree contributed by hyperedges of size k. The total expected degree is simply c = ∑_kc_k.

Technically, we construct realizations of this ensemble by first determining how many k-hyperedges should appear in the graph by drawing a binomially distributed random number from ${{{{{{{\mathcal{B}}}}}}}}\big(\big({N\atop k}\big),{p}_{k}\big)$, since it is infeasible to iterate all $\big({N\atop k}\big)={{{{{{{\mathcal{O}}}}}}}}({N}^{k})$ possible hyperedges of size k and decide whether to include them or not with probability p_k. Since we are interested in sparse hypergraphs, we calculate p_k from the desired mean degree using the relation given by Eq. (4). For large values of N it becomes impractical to draw the number of hyperedges from a binomial distribution. Therefore, for an expected number of hyperedges ${M}_{k}=\big({N\atop k}\big){p}_{k}=N{c}_{k}/k \; > \; 1{0}^{3}$, we switch to the Gaussian ${{{{{{{\mathcal{N}}}}}}}}({M}_{k},\sqrt{{M}_{k}(1-{p}_{k}){p}_{k}})$, ensuring that the error introduced by this approximation is negligible.

Barabási–Albert

Additionally, we introduce a scale-free k-uniform hypergraph, in the sense that the degree distribution—the number of hyper-edges a node belongs to—follows a power-law with an exponent 2 < γ ≤ 3. To construct a realization we perform the preferential attachment procedure of the Barabási–Albert (BA) graph ensemble³¹ with hyperedges, which is a special case of the ensembles introduced in refs. ^32,33. This ensemble offers the parameter m determining the number of hyperedges introduced for each node, which therefore determines the average degree c ≈ mk. We start with a fully connected core, i.e., all subsets of size k are hyperedges, of $M=\max (m-1,k)$ nodes. The remaining nodes are iteratively added. For each node m hyperedges are introduced and their other k−1 neighbours are chosen as members with a probability proportional to their current degree, avoiding identical hyperedges and nodes appearing twice in the same hyperedge. This procedure leads to a scale-free degree distribution P(d) ∝ d^−γ with $\gamma =2+\frac{1}{k-1}$³² and reduces to the well-known BA case for k = 2.

Regular spatial hypergraphs

The DW model was also studied in the square lattice as a very stylized way to introduce a neighbourhood embedded in real space^3,34.

There are different ways to introduce HOI in lattices. Here we propose two regular structures based on the successive neighbours (first, second, third, etc. nearest neighbours) of the dyadic square lattice. The first case is a 3-uniform hypergraph, where hyperedges connect up to the second nearest neighbours as shown on the left of Fig. 10. This results in a mean degree of c = 12. The second case is a five-uniform hypergraph, where hyperedges connect up to the third nearest-neighbour nodes as shown on the right of Fig. 10. This results in a mean degree of c = 15.

Fig. 10: Example of hypergraphs on a lattice.

Two possible hypergraph configurations for lattices with different edge sizes and connectivity, respectively. a k = 3, c = 12 and b k = 5, c = 15. For clarity, a `basis set' of hyperedges is shown for the central node in the foreground (coloured zones). Each node contributes such a basis set to the hypergraph. In the background, with muted colours, all hyperedges are drawn.