Magnonic superradiant phase transition

Abstract

In the superradiant phase transition (SRPT), coherent light and matter fields are expected to appear spontaneously in a coupled light–matter system in thermal equilibrium. However, such an equilibrium SRPT is forbidden in the case of charge-based light–matter coupling, known as no-go theorems. Here, we show that the low-temperature phase transition of ErFeO₃ at a critical temperature of approximately 4 K is an equilibrium SRPT achieved through coupling between Fe³⁺ magnons and Er³⁺ spins. By verifying the efficacy of our spin model using realistic parameters evaluated via terahertz magnetospectroscopy and magnetization experiments, we demonstrate that the cooperative, ultrastrong magnon–spin coupling causes the phase transition. In contrast to prior studies on laser-driven non-equilibrium SRPTs in atomic systems, the magnonic SRPT in ErFeO₃ occurs in thermal equilibrium in accordance with the originally envisioned SRPT, thereby yielding a unique ground state of a hybrid system in the ultrastrong coupling regime.

Introduction

In 1973, it was proposed^1,2 that photon and matter fields spontaneously appear in thermal equilibrium as a static transverse electromagnetic field and a static polarization, respectively, when the photon–matter coupling strength exceeds a certain threshold, entering the so-called ultrastrong coupling regime^3,4,5. This phenomenon is known as the superradiant phase transition (SRPT) or Dicke phase transition, as the Dicke model was used in the theoretical calculations^1,2, having been originally developed to describe the superradiance phenomena⁶.

The realization of the SRPT in thermal equilibrium may be expected to provide a new avenue for decoherence-robust quantum technology because the ground state of the Dicke model provides a quantum-squeezed vacuum on a photon–atom two-mode basis^7,8,9,10,11, and perfect ideal squeezing is obtained at the SRPT critical point, as recently found both numerically and analytically^12,13. In contrast to the standard squeezed state generation in non-equilibrium situations, quantum squeezing at the SRPT critical point is intrinsically stable and resilient against any noise even at finite temperatures¹³. As a result of this stable squeezing, such systems are intrinsically robust against decoherence, which is especially important for quantum sensing and continuous-variable quantum information technology.

A unique aspect of the SRPT is its manifestation as a physical phenomenon associated with the thermal-equilibrium state of a coupled light–matter system. This deviates from typical quantum-optics research that mainly deals with non-equilibrium excited-state dynamics. The occurrence of non-equilibrium SRPTs has been demonstrated in cold-atom systems driven by laser beams^14,15,16,17. Although the temperature of cold atoms in a steady state is usually measured by the variance of their kinetic energy, the non-equilibrium SRPTs are inherently driven, dissipative, and transient phenomena. Effective temperatures defined with the driving power in the non-equilibrium SRPTs have been discussed theoretically¹⁷. However, the realization of SRPTs under pure thermal equilibrium is yet to be achieved. The existence of a SRPT analogue has been theoretically proposed for a superconducting circuit maintained under thermal equilibrium^{18,19,20,21,22,23,24}, but no experimental observations of this effect have been reported.

The present work shows theoretically that the phase transition in erbium orthoferrite (${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$) with a critical temperature$\,{T}_{{{{{{\rm{c}}}}}}}$ of ~4 K, known as the low-temperature phase transition (LTPT), is a magnonic SRPT, that is, an SRPT in which the ${{{{{\rm{Er}}}}}}^{3+}$ spins cooperatively couple with the ${{{{{\rm{Fe}}}}}}^{3+}$ magnonic field (spin-wave field) instead of with a photonic field as in the originally proposed SRPT. Specifically, we found that the LTPT occurs owing to ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling, even in the absence of direct ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions. In addition, we observed that the ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling enhances the ${T}_{{{{{{\rm{c}}}}}}}$ value for LTPT compared to that obtained via direct ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ interactions. These results demonstrate the uniqueness of ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ as a physical system in which SRPT can be experimentally realized under thermal equilibrium.

Results

Principle of magnonic SRPT

The SRPT was first suggested in 1973 by Hepp and Lieb¹, and has been extensively discussed based on the Dicke model⁶, conventionally expressed as

$$\frac{{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}}{\hslash }\equiv {\omega }_{{{{{{\rm{ph}}}}}}}{\hat{a}}^{{{\dagger}} }\hat{a}+{\omega }_{{{{{{\rm{ex}}}}}}}{\hat{S}}_{x}+\frac{{{{{{\rm{i}}}}}}2g}{\sqrt{N}}({\hat{a}}^{{{\dagger}} }-\hat{a}){\hat{S}}_{z}.$$

(1)

Here, $\hat{a}$ is the annihilation operator of a photon in a photonic mode with resonance frequency ${\omega }_{{{{{{\rm{ph}}}}}}}$, ${\hat{S}}_{x,y,z}$ are spin $\frac{N}{2}$ operators representing an ensemble of two-level atoms with a transition frequency ${\omega }_{{{{{{\rm{ex}}}}}}}$, and $N$ is the number of atoms. The last term represents the coupling between the photonic mode and atomic ensemble with strength $g$. In the thermodynamic limit, i.e., in the limit of $N\!\to\! {{\infty }}$, the SRPT arises when $4{g}^{2} \, > \, {\omega }_{{{{{{\rm{ph}}}}}}}{\omega }_{{{{{{\rm{ex}}}}}}}$, i.e., in the ultrastrong coupling regime $g\,\gtrsim\, {\omega }_{{{{{{\rm{ph}}}}}}},{\omega }_{{{{{{\rm{ex}}}}}}}$^3,4,5. Below ${T}_{{{{{{\rm{c}}}}}}}$, the expectation values of the photon annihilation operator $\langle \hat{a}\rangle$ and spin operator $\langle {\hat{S}}_{z}\rangle$ become non-zero, indicating the spontaneous appearance of a static electromagnetic field and static polarization (or a persistent electric current) in thermal equilibrium.

The magnonic SRPT is a phase transition caused by ultrastrong coupling between a magnonic mode and other collective excitations in matter. The spontaneous appearance of magnons, also known as spin waves, reflects the spontaneous ordering of a spin ensemble mediating them in a certain direction. We present an explanation of the magnonic SRPT in the case of ${{{{{{\rm{ErFeO}}}}}}}_{3}$ below.

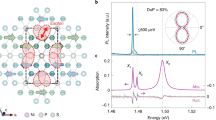
Each unit cell in ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ contains four ${{{{{\rm{Er}}}}}}^{3+}$ ions and four ${{{{{\rm{Fe}}}}}}^{3+}$ ions. The four ${{{{{\rm{Fe}}}}}}^{3+}$ spins, each of which has an angular momentum of $\hslash S=(5/2)\hslash$, are oriented in different directions, even in the absence of an external direct current (DC) magnetic field²⁵. However, it is known that the ${{{{{\rm{Fe}}}}}}^{3+}$ spin resonances (magnon modes) may be described well by considering only two spins ${{\hat{{{{{\bf{S}}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ comprising two real ${{{{{\rm{Fe}}}}}}^{3+}$ spins, which are usually treated as a single spin with $S=5/2$. In such a two-sublattice model of ${{{{{\rm{Fe}}}}}}^{3+}$, as depicted in Fig. 1a, the two spins ${{\hat{{{{{\bf{S}}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ are ordered antiferromagnetically along the $c$ axis at ${T}_{{{{{{\rm{c}}}}}}} \, < \, T\,\lesssim\, 90\,{{{{{\rm{K}}}}}}$, but are slightly canted toward the $a$ axis and show weak magnetization (the ${{{{{\rm{Fe}}}}}}^{3+}$ spins exhibit the so-called spin-reorientation transition at $90\,{{{{{\rm{K}}}}}}\,\lesssim\, T\,\lesssim\, 100\,{{{{{\rm{K}}}}}}$^26,27,28). In contrast, the ${{{{{\rm{Er}}}}}}^{3+}$ spins are paramagnetic at $T \, > \, {T}_{{{{{{\rm{c}}}}}}}$, and they are directed along the $a$ axis by the weak ${{{{{\rm{Fe}}}}}}^{3+}$ magnetization. This phase is called the ${\Gamma }_{2}$ phase²⁹.

Fig. 1: Spin configurations in ErFeO₃ below and above T_c ~ 4 K.

In this study, we considered two-sublattice models both for ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$ and ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ spins. a In the high-temperature (${T}_{{{{{{\rm{c}}}}}}} \, < \, T\,\lesssim\, 90\,{{{{{\rm{K}}}}}}$, ${\Gamma }_{2}$) phase, the ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ spins are ordered antiferromagnetically along the $c$ axis with a slight canting toward the $a$ axis. The ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$ spins are paramagnetic and directed toward the $a$ axis by the weak ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ magnetization. b In the low-temperature ($T \, < \, {T}_{{{{{{\rm{c}}}}}}}$, ${\Gamma }_{12}$) phase, the ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$ spins are ordered antiferromagnetically along the $c$ axis, and the antiferromagnetic (AFM) vector ${{{{{{\bf{S}}}}}}}^{{{{{{\rm{A}}}}}}}-{{{{{{\bf{S}}}}}}}^{{{{{{\rm{B}}}}}}}$ of the ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ spins rotates in the ${bc}$ plane.

At $T \, < \, {T}_{{{{{{\rm{c}}}}}}}$, as shown in Fig. 1b, when a two-sublattice model is used for the ${{{{{\rm{Er}}}}}}^{3+}$ spins, they are ordered antiferromagnetically along the $c$ axis, with a canting toward the $a$ axis due to the ${{{{{\rm{Fe}}}}}}^{3+}$ magnetization. Simultaneously, the ${{{{{\rm{Fe}}}}}}^{3+}$ antiferromagnetism (AFM) vector ${{{{{{\bf{S}}}}}}}^{{{{{{\rm{A}}}}}}}-{{{{{{\bf{S}}}}}}}^{{{{{{\rm{B}}}}}}}$ rotates gradually in the ${bc}$ plane. The rotation angle measured from the $c$ axis, $\varphi$, was estimated to be $4{9}^{\circ }$ at $T=0\,{{{{{\rm{K}}}}}}$²⁹. This low-temperature phase is called the ${\Gamma }_{12}$ phase²⁹.

The second-order phase transition between phases ${\Gamma }_{2}$ and ${\Gamma }_{12}$ at ${T}_{{{{{{\rm{c}}}}}}}\sim 4\,{{{{{\rm{K}}}}}}$ is called the LTPT^27,28. There are at least two contributions to the LTPT, namely the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{{\rm{Er}}}}}}}^{3+}$ and ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ exchange interactions^29,30. Although the former is usually stronger than the latter and is largely responsible for LTPT, the latter is essential for explaining the rotation of the ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector.

In the absence of the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ exchange interactions, as shown in Fig. 1a, the ${{{{{\rm{Fe}}}}}}^{3+}$ spins are ordered antiferromagnetically along the $c$ axis with a slight canting toward the $a$ axis in the ground state of the ${{{{{\rm{Fe}}}}}}^{3+}$ subsystem. Considering that the magnon excitation in this ${{{{{\rm{Fe}}}}}}^{3+}$ subsystem corresponds to the photon excitation in the electromagnetic vacuum, the rotation of the ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector (at $T \, < \, {T}_{{{{{{\rm{c}}}}}}}$ as shown in Fig. 1b) indicates the spontaneous appearance of magnons, corresponding to the appearance of photons (a static electromagnetic field) in the ordinary SRPT, in thermal equilibrium. The ordering of the ${{{{{\rm{Er}}}}}}^{3+}$ spins corresponds to the spontaneous appearance of an atomic field (polarization) in the SRPT.

Owing to the phenomenological similarities between the LTPT and SRPT, the microscopic models governing these phase transitions may be considered transferable. This constitutes the basic concept of magnonic SRPT proposed in this study.

${{{{{\bf{ErFe}}}}}}{{{{{{\bf{O}}}}}}}_{{{{{\bf{3}}}}}}$ spin model

First, we describe a general spin model for ${{{{{\mathrm{Er}}}}}}_{{{{{x}}}}}{{{{{{\mathrm{Y}}}}}}}_{{{{{1}}}}{{{{-}}}}{{{{x}}}}}{{{{{\mathrm{Fe}}}}}}{{{{{{\mathrm{O}}}}}}}_{{{{{3}}}}}$ (${{{{0}}}}{{{{\le }}}}{{{{x}}}}{{{{\le }}}}{{{{1}}}}$), which is consistent with our previous experimental study³¹. The replacement of ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$ ions with non-magnetic ${{{{{{\mathrm{Y}}}}}}}^{{{{{3}}}} + }$ ions simply reduces the density of the rare-earth (${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$) spins without changing the crystal structure or magnetic configuration of ${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ spins in the ${{{{{\Gamma }}}}}_{{{{{2}}}}}$ phase^31,32. Although the present work largely uses ${{{{x}}}} = {{{{1}}}}$ (${{{{{\mathrm{ErFe}}}}}}{{{{{{\mathrm{O}}}}}}}_{{{{{3}}}}}$), the ${{{{x}}}}$-dependence is considered in “Spin resonance frequencies” in Supplementary Methods.

The Hamiltonian for the spins in ${{{{{\rm{Er}}}}}}_{x}{{{{{{\rm{Y}}}}}}}_{1-x}{{{{{\rm{FeO}}}}}}_{3}$ consists of three parts, i.e.,

$${{{{{\mathcal{H}}}}}} = {{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{Fe}}}}}}}+{{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{Er}}}}}}}+{{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{Er}}}}}}-{{{{{\rm{Fe}}}}}}},$$

(2)

where ${{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{Fe}}}}}}}$, ${{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{Er}}}}}}}$, and ${{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{Er}}}}}}-{{{{{\rm{Fe}}}}}}}$ are the Hamiltonians of the ${{{{{\rm{Fe}}}}}}^{3+}$ spins, ${{{{{\rm{Er}}}}}}^{3+}$ spins, and ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ interactions, respectively.

As explained above, we employ the two-sublattice model for the ${{{{{\rm{Fe}}}}}}^{3+}$ spins following Herrmann’s model³³ and the methods of our prior works^31,32,33,34. The Hamiltonian of the ${{{{{\rm{Fe}}}}}}^{3+}$ spins is

$${\hat{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{Fe}}}}}}}=\mathop{\sum}\limits _{{s={{{{{\rm{A}}}}}},{{{{{\rm{B}}}}}}}}\mathop{\sum }\limits_{i=1}^{{N_{0}}}{\mu }_{{{{{{\rm{B}}}}}}}{{\hat{{{{{\bf{S}}}}}}}}_{i}^{s}\cdot {\mathfrak{g}}^{{{{{{\rm{Fe}}}}}}}\cdot {{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}+{J}_{{{{{{\rm{Fe}}}}}}}\mathop{\sum}\limits _{{{{{{{\rm{n}}}}}}.{{{{{\rm{n}}}}}}}}{{\hat{{{{{\bf{S}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}}\cdot {{\hat{{{{{\bf{S}}}}}}}}_{{i^{\prime}}}^{{{{{{\rm{B}}}}}}}$$

$$-\,{D}_{y}^{{{{{{\rm{Fe}}}}}}}\mathop{\sum}\limits _{{{{{{\rm{n.n.}}}}}}}\left({\hat{S}}_{i,z}^{{{{{{\rm{A}}}}}}}{\hat{S}}_{i^\prime ,x}^{{{{{{\rm{B}}}}}}}-{\hat{S}}_{i^\prime ,z}^{{{{{{\rm{B}}}}}}}{\hat{S}}_{i,x}^{{{{{{\rm{A}}}}}}}\right)$$

$$-\mathop{\sum }\limits_{i=1}^{{N_{0}}}\left({A}_{x}{\hat{S}}_{i,x}^{{{{{{\rm{A}}}}}}}{\!\,}^{2}+{A}_{z}{\hat{S}}_{i,z}^{{{{{{\rm{A}}}}}}}{\!\,}^{2}+{A}_{{xz}}{\hat{S}}_{i,x}^{{{{{{\rm{A}}}}}}}{\hat{S}}_{i,z}^{{{{{{\rm{A}}}}}}}\right)$$

$$-\mathop{\sum }\limits_{i=1}^{{N_{0}}}\left({A}_{x}{\hat{S}}_{i,{x}}^{{{{{{\rm{B}}}}}}}{\!\,}^{2}+{A}_{z}{\hat{S}}_{i,z}^{{{{{{\rm{B}}}}}}}{\!\,}^{2}-{A}_{{xz}}{\hat{S}}_{i,x}^{{{{{{\rm{B}}}}}}}{\hat{S}}_{i,z}^{{{{{{\rm{B}}}}}}}\right).$$

(3)

Here, ${{\hat{{{{{\bf{S}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ is the operator of the ${{{{{\rm{Fe}}}}}}^{3+}$ spin $S=5/2$ at the $i$-th site in the A/B sublattice, while ∑_n.n. represents a summation over all nearest-neighbor couplings. The number of nearest neighbors is

$${z}_{{{{{{\rm{Fe}}}}}}}=6.$$

(4)

${N}_{0}$ denotes the number of ${{{{{\rm{Fe}}}}}}^{3+}$ spins in each sublattice and is equal to the unit cell count in ${{{{{\rm{Er}}}}}}{{{{{\rm{Fe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$. A total of $2{N}_{0}$ spins represent the ${{{{{\rm{Fe}}}}}}^{3+}$ subsystem. ${\mu }_{{{{{{\rm{B}}}}}}}$ is the Bohr magneton, and

$${\mathfrak{g}}^{{{{{{\rm{Fe}}}}}}}\equiv \left(\begin{array}{ccc}\mathfrak{g}_{x}^{{{{{{\rm{Fe}}}}}}} & 0 & 0\\ 0 & {{\mathfrak{g}}}_{y}^{{{{{{\rm{Fe}}}}}}} & 0\\ 0 & 0 & {{\mathfrak{g}}}_{z}^{{{{{{\rm{Fe}}}}}}}\end{array}\right)$$

(5)

is the $g$-factor tensor of the ${{{{{\rm{Fe}}}}}}^{3+}$ spins. In the following, the $g$-factor of free electron spin is expressed as ${\mathfrak{g}}$. ${{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}$ is the external DC magnetic flux density. ${J}_{{{{{{\rm{Fe}}}}}}}$ and ${D}_{y}^{{{{{{\rm{Fe}}}}}}}$ are the strengths of the isotropic and Dzyaloshinkii–Moriya-type exchange interaction strengths between the ${{{{{\rm{Fe}}}}}}^{3+}$ spins, respectively. ${A}_{x}$, ${A}_{z}$, and ${A}_{{xz}}$ are the energies expressing the magnetic anisotropy of the ${{{{{\rm{Fe}}}}}}^{3+}$ spins.

Although we expressed the ${{{{{\rm{Er}}}}}}^{3+}$ subsystem using a single spin lattice for the paramagnetic ${{{{{\rm{Er}}}}}}^{3+}$ spins ($T \, > \, {T}_{{{{{{\rm{c}}}}}}}$) in our previous works^31,34, in this study we employ a two-sublattice model for the ${{{{{\rm{Er}}}}}}^{3+}$ spins to describe the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interaction and LTPT. The Hamiltonian of the ${{{{{\rm{Er}}}}}}^{3+}$ spins is

$${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}} = -\mathop{\sum}\limits_{{s={{{{{\rm{A}}}}}},{{{{{\rm{B}}}}}}}}\mathop{\sum }\limits_{i=1}^{{N_{0}}}{{\hat{{{{{\bf{\upmu }}}}}}}}_{i}^{s}\cdot {{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}+{J}_{{{{{{\rm{Er}}}}}}}\mathop{\sum}\limits _{{{{{{{\rm{n}}}}}}.{{{{{\rm{n}}}}}}.}}{{\hat{{{{{\bf{R}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}}\cdot {{\hat{{{{{\bf{R}}}}}}}}_{i\prime }^{{{{{{\rm{B}}}}}}}.$$

(6)

Here, ${{\hat{{{{{\bf{R}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ is the operator of rare-earth (${{{{{\rm{Er}}}}}}^{3+}$ or ${{{{{{\rm{Y}}}}}}}^{3+}$) spin at the site $i$ in the A/B sublattice. For ${{{{{\rm{Er}}}}}}_{x}{{{{{{\rm{Y}}}}}}}_{1-x}{{{{{\rm{Fe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$, the rare-earth spins are represented randomly as $s={{{{{\rm{A}}}}}},{{{{{\rm{B}}}}}}$; i.e.,

$${{\hat{{{{{\bf{R}}}}}}}}_{i}^{s}=\left\{\begin{array}{cc}{{\hat{{{{{\boldsymbol{\sigma }}}}}}}}_{i}^{s} & {{{{{\rm{for}}}}}}\; {{{{{\rm{Er}}}}}}^{3+}\\ {{{{{\bf{0}}}}}} & {{{{{\rm{for}}}}}}\;{{{{{{\rm{Y}}}}}}}^{3+}\hfill\end{array}\right..$$

(7)

We describe each Er³⁺ spin using a vector of Pauli operators ${{\hat{{{{{\boldsymbol{\sigma }}}}}}}}_{i}^{s}\equiv ({\hat{\sigma }}_{i,x}^{s},{\hat{\sigma }}_{i,y}^{s},{\hat{\sigma }}_{i,z}^{s})^{{{{{{\rm{t}}}}}}}$ satisfying ${\hat{\sigma }}_{i,\xi }^{s}{\hat{\sigma }}_{i,\xi }^{s}=1$, $[{\hat{\sigma }}_{i,\xi }^{s},{\hat{\sigma }}_{{i}^{{\prime} },\xi }^{{s}^{{\prime} }}]=0$ ($\xi =x,y,z$), $[{\hat{\sigma }}_{i,x}^{s},{\hat{\sigma }}_{{{i^{{\prime}}} ,y}}^{{s^{{\prime}} }}]={{{{{\rm{i}}}}}}2{\hat{\sigma }}_{i,z}^{s}{\delta }_{s,{s^{{\prime}}}}{\delta }_{i,{i^{{\prime}}}}$, $[{\hat{\sigma }}_{i,y}^{s},{\hat{\sigma }}_{{{i^{{\prime}} },z}}^{{s^{{\prime} }}}]={{{{{\rm{i}}}}}}2{\hat{\sigma }}_{i,x}^{s}{\delta }_{s,{s}^{{\prime} }}{\delta }_{{i,{i^{{\prime} }}}}$, and $[{\hat{\sigma }}_{i,z}^{s},{\hat{\sigma }}_{{{i^{{\prime}} },x}}^{{s^{{\prime} }}}]={{{{{\rm{i}}}}}}2{\hat{\sigma }}_{i,y}^{s}{\delta }_{{s,{s^{{\prime} }}}}{\delta }_{{i,{i^{{\prime}}}}}$, where ${\delta }_{i,j}$ is the Kronecker delta. The ${{{{{{\rm{Y}}}}}}}^{3+}$ ion is non-magnetic, and ${{\hat{{{{{\bf{R}}}}}}}}_{i}^{s}$ is replaced with ${{{{{\bf{0}}}}}}$. The first term in Eq. (6) represents the Zeeman effect, and the magnetic moment is expressed in terms of the anisotropic $g$ factors ${{\mathfrak{g}}}_{x,y,z}^{{{{{{\rm{Er}}}}}}}$ for the ${{{{{\rm{Er}}}}}}^{3+}$ spins as

$${{\hat{{{{{\mathbf{\upmu }}}}}}}}_{i}^{s}\equiv -\frac{1}{2}{\mu }_{{{{{{\rm{B}}}}}}}{({{\mathfrak{g}}}_{x}^{{{{{{\rm{Er}}}}}}}{\hat{R}}_{i,x}^{s},{{\mathfrak{g}}}_{y}^{{{{{{\rm{Er}}}}}}}{\hat{R}}_{i,y}^{s},{{\mathfrak{g}}}_{z}^{{{{{{\rm{Er}}}}}}}{\hat{R}}_{i,z}^{s})}^{{{{{{\rm{t}}}}}}}=-\frac{1}{2}{\mu }_{{{{{{\rm{B}}}}}}}{{\mathfrak{g}}}^{{{{{{\rm{Er}}}}}}}\cdot {{\hat{{{{{\bf{R}}}}}}}}_{i}^{s}.$$

(8)

The factor $1/2$ is added because $(1/2){{\hat{{{{{\boldsymbol{\sigma }}}}}}}}_{i}^{s}$ theoretically corresponds to a spin $\frac{1}{2}$ operator. We define the $g$-factor tensor for the Er³⁺ spins as

$${{\mathfrak{g}}}^{{{{{{\rm{Er}}}}}}}\equiv \left(\begin{array}{ccc}{{\mathfrak{g}}}_{x}^{{{{{{\rm{Er}}}}}}} & 0 & 0\\ 0 & {{\mathfrak{g}}}_{y}^{{{{{{\rm{Er}}}}}}} & 0\\ 0 & 0 & {{\mathfrak{g}}}_{z}^{{{{{{\rm{Er}}}}}}}\end{array}\right).$$

(9)

The second term in Eq. (6) represents the ${{{{{\rm{Er}}}}}}^{3+}-{{{{{\rm{Er}}}}}}^{3+}$exchange interaction with strength ${J}_{{{{{{\rm{Er}}}}}}}$. Because the ${{{{{\rm{Er}}}}}}^{3+}$ ions are diluted in ${{{{{\rm{Er}}}}}}_{x}{{{{{{\rm{Y}}}}}}}_{1-x}{{{{{\rm{Fe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$, the number of nearest-neighbor ${{{{{\rm{Er}}}}}}^{3+}$ spins is effectively given by

$${z}_{{{{{{\rm{Er}}}}}}}=6x.$$

(10)

We describe the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ exchange interactions as

$${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}-{{{{{\rm{Fe}}}}}}}=\mathop{\sum }\limits_{i=1}^{{N}_{0}}\mathop{\sum}\limits_{s,s^{\prime} ={{{{{\rm{A}}}}}},{{{{{\rm{B}}}}}}}\left[J{{\hat{{{{{\bf{R}}}}}}}}_{i}^{s}\cdot {{\hat{{{{{\bf{S}}}}}}}}_{i}^{s^{\prime} }+{{{{{{\bf{D}}}}}}}^{s,s^{\prime} }\cdot ({{\hat{{{{{\bf{R}}}}}}}}_{i}^{s}\times {{\hat{{{{{\bf{S}}}}}}}}_{i}^{s^{\prime} })\right].$$

(11)

In our model, the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ interaction is closed in each unit cell; that is, the ${{{{{\rm{Er}}}}}}^{3+}$ and ${{{{{\rm{Fe}}}}}}^{3+}$ spins in the same unit cell interact with each other but do not interact with the spins in other unit cells. $J$ and ${{{{{{\bf{D}}}}}}}^{s,s^{\prime} }$ are the strengths of the isotropic and antisymmetric exchange interactions, respectively^31,32,33,34. Considering the spin configuration at $T \, < \, {T}_{{{{{{\rm{c}}}}}}}$ with no external DC magnetic field (see more details in “Reduction of number of parameters” in Supplementary Methods), we assume that ${{{{{{\bf{D}}}}}}}^{s,s^{\prime} }$ are expressed in terms of two values ${D}_{x}$ and ${D}_{y}$ as

$${{{{{{\bf{D}}}}}}}^{{{{{{\rm{A}}}}}},{{{{{\rm{A}}}}}}}={({D}_{x},{D}_{y},0)}^{{{{{{\rm{t}}}}}}},$$

(12)

$${{{{{{\bf{D}}}}}}}^{{{{{{\rm{A}}}}}},{{{{{\rm{B}}}}}}}={(-{D}_{x},-{D}_{y},0)}^{{{{{{\rm{t}}}}}}},$$

(13)

$${{{{{{\bf{D}}}}}}}^{{{{{{\rm{B}}}}}},{{{{{\rm{A}}}}}}}={(-{D}_{x},{D}_{y},0)}^{{{{{{\rm{t}}}}}}},$$

(14)

$${{{{{{\bf{D}}}}}}}^{{{{{{\rm{B}}}}}},{{{{{\rm{B}}}}}}}={({D}_{x},-{D}_{y},0)}^{{{{{{\rm{t}}}}}}}.$$

(15)

As explained in detail in the section “Mean-field Calculation Method” we assume that the $y$ components ${\hat{R}}_{i,y}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ of the ${{{{{\rm{Er}}}}}}^{3+}$ spins are not influenced by the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ interactions by implicitly considering a higher energy potential than that of the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ interaction strengths $J$ and ${{{{{{\bf{D}}}}}}}^{{s,s^{\prime}} }$ along the $b$ axis. This assumption helps to obtain an appropriate description of LTPT in accordance with our numerical calculations.

The actual values of the parameters appearing in our proposed spin model are provided in “Parameters” together with a description of how they were determined based on recent experimental results of terahertz magnetospectroscopy³¹ and magnetization measurements²⁶.

LTPT phase diagrams

Next, we show that our spin model certainly describes the thermal equilibrium (average) values of the ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$ spins ${\bar{{{{{{\boldsymbol{\sigma }}}}}}}}^{{{{{{\bf{A}}}}}}/{{{{{\bf{B}}}}}}}$ and ${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ spins ${\bar{{{{{{\bf{S}}}}}}}}^{{{{{{\bf{A}}}}}}{{{{{\boldsymbol{/}}}}}}{{{{{\bf{B}}}}}}}$ in the zero-wavenumber (infinite-wavelength) limit using the mean-field method. Details pertaining to the mean-field method are provided in the section “Mean-field Calculation Method.” Because we simply considered a homogeneous external DC magnetic flux density ${{{{{{\bf{B}}}}}}}^{{{{{{\bf{DC}}}}}}}$, ${\bar{{{{{{\boldsymbol{\sigma }}}}}}}}^{{{{{{\bf{A}}}}}}/{{{{{\bf{B}}}}}}}$ and ${\bar{{{{{{\bf{S}}}}}}}}^{{{{{{\bf{A}}}}}}/{{{{{\bf{B}}}}}}}$ were independent of the site index ${{{{i}}}}$.

Figure 2a–c show the calculated phase diagrams as functions of $T$ and ${{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}$, applied along the $a$, $b$, and $c$ axes, respectively. The difference $|{\bar{\sigma }}_{z}^{{{{{{\rm{A}}}}}}}-{\bar{\sigma }}_{z}^{{{{{{\rm{B}}}}}}}|$ in the $z$ components of the thermal equilibrium values of ${{{{{\rm{Er}}}}}}^{3+}$ spins (AFM vector) is plotted in red. $|{\bar{\sigma }}_{z}^{{{{{{\rm{A}}}}}}}-{\bar{\sigma }}_{z}^{{{{{{\rm{B}}}}}}}|$ is the order parameter for the LTPT in the presence of an external DC magnetic field in general, although the rotation angle of the ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector can be utilized as an alternative order parameter if the external DC field is zero or is along the $a$ axis. The bold solid curves represent phase boundaries. These phase diagrams are consistent with those reported by Zhang et al.²⁶. As shown in Fig. 2a, because ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ possesses a weak magnetization along the $a$ axis, the critical field depends on whether the field is parallel (in the same direction) or antiparallel (in the opposite direction) to the magnetization. The parameters used in the calculations are provided in “Parameters.”

Fig. 2: Phase diagrams of spins in ErFeO₃ calculated using the mean-field method.

An external DC magnetic field was applied along the a $a$. b $b$. c $c$ axes. The difference $|{\bar{\sigma }}_{z}^{{{{{{\rm{A}}}}}}}-{\bar{\sigma }}_{z}^{{{{{{\rm{B}}}}}}}|$ of the $z$ components of the thermal-equilibrium values of ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$ spins is mapped in red. The bold solid curves represent the phase boundaries. The external direct current (DC) magnetic field was varied from zero to positive or negative values at a fixed temperature. As ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ shows weak magnetization along the $a$ axis, the critical field depends on whether the field is parallel or antiparallel to the magnetization in Fig. 2a.

Figure 3 plots the thermal equilibrium values of the ${{{{{\rm{Er}}}}}}^{3+}$ and ${{{{{\rm{Fe}}}}}}^{3+}$ spins in the absence of an external DC magnetic field as functions of temperature. The LTPT, that is, the antiferromagnetic ordering of the ${{{{{\rm{Er}}}}}}^{3+}$ spins along the $c$ axis and the rotation of the ${{{{{\rm{Fe}}}}}}^{3+}$ spins in the ${bc}$ plane²⁹, are reproduced well in our spin model. The rotation angle of the ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector is $\varphi = 46^{\circ }$ at $T = 0\,{{{{{\rm{K}}}}}}$ with our parameters. This value is approximately equal to the experimentally estimated value $\varphi = 49^{\circ }$ ²⁹.

Fig. 3: Thermal equilibrium spin values.

a ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$ spin. b ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ spin calculated using the mean-field method as functions of T in the case of zero external direct current (DC) magnetic field. As shown in Fig. 3a, ${\bar{\sigma }}_{z}={\bar{\sigma }}_{z}^{{{{{{\rm{A}}}}}}}=-{\bar{\sigma }}_{z}^{{{{{{\rm{B}}}}}}}$ spontaneously appears below ${T}_{{{{{{\rm{c}}}}}}}=4.0\,{{{{{\rm{K}}}}}}$, i.e., the ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$ spins are antiferromagnetically ordered along the $c$ axis. They show magnetization along the $a$ axis as ${\bar{\sigma }}_{x}={\bar{\sigma }}_{x}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ due to the ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$–${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ exchange interaction with the weak ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ magnetization along the $a$ axis, whereas ${\bar{\sigma }}_{y}={\bar{\sigma }}_{y}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}=0$. As shown in Fig. 3b, above ${T}_{{{{{{\rm{c}}}}}}}$, the ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ spins are ordered antiferromagnetically along the $c$ axis as ${\bar{S}}_{z}=-{\bar{S}}_{z}^{{{{{{\rm{A}}}}}}}={\bar{S}}_{z}^{{{{{{\rm{B}}}}}}}$, whereas they are slightly canted toward the $a$ axis as ${\bar{S}}_{x}={\bar{S}}_{x}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$, and ${\bar{S}}_{y}={\bar{S}}_{y}^{{{{{{\rm{A}}}}}}}=-{\bar{S}}_{y}^{{{{{{\rm{B}}}}}}}$ = 0. Below ${T}_{{{{{{\rm{c}}}}}}}$, the ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ spins rotate in the ${bc}$ plane, and the rotation angle is $\varphi ={{{{{\rm{arctan }}}}}}({\bar{S}}_{y}/{\bar{S}}_{z})=4{6}^{\circ }$ at $T=0\,{{{{{\rm{K}}}}}}$ with our parameters.

Extended Dicke Hamiltonian

The mean-field method employed in this study, as illustrated in Figs. 2 and 3, is a standard means of analysing magnetic phase transitions. To investigate the analogy between LTPT and SRPT using the Dicke model, we derive an extended version of the Dicke model transformed from the spin model in Eq. (2). This derivation is given in detail in the section “Derivation of Extended Dicke Hamiltonian”.

The extended Dicke Hamiltonian minimally including the terms relevant to the LTPT in an external DC magnetic field applied along the a axis, where the $\Gamma_{12}$ symmetry remains, is

$${\hat{{{{{\mathcal{H}}}}}}}/ {\hslash} \approx \omega_{\pi } {\hat{a}}_{\pi }^{{{\dagger}} } {\hat{a}}_{\pi } + {\omega }_{{{{{{\rm{Er}}}}}}} {\hat{\Sigma}}_{x} + \frac{{2 {z_{{{{{{\rm{Er}}}}}}}}}J_{{{{{{\rm{Er}}}}}}}}{{N {\hslash }}} \left({{{\hat{\Sigma }}_{x}}}^{2}-{{{\hat{\Sigma }}_{z}}}^{2}\right)$$

$$+\frac{{2{g_{x}}}}{\sqrt{N}}({\hat{a}}_{\pi }^{{{\dagger}} }+{\hat{a}}_{\pi }){\hat{\Sigma }}_{x}+\frac{{{{{{{\rm{i}}}}}}2{g}_{z}}}{{\sqrt{N}}}({\hat{a}}_{\pi }^{{{\dagger}} }-{\hat{a}}_{\pi }){\hat{\Sigma }}_{z}.$$

(16)

Here, ${\hat{a}}_{\pi }$ (${\hat{a}}_{\pi }^{{{\dagger}} }$) is the annihilation (creation) operator of an ${{{{{\rm{Fe}}}}}}^{3+}$ magnon in the quasi-antiferromagnetic (qAFM) mode³³. The eigenfrequency ${\omega }_{\pi }=2\pi \times 0.896\,{{{{{\rm{THz}}}}}}$ can be evaluated using Eq. (63). The actual value was evaluated using the parameters shown in “Parameters.” The ${{{{{\rm{Er}}}}}}^{3+}$ resonance frequency is defined as follows.

$${\omega }_{{{{{{\rm{Er}}}}}}}\equiv \frac{{|{E}_{x}+{{\mathfrak{g}}}_{x}^{{{{{{\rm{Er}}}}}}}{\mu }_{{{{{{\rm{B}}}}}}}{B}_{x}^{{{{{{\rm{DC}}}}}}}|}}{{\hslash} }.$$

(17)

$${E}_{x}\equiv 4S(J\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}+{D}_{y}\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}) = h\times 0.023\,{{{{{\rm{THz}}}}}}.$$

(18)

The total number of $\frac{1}{2}$ spins (${{{{{\rm{Er}}}}}}^{3+}$ spins) in the two sublattices is

$$N\equiv 2 x {N}_{0}.$$

(19)

${\hat{\Sigma }}_{x,y,z}$ are spin $\frac{N}{2}$ operators representing the rare-earth spins (a detailed definition is given in Eq. (92)). The two ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling strengths in the last two terms of Eq. (16) are defined as follows.

$${\hslash} {g}_{x}=\sqrt{2{xS}}(J\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}-{D}_{y}\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}){\left(\frac{b+a}{d-c}\right)}^{1/4}=h\,\times \sqrt{x}\,\times 0.051\,{{{{{\rm{THz}}}}}},$$

(20)

$${\hslash} {g}_{z}=\sqrt{2{xS}}{D}_{x}{\left(\frac{d-c}{b+a}\right)}^{1/4}=h\,\times \sqrt{x}\,\times 0.116\,{{{{{\rm{THz}}}}}}.$$

(21)

Comparing Eq. (16) with Eq. (1) (the Dicke model), because ${\hat{a}}_{\pi }$ and ${\hat{\Sigma }}_{x,y,z}$ in Eq. (16) correspond to $\hat{a}$ and ${\hat{S}}_{x,y,z}$ in Eq. (1), respectively, we may observe that the ${g}_{z}$ term in Eq. (16) corresponds to the matter–photon coupling (transverse coupling), that is, the last term in Eq. (1). In addition, the ${g}_{x}$ term represents longitudinal coupling, and the term ${J}_{{{{{{\rm{Er}}}}}}}$ describes the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions in Eq. (16). The coupling strength ${g}_{z}=2\pi \times 0.116\,{{{{{\rm{THz}}}}}}$ shows the system fall into the ultrastrong regime because it is a considerable fraction of the ${{{{{\rm{Er}}}}}}^{3+}$ resonance and qAFM magnon frequencies, ${E}_{x}=h\times 0.023\,{{{{{\rm{THz}}}}}}$ and ${\omega }_{\pi }=2\pi \times 0.896\,{{{{{\rm{THz}}}}}}$. When the ${g}_{z}$ term causes an SRPT, $\langle {\hat{\Sigma }}_{z}\rangle$ spontaneously acquires a non-zero value in thermal equilibrium, corresponding to the antiferromagnetic ordering of the ${{{{{\rm{Er}}}}}}^{3+}$ spins along the $c$ axis. As explained in “Derivation of Extended Dicke Hamiltonian,” the spontaneous appearance of non-zero $\langle {{{{{\rm{i}}}}}}({\hat{a}}_{\pi }^{{{\dagger}} }-{\hat{a}}_{\pi })\rangle$ coupled with ${\hat{\Sigma }}_{z}$ in the ${g}_{z}$ term, corresponds to that of the ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector in the $b$ axis and causes its rotation in the ${bc}$ plane. The ${{{{{\rm{Fe}}}}}}^{3+}$ quasi-ferromagnetic (qFM) magnon mode can be neglected in describing the LTPT, because the AFM ordering of the ${{{{{\rm{Er}}}}}}^{3+}$ spins and the spontaneous appearance of qAFM magnons are rather favoured and they prevent the appearance of qFM magnons, which feel additional energy cost under the ordering of the ${{{{{\rm{Er}}}}}}^{3+}$ spins and the qAFM magnons.

As seen in Eqs. (20) and (21), the transverse coupling strength ${g}_{z}$ depends on ${D}_{x}$, and the longitudinal coupling strength ${g}_{x}$ depends on $J$ and ${D}_{y}$. These expressions are reasonable from the perspective of the spin model in Eq. (11). The ${D}_{x}$ antisymmetric ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ exchange interaction is essential for the LTPT because it couples ${\hat{\sigma }}_{z}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ and ${\hat{S}}_{y}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$, which appear spontaneously at $T \, < \, {T}_{{{{{{\rm{c}}}}}}}$. In contrast, the $J$ and ${D}_{y}$ exchange interactions are not directly related to the LTPT because these interaction terms do not couple ${\hat{\sigma }}_{z}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ and ${\hat{S}}_{y}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ directly.

Evidence of magnonic SRPT

Using the semiclassical method described in “Semiclassical Calculation Method” with the extended Dicke Hamiltonian in Eq. (16), we calculated the thermal equilibrium values of the ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$ and ${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ spins and magnon amplitudes as functions of temperature. Here and also in the calculation of the LTPT phase diagrams by the mean-field approach, we implicitly assumed that a thermal bath is connected to the extended Dicke Hamiltonian in Eq. (16) [and the spin model in Eq. (2)]. The thermal bath simply ensures that the system is in thermal equilibrium at a certain temperature in the present calculations, whereas it causes the energy loss and decoherence in non-equilibrium dynamics of ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$ spins and ${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ magnons.

Figure 4a–c show the thermal equilibrium values of the ${{{{{\rm{Er}}}}}}^{3+}$ spins ${\bar{\sigma }}_{x,y,z}=\langle {\hat{\Sigma }}_{x,y,z}\rangle /(N/2)$, ${{{{{\rm{Fe}}}}}}^{3+}$ spins ${\bar{S}}_{x,y,z}$, and ${{{{{\rm{Fe}}}}}}^{3+}$ qAFM magnons ${\bar{a}}_{r,i}$ as functions of temperature in the absence of an external DC magnetic field, i.e., with ${{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}={{{{{\bf{0}}}}}}$. ${\bar{S}}_{x,y,z}$ were calculated using Eqs. (113)–(115) with $\langle {\hat{a}}_{\pi }\rangle =\sqrt{N}({\bar{a}}_{r}+{{{{{\rm{i}}}}}}{\bar{a}}_{i})$. Figure 4a, b, respectively, reproduce Fig. 3a, b calculated using the mean-field method with the original spin model, including ${T}_{{{{{{\rm{c}}}}}}}$, although ${\bar{S}}_{z}$ differs. As depicted in Fig. 3b, a decrease in temperature causes a reduction in ${\bar{S}}_{z}$ along with the spontaneous appearance of ${\bar{S}}_{y}$, whereas Fig. 4b reveals ${\bar{S}}_{z}$ to remain nearly constant. This difference exists because ${{\bar{S}}_{x}}^{2}+{{\bar{S}}_{y}}^{2}+{{\bar{S}}_{z}}^{2}={S}^{2}$ does not hold in the extended Dicke Hamiltonian derived via magnon quantization (i.e., bosonisation of ${{{{{\rm{Fe}}}}}}^{3+}$ spin modulations). The ultrastrong term ${g}_{z}$, the last term in Eq. (16), causes the spontaneous appearance of ${\bar{\sigma }}_{z}$ and ${\bar{a}}_{i}$, as shown in Fig. 4a, c, respectively, and the latter causes a non-zero ${\bar{S}}_{y}$ through Eq. (114). The ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector is rotated due to the spontaneous appearance of a non-zero ${\bar{S}}_{y}$ when ${{\bar{S}}_{x}}^{2}+{{\bar{S}}_{y}}^{2}+{{\bar{S}}_{z}}^{2}={S}^{2}$ holds. Thus, the LTPT, that is, the spontaneous ordering of ${{{{{{\rm{Er}}}}}}}^{3+}\,$spins (spontaneous appearance of ${\bar{\sigma }}_{z}$) and the spontaneous rotation of ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector (spontaneous appearance of ${\bar{a}}_{i}$ and ${\bar{S}}_{y}$), is caused by the ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling.

Fig. 4: Thermal equilibrium spin and amplitude values.

a ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$ spins. b ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ spins. c ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ magnon amplitudes as functions of $T$. These values were calculated using the semiclassical method with the extended Dicke Hamiltonian in the case of zero external direct current (DC) magnetic field. Figure 4a, b are nearly the same as Fig. 3a, b, respectively, except ${\bar{S}}_{z}$, which changes only slightly due to magnon bosonization. The ${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ spins, ${\bar{S}}_{x,y,z}$, were calculated using Eqs. (113)–(115) with the thermal equilibrium value of the quasi-antiferromagnetic (qAFM) magnon annihilation operator $\langle {\hat{a}}_{\pi }\rangle =\sqrt{N}({\bar{a}}_{r}+{{{{{\rm{i}}}}}}{\bar{a}}_{i})$ plotted in Fig. 4c.

To compare the contributions of the ${{{{{\rm{Er}}}}}}^{3+}$–magnon couplings and ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions for the LTPT, Fig. 5 depicts the phase boundaries calculated using the full Hamiltonian (solid curves) as well as in the absence of ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ exchange interactions (dashed–dotted curve; $J={D}_{x}={D}_{y}={g}_{z}={g}_{x}=0$) and ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions (dashed curve; ${J}_{{{{{{\rm{Er}}}}}}}=0$). Figure 5a, b illustrate the results obtained using the mean-field and semiclassical methods with extended Dicke Hamiltonian, respectively. The solid curve in Fig. 5a is equal to that in Fig. 2a. The slight differences between Fig. 5a, b are discussed in “Aspects of phase boundaries” in Supplementary Methods.

Fig. 5: Phase boundaries of the low-temperature phase transition (LTPT) in ErFeO₃.

Boundaries calculated using the (a) mean-field method and (b) semiclassical method with the extended Dicke Hamiltonian. An external direct current (DC) magnetic field is applied along the $a$ axis. The solid curves are the phase boundaries determined using the full Hamiltonian, and those in Figs. 5a and 2a are equivalent. The dashed-dotted curves are the phase boundaries in the absence of ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$–magnon coupling (${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$–${{{{{\rm{F}}}}}}{{{{{{\rm{e}}}}}}}^{3+}$ exchange interactions). The dashed curves are those obtained in the absence of ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$–${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$ exchange interactions, i.e., the LTPT can be caused solely by the ${{{{{\rm{E}}}}}}{{{{{{\rm{r}}}}}}}^{3+}$–magnon coupling and thus can be interpreted as a magnonic superradiant phase transition (SRPT).

The dashed curves (${J}_{{{{{{\rm{Er}}}}}}}=0$) in Fig. 5 reveal that the phase transition occurs even in the absence of ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions and that T_c equals approximately 1.2 K at ${{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}={{{{{\bf{0}}}}}}$. Thus, ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling alone can cause the LTPT. In this sense, the LTPT can be interpreted as a magnonic SRPT because the ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling is sufficiently strong for the phase transition to occur.

On the other hand, in the absence of ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling, as denoted by the dashed–dotted curves, T_c is approximately 2.6 K at ${{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}={{{{{\bf{0}}}}}}$. This result appears to indicate that the contribution of the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions is larger than that of the ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling. However, the actual ${T}_{{{{{{\rm{c}}}}}}}$ is 4 K; that is, the ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling enhances the T_c of the phase transition. In the same manner, the critical magnetic fields are also enhanced. These facts are similar to the suggestion of ${T}_{{{{{{\rm{c}}}}}}}$ enhancement through photon–matter coupling by Mazza and Georges³⁵; however, in their case, phase transition does not occur solely by photon–matter coupling, and their model does not guarantee gauge invariance^36,37.

Although the ${g}_{z}$ term causes the spontaneous appearance of both ${\bar{\sigma }}_{z}$ and ${\bar{S}}_{y}$ following the above-mentioned description of the SRPT, a non-zero ${\bar{\sigma }}_{z}$ can also spontaneously appear due to the ${J}_{{{{{{\rm{Er}}}}}}}$ term (${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions). Although ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling is inevitable for the spontaneous rotation of the ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector (spontaneous appearance of ${\bar{S}}_{y}$), we quantitatively evaluate the contributions of the ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling and ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions for the LTPT as follows.

The two contributions to the LTPT can be determined by analysing the condition for the SRPT in our extended Dicke Hamiltonian in Eq. (16) under the Holstein–Primakoff transformation^38,39,40. The detailed calculations are discussed in the “Condition for SRPT in Extended Dicke Hamiltonian” section. The condition can finally be expressed as

$$\frac{4{{g}_{z}}^{2}}{{\omega }_{\pi }{\omega }_{{{{{{\rm{Er}}}}}}}}-\frac{4{{g}_{x}}^{2}}{{\omega }_{\pi }{\omega }_{{{{{{\rm{Er}}}}}}}}+\frac{4{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{\hslash {\omega }_{{{{{{\rm{Er}}}}}}}} \, > \, 1.$$

(22)

For ${J}_{{{{{{\rm{Er}}}}}}}={g}_{x}=0$, this expression is reduced to $4{{g}_{z}}^{2} \, > \, {\omega }_{\pi }{\omega }_{{{{{{\rm{Er}}}}}}}$ for the SRPT in the Dicke model, Eq. (1).

The three terms on the left-hand side of Eq. (22) are evaluated as follows.

$${D}_{{g}_{z}}\equiv 4{{g}_{z}}^{2}/({\omega }_{\pi }{\omega }_{{{{{{\rm{Er}}}}}}})=2.65,$$

(23)

$${D}_{{g}_{x}}\equiv -4{{g}_{x}}^{2}/({\omega }_{\pi }{\omega }_{{{{{{\rm{Er}}}}}}})=-0.51,$$

(24)

$${D}_{{J}_{{{{{{\rm{Er}}}}}}}}\equiv 4{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}/(\hslash {\omega }_{{{{{{\rm{Er}}}}}}})=9.29.$$

(25)

In the following, we refer to these quantities as coupling depths. They are dimensionless measures of coupling strength and are determined based on the appearance of the SRPT. As seen in Eq. (22), the SRPT occurs when the sum of these coupling depths exceeds unity, i.e., ${D}_{{g}_{z}}+{D}_{{g}_{x}}+{D}_{{J}_{{{{{{\rm{Er}}}}}}}} \, > \, 1$. The coupling depth ${D}_{{J}_{{{{{{\rm{Er}}}}}}}}$ of the ${J}_{{{{{{\rm{Er}}}}}}}$ term is the largest, which is consistent with Fig. 5. The ${g}_{x}$ term (longitudinal coupling) has a negative contribution to the SRPT (${D}_{{g}_{x}} \, < \, 0$). Among the three couplings, the contribution of the ${g}_{z}$ term is ${D}_{{g}_{z}}/({D}_{{g}_{z}}+{D}_{{g}_{x}}+{D}_{{J}_{{{{{{\rm{Er}}}}}}}})=0.23$, and that of the total ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling is $({D}_{{g}_{z}}+{D}_{{g}_{x}})/({D}_{{g}_{z}}+{D}_{{g}_{x}}+{D}_{{J}_{{{{{{\rm{Er}}}}}}}})=0.19$. These values are roughly equal to $1.3\,{{{{{\rm{K}}}}}}/(1.3\,{{{{{\rm{K}}}}}}+3.4\,{{{{{\rm{K}}}}}})=0.28$, as estimated by Kadomtseva et al.²⁹ However, the longitudinal coupling (${g}_{x}$ term) was not included in their model^41,42, and the parameters were determined only by the phase boundary for ${{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}//a$.

Considering the analogy between an LTPT and SRPT, the coupling depth of the ${g}_{z}$ term satisfies ${D}_{{g}_{z}} \, > \, 1$ and ${D}_{{g}_{z}}+{D}_{{g}_{x}} \, > \, 1$. This result suggests that the transverse ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling is much stronger than the longitudinal coupling (giving a negative contribution) and is sufficiently strong to cause the SRPT alone. In this sense, we can conclude that the LTPT in ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ is a magnonic SRPT obtained in the extended Dicke Hamiltonian with direct atom–atom interaction and longitudinal coupling (${g}_{x}$ term).

Discussion

As shown above, we quantitatively confirmed that the LTPT in ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ is a magnonic version of the SRPT in thermal equilibrium. This is the first confirmation of the SRPT since its proposal in 1973¹.

Early reports on the SRPT suggested its no-go theorems^43,44,45,46, implying that thermal-equilibrium SRPTs cannot be realized in systems described by the minimal-coupling Hamiltonian, that is, charged particles (without spins) interacting with electromagnetic fields. Because the classical treatment of the electromagnetic fields used in proofs of such no-go theorems can be justified only in limited situations^{2,45,46,47,48,49}, proposals of counter-examples against the no-go theorems and criticisms against the counter-examples have been repeated in SRPT research^{35,36,37,50,51,52,53,54,55,56,57}.

One means of evading the no-go theorems involves introducing another degree of freedom, such as spin⁴⁴. For example, it has been shown that the Rashba spin–orbit coupling can cause paramagnetic instability in an ultrastrongly coupled system between a cyclotron resonance and cavity photon field, implying an SRPT³⁷. Further, it has been pointed out recently^37,58,59 that the coupling between matter and a spatially-varying multi-mode cavity fields plays a key role for circumventing the no-go theorem. Another method is to utilize various types of interactions and spin waves in magnetic materials, which cannot be described by the minimal-coupling Hamiltonian.

Ultrastrong photon–magnon coupling has been reported for an yttrium–iron–garnet sphere embedded in a cavity with a resonance frequency in the gigahertz region^{60,61,62,63,64}, where the electromagnetic wave was confined by metallic or superconducting mirrors. Recently, $g/\omega \sim 0.46$ has been achieved to detect dark matter (galactic axions)⁶⁵. Ultrastrong spin–magnon³¹ and magnon–magnon^66,67 couplings have also been observed. However, evidence of an SRPT has not been reported even with those magnonic ultrastrong couplings, although various phase transitions exist in magnetic systems, and it is conceivable that some of the known phase transitions can be understood as the SRPT or an analogue.

The LTPT in ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ has been discussed in relation to the cooperative Jahn–Teller transition^29,41,42, which is analogous to the SRPT^68,69. Vitebskii and Yablonskii proposed a theoretical model for describing the LTPT in 1978³⁰. Further, Kadomtseva et al. theoretically investigated the ratio between the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ and ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ interaction strengths in 1980²⁹. They also mentioned the analogy between the LTPT and cooperative Jahn–Teller transition^41,42. Loos and Larson discussed the analogy between the cooperative Jahn–Teller transition and SRPT in 1984 and 2008, respectively^68,69. However, the analogy between the LTPT and SRPT has not been directly drawn either theoretically or experimentally because the analogies between the LTPT and cooperative Jahn–Teller transition and between the latter and the SRPT have been independently discussed^29,68,69, and no experimental evidence has been shown. The spin-Peierls transitions^70,71 and the spin-reorientation transition in rare-earth iron garnets⁷² have also been discussed as analogous phenomena to the SRPT. However, no experimental evidence has been demonstrated. Structural transitions in ferroelectric materials may also be seen as a SRPT analogue at a first glance⁷³. However, when we map such ferroelectric systems to the Dicke model, we find that the resonance frequency of the electric polarization becomes an imaginary value, which indicates that such ferroelectric phase transitions are caused by the instability of the electric polarization subsystem rather than by the coupling between the polarization and phonon subsystems. Hence, no other SRPT analogue by matter–matter coupling has been confirmed quantitatively.

In 2018, the $\sqrt{N}$-dependence ($N$ is the ${{{{{\rm{Er}}}}}}^{3+}$ density) of the anticrossing frequency, or vacuum Rabi splitting ($2g$), between paramagnetic ${{{{{\rm{Er}}}}}}^{3+}$ spins and a ${{{{{\rm{Fe}}}}}}^{3+}$ magnon mode was experimentally confirmed at $T \, > \, {T}_{{{{{{\rm{c}}}}}}}$³¹. This $\sqrt{N}$-dependence, the Dicke cooperativity, can be taken as evidence that the coupling between the ${{{{{\rm{Er}}}}}}^{3+}$ spin ensemble and ${{{{{\rm{Fe}}}}}}^{3+}$ magnon mode is cooperative, being well described by the Dicke model or its extension.

This study provides the quantitative evidence of magnonic SRPT manifestation. Meanwhile, the existence of photonic SRPT, which was originally proposed in 1973, has yet to be confirmed. Moreover, the possibility of its theoretical existence in materials with spin degree of freedom is still under debate^36,37,58,59. Since the development of the Dicke model, this study is the first to elucidate the occurrence of magnonic thermal-equilibrium SRPT in an actual material, namely ErFeO₃.

Conclusions

In this study, using an ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ spin model reproducing both the phase diagrams obtained via magnetization measurements²⁶ and terahertz magnetospectroscopy results³¹, we derived an extended Dicke Hamiltonian that accounts for ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions as well as the cooperative coupling between the ${{{{{\rm{Er}}}}}}^{3+}$ spins and ${{{{{\rm{Fe}}}}}}^{3+}$ magnon modes. We found that the LTPT in ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ can be caused solely by ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling (in the absence of ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions). From the analytical correspondence between the spin and Dicke models and the quantitative verification that the ${{{{{\rm{Er}}}}}}^{3+}$–magnon coupling solely causes the LTPT, we concluded that the LTPT in ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ is a magnonic SRPT in the extended Dicke model. This is the first confirmation of the SRPT in thermal equilibrium since its proposal in 1973¹. These results are expected to be the first step in finding the (originally proposed) photonic SRPT in magnetic or other materials explicitly including the spin degree of freedom.

The thermal SRPT in ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ would exhibit rich physics beyond the quantum or zero-temperature SRPT that has been demonstrated in laser-driven cold atoms^14,15,16,17. It is known that the thermal and quantum fluctuations of photons and atoms exhibit characteristic behaviours around the SRPT^74,75. Recent studies have reported the occurrence of strong, two-mode quantum squeezing at the SRPT critical point^12,13. In future endeavours, including ongoing terahertz magnetospectroscopy experiments on ${{{{{\rm{Er}}}}}}_{x}{{{{{{\rm{Y}}}}}}}_{1-x}{{{{{\rm{Fe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$ concerning LTPT⁷⁶ and subsequent quantum-fluctuation measurements^77,78 of magnons and Er³⁺ spins, we intend to investigate the occurrence of such quantum-squeezing phenomena during thermal SRPT.

The generation of squeezed states of light has attracted considerable research interest over several decades because they facilitate precision measurements to be performed beyond the limitations encountered owing to the manifestation of quantum vacuum fluctuations and evolution of continuous-variable quantum computing. However, most existing squeezing-generation protocols require a system to be driven to realize transient squeezed states. This limits the realizable degree of squeezing during experiments owing to unpredictable noise. In contrast, quantum squeezing at the SRPT critical point can be stably realized under thermal equilibrium, because an ultrastrong coupled system remains at its most stable in the squeezed state. As a result, such systems are resilient to unpredictable noise. This fundamental stability and resilience are expected to facilitate the realization of novel applications exploring quantum sensing and decoherence-robust continuous-variable quantum computing via the occurrence of quantum squeezing at the SRPT critical point.

Methods

Parameters

Following our previous study³¹, we used the following values for the ${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ subsystem in our numerical calculations, except ${{{{{A}}}}}_{{{{{x}}}}}$, which was determined to fit the spin resonance frequencies to the corresponding terahertz absorption spectrum in our experiments³¹ (see “Spin resonance frequencies” in Supplementary Methods for details).

$${J}_{{{{{{\rm{Fe}}}}}}}=4.96\,{{{{{\rm{meV}}}}}},$$

(26)

$${D}_{y}^{{{{{{\rm{Fe}}}}}}}=-0.107\,{{{{{\rm{meV}}}}}},$$

(27)

$${A}_{x}=0.0073\,{{{{{\rm{meV}}}}}},$$

(28)

$${A}_{z}=0.0150\,{{{{{\rm{meV}}}}}},$$

(29)

$${A}_{{xz}}=0.$$

(30)

The anisotropic $g$-factors for ${{{{{\rm{Er}}}}}}^{3+}$ spins were assumed to be

$${{\mathfrak{g}}}_{x}^{{{{{{\rm{Er}}}}}}}=6,$$

(31)

$${{\mathfrak{g}}}_{y}^{{{{{{\rm{Er}}}}}}}=3.4,$$

(32)

$${{\mathfrak{g}}}_{z}^{{{{{{\rm{Er}}}}}}}=9.6.$$

(33)

These values were utilized to fit the ${{{{{\rm{Er}}}}}}^{3+}$ spin resonance frequencies depicted in Supplementary Figs. 1–3 to their corresponding absorption peak positions observed during experiments³¹ (refer to “Spin resonance frequencies” in Supplementary Methods). They were multiplied by 2 compared to those estimated in our previous study³¹ to compensate for the use of the additional factor of $1/2$ in Eq. (8).

The anisotropic $g$-factors for ${{{{{\rm{Fe}}}}}}^{3+}$ spins were assumed to be

$${{\mathfrak{g}}}_{x}^{{{{{{\rm{Fe}}}}}}}=2,$$

(34)

$${{\mathfrak{g}}}_{y}^{{{{{{\rm{Fe}}}}}}}=2,$$

(35)

$${{\mathfrak{g}}}_{z}^{{{{{{\rm{Fe}}}}}}}=0.6.$$

(36)

Here, ${{\mathfrak{g}}}_{z}^{{{{{{\rm{Fe}}}}}}}$ was determined to reproduce the critical magnetic flux density ${B}_{z}^{{{{{{\rm{DC}}}}}}}\sim 20\,{{{{{\rm{T}}}}}}$²⁶ of the transition between the ${\Gamma }_{2}$ phase and the ${\Gamma }_{4}$ phase, in which the ${{{{{\rm{Fe}}}}}}^{3+}$ spins are ordered antiferromagnetically along the $a$ axis with slight canting toward the $c$ axis, in the case of ${{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}//c$. On the other hand, ${{\mathfrak{g}}}_{x}^{{{{{{\rm{Fe}}}}}}}$ and ${{\mathfrak{g}}}_{y}^{{{{{{\rm{Fe}}}}}}}$ were simply set to the values in the case of free electron spin because the results in the present study are insensitive to these values.

Concerning the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ and ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ exchange interactions, we used the following values.

$${J}_{{{{{{\rm{Er}}}}}}}=0.037\,{{{{{\rm{meV}}}}}},$$

(37)

$$J=0.60\,{{{{{\rm{meV}}}}}},$$

(38)

$${D}_{x}=0.034\,{{{{{\rm{meV}}}}}},$$

(39)

$${D}_{y}=0.003\,{{{{{\rm{meV}}}}}}.$$

(40)

These values were utilized to fit Fig. 2 roughly to the phase diagrams reported by Zhang et al.²⁶. The precise values of ${J}_{{{{{{\rm{Er}}}}}}}$, $J$, and ${D}_{y}$ were mainly determined to fit our calculated spin resonance frequencies ${{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}//c$ to the corresponding terahertz absorption spectrum in our experiments³¹, which are both shown in Supplementary Fig. 3a (see “Spin resonance frequencies” in Supplementary Methods). On the other hand, ${D}_{x}$ was determined to reproduce ${T}_{{{{{{\rm{c}}}}}}}=4.0\,{{{{{\rm{K}}}}}}$.

Although the ratio between the ${{{{{\rm{Er}}}}}}^{3+}\!-\!{{{{{\rm{Er}}}}}}^{3+}$ and ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ interaction strengths was theoretically investigated by the phase boundary for ${{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}//a$²⁹, the phase diagrams (T_c and critical DC fields) themselves were not sufficient to determine all of our parameters, although we do not intend to claim the impossibility of such determination in the present study. The phase diagrams gave only some ranges of the parameters. Because the LTPT is caused by not only the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interaction, but also the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ interactions (${{{{{\rm{Er}}}}}}^{3+}$–magnon couplings), there are at least four parameters (${J}_{{{{{{\rm{Er}}}}}}}$, $J$, ${D}_{x}$, and ${D}_{y}$) even if the number of parameters is reduced according to the analysis in “Reduction of number of parameters” in Supplementary Methods. The anisotropic $g$-factors ${{\mathfrak{g}}}_{x}^{{{{{{\rm{Er}}}}}}}$, ${{\mathfrak{g}}}_{y}^{{{{{{\rm{Er}}}}}}}$, and ${{\mathfrak{g}}}_{z}^{{{{{{\rm{Er}}}}}}}$ of the ${{{{{\rm{Er}}}}}}^{3+}$ spins are free parameters, and could easily change the critical DC fields. T_c and three critical DC fields obtained from the magnetization measurements²⁶ were not sufficient to determine the above parameters.

In determining all of these quantities, the spin resonance frequencies were informative. In particular, as discussed in “Spin resonance frequencies” in Supplementary Methods using the extended Dicke Hamiltonian, the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interaction strength ${J}_{{{{{{\rm{Er}}}}}}}$ clearly appears as the frequency splitting between the ${{{{{\rm{Er}}}}}}^{3+}$ in-phase and out-of-phase resonances. The out-of-phase mode cannot be excited by the terahertz wave unless it couples with the ${{{{{\rm{Fe}}}}}}^{3+}$ magnon modes. In that sense, the anti-crossing between the ${{{{{\rm{Er}}}}}}^{3+}$ in-phase resonances, out-of-phase resonances, and ${{{{{\rm{Fe}}}}}}^{3+}$ qFM magnon mode ${B}_{z}^{{{{{{\rm{DC}}}}}}}\sim 4\,{{{{{\rm{T}}}}}}$ in Supplementary Fig. 3 provides the most important information for determining ${J}_{{{{{{\rm{Er}}}}}}}$ and the other parameters (see “Spin resonance frequencies” in Supplementary Methods).

Mean-field calculation method

Because we simply considered a homogeneous ${{{{{\bf{B}}}}}}^{{{{{{\mathrm{DC}}}}}}}$ in this study, the expectation values of the ${{{{{\mathrm{Er}}}}}}^{{{{{{3}}}}+}}$ spins ${{{{{{\boldsymbol{\sigma }}}}}}}^{{{{{{\mathrm{A}}}}}}/{{{{{\mathrm{B}}}}}}}\equiv {{\langle }}{{\hat{{{{{\boldsymbol{\sigma }}}}}}}}_{{{{{i}}}}}^{{{{{{\mathrm{A}}}}}}{{{{/}}}}{{{{{\mathrm{B}}}}}}}{{\rangle }}$ and ${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ spins ${{{{{{\bf{S}}}}}}}^{{{{{{\mathrm{A}}}}}}{{{{/}}}}{{{{{\mathrm{B}}}}}}}\equiv {{\langle }}{{\hat{{{{{\bf{S}}}}}}}}_{{{{{i}}}}}^{{{{{{\mathrm{A}}}}}}{{{{/}}}}{{{{{\mathrm{B}}}}}}}{{\rangle }}$ were independent of the site index ${{{{i}}}}$. The brackets represent the theoretical expectation values of the operators at a finite temperature in the Heisenberg representation. The brackets also correspond to the ensemble average of the spins in each sublattice. Their equations of motion can be obtained from the Heisenberg equations derived from the Hamiltonian in Eq. (2), as follows (${{{{s}}}} = {{{{{\mathrm{A}}}}}}, {{{{{\mathrm{B}}}}}}$).

$${\hslash} (\partial /\partial t){{{{{{\boldsymbol{\sigma }}}}}}}^{s}=-{{{{{{\boldsymbol{\sigma }}}}}}}^{s}\times {\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{{{{{{\bf{B}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}(\{{{{{{{\boldsymbol{\sigma }}}}}}}^{{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}}\},\{{{{{{{\bf{S}}}}}}}^{{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}}\}),$$

(41)

$${\hslash} (\partial /\partial t){{{{{{\bf{S}}}}}}}^{s}=-{{{{{{\bf{S}}}}}}}^{s}\times {\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{{{{{{\bf{B}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}(\{{{{{{{\boldsymbol{\sigma }}}}}}}^{{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}}\},\{{{{{{{\bf{S}}}}}}}^{{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}}\}).$$

(42)

Here, ${{{{{{\bf{B}}}}}}}_{{{{{{\rm{Er}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ and ${{{{{{\bf{B}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ are the mean fields for the ${{{{{\rm{Er}}}}}}^{3+}$ and ${{{{{\rm{Fe}}}}}}^{3+}$ spins, respectively, and they can be expressed as

$${\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{{{{{{\bf{B}}}}}}}_{{{{{{\rm{Er}}}}}}}^{{{{{{\rm{A}}}}}}}\left(\left\{{{{{{{\boldsymbol{\sigma }}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\right\},\left\{{{{{{{\bf{S}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\right\}\right)={\mu }_{{{{{{\rm{B}}}}}}}{{\mathfrak{g}}}^{{{{{{\rm{Er}}}}}}}\cdot {{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}+2{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}{{{{{{\boldsymbol{\sigma }}}}}}}^{{{{{{\rm{B}}}}}}}$$

$$+\mathop{\sum}\limits _{{s={{{{{\rm{A}}}}}},{{{{{\rm{B}}}}}}}}2\left(\begin{array}{c}J{S}_{x}^{s}-({{{{{{\bf{D}}}}}}}^{{{{{{{\rm{A}}}}}},s}}\times {{{{{{\bf{S}}}}}}}^{s})_{x}\\ 0\hfill\\ J{S}_{z}^{s}-({{{{{{\bf{D}}}}}}}^{{{{{{\rm{A}}}}}},s}\times {{{{{{\bf{S}}}}}}}^{s})_{z}\end{array}\right),$$

(43)

$${\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{{{{{{\bf{B}}}}}}}_{{{{{{\rm{Er}}}}}}}^{{{{{{\rm{B}}}}}}}\left(\left\{{{{{{{\boldsymbol{\sigma }}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\right\},\left\{{{{{{{\bf{S}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\right\}\right)={\mu }_{{{{{{\rm{B}}}}}}}{{\mathfrak{g}}}^{{{{{{\rm{Er}}}}}}}\cdot {{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}+2{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}{{{{{{\boldsymbol{\sigma }}}}}}}^{{{{{{\rm{A}}}}}}}$$

$$+\mathop{\sum}\limits _{{s={{{{{\rm{A}}}}}},{{{{{\rm{B}}}}}}}}2\left(\begin{array}{c}J{S}_{x}^{s}-({{{{{{\bf{D}}}}}}}^{{{{{{\rm{B}}}}}},s}\times {{{{{{\bf{S}}}}}}}^{s})_{x}\\ 0\hfill\\ J{S}_{z}^{s}-({{{{{{\bf{D}}}}}}}^{{{{{{{\rm{B}}}}}},s}}\times {{{{{{\bf{S}}}}}}}^{s})_{z}\end{array}\right),$$

(44)

$${\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{{{{{{\bf{B}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{{{{{{\rm{A}}}}}}}(\{{{{{{{\boldsymbol{\sigma }}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\},\{{{{{{{\bf{S}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\})={\mu }_{{{{{{\rm{B}}}}}}}{{\mathfrak{g}}}^{{{{{{\rm{Fe}}}}}}}\cdot {{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}+\mathop{\sum}\limits _{s={{{{{\rm{A}}}}}},{{{{{\rm{B}}}}}}}x\left(J{{{{{{\boldsymbol{\sigma }}}}}}}^{s}+{{{{{{\bf{D}}}}}}}^{s,{{{{{\rm{A}}}}}}}\times {{{{{{\boldsymbol{\sigma }}}}}}}^{s}\right)$$

$$+\left(\begin{array}{c}{z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}{S}_{x}^{{{{{{\rm{B}}}}}}}+{z}_{{{{{{\rm{Fe}}}}}}}{D}_{y}^{{{{{{\rm{Fe}}}}}}}{S}_{z}^{{{{{{\rm{B}}}}}}}-2{A}_{x}{S}_{x}^{{{{{{\rm{A}}}}}}}-{A}_{{xz}}{S}_{z}^{{{{{{\rm{A}}}}}}}\\ {z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}{S}_{y}^{{{{{{\rm{B}}}}}}}\hfill\\ {z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}{S}_{z}^{{{{{{\rm{B}}}}}}}-{z}_{{{{{{\rm{Fe}}}}}}}{D}_{y}^{{{{{{\rm{Fe}}}}}}}{S}_{x}^{{{{{{\rm{B}}}}}}}-2{A}_{z}{S}_{z}^{{{{{{\rm{A}}}}}}}-{A}_{{xz}}{S}_{x}^{{{{{{\rm{A}}}}}}}\end{array}\right),$$

(45)

$${\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{{{{{{\bf{B}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{{{{{{\rm{B}}}}}}}(\{{{{{{{\boldsymbol{\sigma }}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\},\{{{{{{{\bf{S}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\})={\mu }_{{{{{{\rm{B}}}}}}}{{\mathfrak{g}}}^{{{{{{\rm{Fe}}}}}}}\cdot {{{{{{\bf{B}}}}}}}^{{{{{{\rm{DC}}}}}}}+\mathop{\sum}\limits _{s={{{{{\rm{A}}}}}},{{{{{\rm{B}}}}}}}x\left(J{{{{{{\boldsymbol{\sigma }}}}}}}^{s}+{{{{{{\bf{D}}}}}}}^{s,{{{{{\rm{B}}}}}}}\times {{{{{{\boldsymbol{\sigma }}}}}}}^{s}\right)$$

$$+\left(\begin{array}{c}{z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}{S}_{x}^{{{{{{\rm{A}}}}}}}-{z}_{{{{{{\rm{Fe}}}}}}}{D}_{y}^{{{{{{\rm{Fe}}}}}}}{S}_{z}^{{{{{{\rm{A}}}}}}}-2{A}_{x}{S}_{x}^{{{{{{\rm{B}}}}}}}+{A}_{{xz}}{S}_{z}^{{{{{{\rm{B}}}}}}}\\ {z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}{S}_{y}^{{{{{{\rm{A}}}}}}}\hfill\\ {z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}{S}_{z}^{{{{{{\rm{A}}}}}}}+{z}_{{{{{{\rm{Fe}}}}}}}{D}_{y}^{{{{{{\rm{Fe}}}}}}}{S}_{x}^{{{{{{\rm{A}}}}}}}-2{A}_{z}{S}_{z}^{{{{{{\rm{B}}}}}}}+{A}_{{xz}}{S}_{x}^{{{{{{\rm{B}}}}}}}\end{array}\right).$$

(46)

In Eqs. (43) and (44), the first, second, and third terms represent the Zeeman effect, ${{{{{\rm{Er}}}}}}^{3+}\!-\!{{{{{\rm{Er}}}}}}^{3+}$ exchange interaction, and ${{{{{\rm{Er}}}}}}^{3+}\!-\!{{{{{\rm{Fe}}}}}}^{3+}$ exchange interaction, respectively. In Eqs. (45) and (46), the first, second, and third terms represent the Zeeman effect, ${{{{{\rm{Er}}}}}}^{3+}\!-\!{{{{{\rm{Fe}}}}}}^{3+}$ exchange interaction, and ${{{{{\rm{Fe}}}}}}^{3+}\!-\!{{{{{\rm{Fe}}}}}}^{3+}$ exchange interaction, respectively. The dilution of the ${{{{{\rm{Er}}}}}}^{3+}$ spins is reflected by the factors ${z}_{{{{{{\rm{Er}}}}}}}=6x$ and $x$. ${z}_{{{{{{\rm{Er}}}}}}}$ denotes the number of neighbours of ${{{{{\rm{Er}}}}}}^{3+}$, and its value effectively decreases by a factor of $x$. Because $(1/2){{\hat{{{{{\boldsymbol{\sigma }}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ corresponds to the spin $\frac{1}{2}$ operator, a factor of 2 appears overall in Eqs. (43) and (44). As explained at the end of the section “ErFeO₃,” the $y$ component of the third term in Eqs. (43) and (44) is set to zero by means of implicitly considering a high-energy potential.

The free energy of the system is minimized when the thermal equilibrium values (time averages) of spins ${\bar{{{{{{\boldsymbol{\sigma }}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ and ${\bar{{{{{{\bf{S}}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ are parallel to their mean fields ${\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}\equiv {{{{{{\bf{B}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}(\{{\bar{{{{{{\boldsymbol{\sigma }}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\},\{{\bar{{{{{{\bf{S}}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\})$ and ${\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}\equiv {{{{{{\bf{B}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}(\{{\bar{{{{{{\boldsymbol{\sigma }}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\},\{{\bar{{{{{{\bf{S}}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\})$ as follows.

$${\bar{{{{{{\boldsymbol{\sigma }}}}}}}}^{s}=\langle {{\hat{{{{{\boldsymbol{\sigma }}}}}}}}^{s}\rangle =\langle {\hat{\sigma }}_{\parallel }^{s}\rangle {{{{{{\bf{u}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s},\,{\hat{\sigma }}_{\parallel }^{s}\equiv {{\hat{{{{{\boldsymbol{\sigma }}}}}}}}^{s}\cdot {{{{{{\bf{u}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s},$$

(47)

$${\bar{{{{{{\bf{S}}}}}}}}^{s}=\langle {{\hat{{{{{\bf{S}}}}}}}}^{s}\rangle =\langle {\hat{S}}_{\parallel }^{s}\rangle {{{{{{\bf{u}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s},\,{\hat{S}}_{\parallel }^{s}\equiv {{\hat{{{{{\bf{S}}}}}}}}^{s}\cdot {{{{{{\bf{u}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}.$$

(48)

Here, the unit vectors of the mean fields are defined as

$${{{{{{\bf{u}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}\equiv {\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}/|{\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}|,$$

(49)

$${{{{{{\bf{u}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}\equiv {\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}/|{\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}|.$$

(50)

The thermal equilibrium values ${\bar{{{{{{\boldsymbol{\sigma }}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ and ${\bar{{{{{{\bf{S}}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ can be determined as follows. For given mean fields ${\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}$ and ${\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}$, the effective Hamiltonians of each ${{{{{\rm{Er}}}}}}^{3+}$ and ${{{{{\rm{Fe}}}}}}^{3+}$ can be defined as

$${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}=\frac{1}{2}{\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{{\hat{{{{{\boldsymbol{\sigma }}}}}}}}^{s}\cdot {\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}=\frac{1}{2}{\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{\hat{\sigma }}_{\parallel }^{s}|{\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}|,$$

(51)

$${\hat{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}={\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{\hat{{{{{\bf{S}}}}}}}^{s}\cdot {{\bar{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}={\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}{\hat{S}}_{\parallel }^{s}|{{\bar{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}|.$$

(52)

Subsequently, the partition functions can be expressed as

$${Z}_{{{{{{\rm{Er}}}}}}}^{s}\equiv {{{{{\rm{Tr}}}}}}\left[{{{{{{\rm{e}}}}}}}^{-{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}/({k}_{{{{{{\rm{B}}}}}}}T)}\right]=\mathop{\sum}\limits_{m=\pm 1}{{{{{{\rm{e}}}}}}}^{-m{y}_{s}}=2{{{{{\rm{cosh }}}}}}\,({y}_{s}),$$

(53)

$${Z}_{{{{{{\rm{Fe}}}}}}}^{s}\equiv {{{{{\rm{Tr}}}}}}\left[{{{{{{\rm{e}}}}}}}^{-{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}/({k}_{{{{{{\rm{B}}}}}}}T)}\right]=\mathop{\sum }\limits_{m=-S}^{S}{{{{{{\rm{e}}}}}}}^{-m{x}_{s}}=\frac{{{{{{\rm{sinh }}}}}}\,[(S+1/2){x}_{s}]}{{{{{{\rm{sinh }}}}}}\,({x}_{s}/2)},$$

(54)

where the following are defined.

$${y}_{s}\equiv {\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}|{\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Er}}}}}}}^{s}|/(2{k}_{{{{{{\rm{B}}}}}}}T),$$

(55)

$${x}_{s}\equiv {\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}}|{\bar{{{{{{\bf{B}}}}}}}}_{{{{{{\rm{Fe}}}}}}}^{s}|/({k}_{{{{{{\rm{B}}}}}}}T).$$

(56)

Because ${{\hat{{{{{\boldsymbol{\sigma }}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ is not a standard spin operator with an angular momentum of $\hslash$ or $\hslash /2$ but is a vector of the Pauli operators, the summation is performed for $m=\pm\! 1$. The free energies are given as $-{k}_{{{{{{\rm{B}}}}}}}T{{{{{\rm{ln}}}}}}{Z}_{{{{{{\rm{Er}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ and $-{k}_{{{{{{\rm{B}}}}}}}T{{{{{\rm{ln}}}}}}{Z}_{{{{{{\rm{Fe}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$, and the thermal equilibrium values of the spins are

$$\langle {\hat{\sigma }}_{\parallel }^{s}\rangle =-\frac{\partial }{\partial {y}_{s}}{{{{{\rm{ln}}}}}}{Z}_{{{{{{\rm{Er}}}}}}}^{s}=-{{{{{\rm{tanh }}}}}}({y}_{s}),$$

(57)

$$\langle {\hat{S}}_{\parallel }^{s}\rangle =-\frac{\partial }{\partial {x}_{s}}{{{{{\rm{ln}}}}}}{Z}_{{{{{{\rm{Fe}}}}}}}^{s}=-S{B}_{S}(S{x}_{s}),$$

(58)

where ${B}_{S}(z)$ is the Brillouin function, defined as

$${B}_{J}(z)\equiv \frac{2J+1}{2J}{{{{{\rm{coth }}}}}}\left(\frac{2J+1}{2J}z\right)-\frac{1}{2J}{{{{{\rm{coth }}}}}}\left(\frac{z}{2J}\right).$$

(59)

By consistently solving Eqs. (43)–(48), (57) and (58), ${\bar{{{{{{\boldsymbol{\sigma }}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ and ${\bar{{{{{{\bf{S}}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ can be determined at finite temperatures.

Derivation of extended Dicke Hamiltonian

Here, we describe the transformation of our spin model, Eq. (2), into an extended version of the Dicke Hamiltonian, Eq. (1). We first rewrite the Fe³⁺ subsystem ${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{\mathrm{Fe}}}}}}}$ in terms of the annihilation and creation operators of a magnon in “${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ subsystem.” The ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$ subsystem ${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{\mathrm{Er}}}}}}}$ is rewritten using large spin operators in “${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$ subsystems.” The ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$–${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ exchange interactions, ${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{\mathrm{Er}}}}}}{{{{-}}}}{{{{{\mathrm{Fe}}}}}}}$, are transformed into five ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$–magnon couplings as per “${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }\!-\!{{{{{{\mathrm{Fe}}}}}}}^{{{{{3}}}} + }$ interactions.” Finally, the extended Dicke Hamiltonian is discussed in the section “Total Hamiltonian.”

${{{{{\bf{F}}}}}}{{{{{{\bf{e}}}}}}}^{{{{{{{\bf{3}}}}}}+}}$ subsystem

We assume that the most stable values of the ${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ spins at zero temperature, ${\bar{{{{{{\bf{S}}}}}}}}^{{{{{{\mathrm{A}}}}}}{{{{/}}}}{{{{{\mathrm{B}}}}}}}$, are unchanged even when ${{{{{{\bf{B}}}}}}}^{{{{{{\mathrm{DC}}}}}}}$ ($\lesssim {{{{10}}}}\,{{{{{\mathrm{T}}}}}}$) is applied, as we also assumed in our previous studies^31,34. Under this assumption, as depicted in Fig. 1a, the most stable state (i.e., the ground state) of the ${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ subsystem ${\hat{{{{{{{{\mathcal{H}}}}}}}}}}_{{{{{{\mathrm{Fe}}}}}}}$, Eq. (3), can be expressed as

$${\bar{{{{{{\bf{S}}}}}}}}_{0}^{{{{{{\rm{A}}}}}}}=\left(\begin{array}{c}S\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}\hfill\\ 0\hfill\\ -S\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}\hfill\end{array}\right),\,{\bar{{{{{{\bf{S}}}}}}}}_{0}^{{{{{{\rm{B}}}}}}}=\left(\begin{array}{c}S\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}\hfill\\ 0\hfill\\ S\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}\hfill\end{array}\right).$$

(60)

Here, the canting angle ${\beta }_{0}$ can be expressed as (see “Magnon quantization” in Supplementary Methods and Supplementary Fig. 4 or refs. ^31,33,34)

$${\beta }_{0}=-\frac{1}{2}{{{{{\rm{arctan }}}}}}\frac{{A}_{{xy}}+{z}_{{{{{{\rm{Fe}}}}}}}{D}_{y}^{{{{{{\rm{Fe}}}}}}}}{{z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}-{A}_{x}+{A}_{z}}.$$

(61)

The magnon is the quantum of spin fluctuations (spin waves) from this stable state. As shown in “Magnon quantization” in Supplementary Methods as well as in refs. ^31,34 in the long-wavelength limit, the ${{{{{\rm{Fe}}}}}}^{3+}$ Hamiltonian ${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Fe}}}}}}}$, Eq. (3), can be rewritten in terms of the annihilation (creation) operators ${\hat{a}}_{K}$ (${\hat{a}}_{K}^{{{\dagger}} }$) of ${{{{{\rm{Fe}}}}}}^{3+}$ magnons as

$${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Fe}}}}}}}\approx \mathop{\sum}\limits_{K=0,\pi }\hslash {\omega }_{K}{\hat{a}}_{K}^{{{\dagger}} }{\hat{a}}_{K}+{{{{{\rm{const}}}}}}.$$

(62)

Here, $K=0$ and $\pi$ correspond to the qFM and qAFM magnon modes, respectively³³. The eigenfrequencies can be expressed as follows.

$${\omega }_{K}=\gamma \sqrt{(b\,{{{{{\rm{cos }}}}}}\,K-a)(d\,{{{{{\rm{cos }}}}}}\,K+c)}.$$

(63)

Here, we define

$$a=[S/({\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}})]\left[-{A}_{z}-{A}_{x}-({z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}+{A}_{z}-{A}_{x})\,{{{{{\rm{cos }}}}}}\,(2{\beta }_{0})\right.$$

$$\left.+\,({A}_{{xz}}+{z}_{{{{{{\rm{Fe}}}}}}}{D}_{y}^{{{{{{\rm{Fe}}}}}}})\,{{{{{\rm{sin }}}}}}\,(2{\beta }_{0})\right],$$

(64)

$$b=[S/({\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}})]({z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}),$$

(65)

$$c=[S/({\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}})][({z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}+2{A}_{z}-2{A}_{x})\,{{{{{\rm{cos }}}}}}\,(2{\beta }_{0})+{z}_{{{{{{\rm{Fe}}}}}}}{D}_{y}^{{{{{{\rm{Fe}}}}}}}\,{{{{{\rm{sin }}}}}}\,(2{\beta }_{0})],$$

(66)

$$d=[S/({\mathfrak{g}}{\mu }_{{{{{{\rm{B}}}}}}})][-{z}_{{{{{{\rm{Fe}}}}}}}{J}_{{{{{{\rm{Fe}}}}}}}\,{{{{{\rm{cos }}}}}}\,(2{\beta }_{0})-(2{A}_{{xz}}+{z}_{{{{{{\rm{Fe}}}}}}}{D}_{y}^{{{{{{\rm{Fe}}}}}}})\,{{{{{\rm{sin }}}}}}\,(2{\beta }_{0})].$$

(67)

The operators of the spin fluctuations $\delta {\hat{{{{{\bf{S}}}}}}}_{i}^{{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}}\equiv {\hat{{{{{\bf{S}}}}}}}_{i}^{{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}}-{\bar{{{{{\bf{S}}}}}}}_{0}^{{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}}$ can be expressed as

$$\delta {\hat{{{{{\bf{S}}}}}}}_{i}^{{{{{{\rm{A}}}}}}} = \sqrt{\frac{S}{{2{N_{0}}}}}\left(\begin{array}{c}-({\hat{T}}_{0}-{\hat{T}}_{\pi })\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}\hfill\\ ({\hat{Y}}_{0}-{\hat{Y}}_{\pi })\hfill\\ -({\hat{T}}_{0}-{\hat{T}}_{\pi })\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}\hfill\end{array}\right),$$

(68)

$$\delta {\hat{{{{{\bf{S}}}}}}}_{i}^{{{{{{\rm{B}}}}}}}=\sqrt{\frac{S}{{2{N_{0}}}}}\left(\begin{array}{c}({\hat{T}}_{0}+{\hat{T}}_{\pi })\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}\hfill\\ ({\hat{Y}}_{0}+{\hat{Y}}_{\pi })\hfill\\ -({\hat{T}}_{0}+{\hat{T}}_{\pi })\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}\hfill\end{array}\right),$$

(69)

where the following are defined.

$${\hat{T}}_{K}\equiv {\left(\frac{b\,{{{{{\rm{cos }}}}}}\,K-a}{d\,{{{{{\rm{cos }}}}}}\,K+c}\right)}^{1/4}\frac{({\hat{a}}_{-K}^{{{\dagger}} }+{\hat{a}}_{K})}{\sqrt{2}},$$

(70)

$${\hat{Y}}_{K}\equiv {\left(\frac{d\,{{{{{\rm{cos }}}}}}\,K+c}{b\,{{{{{\rm{cos }}}}}}\,K-a}\right)}^{1/4}\frac{{{{{{\rm{i}}}}}}({\hat{a}}_{-K}^{{{\dagger}} }-{\hat{a}}_{K})}{\sqrt{2}}.$$

(71)

For the subsequent discussion, we define the sum and difference of the spins as

$${{\hat{{{{{\bf{S}}}}}}}}_{i}^{\pm }\equiv {{\hat{{{{{\bf{S}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}}\pm {{\hat{{{{{\bf{S}}}}}}}}_{i}^{{{{{{\rm{B}}}}}}}.$$

(72)

Their equilibrium (most stable) values are

$${\bar{{{{{{\bf{S}}}}}}}}_{0}^{+}\equiv {\bar{{{{{{\bf{S}}}}}}}}_{0}^{{{{{{\rm{A}}}}}}}+{\bar{{{{{{\bf{S}}}}}}}}_{0}^{{{{{{\rm{B}}}}}}}={(2S\,{{{{{\rm{sin }}}}}}\,{\beta }_{0},0,0)}^{{{{{{\rm{t}}}}}}},$$

(73)

$${\bar{{{{{{\bf{S}}}}}}}}_{0}^{-}\equiv {\bar{{{{{{\bf{S}}}}}}}}_{0}^{{{{{{\rm{A}}}}}}}-{\bar{{{{{{\bf{S}}}}}}}}_{0}^{{{{{{\rm{B}}}}}}}={(0,0,-2S\,{{{{{\rm{cos }}}}}}\,{\beta }_{0})}^{{{{{{\rm{t}}}}}}},$$

(74)

and their fluctuations are given by the sum and difference of Eqs. (68) and (69) as follows.

$$\delta {{\hat{{{{{\bf{S}}}}}}}}^{+}\equiv \delta {{\hat{{{{{\bf{S}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}}+\delta {{\hat{{{{{\bf{S}}}}}}}}_{i}^{{{{{{\rm{B}}}}}}}=\sqrt{\frac{2S}{{N}_{0}}}\left(\begin{array}{c}{\hat{T}}_{\pi }\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}\hfill\\ {\hat{Y}}_{0}\hfill\\ -{\hat{T}}_{0}\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}\hfill\end{array}\right),$$

(75)

$$\delta {{\hat{{{{{\bf{S}}}}}}}}^{-}\equiv \delta {{\hat{{{{{\bf{S}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}}-\delta {{\hat{{{{{\bf{S}}}}}}}}_{i}^{{{{{{\rm{B}}}}}}}=\sqrt{\frac{2S}{{N}_{0}}}\left(\begin{array}{c}-{\hat{T}}_{0}\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}\hfill\\ -{\hat{Y}}_{\pi }\hfill\\ {\hat{T}}_{\pi }\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}\hfill\end{array}\right).$$

(76)

${{{{{\bf{E}}}}}}{{{{{{\bf{r}}}}}}}^{{{{{{\bf{3}}}}}} + }$ subsystems

We define the following new operators.

$${{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}\equiv \frac{1}{2}\mathop{\sum }\limits_{i=1}^{{N}_{0}}{{\hat{{{{{\bf{R}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}.$$

(77)

For an ${{{{{\rm{Er}}}}}}^{3+}$ ion, $(1/2){{\hat{{{{{\bf{R}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ is a spin$\,\frac{1}{2}$ operator and ${{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ is a spin$\,\frac{N}{4}$ operator representing the rare earth spins in the A/B sublattice. We also define the sum and difference of the two sublattice spins as

$${{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{\pm }\equiv {{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{{{{{{\rm{A}}}}}}}\pm {{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{{{{{{\rm{B}}}}}}}.$$

(78)

In the long-wavelength limit, all spins in each sublattice have the same values in both static and dynamic situations. Subsequently, the ${{{{{\rm{Er}}}}}}^{3+}$ Hamiltonian in Eq. (6) can be rewritten as

$${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}}\approx \mathop{\sum }\limits_{\xi =x,y,z}{{\mathfrak{g}}}_{\xi }^{{{{{{\rm{Er}}}}}}}{\mu }_{{{{{{\rm{B}}}}}}}{\hat{\Sigma }}_{\xi }^{+}{B}_{\xi }^{{{{{{\rm{DC}}}}}}}+{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}\mathop{\sum }\limits_{i=1}^{{N}_{0}}{{\hat{{{{{\bf{R}}}}}}}}_{i}^{{{{{{\rm{A}}}}}}}\cdot \mathop{\sum }\limits_{i{\prime} =1}^{{N}_{0}}\frac{{{\hat{{{{{\bf{R}}}}}}}}_{i{\prime} }^{{{{{{\rm{B}}}}}}}}{x{N}_{0}}$$

(79)

$$=\mathop{\sum}\limits_{\xi =x,y,z}{{\mathfrak{g}}}_{\xi }^{{{{{{\rm{Er}}}}}}}{\mu }_{{{{{{\rm{B}}}}}}}{\hat{\Sigma }}_{\xi }^{+}{B}_{\xi }^{{{{{{\rm{DC}}}}}}}+\frac{8{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{N}{{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{{{{{{\rm{A}}}}}}}\cdot {{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{{{{{{\rm{B}}}}}}}.$$

(80)

${{{{{\bf{Er}}}}}}^{3+}$–${{{{{\bf{Fe}}}}}}^{3+}$ interactions

In the same manner as in our prior works^31,34, the Hamiltonian of the ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$–${{{{{\mathrm{Fe}}}}}}^{{{{{3}}}} + }$ exchange interactions can be rewritten using Eq. (11), as

$${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}-{{{{{\rm{Fe}}}}}}}\approx 2J\left({{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{+}\cdot {\bar{{{{{{\bf{S}}}}}}}}_{0}^{+}+{{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{+}\cdot \delta {{\hat{{{{{\bf{S}}}}}}}}^{+}\right)+\left(\begin{array}{c}0\hfill\\ 2{D}_{y}\hfill\\ 0\hfill\end{array}\right)\cdot \left({{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{+}\times {\bar{{{{{{\bf{S}}}}}}}}_{0}^{-}+{{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{+}\times \delta {{\hat{{{{{\bf{S}}}}}}}}^{-}\right)$$

$$+\left(\begin{array}{c}2{D}_{x}\hfill\\ 0\hfill\\ 0\hfill\end{array}\right)\cdot \left({{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{-}\times {\bar{{{{{{\bf{S}}}}}}}}_{0}^{-}+{{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{-}\times \delta {{\hat{{{{{\bf{S}}}}}}}}^{-}\right).$$

(81)

In each set of parentheses, the first term represents the influence of the static components (equilibrium values) ${\bar{{{{{{\bf{S}}}}}}}}_{0}^{{{{{{\rm{A}}}}}}/{{{{{\rm{B}}}}}}}$ of ${{{{{\rm{Fe}}}}}}^{3+}$ spins to ${{{{{\rm{Er}}}}}}^{3+}$ spins ${{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{\pm }$, and the second term represents the coupling between the ${{{{{\rm{Fe}}}}}}^{3+}$ fluctuation $\delta {{\hat{{{{{\bf{S}}}}}}}}^{\pm }$ and ${{{{{\rm{Er}}}}}}^{3+}$ spins ${{\hat{{{{{\boldsymbol{\Sigma }}}}}}}}^{\pm }$. We divide these terms into two Hamiltonians as

$${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}-{{{{{\rm{Fe}}}}}}}\approx {{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}-{{{{{\rm{Fe}}}}}}}^{\Sigma }+{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}-{{{{{\rm{Fe}}}}}}}^{{{{{{\rm{coupling}}}}}}}.$$

(82)

The first term gives part of the ${{{{{\rm{Er}}}}}}^{3+}$ spin resonance frequency and can be expressed as follows.

$${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Er}}}}}}-{{{{{\rm{Fe}}}}}}}^{\Sigma }={E}_{x}{\hat{\Sigma }}_{x}^{+}.$$

(83)

Here, we used Eqs. (73), (74) and (18). We neglected $(-4S{D}_{x}\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}){\hat{\Sigma }}_{y}^{-}$ under the assumption explained at the end of the section “ErFeO₃.” The second term in Eq. (82) can be rewritten in terms of the ${{{{{\rm{Fe}}}}}}^{3+}$ fluctuations as

$${{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{{\rm{Er}}}}}}-{{{{{\rm{Fe}}}}}}}}^{{{{{{\rm{coupling}}}}}}}= \,\sqrt{\frac{8S}{{N_{0}}}}\left[(J\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}-{D}_{y}\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}){\hat{T}}_{\pi }{\hat{\Sigma }}_{x}^{+} +J{\hat{Y}}_{0}{\hat{\Sigma }}_{y}^{+}+({D}_{x}\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}){\hat{T}}_{\pi }{\hat{\Sigma }}_{y}^{-}\right.\\ \,\left. +{D}_{x}{\hat{Y}}_{\pi }{\hat{\Sigma }}_{z}^{-}+(-J\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}-{D}_{y}\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}){\hat{T}}_{0}{\hat{\Sigma }}_{z}^{+}\right].$$

(84)

Total Hamiltonian

In terms of the annihilation and creation operators of magnons, the total Hamiltonian can be expressed as

$${\hat{{{{{\mathcal{H}}}}}}}\approx \mathop{\sum}\limits _{K=0,\pi }\hslash {\omega }_{K}{\hat{a}}_{K}^{{{\dagger}} }{\hat{a}}_{K}+{E}_{x}{\hat{\Sigma }}_{x}^{+}+\mathop{\sum}\limits_{\xi =x,y,z}{{\mathfrak{g}}}_{\xi }^{{{{{{\rm{Er}}}}}}}{\mu }_{{{{{{\rm{B}}}}}}}{B}_{\xi }^{{{{{{\rm{DC}}}}}}}{\hat{\Sigma }}_{\xi }^{+}+\frac{8{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{N}{\hat{\Sigma }}^{{{{{{\rm{A}}}}}}}\cdot {\hat{\Sigma }}^{{{{{{\rm{B}}}}}}}$$

$$+\,\frac{2\hslash {g}_{x}}{\sqrt{N}}({\hat{a}}_{\pi }^{{{\dagger}} }+{\hat{a}}_{\pi }){\hat{\Sigma }}_{x}^{+}+\frac{{{{{{\rm{i}}}}}}2\hslash {g}_{y}}{\sqrt{N}}({\hat{a}}_{0}^{{{\dagger}} }-{\hat{a}}_{0}){\hat{\Sigma }}_{y}^{+}+\frac{2\hslash {g}_{y{\prime} }}{\sqrt{N}}({\hat{a}}_{\pi }^{{{\dagger}} }+{\hat{a}}_{\pi }){\hat{\Sigma }}_{y}^{-}$$

$$+\,\frac{{{{{{\rm{i}}}}}}2\hslash {g}_{z}}{\sqrt{N}}({\hat{a}}_{\pi }^{{{\dagger}} }-{\hat{a}}_{\pi }){\hat{\Sigma }}_{z}^{-}+\frac{2\hslash {g}_{z{\prime} }}{\sqrt{N}}({\hat{a}}_{0}^{{{\dagger}} }+{\hat{a}}_{0}){\hat{\Sigma }}_{z}^{+}.$$

(85)

The five coupling strengths are defined as

$${\hslash} {g}_{x}=\sqrt{2{xS}}(J\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}-{D}_{y}\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}){\left(\frac{b+a}{d-c}\right)}^{1/4}=h\times \sqrt{x}\,\times 0.051\,{{{{{\rm{THz}}}}}},$$

(86)

$${{\hslash }}{g}_{y}=\sqrt{2{xS}}J{\left(\frac{d+c}{b-a}\right)}^{1/4}=h\times \sqrt{x}\,\times 0.041\,{{{{{\rm{THz}}}}}},$$

(87)

$$\hslash {g}_{y{\prime} }=\sqrt{2{xS}}({D}_{x}\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}){\left(\frac{b+a}{d-c}\right)}^{1/4}=h\,\times \sqrt{x}\,\times 3.1\times 1{0}^{-5}\,{{{{{\rm{THz}}}}}},$$

(88)

$$\hslash {g}_{z}=\sqrt{2{xS}}{D}_{x}{\left(\frac{d-c}{b+a}\right)}^{1/4}=h\,\times \sqrt{x}\,\times 0.116\,{{{{{\rm{THz}}}}}},$$

(89)

$${\hslash} {g}_{{z{\prime}} }=\sqrt{2{xS}}(-J\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}-{D}_{y}\,{{{{{\rm{cos }}}}}}\,{\beta }_{0})\left(\frac{b-a}{d+c}\right)^{1/4}=h\,\times \sqrt{x}\,\times (-0.040\,{{{{{\rm{THz}}}}}}).$$

(90)

The actual values were evaluated using the parameters shown in “Parameters.”

Compared with the expressions in our previous studies^31,34, the coupling strengths in Eqs. (86)–(87) include additional factors $\sqrt{2}$ and $\sqrt{S}$. First, $\sqrt{2}$ originates from the number of ${{{{{\rm{Er}}}}}}^{3+}$ sublattices in the present study, whereas a single ${{{{{\rm{Er}}}}}}^{3+}$ lattice was considered in our previous studies^31,34. The second factor, $\sqrt{S}$, is a result of the difference in the method of normalizing the ${{{{{\rm{Fe}}}}}}^{3+}$ spins between the present and previous studies^31,34.

Whereas the ${{{{{\rm{Er}}}}}}^{3+}$ spin ensemble is described by six operators ${\hat{\Sigma }}_{x,y,z}^{+}$ and ${\hat{\Sigma }}_{x,y,z}^{-}$ in the extended Dicke Hamiltonian in Eq. (85), only ${\hat{\Sigma }}_{x}^{+}$ and ${\hat{\Sigma }}_{z}^{-}$ are relevant to the LTPT shown in Fig. 1. ${\hat{\Sigma }}_{x}^{+}$ corresponds to the paramagnetic alignment by the ${{{{{\rm{Fe}}}}}}^{3+}$ magnetization along the $a$ axis, and ${\hat{\Sigma }}_{z}^{-}$ corresponds to the antiferromagnetic ordering along the $c$ axis. Subsequently, to analyse the thermal equilibrium values of the spins, it is sufficient to consider only the following two terms in the ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Er}}}}}}^{3+}$ exchange interactions.

$$\frac{8{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{N}{\hat{\Sigma }}^{{{{{{\rm{A}}}}}}}\cdot {\hat{\Sigma }}^{{{{{{\rm{B}}}}}}}=\frac{2{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{N}\mathop{\sum}\limits_{\xi =x,y,z}\left[{({\hat{\Sigma }}_{\xi }^{+})}^{2}-{({\hat{\Sigma }}_{\xi }^{-})}^{2}\right]$$

$$\to \frac{2{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{N}\left[{({\hat{\Sigma }}_{x}^{+})}^{2}-{({\hat{\Sigma }}_{z}^{-})}^{2}\right].$$

(91)

In contrast, while the ${{{{{\rm{Fe}}}}}}^{3+}$ spins are described by the qFM and qAFM magnon modes in Eq. (85), only the qAFM mode is relevant to the LTPT. As shown in Fig. 1, $\delta {\hat{S}}_{y}^{-}$ and $\delta {\hat{S}}_{z}^{-}$ are required to describe the rotation of the ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector in the ${bc}$ plane, and $\delta {\hat{S}}_{x}^{+}$ is required for possible modulation of canting along the $a$ axis. As seen in Eqs. (75) and (76), $\delta {\hat{S}}_{x}^{+}$, $\delta {\hat{S}}_{y}^{-}$, and $\delta {\hat{S}}_{z}^{-}$ are related to the qAFM magnon mode ($K=\pi$), and the qFM mode ($K=0$) plays no role in the LTPT.

Consequently, among the terms in the total Hamiltonian given by Eq. (85), it is only necessary to consider the terms shown in Eq. (16) to describe the LTPT (the other terms are required to fully reproduce the terahertz spectra discussed in “Spin resonance frequencies” in Supplementary Methods). Note that, in Eq. (16), we rewrote the large spin operators representing the ${{{{{\rm{Er}}}}}}^{3+}$ spin ensemble as

$$\left\{\begin{array}{c}{\hat{\Sigma }}_{x}^{+}\to {\hat{\Sigma }}_{x}\equiv \mathop{\sum }\limits_{i=1}^{N}{\hat{\sigma }}_{i,x}/2\\ {\hat{\Sigma }}_{y}^{-}\to {\hat{\Sigma }}_{y}\equiv \mathop{\sum }\limits_{i=1}^{N}{\hat{\sigma }}_{i,y}/2\\ {\hat{\Sigma }}_{z}^{-}\to {\hat{\Sigma }}_{z}\equiv \mathop{\sum }\limits_{i=1}^{N}{\hat{\sigma }}_{i,z}/2\end{array}\right.,$$

(92)

where we re-indexed the Pauli operators representing the ${{{{{\rm{Er}}}}}}^{3+}$ spins in the two sublattices as

$$\left\{\begin{array}{c}{\hat{\sigma }}_{i,x}^{{{{{{\rm{A}}}}}}}\to {\hat{\sigma }}_{2i-1,x}\\ {\hat{\sigma }}_{i,y}^{{{{{{\rm{A}}}}}}}\to {\hat{\sigma }}_{2i-1,y}\\ {\hat{\sigma }}_{i,z}^{{{{{{\rm{A}}}}}}}\to {\hat{\sigma }}_{2i-1,z}\end{array}\right.,\left\{\begin{array}{c}{\hat{\sigma }}_{i,x}^{{{{{{\rm{B}}}}}}}\to {\hat{\sigma }}_{2i,x}\\ {\hat{\sigma }}_{i,y}^{{{{{{\rm{B}}}}}}}\to -{\hat{\sigma }}_{2i,y}\\ {\hat{\sigma }}_{i,z}^{{{{{{\rm{B}}}}}}}\to -{\hat{\sigma }}_{2i,z}\end{array}\right..$$

(93)

Further, in Eq. (16), it was assumed that the external DC magnetic field is applied along the $a$ axis to maintain ${\Gamma }_{12}$ symmetry, where either $|{\bar{\sigma }}_{z}^{{{{{{\rm{A}}}}}}}-{\bar{\sigma }}_{z}^{{{{{{\rm{B}}}}}}}|$ or the rotation angle $\varphi$ of the ${{{{{\rm{Fe}}}}}}^{3+}$ AFM vector from the $c$ axis can be the order parameter for the LTPT. Among the five ${{{{{\rm{Er}}}}}}^{3+}$–magnon couplings in Eq. (85), only the ${g}_{x}$ and ${g}_{z}$ terms are required to consider the coupling between ${\hat{\Sigma }}_{x,z}$ and the qAFM magnons. Although the ${g}_{{y}^{{\prime} }}$ term also couples ${\hat{\Sigma }}_{y}$ and qAFM magnons, its coupling strength is negligible compared with ${g}_{x,z}$, as shown in Eq. (88), which is consistent with the experimentally observed antiferromagnetic ordering of the ${{{{{\rm{Er}}}}}}^{3+}$ spins along the $c$ axis ($\langle {\hat{\Sigma }}_{y}^{-}\rangle =0$).

As demonstrated in Figs. 4 and 5, the LTPT can be quantitatively reproduced as the SRPT in the extended Dicke Hamiltonian, Eq. (85), which was derived from the spin model of ${{{{{\rm{ErFe}}}}}}{{{{{{\rm{O}}}}}}}_{3}$. The essential terms were extracted as shown in Eq. (16). The ${g}_{z}$ term (antisymmetric ${{{{{\rm{Er}}}}}}^{3+}$–${{{{{\rm{Fe}}}}}}^{3+}$ exchange interaction with ${D}_{x}$) corresponds to the matter–photon coupling and causes the antiferromagnetic ordering of ${{{{{\rm{Er}}}}}}^{3+}$ spins along the $c$ axis and the $b$ component of the ${{{{{\rm{Fe}}}}}}^{3+}$ spins through the spontaneous appearance of qAFM magnons.

Semiclassical calculation method

Wang and Hioe demonstrated a simple calculation method for the SRPT in 1973², and Hepp and Lieb confirmed its validity for the Dicke model⁴⁷. In the Dicke model, the partition function at temperature ${{{{T}}}}$

$${{{{{{\mathcal{Z}}}}}}}_{{{{{{\rm{Dicke}}}}}}}(T)\equiv {{{{{\rm{Tr}}}}}}[{{{{{{\rm{e}}}}}}}^{-{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}/({k}_{{{{{{\rm{B}}}}}}}T)}],$$

(94)

in the thermodynamic limit $N\to {{\infty }}$ can be approximately evaluated by replacing the trace over the photonic variables with an integral over coherent states $|\left.\sqrt{N}\bar{a}\right\rangle$ ($\bar{a}\in {\mathbb{C}}$; giving $\left.\hat{a}|\sqrt{N}\bar{a}\right\rangle =\sqrt{N}\bar{a}|\left.\sqrt{N}\bar{a}\right\rangle$) as

$${{\bar{{{{{\mathcal{Z}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}(T)\equiv \int \frac{{{{{{{\rm{d}}}}}}}^{2}\bar{a}}{\pi /N}{{{{{\rm{Tr}}}}}}[{{{{{{\rm{e}}}}}}}^{-{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}^{{{{{{\rm{eff}}}}}}}(\bar{a})/({k}_{{{{{{\rm{B}}}}}}}T)}]$$

(95)

$$=\int \frac{{{{{{{\rm{d}}}}}}}^{2}\bar{a}}{\pi /N}{{{{{{\rm{e}}}}}}}^{-{{\bar{{{{{\mathcal{S}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}(\bar{a},T)/({k}_{{{{{{\rm{B}}}}}}}T)},$$

(96)

where an effective Hamiltonian is defined as given below,

$$\frac{{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}^{{{{{{\rm{eff}}}}}}}(\bar{a})}{\hslash }\equiv N{\omega }_{{{{{{\rm{ph}}}}}}}|\bar{a}{|}^{2}+{\omega }_{{{{{{\rm{ex}}}}}}}{\hat{S}}_{x}+{{{{{\rm{i}}}}}}2g({\bar{a}}^{* }-\bar{a}){\hat{S}}_{z},$$

(97)

as well as an action

$${{\bar{{{{{\mathcal{S}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}(\bar{a},T)\equiv -{k}_{{{{{{\rm{B}}}}}}}T{{{{{\rm{ln}}}}}}{{{{{\rm{Tr}}}}}}[{{{{{{\rm{e}}}}}}}^{-{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}^{{{{{{\rm{eff}}}}}}}(\bar{a})/({k}_{{{{{{\rm{B}}}}}}}T)}]$$

(98)

$$=N\left\{{\hslash} {\omega }_{{{{{{\rm{ph}}}}}}}|\bar{a}{|}^{2}-{k}_{{{{{{\rm{B}}}}}}}T{{{{{\rm{ln}}}}}}{{{{{\rm{Tr}}}}}}[{{{{{{\rm{e}}}}}}}^{-{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}^{{{{{{\rm{a}}}}}}}(\bar{a})/({k}_{{{{{{\rm{B}}}}}}}T)}]\right\},$$

(99)

and an effective Hamiltonian per atom

$$\frac{{{\hat{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}^{{{{{{\rm{a}}}}}}}(\bar{a})}{\hslash }\equiv \frac{{\omega }_{{{{{{\rm{ex}}}}}}}}{2}{\hat{\sigma }}_{x}+{{{{{\rm{i}}}}}}g({\bar{a}}^{* }-\bar{a}){\hat{\sigma }}_{z}.$$

(100)

The normalized expectation value ${\bar{a}}=\langle {\hat{a}}\rangle /\! \sqrt{N}$ of the annihilation operator of a photon at temperature $T$ can be determined to minimize the action, that is, $\partial {\bar{{{{{\mathcal{S}}}}}}}/\partial {{{{{\rm{Re}}}}}}[\bar{a}]=0$ and $\partial {\bar{{{{{\mathcal{S}}}}}}}/\partial {{{{{\rm{Im}}}}}}[{\bar{a}}]=0$. $\bar{a}$ acquires a non-zero value below ${T}_{{{{{{\rm{c}}}}}}}$ when $4{g}^{2} \, > \, {\omega }_{{{{{{\rm{ph}}}}}}}{\omega }_{{{{{{\rm{ex}}}}}}}$ is satisfied ($\sqrt{N} \bar{a}$ gives a finite electric (displacement) field or vector potential even in the thermodynamic limit $N\to \infty$ if the atomic density is fixed). The above approximation is justified if the free energy ${\bar{{{{{\mathcal{F}}}}}}}_{{{{{{\rm{Dicke}}}}}}}(T)\equiv -({k}_{{{{{{\rm{B}}}}}}}T/N){{{{{\rm{ln}}}}}}{{\bar{{{{{\mathcal{Z}}}}}}}}_{{{{{{\rm{Dicke}}}}}}} (T)$ per atom satisfies ${\hslash} {\omega }_{{{{{{\rm{ph}}}}}}}/N\ll | {{\bar{{{{{\mathcal{F}}}}}}}}_{{{{{{\rm{Dicke}}}}}}}(T) |$ in the thermodynamic limit^45,46,48,49.

Following the above treatment, we calculated the expectation values of the ${{{{{\rm{Er}}}}}}^{3+}$ spin and ${{{{{\rm{Fe}}}}}}^{3+}$ qAFM magnon operators in the extended Dicke Hamiltonian, Eq. (16), at a finite temperature. In the thermodynamic limit $N\to {{\infty }}$ the partition function ${{{{{\mathcal{Z}}}}}}(T)\equiv {{{{{\rm{Tr}}}}}} {[{{{{{\rm{e}}}}}}^{{-{\hat{{{{{\mathcal{H}}}}}}}/({k}_{{{{{{\rm{B}}}}}}}T)}}]}$ can be approximately evaluated by replacing the trace over the magnonic variables with an integral over c-numbers ${\bar{a}}_{r},{\bar{a}}_{i}\in {\mathbb{R}}$, giving ${\hat{a}}_{\pi }\to {\sqrt{N}} ({\bar{a}}_{r}+{{{{{\rm{i}}}}}} {\bar{a}}_{i})$, as

$${\bar{{{{{\mathcal{Z}}}}}}} {(T)} \equiv \int \frac{{{{{{{\rm{d}}}}}}{{\bar{a}}_{r}}{{{{{\rm{d}}}}}}{{\bar{a}}_{i}}}}{\pi /N}{{{{{\rm{Tr}}}}}}\left[{{{{{\rm{e}}}}}}^{{-{{\hat{{{{{\mathcal{H}}}}}}}^{{{{{\rm{eff}}}}}}}({\bar{a}}_{r},{\bar{a}}_{i})/({{k}_{{{{{{\rm{B}}}}}}}}T)}}\right]$$

(101)

$$=\int \frac{{{{{{{\rm{d}}}}}}{\bar{a}}_{r}{{{{{\rm{d}}}}}}{\bar{a}}_{i}}}{\pi /N}{{{{{{\rm{e}}}}}}}^{{-{\bar{{{{{\mathcal{S}}}}}}}(\bar{a},T)/({k}_{{{{{{\rm{B}}}}}}}T)}},$$

(102)

where we define an effective Hamiltonian

$${\hat{{{{{\mathcal{H}}}}}}}^{{{{{{\rm{eff}}}}}}} ({\bar{a}}_{r}, {\bar{a}}_{i}) / {\hslash} \equiv N{\omega }_{\pi } ({{\bar{a}}_{r}}^{2} + {{\bar{a}}_{i}}^{2})+{\omega }_{{{{{{\rm{Er}}}}}}} {\hat{\Sigma }}_{x} + \frac{{4{z_{{{{{{\rm{Er}}}}}}}}{J_{{{{{{\rm{Er}}}}}}}}}}{{N{\hslash} }}\left(\langle {\hat{\Sigma }}_{x}\rangle {\hat{\Sigma }}_{x}-\langle {\hat{\Sigma }}_{z}\rangle {\hat{\Sigma }}_{z}\right)$$

$$-\frac{{2{z_{{{{{{\rm{Er}}}}}}}}{J_{{{{{{\rm{Er}}}}}}}}}}{{N{\hslash}}}\left(\left\langle {\hat{\Sigma }}_{x}\right\rangle^{2}-\left\langle {\hat{\Sigma }}_{z}\right\rangle^{2}\right) + 4{g}_{x}{\bar{a}}_{r}{\hat{\Sigma }}_{x} + 4{g}_{z}{\bar{a}}_{i}{\hat{\Sigma }}_{z}$$

(103)

by introducing the ${{{{{\rm{Er}}}}}}^{3+}$ components $\langle {\hat{\Sigma }}_{x,z}\rangle$ of the mean fields of the ${{{{{\rm{Er}}}}}}^{3+}$ ensemble. The action in Eq. (102) is defined as follows.

$${\bar{{{{{\mathcal{S}}}}}}}({\bar{a}}_{r},{\bar{a}}_{i},T)\equiv -{k}_{{{{{{\rm{B}}}}}}}T{{{{{\rm{ln}}}}}}{{{{{\rm{Tr}}}}}}\left[{{{{{\rm{e}}}}}}^{{-{\hat{{{{{\mathcal{H}}}}}}}^{{{{{{\rm{eff}}}}}}}({\bar{a}}_{r},{\bar{a}}_{i})/({k}_{{{{{{\rm{B}}}}}}}T)}}\right]$$

(104)

$$= N\left\{{\hslash} {\omega }_{\pi }\left({{\bar{a}}_{r}}^{2} + {{\bar{a}}_{i}}^{2} \right) - \frac{{2{z_{{{{{{\rm{Er}}}}}}}}{J_{{{{{{\rm{Er}}}}}}}}}}{{N^{2}}}\left(\left\langle {\hat{\Sigma }}_{x}\right\rangle^{2} - \left\langle {\hat{\Sigma }}_{z}\right\rangle^{2}\right)\right\} - N{k}_{{{{{{\rm{B}}}}}}} T {{{{{\rm{ln}}}}}} {{{{{\rm{Tr}}}}}} \left[{{{{{\rm{e}}}}}}^{{-\frac{{{ {\hat{{{{{\mathcal{H}}}}}}}^{{{{{{\rm{a}}}}}}}}({{\bar{a}}_{r}},{{\bar{a}}_{i}})}}{{{k_{{{{{{\rm{B}}}}}}}}T}}}}\right].$$

(105)

Here, we define an effective Hamiltonian per ${{{{{\rm{Er}}}}}}^{3+}$ spin as

$$\frac{{{{\hat{{{{{\mathcal{H}}}}}}}}^{{{{{{\rm{a}}}}}}}({\bar{a}}_{r},{\bar{a}}_{i})}}{\hslash }\equiv \frac{{{\omega }_{{{{{{\rm{Er}}}}}}}}}{2}{\hat{\sigma }}_{x}+\frac{{2{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}}{{N{\hslash} }}\left(\langle {\hat{\Sigma }}_{x}^{+}\rangle {\hat{\sigma }}_{x}-\langle {\hat{\Sigma }}_{z}^{-}\rangle {\hat{\sigma }}_{z}\right)+2{g}_{x}{\bar{a}}_{r}{\hat{\sigma }}_{x}+2{g}_{z}{\bar{a}}_{i}{\hat{\sigma }}_{z}.$$

(106)

The site index $i$ is omitted here because all the spins are identical. The action ${\bar{{{{{\mathcal{S}}}}}}}$ is minimized at $\partial {\bar{{{{{\mathcal{S}}}}}}}/\partial {\bar{a}}_{r}=0$ and $\partial {\bar{{{{{\mathcal{S}}}}}}}/\partial {\bar{a}}_{i}=0$, yielding

$${\omega }_{\pi }{\bar{a}}_{r}+{g}_{x}\langle {\hat{\sigma }}_{x}\rangle =0,$$

(107)

$${\omega }_{\pi }{\bar{a}}_{i}+{g}_{z}\langle {\hat{\sigma }}_{z}\rangle =0,$$

(108)

where the expectation values of the Pauli operators are defined for a given ${\bar{a}}_{r}$ and ${\bar{a}}_{i}$, as

$${\bar{\sigma }}_{\xi }\equiv \langle {\hat{\sigma }}_{\xi }\rangle \equiv \frac{{{{{{\rm{Tr}}}}}}[{\hat{\sigma }}_{\xi }{{{{{{\rm{e}}}}}}}^{-{{\hat{{{{{\mathcal{H}}}}}}}}^{{{{{{\rm{a}}}}}}}({\bar{a}}_{r},{\bar{a}}_{i})/({k}_{{{{{{\rm{B}}}}}}}T)}]}{{{{{{\rm{Tr}}}}}}[{{{{{{\rm{e}}}}}}}^{-{{\hat{{{{{\mathcal{H}}}}}}}}^{{{{{{\rm{a}}}}}}}({\bar{a}}_{r},{\bar{a}}_{i})/({k}_{{{{{{\rm{B}}}}}}}T)}]}.$$

(109)

From Eqs. (107) and (108), the expectation values of the large spin operators can be expressed as

$$\langle {\hat{\Sigma }}_{x}\rangle =\frac{N}{2}\langle {\hat{\sigma }}_{x}\rangle =-\frac{N{\omega }_{\pi }}{2{g}_{x}}{\bar{a}}_{r},$$

(110)

$$\langle {\hat{\Sigma }}_{z}\rangle =\frac{N}{2}\langle {\hat{\sigma }}_{z}\rangle =-\frac{N{\omega }_{\pi }}{2{g}_{z}}{\bar{a}}_{i}.$$

(111)

Substituting these into Eq. (106) gives

$$\frac{{{\hat{{{{{\mathcal{H}}}}}}}}^{{{{{{\rm{a}}}}}}}({\bar{a}}_{r},{\bar{a}}_{i})}{\hslash }=\frac{{\omega }_{{{{{{\rm{Er}}}}}}}}{2}{\hat{\sigma }}_{x}+\left(2{g}_{x}-\frac{{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}{\omega }_{\pi }}{\hslash {g}_{x}}\right){\bar{a}}_{r}{\hat{\sigma }}_{x}+\left(2{g}_{z}+\frac{{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}{\omega }_{\pi }}{\hslash {g}_{z}}\right){\bar{a}}_{i}{\hat{\sigma }}_{z}.$$

(112)

By simultaneously solving Eqs. (107)–(109) and (112) for a given temperature, $T$, we obtain the thermal equilibrium values of the ${{{{{\rm{Er}}}}}}^{3+}$ spins ${\bar{\sigma }}_{x,z}$ and ${{{{{\rm{Fe}}}}}}^{3+}$ qAFM magnons ${\bar{a}}_{r,i}$. From Eqs. (60) and (68)–(71), the thermal equilibrium values of the ${{{{{\rm{Fe}}}}}}^{3+}$ spins can be obtained from those of the qAFM magnons ${\bar{a}}_{r,i}$ as

$${\bar{S}}_{x}\equiv \langle {\hat{S}}_{x}^{{{{{{\rm{A}}}}}}}\rangle =\langle {\hat{S}}_{x}^{{{{{{\rm{B}}}}}}}\rangle =S\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}+\sqrt{2{xS}}\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}{\left(\frac{b+a}{d-c}\right)}^{1/4}{\bar{a}}_{r},$$

(113)

$${\bar{S}}_{y}\equiv \langle {\hat{S}}_{y}^{{{{{{\rm{A}}}}}}}\rangle =-\langle {\hat{S}}_{y}^{{{{{{\rm{B}}}}}}}\rangle =-\sqrt{2{xS}}{\left(\frac{d-c}{b+a}\right)}^{1/4}{\bar{a}}_{i},$$

(114)

$${\bar{S}}_{z}\equiv -\langle {\hat{S}}_{z}^{{{{{{\rm{A}}}}}}}\rangle =\langle {\hat{S}}_{z}^{{{{{{\rm{B}}}}}}}\rangle =S\,{{{{{\rm{cos }}}}}}\,{\beta }_{0}-\sqrt{2{xS}}\,{{{{{\rm{sin }}}}}}\,{\beta }_{0}{\left(\frac{b+a}{d-c}\right)}^{1/4}{\bar{a}}_{r}.$$

(115)

Condition for SRPT in extended Dicke Hamiltonian

To quantitatively evaluate the contributions of the ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$–magnon couplings and ${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$–${{{{{\mathrm{Er}}}}}}^{{{{{3}}}} + }$ exchange interactions to the LTPT, the condition for the SRPT in our extended Dicke Hamiltonian, Eq. (16), can be derived using the Holstein–Primakoff transformation^38,39,40. ${{\hat{{{{\Sigma }}}}}}_{{{{{x}}}}, {{{{y}}}}, {{{{z}}}}}$ can be rewritten using the bosonic annihilation (creation) operator $\hat{{{{{b}}}}}$ (${{\hat{{{{b}}}}}}^{{{{{{{\dagger}} }}}}}$) as

$${\hat{\Sigma }}_{x}\to {\hat{b}}^{{{\dagger}} }\hat{b}-\frac{N}{2},$$

(116)

$${\hat{\Sigma }}_{y}\to \frac{{\hat{b}}^{{{\dagger}} }{(N-{\hat{b}}^{{{\dagger}} }\hat{b})}^{1/2}+{(N-{\hat{b}}^{{{\dagger}} }\hat{b})}^{1/2}\hat{b}}{2},$$

(117)

$${\hat{\Sigma }}_{z}\to \frac{{\hat{b}}^{{{\dagger}} }{(N-{\hat{b}}^{{{\dagger}} }\hat{b})}^{1/2}-{(N-{\hat{b}}^{{{\dagger}} }\hat{b})}^{1/2}\hat{b}}{{{{{{\rm{i}}}}}}2}.$$

(118)

Further, all the operators are replaced by c-numbers ${\bar{a}}_{r},{\bar{a}}_{i},\bar{b}\in {\mathbb{R}}$ as

$$\hat{a}\to \sqrt{N}({\bar{a}}_{r}+{{{{{\rm{i}}}}}}{\bar{a}}_{i}),$$

(119)

$$\hat{b}\to {{{{{\rm{i}}}}}}\sqrt{N}\bar{b}.$$

(120)

Subsequently, the Hamiltonian in Eq. (16) becomes

$$\frac{{\hat{{{{{\mathcal{H}}}}}}}}{N\hslash }\to {\omega }_{\pi }({{\bar{a}}_{r}}^{2}+{{\bar{a}}_{i}}^{2})+{\omega }_{{{{{{\rm{Er}}}}}}}{\bar{b}}^{2}+\frac{4{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{\hslash }{\bar{b}}^{2}({\bar{b}}^{2}-1)$$

$$+\,2{g}_{x}{\bar{a}}_{r}(2{\bar{b}}^{2}-1)-4{g}_{z}{\bar{a}}_{i}\bar{b}\sqrt{1-{\bar{b}}^{2}}+{{{{{\rm{const}}}}}}.$$

(121)

The ground state of the system should satisfy

$$\frac{1}{2}\frac{1}{\hslash N}\frac{\partial {{{{{\mathcal{H}}}}}}}{\partial {\bar{a}}_{r}}={\omega }_{\pi }{\bar{a}}_{r}+{g}_{x}(2{\bar{b}}^{2}-1)=0,$$

(122)

$$\frac{1}{2}\frac{1}{\hslash N}\frac{\partial {{{{{\mathcal{H}}}}}}}{\partial {\bar{a}}_{i}}={\omega }_{\pi }{\bar{a}}_{i}-2{g}_{z}\bar{b}\sqrt{1-{\bar{b}}^{2}}=0,$$

(123)

$$\frac{1}{2}\frac{1}{\hslash N}\frac{\partial {{{{{\mathcal{H}}}}}}}{\partial \bar{b}}={\omega }_{{{{{{\rm{Er}}}}}}}\bar{b}+\frac{4{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{\hslash }\bar{b}(2{\bar{b}}^{2}-1)+4{g}_{x}{\bar{a}}_{r}\bar{b}-2{g}_{z}{\bar{a}}_{i}\frac{1-2{\bar{b}}^{2}}{\sqrt{1-{\bar{b}}^{2}}}=0.$$

(124)

Solving the first two equations, the ${{{{{\rm{Fe}}}}}}^{3+}$ qAFM magnon amplitudes can be expressed as

$${\bar{a}}_{r}=-\frac{{g}_{x}}{{\omega }_{\pi }}(2{\bar{b}}^{2}-1),$$

(125)

$${\bar{a}}_{i}=\frac{2{g}_{z}}{{\omega }_{\pi }}\bar{b}\sqrt{1-{\bar{b}}^{2}}.$$

(126)

By substituting these expressions into Eq. (124), the following equation for the ${{{{{\rm{Er}}}}}}^{3+}$ amplitude can be obtained.

$$\left[{\omega }_{{{{{{\rm{Er}}}}}}}-\frac{4{{g}_{z}}^{2}-4{{g}_{x}}^{2}}{{\omega }_{\pi }}-\frac{4{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{\hslash }\right.\,+\,\left.\left(\frac{8{{g}_{z}}^{2}-8{{g}_{x}}^{2}}{{\omega }_{\pi }}+\frac{8{z}_{{{{{{\rm{Er}}}}}}}{J}_{{{{{{\rm{Er}}}}}}}}{\hslash }\right){\bar{b}}^{2}\right]\bar{b}=0.$$

(127)

For a real non-zero value of $\bar{b}$ to exist, the parameters must satisfy Eq. (22).