Abstract
Unconventional superconductors have Cooper pairs with lower symmetries than in conventional superconductors. In most unconventional superconductors, the additional symmetry breaking occurs in relation to typical ingredients such as strongly correlated Fermi liquid phases, magnetic fluctuations, or strong spin-orbit coupling in noncentrosymmetric structures. In this article, we show that the time-reversal symmetry breaking in the superconductor LaNiGa2 is enabled by its previously unknown topological electronic band structure, with Dirac lines and a Dirac loop at the Fermi level. Two symmetry related Dirac points even remain degenerate under spin-orbit coupling. These unique topological features enable an unconventional superconducting gap in which time-reversal symmetry can be broken in the absence of other typical ingredients. Our findings provide a route to identify a new type of unconventional superconductors based on nonsymmorphic symmetries and will enable future discoveries of topological crystalline superconductors.
Similar content being viewed by others
Introduction
The combination of superconductivity with topology is expected to exhibit new types of quasiparticles such as non-Abelian Majorana zero modes1,2, or fractional charge and spin currents3. Experimental realization of topological superconductivity can also provide new platforms for fault-tolerant quantum computation technologies4. Topological superconductivity can be artificially engineered in hybrid structures5,6,7,8,9 or it can exist intrinsically in certain unconventional superconductors10,11,12,13,14,15. In most intrinsic topological superconductors, the unconventional nature of superconductivity originates from the proximity to magnetic instabilities or strong electronic correlations15. Regardless of how the topological superconducting state is produced, it is well established that there is a vital connection between a material’s symmetries, broken and preserved, and the resulting topology16,17,18,19,20.
We report that the time-reversal symmetry-breaking superconductor LaNiGa2 derives its unconventional superconducting pairing from the previously unknown existence of Dirac lines and Dirac loop in the normal state. These features are pinned at the Fermi energy where they impact low energy properties including superconductivity. The rich topology of the electronic structure originates from the nonsymmorphic symmetry that guarantees band degeneracies, which in turn, enable interband and/or complex superconducting order parameters that can break time-reversal symmetry. Our results illustrate a novel method towards realizing intrinsic (single-material) topological superconductivity wherein the underlying space group symmetry intertwines the topology with the unconventional superconductivity.
The centrosymmetric superconductor LaNiGa2 was previously known to break time-reversal symmetry when it becomes superconducting below Tsc = 2 K21. Subsequent penetration depth, specific heat, and upper critical field studies showed nodeless multigap behavior22, in contradiction with possible single-band spin-triplet pairing22,23. All previous experimental investigations were limited to polycrystalline samples and theoretical considerations were based on the previously reported symmorphic Cmmm (No. 65) space group24. We reveal that single-crystal X-ray diffraction (SCXRD) analysis improves upon previous powder X-ray diffraction (PXRD) work and properly assigns LaNiGa2 to a nonsymmorphic Cmcm (No. 63) unit cell. Difficulty discerning the difference between Cmmm and Cmcm from PXRD data has historical precedent25,26.
The nonsymmorphic symmetries of this new unit cell transform the kz = π/c plane of the Brillouin zone (BZ) into a nodal surface, which hosts fourfold degenerate bands27,28. Here, the band degeneracies form two distinct Dirac crossings between two sets of Fermi surfaces (FSs) precisely at the Fermi level (EF), independent of chemical potential position. There are fluted lines closed by BZ periodicity and a closed loop. Of special note is that the Dirac loop contains two points which are protected against splitting from spin-orbit coupling (SOC). These “touchings” are shown from our band structure calculations, along with angle-resolved photoemission spectroscopy (ARPES) data.
We note that, among non-magnetic materials and outside of intercalated Bi2Se3, no other time-reversal symmetry breaking superconductor has been shown to exhibit a topological band structure (see Supplementary Note 12 and Table S4). Thus making LaNiGa2 unique amongst this small set of bulk superconductors. Lastly, we discuss the impact of the topology of LaNiGa2 as a natural platform for interband pairing and/or complex superconducting order parameter that can break time-reversal symmetry.
Results and discussion
Structural characterization
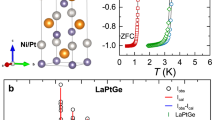
Single-crystalline samples of LaNiGa2 were successfully grown with a Ga deficient self-flux technique. Details about the growth are contained within the “Methods” section below. Highly reflective, plate-like crystals were produced as shown in Fig. 1c.
a Compiled precession image of the hk0 plane from a single-crystal X-ray diffraction data set of LaNiGa2. Overlaid are the predicted diffraction spots with a normalized intensity above 0.1. The diffraction spots are normalized to the 131 diffraction peak. The diffraction spots which are expected for both the original Cmmm24 and our newly proposed Cmcm structures are denoted by the teal squares. The spots which are only expected for the Cmmm and Cmcm structures are shown by the purple circles and orange diamonds, respectively. b A normalized linear cut of the hk0 precession image along the \(h\overline{9}0\), shown by the red triangles in a. The expected intensities for the Cmmm and the Cmcm structures are shown as the purple dashes and the orange crosses, respectively. All intensity data, raw and theoretical, from a and b are normalized to the 131 peak. c Picture of representative single-crystal samples of LaNiGa2. The plate-like samples have the b-axis normal to the surface of the crystals. d A complete superconducting transition is observed with zero-field specific heat capacity (C/T) and zero-field cooled magnetic susceptibility (M/H) data, shown by the red and blue curves, respectively. The susceptibility was collected with an external magnetic field of 1 mT. e The Cmcm unit cell for LaNiGa2.
SCXRD data were collected on several samples and each data set resolved to a LaNiGa2 unit cell with a Cmcm space group (see Supplementary Notes 1 and 2, Fig. S2, and Tables S1 and S2). Given the inherent similarities between the previously reported Cmmm structure24 in real space, nearly all diffraction spots within the reciprocal space are predicted by both structures (see Fig. S1 for PXRD LeBail fittings using each structure and Fig. S3 for a real space comparison between the two structures). This is especially true for the most intense, low-angle diffraction spots. There are, however, a few observable differences amongst the weakly-diffracting high-angle spots that are sufficient to differentiate the two structures, as shown from the compiled hk0 precession image in Fig. 1a.
These discrepancies are highlighted by the differing expected intensities along the normalized \(h\bar{9}0\) line, red arrows in Fig. 1a, between the two structures (Fig. 1b). It should be noted that all peaks along this line from both models are displayed, regardless of intensity. The insufficient intensities for the Cmmm model at these high-angle spots reveal that the previously reported structure inadequately matches the observed diffraction data for this material. The data indicates that the more accurate structure for this material is that of the Cmcm space group.
While this new space group remains centrosymmetric, it adds nonsymmorphic symmetries: a c glide plane perpendicular to the b-axis and a 21 screw axis, \({{{{{{{{\mathcal{S}}}}}}}}}_{2}^{z}\), along the c-axis. First we will discuss the influence of the new symmetry operations on the electronic structure and later we will examine the ramifications on the superconducting pairing state.
Electronic structure and ARPES data
Despite the new structure, Fig. 2a shows that there remain five FSs23,29. Highlighted with the previous space group, there are several regions within the BZ where pairs of FSs are parallel and quasi-degenerate22,23. A crucial difference now is that the nonsymmorphic symmetry operations force the previously quasi-degenerate FS pairs to “touch” on the kz = π/c plane (red plane) in the absence of SOC, turning this plane into a nodal surface27 (see Supplementary Note 11 and the band structures along T − Z − A in Fig. S11 to see bands become degenerate in the Cmcm structure). The combination of \({{{{{{{{\mathcal{S}}}}}}}}}_{2}^{z}\), parity operation, and time-reversal symmetry force bands on the nodal surface to be fourfold degenerate (for the derivation and for the differences in the Cmmm and Cmcm band structures see Supplementary Note 8). This symmetry-enforced degeneracy results in two disjoint sets of Dirac crossings directly at the Fermi level. Both are between bulk bands crossing the nodal surface: fluted lines across the BZ face between FS4/5 and a closed loop between FS2/3 (highlighted lines top panel Fig. 2a). That these crossings occur at the Fermi level make LaNiGa2 uncommon compared to other superconductors with topologically non-trivial band structures10,14,30,31,32,33,34,35,36,37 (see Table S4).
a The five Fermi surfaces (FSs), labeled as FS1−5, within the Brillouin zone (BZ). The Dirac lines (blue lines) and Dirac loop (green line) are highlighted on the nodal surface. The crossings along Z − T (magenta dots) are protected from spin-orbit coupling (SOC). b The BZ showing several high symmetry points and highlights the nodal surface (red plane). The green arrow, ky = 0.516*2π/b, shows where FSs 2 and 3 become degenerate on the nodal surface. The Dirac crossing is shown to remain both without c and with SOC d, where the SOC contribution to anticrossing is seen to be very small. The blue arrow shows the dispersion along kx = 0.236*2π/a without SOC e shows the Dirac lines between FSs 4 and 5. Once SOC is added f, the crossing becomes gapped at the nodal surface.
The Dirac crossings can be observed in the linear band dispersion plots without SOC along \(\overrightarrow{k}=(0,0.516\frac{2\pi }{b},{k}_{z})\) (green arrow) for the Dirac loop (Fig. 2c) and \(\overrightarrow{k}=(0.232\frac{2\pi }{a},0,{k}_{z})\) (blue arrow) for the Dirac lines (Fig. 2e). We note that small shifts of the Fermi energy will shift the k-space location of the Dirac lines and loop. However, since this is a matter of two surfaces intersecting (FS and nodal surface) and nonsymmorphic symmetry enforcement, the nodal lines will persist at the Fermi level as long as the FSs cross the nodal surface. When accounting for SOC, most band crossings become gapped (by a few to 40 meV), as pictured in Fig. 2f. Remarkably, the Dirac points between FS2/3 survive along the Z − T symmetry line under SOC, as seen in Fig. 2d, creating two true-Dirac points at the Fermi level. This protected feature results from the presence of the mirror reflection, \({{{{{{{{\mathcal{M}}}}}}}}}_{x}\), along the Z − T line, therefore, remaining fourfold degenerate even when accounting for SOC (see Supplementary Note 8 for derivation), illustrating that this degeneracy lies precisely at EF, and is robust rather than accidental.
Single crystals of LaNiGa2 do not naturally cleave perpendicular to the crystallographic c-axis, making a direct observation of the Dirac dispersion by ARPES measurements challenging. However, with a photon energy of 144 eV we can probe the ky = 0 plane and confirm the presence of the band touchings (see Supplementary Note 10 and Fig. S10). Figure 3a shows the constant energy map centered at EF and reveals the most prominent features of the spectra: the ruffled cylindrical bands centered on the BZ corners. Given that, near the corner of the BZ, the calculated FSs are very close to each other (see Fig. 3b), it is difficult to discern which bands are observed in the ARPES measurements from just this plane. Overlaid on Fig. 3c are the respective DFT band calculations (dashed lines) which reveal that the most prominent bands in the ARPES data originate from the bands associated with FS2 and FS3. The three parallel horizontal cuts on and near the nodal surface show the band dispersion plots at and below EF (Fig. 3c). The green line, spectrum 2, represents the cut exactly on the nodal surface, while the blue, spectrum 1, and red, spectrum 3, lines are parallel cuts in the first and second BZs, respectively.
Angle-resolved photoemission spectroscopy (ARPES) characterization of LaNiGa2. a Constant energy map with an integration window of ±10 meV around the Fermi energy, EF. The black dotted line indicates the boundary of the Brillouin zone in the ky = 0 plane. The blue, green, and red solid horizontal lines indicate cuts (1), (2), and (3) in panel c, respectively. b Calculated Fermi surfaces (FSs) on the ky = 0 plane with the colors corresponding to FSs in Fig. 2a. See Fig. S10c for an overlay of the ARPES and the calculated FSs on the ky = 0 plane. c Energy vs momentum spectra along cuts indicated in a. The dotted lines are the overlay of electronic structure calculations and the colors show which FSs are associated with each band. The gray bands are low energy bands which do not cross EF. d Momentum distribution curves (MDCs) at EF from the cuts in panel c. Spectra are fit to one (two) Lorentzian peaks (dotted black curve) for cuts 2 (1,3), with a Gaussian background centered on kx = 0. The black curves below the experimental data are the individual Lorentzian peaks marking where the bands cross EF. The peak width for the Lorentzian fit on 2 is a free fitting parameter and fixed to that width for the peaks of cuts 1 and 3.
Each of these cuts was integrated within 50 meV of EF to produce momentum distribution curves (MDCs) shown in Fig. 3d. On the nodal surface, spectrum 2 shows a single clear peak representing the degeneracy of FS2/3. Off the nodal surface, the MDCs for spectra 1 and 3 show that FS2 and FS3 separate and are no longer degenerate. Thus providing direct evidence for the band degeneracy between FS2/3 on the nodal surface. As mentioned above, we expect SOC to split the FS2/3 crossing on the ky = 0 plane of the nodal surface. We note, however, that the SOC gap cannot be resolved because the peaks have a smaller calculated momentum separation than the fitted experimental widths. This result is further evidence for the minimal impact of SOC on the electronic structure of LaNiGa2 in the normal state.
In the normal state and in the absence of SOC, the Cmcm space group makes LaNiGa2 a topological nodal line metal. The line (or loop) is topological38. Nodal lines (lines or loops of degeneracies) in band structures have been found to be rather common39,40. However, LaNiGa2 is so far unique in having the nodal lines lie precisely at the Fermi level. However, this confluence of bands will occur in any nonsymmorphic metal with FSs crossing the nodal surface where bands are guaranteed to be orbitally degenerate.
Pairing model and quasiparticles
Now we examine the consequences of the Cmcm space group assignment for the superconducting state. LaNiGa2 has low symmetry and previous symmetry analysis based on the D2h point group revealed only 4 possible gap functions that break time-reversal symmetry21,41. All of them have nodes inside the BZ, which is incompatible with thermodynamic measurements on polycrystals22, as well as our heat capacity measurements on single crystals which indicate nodeless fully gapped superconductivity (Fig. 1d). The presence of nonsymmorphic symmetries modifies the nodal behavior on the kz = π/c plane with or without SOC (see our classification in Supplementary Note 9), but does not provide a scenario for the absence of nodes inside the BZ. The five FSs in Fig. 2 indicate that the full FS is large and pervasive throughout the zone, thus any superconducting gap nodes in a direction \(\hat{k}\) would produce a gap node on the FS and thus be detectable in thermodynamic measurements. This observation limits the possible superconducting states to A1g with or without SOC (see Supplementary Note 9), but these states do not break time-reversal symmetry. The superconducting properties of LaNiGa2 cannot be understood without involving interband pairing22,23. The topological properties of the normal state now provide a natural platform for such unconventional superconductivity.
As mentioned earlier, the Dirac lines and Dirac loop are gapped by SOC, except for the true-Dirac points surviving on the Z − T line where SOC vanishes. A feature of more interest for the superconducting phase is that, unlike the case for conventional FSs, in Dirac (or Weyl) metals interband transitions persist all the way to zero energy. Any single-band model breaks down, and a two-band model is a minimal model42. LaNiGa2 thereby becomes an intrinsically two, degenerate and topological, band superconductor.
If the interband pairs are symmetric in the band index, then the Cooper-pair wave function will have the same symmetry as the intraband pairs do, s-wave will be spin-singlet and p-wave will be spin-triplet. But if the interband pairs are antisymmetric in the band index, we can have s-wave spin-triplet, or p-wave spin-singlet pairing while still satisfying the overall fermionic nature required for a superconducting order parameter43. If both symmetric and antisymmetric pairing exists simultaneously on the nodal surface (weak SOC) or on the true-Dirac points on the Z − T line (strong SOC), time-reversal symmetry could be broken in two ways: the band (orbital) channel or the spin channel.
In the band-orbital channel, two-gap functions (for example s-wave spin singlet \({A}_{1g}^{s}\) and s′-wave spin-triplet \({A}_{1g}^{t}\)) could form a complex combination similar to \(s+is^{\prime}\) to break time-reversal symmetry. Another possibility is to combine several triplet components. For example, the \({B}_{1g}^{t}\) triplet will be split by SOC into Ag, B2g, and B3g. The complex combination could also break time-reversal symmetry. However, a first-order transition or multiple transitions are expected in these cases22, but there is no such evidence in our heat-capacity measurements (Fig. 1d and Fig. S7). Time-reversal symmetry breaking in the band-orbital channel is therefore unlikely.
Because of the possibility of s-wave spin-triplet pairing on the Dirac lines, loop, or points, time-reversal symmetry could also be broken in the spin channel from an internally antisymmetric nonunitary triplet pairing (INT) state23. The power of symmetry analysis is remarkable in the sense that, even with the incorrect space group, the correct point group (D2h) already led to the conclusion that the INT pairing is the only reasonable solution22,23. However, the necessary degeneracy was not identified because of the wrong space group. An orbital-singlet equal spin pairing has also been proposed for doped Dirac semimetals44. The INT model has also been proposed to explain time-reversal symmetry breaking and fully gapped superconductivity in LaNiC223,45,46. While LaNiGa2 and LaNiC2 are compositionally related, our results on LaNiGa2 highlight new significant differences between the two compounds. LaNiC2 has a symmorphic and noncentrosymmetric space group (Amm2, No. 38), and thus far no topological band crossing has been reported45,47,48,49,50,51,52. In addition, electrical resistivity measurements under pressure showed the proximity to a different state characterized by a high-energy scale53, and magnetic penetration-depth measurements under pressure suggested the proximity of a quantum critical point in LaNiC254. Further studies remain needed on both materials to confirm the validity of the INT model, and the mechanism of time-reversal symmetry breaking. Our discovery of symmetry-imposed band crossing, even under SOC, in LaNiGa2, reinforce the relevance of the INT model for this compound, as well as for other nonsymmorphic superconductors.
Breaking of time-reversal symmetry requires a nonunitary triplet pairing potential \(\hat{{{\Delta }}}=i({{{\Delta }}}_{o}\tilde{{{{{{{{\boldsymbol{\eta }}}}}}}}}\cdot \tilde{{{{{{{{\boldsymbol{\sigma }}}}}}}}}){\sigma }_{y}\otimes i{\tau }_{y}\) where the tensor products include the first (spin, σ matrices) channel σ = ↑, ↓ and the second (band, τ matrices) channel, with the bands labeled by m = ± being degenerate along the Dirac loops, taken to be at k⊥ = 0.
Note that the spontaneous vector field \({{{\Delta }}}_{o}\overrightarrow{\eta }\) couples to spin like a magnetic moment. The pairing matrix describes triplet pairing but is antisymmetric in the band channel (iτy) to ensure the fermionic antisymmetry of the pair wave function22. The experimentally observed time-reversal symmetry breaking is ensured by the non-unitarity, which is characterized by a nonvanishing real vector \(\overrightarrow{\omega }=i(\overrightarrow{\eta }\times {\overrightarrow{\eta }}^{* })\) which satisfies \(| \overrightarrow{\omega }| \le | \overrightarrow{\eta }{| }^{2}=1\). A noteworthy difference with previous INT proposals22,23 is that the true two-band situation in LaNiGa2 is enforced by symmetry, and persists in the Bogoliubov - de Gennes (BdG) quasiparticle bands. Accounting for the linear band coupling βk⊥ away from the nodal surface, the dispersion of the eight BdG quasiparticles (two bands, two spins, electrons and holes) becomes
with degenerate eigenvalues on the nodal surface of \(| {{{\Delta }}}_{o}| \sqrt{1\pm | \overrightarrow{\omega }| }\).
The spectrum, shown in Fig. 4, illustrates the 8-band behavior versus the strength of non-unitarity. The nonsymmorphic operations guarantee that pairs of BdG quasiparticle bands persist in “sticking together” on both sides of the gap at k⊥ = 0, thereby retaining topological character. However, now massive points of degeneracy arise in the BdG band structure, unlike the bands of Ghosh et al.23 which retain no degeneracies and hence no topological character. The linear band mixing results in the gap edges lying slightly away from the plane k⊥ = 0. Unit values of \(| \overrightarrow{\omega }|\) lead to gaplessness, with unusual Weyl dispersion of the BdG quasiparticles. The measured magnetic moment of 0.012 μB, if from spin, corresponds to a small conventional band exchange splitting Δex = m/N(EF) = 1.8 meV. This splitting is comparable to (larger than) the superconducting gap 2Δo ~ 3.5 − 4kBTc ~ 0.7 meV, suggesting it may be central to the exotic pairing mechanism.
Bogoliubov-de Gennes (BdG) quasiparticle bands near the Dirac point for three values of the \(| \overrightarrow{\omega }| =\)a 0.1, b 0.8, and c 1.0 resulting in gapped, weakly nonunitary, and gapless fully nonunitary states, respectively. Energy units correspond to Δo = 0.7 meV, v = 500 and β = 100, see Eq. (1).
In contrast to the INT state, conventional p-wave spin-triplet superconductivity is expected to lead to high upper critical fields, because equal spin pairing is not subject to Pauli limiting, and because most proposed p-wave superconductors are heavy fermion systems with high orbital limit55,56,57,58,59,60. LaNiGa2, however, is not a heavy-fermion material (γn = 14.1 mJ mol−1 K−2) and interband pairing is suppressed by the application of a strong magnetic field. Thus the upper critical field in LaNiGa2 remains low (see Fig. S9), even though time-reversal symmetry breaking superconductivity was observed at zero field in μSR experiments.
Our findings reveal that LaNiGa2 is a topological nonsymmorphic crystalline superconductor61,62,63,64. The normal state electronic structure features Dirac lines and Dirac loop at the Fermi energy enforced by nonsymmorphic symmetries, as well as true-Dirac points that retain their degeneracy under SOC. These findings are expected to be common to a large number of materials with similar crystalline symmetries. In general, when topological materials become superconducting, the superconducting state is unconventional. LaNiGa2 was previously reported as a time-reversal symmetry-breaking superconductor with evidence for a fully gapped superconducting state, but the topological properties were unknown. The topological character now provides a natural platform for the INT state to exist. Further experiments and theoretical proposals are necessary to further elucidate the time-reversal symmetry breaking mechanism.
Because of the possibility of a fully gapped behavior mimicking conventional superconductivity, many other materials could have been overlooked. Our results on LaNiGa2 motivate the need to characterize the time-reversal symmetry, with zero-field μSR experiments or Kerr effect, of other crystalline topological metals18,19,20 that become superconducting. While LaNiGa2 is the only intrinsic topological material with nodal features at the Fermi level which has been experimentally shown to break time-reversal symmetry in the superconducting state without any overlapping magnetic fluctuations or ordering, other materials could soon be discovered based on our findings.
Methods
Sample preparation
Single-crystalline samples of LaNiGa2 were grown with a Ga deficient self-flux technique. Ga (99.99999%) atomic composition ranged from 32–36% Ga and the remaining percentage was equally split between La (99.996%) and Ni (99.999%). Precursor ingots were first synthesized by arc melting all the elements in an argon environment. The ingots were subsequently loaded into an alumina Canfield crucible set65 and sealed in an evacuated quartz ampule. The reaction was heated up to 1150 °C and held at temperature for five hours. The reaction was slowly cooled down to 800 °C over 100 h and then quickly centrifuged. Overall, high-quality single crystals were synthesized and characterized (see Supplementary Notes 3–7, Figs. S4–9, and Table S3).
It was noted that different starting Ga percentages did not produce a noticeable difference in crystal quality, as evaluated by the residual resistivity ratio. However, larger single crystals (up to 7 mm) were obtained in the more Ga deficient syntheses. Additionally, it was also discovered that the superconducting properties were highly sensitive to oxidation throughout the reaction. Lastly, in more Ga deficient growths, below 32% Ga, no crystals were obtained when the reactions were centrifuged at 800 °C.
Crystal Structure Determination
Each synthesis was checked to produce the desired phase by PXRD performed on a Rigaku Miniflex with a Cu X-ray source. LeBail fitting was performed using both the Cmmm and Cmcm space groups in GSAS-II66. Selected samples were aligned using a Laue X-ray diffractometer to distinguish the a- and c-axes directions. SCXRD data were collected on several samples of LaNiGa2 at 100 K using a sealed-tube Mo X-ray source on a Bruker Photon 100 CMOS X-ray diffractometer (Bruker AXS). Across several crystals, obvious twin domains were observed within diffraction space; although not all samples exhibited this. Regardless of the presence of multiple domains, initial unit cell parameters for each sample suggested a C-orthorhombic unit cell that matches well with previous reports: a = 4.2808 Å, b = 17.466 Å, and c = 4.25778 Å (ICSD Nos. 634496 and 634508)24. The collected frames were integrated using SAINT within APEX3 version 2017.3. For every crystal that was diffracted, XPREP suggested the centrosymmetric space group Cmcm (No. 63) and the structure was refined down to a R value of 0.0288 using SHELXL-2018/367. See Tables S1 and S2 for further crystallographic information and Supplementary Data 1 for the CIF file. This Cmcm structure is of the \({{{{{{{{\rm{BaCuSn}}}}}}}}}_{2}\) structure type (ICSD No. 58648). The precession image was compiled within APEX3. Structure factors for the precession image models were calculated from Visualization for Electronic and Structural Analysis (VESTA) Ver.3.4.768.
Physical property measurements
Low-frequency AC resistivity measurements were measured using a four-probe technique on a Quantum Design Physical Property Measurement System (PPMS) from 300–1.8 K. The PPMS was also used to obtain heat capacity data for selected samples using a relaxation technique down to 1.8 K. A 3He insert for the PPMS allowed for measurements of AC resistivity and heat capacity down to 0.4 K. Magnetization measurements were collected in a Quantum Design DC Magnetic Property Measurement System down to 1.85 K.
Electronic structure methods
Density functional-based electronic structures were produced by the precise linearized augmented planewave code Wien2k69,70 using the generalized gradient functional for exchange and correlation. The atomic coordinates used for these calculations were the same as listed above. The sphere sizes were, in Bohr: La, 2.50; Ni, 2.40; Ga, 2.12. The plane-wave cutoff Kmax was determined by RKmax = 7, and the k-point mesh for self-consistency was 14 × 14 × 14. Exchange and correlation contributions to the energy and potential were included by using the generalized gradient approximation functional71. Effects of spin-orbit coupling were included by using second variation method as implemented in WIEN2k.
ARPES measurements
ARPES measurements were performed at Stanford Synchrotron Radiation Lightsource National Laboratory beamline 5–2 using a Scientia DA30 electron spectrometer. Samples were cleaved in-situ at 20 K and with a pressure better than 5 × 10−11 Torr. The nominal resolution for the ARPES measurements was ΔE = 20 meV, the beam spot size was approximately 21μm × 36μm.
Data availability
The data that support the findings of this study are available from the authors upon reasonable request.
References
Kopnin, N. B. & Salomaa, M. M. Mutual friction in superfluid 3He: effects of bound states in the vortex core. Phys. Rev. B 44, 9667 (1991).
Read, N. & Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum hall effect. Phys. Rev. B 61, 10267 (2000).
Volovik, G. E. & Yakovenko, V. M. Fractional charge, spin and statistics of solitons in superfluid 3He film. J. Phys. Condens. Matter 1, 5263 (1989).
Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2 (2003).
Fu, L. & Kane, C. L. Superconducting proximity effect and majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Mourik, V. et al. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003 (2012).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602 (2014).
Fatemi, V. et al. Electrically tunable low-density superconductivity in a monolayer topological insulator. Science 362, 926 (2018).
Sajadi, E. et al. Gate-induced superconductivity in a monolayer topological insulator. Science 362, 922 (2018).
Wray, L. A. et al. Observation of topological order in a superconducting doped topological insulator. Nat. Phys. 6, 855 (2010).
Kobayashi, S., Yanase, Y. & Sato, M. Topologically stable gapless phases in nonsymmorphic superconductors. Phys. Rev. B 94, 134512 (2016).
Kidwingira, F., Strand, J. D., Van Harlingen, D. J. & Maeno, Y. Dynamical superconducting order parameter domains in Sr2RuO4. Science 314, 1267 (2006).
Pustogow, A. et al. Constraints on the superconducting order parameter in Sr2RuO4 from oxygen-17 nuclear magnetic resonance. Nature 574, 72 (2019).
Zhang, P. et al. Observation of topological superconductivity on the surface of an iron-based superconductor. Science 360, 182 (2018).
Ran, S. et al. Nearly ferromagnetic spin-triplet superconductivity. Science 365, 684 (2019).
Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Kitaev, A. Periodic table for topological insulators and superconductors. AIP Confer. Proc. 1134, 22 (2009).
Tang, F., Po, H. C., Vishwanath, A. & Wan, X. Comprehensive search for topological materials using symmetry indicators. Nature 566, 486 (2019).
Vergniory, M. G. et al. A complete catalogue of high-quality topological materials. Nature 566, 480 (2019).
Zhang, T. et al. Catalogue of topological electronic materials. Nature 566, 475 (2019).
Hillier, A. D., Quintanilla, J., Mazidian, B., Annett, J. F. & Cywinski, R. Nonunitary triplet pairing in the centrosymmetric superconductor LaNiGa2. Phys. Rev. Lett. 109, 097001 (2012).
Weng, Z. F. et al. Two-gap superconductivity in LaNiGa2 with nonunitary triplet pairing and even parity gap symmetry. Phys. Rev. Lett. 117, 027001 (2016).
Ghosh, S. K. et al. Quantitative theory of triplet pairing in the unconventional superconductor LaNiGa2. Phys. Rev. B 101, 100506 (2020).
Yarmolyuk, Y. & Grin, Y. Crystal-structure of the rniga2 compounds (r=la, ce, pr, nd, sm, gd). Dopovidi Akademii nauk Ukrainskoi RSR, Seriya A: Fiziko-Matematichni ta Tekhnichni Nauki 44, 71 (1982).
Makarov, E. S. & Bykov, V. N. Crystal structure of compounds of uranium with germanium. Sov. Phys. Crystallogr. 4, 164 (1959).
Oikawa, K., Kamiyama, T., Asano, H., Onuki, Y. & Kohgi, M. Crystal structure of UGe2. J. Phys. Soc. Jpn. 65, 3229 (1996).
Liang, Q.-F., Zhou, J., Yu, R., Wang, Z. & Weng, H. Node-surface and node-line fermions from nonsymmorphic lattice symmetries. Phys. Rev. B 93, 085427 (2016).
Wu, W. et al. Nodal surface semimetals: theory and material realization. Phys. Rev. B 97, 115125 (2018).
Singh, D. J. Electronic structure and fermiology of superconducting laniga2. Phys. Rev. B 86, 174507 (2012).
Zhao, L. et al. Emergent surface superconductivity in the topological insulator Sb2Te3. Nat. Commun. 6, 8279 (2015).
Sakano, M. et al. Topologically protected surface states in a centrosymmetric superconductor β-PdBi2. Nat. Commun. 6, 8595 (2015).
Neupane, M. et al. Observation of the spin-polarized surface state in a noncentrosymmetric superconductor BiPd. Nat. Commun. 7, 13315 (2016).
Guan, S.-Y. et al. Superconducting topological surface states in the noncentrosymmetric bulk superconductor PbTaSe2. Sci. Adv. 2, e1600894 (2016).
Du, G. et al. Drive the Dirac electrons into Cooper pairs in SrxBi2Se3. Nat. Commun. 8, 14466 (2017).
Jin, K.-H. et al. Topological superconducting phase in high-Tc superconductor MgB2 with Dirac-nodal-line fermions. npj Comput. Mater. 5, 57 (2019).
Fang, Y. et al. Discovery of superconductivity in 2M WS2 with possible topological surface states. Adv. Mater. 31, 1901942 (2019).
Gao, Y., Guo, P.-J., Liu, K. & Lu, Z.-Y. RRuB2(R = Y, Lu), topological superconductor candidates with hourglass-type Dirac ring. Phys. Rev. B 102, 115137 (2020).
Allen, P. B. & Pickett, W. E. Accidental degeneracy in k-space, geometrical phase, and the perturbation of π by spin-orbit interactions. Physica C: Supercond. Appl 549, 102 (2018).
Herring, C. Accidental degeneracy in the energy bands of crystals. Phys. Rev. 52, 365 (1937).
Jin, H.-S., Song, Y.-J., Pickett, W. E. & Lee, K.-W. Noncentrosymmetric compensated half-metal hosting pure spin weyl nodes, triple nodal points, nodal loops, and nexus fermions. Phys. Rev. Mater. 3, 021201 (2019).
Annett, J. F. Symmetry of the order parameter for high-temperature superconductivity. Adv. Phys. 39, 83 (1990).
Yanase, Y. Nonsymmorphic Weyl superconductivity in UPt3 based on E2u representation. Phys. Rev. B 94, 174502 (2016).
Black-Schaffer, A. M. & Honerkamp, C. Chiral d-wave superconductivity in doped graphene. J. Phys. Condensed Matter 26, 423201 (2014).
Kobayashi, S. & Sato, M. Topological superconductivity in Dirac semimetals. Phys. Rev. Lett. 115, 187001 (2015).
Csire, G., Ujfalussy, B. & Annett, J. F. Nonunitary triplet pairing in the noncentrosymmetric superconductor LaNiC2. Eur. Phys. J. B 91, https://doi.org/10.1140/epjb/e2018-90095-7 (2018).
Sundar, S. et al. Two-gap time reversal symmetry breaking superconductivity in noncentrosymmetric LaNiC2. Phys. Rev. B 103, 014511 (2021).
Subedi, A. & Singh, D. J. Electron-phonon superconductivity in noncentrosymmetric LaNiC2: first-principles calculations. Phys. Rev. B 80, 092506 (2009).
Laverock, J., Haynes, T. D., Utfeld, C. & Dugdale, S. B. Electronic structure of RNiC2 (R = Sm, Gd, and Nd) intermetallic compounds. Phys. Rev. B 80, 125111 (2009).
Hase, I. & Yanagisawa, T. Electronic Structure of RNiC2 (R = La, Y, and Th). J. Phys. Soc. Jpn. 78, 084724 (2009).
Yanagisawa, T. & Hase, I. Nonunitary triplet superconductivity in the noncentrosymmetric rare-earth compound LaNiC2. J. Phys. Soc. Jpn. 81, SB039 (2012).
Wiendlocha, B., Szczȩśniak, R., Durajski, A. P. & Muras, M. Pressure effects on the unconventional superconductivity of noncentrosymmetric LaNiC2. Phys. Rev. B 94, 134517 (2016).
Zhang, Y., Usman, T., Tao, X.-M. & Tan, M.-Q. A first-principle calculation and de Haas-van Alphen effect simulation in superconductor LaNiC2. J. Supercond. Novel Magnet. 31, 995 (2018).
Katano, S. et al. Anomalous pressure dependence of the superconductivity in noncentrosymmetric LaNiC2: Evidence of strong electronic correlations. Phys. Rev. B 90, 220508 (2014).
Landaeta, J. F., Subero, D., Machado, P., Honda, F. & Bonalde, I. Unconventional superconductivity and an ambient-pressure magnetic quantum critical point in single-crystal LaNiC2. Phys. Rev. B 96, 174515 (2017).
Sheikin, I. et al. Anisotropy and pressure dependence of the upper critical field of the ferromagnetic superconductor UGe2. Phys. Rev. B 64, 220503 (2001).
Aoki, D., Ishida, K. & Flouquet, J. Review of U-based ferromagnetic superconductors: comparison between UGe2, URhGe, and UCoGe. J. Phys. Soc. Jpn. 88, 022001 (2019).
Levy, F., Sheikin, I. & Huxley, A. Acute enhancement of the upper critical field for superconductivity approaching a quantum critical point in URhGe. Nat. Phys. 3, 460 (2007).
Aoki, D. et al. Extremely large and anisotropic upper critical field and the ferromagnetic instability in UCoGe. J. Phys. Soc. Jpn. 78, 113709 (2009).
Knebel, G. et al. Field-Reentrant superconductivity close to a metamagnetic transition in the heavy-fermion superconductor UTe2. J. Phys. Soc. Jpn. 88, 063707 (2019).
Shivaram, B. S., Rosenbaum, T. F. & Hinks, D. G. Unusual angular and temperature dependence of the upper critical field in UPt3. Phys. Rev. Lett. 57, 1259 (1986).
Varjas, D., de Juan, F. & Lu, Y.-M. Bulk invariants and topological response in insulators and superconductors with nonsymmorphic symmetries. Phys. Rev. B 92, 195116 (2015).
Wang, Q.-Z. & Liu, C.-X. Topological nonsymmorphic crystalline superconductors. Phys. Rev. B 93, 020505 (2016).
Shiozaki, K., Sato, M. & Gomi, K. Topology of nonsymmorphic crystalline insulators and superconductors. Phys. Rev. B 93, 195413 (2016).
Yanase, Y. & Shiozaki, K. Möbius topological superconductivity in UPt3. Phys. Rev. B 95, 224514 (2017).
Canfield, P. C., Kong, T., Kaluarachchi, U. S. & Jo, N. H. Use of frit-disc crucibles for routine and exploratory solution growth of single crystalline samples. Philos. Mag. 96, 84 (2016).
Toby, B. H. & Von Dreele, R. B. GSAS-II: the genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 46, 544 (2013).
Sheldrick, G. M. Crystal structure refinement with shelxl. Acta Crystallogr. Sect C 71, 3 (2015).
Momma, K. & Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272 (2011).
Blaha, P. et al. WIEN2k: An augmented plane wave plus local orbitals program for calculating crystal properties (Techn. Universität, Vienna, 2019)
Blaha, P. et al. WIEN2k: an APW+lo program for calculating the properties of solids. J. Chem. Phys. 152, 074101 (2020).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Acknowledgements
We thank Rahim Ullah, Li Si, Jianxin Zhu, Junren Shi, Shingo Yonezawa, Makariy Tanatar, Ruslan Prozorov, Christopher Perez, Donhui Lu, and Makoto Hashimoto for helpful discussions. The synthesis and characterizations were supported by the UC Laboratory Fees Research Program (LFR-20-653926). V.T. also acknowledges funding from GIMRT (19F0502). The ARPES work in this manuscript was supported by AFOSR Grant No. FA9550-18-1-0156. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The work of S. S. is supported by JST CREST Grant No. JPMJCR19T2. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. W.E.P and Y.Q. acknowledge support from U.S. National Science Foundation Grant DMR 1607139. Y.Q. also thank Stony Brook Research Computing and Cyberinfrastructure, and the Institute for Advanced Computational Science at Stony Brook University for access to the innovative high-performance Ookami computing system, which was made possible by National Science Foundation grant #1927880. S.M.K. and K.P.D. acknowledge support from U.S. National Science Foundation Grant DMR-2001156. K.N. and D.S.S. were supported by the NSF-REU programs PHY-1560482 and PHY-1852581.
Author information
Authors and Affiliations
Contributions
J.R.B. and V.T. conceived the project. Single-crystal synthesis work was initiated by K.N. and V.T. J.R.B. completed the synthesis and performed all X-ray crystallography, electrical resistivity, magnetic susceptibility, and heat capacity measurements with assistance from J.C.F., K.P.D., and S.M.K. for single-crystal X-ray diffraction, and P.K., D.A., V.T. for other physical property measurements. Y.Q. and W.E.P. completed the electronic structure calculations and its discussion. M.C.S., A.R., D.S.S., and I.M.V. performed the ARPES measurements and the subsequent analysis. J.R.B., M.C.S., I.M.V., W.E.P., and V.T. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Badger, J.R., Quan, Y., Staab, M.C. et al. Dirac lines and loop at the Fermi level in the time-reversal symmetry breaking superconductor LaNiGa2. Commun Phys 5, 22 (2022). https://doi.org/10.1038/s42005-021-00771-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00771-5
This article is cited by
-
Spin-triplet superconductivity in Weyl nodal-line semimetals
npj Quantum Materials (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.