Emergent colloidal currents across ordered and disordered landscapes

Abstract

Many-particle effects in driven systems far from equilibrium lead to a rich variety of emergent phenomena. Their classification and understanding often require suitable model systems. Here we show that microscopic magnetic particles driven along ordered and defective lattices by a traveling wave potential display a nonlinear current-density relationship, which arises from the interplay of two effects. The first one originates from particle sizes nearly commensurate with the substrate in combination with attractive pair interactions. It governs the colloidal current at small densities and leads to a superlinear increase. We explain such effect by an exactly solvable model of constrained cluster dynamics. The second effect is interpreted to result from a defect-induced breakup of coherent cluster motion, leading to jamming at higher densities. Finally, we demonstrate that a lattice gas model with parallel update is able to capture the experimental findings for this complex many-body system.

Introduction

Interacting particles driven above potential energy landscapes display emergent phenomena that are ubiquitous in condensed matter physics, while posing a considerable challenge in understanding their complex, out of equilibrium dynamics^1,2. Such phenomena include nonlinear current-voltage relationships, plastic or elastic deformations, depinning transitions, locking, and rectification effects. Examples have been reported in disparate systems, including vortices in type II superconductors^3,4, charge density waves^5,6, skyrmions^7,8, sliding frictional surfaces^9,10, and active matter systems^11,12.

Ensembles of polarizable colloidal particles driven across periodic potentials represent a relatively simple, yet nontrivial model system to investigate these many-particle effects. Potential landscapes for colloidal transport have been realized in the past via the use of electric^13,14,15, magnetic^16,17,18 or optical fields^19,20,21. However, previously experimental realizations have often been focused on measuring the speed and the position of a single particle^{16,22,23,24,25} or few interacting ones^26,27, or to demonstrate some technological functionality such as the controlled transport of a microscopic cargos^28,29. However, many fundamental effects arise when raising the system density and forcing the driven particles to interact^30,31. Experimental studies in this situation are scarce³², in particular for disordered energy landscapes³³, and in most of the cases, they involve the use of diffusive rather than driven particles^34,35,36.

Here we use a colloidal model system to investigate the out-of-equilibrium dynamics of particles driven across ordered and disordered traveling-wave-like energy landscapes. In our system, the disorder is induced by the presence of an increasing amount of defects that destroy the orientational symmetry of the lattice. We find that collective interactions between the moving particles lead to a nonlinear current-density relation which is reminiscent of that seen in theoretical studies of driven lattice gases³⁷ and driven Brownian motion across periodic potentials³⁸. At small densities, the colloidal current increases superlinearly, corresponding to a rise of the particle speed with density. This effect contrasts the decrease previously reported in driven systems on a magnetic landscape^17,39. We explain this phenomenon by a commensurability effect of particle clusters with the underlying landscape that causes a stronger synchronization with the energy landscape. When rising the density we find that the collective colloidal speed eventually decreases and the system approaches a jammed state. We argue that such state is induced by the break-up of the cluster motion due to the presence of defects in the lattice. To explain these observations together, we develop a lattice gas model with a parallel update of particle positions. This model is able to capture the experimental findings for both weakly and strongly disordered (i.e. large amount of defects) energy landscapes.

Results

Particle transport on magnetic substrates

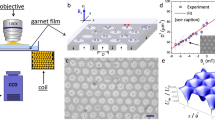
We use an ensemble of paramagnetic polystyrene microspheres of diameter d = 2.8 μm and magnetic volume susceptibility χ ~ 0.4. The particles are diluted in highly deionized water and sediment above a ferrite garnet film (FGF) with uniaxial anisotropy. Such film displays a triangular lattice with lattice constant a = 3 μm, which consists of cylindrical ferromagnetic “bubble” domains immersed in an opposite magnetized film, see Fig. 1(a). Film synthesis and growth process are described in Ref. ⁴⁰. A strong magnetic gradient, ∇ B ~ 0.5 Tm⁻¹ is used to distort the lattice and to introduce a controlled degree of spatial disorder in the bubble arrangement, see Fig. 1(b, c). We quantify such disorder by calculating both the radial distribution function g(r) and the bond correlation function g₆(r) from the bubble positions. We find that the disordered lattices display a positional order similar to the regular one, e.g., the peaks of g(r) have nearly the same locations and amplitudes, see Fig. 1(d). By analyzing the difference between the g(r) for the ordered and disordered lattices, see the inset of Fig. 1(d), we find that the relative separation arises mainly from the first peaks of g(r), which do not exceed 2 μm for the most disordered case. But, as shown in Fig. 1(e), the two phases clearly differ with respect to their orientational order. In the disordered phase, the magnetic domains arrange in a hexatic phase, characterized by an algebraic decay of ${g}_{6}(r) \sim {r}^{-{\eta }_{6}}$, which features dislocations separating regular crystalline domains. Thus, the disorder is mainly present in the orientational degrees of freedom which we quantify via the exponent η₆.

Fig. 1: Transport mechanism and magnetic landscapes.

a Illustration of paramagnetic colloids driven above a ferrite garnet film (FGF), with small arrows indicating the magnetization direction of the bubbles. One unit cell is shown in red with the 12 crystallographic directions, with lattice constant a = 3 μm. The rotating magnetic field is indicated by the arrow in the green circle with the dashed arrows indicating the sense of rotation; the particles move along the direction of the green arrow. b, c Polarization microscope images of a portion of the FGF with (b ordered (η₆ = 0.05) and c disordered (η₆ = 0.45) magnetic bubbles; the scale bar is 20 μm. Colloidal particles appear as dark circles. d Radial distribution g(r) and e g₆(r) for the ordered (blue) and disordered (red) lattices, calculated from a total area of 151 × 113 μm². The inset in g(r) illustrates the difference in absolute value between the two g(r). f Energy landscape of the magnetic lattice (z = 0.4 a) at different times from left to right; scale bar is a/2. Energy minima (dark blue) and maxima (yellow) correspond to (−2000 k_BT) and (−240 k_BT), respectively. The particle moves to the right, the red arrow indicates the direction of motion. g Normalized single-particle speed ${\bar{v}}_{x}^{{{{{{{{\rm{s}}}}}}}}}$ versus angular frequency ω from experiments (scattered data) for ordered case, η₆ = 0.05, and disordered one, η₆ = 0.45; η₆ denotes the exponent of the bond correlation function g₆(r). Continuous lines are fits to the synchronous and asynchronous regimes and yield a critical frequency of ω_c = 37.3 rad s⁻¹. The down-pointing arrow indicates the location of ω_c = 50.3 rad s⁻¹. The experimental data are averaged over different independent measurements, and the error bars (inside the orange circles) indicate the standard error, error bars in the squares are smaller than the symbols.

We induce a directed particle current by applying a magnetic field elliptically polarized and rotating in the xz plane with angular frequency ω, ${{{{{{{\boldsymbol{H}}}}}}}}\equiv (-{H}_{x}\cos (\omega t),0,{H}_{z}\sin (\omega t))$. The amplitudes of the field components are H_x = 590 Am⁻¹ and H_z = 830 Am⁻¹. The external field modulates the heterogeneous stray field of the FGF and produces a traveling-wave like potential moving at a frequency-tunable speed, Fig. 1(f), v_p = aω/(2π). Figure 1(g) shows how the average speed of a single isolated particle ${\bar{v}}_{x}^{{{{{{{{\rm{s}}}}}}}}}$ along the x-direction varies with ω in the noninteracting case. For low frequencies ω < ω_c = 37.3 rad s⁻¹, the motion is field-synchronized and ${\bar{v}}_{x}^{{{{{{{{\rm{s}}}}}}}}}={v}_{p}$ (synchronous regime). For ω > ω_c, the particles desynchronize with the periodic driving, and their average speed decreases as ${\bar{v}}_{x}^{{{{{{{{\rm{s}}}}}}}}}={v}_{p}(1-\sqrt{1-{\omega }_{c}^{2}/{\omega }^{2}})\, < \, {v}_{p}$ (asynchronous regime)⁴¹.

The sequence of images in Fig. 1(f) shows energy landscapes from a magnetostatic field calculation given in the Supplementary Note 2 and illustrates the transport mechanism. For t = 0.5 π/ω, ${{{{{{{\boldsymbol{H}}}}}}}}={H}_{z}\hat{z}$ and a particle is trapped within a magnetic bubble, where is a deep energy minimum (blue region). When t = π/ω, the in-plane field ${{{{{{{\boldsymbol{H}}}}}}}}={H}_{x}\hat{x}$ deforms the landscape, and two energy minima emerge inside the interstitial region along the 01 and 10 directions. Depending on the (fluctuating) particle position within the bubble at that time instant, the particle follows one of these two directions. For t = 1.5 π/ω, the field is antiparallel to the bubble magnetization, ${{{{{{{\boldsymbol{H}}}}}}}}=-{H}_{z}\hat{z}$, and six minima appear in the interstitial region. Finally, for t = 2 π/ω the particle reaches the neighboring bubble. The chirality of the rotating field ensures unidirectional motion between two bubbles. Further, since the depths of the potential wells are ~10² − 10³k_BT for T ~ 290 K, thermal fluctuations are negligible, except for the selection of the two possible paths between the bubbles.

Current-density relation

For investigating the collective particle flux, we vary the normalized density $\tilde{\rho }=N\pi {(d/2)}^{2}/A$ within the observation area A, and keep constant the magnetic field parameters. The flux is quantified by the normalized particle fluxes ${\tilde{j}}_{x,y}=\tilde{\rho }\ {\bar{v}}_{x,y}/{v}_{p}$ along the x- and y-direction. For frequencies in the synchronous regime, particles are coherently dragged by the periodic driving with velocity v_p, yielding $\tilde{j}=\tilde{\rho }$. By contrast, in the asynchronous regime at ω = 50.3 rad s⁻¹ [marked with arrow in Fig. 1(g)], a nonlinear current-density relation is observed, see Fig. 2(a, b). The current ${\tilde{j}}_{x}$ runs through a maximum upon increasing $\tilde{\rho }$, while ${\tilde{j}}_{y}$ is negligible.

Fig. 2: Colloidal current and cluster transport.

a Normalized particle fluxes ${\tilde{j}}_{x}$ (filled symbols), ${\tilde{j}}_{y}$ (empty symbols) and b mean velocities ${\bar{v}}_{x,y}$ versus normalized density $\tilde{\rho }=N\pi {d}^{2}/(4A)$ for low disorder lattices (η₆ < 0.28) and high disordered ones (η₆ > 0.28) in the asynchronous regime at ω = 50.3 rad s⁻¹. Here N is the number of particles in the area A with diameter d, and η₆ is the exponent of g₆(r). The dashed black line in (a) corresponds to the particle flux $\tilde{j}=\tilde{\rho }$ in the synchronous regime (ω < ω_c). The experimental data are averaged over different independent measurements, and the error bars for ${\tilde{j}}_{x}$ are obtained from the standard error. For $\tilde{\rho }$ the statistical errors are smaller than the symbols. In c and d particle trajectories are shown for the ordered and disordered landscape, respectively. Panel c shows the destruction of a seven-particle cluster as it enters a disordered region. The small inset displays an image at t = 3 s, scale bar is 20μm. Panel d shows that both dimers and trimers are faster than single particles. The formers may release a particle and adsorb another giving rise to a new dimer or a trimer. The scale bars for all insets are 2 μm.

We group the experimental data in two classes: a region of low disorder with η₆ < 0.28, and a region of high disorder with η₆ > 0.28. We find that for the distorted lattice ${\tilde{j}}_{x}$ is smaller than for the more regular one. For simplicity, we refer to this lattice with the smallest η₆ as the “ordered lattice” in the following. With an increasing number of defects, the particle motion along the 11 direction becomes progressively disturbed. In general, we find different types of defects such as point defects in form of larger magnetic bubbles, finite dislocation lines or planar defects in form of grain boundaries. Particle clusters break or merge when they are traveling above line defects and grain boundaries. A typical situation is shown in Fig. 2(c), where a seven-particle cluster crosses a grain boundary, which causes its splitting and raises the transverse speed, inducing a corresponding reduction of the longitudinal velocity. The hexatic phase exhibits dislocations which induce the merging of similar crystallographic directions. At these points, colloidal trains from different domains can merge. As we show later, the effect of merging is the main one responsible for the velocity reduction at large density. These implications of the disorder can be well observed in the Supplementary Movie 1. We note that for densities above ρ = 0.6, the paramagnetic colloids start jumping above the close-packed monolayer, and this impedes us to accurately measure the particle speed with our tracking program.

Figure 2(b) shows that the mean particle velocity ${\bar{v}}_{x}={\tilde{j}}_{x}/\tilde{\rho }$ rises for small densities, corresponding to a superlinear increase of ${\tilde{j}}_{x}$ with $\tilde{\rho }$. This effect results from a faster motion of clusters, as we discuss next.

Enhanced cluster transport

The dynamics in the many-particle system is governed by chains of particles along the transport direction, which we refer to as clusters in the following. As can be seen from the slopes of the trajectories shown in Fig. 2(d), these clusters are propelled at a higher average speed than isolated particles. They increase their size for small $\tilde{\rho }$, yielding the rise of ${\bar{v}}_{x}$. Clusters can also reduce in size via breakup processes, which become progressively more important with increasing cluster sizes and cause ${\bar{v}}_{x}$ to decrease with the density at larger $\tilde{\rho }$.

We quantify the cluster speed-up effect by determining the mean velocities of single particles ${\bar{v}}_{x}^{{{{{{{{\rm{s}}}}}}}}}$ and clusters ${\bar{v}}_{x}^{{{{{{{{\rm{cl}}}}}}}}}$. We note that in a more detailed analysis, one could consider the mean velocities ${\bar{v}}_{x}^{(n)}$, n = 1, 2, , …, of clusters composed of n particles (with n = 1 referring to single particles). Such a refinement of the analysis, however, is not essential. The speed ${\bar{v}}_{x}^{{{{{{{{\rm{cl}}}}}}}}}$ corresponds to the average over all n ≥ 2 and can be obtained with better accuracy. Figure 3 shows the results as a function of the driving frequency, wherein the experiments we have included the results for dimers and trimers. While in both the synchronous (ω ≲ ω_c) and the strongly asynchronous (ω ≳ 2ω_c) regimes the two velocities are nearly equal, the clusters are significantly faster in the transient regime ω_c ≲ ω ≲ 2ω_c.

Fig. 3: Enhanced cluster transport. Single particle ${\bar{v}}_{x}^{{{{{{{{\rm{s}}}}}}}}}$ and cluster ${\bar{v}}_{x}^{{{{{{{{\rm{cl}}}}}}}}}$ mean velocities versus frequency ω.

Here, n = 2 and 3 refer to dimers and trimers, respectively. The experimental data are averaged over different independent measurements, and the error bars are obtained from the standard error. The inset shows analytical results according to Eq.(1) for cluster (dimers) and single-particle velocities. They refer to driven Brownian motion in a traveling wave potential U(x, t), with constrained particle distances Δ = a. The calculations are performed for parameters U₀ = 18 k_BT, diffusion coefficient D = 1.3 μm²s⁻¹ and lattice constant a = 3 μm.

Discussion

Commensurability effect – The speed-up of clusters originates from a combination of particle sizes nearly commensurate with the energy landscape periodicity (lattice constant a) and attractive dipolar interactions. These interactions result from the time-averaged modulated stray field of the FGF⁴², and can be estimated for a pair of particles at a distance ~a as U_dd ~ 130k_BT. To understand the speed-up effect, let us consider an idealized situation, where particles are dragged by a traveling wave potential with wavelength a and within clusters are constrained to have a distance Δ commensurate with the wavelength, Δ = a. The distance constraint reflects the interplay of the long-range attractive dipolar interaction and the repulsive volume exclusion, yielding a minimum in the effective pair interaction potential at a distance Δ ≃ d ≃ a. Under the distance constraint, the assembled particles in the clusters replicate the minima of the underlying lattice and thus have a tendency to re-synchronize with the traveling wave even when single particles are in the asynchronous regime. This means that the critical frequency to the asynchronous regime of cluster motion shifts relative to that of single particles. The blue (clusters) and orange (single particles) curves in Fig. 3 demonstrate this behavior. It is important to point out that the upward shift of the critical frequency relies on the commensurability of Δ with a (multiple) of the wavelength a. Considering, e.g., distances Δ ≃ a/2, dimers would be less strongly trapped by the traveling wave potential, because the particles forming the dimer can not be both at potential minima. Accordingly, their motion would start to desynchronize at a lower frequency than that of single particles.

We support these arguments by an exact treatment of driven Brownian motion in a traveling wave potential $U(x,t)={U}_{0}\cos (2\pi x/a-\omega t)$ with constrained particle distances Δ. The detailed derivations in this treatment are given in the Supplementary Note 1. For the mean cluster velocities ${\bar{v}}_{x}^{(n)}$ we obtain

$$\frac{{\bar{v}_{x}^{(n)}}}{{v}_{p}}=1-\frac{1-{e}^{-\omega {\tau }_{n}}}{\omega {\tau }_{n}}G(\omega {\tau }_{n},\beta {U}_{0n})\ .$$

(1)

where

$$G(\omega {\tau }_{n},\beta {U}_{0n})=\frac{1}{\int\nolimits_{0}^{1}{{{{{{{\rm{d}}}}}}}}x\int\nolimits_{x}^{x+1}{{{{{{{\rm{d}}}}}}}}y\ \ g(x;\omega {\tau }_{n},\beta {U}_{0n})/g(y;\omega {\tau }_{n},\beta {U}_{0n})}$$

(2)

and $g(x;\omega {\tau }_{n},\beta {U}_{0n})=\exp [-\beta {U}_{0n}\cos (2\pi x)+\omega {\tau }_{n}x]$. Here β = 1/k_BT, ${U}_{0n}={U}_{0}\sin (nk{{\Delta }}/2)/\sin (k{{\Delta }}/2)$, and τ_n = na²/(2πD) with D the diffusion coefficient of a particle. The dependence of ${\bar{v}}_{x}^{(n)}/{v}_{p}$ for n = 1, 2 predicted by Eq. (1) is displayed in the inset of Fig. 3 and indeed shows the same type of cluster speed-up effect as observed in the experiments. The missing quantitative agreement between the experimental data and theory may be due to different reasons, including the effect of hydrodynamic interactions between the particles. Such interactions may help surmounting energetic barriers⁴³, and thus enhance the speed-up effect, and will be a matter of future studies.

The detailed behavior of cluster speeds is very sensitive to the Δ/a ratio, i.e. the degree of commensurability. Figure 4 shows ${\bar{v}}_{x}^{(n)}/{v}_{p}$ given by Eq. (1) in dependence of the cluster size n at three frequencies in the transient regime for (a) perfect commensurability Δ = a, and (b) a small incommensurability Δ = 0.97a. While for commensurable particle distance the cluster speeds become constant at large cluster sizes, the speed-up at small n is followed by a slowing down at larger n for the slightly incommensurable case. This means that in the experiments, where the commensurability is not perfect, one can expect a rather subtle variation with n.

Fig. 4: Size dependence of the cluster speeds from analytical caluclations [Eq. (1) and Eq. (2)].

The cluster speeds ${\bar{v}}_{x}^{(n)}$ are normalized with respect to the traveling wave speed v_p and shown as a function of the cluster size n for constrained particle distances (a) Δ = a and (b) Δ = 0.97a (a: lattice constant). The behavior is shown for three different frequencies in the transient regime between fully synchronous and fully asynchronous dynamics. Calculations are performed for parameters U₀ = 18 k_BT, D = 1.3 μm²s⁻¹ and a = 3 μm.

From our analysis of particle trajectories in the experiment, mean cluster speeds can be determined for small cluster sizes. At a frequency ω = 44 rad s⁻¹, we found ${\bar{v}}_{x}^{(1)}=9.8\ \mu {{{{{{{{\rm{ms}}}}}}}}}^{-1}$ for single particles, ${\bar{v}}_{x}^{(2)}=13.7\ \mu {{{{{{{{\rm{ms}}}}}}}}}^{-1}$ for dimers, and ${\bar{v}}_{x}^{(3)}=16.7\ \mu {{{{{{{{\rm{ms}}}}}}}}}^{-1}$ for trimers. The increase of ${\bar{v}}_{x}^{(n)}$ with n for these small clusters is in qualitative agreement with our theoretical predictions. Mean cluster speeds for larger n, however, could not be extracted from the trajectories with reliable accuracy.

We also note that the speed-up effect appears to be similar of the concerted cluster motions for single-file transport of molecules in zeolites^44,45 and the simulated Brownian particles forced though an asymmetric ratchet potential⁴⁶. However, in contrast to those cases, the commensurability of the particle size with the underlying lattice is a decisive factor and thermal fluctuations do not play an important role.

Hopping model. – The many-body dynamics at all densities can be captured in a coarse-grained description by a one-dimensional driven lattice gas with parallel update, where the lattice sites represent the potential minima and each site can be occupied by at most one particle. The mean occupation number ρ_lg of lattice sites corresponds to the normalized density $\tilde{\rho }={\rho }_{{{{{{{{\rm{lg}}}}}}}}}[\pi {(d/2)}^{2}\left.\right)/(\sqrt{3}{a}^{2}/2)]$ in the experiment. We develop the model from the experimental observations by considering first an idealized situation, where all clusters have the same speed and cluster breakups are solely induced by defects. Then we take into account variations in cluster speeds in dependence of the cluster size (see Fig. 4) and additional cluster breakups due to limited attraction between particles (unconstrained dynamics). Currents and velocities were determined by kinetic Monte Carlo simulations. Results for the model (lines) are shown in Fig. 5(a) and (b) in comparison with the experimental data for η < 0.28 (circles) and η > = 0.28 (squares).

Fig. 5: Current-density relationship from experiments and hopping model.

a Normalized current ${\tilde{j}}_{x}$ and (b) mean velocity ${\bar{v}}_{x}/{v}_{p}$ vs. normalized density $\tilde{\rho }$ for the lattice gas model (lines) in comparison with the experiments for η₆ < 0.28 (circles) and η₆ > 0.28 (squares). The dashed lines correspond to the idealized model with parameters p₁ = 0.2, p_cl = 0.61 and α = 0.95 for η₆ < 0.28, and p₁ = 0.19, p_cl = 0.5 and α = 1 for η₆ > 0.28. The solid lines mark the results under additional consideration of cluster speeds varying with the cluster size, and cluster breakups due to the limited attraction between particles. The error bars of the experimental data are obtained from the standard error of different experiments.

The particle configurations in the lattice gas are updated in discrete time steps τ = 2π/ω and periodic boundary conditions are used. In one update step, each particle either jumps to a vacant nearest neighbor site along the transport (+x)-direction or it does not move. For a single isolated particle, the jump probability is p₁. In the idealized model, n-clusters composed of n ≥ 2 neighboring particles move as a whole during one time step with a probability p_cl > p₁. The positions of single particles and clusters are updated in sequential order along the (−x)-direction by starting in each step with a randomly selected cluster (including single particles as “1-clusters”).

The effect due to merging of transport lanes from different crystallographic domains, which we consider as the main effect of disorder on the collective dynamics, is taken into account by introducing one representative defect site in the lattice and by requiring a particle to stay at the defect site with a probability q. Since the rate of particle exchange processes at merging points can be expected to increase linearly with the density, we suppose q = αρ_lg with α a proportionality constant. A single particle occupying the defect site then moves with the reduced probability (1 − q)p₁ during one update step. For an n-cluster occupying the defect site with its jth particle [counted from the end along the (+x)-direction], the defect has the following impact: The cluster moves as a whole in one update step with probability (1 − q)p_cl, while it breaks with probability qp_cl. In the case of a breakup, only the (j − 1) particles in front of the defect site move. As before, none of the cluster’s particles moves with probability (1 − p_cl).

The results from this idealized model, shown by the dashed lines in Fig. 5(a) and (b), describe well the defect-induced slowing down of particle transport in the experiments for large $\tilde{\rho }$. As expected, for the higher degree of disorder, we find smaller values of p₁ and p_cl, and a larger α, see the values given in the figure caption. Overall, the refined model reflects already the essential physics observed in the experiments.

However, it is evident from Fig. 5(b) that the cluster speed-up effect is overestimated in the idealized model. This is because of our simple assumption that in the defect-free regions clusters either do not move or move as a whole. In reality, particles in a cluster are held together by the attractive interaction with some probability, implying that clusters can break. To include this in the modeling, the particle positions are sequentially updated in the (−x)-direction against the bias. For an n-cluster in a defect-free region, each of its particles moves with an n-dependent probability p_n. The cluster size dependence of p_n takes into consideration the variation of cluster speeds with the cluster size. In the case that a particle of an n-cluster occupies the defect site, it moves with the reduced probabilitiy (1 − q)p_n. In view of our findings in Fig. 4 and the fact that ${\bar{v}}_{x}^{(n)} \sim {p}_{n}^{n}$ (i.e. large n are less important), we vary p_n for n = 1 − 4, and take p_n = p₄ for all n ≥ 4.

The results from this model refinement are given by the solid lines in Fig. 5 for the parameters given in Table 1. They show a very good quantitative agreement with the experimental data for almost all $\tilde{\rho }$. Deviations from the model are observed above ρ = 0.5. The data trend, even if noisy, excludes the presence of saturation of the current at a large density. This noisy trend could be caused by a lack of statistical accuracy in the experimental data due to the difficulty in tracking large ordered regions of the FGF filled with packed colloids.

Table 1 Parameters of the refined driven lattice gas model for the system with low disorder (η₆ < 0.28) and the disordered one (η₆ > 0.28).

We note that the hopping model is similar to the totally asymmetric simple exclusion process (TASEP) with parallel update^37,47. It differs from this TASEP by the fact that the particles are not moved with the same probability but with the different p_n. Already in the idealized model with just the two different values p₁ and p_cl, this leads to an important qualitative change in the transport behavior: contrary to the TASEP, the mean velocity ${\bar{v}}_{x}$ of a particle increases with ρ for small densities, see Fig. 5(b).

Conclusions

We have investigated the collective transport of colloids across periodic and disordered lattices of magnetic potential wells. Pronounced nonlinear current-density relations are obtained for driving frequencies in the asynchronous regime. For small particle densities, the current along the transport direction increases superlinearly and decreases at large densities due to defect-induced breakup of particle clusters. The superlinear increase is explained by a stronger synchronization of cluster movements with the traveling wave. It occurs for particle interactions favoring particle–particle distances commensurate with the lattice constant. A coarse-grained description of the transport in terms of a driven lattice gas with parallel update is able to capture the experimental findings. In this context, driven colloidal particles above periodic energy landscapes provide a relatively simple experimental model system to investigate basic aspects of nonequilibrium transport across ordered and disordered surfaces. The observed emerging phenomena may equally occur in other condensed matter systems on different length scales from vortices in high Tc superconductor^48,49 to biological transport^50,51,52, traffic flow^53,54, and even surface growth^55,56. Thus, we provide an experimental model system where such general phenomena can be investigated at the single-particle level.

Methods

Details of the experimental setup

We give further details on the sample preparation and on the experimental setup. The strong magnetic attraction of the FGF film is reduced by coating its surface with a h = 1μm thick polymer film (AZ-1512 Microchem, Newton, MA). This is a light-curable polymer matrix that is fixed above the FGF by using spin coating at 3000 rpm for 30 s (Spinner Ws-650Sz, Laurell) and subsequent UV photo cross-linking (Mask Aligner MJB4, SUSS Microtec).

The external magnetic fields are applied via custom-made Helmholtz coils connected to two independent power amplifiers (AMP-1800, Akiyama), which are controlled by a wave generator (TGA1244, TTi). The positions of the particles (Dynabeads M-270, Invitrogen) and their dynamics are recorded using an upright optical microscope (Eclipse Ni, Nikon) equipped with a 100 × 1.3 NA oil immersion objective and a CCD camera (Basler Scout scA640- 74 fc, Basler) working at 75 frames per second. The resulting total field of view is 151 × 113 μm².

We use video microscopy and particle tracking routines to extract the particle positions r_i ≡ {x_i(t), y_i(t)} with i = 1, . . . , N, from which we calculate the mean velocity ${\bar{v}}_{x,y}$ and other statistical quantities.

Correlation functions of disorder

To quantify the spatial disorder, we calculate from the bubble positions: the pair correlation function g(r) for the positional order and the bond orientational correlation g₆(r) for the orientational order. For a two-dimensional pattern of points having number density ρ, the first function is given by

$$g(r)=\frac{1}{2\pi r\rho }\left\langle \mathop{\sum }\limits_{i=1}^{N}\mathop{\sum }\limits_{j=1}^{N}\delta (r-{r}_{ij})\right\rangle \ .$$

(3)

Here δ(r) is the Dirac delta function, r_ij = ∣r_i − r_j∣ is the distance between particles i, j and 〈. . . 〉 denotes an average over all particle positions. To calculate g(r), we counted the particles present in annular rings around each particle.

The second function is given by

$${g}_{6}({r}_{kj})=\langle {\psi }_{6}^{* }({r}_{k}){\psi }_{6}({r}_{j})\rangle \left.\right\rangle \ ,$$

(4)

where ${\psi }_{6}=| \frac{1}{{N}_{b}}\mathop{\sum }\nolimits_{j = 1}^{{N}_{b}}{e}^{6i{\theta }_{kj}}|$, N_b is the number of neighbor particles k of a given particle j, and θ_kj is the angle between a fixed axis, here the x-axis, and the bond joining particles j and k.