Abstract
The creation and annihilation of magnetic skyrmions are mediated by three-dimensional topological defects known as Bloch points. Investigation of such dynamical processes is important both for understanding the emergence of exotic topological spin textures, and for future engineering of skyrmions in technological applications. However, while the annihilation of skyrmions has been extensively investigated in two dimensions, in three dimensions the phase transitions are considerably more complex. We report field-dependent experimental measurements of metastable skyrmion lifetimes in an archetypal chiral magnet, revealing two distinct regimes. Comparison to supporting three-dimensional geodesic nudged elastic band simulations indicates that these correspond to skyrmion annihilation into either the helical and conical states, each exhibiting a different transition mechanism. The results highlight that the lowest energy magnetic configuration of the system plays a crucial role when considering the emergence and stability of topological spin structures via defect-mediated dynamics.
Similar content being viewed by others
Introduction
Topological defects have been shown to mediate phase transitions by breaking local symmetries. For example, Kosterlitz and Thouless suggested that the proliferation and propagation of dislocations and disclinations, respectively breaking translational and rotational symmetry, are responsible for the melting of a 2D crystalline solid into a liquid1. Such discontinuities are excited states, and can be created either in opposing pairs within the system, or singly at the system’s boundaries2. Topological defects have been observed in a range of physical systems, such as in the nematic phase of liquid crystals3, as fluxons in type-II superconductors4, or as magnetic vortices in the two-dimensional X–Y spin model1.
Topological phases have been the focus of recent research due to their unique behaviours and properties. In particular, magnetic skyrmions, stabilised by the Dzyaloshinskii–Moriya interaction (DMI), have been investigated due to their potential applications in future spintronic devices5,6,7. Similar to the melting of solids by dislocations and disclinations, magnetic skyrmions are annihilated by the proliferation and subsequent propagation of magnetic Bloch points8. Such three-dimensional topological defects have been called hedgehog defects, or emergent magnetic monopoles9, due to their singular nature. Finding methods of controlling this behaviour will be crucial for realising reading and writing protocols in proposed skyrmion devices10,11,12.
Due to the focus on thin-film applications, previous investigations into the stability and annihilation mechanisms of skyrmions have largely focused on isolated skyrmions in two-dimensional systems13,14,15. In these confined systems, the energy barrier required to annihilate a skyrmion at the boundary of the system is typically lower than that required for its destruction by direct collapse16,17. Further calculations have demonstrated that entropic considerations, which concern the number of available paths across the annihilation energy barrier, play a more prominent role in determining the lifetime of skyrmions in two-dimensional systems than the energy barrier itself18,19,20,21. This phenomenon has been demonstrated experimentally18,22.
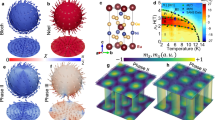
However, while they are commonly portrayed as two-dimensional objects forming a hexagonal skyrmion lattice (SkL), in three dimensions magnetic skyrmions exist as extended tube-like objects23,24. In a bulk skyrmion system, such a skyrmion tube (SkT) can exist within either a helical or conical state, as shown by the visualisations in Fig. 1a, b. These two chiral magnetic states consist of spin spirals aligned along either the easy axes of the system (helical), or along the applied field direction (conical)7,25. In each configuration, the SkT is thought to be annihilated by a different Bloch-point-mediated mechanism, as depicted in Fig. 1c. On the left, the SkT connects with the edge of the nearby helical domain, forming a pair of anti-hedgehog-like Bloch points (H+ and H−), whose subsequent motion joins the SkT to the neighbouring helical domain8. On the other hand, on the right side, the SkT breaks in two, forming a pair of spiral-like Bloch points (C+ and C−), which unwind the SkT into the conical state26. Cross-sections of the system are shown in Fig. 1d, including insets showing the spin configuration surrounding each Bloch point. The chirality of these Bloch points is defined by the local topology of the spin structures (see Supplementary Fig. S1, Supplementary Note 1).
a, b Three-dimensional visualisations of simulations display a skyrmion tube (SkT) embedded in the helical and conical states respectively. The grey contours highlight regions where the magnetisation along the z-axis, sz = 0. The top and bottom layers of spins have been coloured according to their sz component. The back right surface of each simulation has been coloured according to the local sz or sx components respectively, highlighting the orientation of the surrounding helical and conical structures. c Visualisations of the skyrmion to helical (SkL → H), and skyrmion to conical (SkL → C) annihilation mechanisms, where the contour surfaces highlight regions where sz = 0, and the colouration indicates the local sx component. A pair of Bloch points is nucleated where either the SkT connects to the local helical structure (left, H+ and H−), or breaks in two to form the conical state (right, C+ and C−). d Cross-sections of the spin texture around the Bloch-point structures shown in c. Insets display the local spin arrangement around each Bloch point. Colours indicate the mz component.
While there have been previous computational studies into the topological phase transitions governing three-dimensional skyrmion annihilation27,28,29,30, in this work, we undertake a combined experimental and computational investigation into the annihilation dynamics in bulk skyrmion systems. Beyond being vital for technological implementations, such Bloch-point-mediated mechanisms likely hold the key to understanding the stabilisation of more exotic topological phases, for example: the emergence of the low-temperature skyrmion phase from the tilted conical state in Cu2OSeO331,32,33, the transformation of hexagonal skyrmion lattices to meron–antimeron lattices in Co8Zn9Mn334, or future experimental realisation of magnetic hopfion states35.
Results
Metastable skyrmion phase diagram
In bulk chiral crystals, skyrmions typically exist in a small range of temperature and applied magnetic field close to the Curie temperature, TC, of the material25. Previous studies have shown that a metastable skyrmion state can be realised outside this equilibrium region by cooling the sample under an applied magnetic field36,37,38. Being metastable, this state has a finite, temperature-dependent lifetime39, which can be studied with time-resolved measurements40. It has been noted that disorder and defects in the underlying crystal lattice increase the lifetime of the metastable skyrmion state36. Therefore, in order to stabilise metastable skyrmions over the widest possible range of temperature and applied magnetic fields, we chose to investigate a Zn-substituted Cu2OSeO3 sample, which exhibits such an enhanced lifetime41.
Figure 2a shows the magnetic phase diagram of the chosen (Cu1−xZnx)2OSeO3 (x = 0.02) single crystal, with a TC = 57.5 K (see Supplementary Figs. S2-3, Supplementary Note 2). Being multiferroic, the phase diagram was determined by measurements of the electric polarisation, P, along the [001] crystal axis, as a function of the magnetic field applied along the [110] axis42. We chose this sample configuration due to the relative ease of modelling the magnetic phase transitions for these domain orientations (see Supplementary Note 3). At low fields, the ground state consists of helical domains, with their spin modulations oriented along the 〈001〉 axes due to the cubic anisotropy43. With increasing applied field, the conical state is realised, with a propagation vector aligned with the magnetic field direction. The phase diagram illustrates the stabilisation of the equilibrium SkL state over a short range of temperature and applied field around ~56 K, and the comparably larger extent of the metastable SkL state, realised by field cooling at 20 mT.
a The magnetic phase diagram of the (Cu1−xZnx)2OSeO3 sample, as determined by measurements of the electric polarisation P along the [001] crystallographic axis, when the magnetic field is applied along the [110] axis. The phase diagram was determined by field cooling (FC) at 20 mT, as indicated by the green arrow. The uniform magnetisation (UM, white), conical (C, blue), helical (H, red) and equilibrium skyrmion lattice (SkL, yellow) phases are labelled. The metastable SkL phase is divided into two regions, where it overlays the equilibrium conical (yellow hatched) and helical (yellow dotted) phases. b, c The real component of the AC susceptibility data \(\chi ^{\prime}\) measured after zero field-cooling (ZFC, black), high field-cooling (HFC, blue) and field-cooling (FC, blue). The decrease in \(\chi ^{\prime}\) characteristic of the formation of skyrmions is highlighted by the yellow fill. The typical relaxation of \(\chi ^{\prime}\) associated with metastable skyrmion decay is indicated by the green arrow.
Corresponding AC susceptibility measurements are displayed in Fig. 2b, c, performed after zero field cooling (ZFC), high field cooling (HFC) and field cooling (FC) the sample to the target temperature (see Methods). In Fig. 2b, the decrease in the real component of the AC susceptibility, \(\chi ^{\prime}\), around 20 mT is characteristic of the formation of the SkL state44, as highlighted in yellow. Upon FC at 20 mT to 48 K, a similar characteristic decrease in \(\chi ^{\prime}\) is indicative of the presence of metastable skyrmions, as shown in Fig. 2c.
Examination of the magnetic phase diagram reveals that the metastable SkL state overlays both the conical and the helical ground states, as indicated by the yellow hatched and dotted sections on the phase diagram. Therefore, one might expect that the metastable SkL state will decay into either the conical (SkL → C) or helical (SkL → H) states depending on the field applied to the sample. This affords us the opportunity to study the dynamics of both skyrmion annihilation mechanisms proposed in Fig. 1.
Metastable skyrmion lifetime
Measurements of the AC susceptibility, \(\chi ^{\prime}\), as a function of time allow the annihilation of the metastable skyrmion state to be measured. Specifically, we can expect that the difference in the value of \(\chi ^{\prime}\) between the FC and ZFC or HFC measurements is proportional to the population of metastable skyrmions present in the sample, as has been observed in previous works41,45. Thus, when the metastable skyrmions annihilate, the value of \(\chi ^{\prime}\) will relax over time, as indicated by the green vertical arrow in Fig. 2c. We carried out such time-resolved skyrmion lifetime measurements as a function of the applied magnetic field. A selection of the resulting data is displayed in Fig. 3a (full dataset shown in Supplementary Fig. S4 and Supplementary Note 4). Here, the AC susceptibility has been normalised, \({\chi }_{N}^{\prime}=({\chi }_{f}^{\prime}-\chi ^{\prime} (t))/({\chi }_{f}^{\prime}-{\chi }_{0}^{\prime})\), where χ0 is the initial value of \(\chi ^{\prime}\) at t = 0, and χf is the value the system is tending to as t → ∞.
a The normalised real component of the AC susceptibility, \(\chi_{N} ^{\prime}\), measured as a function of time at a range of applied magnetic fields after field cooling the sample at 20 mT from 65 to 49 K. The data is fitted with the stretched exponential decay function, and the corresponding magnetic fields are labelled. b The fitted lifetimes are plotted as a function of the applied magnetic field on a logarithmic axis. The two distinct exponential trends are fitted to \(\tau ={\tau }_{B}\exp (lB)\), where τB is the lifetime at 0 mT, and l is the linear constant in the exponent, to determine how the lifetime varies with the applied field. The extracted parameters for l are 0.066 and − 0.053 mT−1 for the suggested skyrmion lattice to helical (SkL → H) and skyrmion to conical (SkL → C) ranges respectively. c Further lifetimes measured at different fields are plotted as a function of temperature. The datasets are fitted with a modified Arrhenius law to extract a and τ0. d The value of a and τ0 are plotted as a function of the applied field. In the inset, the determined τ0 and a parameters are plotted against one another to test the Meyer-Neldel compensation rule. All error bars indicate the standard error obtained when fitting the data to the relevant function.
The lifetime of the metastable skyrmion state at each field, τ, was extracted by fitting the data to a stretched exponential decay function46,
A stretching parameter of β ≠ 1 indicates that the system displays a range of lifetimes. Such a distribution of lifetimes may be due to inhomogeneous magnetic fields within irregularly shaped samples47,48. Nevertheless, for our measurements, the inclusion of β is necessary to fit the data, and varies between 0.3 and 0.6 for different applied fields.
The resulting metastable skyrmion lifetimes are plotted as a function of magnetic field in Fig. 3b. The lifetime is at a maximum at 24 mT, and decreases at magnetic fields above and below this point. We note that the larger errors bars at both low and high values are due to the difficulty of fitting either very short or long lifetimes—we are effectively exploring the full range of measurable lifetimes for our chosen measurement time. The two distinct exponential trends point towards observation of the two anticipated regimes of the SkL → H and SkL → C annihilation mechanisms, and we tentatively label the corresponding regions of the figure accordingly. In reality, since the decay is a statistical process, one might expect a crossover region in the middle of the field range, with the simultaneous occurrence of both decay pathways.
A modified Arrhenius’ law can be employed to describe the temperature dependence of the skyrmion lifetimes, allowing the energy barrier EB governing the decay mechanism to be determined,
Here, the temperature dependence of the energy barrier is assumed to be approximately linear, with a as the proportional constant, following the relationship EB/kB = a(T − Ts)40. The lifetime can be expected to reach a minimum just below the lowest temperature extent of the equilibrium skyrmion phase, Ts, which we determined to be approximately 4 K below TC (see Supplementary Fig. S2).
Considering equation (2), the two distinct exponential trends in Fig. 3b suggest both a negative or positive linear dependence of a with the applied magnetic field. However, one must also consider the contribution of the τ0 term. This prefactor is typically thought of as a characteristic attempt frequency with which the system attempts to overcome the energy barrier. The term also includes the aforementioned entropic correction which has been shown to play a crucial role in the stability of magnetic skyrmions in thin lamellae22.
In order to separate the contributions of a and τ0, we performed further, temperature-dependent lifetime measurements at five applied magnetic fields between 16 and 34 mT (full data shown in Supplementary Fig. S4). The resulting extracted lifetimes are plotted as a function of temperature in Fig. 3c. By fitting these lifetimes with the modified Arrhenius law in equation (2), the values of a (the gradient) and τ0 (the value of τ at Ts) were determined, and are plotted in Fig. 3d.
Immediately, one can see that a appears to decrease either side of 24 mT, as was indicated by the initial lifetime measurements in Fig. 3b. This supports the interpretation that the energy barrier appears to vary linearly, with either a positive or negative gradient, in two regimes which correspond to the SkL → H and SkL → C transitions respectively. However, the contribution from the τ0 term appears to decrease exponentially across the measured field range. This relationship is significantly different to the one determined by Wild et al. in their thin lamella sample22. Following the phenomenological Meyer–Neldel compensation rule21, they demonstrated that τ0 varied exponentially with the measured energy barrier—concluding that the entropy therefore varies linearly with the energy barrier. However, when plotting our measured a and τ0 values in the inset of Fig. 3d, it is clear that such a dependence is not recovered for our bulk sample, and entropic considerations therefore appear to play a less prominent role.
The discrepancy can be explained by considering that in bulk measurements, the annihilation of skyrmions consists of two processes: the nucleation of Bloch-point pairs, and the subsequent motion of these Bloch points along the length of the skyrmion tube. In bulk systems, τ0 appears to be correlated with increased disorder and defects within the underlying crystal lattice45. Therefore, the decrease of τ0 with increasing magnetic field in our results indicates that the thermally-activated depinning of the Bloch-point from structural defects becomes more energetically favourable at higher applied magnetic fields. Any entropic contributions may well be obscured by these pinning effects.
Energy barrier simulations
To support the interpretation of the experimental measurements, we modelled a chiral magnet by means of a classical spin model with periodic boundaries in the xy plane and open boundaries in the z direction (see Methods). To begin, suitable magnetic configurations for the helical and conical states were prepared and their energy was numerically minimised over the field range. This was repeated for single SkTs embedded within helical and conical states, resulting in the configurations depicted in Fig. 1a, b (see Supplementary Figs. S5, S6, and Supplementary Notes 5–9).
To investigate the transitions of isolated SkTs into helical and conical states, the geodesic nudged elastic band method (GNEBM) was employed13,49. The GNEBM finds minimum energy paths (MEPs) through configuration space, between two equilibrium states by minimising the energy of a chain of copies of the system known as images. This allows the determination of the energy barrier for the transition. (see Methods, Supplementary Notes 10 and 11). Comparing the energies of magnetic states is not sufficient to describe their stability against one another—it is only by considering the microscopic decay pathway, and its associated energy barrier, that one can gain insight into skyrmion stability.
We first applied this algorithm to determine a MEP for a SkT annihilating within a helical state (SkL → H) for applied magnetic fields between bz = 0.04 and 0.16 (in units of exchange, see “Methods”), as shown in Fig. 4a–i (full results shown in Supplementary Fig. S7, Supplementary Movie 1). Since previous measurements suggest that the skyrmion state prefers to annihilate into helical domains with magnetic modulation in the same plane as the skyrmion lattice state8,50, we chose to utilise helical domains aligned along the x-axis accordingly. We found it was necessary to apply a cubic anisotropy of kc = 0.05 in order to stabilise the helical domains against the conical state over the investigated field range.
a–i The results of the simulations for the skyrmion lattice to helical decay mechanism are shown at a range of applied magnetic fields. a, d, g The energy dependence of the magnetic state is plotted as a function of the reaction coordinate X along the minimum energy path (MEP). All data points have been subtracted by the energy of the initial state. b, e, h The z-axis trajectory of the left (L) and right (R) pairs of Bloch points plotted as a function of X as the skyrmion tube is annihilated. Vertical dashed lines highlight images where Bloch points are created or destroyed. Red and blue data points distinguish each Bloch point in a pair. c, f, i Selected three-dimensional visualisations of the simulation at specific points along the MEP at each field, as indicated by the corresponding numeric labels in a, d, g. The surfaces display sz = 0 contours, and have been coloured according to the local value of sx.
As shown by the selected visualisations of the simulated images in Fig. 4c, the SkT decays by forming a pair of Bloch points, whose subsequent motion connects the SkT and the helical domain. The energy of the system along the determined MEP, parameterised by the reaction coordinate X through configuration space, is plotted in Fig. 4a, where each data point is associated with an image of the system. The trajectories of the Bloch points along the z-axis are plotted in Fig. 4b, with the vertical dashed lines indicating images where Bloch points are created or destroyed. By comparison of these panels, one can see that the two energy barriers along the MEP are each associated with the formation of a pair of Bloch points.
We repeated the GNEBM simulations at a range of applied magnetic fields. At some applied fields, both pairs of Bloch points form and annihilate simultaneously, as shown by the simulation performed at bz = 0.10 in Fig. 4d–f. Furthermore, at bz = 0.14 in Fig. 4g–i, we found a simultaneous formation of four pairs of Bloch points. At bz = 0.14 and 0.16, the final state was found to be higher in energy compared to the SkT in helical state, suggesting that, for the chosen parameters, the SkT within the helical state was the lowest energy configuration over a small range of field. Due to the complexity of the transition, there are likely many similar paths through configuration space, all with energy close to the MEP, and therefore we speculate that the formation of different numbers of Bloch points, and whether they form on the left or right of the skyrmion tube, is likely due to the original path interpolation between the specified initial and final states.
There has been a previous work utilising Ginzburg–Landau analysis to investigate energy barriers for a SkT decaying within a helical state. However, the decay mechanism the authors found was more akin to the breaking of the SkT within a conical state27, rather than the joining of the SkT to the helical domains as seen in this work, and other experimental works8,22.
We performed similar GNEBM simulations for the SkT in a conical state (SkL → C) at applied fields between bz = 0.36 and 0.50, as shown in Fig. 5a–i (full results shown in Supplementary Fig. S8, Supplementary Movie 2). With the same cubic anisotropy utilised for the helical simulations, we found that the conical state was only the lowest energy state over a short range of applied field (see Supplementary Fig. S9, Supplementary Movie 3). Therefore, in order to simulate the SkL → C transition over a wide field range, we performed this set of simulations with no cubic anisotropy present.
a–i The results of the simulations for the skyrmion lattice to conical decay mechanism are shown at a range of applied magnetic fields. a, d, g The energy dependence of the magnetic state is plotted as a function of the reaction coordinate X along the minimum energy path (MEP). All data points have been subtracted by the energy of the initial state. b, e, h The z-axis trajectory of the top (T) and bottom (B) pairs of Bloch points plotted as a function of X as the skyrmion tube is annihilated. Vertical dashed lines highlight images where Bloch points are created or destroyed. Red and blue data points distinguish each Bloch point in a pair. c, f, i Selected three-dimensional visualisations of the simulation at specific points along the MEP at each field, as indicated by the corresponding numeric labels in (a,d,g). The surfaces display sz = 0 contours, and have been coloured according to the local value of sx.
Figure 5a–c shows the results of the SkL → C simulation under an applied field of bz = 0.36. In comparison to the SkL → H simulations, the energy landscape is considerably more complex, with many more metastable states possible along the MEP. In Fig. 5c, images of the system along the MEP show the breaking of the SkT into three sections by the formation of two pairs of Bloch points. The sections consist of two chiral bobbers at the open boundary surfaces of the system51, and a short SkT capped by two Bloch points, known as a toron52,53. Following along the MEP, the formation of each Bloch-point pair is once again associated with an energy barrier, as shown in Fig. 5a. In addition, at this lower field there is an energy barrier associated with the collapse of the toron (image 8), and the two chiral bobbers (images 10 and 11), suggesting they are metastable states. We confirmed that these states are indeed local energy minima by energy minimisation. The system behaves similarly at bz = 0.42, as shown in Fig. 5d–f.
At bz = 0.48 and above, the applied field is sufficient to transform the conical state into the uniformly magnetised state. From this point, only one pair of Bloch points is formed during the SkT annihilation, as shown in Fig. 5g–i, which resembles previous computational works28,29. Furthermore, there is no longer an energy barrier associated with the destruction of the torons and chiral bobbers, suggesting they are not metastable configurations at higher applied fields.
To allow comparison of these simulations with the experimental results, we calculated the energy barrier required for the formation of the Bloch-point pairs in each simulation, as indicated by the arrow in Fig. 4d. In cases where two, or four, pairs of Bloch points were formed simultaneously, we divided the energy by the number of pairs. Energy barriers associated with the formation of Bloch-point pairs for the SkL → H and SkL → C transitions are shown as a function of applied field in Fig. 6a, b respectively. In addition, energy barriers for the formation of Bloch-point pairs for SkT tubes annihilating within the uniformly magnetised state (SkL → UM) with cubic anisotropy of kc = 0.05 are shown in Fig. 6c (see Supplementary Figs. S7–S10). Finally, energy barriers associated with the annihilation of toron and chiral bobber states within the conical and uniformly magnetised simulations are shown in Fig. 6d.
a–c The field dependence of the simulated energy barrier which must be overcome to form one pair of Bloch points is plotted as a function of the applied field for the skyrmion lattice to helical (SkL → H) (blue), skyrmion lattice to conical (SkL → C) (red) and skyrmion lattice to uniformly magnetised (SkL → UM) (yellow) simulations. d The simulated energy barrier for the annihilation of a chiral bobber (ChB, squares) or a toron (triangles) is plotted as a function of the applied magnetic field for the SkL → C (red) and SkL → UM (yellow) decay mechanisms. Each dataset has been fitted with a linear trend.
Discussion
Considering Fig. 6a, b, one can see that the energy barrier associated with Bloch-point formation increases as a function of the applied field for the SkT within the helical state, whereas it decreases as a function of field for the SkT within the conical state. This qualitatively agrees with the conclusions drawn from the experimental data in Fig. 3, where we anticipated the energy barriers varying linearly with the applied field, supporting our labelling of the two linear regimes in the lifetime data to the two distinct SkT annihilation mechanisms.
Our results of SkT annihilation to the conical state can be compared to previous results of isolated skyrmions in two-dimensional systems, which typically show two transition paths: either the skyrmion is annihilated at the boundary of the system, or it is directly annihilated within the system’s interior. For direct annihilation, this may occur either by shrinking and flipping the central spin16, or by the newly-coined chimera collapse, where the spin flip occurs at the edge of the skyrmion under an in-plane field54,55. The shrinking annihilation mechanism resembles our results in Fig. 5, where the SkT narrows prior to the nucleation of the Bloch-point pair, at the point where the spin in the centre of the skyrmion flips to align with the applied field. We also investigated the possibility of surface Bloch-point nucleation, as has been done in previous works29,56 (see Supplementary Fig. S11, Supplementary Note 12, Supplementary Movie 4), but when applying the GNEBM, the algorithm appeared to prefer forming Bloch-point pairs within the interior of the system over the simulated field range.
There are a number of limitations in our model which prevent us from reaching a direct quantitative comparison to the experiment. Firstly, in the SkL → H model, we only consider skyrmions decaying directly into helices aligned to the [001] crystal axis. This is because it is simple to conceive of an initial state for a skyrmion embedded in a helical domain with a winding direction in the plane of the skyrmion lattice8, and this also seemed to be the dominant decay pathway in a previous neutron scattering experiment50. This was also our motivation for choosing to measure the sample with the field applied along the [110] axis, rather than the [111] axis, where the helices would all be oriented at some angle to the applied field. However, it is possible that in the measured bulk sample there are additional decay pathways for skyrmions decaying into the helical domains oriented along the [100] and [010] crystal axes, which we have not considered.
Second, due to the considerable complexity of the model, we only consider the annihilation of an isolated skyrmion in our system, whereas in the experimental bulk sample we are measuring the decay of a skyrmion lattice. One could conceive that the lifetime of an isolated skyrmion may differ from one surrounded by other skyrmions57. Third, the decay dynamics in the experimental sample are, by design, influenced by the pinning introduced by defects and impurities in the Zn-substituted sample. Thus, it would make an interesting follow-up study to simulate the effect of defects on the determined energy barriers, as has been done for 2D systems17,58,59.
To summarise, our experimental measurements of field-dependent metastable skyrmion lifetimes indicated two distinct regimes, where skyrmion annihilation is dominated by decay into either the helical or conical states. This conclusion is supported by GNEBM simulations, where the determined energy barriers associated with Bloch-point-mediated skyrmion annihilation to the helical and conical states revealed the same field dependence. In contrast to previous studies of two-dimensional systems, in our bulk sample the effects of defect pinning appear to dominate over entropic contributions. The results highlight that, for technological applications, consideration of the competing magnetic ground state and the dimensionality of the system will be crucial when engineering skyrmion stability for reading and writing processes. Further utilisation of the GNEBM, and similar computational methods, will no doubt prove to be a powerful tool in the understanding of topological defect-mediated phase transitions, particularly when considering the stabilisation of future complex three-dimensional spin textures.
Methods
Sample growth and preparation
A single crystal of (Cu1−xZnx)2OSeO3 was grown from polycrystalline powders using the chemical vapour transport method60. The composition of the resulting crystal was determined by inductively coupled plasma mass spectroscopy, and energy-dispersive X-ray spectroscopy, yielding x = 0.02 (2% Zn substitution), as reported in previous work60. For electric polarisation measurements, the sample was aligned and cut into a plate shape, with two large parallel \(\left\langle 111\right\rangle\) faces.
AC susceptibility magnetometry
AC susceptibility measurements were performed with a MPMS3 Quantum Design magnetometer, fitted with the AC option. The sample was attached to a quartz rod using GE varnish and mounted in the instrument with the [100] crystal direction parallel to the applied magnetic field. AC susceptibility measurements were performed with an oscillating magnetic field amplitude of 0.1 mT and a frequency of 10 Hz. All cooling procedures were performed at a rate of 40 K/min. For the ZFC, FC and HFC measurements, the sample was cooled from 60 K to the target temperature under an applied field of 0, 20 or 200 mT respectively, and measurements subsequently performed as a function of increasing or decreasing magnetic field. For the lifetime measurements, the sample was initialised following the FC process, and the AC susceptibility was then measured as a function of time under stable conditions for three or more hours.
Electric polarisation measurements
For the evaluation of electric polarisation P, silver paste was painted on a pair of [111] surfaces of the Zn-substituted Cu2OSeO3 crystal. With the field applied along the [110] crystal axis, the pyroelectric current was measured during a constant rate of magnetic field sweep using an electrometer (Keithley 6517B), and integrated over time to deduce P42.
Computational modelling
The system was modelled using a cubic lattice of N = 30 × 30 × 30 classical spins with periodic boundaries in the xy plane. The model parameters were chosen in order to fit three helical domains within the specified system size, as has been done in previous works52, and therefore does not directly relate to the experimental values. We are aiming for a qualitative description of the universal skyrmion annihilation mechanisms, rather than a direct quantitative comparison. The system follows a Heisenberg-like Hamiltonian where energy constants of the different interactions are made dimensionless by normalising by the exchange constant,
Here, si are unit vectors denoting spin orientations, d = D/J > 0 is the DMI constant (for a cubic helimagnet), kc = Kc/J > 0 is the cubic anisotropy constant (easy 〈001〉 axes) and bz = (μs/J)Bz is the z-component of the applied field, specified in units of magnetic moment per exchange constant μs/J. The angled brackets in the first two sums denote counting pairs of spins only once.
The magnitude of d ≈ 0.727 was set such that the periodicity of a spin spiral at zero field and in the absence of any anisotropy is 10 lattice sites61,62. The value of the saturation field in the absence of anisotropy is defined as BD = D2/(μsJ) = d2 ≈ 0.5362. To stabilise helical configurations, a cubic anisotropy constant of kc = 0.05 was chosen, while for the conical simulations, kc = 0.00 was specified. Equilibrium states were obtained by initialising the system with a suitable configuration and minimising the energy using an over-damped Landau-Lifshitz-Gilbert (LLG) equation (see Supplementary Figs. S5, S6).
The GNEBM finds minimum energy paths (MEPs) through configuration space between two magnetic states13. Using a suitable initial state, a series of images along the transition path are calculated. During the algorithm, the images follow gradients of energy and are kept distanced in configuration space until reaching a MEP between the initial and final states. Saddle points along the MEP determine the energy barriers of the transitions. In this study, we use a rotation formula for the spin orientations to initiate the algorithm13.
All simulations and GNEBM calculations were obtained using Fidimag16,49. Further details about the simulations and the applied convergence criteria to stop the energy minimisation for both the LLG equation and GNEBM are discussed in the Supplementary Information.
Data availability
All experimental data analysed and presented in the main text and supplementary materials can be found in an online repository63 https://doi.org/10.5281/zenodo.4384569. Further material is available from the corresponding author upon reasonable request.
Code availability
All code utilised in the simulations presented in the main text, supplementary text, and Supplementary Movies 1–4 can be found in an online repository63 https://doi.org/10.5281/zenodo.4384569. Further material is available from the corresponding author upon reasonable request.
References
Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C: Solid State Phys. 6, 1181 (1973).
Mermin, N. D. The topological theory of defects in ordered media. Rev. Mod. Phys. 51, 591 (1979).
Muěvič, I. & Škarabot, M. Two-dimensional nematic colloidal crystals self-assembled by topological defects. Science 313, 954–958 (2006).
Blatter, G., Feigel’man, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125 (1994).
Iwasaki, J., Mochizuki, M. & Nagaosa, N. Current-induced skyrmion dynamics in constricted geometries. Nat. Nanotechnol. 8, 742 (2013).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899 (2013).
Back, C. et al. The 2020 skyrmionics roadmap. J. Phys. D: Appl. Phys. 53, 363001 (2020).
Milde, P. Unwinding of a skyrmion lattice by magnetic monopoles. Science 340, 1076 (2013).
Fujishiro, Y., Kanazawa, N. & Tokura, Y. Engineering skyrmions and emergent monopoles in topological spin crystals. Appl. Phys. Lett. 116, 090501 (2020).
Fert, A., Cros, V. & Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 8, 152 (2013).
Romming, N. et al. Writing and deleting single magnetic skyrmions. Science 341, 636–639 (2013).
Tomasello, R. et al. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 4, 6784 (2015).
Bessarab, P. F., Uzdin, V. M. & Jónsson, H. Method for finding mechanism and activation energy of magnetic transitions, applied to skyrmion and antivortex annihilation. Comput. Phys. Commun. 196, 335–347 (2015).
Rohart, S., Miltat, J. & Thiaville, A. Path to collapse for an isolated Néel skyrmion. Phys. Rev. B 93, 214412 (2016).
Lobanov, I. S., Jónsson, H. & Uzdin, V. M. Mechanism and activation energy of magnetic skyrmion annihilation obtained from minimum energy path calculations. Phys. Rev. B 94, 174418 (2016).
Cortés-Ortuño, D. et al. Thermal stability and topological protection of skyrmions in nanotracks. Sci. Rep. 7, 4060 (2017).
Stosic, D., Mulkers, J., Van Waeyenberge, B., Ludermir, T. B. & Milošević, M. V. Paths to collapse for isolated skyrmions in few-monolayer ferromagnetic films. Phys. Rev. B 95, 214418 (2017).
Hagemeister, J., Romming, N., von Bergmann, K., Vedmedenko, E. Y. & Wiesendanger, R. Stability of single skyrmionic bits. Nat. Commun. 6, 8455 (2015).
Bessarab, P. F. et al. Lifetime of racetrack skyrmions. Sci. Rep. 8, 3433 (2018).
Desplat, L., Suess, D., Kim, J.-V. & Stamps, R. L. Thermal stability of metastable magnetic skyrmions: entropic narrowing and significance of internal eigenmodes. Phys. Rev. B 98, 134407 (2018).
Desplat, L. & Kim, J.-V. Entropy-reduced retention times in magnetic memory elements: a case of the Meyer-Neldel compensation rule. Phys. Rev. Lett. 125, 107201 (2020).
Wild, J. et al. Entropy-limited topological protection of skyrmions. Sci. Adv. 3, e1701704 (2017).
Birch, M. T. et al. Real-space imaging of confined magnetic skyrmion tubes. Nat. Commun. 11, 1726 (2020).
Seki, S. et al. Propagation dynamics of spin excitations along skyrmion strings. Nat. Commun. 11, 256 (2020).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915 (2009).
Kagawa, F. et al. Current-induced viscoelastic topological unwinding of metastable skyrmion strings. Nat. Commun. 8, 1332 (2017).
Schütte, C. & Rosch, A. Dynamics and energetics of emergent magnetic monopoles in chiral magnets. Phys. Rev. B 90, 174432 (2014).
Rybakov, F. N., Borisov, A. B., Blügel, S. & Kiselev, N. S. New Type of Stable Particlelike States in Chiral Magnets. Phys. Rev. Lett. 115, 117201 (2015).
Müller, G. P. et al. Spirit: Multifunctional framework for atomistic spin simulations. Phys. Rev. B 99, 224414 (2019).
Müller, G. P., Rybakov, F. N., Jónsson, H., Blügel, S. & Kiselev, N. S. Coupled quasimonopoles in chiral magnets. Phys. Rev. B 101, 184405 (2020).
Chacon, A. et al. Observation of two independent skyrmion phases in a chiral magnetic material. Nat. Phys. 14, 936 (2018).
Bannenberg, L. J. et al. Multiple low-temperature skyrmionic states in a bulk chiral magnet. npj Quantum Mater. 4, 11 (2019).
Leonov, A. O., Pappas, C. & Kézsmárki, I. Field and anisotropy driven transformations of spin spirals in cubic skyrmion hosts. Phys. Rev. Res. 2, 043386 (2020).
Yu, X. Z. et al. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 564, 95–98 (2018).
Rybakov, F. N. et al. Magnetic hopfions in solids. Preprint at https://arxiv.org/abs/1904.00250 (2019).
Münzer, W. et al. Skyrmion lattice in the doped semiconductor Fe1−xCoxSi. Phys. Rev. B 81, 041203(R) (2010).
Karube, K. et al. Robust metastable skyrmions and their triangular-square lattice structural transition in a high-temperature chiral magnet. Nat. Mater. 15, 1237 (2016).
Okamura, Y., Kagawa, F., Seki, S. & Tokura, Y. Transition to and from the skyrmion lattice phase by electric fields in a magnetoelectric compound. Nat. Commun. 7, 12669 (2016).
Kagawa, F. & Oike, H. Quenching of charge and spin degrees of freedom in condensed matter. Adv. Mater. 29, 1601979 (2017).
Oike, H. et al. Interplay between topological and thermodynamic stability in a metastable magnetic skyrmion lattice. Nat. Phys. 12, 62 (2016).
Birch, M. T. et al. Increased lifetime of metastable skyrmions by controlled doping. Phys. Rev. B 100, 014425 (2019).
Seki, S., Ishiwata, S. & Tokura, Y. Magnetoelectric nature of skyrmions in a chiral magnetic insulator Cu2OSeO3. Phys. Rev. B 86, 060403(R) (2012).
Seki, S., Yu, X. Z., Ishiwata, S. & Tokura, Y. Observation of Skyrmions in a Multiferroic Material. Science 336, 198 (2012).
Wilhelm, H. et al. Precursor phenomena at the magnetic ordering of the cubic helimagnet FeGe. Phys. Rev. Lett. 107, 127203 (2011).
Karube, K. et al. Metastable skyrmion lattices governed by magnetic disorder and anisotropy in β-Mn-type chiral magnets. Phys. Rev. B 102, 064408 (2020).
Karube, K. et al. Skyrmion formation in a bulk chiral magnet at zero magnetic field and above room temperature. Phys. Rev. Mater. 1, 074405 (2017).
Crisanti, M. et al. Position-dependent stability and lifetime of the skyrmion state in nickel-substituted Cu2OSeO3. Phys. Rev. B 102, 224407 (2020).
Reimann, T. et al. Neutron diffractive imaging of the skyrmion lattice nucleation in MnSi. Phys. Rev. B 97, 020406(R) (2018).
Bisotti, M.-A. et al. Fidimag—a finite difference atomistic and micromagnetic simulation package. J. Open Res. Softw. 6, 22 (2018).
Birch, M. T. et al. Anisotropy-induced depinning in the Zn-substituted skyrmion host Cu2OSeO3. Phys. Rev. B 102, 104424 (2020).
Zheng, F. et al. Experimental observation of chiral magnetic bobbers in B20-type FeGe. Nat. Nanotechnol. 13, 451–455 (2018).
Leonov, A. O. & Inoue, K. Homogeneous and heterogeneous nucleation of skyrmions in thin layers of cubic helimagnets. Phys. Rev. B 98, 054404 (2018).
Müller, G. P., Rybakov, F. N., Jónsson, H., Blügel, S. & Kiselev, N. S. Coupled quasimonopoles in chiral magnets. Phys. Rev. B 101, 184405 (2018).
Meyer, S. et al. Isolated zero field sub-10 nm skyrmions in ultrathin Co films. Nat. Commun. 10, 3823 (2019).
Muckle, F. et al. Experimental identification of two distinct skyrmion collapse mechanisms. Nat. Phys. 17, 395–402 (2021).
Li, Y. et al. Tunable terahertz oscillation arising from Bloch-point dynamics in chiral magnets. Phys. Rev. Res. 2, 033006 (2020).
Leonov, A. O., Monchesky, T. L., Loudon, J. C. & Bogdanov, A. N. Three-dimensional chiral skyrmions with attractive interparticle interactions. J. Phys. Condens. Matter 28, 35LT01 (2016).
Uzdin, V. M., Potkina, M. N., Lobanov, I. S., Bessarab, P. F. & Jónsson, H. The effect of confinement and defects on the thermal stability of skyrmions. Phys. B: Condens. Matter 549, 6–9 (2018).
Fernandes, I. L., Bouaziz, J., Blügel, S. & Lounis, S. Universality of defect-skyrmion interaction profiles. Nat. Commun. 9, 4395 (2018).
Štefančič, A. et al. Origin of skyrmion lattice phase splitting in Zn-substituted Cu2OSeO3. Phys. Rev. Mater. 2, 111402(R) (2018).
Buhrandt, S. & Fritz, L. Skyrmion lattice phase in three-dimensional chiral magnets from Monte Carlo simulations. Phys. Rev. B 88, 195137 (2013).
Jin, C. et al. Control of morphology and formation of highly geometrically confined magnetic skyrmions. Nat. Commun. 8, 15569 (2017).
Birch, M. T. & Cortés-Ortuño, D. Data from Bloch point-mediated skyrmion annihilation in three dimensions. Zenodo. Available at https://doi.org/10.5281/zenodo.4384569 (2021).
Acknowledgements
The authors thank P. Steadman, R. Fan and M. Sussmuth at Diamond Light Source for help with the magnetometry measurements. Appreciation is given to K. Matsuura and K. Vilmos for assistance with the electric polarisation measurements. The work was funded by the UK Skyrmion Project EPSRC Programme Grant (EP/N032128/1). M.T.B. acknowledges support from the Max Planck Society.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
M.T.B., D.C.-O. and P.D.H. conceived the project. A.S. and G.B. fabricated the single-crystal sample. N.D.K., S.S. and G.B. performed the electric polarisation measurements with input from Y.T. M.T.B carried out the magnetometry experiments. D.C-O. performed the computational simulations. M.T.B. and D.C-O. wrote the manuscript with input from all authors. All authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Birch, M.T., Cortés-Ortuño, D., Khanh, N.D. et al. Topological defect-mediated skyrmion annihilation in three dimensions. Commun Phys 4, 175 (2021). https://doi.org/10.1038/s42005-021-00675-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00675-4
This article is cited by
-
Three-dimensional neutron far-field tomography of a bulk skyrmion lattice
Nature Physics (2023)
-
Toggle-like current-induced Bloch point dynamics of 3D skyrmion strings in a room temperature nanowire
Nature Communications (2022)
-
Simulating anti-skyrmions on a lattice
Scientific Reports (2022)
-
Formation of magnetic biskyrmions mediated by an intrinsic emergent monopole-antimonopole pair
npj Quantum Materials (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.