Introduction

Harnessing emergent orders in quantum materials has the potential to revolutionise energy and information technologies1. Complex interactions between lattice, electron, and spin degrees-of-freedom in these systems can give rise to emergent physics, such as unconventional superconductivity2, topological protection3,4, or charge density wave (CDW) order and tailored interactions in two-dimensional (2D) materials5. Traditionally, control of materials has been achieved by adiabatic tuning of external parameters. Alternatively, ultrashort light pulses can be employed to perturb and transform states in quantum materials on femtosecond timescales6,7. The quest to probe and control electronic and lattice structural dynamics in solids has driven the utilisation of advanced ultrafast spectroscopies, including ultrafast X-ray and electron diffraction8,9,10,11,12,13, multi-terahertz fields14,15,16, and time-resolved photoemission17,18,19.

Tantalum dichalcogenides (TaX2, X = S, Se, Te) represent a class of materials that are well-matched for this pursuit, and have gained increasing attention as quasi-2D systems with enhanced Coulomb and electron–lattice interactions20,21,22. These compounds exhibit rich phase diagrams, including semi-metallic, charge-ordered, and superconducting behaviours. Multiple CDW phases are observed in 1T-TaS2, which has spawned numerous ultrafast studies to clarify the formation mechanisms and phase competition23,24,25. Moreover, ultrafast driving exposed novel metastable phases in these systems, resulting in a new paradigm of hidden states26,27. Members of the 1T-TaSe2 − xTex family exhibit varying polytypes, CDW ground states, as well as superconductivity depending on composition28. Ultrafast optical melting and switching between CDW phases have so far been demonstrated in TaSe2 and in TaSe2 − xTex alloys, accessing a range of dynamical pathways and timescales29,30,31.

Curiously eluding ultrafast investigation thus far is TaTe2. This compound exhibits markedly different properties with respect to the other Ta dichalcogenides, attributed to weaker electronegativity of Te with respect to Ta leading to a strong propensity for charge transfer and metal–metal bonding32,33,34. TaTe2 exhibits stronger electron–phonon coupling, higher charge-order binding energy, and larger lattice distortions than TaS2 and TaSe2 compounds22,35. The room temperature distorted monoclinic 1T′ crystal structure is characterised by an intra-layer (3 × 1) linear stripe-like order composed of double zigzag Ta trimer chains. A structural transition into a phase with (3 × 3) order occurs at TPT = 174 K, with Ta atoms forming trimer clusters along the linear chains with commensurate CDW-like order33,36,37,38. Unlike other TaX2 CDW systems39,40, the low-temperature (LT) phase ordering of TaTe2 exhibits metallic behaviour, with enhanced conductivity and magnetic susceptibility41. However, the ultrafast response of this compound to optical driving remains unknown. This motivates the use of advanced structural probes to follow the evolution of distortions and periodic order, as a measure of underlying interactions.

We report the ultrafast investigation of TaTe2, demonstrating a rapid picosecond melting of its trimer cluster lattice superstructure in the LT phase. Ultrafast electron diffraction (UED) with relativistic electron bunches is applied using the High Repetition-rate Electron Scattering (HiRES) beamline42,43,44 to probe the time evolution of lattice order after intense near-infrared (near-IR) excitation. We observe photo-induced melting of the LT order on a ≈1.4 ps timescale, indicative of fast switching, followed by recovery into a hot (3 × 3) trimer phase. Insight into the nature of trimer cluster melting is obtained via density functional calculations, which indicate an initial quench driven by charge-transfer transitions from bonding to non-bonding states of the Ta trimer—suggesting pathways for a photo-induced transition that is unique among the family of TaX2 materials. This work establishes TaTe2 as a promising material for optical control, motivating examination of concomitant electronic dynamics for device applications.

Results

Crystal structure and signatures of structural phase transition

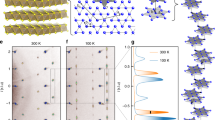
Figure 1a illustrates the crystal structure of TaTe2 in its LT phase. Triple-layer sheets of covalently bonded Ta and Te atoms are separated by weaker van der Waals forces along the stacking direction. Prominent structural elements in this material are Ta trimers—sets of three adjacent Ta atoms in a row that cluster together via enhanced Ta–Ta bonding. Already at room temperature, Ta atoms are ordered in-plane into trimers assembled into double zigzag chains along the b-axis, which breaks hexagonal symmetry and forms a three-layer stacking sequence. In the LT phase, additional ordering emerges in the chains along the b-axis in the form of trimer clusters. This (3 × 3) lattice superstructure represents a distorted 1T′ polytype with C2/m space group symmetry and a monoclinic unit cell45. In this configuration, each Ta atom in the unit cell is coordinated to six Te atoms in a periodically distorted octahedral arrangement.

Fig. 1: Crystal structure and electron diffraction patterns at thermal equilibria.
figure 1

a Layered crystal structure of the low-temperature phase of 1T′-TaTe2. The electron beam is incident perpendicular to Ta and Te planes in the ultrafast electron diffraction (UED) experiments. The a, b, and c lattice vectors shown are those of the monoclinic unit cell. The projection perpendicular to the dashed region is indicated. Black box: Ta trimer clusters forming along the b-axis in the low-temperature (LT) phase. Representations of LT and high-temperature (HT) phases showing enhanced distortions in the LT phase are presented in the top right. Small black arrows denote the movement of atoms towards the central Ta atom. b Static electron diffraction patterns of 1T′-TaTe2 obtained by 0.75 MeV electron pulses at 298 K (HT) and 10 K (LT) along the \([\bar{1}01]\) zone axis. Note the different indices for the LT pattern due to tripling along the b-axis. The inset shows the (3 × 3) periodic lattice distortion satellite (superlattice) peaks that arise in the LT phase. A few additional peaks are present due to diffraction from the Si support frame (see Supplementary Note 2 for sample details). The symmetrised difference pattern between HT and LT phases is shown below the static patterns, with contributions from the Si frame and silicon nitride (Si3N4) membrane removed. The colour scale gives the absolute diffracted intensity change (ΔI).

Full size image

Our density functional theory (DFT) calculations of relaxed structures of TaTe2 confirm the distortions due to an atomic ordering of Ta atoms attributed to metal–metal bonding, in agreement with the structures previously determined by X-ray diffraction33. Moreover, our calculations also reveal enhanced Ta–Ta bonds along the b-axis in the LT phase as highlighted in Fig. 1a, resulting in the tripling along the b-axis corresponding to an overall (3 × 3) superstructure (cf. Supplementary Note 1 for additional details).

Figure 1b shows equilibrium diffraction patterns of a 1T′-TaTe2 flake which we measured with the 0.75 MeV electron bunches at HiRES, comparing the high-temperature (HT) phase at 298 K and LT phase at 10 K. As illustrated in Fig. 1a, the electron beam impinges along the \([\bar{1}01]\) zone axis, i.e., perpendicular to the Ta and Te layers. The measured diffraction patterns exhibit a large number of Bragg spots reaching up to high momentum transfer, demonstrating both a high sample crystallinity and a large scattering range afforded by the relativistic beam energy. More details about the sample and its preparation, including transport measurements, are given in the “Methods” and in Supplementary Note 2.

At 298 K, we observe twofold symmetry exemplified, for instance, by differences of the (020) and (313) Bragg peaks in intensity and their relative distance from the centre. This is consistent with the (3 × 1) periodicity and the monoclinic crystal structure.

The pattern at 10 K in Fig. 1b reveals the appearance of new satellite peaks surrounding the main lattice peaks as a result of the emergent (3 × 3) periodic lattice distortion (PLD), in concordance with Ta trimer cluster formation and the associated unit cell tripling33,36,37,38. Their observation also demonstrates that the transverse coherence length of the electron source is sufficient to track the dynamics of the LT superstructure in 1T′-TaTe2. Analogous satellite peaks in the HT phase are ≈1000 times weaker than the main Bragg peaks and are not observed in these measurements (see Supplementary Note 2).

To determine the signature in the electron diffraction patterns attributed to the structural phase transition, we calculate the difference between HT and LT patterns, following normalisation by the total electron intensity. The resulting changes are shown at the bottom of Fig. 1b. While all superlattice satellites associated with the (3 × 3) trimer superstructure are suppressed, the main Bragg peaks exhibit a mixture of positive and negative intensity changes. This complex response deviates from observations in TaS2 and TaSe2, where all primary Bragg peaks increased in intensity, opposite to the suppression of the PLD satellites23,46. We attribute this positive–negative intensity change signature to the symmetry of the superstructure formation within the distorted monoclinic unit cell, leading to mixed structure factor changes for different diffraction orders as supported by our simulations (see Supplementary Note 3)47,48.

Ultrafast optical melting of trimer clusters

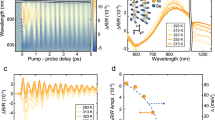
We utilise the HiRES beamline for UED. The sample was first cooled into the LT ordered phase at 10 K, and then photo-excited with near-IR femtosecond pulses (1030 nm wavelength). Time-delayed electron pulses at 0.75 MeV are used as structural probe, as illustrated in Fig. 2a. Recorded diffraction patterns with and without excitation provide signatures of photo-induced changes for each pump-probe time delay.

Fig. 2: Ultrafast electron diffraction of TaTe2.
figure 2

a Illustration of the optical pump, electron diffraction probe experiment. b Photo-induced changes in the diffraction patterns, for selected time delays. The colour scale gives the absolute diffracted intensity change (ΔI). The patterns have been symmetrised for visualisation purposes only. c Temporal evolution of the signals from the main lattice Bragg peaks, separately for the increasing and decreasing subsets, and of the low-temperature (LT) phase superlattice peaks. Solid lines: fits with an exponential function convolved with the time resolution of 0.75 ps, up to 7 ps delay time. The corresponding time constants are τPLD = 1.44 ± 0.27 ps for the superlattice peaks and τBragg↑ = 2.44 ± 0.81 ps and τBragg↓ = 2.25 ± 1.34 ps for the main lattice peak subsets. Error bars in the data indicate standard error calculated using the distribution of laser-off signals compared to the mean laser-off signal over the course of the measurement.

Full size image

Difference maps of the diffraction intensity at selected time delays Δt are shown in Fig. 2b for a pump fluence of 2.3 mJ cm−2, indicating structural changes on a picosecond timescale. For clearer visualisation, these maps are symmetrised by averaging signals across the vertical and horizontal mirror plane symmetries (the process is described in Supplementary Note 4). At early times, the signals exhibit a characteristic pattern of changes, including a decrease of the (3 × 3) PLD satellites, and a mixture of increased and decreased intensities of the main lattice Bragg peaks (see diffraction pattern at Δt = 4 ps in Fig. 2b). This pattern strongly resembles that of the HT–LT phase transition obtained from the equilibrium data in Fig. 1a. This indicates that the intense near-IR excitation induces a melting of the LT trimer clusters and an ultrafast phase transition to the (3 × 1) ordered HT state in TaTe2.

In order to track the structural kinetics, we fit all peaks for each time-delayed UED pattern, summing the photo-induced changes of specific subsets for optimal signal-to-noise (the peak fitting procedure is provided in Supplementary Note 5). Figure 2c plots the dynamics of the set of lattice Bragg peaks exhibiting an intensity increase (Bragg↑) or decrease (Bragg↓) in the pattern, as well as the changes of the superlattice satellites. Normalised to their intensities before excitation, the PLD satellites undergo ≈55% suppression with a time constant of τPLD ≈ 1.4 ps (details of the fitting are provided in Supplementary Note 6). This time constant provides a measure of the (3 × 3) trimer superstructure melting time in TaTe2 in our experiments. We note this is likely preceded by a faster electronic melting time, which we cannot access here, but could be a subject of future spectroscopic investigations17.

Alongside the PLD suppression, the primary lattice Bragg peaks also exhibit strong changes with slower dynamics corresponding to time constants of τBragg↑ ≈ 2.4 ps and τBragg↓ ≈ 2.3 ps. The underlying diffraction orders show comparable dynamics (see Supplementary Note 7). Moreover, an oscillation seems to appear in the Bragg↓ trace, with a period of ≈2 ps. While this may be linked to excitation of coherent phonons, the ≈0.5 THz frequency does not match vibrational modes identified by theory (cf. Supplementary Note 1). The lack of a similar feature on the Bragg↑ curve does not rule out a coherent phonon origin. However, the error bars in the Bragg↓ trace are larger due to its weaker constituent high-q peaks (cf. Supplementary Note 7) and the fluctuation is comparable to measurement error. While beyond the scope of our present work, future investigations are warranted to clarify the presence of coherent lattice motion. We also note that at negative time delays, a few-percent intensity reduction is observed in both the superlattice and Bragg↓ peaks, which we attribute to residual heating accumulated over several laser pulses.

Re-formation of lattice superstructure

Following the melting of the trimer clusters, further structural dynamics ensues that is marked by the recovery of the (3 × 3) superstructure due to lattice thermalisation. Figure 3a shows transient difference maps, where the data have been averaged for two representative time ranges corresponding to early (Δt = 3–5 ps) and late (50–80 ps) time delays. The pattern at early times exhibits the clear signature of the (3 × 3) trimer superstructure melting discussed above, while at later times such signature disappears and the pattern recovers the LT superlattice. The broad overall reduction of the peak intensities in this time range is that expected of a heated state with incoherent thermal atomic motions via the Debye–Waller effect46,49. Between these time ranges, we note that diffraction peaks on one side of the pattern increase while those on the other side decrease, indicating mechanical buckling of the sample as it accommodates the structural phase change and lattice heating50,51. Difference images from these time ranges are shown in Supplementary Note 4.

Fig. 3: Re-formation of superstructure and Debye–Waller dynamics.
figure 3

a Representative symmetrised difference images for early (centred around ≈4 ps) and late (around ≈65 ps) time delays. The colour scale gives the absolute diffracted intensity change (ΔI). For improved signal-to-noise these are calculated by averaging difference patterns over time ranges, i.e., 3–5 ps for early and 50–80 ps for late time delays. For the late time delays, all Bragg peaks exhibit a loss of intensity indicative of a Debye–Waller effect. b Dynamics of the superlattice peaks over an extended timescale. Yellow shading indicates time ranges that were averaged to generate the difference images. A partial recovery is observed, fit with an exponential relaxation with offset (red line) with time constant τ = 6.6 ± 2.6 ps. The long-lived suppression indicates that the lattice system has thermalised at an elevated temperature. Error bars in the data indicate standard error calculated using the distribution of laser-off signals compared to the mean laser-off signal over the course of the measurement.

Full size image

As seen in Fig. 3b—which plots the time evolution of the PLD side peaks over the entire measurement window—the suppressed trimer order recovers ≈20% of the original intensity with a ≈7 ps time constant. We note that this timescale may be influenced by simultaneous contribution from mechanical buckling. The overall suppression of the diffraction peaks relative to the LT ground state indicates the thermalisation of the lattice degrees-of-freedom into a “hot” (3 × 3) trimer superstructure at longer delays. We can estimate the maximum lattice thermalised temperature due to full thermalisation of the absorbed laser energy. For the given 2.3 mJ cm−2 fluence, this results in a temperature of 177 K, based on the 1T′-TaTe2 heat capacity33 and the optical constants we measured of our 60-nm thick flake (see Supplementary Notes 8 and 9). We also performed experiments on the same sample at 1.75 and 1.5 mJ cm−2 fluence. The signature of the structural phase transition was reproduced for these fluences with reduced magnitude (see Supplementary Note 9).

Discussion

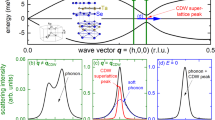
Figure 4 illustrates the proposed sequence of phases in the ultrafast dynamics of TaTe2. Photo-excitation with intense pulses leads to the excitation of energetic carriers and picosecond melting of the LT (3 × 3) trimer superstructure phase. The transient phase that results corresponds to a (3 × 1) trimer chain order, as inferred from the close overlap of the photo-induced change in the diffraction pattern with the fingerprint of the LT–HT transition. In the subsequent picoseconds, the lattice degrees-of-freedom thermalise, enhancing Ta–Ta bonds and thereby switching into a hot (3 × 3) superstructure state. The latter persists for extended times (≫80 ps) until thermal diffusion transfers heat into the substrate.

Fig. 4: Proposed stages of the photo-induced dynamics in 1T′-TaTe2.
figure 4

The system starts in the low-temperature (LT) phase with a (3 × 3) superstructure of Ta trimer clusters (I). Near-infrared excitation promotes carriers from bonding to non-bonding states via a charge-transfer excitation, which results in melting of the trimer clusters and leaves behind stripe-like trimer chains (II). Subsequently, the lattice subsystem thermalises, causing the (3 × 3) superstructure to re-establish and stablise at elevated temperatures (III). Inset: density of states (DOS) projected onto Ta and Te atoms as calculated using density functional theory, along with schematic optically induced promotion from bonding to non-bonding Ta orbitals, which lie in the plane. EF denotes the Fermi level. The participating Ta trimer bonding and non-bonding (with a node in the middle) orbitals are shown.

Full size image

DFT calculations clarified the electronic states involved in the photo-excitation. We computed the projected density of states and crystal orbital Hamilton population (COHP) of the relaxed LT and HT structures of TaTe2, revealing the nature of occupied and unoccupied states, as shown in Fig. 4 (see Supplementary Note 1 for details and Supplementary Data 1 for atomic coordinates of the calculated relaxed structures). In the LT phase, the lower-energy region of the valence band (i.e., below −4 eV) consists of Te p-states with a small contribution from Ta d-states, whereas the upper region of the band (i.e., above −2 eV) has mostly Ta character. Negative COHP values in the upper valence band indicate the bonding nature of Ta trimer states in this energy region. Trimer formation is enabled by partial charge transfer from Te to Ta involving dxz and dxy states, which leaves uneven charges on Ta sites and enhanced Ta–Ta bonding36. Meanwhile, conduction band states near the Fermi level belong to non-bonding states of Ta trimers, with anti-bonding states lying higher in energy (≈4 eV above EF).

Optical absorption in 1T′-TaTe2 involves mainly two kinds of dipole-allowed charge-transfer transitions (see Supplementary Note 1): promoting either Te p to Ta anti-bonding states (type-I), or depopulating bonding states while populating non-bonding states of the b-axis trimers above the Fermi level (type-II). Photo-excitation around 1.2 eV chiefly involves the latter, which weakens the original charge disproportionation between Ta sites within these trimers, thus triggering the “melting” of the (3 × 3) order. The calculations also identified several strongly coupled phonons, including a mode around 2.7 THz involving Te motions and displacements of the Ta ions along the trimer axes that may be set into motion after optical charge-transfer excitation. This predicts a cooperative mechanism for photo-induced trimer cluster dissolution in TaTe2, which can be addressed in future diffraction studies with higher temporal resolution and time-resolved diffuse scattering to directly track the phonon modes participating in the transformation.

Our study hence represents the first ultrafast measurement of TaTe2, utilising short MeV electron bunches to resolve a picosecond atomic-scale melting of its intriguing trimer clusters and the subsequent thermalisation into a hot (3 × 3) superstructure phase. In these and other MTe2 systems (where M = transition metal), changes in the lattice structure are linked to anomalous changes in conductivity and magnetic susceptibility. The light-driven toggle and recovery seen here to occur between different lattice symmetries may thus enable applications, e.g., for ultrafast switching. Moreover, the associated trimer dynamics in this material opens the possibility for control of the related electronic modulations in TaTe2 on even faster timescales.

Methods

Ultrafast electron diffraction

The UED experiments were performed at the HiRES beamline at Lawrence Berkeley National Laboratory (LBNL). The instrument exploits a one-of-a-kind technology developed at LBNL to provide unique beam properties for ultrafast structural dynamics studies, coupling relativistic electrons and high repetition rates. The results reported in the paper validate the technological breakthrough, which has the potential of broadening the scientific reach of ultrafast tools. Near-IR laser pulses centred at ≈1030 nm wavelength and with ≈350 fs duration (full-width at half-maximum, FWHM) were used to photo-excite the sample. Synchronised electron pulses with 0.75 MeV kinetic energy (de Broglie wavelength λ = 0.01 Å) were delivered to the sample for electron diffraction. Experiments were performed at 0.5 kHz repetition rate, recording ten frames with the pump beam OFF and ten frames with the pump ON for each time delay. Each frame was recorded for an exposure time of 8 s. A home-built sample stage interfaced to a closed-cycle cryostat was used to cryogenically cool the samples down to 10 K. Laser and electron beams impinged on the TaTe2 sample surface, transmitting through a supporting silicon nitride window. The electron beam diameter at the sample was ≈450 μm FWHM, while the pump beam was adjusted to ≈750 μm FWHM to ensure homogeneous excitation across the probe volume. The beam charge was ≈2.5 fC corresponding to 1.6 × 104 electrons/pulse. We confirmed sample reversibility by measuring intensities of the diffraction peaks in pump OFF images normalised to their intensities before excitation as a function of pump laser shots (see Supplementary Note 10).

TaTe2 samples

Single crystals of 1T′-TaTe2 were grown by the chemical vapour transport technique52 at 700–800 °C for 14 days using iodine as a transport agent. The crystals were repeatedly mechanically exfoliated with Scotch tape until optically transparent and then dry transferred onto 20-nm thick Si3N4 windows using polydimethylsiloxane stamps53. The thickness of the TaTe2 flake was determined to be ≈60 nm using atomic force microscopy (AFM; see Supplementary Note 2).

Simulations, image analysis, and standard error

Details of DFT calculations, electron diffraction simulations, and diffraction image analysis methods are provided in Supplementary Notes 1, 3, and 4, respectively. The Supplementary Data 1 file contains the atomic coordinates of the relaxed structures. The error bars in Figs. 2c and 3b represent the standard error for the given number of averaged frames. The corresponding standard deviation per frame is derived (for each peak set Bragg↑, Bragg↓, and superlattice) from the distribution of laser-off frames, multiplied by \(\sqrt{2}\) to account for the total standard deviation when subtracting (laser on) − (laser off) frames.