Introduction

Rydberg-state atoms provide a strong dipole–dipole interaction (DDI) and a dipole blockade mechanism1,2,3,4 suitable for applications in quantum information processing, such as quantum simulators5,6,7, quantum logic gates8,9,10,11, and single-photon sources12,13,14. The effect of electromagnetically induced transparency (EIT) reduces the propagation speed of light in media and significantly increases the light-matter interaction time15,16,17,18,19. Thus, the EIT effect involving the Rydberg atoms can efficiently mediate significant photon–photon interactions20,21,22,23,24,25, and this issue has attracted a great deal of attention recently. Most of the previous Rydberg-EIT studies concentrated on strongly-correlated photons in the dipole blockade regime, which emerges for the strongly-interacting Rydberg atoms with a high principal quantum number, n, close to 100. This leads to, for example, the two-body photon–photon gates11,22 and strongly-correlated many-body phases21,25.

The system of the Rydberg EIT polaritons is an ensemble of bosonic quasiparticles26,27. The dispersion relation and momentum distribution of the Rydberg polaritons can be associated with their effective mass and the temperature28. The phase shift and attenuation of the output light induced by the DDI can be viewed as a consequence of the elastic and inelastic collisions among the polaritons. Hence, the change rates of the phase shift and attenuation are related to the elastic and inelastic collision rates, respectively. Finally, the propagation time of slow light or the diffusion time of stationary light in the EIT system is exactly the interaction time of the particles.

Here we proposed and experimentally demonstrated an innovative idea of utilizing a medium with a high optical depth (OD) and Rydberg atoms with a low principal quantum number to create a weakly-interacting many-body system based on the EIT effect. In this work, OD ≈ 80 and n = 32 were used. We studied the EIT polaritons also known as the dark-state polaritons26,27,29, which, in the case of the Rydberg EIT, are quasi-particles representing superpositions of photons and Rydberg coherences. The Rydberg coherence is the coherence between the atomic ground and Rydberg states. Weakly-interacting Rydberg polaritons under an OD-enhanced interaction time can be employed in the study of many-body physics, such as the Bose–Einstein condensation (BEC)28,30,31,32,33,34,35,36.

The low-n Rydberg state, together with a moderate polariton density, ensured the weak-interaction regime in our experiment, i.e., \({r}_{B}^{3}/{r}_{a}^{3}\ll 1\), where rB is the blockade radius and ra is the half mean distance between Rydberg polaritons. In this regime, the mean number of Rydberg polaritons in a blockade sphere is much less than the unity, and thus attenuation due to the blockade effect occurs rarely. The collision cross-section of polaritons due to the DDI is around μm2 in the Rydberg state of n = 32, leading to the elastic collision rate of a few MHz at the Rydberg-polariton density of 2 × 109 cm−3 used in this work. On the other hand, the high-OD medium provides for the Rydberg polaritons a long interaction time of a few μs, as demonstrated here and in our previous works17,18. Therefore, a high OD can result in a sufficiently large product of the collision rate and interaction time for weakly-interacting Rydberg polaritons, enabling them to exhibit many-body phenomena28,37,38.

In this work, we systematically studied the phase shift and attenuation of an output probe light for the EIT involving a Rydberg state of \(\left|32{D}_{5/2}\right\rangle\). Owing to the high OD and low intrinsic decoherence rate in the system, to the best of our knowledge, our experiment is the first one to demonstrate the DDI effect in the truly weak-interaction regime, i.e., \({r}_{B}^{3}/{r}_{a}^{3}\,<\,0.1\), as compared with previous experiments20,21,22,39,40,41,42,43,44. We were able to clearly observe the DDI-induced attenuation and phase shift even at \({r}_{B}^{3}/{r}_{a}^{3}=0.02\). Furthermore, we varied the DDI strength via the input photon flux and measured the transverse momentum distribution of the Rydberg polaritons. A larger DDI strength caused the width of the momentum distribution to become notably smaller, indicating the thermalization process was driven by elastic collisions28,45,46. The observed reduction of the momentum distribution width suggested that the combination of the μm-range DDI strength and the μs-long light-matter interaction time can make the BEC of the Rydberg polaritons feasible.

Results

Experimental setup

We carried out the experiment in cold 87Rb atoms produced by a magneto-optical trap (MOT). There were typically 5 × 108 trapped atoms with a temperature of about 350 μK in the MOT47,48. The cigar-shaped atomic cloud had a dimension of 1.8 × 1.8 × 6.0 mm3. Before each measurement, we first turned off the magnetic field of the MOT and then performed the dark MOT for 2.5 ms to increase the OD of the system18,49. The OD of the atomic cloud was 81 ± 3. When the experimental condition of a low OD was needed, we were able to adjust the dark-MOT parameter to reduce the OD of the system by about fourfolds.

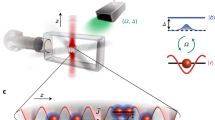
Figure 1a shows the transitions driven by the probe and the coupling fields in the EIT system. We optically pumped all population to a single Zeeman state \(\left|F=2,{m}_{F}=2\right\rangle\) at the ground level \(\left|5{S}_{1/2}\right\rangle\)49. Since the probe and coupling fields were σ+-polarized, each of the energy levels \(\left|1\right\rangle\), \(\left|2\right\rangle\) and \(\left|3\right\rangle\) shown in Fig. 1a was a single Zeeman state. The spontaneous decay rate, Γ, of \(\left|3\right\rangle\) is 2π × 6 MHz, and \(\left|1\right\rangle \leftrightarrow \left|3\right\rangle\) is a cycling transition. The lifetime, \({{{\Gamma }}}_{2}^{-1}\), of \(\left|2\right\rangle\) is about 30 μs50, and Γ2 ≪ γ0 in this work, where γ0 is the intrinsic decoherence rate of the system. Thus, the influence of Γ2 was negligible. We estimated natom ≈ 5 × 1010 cm−3 in the experiment, and C6 = −2π × 260 MHz· μm6 for \(\left|32{D}_{5/2},{m}_{J}=5/2\right\rangle\) by using Dφ = 0.343, where Dφ is the coefficient resulted from the angular momentum states of two interacting Rydberg atoms being \(\left|J=5/2,{m}_{J}=5/2\right\rangle\)51. Such C6 together with natom can make the DDI effect unobservable under a small Ωp or a low OD20,39,52,53.

Fig. 1: Transition scheme and experimental setup.
figure 1

a Relevant energy levels and laser excitations in the experiment. States \(\left|1\right\rangle\), \(\left|2\right\rangle\), and \(\left|3\right\rangle\) correspond to the ground state \(\left|5{S}_{1/2},F=2,{m}_{F}=2\right\rangle\), Rydberg state \(\left|32{D}_{5/2},{m}_{J}=5/2\right\rangle\), and excited state \(\left|5{P}_{3/2},F=3,{m}_{F}=3\right\rangle\) of 87Rb atoms. Ωc and Ωp denote the coupling and probe Rabi frequencies, and Δc and Δp represent their detunings. b Experimental setup. AOM acousto-optic modulator, BSa, BSb: beam splitters, CLa, CLb, CLc: collimation lenses, PMF polarization-maintained optical fiber, BB beam block, Ma: mirror, Mb: movable mirror on a flip mount, PD photodetector (Thorlabs APD110A), PBS polarizing beam splitter, DM dichroic mirror, L1, L2, L3: lenses, QWP quarter-wave plate, EMCCD electron-multiplying charge-coupled device camera (Andor DL-604M-OEM), MMF multimode optical fiber, PMT photomultiplier tube and amplifier (Hamamatsu H6780-20 and C9663). Blue, red, and brown arrowed lines indicate the optical paths of the coupling, probe, and AOM’s zeroth-order beams, respectively.

Full size image

Figure 1b shows the experimental setup. The probe field came from the first-order beam of an acousto-optic modulator (AOM) and was coupled to a polarization maintained fiber (PMF). The PMF delivered the probe field to the cold atoms. The probe field was twice diffracted from the AOM in the double-pass scheme. The AOM was used to shape the probe pulse, and its driving rf frequency and amplitude were precisely tuned or varied by a function generator. We used a rubidium atomic standard (SRS FS752) as the external clock of the function generator. The blue path in Fig. 1b represents the coupling field, which was switched on and off with another AOM not drawn in the figure. Inside the atom cloud, the probe and coupling fields counter-propagated and completely overlapped to minimize the Doppler effect. The e−1 full widths of the probe and coupling beams were 130 and 250 μm, respectively. After passing through the atoms, the probe field was detected by a photomultiplier tube (PMT). A digital oscilloscope (Agilent MSO6014A) acquired the signal from the PMT and produced raw data.

The entire setup of red and brown optical paths shown in Fig. 1b formed the beat-note interferometer, which measured the phase shift of the output probe field (see beat-note interferometer in “Method”). The brown optical paths were present only in the phase shift measurement.

Theoretical model

The mean-field model developed in Ref. 54, which describes the DDI-induced attenuation and phase shift in the system of weakly-interacting Rydberg polaritons, is summarized in this section. Rydberg polaritons are randomly distributed and can be considered approximately as particles of a nearly ideal gas due to their weak interaction. Thus, the nearest-neighbor distribution55 was utilized in our theory. Using the probability function of the nearest-neighbor distribution and the atom-light coupling equations of an EIT system, we derived the following analytical formulas of the steady-state DDI-induced attenuation coefficient Δβ and phase shift Δϕ:

$${{\Delta }}\beta =2{S}_{{\rm{DDI}}}\left(\frac{\sqrt{{W}_{c}-2{{{\Delta }}}_{c}}}{{W}_{c}}-\frac{3{\gamma }_{0}\sqrt{{W}_{c}+2{{{\Delta }}}_{c}}}{{{{\Omega }}}_{c}^{2}}\right){{{\Omega }}}_{p}^{2},\,\,$$
(1)
$${{\Delta }}\phi ={S}_{{\rm{DDI}}}\left(\frac{\sqrt{{W}_{c}+2{{{\Delta }}}_{c}}}{{W}_{c}}-\frac{3{\gamma }_{0}\sqrt{{W}_{c}-2{{{\Delta }}}_{c}}}{{{{\Omega }}}_{c}^{2}}\right){{{\Omega }}}_{p}^{2},\,$$
(2)
$${S}_{{\rm{DDI}}}\equiv \frac{{\pi }^{2}\alpha {{\Gamma }}\sqrt{| {C}_{6}| }{n}_{{\rm{atom}}}\varepsilon }{3{{{\Omega }}}_{c}^{3}},$$
(3)
$${W}_{c}\equiv \sqrt{{{{\Gamma }}}^{2}+4{{{\Delta }}}_{c}^{2}},$$
(4)

where α is the OD of the system, Γ is the spontaneous decay rate of the excited state \(\left|3\right\rangle\), γ0 is the intrinsic decoherence rate in the system, C6 is the van der Waals coefficient in SI units of Hz· m6, natom is the atomic density, and ε is a phenomenological parameter. In the above equations, we assume \({{{\Omega }}}_{p}^{2}\ll {{{\Omega }}}_{c}^{2}\) and \({r}_{B}^{3}\ll {r}_{a}^{3}\), and consider the case that the two-photon detuning δ is much smaller than the EIT linewidth and its influence on Δβ and Δϕ is negligible. Furthermore, ε is utilized to relate the average Rydberg-state population (ρ22) to the input probe and coupling Rabi frequencies (Ωp and Ωc) as \({\rho }_{22}=\varepsilon {{{\Omega }}}_{p}^{2}/{{{\Omega }}}_{c}^{2}\). Equations (1) and (2) are for the case of C6 < 0. They qualitatively agree with those in the pioneering work of Ref. 56 and served as the theoretical references for the experimental data in this work.

The attenuation coefficient β and phase shift ϕ of the probe field is defined by the output-input (\({{{\Omega }}}_{p}^{\prime}\)–Ωp) relation of \({{{\Omega }}}_{p}^{\prime}={{{\Omega }}}_{p}\exp (i\phi -\beta /2)\). Thus,

$$\beta ={\beta }_{0}+{{\Delta }}\beta \approx \frac{2\alpha {\gamma }_{0}{{\Gamma }}}{{{{\Omega }}}_{c}^{2}}+{{\Delta }}\beta ,$$
(5)
$$\phi ={\phi }_{0}+{{\Delta }}\phi \approx \frac{\alpha {{\Gamma }}\delta }{{{{\Omega }}}_{c}^{2}}+{{\Delta }}\phi ,$$
(6)

where β0 and ϕ0 are the attenuation coefficient and phase shift in the absence of DDI54, δ( = Δp + Δc) is the two-photon detuning. The mean-field theory predicted that both β and ϕ depend on \({{{\Omega }}}_{p}^{2}\) linearly, and the dependence of \({{{\Omega }}}_{p}^{2}\) comes from the Rydberg-state population ρ22. In addition, the slope of β or ϕ versus \({{{\Omega }}}_{p}^{2}\) is asymmetric with respect to Δc = 0.

DDI-induced attenuation and phase shift

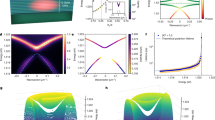
We first verified that the DDI effect can be observed in the system consisting of weakly-interacting Rydberg polaritons. The attenuation coefficient β and phase shift ϕ were measured as functions of the square of the probe Rabi frequency \({{{\Omega }}}_{p}^{2}\), as shown in Fig. 2a, b. A nonzero two-photon detuning, δ, can significantly affect the phase shift and attenuation of the output probe light in the EIT medium. Thus, we utilized a beat-note interferometer to carefully determine the probe frequency for δ = 0 (see beat-note interferometer in “Method”). The uncertainty of δ/2π was ±30 kHz, including the accuracy of the beat-note interferometer of ±10 kHz and the long-term drift of the two-photon frequency of ±20 kHz.

Fig. 2: Attenuation coefficient and phase shift due to the dipole–dipole interaction (DDI).
figure 2

a, b Attenuation coefficient β and phase shift ϕ at δ = 0 as functions of \({{{\Omega }}}_{p}^{2}\) in the presence of the DDI. Circles are the experimental data taken with α (optical depth) = 81 ± 3, Ωc = 1.0Γ, and Δc = −2Γ (black), −1Γ (red), 0 (blue), 1Γ (magenta), and 2Γ (olive), where Γ = 2π × 6 MHz. Straight lines are the best fits. c, d Circles are data points of the slope of a straight line in (a) and (b) versus the corresponding Δc. Black lines are the best fits, which determine SDDI = 37/Γ3/2 in (c) and 38/Γ3/2 in (d). The error bars represent the standard deviation of measured values.

Full size image

At δ = 0, we applied a square input probe pulse and measured the steady-state attenuation coefficient β and phase shift ϕ of the output probe pulse. The measurement procedure and representative data can be found in Supplementary Note 3. Figure 2a (and b) shows β (and ϕ) versus \({{{\Omega }}}_{p}^{2}\) at various Δc, where \({{{\Omega }}}_{p}^{2}\) corresponds to the peak or center intensity of the input Gaussian beam. At a given Δc, the data points approximately formed a straight line, as expected from the theory. We fitted the data with a linear function and plotted the slope of the best fit against Δc, as shown in Fig. 2c, d. It can be noticed that the y-axis interceptions of best fits were scattered in Fig. 2b. Since a change of 30 kHz in δ/2π resulted in that of 0.4 rad in phase, the uncertainty of δ made the interceptions scatter around zero.

The strengths of the DDI effect on β and ϕ, i.e., the slope of β versus \({{{\Omega }}}_{p}^{2}\) and that of ϕ versus \({{{\Omega }}}_{p}^{2}\) (denoted as χβ and χϕ), were asymmetric with respect to Δc = 0 as shown in Fig. 2c, d. Such asymmetries are expected from the theory, as demonstrated by Eqs. (1) and (2). Considering the coupling detunings of −∣Δc∣ and ∣Δc∣, χβ (or χϕ) of −∣Δc∣ was always larger (or smaller) than that of ∣Δc∣. The physical picture of the asymmetries is discussed in Ref. 54. We fitted the data points in Fig. 2c, d with the functions of χβ and χϕ, where γ0 was set to 0.012Γ, and SDDI was the only fitting parameter. The SDDI of the best fit shown in Fig. 2c is in good agreement with that of Fig. 2d. Using Eq. (3) and the values of SDDI, C6, natom, and Ωc, we obtained ε = 0.43 ± 0.05. Considering that ε related the average Rydberg-state population to \({{{\Omega }}}_{p}^{2}\) and that \({{{\Omega }}}_{p}^{2}\) corresponded to the center intensity of the input Gaussian beam, the measured value of SDDI is also reasonable. Thus, the experimental data are in good agreement with the theoretical predictions, revealing that the low-n Rydberg polaritons in the high-OD medium can form a weakly-interacting many-body system.

Feasibility of thermalization process

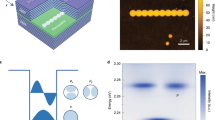
To observe the thermalization process in this weakly-interacting system, we varied the DDI strength and measured the transverse momentum distribution of the Rydberg polaritons. The moveable mirror Mb has shown in Fig. 1b was installed to direct the output probe beam to the EMCCD. Figure 3 shows the key elements for the EMCCD image of the probe beam. We reduced the waist of the input probe beam by adding the lens pair of L4 and L5, as shown in the figure, and made the input photons or initial Rydberg polaritons have a large transverse momentum distribution. In the measurements of Figs. 4–7, the e−1 full width of the probe beam at the center of the atomic cloud was reduced to 39 μm, while we kept the coupling beam size the same as before. Since the coupling beam size was 6.4 times larger than the probe beam size, the waveguide effect due to the coupling intensity profile should play little role in the data of these figures. Furthermore, the attenuation of Rydberg polaritons decreases the particle density and consequently the collision rate. While the propagation delay time, i.e., the interaction time, at Δc of a small magnitude can be maintained approximately the same, the DDI-induced attenuation coefficient of Δc = +1Γ is significantly smaller than those of Δc = 0 and −1 Γ. Hence, we chose the experimental condition of Δc = +1Γ in the study.

Fig. 3: Sketch of key elements for taking images of the probe beam.
figure 3

Values of f indicate the focal lengths of lenses. PMF polarization-maintained optical fiber; CLb: collimation lenses, L2 and L3: lenses, EMCCD electron-multiplying charge-coupled device camera (Andor DL-604M-OEM). The probe beam coming out of CLb was collimated and had the e−1 full width of 0.92 mm. We adjusted the separation between L4 and L5 such that the beam was focused on nearly the center of the atomic cloud by L2, and had the width of 39 μm at the focal point.

Full size image
Fig. 4: Determination of the two-photon detuning for the zero phase shift.
figure 4

Black (or red) circles are the experimental data of phase shift versus two-photon detuning measured at α (optical depth) = 82, Ωc = 1.0Γ, Δc = 1.0Γ, and Ωp = 0.10Γ (or 0.20Γ). Black and red lines represent the linear best fits. We determined the two-photon detuning, δ0, for the zero phase shift, i.e., ϕ = 0, by the intersection between the best fit and the gray dashed line. As references, blue and green lines are the theoretical predictions calculated numerically54. The error bars represent the standard deviation of measured values.

Full size image

Following the idea in Ref. 28, we estimate the elastic collision rate, which is responsible for the thermalization, of the Rydberg polaritons from the formula below:

$$\frac{d\phi }{dt}={R}_{c}{\phi }_{c},$$
(7)

where dϕ/dt is the phase shift per unit time, Rc denotes the collision rate, and ϕc represents the phase shift per collision. Note that in the case of Δc = −1 Γ, for example, some collisions result in positive phase shifts and some result in negative phase shifts54, and thus the net phase shift is close to zero. Such a case cannot be used to make an estimation of the collision rate. To ensure that the phase shifts induced by the collisions are all positive, we should use the case of Δc = 0 or +1 Γ in the estimation. The value of dϕ/dt can be estimated from the experimentally observed value of Δϕ/τd, where Δϕ is the DDI-induced phase shift measured at the output of the medium and τd is the propagation delay time, i.e., the interaction time of Rydberg polaritons. Using τd = 2.1 μs and the data point is shown in Fig. 2b of Δc = +1Γ and Ωp = 0.2Γ resulted in dϕ/dt = 0.64 rad/μs. Note that the experimental condition of Ωp = 0.2 Γ corresponded to the Rydberg-polariton density of 2 × 109 cm−3. Considering the hard-sphere collision, \({\phi }_{c}=\bar{k}a\) where \(\hslash \bar{k}\) is the root-mean-square value of the relative momentum between two colliding bodies, and a is the radius of a hard-sphere. In view of the Rydberg polaritons, a can be treated as the blockade radius57, which was about 2.1 μm in our case according to the formula21 of \({r}_{B}={(2{C}_{6}{{\Gamma }}/{{{\Omega }}}_{c}^{2})}^{1/6}\). The momentum distribution, which we measured in this study and will be shown later, indicated \(\bar{k}=0.051\) μm−1. The values of \(\bar{k}\) and a result in ϕc = 0.11 rad. Thus, we obtain Rc = 6.0 MHz by inserting the values of dϕ/dt and ϕc in Eq. (7). Under such an elastic collision rate, it was feasible to observe the thermalization effect in our experiment.

Procedure of the beam profile measurement

We measured the output probe beam size on the EMCCD at Δc = 1Γ. To avoid the lensing effect58, we set the two-photon detuning, δ0, corresponding to the zero phase shift, giving ϕ = 0 in the measurement. That is, at the two-photon resonance (δ = 0) there is a positive DDI-induced phase shift (ϕ > 0), and we deliberately set a negative two-photon detuning, δ0, to eliminate the phase shift, i.e., ϕ = 0 at δ = δ0 where δ0/2π was equal to −85 or −180 kHz in the measurement of Ωp = 0.1Γ or 0.2Γ, respectively. Please note ϕ = 0 is the condition that the phase shift due to the ordinary EIT effect at δ0 cancels out the phase shift due to the DDI effect. Details of the measurement of the probe beam size, i.e., the transverse momentum distribution of the Rydberg polaritons, and those of the study on the lensing effect can be found in Supplementary Notes 4 and 5.

The procedure of taking the image of the output probe beam profile is summarized in the following steps: (i) the experimental parameters were determined and set to the designed values. (ii) The probe frequency for δ = 0 was determined by the method of the beat-note interferometer. (iii) At the above experimental parameters, we measured SDDI, and confirmed that the measured value was consistent with the SDDI shown in Fig. 2. (iv) The two-photon detuning, δ0, corresponding to ϕ = 0 was determined. Representation data are shown in Fig. 4. We fitted the data with a straight line, and the best fit determined δ0. The uncertainty of δ0 was ±2π × 30 kHz. (v) At δ0, we took images of the output probe beam profile. We repeated the steps (iv) and (v) for different values of Ωp. (vi) The value of SDDI was measured again to verify it was unchanged during the steps (iv) and (v).

Images of the probe beam profile

Figure 5a shows the probe beam profile in the absence of the atom, while Fig. 5b, c show those in the presence of the atoms. It can be clearly observed that a larger value of \({{{\Omega }}}_{p}^{2}\), i.e., a higher density of Rydberg polaritons because of \({n}_{{\rm{atom}}}{\rho }_{22}\propto {{{\Omega }}}_{p}^{2}\), caused the beam size to become smaller. Since transverse momentums of the Rydberg polaritons were carried by the probe photons leaving the medium, the intensity profile of the output probe beam was able to be used to derive the transverse momentum distribution28,33. We fitted the intensity profiles of three images with a two-dimension Gaussian function and utilized the results of the best fits to construct the momentum distributions shown in Fig. 5d–f. The relation between the transverse momentum distribution of photons at the atom cloud and the intensity profile of an EMCCD image can be found in Supplementary Note 6. As the Rydberg-polariton density increased, the elastic collision rate also increased. Due to Ωc = 1.0Γ, the values of Ωp in the cases of Fig. 5b, c well satisfied the perturbation condition. Thus, the propagation times of the probe light, i.e., the interaction times of the Rydberg polaritons, were approximately the same in the two cases. Under the same interaction time, the higher collision rate due to the larger Rydberg-polariton density produced a smaller width of the transverse momentum distribution or a lower effective transverse temperature, which is the expected outcome of the thermalization process.

Fig. 5: Images of the output probe beam profile and transverse momentum distributions of the Rydberg polaritons.
figure 5

a–c Images of the probe beam profile taken by the electron-multiplying charge-coupled device camera (EMCCD) at Ωp = 0.2Γ in the absence of the atoms, and at Ωp = 0.1Γ and 0.2Γ in the presence of the atoms, respectively. Color represents the gray level detected by the EMCCD. We fit each image with a Gaussian function and draw a white-dashed-line circle of the diameter equal to the e−1 full width of the best fit. The diameters of the circles from top to bottom are 2.6, 2.2, and 1.6 mm. d–f Transverse momentum distributions of the probe photons at the output, i.e., the Rydberg polaritons in the atomic cloud, derived from the best fits of the images in (a)–(c), respectively. Color represents the normalized probability density. The e−1 full widths of the distributions from top to bottom are 0.10, 0.087, and 0.065 μm−1.

Full size image

To check whether the uncertainty of δ0 could be significant on the probe beam profile due to the lensing effect, we measured the probe beam size not only at δ0 but also at δ0 ±2π × 50 kHz. Figure 6 shows the measured beamwidths at these two-photon detunings. As Ωp = 0.1Γ, δ0 = −2π × 85 kHz. As Ωp = 0.2Γ, δ0 = −2π × 180 kHz. Both values of δ0 were determined in the way illustrated by Fig. 4. In Fig. 6, the gray dashed line is the beamwidth measured without the presence of the atoms, and the black and red solid lines are the linear best fits of the experimental data. It is verified by the gentle slopes of the best fits that the uncertainty in δ0 and the lensing effect played insignificant roles in the measurement of the probe beamwidth.

Fig. 6: The output probe beam width as a function of the two-photon detuning.
figure 6

Black and red circles are the experimental data of the e−1 full width of the output probe beam versus the two-photon detuning. The black (or red) data points were taken at α (optical depth) = 82, Ωc = 1.0Γ, Δc = 1.0Γ, and Ωp = 0.10Γ (or 0.20Γ). Black and red lines are the linear best fits of the experimental data, and their slopes are 2.5 μm/kHz and 2.1 μm/kHz, respectively. The Gray dashed line indicates the probe beamwidth measured without the presence of the atoms, i.e., the input probe beamwidth. The error bars represent the standard deviation of measured values.

Full size image

To verify that the observed reduction of the beam size on the EMCCD image is not caused by the nonlinear self-focusing effect of the probe beam, we also measured the probe beam size at Δc = −1 Γ. As demonstrated by Fig. 2d, the DDI-induced phase shift at Δc = −1Γ is 5–6 times smaller than that of at Δc = +1 Γ. Consequently, the nonlinear self-focusing effect at Δc = −1 Γ is little as compared with that at Δc = +1 Γ. Figure 7 shows the EMCCD images taken at Δc = −1 Γ with the same procedure and method as those in Fig. 5. The reduction of the probe beam size is still observed at Ωp = 0.1Γ (or 0.2 Γ) by comparing Fig. 7a, b (or c) without and with the presence of atoms, respectively. Due to the large attenuation coefficient at Δc = −1Γ, the degree of the reduction in Fig. 7c is not as significant as that in Fig. 5c, but they are comparable. Thus, the reduction of the probe beam width cannot be explained by the nonlinear self-focusing effect, and it is the consequence of the transverse momentum distribution of the Rydberg polaritons being narrowed the thermalization process.

Fig. 7: Images of the output probe beam profile taken at Δc = −1Γ.
figure 7

Here, the phase shift induced by the dipole–dipole interaction is minimal. a The image was taken in the absence of the atoms and at Ωp = 0.1Γ. b, c The images were taken in the presence of the atoms, and Ωp = 0.1 Γ and 0.2 Γ, respectively. Color represents the gray level detected by the electron-multiplying charge-coupled device camera. We fit each image with a Gaussian function and draw a white-dashed-line circle of the diameter equal to the e−1 full width of the best fit. The diameters of the circles in (a), (b), and (c) are 2.6, 2.0, and 1.8 mm, respectively.

Full size image

It is noteworthy that we did not observe any asymmetry in the images of Fig. 5b, c. In Ref. 59, two Rydberg atoms were trapped in two microscopic dipole traps. The angle between the interatomic axis and the propagation direction of light fields was well defined. Thus, an anisotropic interaction as a function of the angle due to the Rydberg D state was observed. In this work, the Rydberg atoms were randomly distributed. Angles between the interatomic axes and the propagation direction of light fields were also randomly distributed. Furthermore, we took the probe beam images or Rydberg-polariton momentum distributions in the plane transverse to the propagation direction of light fields or the quantization axis. As expected, the images of Fig. 5b, c do not reveal any anisotropic interaction of the Rydberg D state.

Discussion

Let us estimate the effective transverse temperature from Fig. 5 to show the thermalization efficiency. Following the idea in Ref. 28, the effective mass of Rydberg polaritons in the transverse direction is \({m}_{\perp }=\eta \hslash {k}_{p}{{\Gamma }}/{{{\Omega }}}_{c}^{2}\), where η is the OD per unit length and kp is the wave vector of the probe light. Suppose the Rydberg polaritons obey the Maxwell–Boltzmann distribution. Then, the effective temperature in the transverse direction is given by

$${T}_{{\rm{eff}}\perp }={\hslash }^{2}{{{\Delta }}}_{k}^{2}/(2{m}_{\perp }{k}_{B}),$$
(8)

where Δk is the e−1 half-width of the momentum distribution and kB is the Boltzmann constant. Using the above formulas, we estimate the values of Teff⊥ corresponding to Fig. 5d, f (or equivalently Fig. 5a, c) to be about 3.1 and 1.2 μK, respectively. Thus the effective temperature Teff⊥ experiences a 2.6-fold reduction, as the Rydberg polaritons with the initial density of 2 × 109 cm−3 (Ωp = 0.2Γ) traverse the medium. Furthermore, Fig. 5e (or b) for Ωp = 0.1Γ indicates Teff⊥ = 2.0 μK. As Teff⊥ of Fig. 5f is compared with that of Fig. 5e, a larger Ωp corresponding to a higher polariton collision rate results in a better cooling effect.

In addition to the elastic collision, the observed cooling effect can be assisted by the EIT bandwidth. After an elastic collision between two Rydberg polaritons, one polariton can increase the momentum and the other can decrease the momentum. The one with a larger momentum has a higher frequency of two-photon detuning and is more likely dissipated in the medium due to the EIT bandwidth, while the other with a smaller momentum has a lower frequency and can survive well. After many elastic collisions, the average energy or temperature of the Rydberg-polariton system becomes reduced.

The authors of Ref. 28 proposed to utilize stationary dark-state polaritons, i.e., stationary light based on the Λ-type EIT, to form the Bose–Einstein condensation (BEC). Please note that the interaction between such dark-state polaritons is induced by a far-detuned coupling scheme, e.g., the detuning used in Ref. 28 is 50 times exceeding the spontaneous decay rate. Thus, the scattering cross-section of dark-state polaritons is far smaller than that of Rydberg polaritons interacting due to the strong interaction between the Rydberg atoms. Once Rydberg polaritons are made stationary, the BEC formulism in Ref. 28 can be readily applied to the Rydberg-polariton system. The critical temperature Tc for the polariton BEC under the cylindrical symmetry is given by28

$${T}_{{\rm{c}}}=\frac{\pi {\hslash }^{2}\root{3}\of{{n}_{p}^{2}}}{{k}_{B}\root{3}\of{{m}_{\perp }^{2}{m}_{\parallel }}},$$
(9)
$${m}_{\perp }=\frac{\hslash \eta {k}_{p}{{\Gamma }}}{{{{\Omega }}}_{c}^{2}},$$
(10)
$${m}_{\parallel }=\frac{\hslash {\eta }^{2}{{{\Gamma }}}^{2}}{8{{{\Omega }}}_{c}^{2}{{{\Delta }}}_{c}},$$
(11)

where np is the Rydberg-polariton density, m⊥ and m∥ are the transverse and longitudinal effective masses, η is the OD per unit length, and kp is the wave vector of the probe light. However, in the present study, we dealt with a two-dimensional Rydberg-polariton system. The Rydberg polaritons propagated along the longitudinal direction. The average longitudinal kinetic energy of each Rydberg polariton (=ℏkpvg/kB where vg is the group velocity) given by 140 mK was much larger than the transverse temperature. To achieve BEC, we need to make Rydberg polaritons stationary and further enhance OD to have a sufficient interaction time, i.e., a lifetime of the stationary light17. It is also desirable to add an artificial trap to enable efficient evaporative cooling or energy dissipation. Using η = 160 cm−1, Ωc = 1.0Γ, and Δc = 1.0Γ, we estimate Tc = 2.0 mK for the stationary Rydberg polaritons of np = 2 × 109 cm−3.

Up to now, the BECs of various kinds of polaritons have been realized in cavity systems33,34,35,36. This work deals with the cavity-free high-OD medium, in which the interaction time between the Rydberg polaritons is analogous to the storage time of polaritons in a cavity with a Q factor greater than 109. While the current systems of polariton BECs are all two-dimensional, a three-dimension BEC can be formed in the system of Rydberg or dark-state polaritons28. In addition, as compared with other kinds of polaritons, the condensate of Rydberg polaritons can have a much longer lifetime due to a low decoherence rate in the Rydberg-EIT system, offering more opportunities for many-body physics of polariton systems.

Method

Laser fields preparation

The probe and coupling fields were generated by a homemade diode laser and a blue laser system (Toptica TA-SHG pro), respectively. The frequency stabilizations of the probe and coupling lasers are described as follows. We utilized the injection lock scheme to stabilize the frequency of the probe laser. In the scheme, the probe laser was used as the slave, and an external-cavity diode laser (ECDL) of Toptica DLC DL pro with a wavelength of about 780 nm was employed as the master. We utilized the Pound–Drever–Hall scheme and the saturated absorption spectroscopy to lock the frequency of the ECDL with a heated vapor cell of Rb atoms. The blue laser had a wavelength of about 482 nm. Furthermore, we used the Pound–Drever–Hall scheme and the EIT spectrum to lock the frequency of the blue laser with another heated vapor cell. The ECDL and blue laser fields counter-propagated in the measurement. We were able to lock the sum of the two laser frequencies to the EIT transition with the root-mean-square fluctuation of around 150 kHz47.

Determination of experimental parameters

The parameters of the OD (α), coupling Rabi frequency (Ωc), and intrinsic decoherence rate (γ0) were determined experimentally with the same method used in Ref. 47. Details of the determination procedure can be found in Supplementary Note 2. We set Ωc = 1.0Γ and were able to maintain γ0 around 0.012(1)Γ throughout the experiment. This γ0 included the effects of laser frequency fluctuation, Doppler shift, and other decoherence processes that appear in the Λ-type EIT system47.

Beat-note interferometer

We employed the beat-note interferometer to measure the phase shift of the probe field induced by the atoms. The concept and illustration of the beat-note interferometer can be found in Refs. 60,61. In the absence of the DDI, the phase shift of the probe field also enabled us to precisely determine the probe frequency for the zero two-photon detunings, i.e., δ = 0, at a given coupling detuning, Δc. This is because the phase shift is equal to τdδ according to the non-DDI EIT theory, where τd is the propagation delay time. The data of attenuation coefficients and phase shifts under the DDI effect presented in Fig. 2 were taken at δ = 0. See Supplementary Note 1 for more details.