Deconvolution of dissipative pathways for the interpretation of tapping-mode atomic force microscopy from phase-contrast

Abstract

Phase-contrast in tapping-mode atomic force microscopy (TM-AFM) results from dynamic tip-surface interaction losses which allow soft and hard nanoscale features to be distinguished. So far, phase-contrast in TM-AFM has been interpreted using homogeneous Boltzmann-like loss distributions that ignore fluctuations. Here, we revisit the origin of phase-contrast in TM-AFM by considering the role of fluctuation-driven transitions and heterogeneous loss. At ultra-light tapping amplitudes <3 nm, a unique amplitude dependent two-stage distribution response is revealed, alluding to metastable viscous relaxations that originate from tapping-induced surface perturbations. The elastic and viscous coefficients are also quantitatively estimated from the resulting strain rate at the fixed tapping frequency. The transitional heterogeneous losses emerge as the dominant loss mechanism outweighing homogeneous losses at smaller amplitudes for a soft-material. Analogous fluctuation mediated phase-contrast is also apparent in contact resonance enhanced AFM-IR (infrared), showing promise in decoupling competing thermal loss mechanisms via radiative and non-radiative pathways. Understanding the loss pathways can provide insights on the bio-physical origins of heterogeneities in soft-bio-matter e.g., single cancer cell, tumors, and soft-tissues.

Introduction

Since inception¹ atomic force microscopy (AFM) has emerged as a key nanoscale surface metrology tool for scientists and engineers alike^2,3. Tapping mode AFM⁴ (TM-AFM) deserves a special mention in this regard for its ability to nondestructively characterize soft bio-interfaces^5,6 at the nanoscale. In recent years it has found renewed popularity in the study of nonequilibrium (NE) energetics of protein and DNA/RNA^7,8 folding landscapes. NE energy routes underpin fundamental bio-physical mechanisms like cell migration, cell signaling, tissue—self-repair, damage evolution, and toughening, among others^9,10,11,12. An apparently homogeneous surface locally deviates off equilibrium to metastable states and eventually restores back via NE dissipative routes. Fluctuations mediate the thermodynamic cost of such excursions. These are pivotal to the evolution of mechano-biological functions³ that closely imitate soft glassy dynamics¹³ yielding to viscous relaxations at nanoscale heterogeneities. New knowledge in macroscopic and biological phenomena from nanoscale and molecular heterogeneity perspectives has emerged^14,15,16. Yet, our predictability of NE pathways in biology is still in its infancy. This is because of our general lack of understanding of the role of heterogeneities in NE dissipative pathways. Methods that can connect local fluctuations at heterogeneities to energy losses are thus becoming more general and broader to elucidate insights on such mechanisms^17,18. TM-AFM with microcantilevers, which have tapping frequencies in the order of $\sim 10^2$ kHz, is a unique platform to study such intricate energetics in soft-bio-matter at the nanoscale¹⁹. Typically, nondestructive bio-TM-AFM has been executed at the large tip–surface separations with high amplitude tapping ensuring that the tip–surface interaction potentials remain predominantly conservative^20,21. Yet, losses originate from inelastic interactions and are reflected as a phase-contrast²². These constitute loss contributions that are intrinsic to the cantilever and from tip–surface interactions including the hysteretic losses from indentations that cannot be decoupled. This is because the tip is invariably exposed to nonconservative interaction potentials every cycle on tip-approach^20,21, even if for a fraction of its oscillation-period²². The conservative interactions typically overshadow the nonconservative effects at large oscillation amplitudes since a greater percentage of cantilever motion occur at large separations. However, at small separations nonconservative or inelastic effects dominate which are of particular interest from a bio-physical perspective, since they carry the signatures of the NE loss pathways. Deconvoluting the nonconservative loss mechanisms is thus essential to gain insights on the role of nanoscale heterogeneities. Surfaces begin to deform even without indentation at small separations²⁰. The very nature of such induced deformation introduces two possibilities depending on the material’s relaxation characteristics at the tapping perturbation rate. If the perturbation rate is high enough, the surface deformations would exhibit inelastic viscous relaxations manifesting over multiple-length and timescales¹³ adopting NE dissipative routes. Biophysical mechanisms adopt such NE energy routes in bio-evolutionary processes, relentlessly competing over local fluctuations. For example, to maintain equilibrium at room temperature, single biomolecule dissipates energy at the rate of $10^{ - 20} - 10^{ - 19}\;{\rm{J/s}}$, competing over thermal fluctuations that are in the order of $\sim 10^{ - 20}\;{\rm{J/s}}$. Interrogating such non-conservative losses without indentation may prove invaluable in deciphering signatures of such multiscale NE relaxation mechanisms^13,23.

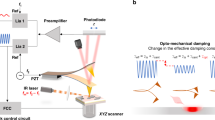
TM-AFM’s operation typically relies on $1\;{\rm{pN}}-100\;{\rm{nN}}$ forces that manifest at a tip–surface junction in the limit where constitutive continuum laws breakdown and nanoscale effects takeover. Complex multiscale energy interplay takes predominance linking molecular (or atomic scale) forces at the tip to macroscale cantilever dynamics^20,24. The dynamics capture surface deformation modalities as topography, amplitude, and phase-contrast images through raster scans that form the backbone of any TM-AFM study. At each oscillation cycle, the tip experiences a gradient of forces with loss of energy. The oscillation amplitude decreases linearly starting with negligible interaction (mostly fluid media loss) when the tip is furthest from the surface $\to$ long-range attractive force (non-contact regime) $\to$ repulsive forces (contact regime) (Fig. 1). The reverse happens in the retraction cycle. The energy losses in the repulsive and attractive regimes have been explained to appear as a phase-change ${\Delta}\phi$ in the cantilever dynamics with respect to the external drive. ${\Delta}\phi$ essentially displays compositional contrast of the heterogeneous boundaries. By convention, the repulsive and attractive regimes are characterized by positive ($+ {\Delta}\phi$) and negative ($- {\Delta}\phi$) phase shifts, respectively, arising from the energy dissipated, $E_{\rm{dis}}$, during tip–surface interactions^25,26 as

$$E_{\rm{dis}} = \frac{{\pi kA_0A}}{Q}\left[ {\sin \left( {{\Delta}\phi } \right) - \frac{A}{{A_0}}} \right].$$

(1)

$E_{\rm{dis}}$ presents an accurate approximation of the net dissipated energy when the free amplitude quality factor $Q = \frac{{\omega _0}}{{2{\Gamma}}}$ is relatively high $\sim 100 - 1000$ (oscillation decay rate ${\Gamma}$ widely separated from the resonance frequency of the AFM cantilever $\omega _0$), and the damped tapping amplitude $A = A_0 - A_{\rm{sp}}$ is sufficiently large $> 15\;{\rm{nm}}$ ensuring that the tip-motion accesses the contact regime every cycle^22,27,28 (Fig. 1). Here, $k$ is the spring constant with $A_0$ the free amplitude set by tuning and $A_{\rm{sp}}$ the operational amplitude setpoint in nanometers, both calibrated from volt units (V) from the AFM’s optical deflection measurements. True atomic²⁹ and bond-level^30,31 resolutions have been demonstrated exploiting large-amplitude techniques relying on dynamic tip-surface interactions. However, the steady-state dissipation approximation of Eq. (1) necessarily rests on the assumption of a constant $Q$ even on intermittent contact at large $A$. In addition, for large $A$, the effective tip-surface interaction time is a fraction of the cantilever oscillation time-period²² (Fig. 1). Thus, in principle, a soft-surface gets enough time to relax to its equilibrium state before the tip interacts again in the next cycle. This essentially results in homogeneous Boltzmann-like distributions³² in ${\Delta}\phi$ reflecting equilibrium tip–surface interactions (black curve in phase histogram plot of Fig. 1). The captured surface modalities end up being analyzed from a conservative interactions perspective. E.g., relatively hard materials with interatomic spacing $\sim 2 - 3$ Å are typically modeled as simple-solids exhibiting pure elasticity (Young’s-moduli in the order of $\ge \!10\;{\rm{GPa}}$), with no dissipation. The assumption is that deformations at the molecular length scales ($\sim$Å) relax so quickly (picoseconds) in comparison to the cantilever’s timescale (micro–milliseconds) that the microscopic components of the material behave as if they are locally at equilibrium³³. This is intuitively valid for atoms in crystal lattices ($\sim$Å) and small molecules like H₂O (mean diameter $\simeq 2.7$ Å) that invariably adsorb at nanometric imperfections of bio-interfaces. However, in bio-materials with larger constituent components (typically $\ge$10 Å) relaxation rates become comparable to nanometer order strain rates. The assumption of local equilibrium on deformation no longer holds in such a case and is bound to have metastable states¹³. A more intricate experimental description thus becomes necessary to correctly account for the metastable relaxation phenomenon from the resulting phase-contrast. Dissipative features have so far been qualitatively explained in terms of an apparent lighter contrast in the noncontact regime ($- {\Delta}\phi$ phase shift) and a darker contrast in the contact regime ($+ {\Delta}\phi$ phase shift). Such interpretations directly follow from the sudden changes in phase observed in large amplitude tapping experiments^34,35,36,37 agreeing to Eq. (1). Yet, the origin of phase shift remains ambiguous for apparent erroneous invoking of elastic and/or inelastic interactions³⁴. Inherent tip–surface hysteretic interactions from capillary effects^35,36, chemical affinity³⁷, solid-mechanics assumptions of tip–surface indentation models²⁴, artifacts from control system feedback³⁸, presence of intrinsic stochasticity at the nanoscale³⁹, the combination of many several possible mechanisms like the hydrodynamic effects^40,41 and the controversial nature of friction at the nanoscale^42,43,44, all of these could contribute simultaneously to the ambiguities. It must be noted here that previous efforts in generating decent phase-contrast images have necessarily adopted surface indentation methodology with high amplitude oscillations $\sim \!A > 15\;{\rm{nm}}$ but without the means to decouple the hysteretic effects. This is to specifically conform to steady-state loss descriptions that satisfy Eq. (1) despite compromising on the tip–surface interaction time. In principle, to accurately quantify viscous relaxations the tip–surface interaction time per oscillation cycle should sufficiently be close to the viscous relaxation timescale. Previously, contact time has been argued to be independent of topographic features²², while others contradicted with models decomposing phase-contrast into moments of topography⁴⁵. Both, however, agreed on the criticality of tip–surface equilibrium separation $z_c$, typically $> 20\;{\rm{nm}}$, to correctly reflect on the qualitative interpretation of soft and hard features from the generated ${\Delta}\phi$. Nevertheless, viscoelasticity has an inherent time dependence and phase data from high-amplitude tapping experiments makes such interpretations erroneous and inconclusive for the insufficient tip–surface interaction time. The cantilever dynamics basically fails to follow the surface relaxation dynamics that are crucial for decoupling the viscous loss pathways originating from the strain rate or strain history of the interface deformations. On the other hand, matching tip–surface interaction time to the oscillation timescale invokes the promise of reconceptualizing phase-contrast where the microcantilever tip has access to the surface relaxations during its entire tapping cycle, without necessarily indenting the surface.

Fig. 1: Experimental schematic.

The exploitation of fluctuations in the near-contact crossover regime at tip–surface separations z_c = 2.5–3.5 nm with ultra-light tapping amplitude (A < 3 nm). Free amplitude A₀ and setpoint amplitude A_sp are judiciously optimized. The dynamic response of interaction with soft drug clusters leads to a two-stage distribution in phase giving an apparent phase contrast $\phi ^ \ast$. DxO@mGO and MxD@mGO represent Doxorubicin and Minoxidil clusters on multilayered graphene oxide (mGO) respectively.

Here, with our ultra-light tapping amplitudes A < 3 nm, we demonstrate the emergence of a complex double-stage phase-contrast (red curve in phase histogram plot in Fig. 1) as evidence of energy losses from metastable relaxation in a soft-material. We decouple a heterogeneous loss component from the appearing Δ$\phi$ distributions. Previously ultra-low amplitude tapping has been implemented at subharmonics, successfully decoupling hysteretic interactions in metal lattices²¹. Our experimental outcome reveals an intricate phase distribution response (Fig. 1) where the single Boltzmann peak (black curve A₀ > 15 nm) bifurcates to two peaks (red curve A₀ < 10 nm). We explain this from fluctuational excursions of microcantilever dynamics in the limit of ${\Delta}\phi \to 0$ (Fig. 1). Such distribution in context has never been observed or explained. We must note here that ${\Delta}\phi$ appearing from dynamic losses of an oscillating microcantilever is expected to be maximized at the condition of resonance since loss pathways maximize variationally at resonance⁴⁶. Uniquely, resonance provides access to two timescales: the oscillator timescale (faster—resonance frequency) referred to here as $\tau _{\rm{osc}}$ and a dissipation timescale (slower—the resonance width), that essentially reflect the cumulative result of phase-trajectory excursions in the underlying dynamics. We exploit these two timescales with controlled tip–surface interactions and demonstrate the emergence of the intricate distribution of phase-change ${\Delta}\phi$ that surprisingly deviates from a standard Boltzmann distribution. We analyze it in detail to reflect on the dissipative pathways at the tip–surface junction. We go on to explain that the key to obtaining such a distribution lies in the close matching of the tip–surface interaction timescale $\tau$ to the cantilever resonance timescale, whereby, the multi-time scale relaxation processes are encoded in the resonance width as an integral of dissipation functions; the secondary peak signifying a unique dissipation timescale corresponding to metastable relaxations of the soft surface. We further comment on the origins of ${\Delta}\phi$ from the aspect of energy exchange through time-dependent adiabatic and anti-adiabatic routes and connect them to fluctuational dynamics of the AFM microcantilever tip in response to heterogeneous interactions at the nanoscale. Earlier implemented nonresonant frequency scanning based AFM techniques do not provide the means to access this dissipation or non-conservative timescale since they follow steady-state deformation dynamics. Such steady-state deformations are expected to be predominantly elastic since the probe cantilever behaves as an elastic element at the dynamic frequencies employed in such a study. The small-amplitude resonant tapping mode method we expound here will particularly be applicable for a broad class of soft-bio matter such as soft tissues, cells, DNA, proteins, and drug molecule clusters with intercalated H₂O, that exhibit means to simultaneously store (solid-like) and dissipate (liquid-like) energy from the tip–surface interactions.

Results and discussion

Experimental technique

At the nanoscale, viscosity manifests from the diffusion of atom centers when perturbed. Heterogeneities accentuate such manifestations. The perturbation rate is important since it continuously works against the material’s stress relaxation or dissipation mechanisms. On tapping, a phase-change, ${\Delta}\phi$, thus appears from the mismatch of the applied and induced surface strain rates owing to the soft-material dynamics. Considering resonance, ${\Delta}\phi$ signify a delay-bandwidth product ${\Delta}\phi = \delta \omega \cdot \tau$ vide $A = A_0e^{ - i\left( {\delta \omega \cdot \tau } \right)}$, where $\delta \omega = \omega - \omega _0$ is the shift in fundamental resonance frequency $\omega _0$ on tip approach. The steady state damped amplitude $A$ evolves as a function of the delay bandwidth product with $- i{\Delta}\phi$ necessarily capturing the time dependance. Therefore, in principle, ${\Delta}\phi$ have both a steady state solution (contact and noncontact regime) and a transitional component that depends on how ${\Delta}\phi$ gets influenced as a function of tip–surface interactions. We focus on the transitions in the limit ${\Delta}\phi \to 0$ with small tapping amplitudes. We are specifically considering the effect of small fluctuations on an otherwise deterministic dynamical system that have been described by phenomenological laws of equilibrium energetics³². We determine the dynamic crossover ${\Delta}z \cong 4 - 7\;{\rm{nm}}$ from snap-in lengths having equilibrium tip–surface separation $z_c \approx 2.5 - 3.5\;{\rm{nm}}$ for different samples under study as shown in Fig. 1. We carefully restrict the dynamics in this near-contact crossover regime ensuring that the damped amplitude $A$ stayed within the fluctuational ${\Delta}z$ as shown in Fig. 1. This we enforce with ultra-light tapping with a gradual controlled tip–surface approach as a function of $A_{\rm{sp}}$ and an integral time optimization. On optimization, constant amplitude TM images were captured as a function of varying $A_{\rm{sp}}$. The phase at free amplitude $A_0$ is zeroed at each run corresponding to a particular $A_{\rm{sp}}$ allowing the precise monitoring of the phase changes ${\Delta}\phi$ at the ultra-light tapping condition. Fluctuations would be dominant in this operational regime with $z_c$ as the boundary of crossover in our consideration. In the short run, we cannot expect large deviations from a deterministic equilibrium behaviour^{33,34,35,36,37}. Yet, if enough equilibrium time is allowed per scanning point (pixel) for the system to settle down, the cumulative effect of the fluctuations may become pronounced, albeit the rare events become more probable on account of synchronization of tip oscillation with the surface relaxations⁴⁷. This we ensure by an optimized scan rate and controller integral time that caters to the necessary timescale conditions. In view of the fluctuational phenomenon in context, the recorded amplitude, phase, and topography data channels at each $A_{\rm{sp}}$ have important statistical significance in the appearance of a surprising two-stage phase contrast as shown in Fig. 2a–f. We have selected Doxorubicin (DxO) and Minoxidil (MxD) drug clusters on multilayered graphene oxide (mGO) as the model soft-matter systems (DxO@mGO and MxD@mGO, respectively). Invariably, the samples will have intercalated H₂O at the nanometric imperfections. DxO ($\sim 15$ Å)⁴⁸ and MxD ($\sim 10$ Å) [ChemDraw] molecules are expected to exhibit finite relaxation rates making it an ideal soft-matter candidate to investigate. Such drug@mGO systems are gaining interest in drug delivery systems^49,50, where the correct interpretation of the loading condition is crucial for drug delivery efficiency and their therapeutic success. Accurate estimations of surface energy play a vital role in controlling drug release. From the distribution results of DxO@mGO and MxD@mGO samples, we quantify the surface energy in terms of the elastic and viscous components and compare them to bare mGO samples, where the appearance of a secondary peak is not prominent. On the fundamental side, exploiting the fluctuational regime serves us two purposes: (a) determine the basis of the intermediate energetics in the origin of ${\Delta}\phi$ and (b) link them to the dissipative pathways.

Fig. 2: 3D Stacked phase images and their corresponding histogram distributions obtained for varying amplitude setpoints A_sp.

a, d mGO; b, e DxO@mGO; c, f MxD@mGO. Experimental free amplitude A₀ for mGO is 6.2 nm while that for DxO@mGO is 6.32 and 6.34 nm in the case of MxD@mGO. Curiously enough, the soft DxO@mGO and MxD@mGO surfaces show the multi-peak distribution in comparison to simpler single peak distribution in mGO. The appearance of the secondary peak is direct evidence of the interplay of the metastable relaxation timescale of a soft-surface as interrogated by ultra-light tapping conditions enforced here. The relative position and amplitude of the distribution peaks change as a function of setpoint amplitude A_sp. At higher A_sp, i.e., lower tapping A at tip–surface approach, the fluctuational probability transition from surface heterogeneity is expected to be high since damping is low at small A. This is evident in a relative increase in phase delay ${\Delta}\phi _ -$ peak with respect to ${\Delta}\phi _ +$ at higher A_sp in both DxO@mGO and MxD@mGO samples. DxO- Doxorubicin, MxD- minoxidil, mGO- multilayered graphene oxide.

Timescales and significance of fluctuations

Soft surfaces typically relax over multiple timescales with the system hopping between metastable and equilibrium states attesting to their unique NE loss mechanisms¹³. The energy loss corresponding to the metastable hops typically signifies a heterogeneous loss path that rides over the equilibrium homogenous loss path and may appear as small fluctuations of the steady-state energy landscape. Necessarily, the timescale separation of the states needs to be small for both the loss pathways to reflect simultaneously in the dynamics. In its limiting case, when the states are widely separated in timescales, the excursions amongst the states become statistically independent. In that case, the energy loss follows a typical homogenous Gaussian distribution with vanishingly small relative fluctuations $\frac{{\sigma _{\rm{dis}}}}{{\left\langle {E_{\rm{dis}}} \right\rangle }} \sim 0.1$, $\left\langle {E_{\rm{dis}}} \right\rangle$ and $\sigma _{E_{dis}}^2$ being the mean and variance of the dissipated energy as described by Eq. (1). This is apparently evident in the generated ${\Delta}\phi$ distributions in our experimental outcomes at high amplitude (Fig. 2b, d), similar to the previous experiments^35,40,51,52 with surface indentation and where the interaction time $\tau$ is negligible compared to the perturbation timescale. However, subject to the condition that the timescale separation is short, the energy landscape of a soft-material deviates from a single-stage Boltzmann potential. A kinetic variant becomes essential to account for and explain a succession of NE states. This was postulated in Onsager’s principle of least dissipation of energy. This manifests at near contact conditions where the tip interaction time $\tau$ (Fig. 1) renders fluctuations relevant to the underlying dynamics making the states and their probability of excursions in between the states statistically correlated. Onsager attributed this statistical significance to the time integral of dissipation functions⁴⁷. Variationally this has the means to be effectively encoded in resonance width broadening timescale⁴⁶. This is because when enough interaction time is allowed the microcantilever dynamics essentially start to follow the multi-time scale dynamical relaxations of the soft viscous material^13,23 typically adopting two or more timescales. In principle, the shortest timescale (resonance timescale) relates to dynamical trapping of oscillator around one of the equilibrium states (contact/non-contact in our case) while the longest (resonance broadening timescale) signifies relaxation time towards a (unique) dynamic steady state. For soft-material, this typically signifies a structurally disordered metastable state^13,23. Phenomenologically, the energy states of soft material can be modeled to be confined in a double-well free energy landscape with the system spontaneously hopping between the potential wells when externally perturbed, i.e., by the periodic tapping mechanism in our case. Specific to a material, the double-well free-energy landscape will exhibit a characteristic relaxation time that is inversely proportional to Kramer’s rate of hop in between the wells. When the interaction time $\tau$ relevant to the perturbations, closely matches this inherent rate of hop, a state of dynamic stochastic resonance emerges; the excursion between the minima states starts to synchronize with the external perturbation dynamics. I.e., the microcantilever dynamics sync to fluctuational dynamics about $\phi = 0$ (in the near-contact regime) deviating from equilibrium (Fig. 1). Physically, the microcantilever follows the surface’s excursions to the metastable state in time. These transitional excursions amongst the fluctuational and the steady states thus become relevant to the dynamics reflecting phase distributions that deviate from standard Gaussian as two-stage distribution in ${\Delta}\phi$ (Fig. 2). Basically, two markedly distinct regimes of energy interactions are possible (i) the anti-adiabatic case: when the cantilever dynamics does a fast transition between equilibrium states remaining oblivious to the intermediate metastable state⁵³ and (ii) the opposite adiabatic case: where the oscillator dynamics is very slow compared to the faster relaxation processes at the interface, thus susceptible to nonlinear damping effects⁵⁴. A third crossover regime at a comparable timescale $\tau _{\rm{osc}} \cong \tau _{\rm{sur}}$ has the fluctuational relevance as described above. I.e., when the enforced dynamics is slow enough to reversibly follow the transitional excursions at small-separation deformations where $\tau _{\rm{sur}}$ is the inherent metastable relaxation timescale of the surface in question. Our experimental description institutes this premise to faithfully follow the transitional adiabatic $\rightleftharpoons$ anti-adiabatic crossovers in between the equilibrium and metastable states. In effect, enforcing oscillations within the crossover regime renders the tip–surface interaction correlation time $\tau _c$ finite, allowing the interrogation of a heterogeneous interaction scale at the tip–surface junction (see “Methods”) in addition to inherent homogeneous loss timescale from the cantilever’s oscillatory dynamics.

The appearance of two-stage phase contrast

The enforcement of a finite correlation time $\tau _c \to \tau _{\rm{osc}} \approx \tau _{\rm{sur}}$ is optimized in our experiments in terms of $A_{\rm{sp}}$ and the integration time of the PI controller. The choice of P and I gains is critical at our operational low scanning rates $\sim 0.05\;{\rm{Hz}}$, giving the tip enough time to equilibrate at every pixel of the image (pixel data is sampled over an average of 40,000 cycles). The P and I gain are set such that the integral timescale is of the order $\tau _c = 6.430\;{\rm{ms}},$ sufficiently close to $\tau _{\rm{osc}} = \frac{{2\sqrt 3 Q}}{{\omega _0}} \simeq 0.55 - 0.64\;{\rm{ms}}$, within 1 order of magnitude, corresponding to the fundamental resonance frequencies $\sim 302\;{\mathrm{and}}\;309\;{\rm{kHz}}$ and $Q\sim 355\;{\mathrm{and}}\;{\mathrm{254}}$ of the tapping mode cantilevers employed in cases of DxO@mGO and MxD@mGO, respectively. Such sampling satisfies the condition of ergodicity making the collected data every channel and their probability distributions statistically relevant to the fluctuational transitions about $\phi = 0$. In addition, when $\tau _{\rm{osc}} \approx \tau _{\rm{sur}}$ within same order of magnitude, the underlying dynamics start following the viscous relaxation scale of the soft-surface. Thus, for $\tau _c > \tau _{\rm{osc}}$ in the limit $\tau _c \to \tau _{\rm{osc}}$ at our ultra-light tapping implementation, the mean surface deformation and the fluctuations about the mean also become a function of the cantilever’s mean amplitude evolution at every pixel. The frequency fluctuations and the time delay associated with such evolution thus should reflect a unique distribution relevant to the enforced conditions. Contrarily, large amplitude oscillations approximate steady-state dynamics when $\tau _c < \tau _{\rm{osc}}$. The phase crossover between the equilibrium states is sudden, necessarily satisfying the Gaussian distribution approximation of the central limit theorem in the limit that the fluctuations become statistically insignificant and dynamically irrelevant.

Under our enforced fluctuational conditions ($\tau _c > \tau _{\rm{osc}}$), however, we may infer that the dynamic amplitude measured at each pixel will be proportional to a phase lag ${\Delta}\phi {\mathrm{ = }}\tau _c \cdot \left( {\omega - {\Delta}_\omega } \right)$ (see “Methods”) as

$$A + {\Delta}a = {\rm{X}}\left( \omega \right)A_0e{\,}^{ - i{\Delta}\phi },$$

(2)

${\Delta}a$ being the mean deformation at each amplitude setpoint. Herein lies the significance of fluctuations or the adiabatic $\rightleftharpoons$ anti-adiabatic crossover as the fundamental basis of origin of ${\Delta}\phi$ in our experimental description. The mean deformation ${\Delta}a$ for each operational $A_{sp}$ were determined from the Lorentzian width (heterogeneous broadening) of the normalized amplitude histograms as shown in Fig. S1. Following the premise of Eq. (2), phase lag ${\Delta}\phi$ is expected to follow a complex probability distribution in the zeroth order of $\tau _c{\Delta}_\omega$, signifying energy losses via both homogeneous (inherent steady state losses) and heterogeneous (dynamic interaction losses) mechanisms. Indeed, complex distributions in ${\Delta}\phi$ appear in the form of convoluted peaks centered at ${\Delta}\phi _ +$ and ${\Delta}\phi _ -$ changing in form as a function of $A_{\rm{sp}}$ for DxO@mGO and MxD@mGO samples as evident from the phase histograms (Fig. 2e, f) of the phase images (Fig. 2b and 2c). For the control sample mGO, the phase responses resemble homogeneous distributions (Fig. 2d and Fig. S2), since deformations are expected to be predominantly elastic at this perturbation frequency. The two-stage distribution for the drug@mGO samples is significant from the fact, that it appears from dynamic tip interactions at the nanoscale and not from typical resonance bi-stability on account of amplitude nonlinearity⁵⁵. The span of the two fluctuational peaks $\phi ^ \ast = {\Delta}\phi _ + - {\Delta}\phi _ -$ becomes a measure of the apparent phase-contrast that highlights distinctive phase features obtained in our experiments (Fig. 2b, c). The individual peaks encode the dynamic loss mechanisms which essentially materialize from two disparate timescale events relative to the operational correlation timescale $\tau _c.$ It must be noted here that $\tau _c$ is not strictly independent of $A_{\rm{sp}}$ at constant P and I, since cantilever steady-state time has a strong frequency and Q dependence when dissipation dominates and deviates from linearity. Operationally in our experiments P and I were optimized to an order of few % at each $A_{\rm{sp}}$ to ensure conformed trace-retrace scans. The separation of the obtained two-stage phase peaks $\phi ^ \ast$ signifies the separation of interaction timescales as captured by the underlying dynamics via fluctuational crossovers as explained in detail in the “Timescales and significance of fluctuations” section before. A longer timescale ensues from slower surface relaxation events. The tip follows the strain history via interactions that are finite time-correlated every successive oscillation cycle at a pixel. These reflect as a phase-lag ${\Delta}\phi _ -$ probability transition. The very nature of time-correlated interactions is suggestive of a heterogeneous (Cauchy) distribution. A second inherently faster oscillatory timescale results from surface interactions that are uncorrelated (spatial and temporal) down to nearest neighbor pixels. A phase-lead ${\Delta}\phi _ +$ probability transition results with an apparent homogeneous (Gaussian) distribution. This heterogeneous phase-lag transition peak centered at ${\Delta}\phi _ -$ appears in the case of viscoelastic DxO@mGO and MxD@mGO but is absent in mGO (Fig. 2d and Fig. S2).

The loss mechanisms at either peak demand elaboration. We consider a minimal scalar model here with the least number of parameters to explain the transitions phenomenologically. A more detailed exact solution model can be formulated in the likes of Sollich’s exposition²³ incorporating multiscale dynamics, essentially giving the same conclusions. Normalized cumulative density graphs (Fig. 3a, c) for each $A_{sp}$ as a function of ${\Delta}\phi$ highlight a clear two-stage transition in dissipated energy ${\Delta}E_{\rm{dis}}$. In comparison, the same for mGO depicts a more homogeneous Boltzmann-like transition as discussed in Fig. S2. For our case where the distributions deviate from a single homogeneous distribution, it is important to consider how a change in a parameter, $A \to A + {\Delta}a$, would affect a change in the average value of its dependent variable $\left\langle {{\Delta}\phi } \right\rangle$. Under a generalized assumption of coupled homogeneous and heterogeneous loss mechanisms⁵⁶ from disparate interaction timescales as elucidated before, a measure of the net energy dissipation as a function of appearing ${\Delta}\phi$ can be formulated as

$${\Delta}E_{\rm{dis}} \equiv \left\langle {{\Delta}\phi } \right\rangle _{A + {\Delta}a} - \left\langle {{\Delta}\phi } \right\rangle _A \propto \;{\mathrm{exp}}\left( { - \frac{{\sigma _{AG}^2}}{{\sigma _{AL}^2}}} \right)$$

(3)

where $\sigma _{AG}$ and $\sigma _{AL}$ are the respective homogeneous and heterogeneous standard deviations of ${\Delta}\phi _ +$ & ${\Delta}\phi _ -$ for a surface deformation ${\Delta}a$ at the oscillation amplitude of $A$. In principle, $\left\langle {{\Delta}\phi } \right\rangle _x$ is the ensemble average that is proportional to its variance at the parameter value $x$; $x$ taking the values $A$ and $A + {\Delta}a$. For example, $\left\langle {{\Delta}\phi } \right\rangle _A$ explicitly represents a probability density $\left\langle {{\Delta}\phi } \right\rangle _A = {\int}_{\Omega} {\left( {{\Delta}\phi } \right)P\left( {A,\left( {{\Delta}\phi } \right)} \right)d\left( {{\Delta}\phi } \right)}$⁵⁷ with $P\left( {A,\left( {{\Delta}\phi } \right)} \right)$ the normalized distribution function. The integral range ${\Omega}$ denotes the ${\Delta}\phi$ span obtained in an experiment for a particular $A_{sp}$, thus accounting for an estimate of the net dissipated energy ${\Delta}E_{\rm{dis}}$ as in Eq. (3). We further re-cast Eq. (3) to a fitting function of coupled cumulative energy densities (see Supplementary Section C and Fig. S3 for the goodness of fit) from which the respective homogeneous and heterogeneous probability densities centered at ${\Delta}\phi _ +$ and ${\Delta}\phi _ -$ are determined. $P\left( {{\Delta}\phi _ + } \right)$ and $P\left( {{\Delta}\phi _ - } \right)$ thus essentially represent the relative energy losses via homogeneous and heterogeneous routes, respectively.

Fig. 3: Normalized cumulative density graphs of phase histograms.

a DxO@mGO and c MxD@mGO at low A₀ depicting the net dissipated energy from the fluctuational probability transitions at light tapping in the limit ${\Delta}\phi \to 0$. The two-level transition originates from both heterogeneous and homogeneous energy losses. Phase images of b DxO@mGO and d MxD@mGO at low and high amplitudes and comparable A_sp/A₀ ratios. The absence of the secondary heterogeneous transition at higher A₀ = 25 and 15.54 nm (traditional hard tapping) is apparent. The histogram peaks in (b) and (d) highlight the separation of the timescales in the underlying dynamics accentuated by the fluctuations. The transitions at A₀ = 25 and 15.54 nm are centered at 0 with a positive ${\Delta}\phi$ skew signifying an apparent contact regime operation.

The phase image and histograms for DxO@mGO and MxD@mGO obtained at high amplitude oscillations are also shown in comparison (Fig. 3b, d). The absence of any secondary transition at ${\Delta}\phi _ -$ is apparent. Imaging at lower amplitude $A$ increases the probability of tracking the ${\Delta}\phi _ -$ transitions at the heterogeneities since the correlation time $\tau _c$ theoretically tends to $\infty$ when ${\Delta}\phi = 0$. This promotes a relative skew in the ${\Delta}\phi _ -$ transition density at very high $A_{\rm{sp}}$’s (Fig. 2e, f). In principle, the secondary ${\Delta}\phi _ -$ transition suggests a negative shift in the eigen frequency with acute losses. This is rather very interesting from the aspect of fluctuational trajectories and Lyapunov exponents in phase space. An in-depth theoretical treatment on this will be taken up elsewhere. This secondary transition is clearly absent in mGO, which is expected to exhibit predominant equilibrium behavior at our perturbation rates $\sim 10^2\;{\mathrm{s}}^{ - 1}$. The probability distribution in ${\Delta}\phi$ appearing for bare mGO is centered around ${\Delta}\phi = 0^ \circ$ with a longer positive tail (Fig. S2). The phase-contrast and peak height decrease at lower $A$, signifying lower energy losses as expected for materials with dominant elasticity. The positive skew in ${\Delta}\phi$ is suggestive of a positive shift in eigenfrequency. For pure elastic deformations, this is reminiscent of an effective increase in surface stiffness as has been considered earlier²² at high amplitude tapping. Further, to decouple noise correlation effects, the correlation length results of the height and phase images were taken into consideration and compared to previous results³² (see Supplementary section D and Fig. S4 for details).

Importance of captured strain rate

The energy losses as captured in Fig. 3a, c provides access to both the elastic and time-dependent viscous interactions as a function of ${\Delta}\phi$ distributions since the cumulative energy losses have nonconstant zero-crossovers. Specifically, ${\Delta}E_{\rm{dis}}$ at ${\Delta}\phi = 0^o$ provides a measure of conserved energy in the underlying dynamics. In our notation, the conserved energy is the same as energy stored ${\Delta}E_{\rm{stored}}$. Elastic deformation caters to this conserved energy scale providing a means to determine variations in elastic surface energy $\gamma _{el}$ on tip interactions. The viscoelastic deformation on the other hand is inelastic, and causes variations in surface stress as a function of the strain rate. This can be estimated from the net steady state ${\Delta}E_{\rm{dis}}$ as a function of apparent phase-contrast $\phi ^ \ast$ obtained in experiments using Eq. (1). The effective surface deformation in each case changes with the effective interaction area over which tip–surface energetics take root. The deformation-dependent changes in the interaction area were approximated as $A_{{\mathrm{interac}}} = 2\pi R \cdot {\Delta}a$ with $R \approx 12\;{\rm{nm}}$ (Fig. S5) alongside the deformation rates ${\Delta}\dot a \cong \omega \cdot {\Delta}a$ in units of ${\mathrm{m}} \cdot {\mathrm{s}}^{ - 1}$. The deformation rate represents a measure of the strain rate scale in the underlying dynamics as highlighted in Fig. 4 color bars. ${\Delta}E_{\rm{stored}}$ and ${\Delta}E_{\rm{dis}}$ are plotted against the estimated deformation dependencies, to determine the elastic $\gamma _{el}$ and viscosity coefficient $\eta$ as ${\Delta}E_{\rm{stored}} = - \gamma _{el}{\Delta}A_{{\mathrm{interac}}}$ and ${\Delta}E_{\rm{dis}} = \exp \left( { - \eta A_{{\mathrm{interac}}}{\Delta}\dot a} \right)$ vide⁵⁸ as shown in Fig. 4. The relative variations in energy stored and dissipated vs the strain rate amplitude (s⁻¹) are also suggestive as clear from the color bars in Fig. 4. For an elastic material, higher strain rate amplitude leads to more energy storage and loss, while in case of a viscoelastic material the energy storage reverses at higher strain rate amplitudes with the dissipated energy remaining higher for higher strain rate amplitudes as expected. It must be noted here that since TM-AFM is a fixed frequency method, the variation in strain rate in our experiments is obtained via a statistically relevant deformation scale ${\Delta}a$ that corresponds to a fixed oscillating amplitude $A$ as set by the amplitude setpoint $A_{{\mathrm{sp}}}$. In essence, ${\Delta}a$ is the mean deformation the surface encounters at a fixed tapping amplitude and frequency, depicting the viscoelastic dependencies in our experiments. The variations in ${\Delta}a$ are thus indeed a function of different strain amplitude at a fixed frequency. The energy losses or the equivalent viscoelastic behavior show an exponential dependence as a function of the strain rate scale ${\Delta}\dot a$ in units of ${\mathrm{m}} \cdot {\mathrm{s}}^{ - 1}$ for a fixed perturbation frequency.

Fig. 4: Estimations of surface energy and viscosity coefficients from the dynamic responses.

The exponential trend of dissipated energy clearly depicts a changing viscoelastic behavior as a function of strain rate. Error bars of the energy estimations from the experimental data are in the order of 1%. Error bars are computed from the standard deviations of individual measurands used to compute the energy estimates. The shaded area represents the 95% confidence band of the data fits. The estimated surface energy: $\gamma _{el}$ and viscosity coefficient: $\eta$ indicate an intrinsic strength in the order of kPa for DxO and MxD on mGO systems at the operational fixed perturbation rates $\sim$302 and 309 kHz, respectively. This is a relevant scale for biomolecules and tissues behaving like metallic glass^32,62. MxD being a smaller molecule is expected to reflect a higher intrinsic strength at a comparable perturbation rate. Comparatively for mGO results indicate an intrinsic strength in the order of MPa that matches well to the previous literature⁶³. Note: for mGO elastic deformation acts against the change in surface energy and thus the x-axis scale needs to be reversed in sign to correctly estimate as to the positive slope of the fitting line.

Theoretical consideration

For a detailed theoretical understanding, a comprehensive stochastic-dynamics model of motion is necessary to explain the probability of transitions or hopping between the states ${\Delta}\phi _ +$ and ${\Delta}\phi _ -$ as captured with ultra-light tapping. One approach can be the probability of achieving states $U\left( {{\Delta}\phi _ + } \right)$ and $U\left( {{\Delta}\phi _ - } \right)$ as a function of $\tau _c$, $U\left( {{\Delta}\phi } \right)$ being the potential function defining the energy of the states as depicted in (Fig. 5). Establishing such dependence will be crucial for identifying the stochastic parameters that are relevant to the underlying fluctuational dynamics appearing from tip–surface interactions in the limit ${\Delta}\phi \to 0$. However, such a detailed theoretical exposition is avoided here for the sake of brevity. Instead, we postulate and outline an energy partitioning approach that faithfully explains our results and institutes a general framework for explaining similar stochastic-resonance conditions²¹ that may arise in an experimental realization. The energy ${\Delta}E_{\rm{osc}}$ required to attain the minima at ${\Delta}\phi _ +$ and ${\Delta}\phi _ -$ appear from the losses in the driven oscillatory dynamics that are above the thermal noise potential $E_{\rm{noise}}$. It goes without saying that the operational parameters in the experiments are set to ensure that the deformations ${\Delta}a$ that result in the ${\Delta}\phi$ distributions in the first place are greater than the noise equivalent amplitude $A_{\rm{noise}} = \sqrt {\frac{{k_BT}}{k}} \approx 1.2\;{\rm{pm}}.$This corresponds to $E_{\rm{noise}} \sim 10^{ - 23}{\rm{J}}$. Error calibration analysis are provided in Fig. S6. Independent of the exact functional form of the chosen $U\left( {{\Delta}\phi } \right)$, Eq. (3) describes the fluctuation-induced hopping probability among the metastable and equilibrium states centered at ${\Delta}\phi _ +$ and ${\Delta}\phi _ -$ . Under very general assumptions Eq. (3) may be re-casted in the Gibbs measure form as⁵⁷

$${\Delta}E\left( {\phi ^ \ast } \right) = \frac{{E_{\phi ^ \ast }}}{{E_0}} = \exp \left( { - \frac{{{\Delta}E_{\rm{fluc}}}}{{{\Delta}E_{\rm{osc}}}} \cdot \phi ^ \ast } \right)$$

(4)

where ${\Delta}E_{\rm{fluc}}$ represents the energy losses from the transitional probabilities corresponding to $P\left( {{\Delta}\phi _ - } \right)$ appearing from interactions at the interface heterogeneities. This probability density $P\left( {{\Delta}\phi _ - } \right)$ signifies the relative strength of transitional loss pathways. ${\Delta}E_{\rm{osc}}$ on the other hand, corresponds to energy losses from the oscillatory dynamics with $P\left( {{\Delta}\phi _ + } \right)$ signifying the probability density of achieving the equilibrium states while $E_0$ accounts for the average energy conserved. The rationale behind casting Eq. (3) in the generalized Gibbs measure form (Supplementary Section G) is the assumption that fluctuations from interactions at the interface heterogeneities become more probable in the limit ${\Delta}\phi \to 0$ at small amplitudes $A$ and at smaller equilibrium separations $z_c$. The fluctuational transitions augment the homogeneous energy losses centered at ${\Delta}\phi _ +$ with an additional phase lag probability centered at ${\Delta}\phi _ -$ reflecting the overall phase contrast $\phi ^ \ast = {\Delta}\phi _ + - {\Delta}\phi _ -$ in our phase images (Fig. 3b, d). The appearing ${\Delta}\phi _ +$ and ${\Delta}\phi _ -$ distribution peaks, respectively, correspond to the faster resonance and the slower resonance broadening timescale affected by the tip–surface interactions. Equation (4) remarkably agrees with our experimental results for DxO@mGO and MxD@mGO normalized on the same scale, showing that the ratio of the fluctuational probability transitions to the equilibrium losses $\frac{{P\left( {{\Delta}\phi _ - } \right)}}{{P\left( {{\Delta}\phi _ + } \right)}}$ in the limit ${\Delta}\phi \to 0$ is exponentially related to the apparent phase-contrast $\phi ^ \ast$as shown in Fig. 6a justifying our Gibbsian approach. As evident from this result, the cantilever tip is more susceptible to experience fluctuational losses at low $A$ near-contact imaging, though yielding a smaller net phase contrast $\phi ^ \ast$ (Fig. 6b). The molecular clusters of DxO and MxD on mGO indeed are expected to exhibit surface heterogeneities, as the results indicate, owing to its viscoelastic properties which pronounce transitional losses from the viscous tip–surface interactions. The probability transition ratio $\frac{{P\left( {{\Delta}\phi _ - } \right)}}{{P\left( {{\Delta}\phi _ + } \right)}}$ (Fig. 6a) provides the Gibbs measure partitioning of heterogeneous losses over homogeneous losses. mGO, on the other hand, undergoes predominant elastic deformation and thus the heterogeneous effects are nonsignificant at the probing frequency. The transition ratio curve thus flattens out to an extent of small oscillations around a linear dependence in $\phi ^ \ast$ (Fig. 6a inset).

Fig. 5: Potential function $U\left( {{\Delta}\phi } \right)$ for the generalized theoretical consideration.

The AFM-cantilever translates $U\left( {{\Delta}\phi } \right)$ in the ultra-light tapping mode operation. $U\left( {{\Delta}\phi } \right)$ in the case of soft-matter is expected to typically exhibit two minima¹³ that correspond to steady-state and second metastable energy. This is dynamically captured by the cantilever as minima at ${\Delta}\phi _ +$ and ${\Delta}\phi _ -$ while translating between the states. The minima are separated with a potential barrier ${\Delta}E_{\rm{fluc}}$. It must be noted here, the potential barrier can consist of multiple transitional levels each having its own characteristics of relaxation timescale that would account for a phase delay ${\Delta}\phi$ proportional to the bandwidth product ${\Delta}_\omega \cdot \tau _c,$ where ${\Delta}_\omega$ is the frequency dispersion and $\tau _c$ is the correlation time. Energy losses from fluctuations in the limit ${\Delta}\phi \to 0$ compensates the thermodynamic cost of transition to the metastable state ${\Delta}\phi _ -$ from the steady state ${\Delta}\phi _ +$.

Fig. 6: Energy partitioning and apparent phase-contrast.

a The ratio of fluctuational probability density as a function of apparent phase contrast $\phi ^ \ast$. The shaded area represents 95% confidence bands of the fits. The error bars in the probability estimates are in the order of less than 1%, computed from the area standard deviations of the phase histograms obtained at each amplitude setpoint. The red square denotes a sole outlier of the experimental fit. b Highlights the evolution of apparent phase-contrast as a function of the tapping amplitudes. The nonlinear behavior observed for DxO and MxD is indicative of inelastic deviations yielding to viscous relaxations at the heterogeneities. The error bars in the apparent phase contrast $\phi ^ \ast$ are obtained from the standard deviations of measured phase histograms and the dynamic amplitude A.

Conclusions on ultra-light tapping mode AFM

Exploiting the fluctuational regime in TM-AFM with ultra-light tapping allows us to make the following important conclusions:

• (i) Phase imaging with ultra-light tapping ($A < 3\;{\rm{nm}}$) can discern both heterogeneous and homogeneous loss mechanisms as unique probability distributions centered at ${\Delta}\phi _ -$ and ${\Delta}\phi _ +$, but at the cost of low apparent phase-contrast $\phi ^ \ast = {\Delta}\phi _ + - {\Delta}\phi _ -$. $\phi ^ \ast$ marks out the separation of the characteristic relaxation timescales that describe the underlying transitional dynamics.

• (ii) Homogeneous losses stem from hopping between equilibrium states while heterogeneous losses originate from fluctuational transitions to metastable states of equilibrium. The latter dominates at small $A$ but are averaged out in high amplitude hard tapping. Fast transition between equilibrium states at high $A$ approximates monostable dynamics⁵⁵.

• (iii) Despite fluctuations at small $A$, a unique steady state irrespective of its evolving tip–surface potential $U\left( {{\Delta}\phi } \right)$ in ${\Delta}\phi$ is exhibited, and is approached throughout the transitional dynamics following Gibbs measure of energy partitioning. The unique steady-state denotes the metastable relaxation state in the case of soft-matter.

• (iv) The exponential fitting coefficient signifies a dimensionless damping parameter characterizing the underlying fluctuational dynamics off equilibrium. Our obtained experimental fit value = 0.11 on imaging DxO@mGO and MxD@mGO (Fig. 6a) matches well to a generalized theoretical estimate of damping coefficient of order $10^{ - 1}$ that considers similar dynamics⁵³; attesting merit to our analysis.

Application: transitional phase-contrast at contact resonance-enhanced AFM-IR can decouple thermal loss pathways in AFM-IR

The relevance of the crossover regime and the underlying transitional dynamics as argued above becomes even more crucial in studying and understanding thermal dissipative pathways in contact resonance-enhanced AFM-IR. Resonance-enhanced AFM-IR is emerging as a critical tool in characterizing compositional heterogeneities in addition to mechanical heterogeneities in bio-interfaces. This has been attempted with extracellular vesicles to aid with early diagnosis of diseases⁵⁹, miscibility of pharmaceutical blends for therapeutic drug delivery applications, and with the composition of extra-cellular-matrix at the nanoscale boundaries of cells⁶⁰ to study cell kinetics and cell signaling. The correct interpretation of the heterogeneities is crucial, and this is where our fluctuational understanding as argued above can create inroads.

Pseudo-ultra-light AFM-IR tapping mode

In contact resonance-enhanced AFM-IR, while a tip is scanned in the contact mode, a focused IR beam is simultaneously pulsed at the tip–surface junction. The IR pulsing rate is tuned to the contact resonance harmonic mode of the tip; the tip–surface interface essentially behaving like a viscoelastic contact junction. At the right IR wavelength, the absorption of IR energy resonantly excites vibrational states of molecules on the surface at the tip–surface junction. Nonradiative decay of these excited states causes thermal changes at the tip junction through multi-photon relaxation processes. The locally generated heat needs to dissipate at the nanoscale junction and there arise two possible routes: (i) a long-timescale conduction pathway and (ii) a faster dynamic dissipation route via a radiative coupling. Typically, in response to the long-timescale conduction pathway, the cantilever bends on heating generating a steady-state deflection giving IR-contrast as contact resonance (CR) amplitude (CR-amplitude in Fig. 7a, b). The dynamic dissipation route (fast timescale) on the other hand, manifests in the underlying CR dynamics. Details on optimization steps for the AFM-IR experiments is provided in the methods section. Essentially, thermal fluctuations at the tip–surface junction from IR absorption, instigate the probe cantilever to oscillate in a pseudo tapping mode with the active drive being at the tip of the cantilever. This establishes the pseudo-ultra-light AFM-IR tapping mode giving us the AFM-IR phase images. Radiative phonons instigated from the thermal fluctuations at the tip-junction have a finite probability to couple to acoustic phonon states of the probe tip (Fig. 8a), the tip–surface being a very low thermal mass junction. Such phonon couplings may promote transitional fluctuations in the underlying CR dynamics (Fig. 8b). The mechanism surrounding the energy dissipation probability from fluctuational transitions is illustrated in Fig. 8. Typically, radiative phonons relax over timescales that are in the order of ns, much faster compared to the contact resonance timescale in the order of a few microseconds. Thus, vide discussions of interaction timescales before, phonon coupling would result in an inherent fast interaction timescale in the underlying dynamics with respect to IR drive frequency. An apparent $+ {\Delta}\phi$ phase shift would result in giving a phase-contrast image (CR-phase in Fig. 7a, b). The fluctuational phase characteristics as a function of contact resonance amplitude are shown in Fig. 8d, e. Surface phonon excitations by IR and their subsequent coupling to acoustic phonon states of the cantilever, perturb the contact potential gradient. This enhances the probability transition into the transitional states from minute changes in heat. The modification of tip–surface potential function as shown in Fig. 8b in principle leads to multiple relaxation timescales. This is reflected as an apparent broadening of the fluctuational regime (Fig. 8b). The interplay of these multiple timescales is reflected in the apparent skewness of the phase lag distributions (Fig. 8d, e). In principle, following Eq. (3), the net dissipated energy is proportional to the standard deviation of the phase lag fluctuations. The slowest timescale being the rate-determining step of the underlying fluctuational dynamics, the effective phase contrast $\phi ^ \ast$ becomes the harmonic mean of the asymmetric Gaussian distribution fits (Fig. 8d, e) and is plotted in Fig. 8c inset. An apparent skewness toward $+ {\Delta}\phi$ is evident in both DxO and MxD molecules due to inherent viscous and compositional heterogeneities. Such behavior is absent in the case of bare mGO as detailed in Fig. S7 along with IR contact resonance-enhanced dynamics.

Fig. 7: Contact resonance-enhanced dynamic contrasts of infrared (IR) amplitude and phase contrast.

Contact resonance-enhanced amplitude contrast (left—CR-Amp) and contact resonance-enhanced phase contrast (right – CR-Phase) variations with setpoint @ 1416 cm⁻¹ on a DxO@mGO and b @ 1455 cm⁻¹ on MxD@mGO. The x-axis and y-axis scales of a DxO@mGO is 0.49 µm × 0.39 µm and that of b MxD@mGO is 3.66 µm × 3.6 µm. The long-timescale conduction dissipation path is measured from the cantilever deflection as IR amplitude contrast while the transitional dissipation path is measured from resonance fluctuations from the phase signal locked in at the contact resonance IR pulsing frequency. As clear from the results DxO has IR absorbance peak at 1416 cm⁻¹, while MxD has an absorption peak at 1455 cm⁻¹. The IR peak observed at 1416 cm⁻¹ for DxO@mGO is a representative signature of the vibration modes of skeletal rings of a DxO molecule (four rings per molecule)^64,65. The 1455 cm⁻¹ peak of for MxD@mGO is attributed to the vibration mode corresponding to aromatic C=C stretch (three bonds per molecule)^66,67. In contrast, the generated IR-contrast and phase lag contrast in the case of mGO shows no variations as a function of contact setpoint or its equivalent A_cr/A₀, where A₀, in this case, is the contact mode mean deflection and A_cr is the contact resonance amplitude at 100% IR power. Contact resonance characteristics relevant to the experiments are discussed in the Supplementary section H. DxO and MxD clusters on the other hand have appreciable IR absorbance and are reflected in the IR and phase-contrast images. Essentially IR-contrast (CR-Amplitude) and phase-contrast (CR-Phase) are complementary – locations having higher long-timescale dissipation reflect lesser dissipation by the transitional path and vice versa. These are more evident in the phase-contrast probability distributions showing an increase in phase contrast as a function of the contact mode setpoint in the case of DxO@mGO and MxD@mGO, respectively. mGO on the other hand does not show any variation since the contact resonance is not initiated.

Fig. 8: Contact resonance-enhanced infrared atomic force microscopy schematic.

a Illustration of IR-induced fluctuational enhancement. b describes the change in interaction potential function as a function of external IR excitation that brings about higher fluctuational probability transitions. c Energy dissipation probability as a function of phase contrast, the gray areas represent 98% confidence bands; Insets depict the apparent phase-contrast as function of the contact resonance amplitude (CR-Amplitude) ratios. d, e shows the IR phase-contrast characteristics in DxO@mGO and MxD@mGO, respectively. Error bars are computed from the standard deviations of the measured phase histograms and the dynamic amplitude A.

Conclusions and broad applicability

The exploitation of the transitions can thus be crucial in determining surface mechanical and chemical heterogeneities of pharmaceutical blends with relevance to drug delivery and therapeutic applications. A further detailed study on the transitional dynamics from the aspect of probability distributions is imperative which can link the coupling of IR-induced surface phonon and cantilever tip phonon states. These will be taken up elsewhere. A higher resolvability of the noise and contact resonance amplitudes and exploitation of higher contact harmonic modes may prove beneficial in nanoscale imaging of phonon density of states from surface heterogeneities. High resolution ${\Delta}\phi$ distributions at heterogeneous bio-interfaces of DNA, proteins, cells, and tissues augmented via CR enhanced AFM-IR contrast signatures, can provide insights on mechanical cues that bio-systems adopt to bring about irreversible evolutionary changes.

Methods

Materials

Silicon wafer (Si-w) was immersed in piranha solution for 1h to introduce an oxide layer on the surface of the wafer. The oxidized Si-w was immersed in 3% of (3-aminopropyl) triethoxysilane (APTES) ethanol solution to produce a positively charged amine group on the surface. After washing with fresh ethanol, the negatively charged GO solution at concertation of 1mg/mL was poured on the APTES functionalized Si-w for 10 min. Then, the prepared sample was spin-coated at 100 rpm for 2 s and 2000 rpm for 1 min to obtain mGO coated Si-w. Doxorubicin hydrochloride solution at a concentration of 0.1 mg/mL was prepared in deionized (DI) water and the pH of the solution was adjusted to pH 9 using NaOH. Then, the DxO solution was loaded on the mGO coated Si-w (mGO-Si-w) surface for 24 h. The DxO loaded mGO-Si-w (DxO@mGO) was washed with fresh DI water thrice to remove the unbounded DxO from the surface. Minoxidil loaded mGO (MxD@mGO) was prepared by the same method used for DxO@mGO, where minoxidil solution was initially prepared in ethanol at a concentration of 1 mg/mL and then diluted in DI water with a final concentration of 0.1 mg/mL before loading on mGO. Before each run samples were dried, and AFM was conducted in a continuous dry nitrogen environment. A comparative result of DxO@Si is provided in Fig. S8—small and high amplitude tapping highlighting the multi-stage phase distribution response. In our experiments, the tip-radius of the AFM probes are in the order of $\sim 12\;{\rm{nm}}$. This limits imaging DxO and MxD clusters of roughly 8–15 molecules with intercalated water in our case.

Equipment

Bruker’s ANASYS Nano IR2 system was used to run experiments. The tapping mode AFM images were obtained with soft tapping mode—PR-EX-TnIR-A probe cantilevers supplied by Bruker. Low amplitude runs within the fluctuational regime were optimized in steps starting with high amplitude tapping $A_0$ in the order of 10–12 nm till cantilever dynamics stabilize to give decent overlap of trace and retrace plots every scan. Subsequently, $A_0$ is brought down to the operational free amplitudes as annotated in Fig. 1 to achieve desired ultra-light tapping at amplitudes $A$ in the order of 1–2 nm. Low damping at the operational small $A$ gives us control over the dynamics to navigate the transitional excursions about the steady-state as highlighted in the Fig. 1. Setpoint amplitude was similarly optimized from low to high to obtain clean scans via overlap of trace and retrace scans. Images were captured with alternate low and high amplitude setpoint $A_{\rm{sp}}$ following bisection rule to negate the charge saturation effects at near-contact closest separations of tip and sample. The representative frequency response characteristics of the tapping mode cantilevers used in our analysis of mGO, DxO@mGO, and MxD@mGO data are shown in Fig. S9. Multiple scans were conducted at each optimized setpoint to ensure minimization of drift and artifacts, though at the cost of low throughput.

For the contact resonance-enhanced AFM-IR experiments, the same Nano IR2 system was used in conjunction with a tunable quantum cascade IR laser from Pranalytica as the high-power IR source. Bruker’s PR-EX-TnIR contact mode probes were used for getting the AFM-IR images. IR laser focus at the tip–surface junction was optimized with tip-engage to ascertain maximum contact resonance amplitude and establish the contact resonance-enhanced operation for AFM-IR runs (Fig. S7). The contact force was varied as a function of the contact mode setpoints at each run and the corresponding contact resonance-enhanced amplitudes $A_{\rm{cr}}$ were determined from the amplitude spectra collected as an independent data channel. The contact resonance amplitude $A_{\rm{cr}}$ varies as a function of the contact mode setpoint set in an experiment and a representative response spectrum (first contact resonance-enhanced mode) is shown in Fig. S7. The mean contact mode deflection for a given amplitude setpoint is obtained as a function of the spring constant of the probe cantilever. This along with the contact resonance noise spectra (Fig. S7) is used to determine the pseudo-ultra-light tapping AFM-IR free amplitudes $A_0$. These corresponding AFM-IR response characteristics as a function of $\frac{{A_{\rm{cr}}}}{{A_0}}$ are plotted as represented in Figs. 7, 8, and S7.

Exploiting fluctuations by the correlation timescale τ_c

To explain how fluctuations affect dynamics, it is convenient to start with the oscillator’s susceptibility ${\rm{X}}\left( \omega \right),$ which relate the average value of damped amplitude $A$ as $\left\langle A \right\rangle = {\rm{X}}\left( \omega \right)A_0e^{ - i\omega \tau }$; with $\left\langle A \right\rangle = 0$ in the absence of external drive and $\omega$ the frequency on tip–surface approach from amplitude damping. To capture the transients, correct ensemble averaging over the timescale $\tau$ is important such that the correlation timescale $\tau _c$ of two successive data cycles at every pixel is finite. A linear amplitude damping on tip approach is a direct outcome of the oscillator’s frequency dispersion ${\Delta}_\omega = \left\langle {\left[ {{\Delta}\left( \omega \right) - \left\langle {{\Delta}\left( \omega \right)} \right\rangle } \right]^2} \right\rangle ^{\frac{1}{2}}$ accentuated by frequency fluctuations ${\Delta}\left( \omega \right)$ near resonance. The regime of interest is the condition where the reciprocal of correlation timescale $\tau _c^{ - 1}$ becomes comparable to the standard deviation of the fluctuations ${\Delta}_\omega$. With the free amplitude frequency $\omega _0$, the largest frequency in the system, the rest of frequency scales ${\Gamma},\;{\Delta}_\omega \approx \tau _c^{ - 1}\;{\mathrm{and}}\;\left| {\delta \omega } \right|$ satisfy the condition to be $\ll \omega$ near resonance. In effect, the frequency fluctuations ${\Delta}\left( \omega \right)$ becomes the parameter of significance dictating the linewidth of ${\rm{X}}\left( \omega \right)$ near resonance $\left| {\omega - \omega _0} \right| \ll \omega$ when simultaneously ${\Gamma},\;\tau _c^{ - 1} \approx {\Delta}_\omega$ is satisfied. In the limit when $\tau _c^{ - 1}$ is finite and nonzero, and $\tau _c \to \tau _{\rm{osc}}$ ($\tau _c > \tau _{\rm{osc}}$ as in our case), the energy interactions at the tip–surface junction becomes heterogeneous; leading to a Lorentzian linewidth spread in $Im{\rm{X}}\left( \omega \right)$ centered at $\omega - {\Delta}_\omega$ with no averaging of the eigenfrequency⁵⁷. Corresponding variations in amplitude of oscillation would then resolve as $A + {\Delta}a$ with ${\Delta}a$ being the standard deviation (Lorentzian width) of the normalized amplitude histogram obtained in an experiment for a particular $A_{\rm{sp}}$. ${\Delta}a$ essentially becomes the surface deformation at the interaction timescale of $\tau _c \to \tau _{\rm{osc}}$ $\left( {\tau _c > \tau _{\rm{osc}}} \right)$ that is in the same order as $\tau _{\rm{sur}} \approx 10^2 - 10^4\;{\rm{ns}}$⁶¹. In the opposite limit $\tau _c < \tau _{\rm{osc}}$ however, the oscillator cannot resolve the frequency variations and are thus averaged out giving $\left\langle {{\Delta}_\omega } \right\rangle \cong 0$. The linewidth shape of $Im{\rm{X}}\left( \omega \right)$ remains a Lorentzian ${\Gamma}$ centered at $\omega - \left\langle {{\Delta}_\omega } \right\rangle$ with $\left\langle {{\Delta}_\omega } \right\rangle \cong 0$. The limit $\tau _c < \tau _{\rm{osc}}$^35,40,51,52 has been the premise of hard tapping operation that satisfies Eq. (1) for both hard elastic and soft viscoelastic surfaces at higher tapping amplitudes. However, the data captured under such conditions, convey energetics that asymptotically tend to the steady state dynamics overlooking the fluctuations. The fluctuations near equilibrium are thus averaged out as explained, missing out on the critical NE energetics of tip–surface interactions.