Introduction

Network science has been successful in describing the structure and dynamics of complex systems in many fields of science. Nevertheless, in the vast majority of studies, the mathematical and computational descriptions of these networks are limited to pairwise interactions. In most cases, this order of interaction is a good approximation, describing real phenomena1,2,3,4. Recently, it has become increasingly evident that simplifying higher-order interactions as a set of pairwise ones can be misleading in many situations5,6, as it is the case, for instance, when comparing triangles and clustering6. An attempt to formally solve this problem is represented by the introduction of the simplicial complexes approach7,8. Although very powerful, as a topological space, simplicial complexes require mutual inclusion for the interactions9, which is too restrictive for general purposes. To face this problem, one needs to resort to the use of hypergraphs, which by relaxing the assumption of mutual inclusion, allow the representation of a broader range of systems.

Admittedly, the attention to higher-order systems has proliferated lately 5,6,8,10,11,12,13,14,15,16,17,18,19,20, with an increasing focus on hypergraphs in fields such as mathematics6,12,13,15,16,21,22, physics8,10,11,17,18,19,23,24,25, and computer science26,27,28,29,30,31,32,33,34. In many fields, the dynamical systems approach appears naturally. This is the case of many problems tacked in the physics literature mentioned above, where we are interested in macroscopic changes that emerge from local interactions. Specifically, this viewpoint was explored in social contagion models in refs. 8,17, where first- and second-order transitions and hysteresis were found. Along the similar lines, the problems of evolutionary game theory18, synchronization23,24,25, and random walks19,33,34 were also explored. Each field’s focus is different, but it is often useful to use an abstract model that has a direct physical interpretation. Perhaps, the simplest example of this is the use of random walks in deep learning and machine learning techniques33,34. Despite this interest, a general theory of dynamical processes on higher-order structures is still largely missing.

Here we address this open problem by building a mathematical framework that allows performing a linear stability analysis for general processes on arbitrary hypergraphs. This approach highlights the importance of the graph projection—an underlying weighted graph representation of a hypergraph—for the dynamics. The proposed methodology makes it possible to decompose a hypergraph in uniform structures, hence enabling the characterization of their role in the system’s dynamics. Finally, to show the usefulness of our approach, we analytically study and recover some results reported for social contagion8,17, and diffusion processes, also providing new key insights into these paradigmatic dynamics. The framework discussed in this paper could be used to explore different processes when pairwise interactions are an oversimplification of the system, which has the potential to bring more insights into the understanding of higher-order dynamics of interacting systems.

Results and discussion

A hypergraph, \({\mathcal{H}}=\{{\mathcal{V}},{\mathcal{E}}\}\), is defined as a set of nodes, \({\mathcal{V}}=\{{v}_{i}\}\), with \({v}_{i}\in {{\mathbb{Z}}}^{+}\), \(N=| {\mathcal{V}}|\) the number of nodes and a set of hyperedges \({\mathcal{E}}=\{{e}_{j}\}\), where ej is a subset of \({\mathcal{V}}\) with arbitrary cardinality ∣ej∣. We also denote \({{\mathcal{E}}}_{i}\) as the set of hyperedges that contain the node i. Note that if \(\max (| {e}_{j}|)=2\), we recover a graph, whereas one has a simplicial complex if for each hyperedge with ∣ej∣ > 2, its subsets are also contained in \({\mathcal{E}}\). The adjacency matrix15 can be defined as

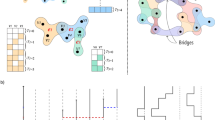
$${\bf{A}}_{ik}=\sum\limits_{{{{{e}_{j}\in{\mathcal{E}}}\atop {i,k\in {e}_{j}}}\atop {i\ne k}}}\frac{1}{| {e}_{j}| -1},$$
(1)

which can be interpreted as a weighted projected graph. Note that Aii = 0 for all i. An example of a hypergraph and its graph projection is shown in Fig. 1. A more general definition of the adjacency matrix, including also diagonal elements, can be expressed in terms of its weighted counterpart defined as

$${{\bf{W}}}_{ik}=\sum\limits_{{{e}_{j}\in{\mathcal{E}}}\atop {i,k\in {e}_{j}}}\frac{{w}_{ik}({e}_{j})}{| {e}_{j}| -1},$$
(2)

where wik(ej) is an arbitrary number. When wik(ej) = w(∣ej∣), the weight is a function of the cardinality of the hyperedge, ej, weighting differently the contribution of each hyperedge. For instance, if we consider w(∣ej∣) = ∣ej∣ − 1, we recover the adjacency matrix used in ref. 19. Furthermore, the Laplacian matrix is defined as L = D − A, where D = diag(ki) and the degree is given as \({k}_{i}=\mathop{\sum }\nolimits_{j = 1}^{N}{{\bf{A}}}_{ij}\). Note that, in order to define the Laplacian matrix on the weighted case we also need to redefine D accordingly.

Fig. 1: Graphical representation of a hypergraph.
figure 1

The hypergraph in a, its projection in b, and structural decomposition in c. Mathematically, The set of nodes was represented by \({\mathcal{V}}=\{{v}_{1},{v}_{2},{v}_{3},{v}_{4},{v}_{5},{v}_{6},{v}_{7},{v}_{8}\}\), while the set of hyperedges was \({\mathcal{E}}=\{{e}_{1},{e}_{2},{e}_{3},{e}_{4}\}\), where the hyperedges are e1 = {v1, v2, v3}, e2 = {v3, v4, v5, v6}, e3 = {v6, v7}, and e4 = {v8}. We show how the original hypergraph (a) can be represented both by c decomposing it into m-uniform hypergraphs (color-coded) or by b projection—where hyperedges are simplified as ∣ej∣-cliques, with j = 1, ..., 4.

Full size image

We can also decompose the hypergraph into m-uniform hypergraphs, as motivated in ref. 16. Formally,

$${{\bf{A}}}_{ik}^{m}=\sum\limits_{{{{{e}_{j}\in {\mathcal{E}},| {e}_{j}| =m}\atop i,k\in {e}_{j}}\atop {i\ne k}}}\frac{1}{| {e}_{j}| -1},$$
(3)

therefore A = ∑mAm as showed in Fig. 1. Consequently, we can also define Dm, Lm, and Wm.

Linear stability analysis (LSA)

A general dynamical process on the hypergraph can be written as

$$\frac{d{x}_{i}}{dt}={f}_{i}({x}_{i})+\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}{g}_{j}({x}_{\{{e}_{j}\}}),$$
(4)

where xi is the state of the node i, fi(xi) is a \({\mathbb{R}}\to {\mathbb{R}}\) function that depends only on the state of node i and \({g}_{j}({x}_{\{{e}_{j}\}})\) is a \({{\mathbb{R}}}^{| {e}_{j}| }\to {\mathbb{R}}\) function that takes all the states of the nodes on the hyperedge ej, here denoted as \({x}_{\{{e}_{j}\}}\), and compute its contribution to xi. While fi(xi) represents the internal dynamics of the node, \({g}_{j}({x}_{\{{e}_{j}\}})\) is the external interaction, expressed as the hyperedge contribution.

Linear stability analysis for higher-order systems has been explored both in simplicial complexes24,25, where the mutual inclusion constrain imposes a limit on the dynamics, and for particular dynamics with a specific Laplacian for hypergraphs23. Despite these efforts, a general theory of dynamical processes on higher-order structures is still largely missing. Similarly to ref. 2, we can perform a linear stability analysis for Eq. (4) around a known fixed point, \({x}_{i}={x}_{i}^{* }\). The linearized equations are expressed as

$$\frac{d{\epsilon }_{i}}{dt}=\left.\frac{d{f}_{i}({x}_{i})}{d{x}_{i}}\right|_{{x}_{i} = {x}_{i}^{* }}{\epsilon }_{i}+\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}\left.\sum\limits_{k\in {e}_{j}}{\partial }_{{x}_{k}}{g}_{j}({x}_{\{{e}_{j}\}})\right|_{{\bf{x}} = {{\bf{x}}}^{* }}{\epsilon }_{k},$$
(5)

where x is a vector whose components are xi. We can express Eq. (5) in its matrix form decomposing a general hypergraph into uniform hypergraphs as

$$\frac{d{\boldsymbol{\epsilon }}}{dt}=\left({\bf{F}}({{\bf{x}}}^{* })+{\bf{G}}({{\bf{x}}}^{* })\right){\boldsymbol{\epsilon }}={\bf{M}}{\boldsymbol{\epsilon }},$$
(6)

where

$${{\bf{F}}}_{ii}({{\bf{x}}}^{* })=\left\{\begin{array}{ll}\frac{d{f}_{i}({x}_{i})}{d{x}_{i}}{\left|\right.}_{{x}_{i} = {x}_{i}^{* }}&i=j\\ 0\hfill&\,\text{otherwise}\,\end{array}\right.$$
(7)
$${{\bf{G}}}_{ik}({{\bf{x}}}^{* }) =\left.\sum \limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}{\partial }_{{x}_{k}}{g}_{j}({x}_{\{{e}_{j}\}})\right|_{{\bf{x}} = {{\bf{x}}}^{* }}\\ =\left.\sum\limits _{{e}_{j}\in {{\mathcal{E}}}_{i}}{{\mathbb{1}}}_{\{k\in {e}_{j}\}}{\partial }_{{x}_{k}}{g}_{j}({x}_{\{{e}_{j}\}})\right|_{{\bf{x}} = {{\bf{x}}}^{* }},$$
(8)
$${\bf{M}}({{\bf{x}}}^{* })={\bf{F}}({{\bf{x}}}^{* })+{\bf{G}}({{\bf{x}}}^{* }).$$
(9)

The fixed point x* is stable if

$${{{\Lambda }}}_{i}({\bf{M}})<0\ \forall i\in \{1,2,...,N\},$$
(10)

where Λi(M) is the ith eigenvalue of the Jacobian M. Note that the indicator function \({{\mathbb{1}}}_{\{k\in {e}_{j}\}}\), which is one if the node k is inside the hyperedge ej, and zero otherwise, in this case is redundant, considering that gj depends only on the states of the nodes inside ej. The general form of the adjacency matrix in Eq. (2) can be expressed as

$${{\bf{W}}}_{ik} =\sum\limits_{{{e}_{j}\in {{\mathcal{E}}}}\atop{k\in {e}_{j}}}{w}_{ik}({e}_{j})\\ =\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}{{\mathbb{1}}}_{\{k\in {e}_{j}\}}{w}_{ik}({e}_{j}),$$
(11)

when \({w}_{ik}({e}_{j})=(| {e}_{j}| -1){\partial }_{{x}_{k}}{g}_{j}({x}_{\{{e}_{j}\}})\) calculated at the fixed point x*, G = W. This shows that, although we have a high-order structure (\({N}^{\max (| {e}_{j}| )}\) in the tensorial representation13), near the fixed point, the dynamics is described only by \({\bf{G}}\in {{\mathbb{R}}}^{N\times N}\), which is a weighted graph-projection of the hypergraph, the weights being determined by the dynamics. In special cases, as shown next, this projection appears in the form of the Laplacian or the adjacency matrix A in Eq. (1).

Moreover the matrix G can be decomposed in m-order contributions Gm that correspond to the mth uniform hypergraph in the structural decomposition, such that

$${{\bf{G}}}_{ik}^{m}({{\bf{x}}}^{* })=\sum\limits _{{{{{e}_{j}\in {{\mathcal{E}}}_{i}}\atop | {e}_{j}| =m}}}{\partial }_{{x}_{k}}{g}_{j}({x}_{\{{e}_{j}\}})|_{{\bf{x}} = {{\bf{x}}}^{* }},$$
(12)
$${\bf{G}}({{\bf{x}}}^{* })=\mathop{\sum }\limits_{m=1}^{\max \left(| {e}_{j}| \right)}{{\bf{G}}}^{m}({{\bf{x}}}^{* }).$$
(13)

The structures of cardinality m do not contribute to the stability of the fixed point x* if \({{\bf{G}}}_{ik}^{m}({{\bf{x}}}^{* })=0\) ∀i, k. A similar approach can be tackled by the bipartite representation of the hypergraph, as shown in the next section.

Linear stability analysis: comparison with the bipartite representation

In order to define the bipartite representation of a hypergraph, we have to introduce the incidence matrix. The common definition is given by

$${{\mathcal{I}}}_{ij}=\left\{\begin{array}{l}1\ \,\text{if}\,\ i\in {e}_{j}\\ 0\ \,\text{if}\,\ i\,\notin\, {e}_{j}\end{array}\right.,$$
(14)

where \({\mathcal{I}}\in {{\mathbb{R}}}^{N\times M}\) as shown in refs. 19,20,23. In this case, we have two sets of nodes, one representing the hypergraph nodes, and the other the hyperedges. The relative projection is encoded in the weighted adjacency matrix19

$$\tilde{{\bf{A}}}={\mathcal{I}}{{\mathcal{I}}}^{T}-{\bf{D}},$$
(15)

where D = diag(ki) is a diagonal matrix whose diagonal elements are the degrees. The element \({\tilde{{\bf{A}}}}_{ij}\) can be interpreted as the number of hyperedges shared by nodes i and j. Notice that \({\sum }_{j}{\tilde{{\bf{A}}}}_{ij}\) is the number of neighbors of i, which can be different from the degree. On the other hand, the projection in Eq. (1), can be defined as

$${\bf{A}}={\mathcal{B}}{{\mathcal{B}}}^{T}-\hat{{\bf{D}}},$$
(16)
$${\hat{{\bf{D}}}}_{ii}=\sum\limits_{{e}_{j}\cap \{i\}\ne {{\emptyset}}}\frac{1}{| {e}_{j}| -1},$$
(17)

where the weighted incidence matrix is

$${{\mathcal{B}}}_{ij}=\left\{\begin{array}{ll}{\left(| {e}_{j}| -1\right)}^{-\frac{1}{2}}&\,\text{if}\,\ i\in {e}_{j}\\ 0\hfill&\,{\text{if}}\,\ i \, \notin \, {e}_{j}\end{array}\right.$$
(18)

and \(\hat{{\bf{D}}}\) is a diagonal matrix. In this case, ∑jAij correctly represents the degree, like in standard graph theory. Moreover, the projection in Eq. (15) can represent multiple hypergraphs, as shown in Fig. 2a, b, while, in the case of Eq. (16) we could not find the same projection for two different hypergraphs (Fig. 2b, c). To the best of our knowledge, the proof of the one to one mapping is an open problem.

Fig. 2: Different hypergraph projections.
figure 2

Projection of two different hypergraphs built on the same set of nodes, \({\mathcal{V}}=\{{v}_{1},{v}_{2},{v}_{3},{v}_{4},{v}_{5}\}\). In a projection following the incidence matrix in Eq. (15), b original hypergraphs, and c the weighted projection for the model presented in Eq. (16). In a and c, the edges' colors represent their weights as indicated next to each edge.

Full size image

From a dynamical point of view, Eq. (4) can be written in terms of the bipartite representation as

$$\frac{d{x}_{i}}{dt}={f}_{i}({x}_{i})+\mathop{\sum }\limits_{j=1}^{M}{{\mathcal{B}}}_{ij}{g}_{j}({x}_{\{{e}_{j}\}}).$$
(19)

In this case, the linear stability is expressed by

$$\frac{d{\epsilon }_{i}}{dt}=\left.\frac{d{f}_{i}({x}_{i})}{d{x}_{i}}\right|_{{x}_{i} = {x}_{i}^{* }}{\epsilon }_{i}+\left.\mathop{\sum }\limits_{j=1}^{M}\mathop{\sum }\limits_{k=1}^{M}{{\mathcal{B}}}_{ij}{{\mathcal{B}}}_{kj}{\partial }_{{x}_{k}}{g}_{j}({x}_{\{{e}_{j}\}})\right|_{{\bf{x}} = {{\bf{x}}}^{* }}{\epsilon }_{k},$$
(20)

recovering Eq. (5).

Linear stability analysis of separable interacting functions (LSA-SIF)

We now focus on the special case of a diffusion-like process on hypergraphs. In this case, \({g}_{j}({x}_{\{{e}_{j}\}})\) is separable and we can express the interaction function as

$${g}_{j}({x}_{\{{e}_{j}\}})=\frac{1}{| {e}_{j}| -1}\sum\limits_{k\in {e}_{j} \atop k\ne i}\left(g({x}_{i})-g({x}_{k})\right),$$
(21)

where the weight \({(| {e}_{j}| -1)}^{-1}\) is necessary due to conservation purposes. Assuming that fi(xi) is the same for all nodes, the fixed point is symmetrical, i.e., \({x}_{i}^{* }={x}_{j}^{* }\) for any pair i, j. In this case, Eqs. (7) and (8) reduce to

$${\bf{F}}=\alpha {\bf{I}}\ \,\text{and}\,\ {\bf{G}}=\beta {\bf{L}},$$
(22)

where \({\bf{I}}\in {{\mathbb{R}}}^{N\times N}\) is the identity matrix, and

$$\alpha =\frac{df(x)}{dx}{\left|\right.}_{{\bf{x}} = {{\bf{x}}}^{* }}\ \,\text{and}\,\ \beta =\frac{dg(x)}{dx}{\left|\right.}_{{\bf{x}} = {{\bf{x}}}^{* }}.$$
(23)

Therefore, Eq. (5) is expressed as

$$\frac{d{\epsilon }_{i}}{dt}=\left(\alpha +\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}\sum\limits_{k\in {e}_{j}}\frac{\beta }{| {e}_{j}| -1}\right){\epsilon }_{i}-\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}\sum\limits_{k\in {e}_{j}}\frac{\beta {\epsilon }_{k}}{| {e}_{j}| -1},$$
(24)

which in matricial form reads

$$\frac{d{\boldsymbol{\epsilon }}}{dt}=\left(\alpha {\bf{I}}+\beta {\bf{L}}\right){\boldsymbol{\epsilon }},$$
(25)

where ϵ is the vector whose components are ϵi. If μi are the eigenvalues of L, the stability condition for the fixed point x* can be written as α + βμi < 0, for all i. Next, considering that the Laplacian matrix is semi-positive definite, the former condition in terms of the largest eigenvalue, μn, is

$$\frac{1}{{\mu }_{n}}> -{\left[\frac{dg(x)}{dx}/\frac{df(x)}{dx}\right]}_{{x}_{i} = {x}_{i}^{* }}.$$
(26)

Linear stability analysis of interacting functions with symmetrical derivatives (LSA-SD)

Now, let us consider a second scenario for \({g}_{j}({x}_{\{{e}_{j}\}})\) such that

$${g}_{j}^{* }({x}_{\{{e}_{j}\}})=\frac{1}{(| {e}_{j}| -1)}{g}_{j}({x}_{\{{e}_{j}\setminus \{i\}\}}),$$
(27)

which depends, for a node i, only on xk, where k ∈ ej and k ≠ i, and the weight is the same as for Eq. (21). Assuming that fi(xi) is the same for all nodes, and also all the derivatives of \({g}_{j}^{* }\) are all the same in the fixed point, Eq. (7) reduces to

$$\frac{d{\epsilon }_{i}}{dt}=\alpha {\epsilon }_{i}+\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}\sum\limits_{k\in {e}_{j}}\frac{\beta {\epsilon }_{k}}{| {e}_{j}| -1},$$
(28)

or, equivalently,

$$\frac{d{\boldsymbol{\epsilon }}}{dt}=\left(\alpha {\bf{I}}+\beta {\bf{A}}\right){\boldsymbol{\epsilon }}.$$
(29)

Note that, the former restriction covers the wide class of normalized symmetric functions23. Denoting by λi, the eigenvalues of A, the stability condition reads

$$\frac{1}{{\lambda }_{n}}<-{\left[\frac{dg(x)}{dx}/\frac{df(x)}{dx}\right]}_{{x}_{i} = {x}_{i}^{* }}<\frac{1}{{\lambda }_{1}}.$$
(30)

In these two general cases, the projected adjacency matrix, Eq. (1), arises naturally from the linear stability analysis around the fixed point, which means that only the projected structure is relevant for the dynamics. Moreover, as it can be seen from Eqs. (26) and (30), we can decouple the structural and dynamical contributions to the stability conditions.

Linear stability analysis of uniform hypergraphs (LSA-UH)

So far we have focused on arbitrary structures. However, it is worth emphasizing that structural constraints might allow for a simplification of the linear stability condition. A special class of hypergraphs that allows for that are uniform hypergraphs, for which all hyperedges have the same cardinality. Note that although the cardinality of the hyperedges is the same, the degree distribution could be arbitrary. Moreover, even if constrained, this class of hypergraphs was used to study epidemic spreading35 and evolutionary games18. As all the hyperedges have the same cardinality, the interacting functions will be the same, i.e., \({g}_{j}({x}_{\{{e}_{j}\}})=g({x}_{\{{e}_{j}\}})\). Assuming symmetric derivatives and denoting them by β as in Eq. (21), and, given that we are restricted to undirected hypergraphs, G will comply with one of the three following cases: (i) separable functions, thus G = βL, (ii) normalized functions of its entries23, where \(g({x}_{\{{e}_{j}\}})\) does not distinguish between xi and the other arguments, in this case G = β(A + D), which has the same form of sing-less Laplacian in graph theory, (iii) independent of xi, i.e., \(g({x}_{\{{e}_{j}\}})={g}_{j}({x}_{\{{e}_{j}\setminus \{i\}\}})\), thus G = βA.

Note that although the former derivations are specific for these cases, Eq. (10) holds for general dynamics in an arbitrary hypergraph. The framework outlined up to now is general and can be readily applied to many dynamical processes in which one is forced to go beyond pairwise interactions. In what follows, we discuss two of such applications, namely, social contagion8,17 and diffusion processes. For the social contagion case, the stability of the process is related to the adjacency matrix, following a similar form as Eq. (30), where we were able to employ the structural decomposition to evaluate the role of pairwise and higher-order structures. On the other hand, for the diffusion, the stability depends on the Laplacian matrix, yielding to a condition of the form of Eq. (26). In this case, we show that hypergraphs’ structural organization may introduce a nontrivial behavior, and we remark that the Laplacian operator is connected to many other dynamical processes, such as random walks and synchronization. With these two processes, we exemplify possible applications of the linear stability analysis and the structural decomposition, providing insights about these dynamics in hypergraphs and suggesting further implications in other processes.

Application to a process of social contagion

In this dynamical process, the state xi represents the probability of an individual to be active. The deactivation mechanism is given by fi(xi) = −δxi and the interaction functions \({g}_{j}({x}_{\{{e}_{j}\}})\) are given by the product of the probability that i is inactive and the other nodes in the hyperedge ej are active times a contact rate, \({\beta }_{| {e}_{j}| }\). Hence,

$${g}_{j}({x}_{\{{e}_{j}\}})=\frac{{\beta }_{| {e}_{j}| }}{| {e}_{j}| -1}(1-{x}_{i})\prod\limits_{k\in {e}_{j} \atop{k\ne i}}{x}_{k}.$$
(31)

Separating the pairwise and higher-order contributions to the state of the node, we have

$$\frac{d{x}_{i}}{dt} = -\delta {x}_{i}+{\beta }_{2}\sum\limits_{{{e}_{j}\in {{\mathcal{E}}}_{i}\atop | {e}_{j}| =2}\atop {k\in {e}_{j},k\ne i}}(1-{x}_{i}){x}_{k}+\\ +\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}\atop | {e}_{j}| > 2}\frac{{\beta }_{| {e}_{j}| }}{| {e}_{j}| -1}(1-{x}_{i})\prod\limits_{k\in {e}_{j}\atop k\ne i}{x}_{k}.$$
(32)

Assuming a symmetric fixed point, i.e., xi = x*,

$$\frac{d{\epsilon }_{i}}{dt} = \left(-\delta -\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}\frac{{\beta }_{| {e}_{j}| }{({x}^{* })}^{(| {e}_{j}| -1)}}{| {e}_{j}| -1}\right){\epsilon }_{i}\\ +\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}\sum\limits_{k\in {e}_{j}\atop k\ne i}\frac{{\beta }_{| {e}_{j}| }(1-{x}^{* }){({x}^{* })}^{(| {e}_{j}| -2)}}{| {e}_{j}| -1}{\epsilon }_{k},$$
(33)

where we can apply Eq. (10) to evaluate the stability of the system’s dynamics. The mean-field form of Eq. (32) is given by

$$\frac{dx}{dt}=-\delta x+{P}^{\nu }(x)=-\delta x+\mathop{\sum }\limits_{k=1}^{\nu }{\beta }_{k}c(k)(1-x){x}^{k-1},$$
(34)

where \(\nu ={\max }_{j}\{| {e}_{j}| \}\) is the maximum cardinality and c(k) is the ratio between the number of hyperedges with cardinality k and the number of pairwise interactions, which characterizes the structure of the hypergraph. In the steady state this is a polynomial equation whose solutions are the fixed points of the process and their stability can be evaluated using Eq. (33).

Social contagion: general behavior

A fundamental observation from Eq. (33) is that only pairwise interactions, given by the off-diagonal terms, are responsible for the stability of the absorbing state, the fixed point xi = 0. Specifically, the stability condition for this state depends on the second-order adjacency matrix from Eq. (3) and is given by

$$\frac{\beta }{\delta }<{\left({{{\Lambda }}}_{\max }({{\bf{A}}}^{2})\right)}^{-1}.$$
(35)

Interestingly enough, in this scenario, the dynamics behaves like an SIS process on complex networks, and is characterized by a continuous phase transition36. Therefore, we claim that in a social contagion model, pairwise interactions are a necessary condition for a continuous phase transition. We can support this claim using an argument by contradiction as follows. Near the absorbing state the probability for a node to be active is very small, hence, assuming an arbitrary small number η ≈ 0, we can consider xi ∈ O(η). Therefore, from Eq. (32), the coefficients \({\beta }_{| {e}_{j}| }\) are multiplying terms of order \(O({\eta }^{(| {e}_{j}| -1)})\). At the steady state, \(\delta {x}_{i} \sim {\beta }_{| e{| }_{j}}{x}_{i}\), assuming δ ∈ O(1) without loss of generality. From this point, we can differentiate three cases depending on \({\beta }_{| {e}_{j}| }\):

  1. (i)

    If \({\beta }_{| {e}_{j}| }\in O(1)\) for all \(| {e}_{j}| \in \{1,2,...,\max (| {e}_{j}| )\}\), then the leading coefficient is β2 therefore β2xi ∈ O(η) as assumed. In this case we have a continuous phase transition with respect to the control parameter β2;

  2. (ii)

    If β2 ∈ O(1) and \({\beta }_{| {e}_{j}| }\in O({\eta }^{-(| {e}_{j}| -2)})\), for ∣ej∣ > 2, then the leading coefficient is \({\beta }_{| {e}_{j}| }{x}_{i}\in O(\eta )\), thus the transition can be either continuous or discontinuous;

  3. (iii)

    If \({\beta }_{| {e}_{j}| }\in O({\eta }^{-(| {e}_{j}| -1)})\) for all \(| {e}_{j}| \in \{1,2,...,\max (| {e}_{j}| )\}\), then the leading coefficient is \({\beta }_{| {e}_{j}| }{x}_{i}\in O(1)\), which contradicts the initial assumption of xi ∈ O(η). This suggests a discontinuity if β2 ∈ O(1) and at least one of the higher-order coefficients is \(O({\eta }^{-(| {e}_{j}| -1)})\).

Social contagion: mean-field approach

To further extend the analysis in ref. 8, in order to compute c(k), we consider higher-order contact patterns from two real datasets. The data were collected with proximity sensors in a high school14,37, and a primary school14,38. Our results are summarized in Fig. 3a, b, where we consider the feasible fixed points and their stability. In this case, we assume β2 = β and βk = βek, in order to emphasize the role of lower and higher-order structures. Notice that, given the same parameters, we can have either continuous or discontinuous phase transitions with hysteresis, depending only on the structure of the hypergraph. Considering the graph case, i.e., \({\max }_{j}\{| {e}_{j}| \}=2\), the social contagion model is an SIS epidemic spreading. Thus, the behavior near the fixed point x* = 0 is

$$\frac{d{\epsilon }_{i}}{dt}=-\delta {\epsilon }_{i}+{\beta }_{2}\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}{\epsilon }_{k}.$$
(36)

Note that the stability of the absorbing state is given by \({\lambda }_{\max }<\frac{\delta }{{\beta }_{2}}\), as for the quenched mean-field39.

Fig. 3: Stability analysis of a social contagion dynamics on real-world, and synthetic hypergraphs.
figure 3

In a, the substrate is a high school contact pattern, while in b, a primary school contact pattern. The order parameter, X, is the fraction of active nodes, while β is the spreading rate. c–f Results for the stability analysis of a simplicial complex in the space of the spreading rates for pairwise interactions, β2, and triangles, β3. c, e Correspond, respectively, to the solution \({{x}^{* }}_{2}^{-}\) (Eq. (37)) and its stability (Eq. (38)), whereas d, f represent the solution \({{x}^{* }}_{2}^{+}\) (Eq. (37)) and its stability (Eq. (38)), respectively. Here, \({{x}^{* }}_{2}^{+}\) and \({{x}^{* }}_{2}^{-}\) are solutions of the mean-field equation that describes the social contagion model. In e, f, U and S stand for unstable and stable, respectively.

Full size image

Next, we analyze the simplicial complex case, where the structure is homogeneous and consists only of pairwise interactions and triangles, hence n = 3. In this case, Eq. (34) has the three solutions, \({{x}^{* }}_{1}=0\), and

$${{x}^{* }}_{2}^{\pm }=\frac{(\frac{{\beta }_{3}}{2}-{\beta }_{2})\pm \sqrt{{({\beta }_{2}-\frac{{\beta }_{3}}{2})}^{2}-2{\beta }_{3}(\delta -{\beta }_{2})}}{{\beta }_{3}}.$$
(37)

From Eq. (33) we derive the following condition

$$\left(-\delta -{\beta }_{2}{x}^{* }-\frac{{\beta }_{3}{{x}^{* }}^{2}}{2}+{\beta }_{2}(1-{x}^{* })+{\beta }_{3}(1-{x}^{* }){x}^{* }\right) \, < \, 0,$$
(38)

thus, \({{x}^{* }}_{1}=0\) is stable for β2 < δ. The feasibility of the solution \({{x}^{* }}_{2}^{\pm }\) was shown in ref. 8. Complementarily, Fig. 3c–f shows the results of the corresponding stability analysis, illustrating how our approach could provide new insights. As noted before, we stress that Eq. (33) is not limited to the case of simplicial complexes, but it can be used to further explore higher-order structures. Our findings are in alignment with ref. 40.

Social contagion: uniform hypergraphs

Restricting our analysis to uniform hypergraphs, Eq. (32) reduces to

$$\frac{d{x}_{i}}{dt}=-\delta {x}_{i}+\frac{{\beta }_{| {e}_{j}| }}{| {e}_{j}| -1}\sum\limits_{{e}_{j}\in {{\mathcal{E}}}_{i}}(1-{x}_{i})\prod\limits_{k\in {e}_{j} \atop{k\ne i}}{x}_{k},$$
(39)

whose solutions are

$${\bf{x}}={\beta }^{* }\left({\bf{A}}{{\bf{x}}}^{[| {e}_{j}| -1]}-{\bf{A}}{{\bf{x}}}^{[| {e}_{j}| ]}\right),$$
(40)

where the \({\beta }^{* }=\frac{{\beta }_{| {e}_{j}| }}{\delta (| {e}_{j}| -1)}\) is the scaled spreading rate and x[k] is the element-wise kth power vector, i.e., \({{\bf{x}}}^{[k]}={\left[{x}_{i}^{k}\right]}^{T}\). We now focus on homogeneous degree distributions where all the nodes have the same degree. In this case, x = xi, \(\forall i\in {\mathcal{V}}\) and the solutions, x*(β*), of Eq. (40) are the roots

$${\beta }^{* }\langle k\rangle ({x}^{| {e}_{j}| -1}-{x}^{| {e}_{j}| })-x=0,$$
(41)

which are stable if

$$-\delta -{\beta }^{* }\langle k\rangle \delta (| {e}_{j}-1| )(1-{x}^{* }){({x}^{* })}^{| {e}_{j}| -2} \, < \, 0.$$
(42)

We observe numerically that Eq. (41) has three feasible solutions, of which two are stable, including the absorbing state x* = 0, and one unstable. The first non-zero positive value of the stable solution is denoted by \({Q}_{l}({\beta }_{c}^{* })\), where \({\beta }_{c}^{* }\) is the tipping point, using the same notation as ref. 17. As shown in Fig. 4a, b, both \({Q}_{l}({\beta }_{c}^{* })\) and \({\beta }_{c}^{* }\) increase with the cardinality, in particular the last one follows a linear trend as shown in Fig. 4c. Notice that in this annealed approach we can consider 〈k〉 just as a scaling factor of β*.

Fig. 4: Numerical results for the social contagion dynamics on uniform hypergraphs.
figure 4

a The feasible stable solution as a function of the scaled spreading rate β* for different values of cardinality (color-coded), in the range from ∣ej∣ = 3 in blue, to ∣ej∣ = 30 in light gray. b The first non-zero positive value of the stable solution, Ql, as a function of the cardinality. c Depicts the behavior of β* at the tipping point, \({\beta }_{c}^{* }\), as a function of the cardinality, revealing a linear behavior.

Full size image

From Eq. (41), considering that β* is a free parameter, x = 0 is always a solution. Moreover, for finite β* and in the limit of infinite cardinality, in the range of 0 ≤ x ≤ 1, x = 0 is the only solution. Finally, in the case of infinite β*, the only feasible solution is x = 1. This argument aligns with the numerical results of Fig. 4c. For ∣ej∣ = 2, trivially we have an SIS dynamics and a continuous phase transition. On the other hand, in the limit of infinite cardinality, the system displays a discontinuous phase transition and \({\beta }_{c}^{* }\to \infty\) and \({Q}_{l}({\beta }_{c}^{* })=1\). For finite cardinalities the tipping point is also finite.

Application to diffusion processes

Another immediate application is the diffusion process2. In this case, \({g}_{j}({x}_{\{{e}_{j}\}})\) is separable and g(xi) = xi. The dynamics of the process is given by

$$\frac{d{\bf{x}}}{dt}=-D{\bf{L}}{\bf{x}}.$$
(43)

where D is the diffusion constant and the minus sign is a consequence of the stability condition in Eq. (26). We can arbitrarily decompose the Laplacian in m-uniform hypergraphs as done for the adjacency matrix in Eq. (3). In particular, we want to consider if the lower-order contributions are enough to describe the dynamics. To this end, we can separate the Laplacian in two components L = LO(θ) + LR(θ) given by

$${{\bf{L}}}_{O}(\theta )=\mathop{\sum }\limits_{m=1}^{\theta }{{\bf{L}}}^{m}\ \,\text{and}\,\ {{\bf{L}}}_{R}(\theta )=\mathop{\sum }\limits_{m=\theta +1}^{\max (| {e}_{j}| )}{{\bf{L}}}^{m},$$
(44)

where θ differentiates between higher and lower-order Laplacian, LR(θ) and LO(θ), respectively. In order to underline the important role played by the structure on the dynamics, we next analyze a diffusion process on both a synthetic hypergraph generated according to a power-law cardinality distribution, P(∣e∣) ~ ∣e∣−2.05, and a real hypergraph using data from email exchange at a European research institution14,41,42. In Fig. 5a, b, we show the variance of \({x}_{O}(\theta ,t)={e}^{-D{{\bf{L}}}_{O}(\theta )t}x(0)\), which is the solution of the diffusion process on the lower-order Laplacian LO. For a small enough θ, we have disconnected components and the process does not reach the final state of the complete Laplacian. On the other hand, when the final state is reached, different θ’s correspond to different timescales, and in particular, convergence is faster when increasing θ. In fact, for the synthetic case we need less information (structures) to represent the whole process, in the email dataset the convergence is only reached for θ − 1, as shown in Fig. 5b. The relative error can be estimated as

$${E}_{2}=\frac{| | x(t)-{x}_{O}(\theta ,t)| {| }_{2}}{| | x(t)| {| }_{2}}.$$
(45)

For the synthetic case, as shown in Fig. 5c, the error curves show peaks that are higher for lower values of θ. For long enough times, different plateau is reached depending on how many components are considered. The same is true for the email case, Fig. 5d, however we have a multiple peaked pattern, suggesting that we have various structures, each one with a different time scale. As expected, only for θ = 39, the error goes to zero, highlighting that real structures might have nontrivial behavior.

Fig. 5: Caracterization of diffusion on real and synthetic hypergraphs.
figure 5

a–c Represents real hypergraphs, while e–g synthetic ones. a, b The variance of states, xO(θ, t), up to order θ, in the diffusion, while c and d display the error E2, both as a function of time and structures considered, θ (color-coded). To represent the hypergraphs, we used in a and c, a power-law distribution of cardinalities, whereas in b and d, the hypergraph is given by the real email data (see text). The three panels to the right (e–g) show results obtained for weighted diffusion on hypergraphs, in terms of the variance of the state of the complete system x, defined by Eq. (43). e, f The effect of the different weights as a function of the cardinality, Eq. (2), see the legend. e Corresponds to a synthetic hypergraph with a power-law distribution of cardinalities, P(∣e∣) ~ ∣e∣−2.05, and f to the email hypergraph. g Explores the dependency with the exponent of the power-law weighting function.

Full size image

Another important aspect is the role on the dynamics of considering different weights for the hyperedges8,17,18. In particular, by redefining the Laplacian with the weighted adjacency matrix, Eq. (2), different choices of w(∣ej∣) can be used, as shown in Fig. 5e–g. As expected, increasing the weights reduces the convergence time. Aside from the different timescales in the two examples, we show that real data might also have a qualitatively different behavior, as shown in Fig. 5f, g. In particular, we focus on the power-law weighting functions, w(∣ej∣) = ∣ej∣−γ, in Fig. 5g. In this case, since higher-order structures are heavily penalized, we observe a greater time modulation by increasing γ. We also note that a well-established approach to this problem could be the analysis of some of the spectral modes of the Laplacian. In this case, it is not possible to decouple the contributions of different orders from the spectrum. On the other hand, the structural decomposition explicitly takes into account each order, allowing a straightforward analysis of the dynamics.

Conclusions

In this paper, we have developed a framework that allows to describe the relationship between the structural organization of hypergraphs and a highly general class of dynamical processes, beyond pairwise interactions. Within this framework, the graph projection appears naturally from a linear stability analysis around a given fixed point. Therefore, the dimensionality of the hypergraph, \({N}^{\max (| {e}_{j}| )}\) in its tensor representation, around the fixed point is reduced to a N2 space. Moreover, we showed that using a structural decomposition in m-uniform hypergraphs, given by Eq. (3), enables the individual analysis of each mth order component. Altogether, the methodology provides the stability condition for a general class of dynamical process and also allows to identify the structural components that play a role in the stability of any known fixed point. Of particular interest are the special cases LSA-SIF, LSA-SD and LSA-UH as one is able to separate the structural and dynamical contributions to stability. We also applied the proposed framework to two relevant dynamical processes, namely, social contagion and diffusion dynamics. For the former, we not only recovered known results for graph-based and simplicial complexes, but we obtained a necessary condition for the stability of the absorbing state, showing that only pairwise interactions play a role for such a state. In addition, our analysis revealed the conditions for the continuity of the phase transition also for real systems, where different kinds of bifurcations might appear. Furthermore, in the special case of uniform hypergraphs, we have shown that both the tipping point and \({Q}_{l}({\beta }_{c}^{* })\) increase with the cardinality. In particular, for finite cardinalities the tipping point is also finite, whereas in the infinite limit the two possible solutions are x = 0 and x = 1, being the latter only possible for β* → ∞. Finally, with regard to diffusion processes, we characterized the role played by the structural decomposition of the hypergraph and different weighting functions for the hyperedges on the dynamics of the system. In conclusion, we are confident that this investigation will motivate further research on the spectral properties of hypergraphs, their structural characterization, and in providing relevant insights in different areas where higher-order interactions can not be neglected, also beyond the community of dynamical processes on complex networks.