Cavity buildup dispersion spectroscopy

Abstract

Measurements of ultrahigh-fidelity absorption spectra can help validate quantum theory, engineer ultracold chemistry, and remotely sense atmospheres. Recent achievements in cavity-enhanced spectroscopy using either frequency-based dispersion or time-based absorption approaches have set new records for accuracy with uncertainties at the sub-per-mil level. However, laser scanning or susceptibility to nonlinearities limits their ultimate performance. Here we present cavity buildup dispersion spectroscopy (CBDS), probing the CO molecule as an example, in which the dispersive frequency shift of a cavity resonance is encoded in the cavity’s transient response to a phase-locked non-resonant laser excitation. Beating between optical frequencies during buildup exactly localizes detuning from mode center, and thus enables single-shot dispersion measurements. CBDS can yield an accuracy limited by the chosen frequency standard and measurement duration and is currently 50 times less susceptible to detection nonlinearity compared to intensity-based methods. Moreover, CBDS is significantly faster than previous frequency-based cavity-enhanced methods. The generality of CBDS shows promise for improving fundamental research into a variety of light–matter interactions.

Introduction

Highly accurate models of light-matter interactions are important for fundamental studies of molecular hydrogen^1,2, engineering of ultracold chemistry³, tests of molecular structure calculations^4,5, modelling of planetary atmospheres^6,7, and the development of advanced spectroscopic databases⁸. The latter application is crucial for improvements in remote sensing and measurements of variations in greenhouse gas concentrations at 0.1% uncertainty levels required to better predict changes in Earth’s climate⁹. To develop and test these models using first-principles approaches, accurate experimental techniques are required.

Recent achievements in cavity-enhanced spectroscopy using either frequency-based dispersion¹⁰ or time-based absorption¹¹ approaches have set new records for accuracy with uncertainties at the sub-per-mil level. However, laser scanning¹⁰ or susceptibility to nonlinearities¹¹ limits their ultimate performance. While cavity mode-dispersion spectroscopy¹² (CMDS) yields absorption spectra entirely in terms of measured optical frequency shifts, the shifts are not read out instantaneously. This is also true for multiplexed approaches to CMDS performed with a broadband optical frequency comb^13,14. Consequently, these CMDS techniques are susceptible to drifts. Although frequency-agile rapid scanning (FARS) spectroscopy¹⁵ provides single-shot acquisition of local absorption limited only by the cavity response time, it is an intensity-based technique and inherently susceptible to nonlinearities in the detection system¹¹. Therefore, each of these established techniques in ultrasensitive absorption spectroscopy has a critical weakness.

Cavity-enhanced condensed-phase sensing techniques face similar problems. Recently reported techniques use micro-resonators with optical quality factors of Q ≤ 10⁸ to readout dispersive signals on nanosecond timescales^16,17. As described by Yang et al.¹⁸, those approaches leverage heterodyne¹⁹ and rapidly swept laser^20,21 cavity ring-down readout concepts developed decades ago to reduce technical noise and improve sensitivity.

Here, we present cavity buildup dispersion spectroscopy (CBDS): an accurate measurement of cavity mode frequency that can be implemented on time scales that are substantially shorter than the cavity buildup time. In CBDS, a frequency-locked non-resonant laser beam is instantaneously injected into a high-finesse cavity followed by observation of the transient transmitted signal. The net response involves optical interference between the excitation and the transient cavity fields, with the latter field always occurring at the local cavity resonance frequency²² and in opposition to the former field. Thus, measurement of the resulting heterodyne beat frequency provides the local cavity mode position. In practice, absorption-induced dispersion within the resonator leads to changes in the measured mode-by-mode beat frequencies, which yield dispersion spectra. The CBDS approach requires the sequential injection of discrete and arbitrarily detuned laser fields which are optically phase-coherent with the resonant cavity field²³. We demonstrate use of this technique to measure broadband phenomena using measurement of a CO rovibrational line as an example.

We show that CBDS measurements can be made on timescales equal to or significantly less than the buildup duration, making possible studies in dynamic cavity response for physical sensing, as well as time-resolved spectroscopy of transient free radicals and other short-lived species in both thermal and non-thermal gases. The use of high-Q, macroscopic-length resonators allows one to set acquisition times in the microsecond range. Therefore, we achieve a frequency-based measurement without sacrificing the ability to study a wide range of dynamic phenomena. In addition, we establish the immunity of CBDS to common nonlinearities and biases which may occur with conventional intensity-based cavity-enhanced spectroscopy methods^11,24.

Results

Transient cavity response to single-mode, non-resonant excitation

Consider a conventional, linear optical cavity formed by two mirrors having intensity reflectivity R and separated by a distance L. The cavity is filled with an intracavity gas medium described by an absorption coefficient α. Assuming lossless mirrors, we define an effective mirror reflectivity and round-trip time of the empty cell as R_eff = Re^−αL and t_r = 2nL/c = 1/δv_FSR, respectively, where c is the speed of light in vacuum, n is the refractive index of the absorptive medium and δv_FSR is the cavity free spectral range (FSR). Let us consider the single excitation of cavity longitudinal mode order q of angular frequency ω_q by an optical electric field of angular frequency ω_c and amplitude ${\it{\epsilon }}$ given by $E_{\mathrm{i}}\left( t \right) = {\it{\epsilon }}e^{i\omega _{\mathrm{c}}t}$, which is instantaneously switched on at time t = 0. The net time response of the field transmitted by the cavity E_out(t) can be calculated by summing contributions over a finite number of passes in the cavity realized from t_r/2 to t²⁵ and leads to the following form

$$E_{{\mathrm{out}}}\left( t \right) = E_{{\mathrm{out}}}^0\left[ {e^{i\omega _{\mathrm{c}}t} - e^{ - {\Gamma}_{\it{q}}t}e^{i\omega _qt}} \right],$$

(1)

where $E_{{\mathrm{out}}}^0 = \frac{{\it{\epsilon }}}{{t_{\mathrm{r}}}}\,\frac{{\left( {1 - R} \right)e^{ - \alpha L/2}}}{{{\Gamma}_q + i\delta \omega }}$, and ${\Gamma}_q = - t_{\mathrm{r}}^{ - 1}{\mathrm{ln}}\left( {R_{{\mathrm{eff}}}} \right)$ describes the width (HWHM) of q-th cavity mode. The resulting field involves the sum of two fields: the excitation term proportional to $e^{i\omega _ct}$ and the transient response of the cavity (Green’s function) given by $e^{ - {\Gamma}_qt}\,e^{i\omega _qt}$. It can be easily shown that (2Γ_q)⁻¹ is the conventional intensity-based time constant, τ, of a light decay measured in cavity ring-down spectroscopy (CRDS). The structure of Eq. (1) illustrates how the induced transient field of the cavity tends to oppose the driving field and causes interference which is manifest as a decaying beat signal at angular frequency $\delta \omega = \omega _{\mathrm{c}} - \omega _q$.

In order to compute the intensity, we square the real-valued part of the complex-analytic field from Eq. (1). To account for the finite detector bandwidth, we ignore the resulting optical frequency terms in the beat signal. These operations yield the detected intensity exiting the cavity as

$$I_{{\mathrm{out}}}\left( t \right) = I_{{\mathrm{out}}}^0\left[ {1 + e^{ - 2{\it{{\Gamma}}}_qt} - 2e^{ - {\it{{\Gamma}}}_qt}\cos \left( {\delta \omega t} \right)} \right],$$

(2)

where $I_{{\mathrm{out}}}^0 = \left| {E_{{\mathrm{out}}}^0} \right|^2/2$. Equation (2) describes the time-dependent buildup signal in the CBDS method. Note the occurrence of two characteristic rates, one at 2Γ_q equal to the familiar ring-down intensity decay rate, and the other at half of this value, which corresponds to the decay rate of the induced transient cavity field.

For reasons discussed below, it is useful to analyze CBDS signals in the frequency domain. Taking the Fourier transform of I_out(t) and neglecting the DC term gives the function

$${\cal{F}}\left( \omega \right) = I_{{\mathrm{out}}}^0\left( {\frac{1}{{2{\mathrm{{\Gamma}}}_q - i\omega }} - \frac{1}{{{\mathrm{{\Gamma}}}_q - i\left( {\omega + \delta \omega } \right)}} - \frac{1}{{{\mathrm{{\Gamma}}}_q - i(\omega - \delta \omega )}}} \right),$$

(3)

which is the sum of three complex Lorentzian resonances. The first resonance is centered at ω = 0, and corresponds to decay of intensity in the transient field. The other two resonances are at $\omega = \pm \delta \omega$ and describe the slower decay of the intensity in the beat signal caused by interference between the two fields. In practice, we can use Eq. (3) to calculate the real-valued quantity, $\left| {{\cal{F}}\left( \omega \right)} \right|^2$, to model the power spectral density of the measured CBDS signal. Evaluation of $\left| {{\cal{F}}(\omega )} \right|^2$ leads to three symmetric Lorentzian components and three asymmetric, dispersive components associated with the off-diagonal terms.

We have generalized the preceding analysis to account for a driving laser field that does not switch on instantaneously. Derivations and full expressions for this case are given in the Methods. To this end, we model this field by $E_{\mathrm{i}}\left( t \right) = {\it{\epsilon }}\left( {1 - e^{ - {\Gamma}_0t}} \right)e^{i\omega _{\mathrm{c}}t}$, where the switch-on time constant is $\tau _0 = {\Gamma}_0^{ - 1}$. In the limit that τ₀ << τ the resulting expressions are qualitatively similar to those presented in Eqs. (1)–(3), and reduce exactly to the present formulas as τ₀ → 0. We note however, that for the typical case of a finite switch-on rate that is fast compared to the cavity decay time, there is a constant phase shift, φ, introduced in the cosine term of Eq. (2) which depends on Γ_q, Γ₀, and δω. Unless otherwise noted, all final calculations and fits of the model to measurements utilized the full model given in the Methods.

In Fig. 1 we present simulated CBDS signals in the time and frequency domains assuming a detuning of δω/2π = 100 kHz, δω/Γ_q ≈ 30 and τ₀ = 50 ns. These parameters correspond to our experimental conditions. The time-dependent buildup signal in the first panel exhibits large damped oscillations with a peak signal that is four times greater than the asymptotic value reached at long times. These strong oscillations occur when the frequency detuning is greater than the cavity linewidth, (i.e. δω/Γ_q > 1). For smaller frequency detuning values (not shown), the period of oscillation is longer than the cavity decay time so that $I_{{\mathrm{out}}}\left( t \right) \to I_{{\mathrm{out}}}^0\left[ {1 - e^{ - {\Gamma}_qt}} \right]^2$, which as expected for on-resonance excitation of the ring-down cavity, reduces to a monotonically increasing field amplitude described by the complement of the exponential decay function. In Fig. 1b, we compare the power spectral density obtained from the fast Fourier transform (FFT) of the time domain signal and the analytical Fourier transform given in Eq. (20) of Methods. The two spectra are indistinguishable at the 10⁻⁷ level. Moreover, even greater relative accuracy, of 10⁻⁹, is observed for retrieved values of $\delta \nu = \delta \omega /(2\pi )$. Two of the resonances (one at DC and the other at the positive value of the beat frequency) are evident, whereas the other resonance at negative frequencies contributes via its wing. In contrast, ignoring the three dispersive terms in $\left| {{\cal{F}}\left( \omega \right)} \right|^2$and using a simplified three-component symmetric Lorentzian model for this quantity leads to systematic residuals at the 1% level.

Fig. 1: Transient cavity response to single-mode, non-resonant excitation.

a Simulated buildup signal for frequency detuning between laser and cavity mode $\delta \nu = 100$ kHz and a driving field switch-on time of 50 ns. For clarity, the initial 150 µs of the signal is shown. b The fast Fourier transform (FFT) spectrum of the buildup signal from the panel (a) and residuals from fits of Lorentzian (orange) and our full (blue) model given by Eq. (20) in the Methods.

Sensitivity of CBDS to absorption coefficient and measurement speed

The CBDS buildup signal, I_out(t), depends on the sample absorption coefficient, α_q through the mode width, Γ_q, as well as the beat frequency term $\delta \omega$ which encodes information about the position of mode ω_q. The change of mode width ${\mathrm{{\Delta}}}{\Gamma}_q$ caused by absorption α_q in the cavity medium is ${\mathrm{{\Delta}}}{\Gamma}_q = \frac{c}{2}\alpha _q$ and is linked to the corresponding dispersive cavity mode shift, $\delta \omega _D$, by the complex-valued refractive index $n\left( \omega \right) = n_0 + \chi \left( \omega \right)/(2n_0)$ and resonant susceptibility $\chi \left( \omega \right) = \chi ^{\prime}\left( \omega \right) - i\chi ^{\prime\prime}\left( \omega \right)$²⁵, which for an isolated spectral line may be written using the complex-valued line shape function ${\cal{L}}(\omega )$^26,27

$$\frac{{\delta \omega _D}}{{{\mathrm{{\Delta}}}{\Gamma}_q}} = - \frac{{\chi ^{\prime}}}{{n_0\chi ^{\prime\prime}}} = \frac{{{\mathrm{Im}}\{ {{\cal{L}}( {\omega _q - \omega _0})} \}}}{{n_0\,{\mathrm{Re}}\{ {{\cal{L}}( {\omega _q - \omega _0} )} \}}},$$

(4)

where n₀ is non-resonant refractive index of the sample and $\omega _0$ is the center of spectral line. For derivation of Eq. (4) see the Methods.

To assess the theoretical precision and speed limits of CBDS compared to CRDS, we fitted the appropriate model for each method to I_out(t) signals simulated with Gaussian noise. For both techniques, we considered signals with identical signal-to-noise-ratio levels of SNR = 3000, $\frac{{\chi ^{\prime}}}{{n_0\chi ^{\prime\prime}}} = 1$ (which corresponds to a Lorentzian line shape at the point of maximum dispersion), ring-down time constant $\tau _q = {\Gamma}_q^{ - 1}$ = 30 µs, and various laser detuning frequencies $\delta \nu = \delta \omega /(2\pi )$. Here we used Eq. (2), assuming infinitely fast laser switching. Fitted values of $\delta \nu$ from CBDS and ${\Gamma}_q$ from CRDS were converted to equivalent absorption coefficient quantities, and the standard deviations of these values, $\sigma _\alpha$, were evaluated from the resulting distributions and treated as sensitivity parameters for each technique. In Fig. 2, the data points show the dependence of $\sigma _\alpha$ in both cases upon the width of the fitting time window, T. Superimposed on the data points from our fitted numerical simulations are solid lines calculated from analytical solutions for $\sigma _\alpha$ as a function of T which arise from an assumed least-squares fitting routine²⁸. To calculate the analytical solutions for CBDS, we again used Eq. (2) assuming infinitely fast laser switching and followed a procedure like the CRDS treatment of Huang and Lehmann²⁹.

Fig. 2: Comparison of simulated sensitivity of CBDS and CRDS.

Dependence of the standard deviation $\sigma _\alpha$ of the absorption coefficient obtained from fits of simulated cavity ring-down spectroscopy (CRDS) and cavity buildup dispersion spectroscopy (CBDS) signals on the fitting time window T (or on the ratio $T/\tau _q$ – top horizontal axis). CBDS signals were generated for several laser frequency detunings $\delta \nu$ from the cavity mode center and ring-down time constant $\tau _q$ = 30 μs. The time window begins at the moment the excitation light is switched on (CBDS) or off (CRDS). Dots correspond to numerical simulation results and curves are full analytical solutions.

It is apparent that CBDS has substantially improved sensitivity relative to CRDS as T decreases and $\delta \nu$ increases. Most interestingly, CBDS has an inherent sensitivity advantage for shorter measurement times, especially for fit windows where $T/\tau _q \, < \, 1$. Notably, when $T/\tau _q = 0.1$ and δv ≥ 500 kHz, CBDS provides a 30-fold reduction in $\sigma _\alpha$ relative to CRDS. Calculations not shown here also reveal that CBDS measurements are subject to substantially smaller biases than CRDS when $T/\tau _q \, < \, 1$. For each chosen value of $\delta \nu$, the CBDS sensitivity advantage over CRDS is maximized once $T\delta \nu \, > \, 1$. Further, the CBDS advantage over CRDS converges to a constant value, independent of $\delta \nu$, once $T\delta \nu \, > \, 1$ for all $\delta \nu$. Generally, the advantage of CBDS disappears when T is shorter than the half-period of the beat frequency $1/(2\delta \nu )$. For long measurement times, when $T/\tau _q \gg 1$, the CBDS sensitivity converges to a value which is larger than the CRDS sensitivity by a factor of 2. This apparent twofold disadvantage predicted for CBDS when $T/\tau _q \gg 1$ could be fully recovered in a two-point measurement scheme where, for CBDS, the chosen two points are at the extrema of the imaginary line shape profile. Finally, the vertical axis of Fig. 2 can be rescaled by the factor proportional to $(1 - R)/L$ to further generalize these results for cavities of other lengths L and mirror reflectivities R. Therefore, we expect that the advantages of the CBDS can be also exploited in systems with compact cavities.

The above discussion assumed the realistic case in which optimized measurements of the light transmitted by the ring-down cavity are not limited by the available laser power. However, when noise in the buildup signal is laser-power-limited, then increases in $\delta \nu$ will lead to decreases in the SNR, because less radiation is coupled into the cavity mode.

Immunity of CBDS accuracy to detection system nonlinearity

To quantify the effect of detection system nonlinearity on the accuracy of CBDS, we simulated buildup signals and assumed nonlinear quadratic or power-law deviations from linearity of the signal amplitude. Conventional CRDS absorption spectra also were analyzed in the same fashion. Given the same degree of assumed nonlinear response, the maximum relative errors in CBDS analyzed in the time-domain (TD) and frequency-domain (FD) were found to be independent of detuning $\delta \nu _{{\mathrm{meas}}}$ and 6 and 50 times smaller, respectively than those acquired using CRDS. For the frequency-domain CBDS case, maximum errors were 0.02% for realistic non-linearities at the 2% level^11,24.

We performed simulations of normalized buildup signals, $T(t)/T_{{\mathrm{max}}}$, with their amplitudes multiplied by the function $y_1\left( t \right) = 1 - a\left[ {T(t)/T_{{\mathrm{max}}}} \right]$, where a is a constant factor which scales the degree of nonlinearity and $T_{{\mathrm{max}}}$ is the maximum amplitude of $T(t)$ for the whole spectrum (Fig. 3). In the case of the CRDS signal (TD) we fitted the amplitude, baseline and time constant from which the absorption spectrum was derived. For the time-domain analysis of the CBDS signal (TD), we fitted the amplitude, baseline and parameters D, ${\Gamma}_q$, $\varphi$ and $\delta \omega$ of Eq. (18). For the frequency-domain analysis of the CBDS signal (FD) we fitted the amplitude, baseline and parameters D, Γ_q, $\varphi$ and $\delta \omega$ of Eq. (20). For both the (TD) and (FD) cases, the CBDS spectrum was derived from fitted $\delta \omega = 2\pi \delta \nu _{{\mathrm{meas}}}$. We found a 0.1–4% systematic bias in the y axis of the CRDS spectra and a 1–20% maximum systematic error for 2% < a < 30% (Fig. 3b). For CBDS spectra retrieved from frequency-domain (FD) analyses of buildup signals, the maximum systematic error is up to 50 times smaller than that predicted for CRDS spectra and is independent of detuning $\delta \nu _{{\mathrm{meas}}}$. The systematic bias of the FD CBDS spectra averages close to zero within the entire spectrum (Fig. 3a). We estimate sub-per-mil accuracy in the FD CBDS even when the detector nonlinearity is as high as 8%. Moreover, we noticed that the choice of fitting the buildup signals in the time or frequency domain has a large impact on the sensitivity to detector nonlinearity. Dispersive spectra obtained through time-domain (TD) analyses of buildup signals have a nonlinear susceptibility intermediate between those of the CRDS and FD CBDS cases, i.e. 6 times lower by comparison to the CRDS absorption case. In the case of the TD CBDS spectrum, we also calculate a systematic bias of the y axis ranging from 0.01–0.2% and we observed a slight asymmetry in the TD CBDS spectra (Fig. 3a). As a further exploration of the effect of non-linearity, we assumed its power law response model has the form $y_2\left( t \right) = [T(t)/T_{{\mathrm{max}}}]^a$, which in conventional CRD spectroscopy would lead to measured decay rates $\tau ^{ - 1}$ biased by the constant fractional amount, $a$. Notably, this type of nonlinearity would not be evidenced in the fit residuals of individual decay signals because the decay signals would remain exponential in form. As can be seen in Fig. 3b, this type of nonlinearity augments the bias for both the CRDS and TD CBDS spectra, by comparison to $y_1\left( t \right)$, but yields nearly identical results for the FD CBDS case.

Fig. 3: Influence of detection system nonlinearity on the spectrum accuracy.

a Relative systematic differences between absorptive/dispersive spectra obtained from fits of ring-down/buildup signals simulated with and without nonlinearity of the amplitude for corresponding nonlinear factors a: 2%, 10% and 30% for spectra corresponding to the R23 CO molecular line from (3-0) band centered at frequency $\nu _0$ and at CO pressure of 530 Pa. The buildup signals were analyzed in the time and frequency (as a power spectral density) domains leading to spectra denoted as “TD” and “FD”, respectively. For dispersion, we chose a detuning of laser from the cavity mode center $\delta \nu _{{\mathrm{meas}}} \approx 100$ kHz, corresponding to $\approx$30 cavity mode half-widths (HWHM). We modeled nonlinear distortion of the spectrum by multiplying the normalized time response of the cavity $T(t)/T_{{\mathrm{max}}}$ (buildup and ring-down signals) by $y_1\left( t \right) = 1 - a\left[ {T(t)/T_{{\mathrm{max}}}} \right]$, where T_max is the maximum amplitude of $T(t)$. b Solid lines - maximum relative systematic errors of absorptive and dispersive spectra from the panel (a) versus detection nonlinearity a for various detunings $\delta \nu _{{\mathrm{meas}}}$. Dashed lines - similar results when using the power-law model of detector nonlinearity given by $y_2(t) = \left[ {T(t)/T_{{\mathrm{max}}}} \right]^a$ and detuning $\delta \nu _{{\mathrm{meas}}} \approx 100$ kHz.

Experimental setup

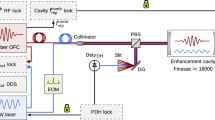
The setup for experimental realization of CBDS is illustrated in Fig. 4. The CBDS method utilizes a single-frequency light source that is frequency-locked to the optical resonator. We use a double-polarization frequency-locked laser scheme^10,15 where one linear polarization of laser light is frequency-locked to a cavity mode while the orthogonal polarization (having a well-controlled, constant frequency detuning v_MW from the locking point) is used for non-resonant excitation of the measured cavity mode (Fig. 4a). Additionally, the cavity length is stabilized to prevent thermal drift of the comb of modes over time scales >1 s. The Nd:YAG laser frequency-locked to an I₂ line and having frequency instability <1 kHz is used here as a reference. The buildup signal is initiated after rapidly switching on the frequency-detuned probe beam at the measurement mode, and the locking beam remains on during the entire cavity pumping process, but does not contribute to the CBDS signal because of a polarization-dependent optical filter and the large frequency difference between probe and locking beams. Coherent averaging of repeated events in the time-domain is readily achieved because of the tight frequency-locking scheme. The Fourier spectrum of the beating signal appearing in the transmitted light allows determination of the frequency detuning $\delta \nu _{{\mathrm{meas}}}$ of the cavity resonance with respect to the probe beam frequency v_P. The relation $k\delta \nu _{{\mathrm{FSR}}} - \left( {\nu _{{\mathrm{MW}}} + \delta \nu _{{\mathrm{meas}}}} \right)$ yields the dispersive shift $\delta \nu _{\mathrm{D}}$ of the cavity resonance relative to the locking point frequency v_L (Fig. 4a). Here, $\delta \nu _{{\mathrm{FSR}}}$ is the FSR corresponding to cavity conditions outside the molecular resonance with potential contribution from the broadband intracavity dispersion, and k is the integer number of modes between the locking point and the measured cavity mode.

Fig. 4: Cavity mode localization and schematic of CBDS apparatus.

a The laser frequency $\nu _{\mathrm{L}}$ is frequency-locked to a transverse electro-magnetic TEM₀₀ cavity mode, which is a local resonance of the cavity transmission spectrum indicated by the thick black line. An orthogonally polarized beam with frequency $\nu _{\mathrm{P}}$, is detuned from $\nu _{\mathrm{L}}$ by frequency $\nu _{{\mathrm{MW}}}$ (a sum of driving frequencies of EOM_P and AOM) and excites another TEM₀₀ mode shifted by dispersion. For non-resonant excitation, an oscillation on the transmitted buildup signal with a frequency $\delta \nu _{{\mathrm{meas}}}$corresponds to heterodyne beating between the non-resonant driving field and the resonant transient response of the cavity. For a given mode k relative to the locking point and cavity free spectral range $\delta \nu _{{\mathrm{FSR}}}$, the dispersive shift $\delta \nu _{\mathrm{D}}$ of the cavity mode can be retrieved from $\delta \nu _{{\mathrm{meas}}}$. b Schematic of the cavity mode dispersion spectroscopy (CBDS) experiment. A broadband electro-optic modulator EOM_P, driven by the microwave source MW, rapidly detunes the external cavity diode laser (ECDL) beam with frequency $\nu _{\mathrm{P}}$ from the locking point. An acousto-optic modulator AOM prevents cavity excitation by the carrier frequency. A photodiode PD_P records the buildup signal. Here the experimental signal for $\delta \nu _{{\mathrm{meas}}} = 5$ MHz and time interval 3 μs, measured with cavity finesse 2360 is shown. Electro-optic modulator (EOM_L), circulator (Circ.), photodiode (PD_L): elements in the Pound-Drever-Hall (PDH) phase-locking loop.

Frequency detuning and intracavity gas sample

Finally, frequency agile rapid scanning for fast spectral acquisition is achieved by adjusting the detuning frequency $\nu _{{\mathrm{MW}}}$ using a high-bandwidth (~20 GHz) electro-optic modulator^10,15. We ensure that only a single sideband of EOM_P excites the cavity mode and all other sidebands as well as the carrier are fully reflected from the cavity. For this purpose, the output of EOM_P is additionally frequency shifted by a fraction of the FSR with an acousto-optic modulator (AOM). In practice this offset frequency can be fine-tuned to prevent accidental excitation of higher-order transverse modes by any of the EOM_P sidebands in the case of imperfect mode-matching of the probe laser to TEM₀₀. Using a macroscopic-length (0.73 m) resonator containing, a sample of carbon monoxide (CO) and tuning our laser frequency to probe the peak absorption, we observe signals with τ as short as 0.3 μs with cavity Q = 3.6 × 10⁸ (Fig. 4b), as well as τ as long as 24 μs with Q = 2.9 × 10¹⁰ (Fig. 5a) for the empty-cavity cases.

Fig. 5: Cavity buildup dispersion spectroscopy.

a Buildup signals recorded for cavity modes around the R23 CO molecular line from (3-0) band, centered at $\nu _0 = 192193.3341$ GHz and having an intensity of 8.056 × 10⁻²⁵ cm/molec. CO pressure was 530 Pa and the cavity finesse was 194,000. Each signal is an average over 150 scans recorded one by one and separated by 1.4 ms (0.2 ms for the buildup signal and 1.2 ms for the subsequent ring-down decay and change of microwave generator frequency $\nu _{{\mathrm{MW}}}$). b The fast Fourier transform (FFT) spectrum of buildup signals from the panel (a). Absorptive broadening and dispersive shift of the FFT peaks (cavity modes) are visible. Fitting of the frequency-domain spectrum provides accurate positions $\delta \nu _{{\mathrm{meas}}}(\nu - \nu _0)$ of cavity modes within the molecular line. c The dispersive spectrum $\delta \nu _{\mathrm{D}}(\nu - \nu _0)$ reconstructed from the FFT peak frequencies shown in the panel (b). The absorptive spectrum (gray line) is calculated from the dispersive spectrum using Eq. (4). d Allan deviations $\sigma _{AD}$ of δv_meas versus the number of samples N for two different time intervals dt between samples. The vertical axis is expressed in terms of frequency shift (left) and corresponding absorption units (right).

Molecular spectra retrieval

For each cavity resonance, a buildup signal was recorded at a new value of $\nu _{{\mathrm{MW}}}$ (Fig. 5a). Corresponding FFT spectra, presented in Fig. 5b, show absorptive and dispersive changes in the width and position of cavity modes within the frequency range of the measured molecular line. Measured dispersive shifts $\delta \nu _{\mathrm{D}}(\nu - \nu _0)$, determined for each cavity mode, were used to reconstruct the purely frequency-based complex-valued (absorption and dispersion) line shape of a carbon monoxide (CO) transition of central frequency $\nu _0$ (Fig. 5c). The absorption was calculated from the measured dispersion using Eq. (4) with Hartmann-Tran model^30,31 of line shape ${\cal{L}}\left( \omega \right)$. Allan deviation plots of $\delta \nu _{{\mathrm{meas}}}$, Fig. 5d, demonstrate excellent stability of the frequency measurement in the CBDS experiment yielding an equivalent absorption coefficient detection limit less than 3 × 10⁻¹¹ cm⁻¹, corresponding to a detection limit for $\frac{{\delta \omega _{\mathrm{D}}}}{{2\pi }}$ of ~100 mHz. Moreover, consistent with the rapid phase-coherent nature of the measurement, a short-term 22-Hz sensitivity to cavity resonance shifts was obtained in 200 µs.

Comparison of spectra from CBDS and CMDS

We verified the accuracy of CBDS by comparing the measured spectra of the R23 CO molecular line from (3-0) band with those obtained from a reference CMDS method at the same temperature and pressure of the CO gas sample. In Fig. 6a-b we demonstrate excellent agreement between CO spectra and peak areas obtained from the CMDS and CBDS experiments for a range of detuning $\delta \nu _{{\mathrm{meas}}}$ from −200 kHz to +200 kHz. We found that systematic differences between line areas determined from the CBDS and CMDS methods are only 0.1% on average, with a standard deviation of 0.2% and this agreement is independent of the chosen frequency detuning $\delta \nu _{{\mathrm{meas}}}$, see Fig. 6b. These observations indicate that the accuracy of these first CBDS measurements is already similar to some of the most accurate techniques currently available^10,11. We emphasize that this level of agreement requires the proper frequency-domain modelling (Fig. 6c) of the transmission signals. Moreover, we note that the CBDS spectrum was measured more than 100 times faster than that of CMDS. While the density of points in presented CBDS spectrum was determined by the cavity FSR, we should note that it can be increased to any desired level by interleaving dispersion spectra for cavity lengths varied in a controlled way, as was demonstrated for CMDS¹².

Fig. 6: Accuracy of CBDS spectra.

a Comparison of experimental dispersive spectra ${\mathrm{{\Delta}}}\nu _{\mathrm{D}}\left( {\nu - \nu _0} \right)$ using cavity buildup dispersion spectroscopy CBDS (orange points) and cavity mode dispersion spectroscopy CMDS (blue points). Below are residuals from the fit with the Hartmann-Tran profile^30,31. b Line areas obtained from CBDS relative to CMDS as a function of detuning δv_meas of laser from the cavity mode center. The error bars correspond to standard deviations of the fitted areas. The green shaded region corresponds to ±1σ standard deviation for all results. c The fast Fourier transform (FFT) power spectral density of buildup signals measured for δv_meas ≈ 30 kHz and 100 kHz, for cavity modes located on and off the molecular resonance - green circles on the panel (a). Visible asymmetry of the FFT peaks increases with smaller detuning δv_meas. Our model for the Fourier spectrum reproduces well the experimental data enabling accurate determination of cavity mode position.

Discussion

CBDS achieves high accuracy through precise measurement of the cavity resonance frequencies resulting from accurate modeling and fitting of the buildup signals in the frequency domain. The generality of our field-based method enables applications to dynamic cavity-enhanced sensing throughout the electromagnetic spectrum, making the method amenable to the analysis of intermode³² and multiplexed³³ buildup signals with detuned local excitation fields. The tightly frequency-locked optical scheme allows for coherent time-domain averaging of CBDS signals, and therefore ultrahigh precision with minimal data storage. We see the potential of CBDS for improving the accuracy of fundamental and atmospheric absorption spectroscopy studies as well as metrological applications which to date have depended exclusively on intensity-based experiments. The rapidity and sensitivity of CBDS should also render it useful in fast biological processes and single-particle spectroscopy. Moreover, CBDS methods are expected to be readily extendable to broadband spectroscopic techniques using an optical frequency comb, which could open new possibilities for high-accuracy measurements in this field³⁴. We also note that in classical dual-comb spectroscopy³⁵ information about the absorptive and dispersive components of the sample spectrum is encoded in the amplitude and phase shift of the detected beat notes, respectively, whereas in CBDS this information would be encoded directly in the measured mode widths and mode frequencies.

As recounted by T. Hänsch in his 2005 Nobel Prize Lecture, A. Schawlow of Stanford University emphatically advised his students to “Never measure anything but frequency!”³⁶. These words of advice were grounded in the inherently digital nature and resulting noise immunity of frequency measurements: properties making frequency the quantity in nature that can be determined with the highest precision and accuracy. Given this perspective, the CBDS technique also aligns well with general efforts to express physical quantities in terms of frequency³⁷. Atomic and molecular spectra entirely measured in terms of cavity resonance frequencies can be easily referenced to the atomic frequency standard³⁸. Thus, we anticipate that CBDS will result in robust SI-referenced uncertainties and will greatly facilitate interlaboratory comparisons of data. In this context, we see clear applications of CBDS e.g. to Doppler³⁹ and ro-vibrational⁴⁰ thermometry as well as to a new gas pressure standard currently being developed which is based on precisely measuring the dispersive shifts of optical cavity modes⁴¹. Also, recent nondestructive detection of Rydberg atoms based on cavity dispersion⁴² as well as chemical kinetic study of radicals⁴³ indicates the potential of CBDS in terms of both speed and accuracy for determination of atomic and molecular populations.

Methods

Transient cavity response to single-mode, non-resonant excitation with finite switch-on time of the electric field

Consider a conventional, linear optical cavity formed by two mirrors having intensity reflectivity R and separated by a distance L. The cavity is filled with an intracavity gas medium described by an absorption coefficient $\alpha$. We define an effective mirror reflectivity and round-trip time of the empty cell as $R_{{\mathrm{eff}}} = Re^{ - \alpha L}$ and $t_{\mathrm{r}} = 2nL/c = 1/\delta \nu _{{\mathrm{FSR}}}$, respectively, where c is the speed of light in vacuum, $n$ is the refractive index of absorptive medium and $\delta \nu _{{\mathrm{FSR}}}$ is the cavity free spectral range. Let us consider excitation of the cavity by light electric field $E_{\mathrm{i}}\left( t \right) = {\it{\epsilon }}\left( {1 - e^{ - {\Gamma}_0t}} \right)e^{i\omega _{\mathrm{c}}t}$ characterized by an arbitrary angular frequency $\omega _{\mathrm{c}}$ and amplitude ${\it{\epsilon }}$. Here, we assume a finite switch-on time $\tau _0 = {\Gamma}_0^{ - 1}$ of the electric field. The time response of the cavity $E_{{\mathrm{out}}}(t)$ can be calculated at a given time by summing the contribution of a finite number of M passes in the cavity realized up to this moment²⁵

$$E_{{\mathrm{out}}}\left( t \right) = \left( {1 - R} \right)e^{ - \alpha L/2}\sum_{m = 0}^M {R_{{\mathrm{eff}}}^m\,E_{\mathrm{i}}\left( {t - mt_{\mathrm{r}}} \right)} .$$

(5)

We assumed that t = 0 corresponds to the moment when the first transmitted field contribution leaves the cavity. Further expansion of Eq. (5) leads to the sum of two finite geometric series

$$E_{{\mathrm{out}}}\left( t \right) = A\left( \alpha \right)e^{i\omega _{\mathrm{c}}t}\left[ {\sum_{m = 0}^M {\left( {R_{{\mathrm{eff}}}e^{ - i\delta \omega t_{\mathrm{r}}}} \right)^m} - e^{ - {\Gamma}_0t}\sum_{m = 0}^M {\left( {R_{{\mathrm{eff}}}e^{{\Gamma}_0t_{\mathrm{r}}}e^{ - i\delta \omega t_{\mathrm{r}}}} \right)^m} } \right],$$

(6)

where the factor

$$A\left( \alpha \right) = {\it{\epsilon }}\left( {1 - R} \right)e^{ - \alpha L/2}$$

(7)

describes modification of the electric field amplitude after the first pass through the cavity. In transition from Eq. (5) to Eq. (6) we replaced the expression $e^{ - i\omega _{\mathrm{c}}t_{\mathrm{r}}}$ by $e^{ - i\delta \omega t_{\mathrm{r}}}$, since the electric field angular frequency can be rewritten as $\omega _{\mathrm{c}} = 2\pi (N\delta \nu _{{\mathrm{FSR}}} + \delta \nu )$, where N is the cavity mode number and $\delta \omega = 2\pi \delta \nu$ is detuning of the light angular frequency from the cavity mode center. Small values of the round-trip time t_r allow us to replace the discrete time values $mt_{\mathrm{r}}$ by the continuous quantity t and consequently enable us to use integrals instead of sums in Eq. (6)

$$E_{{\mathrm{out}}}\left( t \right) = A\left( \alpha \right)e^{i\omega _{\mathrm{c}}t}t_{\mathrm{r}}^{ - 1}\left[ {{\int}_{0}^t {e^{\left( {t_{\mathrm{r}}^{ - 1}{\mathrm{ln}}\left( {R_{{\mathrm{eff}}}} \right) - i\delta \omega } \right)t^{\prime}}dt^{\prime}} - e^{ - {\Gamma}_0t}{\int}_{0}^t {e^{\left( {t_{\mathrm{r}}^{ - 1}{\mathrm{ln}}\left( {R_{{\mathrm{eff}}}} \right) + {\Gamma}_0 - i\delta \omega } \right)t^{\prime}}} dt^{\prime}} \right].$$

(8)

Here, for the convenience of calculations we expressed $R_{{\mathrm{eff}}}^{t/t_{\mathrm{r}}}$ as ${\mathrm{exp}}\left[ {t/t_{\mathrm{r}}{\mathrm{ln}}\left( {R_{{\mathrm{eff}}}} \right)} \right]$. Evaluation of Eq. (8) leads to the final complex-valued expression for the electric field leaving the cavity

$$E_{{\mathrm{out}}}\left( t \right) = E_{{\mathrm{out}}}^0\left( t \right)\left[ {e^{i\omega _{\mathrm{c}}t} - D(t)e^{ - {\Gamma}_qt}e^{i(\omega _{\mathrm{c}} - \delta \omega )t}} \right],$$

(9)

where

$$E_{{\mathrm{out}}}^0\left( t \right) = B\left( {1 - Ce^{ - {\Gamma}_0t}} \right),$$

(10)

$$B = \frac{{A\left( \alpha \right)}}{{t_{\mathrm{r}}}}\frac{1}{{{\Gamma}_q + i\delta \omega }},$$

(11)

$$C = \frac{{{\Gamma}_q + i\delta \omega }}{{{\Gamma}_q - {\Gamma}_0 + i\delta \omega }},$$

(12)

$$D(t) = \frac{{1 - C}}{{1 - Ce^{ - {\Gamma}_0t}}},$$

(13)

and ${\Gamma}_q = - t_{\mathrm{r}}^{ - 1}{\mathrm{ln}}(R_{{\mathrm{eff}}})$ describes the width (HWHM) of q-th cavity mode having angular frequency $\omega _q = \omega _{\mathrm{c}} - \delta \omega$. It can be easily shown that $( {2{\Gamma}_q})^{ - 1}$ is the conventional intensity-based time constant of a light decay, $\tau _q$, measured in cavity ring-down spectroscopy. The structure of Eq. (9) illustrates how the transient field tends to oppose the driving field and gives rise to interference between the two fields at angular frequencies $\omega _{\mathrm{c}}$ and $\omega _q$, respectively. Taking the real part of the field defined by Eq. (9) gives

$${\mathrm{Re}}\left\{ {E_{{\mathrm{out}}}\left( t \right)} \right\} = \left| {E_{{\mathrm{out}}}^0\left( t \right)} \right|\cos \left( {\omega _{\mathrm{c}}t + \varphi _1} \right) - \left| {E_{{\mathrm{out}}}^0\left( t \right)D\left( t \right)} \right|e^{ - {\Gamma}_qt}\cos \left[ {\left( {\omega _{\mathrm{c}} - \delta \omega } \right)t + \varphi _2} \right],$$

(14)

where

$$\varphi _1\left( t \right) = {\mathrm{arctg}}\left\{ {{\mathrm{Im}}\left[ {E_{{\mathrm{out}}}^0\left( t \right)} \right]/{\mathrm{Re}}\left[ {E_{{\mathrm{out}}}^0\left( t \right)} \right]} \right\},$$

(15)

$$\varphi _2\left( t \right) = {\mathrm{arctg}}\left\{ {{\mathrm{Im}}\left[ {E_{{\mathrm{out}}}^0\left( t \right)D(t)} \right]/{\mathrm{Re}}\left[ {E_{{\mathrm{out}}}^0\left( t \right)D(t)} \right]} \right\}.$$

(16)

In order to compute the intensity, we square the real-valued field (Eq. 14) and average all sinusoidal terms over optical cycles to account for the finite detector bandwidth. Ignoring the sum frequency term occurring at optical frequencies, this operation yields the intensity exiting the cavity as

$$I_{{\mathrm{out}}}\left( t \right) = I_{{\mathrm{out}}}^0\left( t \right)\left\{ {1 + \left| {D\left( t \right)} \right|^2e^{ - 2{\Gamma}_qt} - 2\left| {D\left( t \right)} \right|e^{ - {\Gamma}_qt}\cos \left[ {\delta \omega t - \varphi \left( t \right)} \right]} \right\}.$$

(17)

that fully describes the shape of the buildup signal measured in the CBDS method. Here, the amplitude of the transmitted signal is defined as $I_{{\mathrm{out}}}^0(t) = \left| {E_{{\mathrm{out}}}^0\left( t \right)} \right|^2/2$. The intensity function given by Eq. (17) exponentially approaches a constant value for long times and exhibits damped oscillations at the beat angular frequency, $\delta \omega$ between that of the excitation field, $\omega _{\mathrm{c}}$ and the cavity resonance frequency, $\omega _q$. Note the occurrence of two characteristic rates, one at 2Γ_q equal to the familiar ring-down intensity decay rate, and the other at half of this value, which corresponds to the characteristic decay rate of the oscillating intensity amplitude.

In general, the amplitude $I_{{\mathrm{out}}}^0(t)$, the factor $\left| {D\left( t \right)} \right|$ and the phase $\varphi \left( t \right) = \varphi _2{\mathrm{(t)}} - \varphi _1{\mathrm{(t) = arctg}}\left\{ {{\mathrm{Im}}\left[ {D\left( t \right)} \right]/{\mathrm{Re}}\left[ {D\left( t \right)} \right]} \right\}$ in Eq. (17) are time-dependent functions. However, for small values of $\tau _0$ all these functions can be treated as time independent. In practice, for $\tau _0 = 50$ ns the expression $e^{ - {\Gamma}_0t}$ is of the order of 10⁻⁹ for $t \, > \, 1\,{\upmu} {\mathrm{{s}}}$, so it can be neglected in $I_{{\mathrm{out}}}^0\left( t \right)$ and $D\left( t \right)$ leading to time-independent functions $I_{{\mathrm{out}}}^0$ and $D$. For the limiting case $\tau _0 \to 0$ (${\Gamma}_0 \to \infty$), which corresponds to an immediate switch-on of the incident light electric field, $I_{{\mathrm{out}}}^0(t) \to \left| B \right|^2$, $D(t) \to 1$ and $\varphi (t) \to 0$ (because $C \to 0$).

Spectrum model of the buildup signal

For practical reasons in the realistic case mentioned above let us consider the buildup function $I_{{\mathrm{out}}}\left( t \right)$ approximating the Eq. (17) in the form

$$I_{{\mathrm{out}}}\left( t \right) = I_{{\mathrm{out}}}^0\left\{ {1 + D^2\exp ( { - 2{\Gamma}_qt}) - 2D\exp( { - {\Gamma}_qt} )\cos \left( {\delta \omega t - \varphi } \right)} \right\},$$

(18)

where $I_{{\mathrm{out}}}^0$, D and φ are real, time-independent parameters corresponding to original time-dependent quantities $I_{{\mathrm{out}}}^0(t)$, $\left| {D\left( t \right)} \right|$, φ(t), respectively. The Fourier transform ${\cal{F}}\left( \omega \right) = {\int}_0^\infty {I_{{\mathrm{out}}}\left( t \right)\exp (i\omega t)dt}$ leads to the formula

$${\cal{F}}\left( \omega \right) = I_{{\mathrm{out}}}^0\left\{ {\frac{{D^2}}{{2{\Gamma}_q - i\omega }} - D\left[ {\frac{{e^{ - i\varphi }}}{{{\Gamma}_q - i\left( {\omega + \delta \omega } \right)}} + \frac{{e^{i\varphi }}}{{{\Gamma}_q - i\left( {\omega - \delta \omega } \right)}}} \right]} \right\},$$

(19)

in which we have omitted the Dirac delta function term. The Fourier transform power spectrum $\left| {{\cal{F}}\left( \omega \right)} \right|^2$ of the buildup signal is given as

$$\begin{array}{l}\left| {{\cal{F}}\left( \omega \right)} \right|^2 = \left| {I_{{\mathrm{out}}}^0} \right|\left\{ {\frac{{D^2}}{{\left( {2{\Gamma}_q} \right)^2 + \omega ^2}} + D^2\left[ {\frac{1}{{{\Gamma}_q^2 + \left( {\omega - \delta \omega } \right)^2}} + \frac{1}{{{\Gamma}_q^2 + \left( {\omega + \delta \omega } \right)^2}}} \right] + 2D^2\frac{{\left( {{\Gamma}_q^2 + \omega ^2 - \delta \omega ^2} \right){\mathrm{cos}}\left( {2\varphi } \right) + \left( {2{\Gamma}_q\delta \omega } \right){\mathrm{sin}}\left( {2\varphi } \right)}}{{\left( {{\Gamma}_q^2 + \omega ^2 - \delta \omega ^2} \right)^2 + \left( {2{\Gamma}_q\delta \omega } \right)^2}} - } \right.\\ \quad \quad \left. {2D^3\left[ {\frac{{\left[ {2{\Gamma}_q^2 + \omega \left( {\omega + \delta \omega } \right)} \right]{\mathrm{cos}}\left( \varphi \right) + \left[ {2{\Gamma}_q\left( {\omega + \delta \omega } \right) - {\Gamma}_q\omega } \right]{\mathrm{sin}}\left( \varphi \right)}}{{\left[ {2{\Gamma}_q^2 + \omega \left( {\omega + \delta \omega } \right)} \right]^2 + \left[ {2{\Gamma}_q\left( {\omega + \delta \omega } \right) - {\Gamma}_q\omega } \right]^2}} + \frac{{\left[ {2{\Gamma}_q^2 + \omega \left( {\omega - \delta \omega } \right)} \right]{\mathrm{cos}}\left( \varphi \right) - \left[ {2{\Gamma}_q\left( {\omega - \delta \omega } \right) - {\Gamma}_q\omega } \right]{\mathrm{sin}}\left( \varphi \right)}}{{\left[ {2{\Gamma}_q^2 + \omega \left( {\omega - \delta \omega } \right)} \right]^2 + \left[ {2{\Gamma}_q\left( {\omega - \delta \omega } \right) - {\Gamma}_q\omega } \right]^2}}} \right]} \right\}.\end{array}$$

(20)

This function, apart from Lorentzian components, also contains asymmetric, dispersive terms.

Relation between cavity mode width and shift due to resonant absorption

For cavity buildup dispersion spectroscopy (CBDS) and in the limit of infinitely fast switching on of the laser at angular frequency $\omega$, the transmitted intensity associated with excitation of mode q located at $\omega _q = \omega - \delta \omega$ is given by Eq. (17) with $D\left( t \right) = 1$ and $\varphi \left( t \right) = 0$

$$I_{{\mathrm{out}}}\left( t \right) = I_{o{\mathrm{ut}}}^0\left( t \right)\left\{ {1 + e^{ - 2{\Gamma}_qt} - 2e^{ - {\Gamma}_qt}{\mathrm{cos}}\left[ {\delta \omega \,t} \right]} \right\}.$$

(21)

In the context of saturation-free CRDS, Lehmann²⁶ derived the relation between absorption in the cavity medium and concomitant perturbations on the cavity mode frequencies. To this end, the frequency-dependence of the real and imaginary parts of the index of refraction $n\left( \omega \right) = n_0 + \chi \left( \omega \right)/(2n_0)$ of the absorbing cavity gas can be expressed in terms of the absorptive and dispersive components of the complex-valued resonant susceptibility $\chi \left( \omega \right) = \chi^{\prime}\left( \omega \right) - i\chi^{\prime\prime}\left( \omega \right)$. The real and imaginary components of $\chi$ are tied by causality considerations that ensure zero impulse response for t < 0²⁶. Absorption and dispersion are thus given by

$$\alpha _q = \frac{{\omega _q\chi^{\prime\prime}(\omega )}}{{cn_0}},$$

(22)

and

$${\mathrm{{\Delta}}}\omega _q = - \omega _q\frac{{\chi^{\prime}\left( \omega \right)}}{{2n_0^2}},$$

(23)

respectively. Here ${\mathrm{{\Delta}}}\omega _q = \omega _q - \omega _q^{(0)}$ is the absorption-induced shift of the unperturbed mode position, $\omega _q^{(0)}$. The ratio of mode shift ${\mathrm{{\Delta}}}\omega _q$ to absorption coefficient, $\alpha _q$ reduces to

$$\frac{{{\mathrm{{\Delta}}}\omega _q}}{{\alpha _q}} = - \frac{c}{{2n_0}}\frac{{\chi^{\prime}\left( \omega \right)}}{{\chi^{\prime\prime}\left( \omega \right)}},$$

(24)

where c is the speed of light and $n_0$ is non-resonant refractive index of the sample.

Substituting $\alpha _q = (1/c)( {1/\tau _q - 1/\tau _{q,0}})$, with $\tau _{q,0}$ equal to the cavity time constant in the absence of absorption, and the uncertainty relation $2{\mathrm{{\Gamma}}}_q\tau _q = 1$ into Eq. (23) gives the ratio of the frequency shift to the increase in decay rate, ${\Delta}{\mathrm{{\Gamma}}}_q = {\mathrm{{\Gamma}}}_q - {\mathrm{{\Gamma}}}_{q,0}$, as

$$\frac{{{\Delta}\omega _q}}{{{\Delta}{\Gamma}_q}} = - \frac{{\chi^{\prime}\left( \omega \right)}}{{n_0\chi^{\prime\prime}\left( \omega \right)}}.$$

(25)

For measurements of isolated line shapes, one can write the resonant susceptibility for a line located at ω_j as

$$\chi \left( \omega \right) = - i\,n_0\frac{c}{\omega }{\cal{L}}^ \ast (\omega - \omega _j)n_{\mathrm{a}}S_j,$$

(26)

Here * denotes complex conjugate, S_j is the line intensity given by$2\pi cS_{\tilde \nu ,j}$ in which $S_{\tilde \nu ,j}$ is the intensity in standard dimensions of line area × wave number per molecule, $n_{\mathrm{a}}$ is the number density of the absorber and ${\cal{L}}\left( \omega \right)$ is the complex-valued line profile function²⁷ normalized so that ${\smallint }{\cal{L}}\left( \omega \right)d\omega = 1$. Equation (25) can be rewritten using complex line shape function ${\cal{L}}\left( \omega \right)$

$$\frac{{\delta \omega _D}}{{{\mathrm{{\Delta}}}{\Gamma}_q}} = \frac{{{\mathrm{Im}}\{ {{\cal{L}}( {\omega _q - \omega _0} )} \}}}{{n_0{\mathrm{Re}}\{ {{\cal{L}}( {\omega _q - \omega _0})}\}}}.$$

(27)

For symmetric line profiles ${\mathrm{Re}}\{ {\cal{L}}( {\omega - \omega _j} )\}$, ${\mathrm{Im}}\{ {\cal{L}}( {\omega - \omega _j})\}$ is an odd function centered on $\omega _j$, such that ${\mathrm{{\Delta}}}\omega _q$ > 0 for $\omega \, > \, \omega _j$ and ${\mathrm{{\Delta}}}\omega _q$ < 0 for ω < ω_j. This means that absorption-induced dispersion tends to “push” local cavity modes away from their unperturbed positions. In practice, this result can be used to disambiguate the signs of measured heterodyne beat frequencies.