Abstract
Tin is the chemical element with the largest number of stable isotopes. Its complete proton shell, comparable with the closed electron shells in the chemically inert noble gases, is not a mere precursor to extended stability; since the protons carry the nuclear charge, their spatial arrangement also drives the nuclear electromagnetism. We report high-precision measurements of the electromagnetic moments and isomeric differences in charge radii between the lowest 1/2+, 3/2+, and 11/2− states in 117–131Sn, obtained by collinear laser spectroscopy. Supported by state-of-the-art atomic-structure calculations, the data accurately show a considerable attenuation of the quadrupole moments in the closed-shell tin isotopes relative to those of cadmium, with two protons less. Linear and quadratic mass-dependent trends are observed. While microscopic density functional theory explains the global behaviour of the measured quantities, interpretation of the local patterns demands higher-fidelity modelling.
Similar content being viewed by others
Introduction
Nuclear science greatly relies on observations, not only in naturally-occurring, but also in laboratory-synthesized nuclides, which represent the majority of approximately 3000 species discovered to date1. Either type can be studied by laser spectroscopy, a non-destructive experimental technique probing the hyperfine splitting of atomic energy levels induced by the nuclear electromagnetism. An electric quadrupole moment, for instance, reflects an anisotropic (deformed) charge distribution within the nucleus2. Appreciable nuclear deformation is primarily found in species with open shells for both protons and neutrons3,4. The tin isotopes, with their proton core complete (spherical), may still acquire quadrupole moments through the geometry of valence neutron orbitals. Those can be discussed in terms of schematic theoretical descriptions such as the seniority or generalized-seniority models5,6, which explain the striking regularities previously observed, e.g., the nearly-constant energy of excited states and simple patterns exhibited by other quantities7,8,9. When looking into details, however, deviations from regular behavior are revealed as fingerprints of the underlying nucleonic shell structure and many-body correlations10,11,12,13.
Here we study the odd-mass isotopes 117–131Sn. An 11/2− state with an unpaired neutron confined by the rules of quantum mechanics to the unique-parity h11/2 orbital is present in each case. The remaining valence orbitals in the neutron shell have the opposite parity and considerably lower angular momenta, which results in isomerism (metastability of an excited nuclear state). Quadrupole moments in the closed-shell tin isotopes are found at variance with those in the cadmium isotopes having two protons less. Differences in radii between nuclear ground and isomeric states, on the other hand, are shown to remain surprisingly similar. Calculations in the framework of nuclear density functional theory with recently optimized input describe the global behavior of the experimental observables. Interpretation of the local patterns, however, calls for a dedicated microscopic modeling.
Results and discussion
Measurements
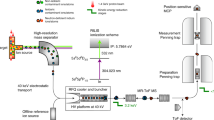
Short-lived nuclei, naturally occurring only in astrophysical phenomena such as supernovae explosions14, are synthesized on Earth using particle accelerators. The tin isotopes for this study were produced at the CERN-ISOLDE laboratory15 by uranium fission using fast protons traveling with more than 90% of the speed of light. Prior conversion to neutrons increased the fission purity16. Tin atoms were laser ionized, accelerated to an energy of 40 or 50 keV to form a continuous beam of fast-traveling ions, and mass separated. Typically, each 100-ms segment of the beam was compressed into an ion bunch with a temporal width of less than 10 μs using a linear Paul trap17. Individual bunches were subsequently released, re-accelerated, and guided with a dedicated set of electrostatic optics into a volume of vaporized sodium for neutralization. Narrow-bandwidth continuous-wave laser light was introduced along the axis of ion/atom propagation. The atomic-beam energy and the associated Doppler-shifted laser frequency were defined at the sodium charge-exchange cell, whose electrostatic potential was scanned in search of resonant atomic-beam fluorescence. The latter was collected by telescopes of aspheric lenses and imaged onto the photocathodes of photomultiplier tubes for single-photon counting. The measurements were correlated with the timing structure of the atomic beam, which allowed substantial background suppression and high sensitivity. A sketch of the experimental arrangement is shown in Fig. 1a.
a From left to right: linear Paul trap for ion-beam bunching; continuous-wave laser beams; electrostatic elements: deflector, quadrupole triplet, cylinder lens; alkali-vapor cell; optical detection: fused-silica aspheric lenses, photomultiplier tubes. b Partial energy level scheme of neutral tin indicating the studied excitations and the subsequent fluorescence used for detection. The shaded areas indicate the groups of 5p2 and 5p6s levels.
Laser excitation of tin atoms was performed using the two complementary transitions in Fig. 1b to resolve the nuclear properties, as described in “Methods”. The laser system comprised a diode-pumped solid-state laser, a tunable laser using either dye or titanium–sapphire as the active medium, and a second-harmonic-generation cavity. Two nuclear states were detected for each odd-mass isotope in the range 117–131Sn, as shown in Fig. 2. The hyperfine structure is characterized by a sizeable quadrupole splitting in the \(5p6s\,^1\!P_1^{\mathrm{o}}\) state and a large magnetic splitting in the \(5p6s\,^3\!P_1^{\mathrm{o}}\) state. The two are correlated through the nuclear electromagnetic properties and are thus fitted simultaneously. All results are shown in Table 1. The magnetic moments therein incorporate the latest computation of the absolute shielding constant in tin18. The accuracy of quadrupole moments is ensured by the theoretical work outlined in the following.
Hyperfine structure in the a \(5p6s\,^1P_1^{\mathrm{o}}\) state and b \(5p6s\,^3P_1^{\mathrm{o}}\) state. The fitted black curves comprise a 3/2+ nuclear ground state, represented by the dashed white lines, and an 11/2− isomer, represented by the solid blue lines. Hyperfine levels are denoted by the individual total angular-momentum quantum number.
Atomic structure calculations
The fully relativistic multiconfiguration Dirac–Hartree–Fock (MCDHF) method was employed to calculate the magnetic dipole hyperfine-structure constants and electric-field gradients in the \(5p6s\,^1\!P_1^{\mathrm{o}}\) and \(5p6s\,^3\!P_1^{\mathrm{o}}\) states of tin (see “Methods” for the definition of these quantities). Three independent series of large-scale calculations were performed, adopting different computational strategies and correlation models using the General Relativistic Atomic Structure Package computer codes GRASP2K19 and GRASP201820, based on the same relativistic MCDHF theory and methodology21,22. Classes of electron excitations adopting different multireference spaces and active orbital sets were investigated in detail to clarify the role of electron correlation in the relevant matrix elements. A combined effort was put in assessing the reliability of the resulting ab initio electronic factors involved in M1 and E2 hyperfine interactions for both levels (Papoulia, A. & Schiffman, S. et al. mansuscript in preparation). The quadrupole moments from this work are obtained with the electric-field gradient 706(50) MHz/b in the singlet state, which is the mean value resulting from the aforementioned calculations. With regard to the dipole hyperfine constants in the triplet state, cross-checking calculations were performed using the configuration interaction Dirac–Fock–Sturm (CI-DFS) method23. The hyperfine anomaly (see “Methods”) was estimated in separate multireference calculations for each isotope using a Fermi charge distribution with adopted root mean square radius and a parametrized squared harmonic-oscillator wave function of the last unpaired neutron as magnetization distribution24. It reaches a maximum at 119gΔ131m = 0.05% due to the limited overlap between the 3s and 1h nuclear wave functions and partly due to the increase in the charge radius between the two isotopes. The anomaly between positive-parity states was found to be negligible with respect to the experimental precision.
Experimental trends
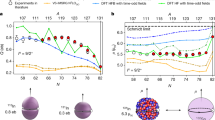
The data on quadrupole moments and differences in mean square charge radii between nuclear ground and isomeric states are compared in Fig. 3 with values measured in the cadmium isotones25,27,27. A number of key observations are worth being pointed out: (i) There is a significant attenuation of the quadrupole moments of tin (Z = 50) with respect to cadmium (Z = 48). Note that the observed charge (proton) quadrupole moment originates from the nuclear response to an odd neutron in a d3/2 or an h11/2 single-particle state. (ii) The fitted trends in Fig. 3a, b cross each other close to zero, i.e., the h11/2 orbital is half full5,6 for both tin and cadmium at N = 73, as is d3/2 at N = 75. (iii) The quadrupole moments of tin in the 11/2− states are by a factor of about two larger in magnitude than those in the 3/2+ states. This is consistent with a stronger quadrupole polarization exerted by unique-parity h11/2 nucleons. (iv) All trends are remarkably smooth, often near linear, at most quadratic. (v) The quadrupole moments of the 11/2− states in tin exhibit a quadratic behavior with changing neutron number, strikingly different from the linear trend observed along the cadmium chain. (vi) The pattern is unexpectedly reversed for the 3/2+ states whose quadrupole moments change linearly for tin and quadratically for cadmium. (vii) Re-evaluated values for 113,115,119Sn28 in Fig. 3a, b are consistent with the trends defined by the heavier isotopes. These are independently calibrated to experimental γ-decay rates, thus showing consistency between nuclear data and atomic theory. (viii) The measured mean square charge-radii changes in Fig. 3c are fairly similar for tin and cadmium. All these features are discussed in the following.
a 11/2− quadrupole moments. b 3/2+ quadrupole moments. Correlated uncertainties originating from the electric-field gradients are smaller than the dots. c Mean square charge-radii changes for the 11/2− states relative to the 1/2+ (N ≤ 71) and 3/2+ (N ≥ 71) states. Shaded bands represent systematic uncertainties originating from the field-shift coefficients. The literature values are taken from refs. 25,26,28.
Nuclear structure calculations
The theoretical analysis at the level of nuclear density functional theory29 (DFT) employs the standard Skyrme functional SV-min30 and the recently optimized Fayans functional Fy(Δr, HFB)31, the latter containing gradient terms in surface and pairing energies32,33. Both models are optimized to the same large set of basic ground-state nuclear data30. In addition, Fy(Δr, HFB) accommodates the isotopic shifts of charge radii in the calcium chain, a feature which could only be achieved by invoking the Fayans gradient terms31,34. The calculations for the charge radius, which is an isotropic observable, were done in spherical approximation with pairing handled at Hartree–Fock–Bogoliubov (HFB) level. The odd nucleons were treated within the blocking ansatz35. In principle, the odd nucleon polarizes the nucleus and so perturbs the spherical shape. The impact of this polarization effect on charge radii and correlations beyond mean field are small for heavier spherical species as the tin isotopes36,37. To check the uncertainty from the spherical mean-field approximation, we performed more elaborate blocked HFB calculations allowing axial deformations and spin polarization for the case of the SV-min model. In this variant, each magnetic sub-state produces a slightly different radius whose average is very close to the spherical result. This supports our spherical calculations and the variance of charge radii within a jm shell delivers an estimate of their theoretical uncertainties.
Figure 4a shows the quadrupole moments of 11/2− states in tin and cadmium which were obtained by blocking the m = 11/2 magnetic substate of the h11/2 orbital in calculations that break spherical symmetry. It is satisfactory to see that the general experimental pattern in Fig. 3a is reproduced. Namely, the quadrupole moments exhibit a smooth increase as a function of the neutron number, with the quadrupole moments of tin being reduced in magnitude relative to cadmium. The enhanced quadrupole correlations in cadmium stem from the enhanced polarizability through the two g9/2 proton holes38,39. Indeed, in the nuclear shell model40 and in nuclear DFT41, deformation is primarily driven by the isoscalar neutron–proton (quadrupole) interaction, acting against the sphericity-favoring monopole force, which includes the isovector pairing interaction. According to the seniority coupling scheme5,6,7, the spectroscopic quadrupole moment should vanish at mid-shell. In SV-min, the neutron h11/2 shell becomes half-filled at N = 75, as seen in Fig. 4a. Experimentally, the zero crossover point is at N = 73, which suggests that the single-particle energy of the h11/2 shell is perhaps not optimal in our model. This nicely demonstrates that the present high-precision data on quadrupole moments deliver extremely sensitive criteria for probing the shell structure of a model.
Theoretical values for the isomeric charge-radii shifts of the odd-mass tin isotopes are displayed in Fig. 4b, c. The error bars on the SV-min results indicate the estimated uncertainty of the spherical approach as compared to calculations allowing shape deformation as well as spin polarization and subsequent angular momentum projection, as explained above. We expect similar uncertainty for the Fy(Δr, HFB) model. One finds an acceptable agreement for the charge radii difference between the 11/2− and the 3/2+ states, with a preference towards the Fy(Δr, HFB) description, especially when considering the theoretical uncertainty. This is not the case for the radii changes between the 11/2− and the 1/2+ states, since the experimental data approach the upper end of theoretical results in Fig. 4b. A word of caution is in order here: the 1/2+ state is particularly prone to a dynamical coupling with low-energy quadrupole vibrations which is expected to enhance the charge radius.
The trends of quadrupole moments, linear vs. quadratic, are different for cadmium and tin owing to a significant configuration dependence. The latter does not cause a substantial deviation between the corresponding mean square charge-radii changes. The future theoretical analysis would need to address these features in greater detail together with variations of the magnetic moments shown in Fig. 5. Any connection with the quadrupole moments of the lowest 2+ states in the even–even isotopes42,43 should also be examined.
Perspective
Complex systems often display regular patterns. Atomic nuclei, composite structures consisting of hundreds of nucleons, are no exception; they often behave as ordered systems obeying elementary rules5. The reason for such simplicities is the presence of many-body symmetries resulting in a collective nucleonic motion. A challenge for the modern microscopic theory is to explain the origin of underlying symmetries.
In this work, we showed that electromagnetic properties of tin nuclei evolve from one isotope to another in a simple way: along a line or parabola. The microscopic mechanisms behind the observed behavior are rooted in many-body polarization effects. While the general trends are explained by theory, the regularities seen at high experimental resolution provide a strong motivation for further theoretical developments.
Similar effects are expected to be common for nuclei whose valence nucleons move in a unique-parity shell. Dedicated studies would be required to refine the systematics in lead and mercury isotopes44, which are the closest analogues of tin and cadmium in terms of nuclear structure. While initial assessments could be made by in-source measurements45,46, the high-resolution spectroscopic techniques employed here, in combination with advanced atomic calculations, will be essential for developing further understanding of complex nuclear systems.
Methods
Hyperfine structure
The electromagnetic interaction of the nucleus with the electron environment in an atom causes splitting of the energy levels which is about a millionth of the fine-structure splitting, hence the term hyperfine structure. The energy shift of the individual hyperfine components equals
where A = μB0/(IJ) is proportional to the nuclear magnetic moment μ and the average magnetic-flux density at the origin B0, B = eQVJJ is proportional to the nuclear quadrupole moment Q and the average electric-field gradient at the origin VJJ, F = I + J is the total angular momentum of the atom, and k = F(F + 1) − I(I + 1) − J(J + 1). The hyperfine-structure splitting is determined by the A and B parameters whose values are obtained from the experiment. The decay rate per atom, commonly referred to as Racah intensities47, is given by
where τ is the lifetime of the excited atomic state and γ is the ratio between the induced and spontaneous emission coefficients, which incorporates the laser intensity and the spectral lineshape.
Hyperfine anomaly
The A hyperfine constant is influenced by the extended nuclear magnetization, known as Bohr–Weisskopf effect, and the extended nuclear charge distribution, known as Breit–Rosenthal–Crawford–Schawlow correction. Both contribute to the hyperfine anomaly:
Following justification by atomic calculations, the anomaly is neglected in our analysis. However, its estimated contribution to the 11/2− magnetic moments is predicted to be on the level of the experimental precision and it is therefore incorporated into the final uncertainties quoted in Table 1, as further discussed.
Isomer shifts
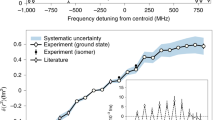
A change in the nuclear mean square charge radius between a nuclear ground state and an isomer results in a common energy displacement of all levels in a given hyperfine multiplet. The combined effect in a transition between two atomic levels is manifested in spectra from laser spectroscopy as an apparent “isomer shift”. For example, in Fig. 6, this causes the pattern of peaks associated with the 11/2− state in the right column to “walk” towards higher frequencies in the heavier isotopes. The isomer (frequency) shift is a product of the electronic factor, related to a change in the total electronic charge density at the site of the nucleus, and a change in the nuclear mean square charge radius:
The common frequency scales are relative to the fine-structure splittings in the transitions \(5p^2\,^3P_0 \to 5p6s\,^3P_1^{\mathrm{o}}\) and \(5p^2\,^1S_0 \to 5p6s\,^1P_1^{\mathrm{o}}\). Positive- and negative-parity states are represented by dashed and solid lines, respectively. Solid lines in the right column also show the sum fit function. 119Sn is studied from a mass marker to observe only the stable 1/2+ g.s., and after target irradiation to detect the radioactive 11/2− state. Spectra of the stable g.s. in 115,117Sn (similar to 119Sn g.s.) are not shown. 133Sn, used together with 109Sn for calibration of the B-ratio, will be published elsewhere.
Distinction should be made between Fλ and the total angular-momentum quantum number F introduced earlier. The effect from a change in the nuclear mass is negligible.
Fitting of multiple spectra
Routines for fitting multiple spectra were developed in the ROOT data analysis framework48, making use of the WrappedMultiTF1 class for enveloping individual fit functions under a common χ2. Spectra of the stable 1/2+ ground states in 115,117,119Sn, free of quadrupole splitting, were used to determine the proportionality of A factors between the singlet and the triplet state. With this condition applied to the spectra of 109Sn and 133Sn, which are unperturbed by the presence of an isomer, one obtained the ratio of B factors. Individual masses were used for ground and isomeric states49. The isomer shifts were constrained to one another by a King plot50 of data on the even–even isotopes. The three aforementioned ratios are presented in Table 1. Voigt lineshapes were used with a predominant Lorentzian component emerging from the fits. Resolved lines were fitted with free intensities. The heights of overlapping lines were locked to each other, or to other resolved lines when available, by using the Racah intensities. As constrained above, the fits fully determine the nuclear spins.
Nuclear properties
Using frequency ratios from the nuclear magnetic resonance of the 1/2+ states in 115,117,119Sn51, and the latest evaluation of the magnetic moment of 119Sn18 with an adopted uncertainty of 0.01%52, one arrives at a high-precision magnetic moment for each of the three isotopes, as given in Table 1. These in combination with their corresponding A factors in the triplet state are used to determine the ratio AIµN/(hµ) = 2396.6(7) MHz through a weighted mean, which is then used to extract magnetic moments for the rest of the isotopes. A small hyperfine-anomaly contribution of 0.05% (see the main text) is added in quadrature to the uncertainties of the 11/2− magnetic moments. The quadrupole moments are determined in the singlet state with the electric-field gradient B/(hQ) = 706(50) MHz/b from this work. Using the B ratio reported in Table 1, the electric-field gradient in the triplet state is found to be −173(17) MHz/b. Both are substantially stronger in comparison with semi-empirical estimates adopted in former studies53,55,55. This has had an impact on the results of a recent phenomenological analysis56. Mean square charge-radii changes are extracted in the triplet state with the field shift δν/δ〈r2〉 = 0.274(57) MHz/μb37.
Data availability
The authors declare that the data supporting this study are published within the paper as histograms in Fig. 6.
References
Thoennessen, M. The Discovery of Isotopes. (Springer: Cham, Switzerland, 2016).
Bohr, A. & Mottelson, B. R. Nuclear Structure, Vol. 2 (W. A. Benjamin, Inc.: Singapore, 1975).
Reinhard, P.-G. & Otten, E. W. Transition to deformed shapes as a nuclear Jahn–Teller effect. Nucl. Phys. A 420, 173 (1984).
Nazarewicz, W. Microscopic origin of nuclear deformations. Nucl. Phys. A 574, 27 (1994).
Casten, R. F. Nuclear Structure from a Simple Perspective. (Oxford University Press: New York, 1990).
Talmi, I. Simple Models of Complex Nuclei. (Harwood Academic Publishers: Switzerland, 1993).
Talmi, I. The shell model—simplicity from complexity: some of my best nuclei are spherical. Phys. Scr. 92, 083001 (2017).
Morales, I. O., Van Isacker, P. & Talmi, I. Generalized seniority and E2 transitions in the tin isotopes. Phys. Lett. B 703, 606 (2011).
Stuchbery, A. E. Simple structures in complex nuclei versus complex structures in simple nuclei: a nuclear moments perspective. J. Phys.: Conf. Ser. 366, 012042 (2012).
Morris, T. D. et al. Structure of the lightest tin isotopes. Phys. Rev. Lett. 120, 152503 (2018).
Togashi, T., Tsunoda, Y., Otsuka, T., Shimizu, N. & Honma, M. Novel shape evolution in Sn isotopes from magic numbers 50 to 82. Phys. Rev. Lett. 121, 062501 (2018).
Siciliano, M. et al. Pairing-quadrupole interplay in the neutron deficient tin nuclei: first lifetime measurements of low-lyingstates in 106,108Sn. Preprint at https://arxiv.org/abs/1905.10313 (2019).
Zuker, A. P. Quadrupole dominance in light Cd and Sn isotopes. Preprint at https://arxiv.org/abs/1905.11479 (2019).
Burbidge, E. M., Burbidge, G. R., Fowler, W. A. & Hoyle, F. Synthesis of the elements in stars. Rev. Mod. Phys. 29, 547 (1957).
Neugart, R. et al. Collinear laser spectroscopy at ISOLDE: new methods and highlights. J. Phys. G 44, 064002 (2017).
Köster, U. et al. Progress in ISOL target-ion source systems. Nucl. Instrum. Methods Phys. Res., Sect. B 266, 4229 (2008).
Mané, E. et al. An ion cooler-buncher for high-sensitivity collinear laser spectroscopy at isolde. Eur. Phys. J. A 42, 503 (2009).
Malkin, E., Komorovsky, S., Repisky, M., Demissie, T. B. & Ruud, K. The absolute shielding constants of heavy nuclei: resolving the enigma of the 119Sn absolute shielding. J. Phys. Chem. Lett. 4, 459 (2013).
Jönsson, P., Gaigalas, G., Bieroń, J., Froese Fischer, C. & Grant, I. P. New version: Grasp2K relativistic atomic structure package. Comput. Phys. Commun. 184, 2197 (2013).
Froese Fischer, C., Gaigalas, G., Jönsson, P. & Bieroń, J. GRASP2018—A Fortran 95 version of the general relativistic atomic structure package. Comput. Phys. Commun. 237, 184 (2019).
Froese Fischer, C., Godefroid, M., Brage, T., Jönsson, P. & Gaigalas, G. Advanced multiconfiguration methods for complex atoms: I. Energies and wave functions. J. Phys. B 49, 182004 (2016).
Grant, I. P. Relativistic Quantum Theory of Atoms and Molecules. Theory and Computation. (Springer-Verlag: NY, USA, 2007).
Tupitsyn, I. I. & Loginov, A. V. Use of Sturmian expansions in calculations of the hyperfine structure of atomic spectra. Opt. Spectrosc. 94, 319 (2003).
Ekman, J., Li J., Jönsson P., Godefroid M. & Gaigalas G. Modeling hyperfine anomalies using GRASP. Proc. EOS workshop on Electronic Atomic Factors and Hyperfine Anomalies for Nuclear Physics (Brussels, Belgium, 2019).
Yordanov, D. T. et al. Spins, electromagnetic moments, and isomers of 107–129Cd. Phys. Rev. Lett. 110, 192501 (2013).
Yordanov, D. T. et al. Simple nuclear structure in 111–129Cd from atomic isomer shifts. Phys. Rev. Lett. 116, 032501 (2016).
Frömmgen, N. et al. Collinear laser spectroscopy of atomic cadmium. Eur. Phys. J. D 69, 164 (2015).
Haas, H. Data re-evaluation. Private Communication (2019).
Bender, M., Heenen, P.-H. & Reinhard, P.-G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 75, 121 (2003).
Klüpfel, P., Reinhard, P.-G., Bürvenich, T. J. & Maruhn, J. A. Variations on a theme by Skyrme: a systematic study of adjustments of model parameters. Phys. Rev. C 79, 034310 (2009).
Miller, A. J., Minamisono, K. & Klose, A. et al. Proton superfluidity and charge radii in proton-rich calcium isotopes. Nat. Phys. 15, 432 (2019).
Fayans, S. A. Towards a universal nuclear density functional. JETP Lett. 68, 169 (1998).
Fayans, S. A., Tolokonnikov, S. V., Trykov, E. L. & Zawischa, D. Nuclear isotope shifts within the local energy-density functional approach. Nucl. Phys. A 676, 49 (2000).
Reinhard, P.-G. & Nazarewicz, W. Toward a global description of nuclear charge radii: exploring the Fayans energy density functional. Phys. Rev. C 95, 064328 (2017).
Ring, P. & Schuck, P. The Nuclear Many-Body Problem. (Springer-Verlag: Berlin, 1980).
Hammen, M. & Nörtershäuser, W. et al. From calcium to cadmium: testing the pairing functional through chargeradii measurements of 100–130Cd. Phys. Rev. Lett. 121, 102501 (2018).
Gorges, C. et al. Laser spectroscopy of neutron-rich tin isotopes: a discontinuity in charge radii across the N = 82 shell closure. Phys. Rev. Lett. 122, 192502 (2019).
Zhao, P. W., Zhang, S. Q. & Meng, J. Explanation of the simplicity of the quadrupole moments recently observed in Cd isotopes from covariant density functional theory. Phys. Rev. C 89, 011301(R) (2014).
Yordanov, D. T. et al. Spins and electromagnetic moments of 101–109Cd. Phys. Rev. C 98, 011303(R) (2018).
Federman, P. & Pittel, S. Unified shell-model description of nuclear deformation. Phys. Rev. C 20, 820 (1979).
Dobaczewski, J., Nazarewicz, W., Skalski, J. & Werner, T. Nuclear deformation: a proton–neutron effect? Phys. Rev. Lett. 60, 2254 (1988).
Esat, M. T., Kean, D. C., Spear, R. H. & Baxter, A. M. Mass dependence of the static quadrupole moments of the first 2+ states in the cadmium isotopes. Nucl. Phys. A 274, 237 (1976).
Allmond, J. M. et al. Investigation into the semimagic nature of the tin isotopes through electromagnetic moments. Phys. Rev. C 92, 041303(R) (2015).
Neyens, G. Nuclear magnetic and quadrupole moments for nuclear structure research on exotic nuclei. Rep. Prog. Phys. 66, 633 (2003).
Ferrer, R. et al. Towards high-resolution laser ionization spectroscopy of the heaviest elements in supersonic gas jet expansion. Nat. Commun. 8, 14520 (2017).
Sels, S. et al. Shape staggering of midshell mercury isotopes from in-source laser spectroscopy compared with density-functional-theory and Monte Carlo shell-model calculations. Phys. Rev. C 99, 044306 (2019).
Magnante, P. C. & Stroke, H. H. Isotope shift between 209Bi and 6.3-day 206Bi. J. Opt. Soc. Am. 59, 836 (1969).
Brun, R. & Rademakers, F. ROOT—an object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res., Sect. A 389, 81 (1997).
Audi, G., Kondev, F. G., Wang, M, Huang, W. J. & Naimi, S. The NUBASE2016 evaluation of nuclear properties. Chin. Phys. C 41, 030001 (2017).
King, W. H. Comments on the article: Peculiarities of the isotope shift in the samarium spectrum. J. Opt. Soc. Am. 53, 638 (1963).
Makulski, W. Tetramethyltin study by NMR spectroscopy in the gas and liquid phase. J. Mol. Struct. 1017, 45 (2012).
Makulski, W., Jackowski, K., Antušek, A. & Jaszuński, M. Gas-phase NMR measurements, absolute shielding scales, and magnetic dipole moments of 29Si and 73Ge nuclei. J. Phys. Chem. A 110, 11462 (2006).
Anselment, M. et al. Charge radii and moments of tin nuclei by laser spectroscopy. Phys. Rev. C 34, 1052 (1986).
Le Blanc, F. et al. Charge-radius change and nuclear moments in the heavy tin isotopes from laser spectroscopy: charge radius of 132Sn. Phys. Rev. C 72, 034305 (2005).
Eberz, J. et al. Nuclear spins, moments and charge radii of 108–111Sn. Z. Phys. A 326, 121 (1987).
Maheshwari, B., Abu Kassim, H., Yusof, N. & Jain, A. K. Evolution of nuclear structure in and around Z = 50 closed shell: generalized seniority in Cd, Sn and Te isotopes. Nucl. Phys. A 992, 121619 (2019).
Raghavan, P. Table of nuclear moments. At. Data Nucl. Data Tables 42, 189 (1989).
Acknowledgements
The authors thank the ISOLDE technical group for their professional assistance and Heinz Haas for re-evaluating the quadrupole moments of the very short-lived isomers in 113,115,119Sn. This work has been supported by the Max Planck Society, the German Federal Ministry for Education and Research under Contract No. 05P15RDCIA, the Helmholtz International Center for FAIR within the LOEWE program by the State of Hesse, the Belgian IAP Project No. P7/12, the FWO-Vlaanderen, GOA 15/010 from KU Leuven, the European Union seventh framework through ENSAR under Contract No. 262010, the Science and Technology Facilities Council (ST/P004423/1 and ST/P004598/1), and by the Office of Science, U.S. Department of Energy under Grant Nos. DE-SC0013365 and DE-SC0018083 (NUCLEI SciDAC-4 Collaboration). D.L.B. acknowledges support from the EU Development Fund and Competitiveness Operational Program for the ELI-NP Project Phase II (1/07.07.2016, COP, ID1334), M.R.G. from the FWO & FNRS Excellence of Science Programme (EOS-O022818F), A.P., J.E., and P.J. from the Swedish Research Council (VR) under Contract No. 2015-04842, and P.P. from the Magnus Ehrnrooth Foundation.
Author information
Authors and Affiliations
Contributions
M.L.B., R.F.G.R., C.G., H.H., S.K., V.L., S.L., S.M.-E., L.V.R., S. Sailer, L.X., X.Y., and D.T.Y. prepared the instrumentation and contributed to the on-line measurements along with D.L.B., K.B., B.C., G. Georgiev, W.G., A.K., B.M., R.N., G.N., W. Nörtershäuser, R.S., S. Schmidt, L.W., C.W., and Z.X. L.V.R. developed routines for the fitting of multiple spectra. Nuclear DFT analysis was carried out by W. Nazarewicz and P.-G.R. J.B., J.E., G. Gaigalas, M.R.G., Z.H., P.J., C.H.K., N.S.O., A.P., P.P., and S. Schiffmann contributed to the ab initio large-scale MCDHF and CI-DFS calculations of the relevant electronic parameters and to their reliability assessment. J.E. computed the hyperfine anomalies. D.T.Y. proposed the measurements and prepared the manuscript with input from all authors. These results are part of the PhD theses of C.G. and L.V.R.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yordanov, D.T., Rodríguez, L.V., Balabanski, D.L. et al. Structural trends in atomic nuclei from laser spectroscopy of tin. Commun Phys 3, 107 (2020). https://doi.org/10.1038/s42005-020-0348-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0348-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.