Abstract
Hybrid organolead perovskites (HOP) have started to establish themselves in the field of photovoltaics, mainly due to their great optoelectronic properties and steadily improving solar cell efficiency. Study of the lattice dynamics is key in understanding the electron-phonon interactions at play, responsible for such properties. Here, we investigate, via neutron and Raman spectroscopies, the optical phonon spectrum of four different HOP single crystals: MAPbBr3, FAPbBr3, MAPbI3, and α-FAPbI3. Low temperature spectra reveal weakly dispersive optical phonons, at energies as low as 2-5 meV, which seem to be the origin of the limit of the charge carriers mobilities in these materials. The temperature dependence of our neutron spectra shows as well a significant anharmonic behaviour, resulting in optical phonon overdamping at temperatures as low as 80 K, questionning the validity of the quasi-particle picture for the low energy optical modes at room temperature where the solar cells operate.
Similar content being viewed by others
Introduction
Over the last few years, halide perovskites have emerged as a promising class of materials for high-performing photovoltaic (PV) cells1,2,3. The hybrid organolead perovskites (HOPs) adopt an APbX3 structure, where A is an organic cation (methylammonium, MA, or formamidinium, FA) and X is an halide (Cl, Br, I) and their optoelectronic properties, as well as easy and cost-effective production (from abundant chemical elements), make HOPs not only attractive for PV applications4,5,6,7,8, but also for light-emitting devices (LEDs) and many other application based on thin films or even single crystals9,10,11,12.
Several of the properties responsible for the outstanding performance of hybrid perovskites are connected with electron–phonon interactions, which have been under intense debate13,14,15,16,17. Besides governing their emission line broadening, phonon scattering is among the factors setting a fundamental intrinsic limit to the mobility of charge carriers in these materials. From the inspection of photoluminescence (PL) lineshape broadening in the high-temperature regime of 3D perovskite thin films, it was deduced that carriers scattering is dominated by Fröhlich coupling between charge carriers and longitudinal optical (LO) phonon modes, rather than with acoustic phonons13,15. This was later reinforced from the analysis of elastic constants among different 3D hybrid perovskites18,19. More, optical phonons were shown to play a central role in the slow carriers relaxation in colloidal quantum dots (CQD) of FAPbI3 and FAPbBr3, from the exciton bright triplet to the dark singlet through a second-order process20, with strong consequences for CQD brightness and quantum efficiency of CQD light-emitting devices20,21. This mechanism is an alternative to the Rashba effect, which was proposed to lead to an inversion of dark and bright exciton states in CQDs22. Further, the potential of perovskite CQDs for hot-carriers solar cell applications has also been stressed23: the suppression of the LO relaxation process to longitudinal acoustic (LA) phonons was attributed to an optical phonon bottleneck effect24, and later on related to the anharmonicity of the acoustic modes25. Then, a direct measurement of optical phonons branches with the same methodology as for the acoustic modes18,19 becomes a necessary step to completely uncover carrier–phonon coupling dynamics and to assess the fundamental intrinsic limit of the mobility of charge carriers in these materials.
HOPs are composed of two sub-lattices: the inorganic sub-lattice, composed of covalently bonded PbX3 octahedra, and the organic sub-lattice consisting of the MA/FA molecular cations inside cuboctahedral perovskite cavities. They have been well documented to undergo a series of crystallographic transitions which differ slightly depending on the organic cation or the halide atom. It typically goes from the high-temperature cubic phase (Pm\(\overline{3}\)m), passing by a tetragonal phase (I4/mcm for MAPbI3 and MAPbBr3 and P4/mbm for FAPbBr326) down to the low-temperature orthorhombic phase (Pnma for all compounds except for FAPbI3 where a trigonal phase P3m1 has been reported at low temperature)27,28,29,30,31. In general, these phase transitions originate from the tilting of the PbX3 cage and the orientational ordering of MA/FA molecules, which is reconstructive for the low-temperature transformation in MA-based compounds18,32,33,34,35,36. Note that the first-order character of the low-temperature phase transition is less prononced in FA-based compounds than in MA-based ones. By inducing more complex octahedra tiltings in the perovskite lattice, organic cations may indirectly affect their electronic structure.
While the molecular cations are not expected to directly contribute to the electronic band structure37,38, they are thought to indirectly influence the electronic band edge states through the induction of distortions in the PbX3 framework38,39. Effective volume in the A-site—which is increasing from K+, Rb+, Cs+ inorganic compounds to MA+ and FA+40—is for one affecting the Pb-X elongation. Also, the MA/FA molecules have been suggested to interact with the Pb-X network via hydrogen bonding between the ammonium hydrogens and the halide atoms, perturbing in this way the conduction band minimum, increasing diffusion length and suppressing electron–hole recombination41,42,43,44. Therefore, the interplay between the molecular groups and the inorganic network presents itself as an additional factor affecting both in the charge-recombination dynamics and the above-mentioned electron–phonon interactions.
On the other hand, the intrinsic anharmonicity of the perovskite lattice is expected to play a more important role17. Lattice dynamic calculations from density functional theory (ab initio atomic-level description) of HOPs is complicated and generally not reliable due to the hybrid nature of these compounds, where molecules perform stochastic motions at ambient temperature17. More generally though, the strongly anharmonic character of the lattice dynamics is not taken into account in recent phonon calculations for both inorganic and hybrid compounds. Typically, the lowest energy phonons, related to Pb-halogen vibrations, are found unstable with imaginary mode frequency in almost all available theoretical calculations within the harmonic approximations25,45. It is therefore interesting to rely on frozen-phonon calculations46 or molecular dynamics47 to get a first theoretical insight into anharmonic effects.
In this work, we employed both time-of-flight (TOF) and triple-axis (TAS) inelastic neutron scattering (INS) techniques (see Methods) to investigate four different hybrid perovskite single crystals: MAPbBr3, FAPbBr3, MAPbI3 and α-FAPbI3; from now on referred to as MAPB, FAPB, MAPI and FAPI, respectively. Complementary Raman scattering spectroscopy is also used. At low temperatures, well-defined optical phonons are observed. Mode attribution to the respective structural vibrations has been discussed and a comparison has been made between the four compounds. We also find the optical excitations to be very weakly propagating, particularly in MA-based compounds. Moreover, the temperature dependence of the TAS spectra reveals a significant anharmonic behaviour, resulting in optical phonon overdamping at temperatures as low as 80 K. We argue for the importance of the acoustic and optical phonon coupling on the harmonicity of the lattice.
Results
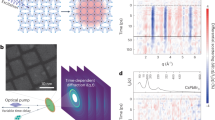
From an experimental perspective, INS allows for direct measurement of the phonon spectrum over the reciprocal space that covers the full Brillouin zone (Fig. 1a, b), thus offering the most complete approach. Raman spectroscopy is also a very powerful and precise technique to measure optical phonons and quasielastic contributions, but restricted to the centre of the Brillouin zone (Γ-point) and limited by specific selection rules.
a Schematic representation of lattice vibrations (phonons) interacting with neutrons with incident and final momentum, ki and kf, respectively. Panel b shows kinematic condition for the conservation of momentum during the INS experiment measuring a phonon at a momentum Q in the reciprocal (or momentum) space, from which one can deduce the phonon wave vector q from the relation Q = τ + q, where τ is the nearest Bragg peak position.
Room temperature phonon spectra
In Fig. 2, both room temperature (RT) and low temperature (5 K) TOF and TAS measurements are presented. As a first remark, it is necessary to cool the samples down to the lowest temperature to observe well-defined optical phonon branches. Indeed, the INS spectrum recorded at RT in MAPI shows no well-defined optical phonon modes at any energy range as a result of all modes being overdamped in all momentum points (Fig. 2a). Only low-energy acoustic phonons can be actually identified (see also Supplementary Fig. 1), in agreement with the report of RT acoustic phonons in the same four HOP compounds18,19. Above ~3 meV, the acoustic branches vanish19 as observed in the broadening of the acoustic branches at the zone boundary in deuterated MAPI48 and in MAPbCl3 (ref. 49). The absence of optical phonons at RT is also observed in TAS spectra of the other three systems in the Supplementary Fig. 2, all of which is in line with a previous report on MAPI50. Accordingly, only a broad inelastic contribution was observed around 12 meV in MAPB at RT and a tentative attribution of the various phonon modes inside this bundle was only possible through the numerical fitting of the experimental spectrum by a superposition of damped harmonic oscillators (DHOs)18. This is also consistent with the high-temperature Raman spectrum of MAPbBr3 (vide infra)51. The dispersive optical phonon modes reported at RT by inelastic X-Ray scattering in MAPI and MAPB45, with its broader energy resolution (i.e. ~1.5 meV) and its Lorentzian instrumental shape, are then put into question.
Data obtained with both neutron time-of flight (TOF) and triple-axis spectrometer (TAS) measurements. The TOF instruments allow a mapping of optical modes in the momentum space whereas TAS focuses on particular Q-points to follow phonon modes versus momentum or energy. a–c TOF contour plots of MAPbI3: a at room temperature (RT), between 0 and 13 meV, and at 5 K at b low-energy range (below 6 meV) and c between 10 and 14 meV. Also at 5 K, TAS measurements along high symmetry directions, going through the reciprocal space, in d MAPB, e FAPB and f FAPI. The insets of panels d–f show the related TAS measurement trajectories in the first Brillouin zone. The inelastic neutron scattering measurements in the orthorhombic phase (5 K) of all four perovskites, suggesting little to no dispersion of the optical phonon modes. In panels d–f, error bars (of the order of the symbol size) represent one standard deviation.
Lack of dispersion in momentum space
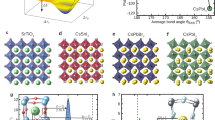
In order to be able to observe sharp optical phonon features, recording neutron spectra at 5 K (Fig. 2b–f) is necessary as cooling down to the lowest temperature substantially reduces phonon damping. In MA-based HOP compounds, the phonons are typically resolution-limited in energy at 5 K, whereas in FA-based systems the phonon features remain broad even at 5 K (see e.g. Fig. 3a–h). Showing relatively broad peaks that apparently represent scattering from a bundle of modes, it should be emphasized that the INS technique is incapable of detecting a specific phonon dispersion in such closely packed optical modes which might overlap. However, this experimental limit depends greatly on the instrumental energy resolution which is very much improved for cold neutron spectrometers (see Fig. 3 caption).
Triple-axis spectrometer (TAS) neutron spectra measured at 5 K, at the R bragg reflection (1/2, 1/2, 3/2) of a, b MAPB, c, d MAPI, e, f at the M point (5/2, 1/2, 0) of FAPB and g at the R point of FAPI. For each compound, each row shows the measurements either using a thermal (a, c, e) or a cold (b, d, f) neutron instrument, with the exception of FAPI only using cold TAS (g). The energy resolution using TAS varies considerably with experimental conditions and the neutron energies. It is broader on thermal instrument (1–3 meV from 0 to 40 meV energy transfer) than on cold neutron instruments (0.2–0.4 meV from 0 to 15 meV energy transfer). The experimental TAS data (black scatter points) are fitted (full red line) with a sum of damped harmonic oscillators and are presented with a removed constant background. Individual fitted peaks are labelled (filled-coloured area). h Comparison of the Raman scattering responses above (170 K) and below (20 K) the orthorhombic–tetragonal transition. Error bars (sometimes smaller than the symbol size) represent one standard deviation.
Having said that, one observes that all phonon modes (or mode bundles) show little to no dispersion as shown by TOF in MAPI (Fig. 2b, c). The low-temperature TAS measurements along high symmetry directions (Γ → M or Γ → R) in MAPB, FAPB and FAPI show no dispersion either within a 0.1 meV error, and only the amplitudes of the modes vary (Fig. 2d–f). That shows that optical excitations are almost non-propagating as summarized in Fig. 4 for MAPB, suggesting a localized character in real space.
However, we need to temper this observation. Indeed, as pointed out in Supplementary Note 1, the neutron intensities correspond to the sum of coherent and incoherent cross-sections. In case of incoherent scattering, the phonon momentum information is lost. As hydrogen atom has a large incoherent scattering length, the phonon peaks involving hydrogen would roughly correspond to the incoherent cross-section. In contrast, the phonon peaks from the PbX3 cage are related to the coherent cross-section, which typically corresponds to the lowest energy bundle a (as discussed below) showing as well no dispersion (see e.g. the TOF data in MAPI, Fig. 2b). Furthermore, even for incoherent scattering, some information can be obtained from the sharpness of the measured peaks. Energy resolution-limited peaks, as we observed for MA-based HOP, can only be accounted for by dispersionless phonons even for incoherent scattering. It is interesting to compare our data with the neutron scattering studies of HOP powder samples where the q dependence is also lost by averaging over all orientational directions. It appears that the powder sample spectra of MAPB52 and MAPI53 also show sharp phonon modes at the same energy than in our experiments, suggesting once more the dispersionless nature of these phonon modes. The neutron powder sample spectrum observed in MAPbCl3 (ref. 53) does not show any sharp features in clear contrast with MAPI, suggesting again that optical phonons exhibit no dispersion in MA-based HOPs.
It should be further stressed that the lowest energy mode at 5 meV in MAPB52 is found at the same position in protonated and deuterated samples, showing that it is not related to a molecular vibration. The lowest energy mode is therefore necessarily associated to the coherent neutron cross-section, corroborating the lack of dispersion in MA-based HOPs of the lowest frequency modes. In contrast, the observation of broader phonons modes in FA-based HOPs (see below) may question the dispersionless nature in FAPB and FAPI (for instance, the modes above ~7 meV in Fig. 3e–g involving molecular vibrations). Indeed, the origin of broader phonon peaks can be either due to a larger damping or related to moderately dispersive phonons in FA-based HOP.
The observation of dispersionless phonon is opposed to what has been previously predicted using density functional perturbation theory in the frozen-phonon approximation in MA-based HOPs25,45, where dispersive phonon branches were computed. It is worth to emphasize that this lack of dispersion concerns both longitudinal and transverse optical phonons. For FA-based HOP, due to the large broadening still observed at low temperature, slight phonon dispersion associated to crossing of branches inside the three bundles cannot be completely ruled out.
Raman scattering spectroscopy has been performed as well in the MAPB single crystal as a control experiment (see Methods). Figure 5 shows the comparison of the low-temperature (20 K) spectra of MAPB, between INS on a thermal instrument and Raman scattering (that agrees with a previous Raman scattering report54). Raman spectra are recorded at very low q, whereas the INS experiments are measured at a Bragg peak position Q = (0, 0, 2), both are therefore probing optical phonons at the Γ point in the Brillouin zone. The energy positions of the optical phonon modes here identified from INS and Raman are consistent, especially the Raman mode bundles around 5, 12 and 18 meV (inset). However, the modes below 9 meV are significantly broader and less intense in INS than in Raman scattering. This may be attributed to a poorer energy resolution in INS for thermal TAS (1–2 meV) as compared to Raman (0.125 meV) as well as to the different scattering efficiency between both techniques. Figure 2 shows as well that each optical phonon mode can be defined by almost the same energy for any Q-point of the Brillouin zone, although mode broadening related to instrumental resolution is more important for neutron scattering than for Raman scattering.
Comparison of the triple-axis spectrometer (TAS) neutron data using the thermal beam instrument 1T (5 K) and Raman scattering (20 K) optical phonon spectra in MAPB, at the Γ point (≡ (0, 0, 2) Bragg position for neutron data). Inset shows a magnification of the Raman scattering spectra in the 10–20 meV range. The energy resolution of Raman scattering is here 0.125 meV compared to the energy resolution of ~ 1–2 meV for a thermal TAS. Error bars (smaller than the symbol size) represent one standard deviation.
Optical phonons in the orthorhombic phase
Systematic low-temperature INS experiments were performed with medium- and high-energy resolutions from, respectively, thermal and cold beams (see Methods). The optical phonon spectra (obtained at either the M point or R point) for all four compounds are presented in Fig. 3. Each compound studied undergoes structural distortions at low temperature, giving rise to atomic superstructures at either or both the M and R points. At low temperature, phonon spectra have been recorded at both momentum points. As no noticeable difference can be observed between these spectra (related to the lack of dispersion of the phonon modes), we here report the phonon spectrum measured at the R point for most compounds, except for FAPB, where it is shown at the M point (see also Supplementary Fig. 3). As already stated, a series of prominent optical phonon bundles of modes are observed at different energy ranges. Each phonon mode is usually accounted for by a DHO. Therefore, a model with a sum of DHOs convoluted by the spectrometer energy resolution is used to describe the neutron spectra, including a constant background (see Methods). The neutron spectra of Fig. 3 have been fitted using Eq. (1) and the obtained phonon energies are summarized in Table 1.
For a first analysis, we define three energy ranges where the different optical modes are located. These modes have been arbitrarily labelled as low (2–10 meV), medium (10–20 meV) and high (>20 meV). More specifically, in MAPB we find a low-energy mode at 5 meV; an intense peak at 11.6 meV followed by two smaller shoulders at 13.5 and 16.9 meV; and relatively broader bands at 23.2, 27.2 and 36.6 meV (Fig. 3a, b). These results match well with a previous INS experiment on an MAPB powder sample52.
Similarly in MAPI, we obtained two low-energy modes located at 2.3 and 3.8 meV, an intense peak centred at 11.7 meV surrounded by two smaller shoulders at 10.8 and 12.8 meV followed by two bundles at 15.5 and 18.3 meV and at higher energy range, other ones at 23.5, 28.5 and 38.3 meV (Fig. 3c, d). These again are directly comparable with previous INS studies50,55 where two additional small modes in the 2–5 meV range (~3.1 and ~4.3 meV) were reported.
In FAPB, we note a broader central feature dominating the medium-energy range (Fig. 3e, f), while three distinct bundles can be identified at 5.5, 13.1 and 22.2 meV. These results on FAPB are in line with the ones observed in MAPB, although much broader phonon bundles are systematically observed in FAPB compared to the more numerous (and narrower) modes that appear for MAPB. These two compounds share the same space group (Pnma) at low temperature although the static structural distortions characteristic of the orthorhombic phase are smaller in FAPB26. This may be connected to a different dynamics of the FA cation and its coupling to the perovskite lattice, by comparison to the MA cation (vide infra)47.
Finally, in FAPI—a sample requiring specific procedures and a proper storage to avoid the transformation to its yellow non-perovskite δ-phase at high temperature before cooling56 and, therefore, scarcely studied at such a low temperature in the literature—we could only perform measurements on the 4F2 cold neutron spectrometer (Fig. 3g). Nevertheless, in the accessible energy range, we detect large optical phonons at 3.9, 9.8 and ~5.1 meV. PL studies on single CQDs20 have identified exciton side-bands at 3.2, 7.8 and 15.4 meV, which match rather well with our TAS results on FAPI. The intermediate mode seemingly exhibits a slight discrepancy, but as reported in ref. 20, it undergoes temporal fluctuations under high-energy excitation, and is roughly spread between 7.5 and 12.5 meV. Again, our TAS results on FAPI show a significantly broad profile, as in FAPB.
According to nuclear magnetic resonance (NMR) measurements57, the broader nature of the optical modes of FA-based compounds, compared to their MA-based counterparts, may be attributed to the fact that the FA reorientation in FA-containing materials is faster than that of MA in the MA-based perovskite, despite the fact that FA is larger than MA. This has an impact on the charge carriers lifetime in these compounds. In addition, the acoustic density of states is located at lower energy in FA-based compounds as compared to the MA based19, thus leading to enhanced scattering between acoustic and optical phonons and related increased anharmonicity.
In Fig. 3h we further compare Raman scattering spectra in MAPB, above and below the orthorhombic to tetragonal first-order transition ~50 K. When passing the phase transition and on cooling down to 20 K one notices a considerable narrowing of the phonons lines below 10 meV, while higher-frequency vibrations evolve much more smoothly and continuously. Furthermore, phonon modes are split at low temperature below 10 meV (Fig. 5). These additional Raman scattering modes (listed in Table 1) result from the band folding in the low-temperature phase, induced by the structural distortion caused by the phase transition.
Overall, a commonality between the different perovskite systems has now been identified. By cross-referencing our results with the above-mentioned previous works and other literature on the subject, we can assign the identified features of the low-temperature spectra to the respective vibrational modes. In recent lattice dynamics calculations, Ponce et al.58 predict five modes for MAPI at 3, 4.3, 10.2, 14.4 and 21 meV. A-site displacement (i.e. rattling of the organic molecule within the cage) is said to be responsible for the peak at 10.2 meV, while scattering at 21 meV results from libration motions of the organic cations. On the other hand, the modes at 3, 4.3 and 14.4 meV are claimed to be related to the inorganic sub-lattice and arise from the rocking, bending and stretching motions of the PbI3 network, respectively, the latter one involving hybridization with organic cation motions. The calculated modes match well with our measurements and previous INS studies50,53,55 and the identifications made based on associated density functional theory (DFT) calculations55.
Regarding MAPB, one is compelled to draw parallel conclusions with those made about MAPI. Besides, in the work by Swainson et al.52 on MAPB, the 5 meV mode is again associated to vibrations of the PbX3 network. Furthermore, their comparative study between non-deuterated and deuterated samples clearly evidenced the influence of the organic cation motions on the modes at 11.5 and 13.7 meV.
In the PL study on FAPI CQDs20, the authors compared their study with the theoretical predictions and near-infrared spectroscopic measurements on MAPI59 and, as a result, ascribe the observed side-bands to LO phonon modes related to bending (3.5 meV) and stretching (15 meV) motion of the PbI3 cage, and to rigid-body motions of FA cations (11 meV).
As far as the mode at ~37 meV is concerned, there is a consensus that it originates from organic molecular vibrations55,60,61, although there is a debate about the exact nature of the involved atomic motions. Park et al.60 describe MA vibrations involving MA wagging, MA rotation and MA–MA stretch. Quarti et al.61, as well as Drużbicki et al.55, suggest a torsional MA vibration (also called disrotatory vibrations) that involves the terminal NH3 and CH3 moieties, which is also in line with the vibrational mode found near 300 cm−1 (i.e. 37.2 meV) in isolated MA calculations61,62.
Anharmonic behaviour of lattice dynamics
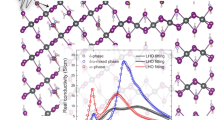
As mentioned above, anharmonicity of the hybrid halide perovskite lattice is expected to play a considerable role in electron–phonon interactions. In Fig. 6 we show the temperature behaviour of the INS optical phonon spectra of the four compounds, up to 120 K. The anharmonicity manifests already at low temperatures well below RT, where optoelectronic devices and solar cells are usually operating. The increased phonon damping is observed in Fig. 6 above ~30 K, together with an increase of the low-energy quasielastic signal and a reduced phonon intensity. The weaker phonon intensity upon warming corresponds to a decrease of the phonon Debye–Waller factor, meaning the increase of atomic mean displacements. However, consistent DHO fitting of the temperature data has also proven difficult due to the strong anharmonic behaviour. These effects lead to a rather quick overdamping of certain phonon modes at temperatures as low as 80 K, making it difficult to properly assign the exact contribution of each phonon mode to the overall spectra at higher temperatures.
Optical phonon spectra as a function of temperature, at the R point of a MAPI, b MAPB, c FAPI and d at the M point of FAPB. Measurements in c were performed on a cold neutron source, hence the difference in energy range, as compared to the a, b and d scans (thermal instrument). Error bars (sometimes smaller than the symbol size) represent one standard deviation.
Discussion
The low-temperature INS (and Raman) optical phonon spectra in our four HOP single crystals reveal a number of characteristic features down to very low energy. It is now accepted that carriers scattering in HOPs is dominated by Fröhlich coupling between charge carriers and optical phonon modes. This phonon scattering is believed to be the key fundamental factor in establishing the intrinsic limit of the charge carriers mobility. More specifically, it has been recently suggested that this limit is set by the lower-energy LO modes (3–20 meV)58. Therefore, the observed presence of such modes, common in all four compounds, seems to be the reason for the relatively low mobilities compared to classical inorganic semiconductors like Si and GaAs. Nevertheless, our experimental study clearly indicates that a missing ingredient of current attempt to reproduce the observed temperature dependence of charge carriers mobilities in HOPs is related to the underlying harmonic or quasi-harmonic assumptions of phonon modelling. Defining optical phonons as well-defined quasi-particles above 80–100 K is actually questionnable according to the present experimental observations. Therefore, the apparent discrepancy between the experimental acoustic-like temperature dependence of carriers mobilities and the expected dominant process (Fröhlich interaction) may be an unexpected consequence of the HOPs lattice softness.
Three different energy ranges have been identified in the spectra and gathered the modes or bundles of modes for each compound in three categories (a, b and c), as can be seen in Fig. 3. The following conclusions are drawn from our experimental data and based on earlier literature. Modes in the low-energy range (below 10 meV) are associated with vibrations of the PbX3 network, mainly rocking and bending. As for the intermediate energy range, between 10 and 20 meV, a series of mutually coupled modes are observed which arise from both the organic and inorganic sub-lattices and, therefore, show a highly hybridized nature. Here, a prominent feature is the stretching of PbX3, which is predicted to be coupled with the organic sub-lattice. An additional proof of this coupling comes from the comparison between non-deuterated and deuterated samples52. This further corroborates the increased broadening observed in FA-based systems, especially in this medium-energy range. This enhanced broadening is consistent with the difference in the dynamics of the FA and MA cations previously reported by NMR57, and molecular dynamics simulations47. It has also been shown by PL studies that the phase transition down to the lowest temperature is much smoother (weaker distortion) in FA-based compounds26,31 than in MA-based ones63. However, it should be stressed that the broadening in the FA compounds can be affected by the possible dispersion of bundles b and c due to the incoherent nature of these peaks in INS experiments. Also, still for the bundle b, a phonon related to the A-site displacement is identified at least in MAPI. Above 20 meV, optical features are essentially a result of molecular motions, although there could be some inorganic contributions to the cation librations of bundle c, at least for MA-containing perovskites. Meanwhile, direct comparison between the MAPB and FAPB spectra leads us to believe that the same mechanisms are possibly at play in the latter. It is apparent that in FA-based compounds there is significantly more contribution stemming from the coupling between inorganic and organic sub-lattices, as a result of the more hybridized nature of the lowest energy modes.
In Fig. 7, the relative energy shifts of the labelled phonon bundles, between the four compounds, is presented. One can see that the low-energy bundles a have lower energy in compounds that contain I− as opposed to Br−. Likewise, there is a significant decrease in energy in the medium/high-energy bundles when coming from MA-based compounds to FA ones. Reminding that the phonon energy is generally proportional to the square root of the inverse of atomic mass (E \(\sim 1/\sqrt{M}\)) and that FA+ and I− are heavier than MA+ and Br−, respectively, we can conclude that such trends agree with the attribution regarding the origin of the respective modes (see Supplementary Note 2). Actually, the relative shifts observed here, i.e., lower energy in FA+ and I− based compounds when comparing with MA+ and Br−, are also consistent with the smaller elastic constants obtained in our previous INS study19.
In 3D hybrid peroskites, substantial interactions between the organic and Pb-halogen neighbouring networks are typically expected; however, besides being located in low-energy range, the optical lattice excitations measured here appear to be basically non-propagating (Figs. 2 and 4), exhibiting nearly no dispersion in the Brillouin zone, and thus contradicting existing reports on phonon simulations based on the harmonic approximation. Similarly to phonon modes in thermoelectric clathrates 64, strong anharmonic phonon–phonon scattering processes may lead to a series of anticrossings flattening phonons dispersions. For instance, this strong hybridization between phonons would typically involve rattling of the organic molecule within the PbX cage. Furthermore, rattling phonon modes are generally associated with anharmonicity and lower thermal conductivities65,66 as it has been discussed through a crystal–liquid duality of HOPs67.
While the anharmonicity of halide perovskites leads to low-frequency acoustic phonons, characteristic of a soft lattice19, it occurs for optical phonons through an overdamped behaviour over the entire Brillouin zone at RT, and weakly dispersing branches at low temperature. The overriding anharmonic character of optical phonons specific to halide perovskites is most probably an important missing link for a proper account of the leading Fröhlich carrier–phonon interaction for this class of soft semiconductors. The size of the cation and the nature of the halogen are additional features known to strongly influence the softness of the lattice19. They also have a direct impact on the damping of the optical modes. Therefore, this suggests that the coupling between acoustic and optical phonons may play a role in the harmonicity of the lattice, besides non-linear coupling between optical phonons.
The lack of dispersion of such low optical modes overlapping with the upper part of the acoustic phonon dispersions is expected to be at the origin of several specific physical properties of HOPs. We first note a significant anharmonic behaviour that manifests itself in phonon overdamping at temperatures well below the ones used for operating optoelectronic devices and solar cells. Therefore, the current modelling of charge carriers mobilities based on a quasi-particle picture for low-energy optical lattice modes is questionable. Together with an apparent correlation between lattices softness (i.e. elastic constants) and optical phonon energy/frequency, our results point to the influence of acoustic and optical phonon coupling on the harmonicity of the lattice and the Fröhlich interaction between charge carriers and optical phonons. Moreover, this coupling occurs as well in the anharmonicity of the upper part of the acoustic phonon branches.
In conclusion, we present here an extensive comparison of optical phonon excitations in four different HOP compounds. INS and complementary Raman scattering measurements revealed various features of the low-temperature phonon spectra, which we have assigned to possible structural vibrations. The dispersionless nature of these optical modes is a first characteristic feature of HOPs. The optical phonons overdamping upon warming for temperatures as low as ~80 K demonstrate the strong anharmonicity in these materials. We believe that the following experimental report could serve as a solid base in future theoretical calculations and modelling for improved mode assignment and understanding of the electron–phonon interactions, especially for FA-based compounds where measurements of their optical phonon spectrum have been lacking.
Methods
Sample preparation
Single crystals of four different hybrid lead halide perovskites have been grown by the inverse temperature crystallization method (see Supplementary Note 3). The perovskite compounds are MAPbBr3 (MAPB), FAPbBr3 (FAPB), MAPbI3 (MAPI), and α-FAPbI3 (FAPI). MA and FA stand for MA and FA molecules, respectively. All single crystals of typical size of 200 mm3 for all compounds (except for FAPI where only a volume of ~50 mm3 could be achieved) were synthesized at the Institut des Sciences Chimiques de Rennes (ISCR).
INS spectroscopy
INS measurements were conducted using both triple-axis spectrometers (TAS) and time-of-flight spectrometers (TOF). On all TAS instruments, monochromators and analysers were made from the 002 reflection of pyrolithic graphite (PG). Cold (below ~15 meV) and thermal TAS have been used to cover the full energy range of the phonon spectrum in the three hybrid lead halide perovskites, MAPI, MAPB and FAPB. On 4F1/4F2 and IN12 TAS located (on cold neutron sources), respectively, at the reactor Orphée/Laboratoire Léon Brillouin (LLB), in CEA Saclay and at the Institut Laue-Langevin (ILL) in Grenoble, a constant final neutron wave vector of kf = 1.55 Å−1 was utilized with a beryllium (Be) filter to remove high-order neutrons in the beam. In addition for the measurement on IN12, a velocity selector was used to remove neutrons with high-order harmonics from the incident beam. At the thermal TAS 1T at LLB, a constant final neutron wave vector of kf = 2.662 Å−1 was used with a pyrolytic graphite filter to remove neutrons with high-order harmonics. The energy resolution of cold TAS goes from ~0.2 to 0.4 meV for an energy transfer ranging from 0 to 15 meV, while for the thermal TAS (1T) it goes from ~1 to 3 meV for an energy transfer ranging from 0 to 40 meV.
In MAPI, mapping of the phonon spectrum has been performed using the TOF instrument IN5 at the Institut Laue-Langevin (ILL) in Grenoble with an incident neutron wavelength of λ = 2 Å (≡3.14 Å−1), corresponding to an energy resolution which varies from 1.15 meV at elastic position to 0.8 meV at 15 meV energy transfer. The four-dimension S(q, ω) data measured on IN5 were reduced and visualized using the Horace software suite. Cuts shown in Fig. 2a–c were made along [hh2] direction, with an integration over −0.1 < l < 0.1 (i.e. [002+l]) and −0.1 < η < 0.1 in [η, −η, 0].
All samples have been attached to the cold head of the cryogenerator at LLB or a cryostat at ILL, reaching a low temperature of 5 K where all these HOPs are in the orthorhombic phase. However, throughout the present manuscript, the Miller indices refer to the high-temperature cubic phase of the perovskite lattice. Samples were mounted in a scattering plane such that the high symmetry reciprocal directions [001] and [110] were within the horizontal plane, except for FAPB which mounted with directions [100] and [010] within the horizontal scattering plane. When necessary, goniometers were used to reach out-of-plane momentum position. It should be stressed that MA and FA molecules were not deuterated giving rise to a large incoherent neutron scattering from the various hydrogen atoms from the organic part of the compounds. The fact that the samples are fixed onto a vanadium sheet also results in additional incoherent elastic scattering.
Raman scattering spectroscopy
Raman scattering in MAPB has been performed under an optical microscope and a T64000 Jobin-Yvon double pass diffractometer working with 18000 trts/mm gratings. The radiation of a krypton laser emitting at 647 nm was tightly focused into the sample with a ×100 objective. In order to avoid photo-induced effects, the incident power was always kept lower than 2 mW. The spectra have been obtained in the backscattering geometry with the incident light parallel to the [001]-cubic crystallographic direction of the sample. The incident polarization was parallel to the [110] direction and the results shown in Figs. 2 and 3 of the main text correspond to the polarized spectra (i.e. scattered light // [1\(\overline{1}\)0]).
Experimental data fitting
The experimental TAS spectra can be described by a sum of phonon terms on top of a flat background (BG). Each phonon is typically accounted for by a DHO68. The neutron spectra can then be described by the following expression:
where ωj represents the energy, Γj the damping and Fj(Q) is the dynamical structure factor of the jth phonon. The number of mode depends on how many peaks are visible. The prefactor of DHOs is the phonon population factor. This full scattering function, I(Q, ω), is next convoluted by the 4D spectrometer resolution function of the instrument as explained in ref. 68, and used to fit the experimental data. The presence of several phonon lines in a given phonon bundle would have the effect to increase the damping when fitted by a DHO due to the energy resolution function.
Data availability
Data collected on IN12 and IN5 are available at https://doi.org/10.5291/ILL-DATA.7-02-172 and https://doi.org/10.5291/ILL-DATA.TEST-2912, respectively. The rest of the data that support the findings of this study is available from the corresponding authors upon request.
References
Correa-Baena, J.-P. et al. Promises and challenges of perovskite solar cells. Science 358, 739–744 (2017).
Snaith, H. J. Present status and future prospects of perovskite photovoltaics. Nat. Mater. 17, 372–376 (2018).
Jena, A. K., Kulkarni, A. & Miyasaka, T. Halide perovskite photovoltaics: background, status, and future prospects. Chem. Rev. 119, 3036–3103 (2019).
Yang, W. S. et al. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 348, 1234–1237 (2015).
Anaraki, E. H. et al. Highly efficient and stable planar perovskite solar cells by solution-processed tin oxide. Energy Environ. Sci. 9, 3128–3134 (2016).
Tan, H. et al. Efficient and stable solution-processed planar perovskite solar cells via contact passivation. Science 355, 722–726 (2017).
Kojima, A., Teshima, K., Shirai, Y. & Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 131, 6050–6051 (2009).
Extance, A. The reality behind solar poweras next star material. Nature 570, 429–432 (2019).
Yuan, Z. et al. One-dimensional organic lead halide perovskites with efficient bluish white-light emission. Nat. Commun. 8, 14051 (2017).
Akkerman, Q. A., Rainò, G., Kovalenko, M. V. & Manna, L. Genesis, challenges and opportunities for colloidal lead halide perovskite nanocrystals. Nat. Mater. 17, 394–405 (2018).
Smith, M. D., Connor, B. A. & Karunadasa, H. I. Tuning the luminescence of layered halide perovskites. Chem. Rev. 119, 3104–3139 (2019).
Fu, Y. et al. Metal halide perovskite nanostructures for optoelectronic applications and the study of physical properties. Nat. Rev. Mater. 4, 169–188 (2019).
Wright, A. D. et al. Electron-phonon coupling in hybrid lead halide perovskites. Nat. Commun. 7, 11755 (2016).
Chen, Y. et al. Extended carrier lifetimes and diffusion in hybrid perovskites revealed by Hall effect and photoconductivity measurements. Nat. Commun. 7, 12253 (2016).
Even, J. et al. in Physics, Simulation, and Photonic Engineering of Photovoltaic Devices V (eds Freundlich, A., Lombez, L. & Sugiyama, M.) Vol. 9743, 78–85 (International Society for Optics and Photonics, SPIE, 2016).
Miyata, K. et al. Large polarons in lead halide perovskites. Sci. Adv. 3, e1701217 (2017).
Katan, C., Mohite, A. & Even, J. Entropy in halide perovskites. Nat. Mater. 17, 377–379 (2018).
Létoublon, A. et al. Elastic constants, optical phonons, and molecular relaxations in the high temperature plastic phase of the CH3NH3PbBr3 hybrid perovskite. J. Phys. Chem. Lett. 7, 3776–3784 (2016).
Ferreira, A. et al. Elastic softness of hybrid lead halide perovskites. Phys. Rev. Lett. 121, 085502 (2018).
Fu, M. et al. Unraveling exciton-phonon coupling in individual FAPbI3 nanocrystals emitting near-infrared single photons. Nat. Commun. 9, 3318 (2018).
Tamarat, P. et al. The ground exciton state of formamidinium lead bromide perovskite nanocrystals is a singlet dark state. Nat. Mater. 18, 717–724 (2019).
Becker, M. A. et al. Bright triplet excitons in caesium lead halide perovskites. Nature 553, 189–193 (2018).
Li, M., Fu, J., Xu, Q. & Sum, T. C. Slow hot-carrier cooling in halide perovskites: prospects for hot-carrier solar cells. Adv. Mater. 31, 1802486 (2019).
Yang, Y. et al. Observation of a hot-phonon bottleneck in lead-iodide perovskites. Nat. Photonics 10, 53–59 (2015).
Yang, J. et al. Acoustic-optical phonon up-conversion and hot-phonon bottleneck in lead-halide perovskites. Nat. Commun. 8, 14120 (2017).
Schueller, E. C. et al. Crystal structure evolution and notable thermal expansion in hybrid perovskites formamidinium tin iodide and formamidinium lead bromide. Inorg. Chem. 57, 695–701 (2017).
Onoda-Yamamuro, N., Matsuo, T. & Suga, H. Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenoplumbates (II). J. Phys. Chem. Solids 51, 1383–1395 (1990).
Swainson, I., Hammond, R., Soullière, C., Knop, O. & Massa, W. Phase transitions in the perovskite methylammonium lead bromide, CH3ND3PbBr3. J. Solid State Chem. 176, 97–104 (2003).
Stoumpos, C. C., Malliakas, C. D. & Kanatzidis, M. G. Semiconducting tin and lead iodide perovskites with organic cations: phase transitions, high mobilities, and near-infrared photoluminescent properties. Inorg. Chem. 52, 9019–9038 (2013).
Baikie, T. et al. A combined single crystal neutron/x-ray diffraction and solid-state nuclear magnetic resonance study of the hybrid perovskites CH3NH3PbX3 (X = I, Br and Cl). J. Mater. Chem. A 3, 9298–9307 (2015).
Fang, H.-H. et al. Photoexcitation dynamics in solution-processed formamidinium lead iodide perovskite thin films for solar cell applications. Light Sci. Appl 5, e16056 (2015).
O’Leary, G. P. & Wheeler, R. G. Phase transitions and soft librational modes in cubic crystals. Phys. Rev. B 1, 4409–4439 (1970).
Glazer, A. M. The classification of tilted octahedra in perovskites. Acta Cryst. B 28, 3384–3392 (1972).
Swanson, B. I. Displacive phase transformations in K2SnBr6. Phys. Stat. Sol. (A) 47, K95–K98 (1978).
Benedek, N. A. & Fennie, C. J. Why are there so few perovskite ferroelectrics? J. Phys. Chem. C 117, 13339–13349 (2013).
Beecher, A. N. et al. Direct observation of dynamic symmetry breaking above room temperature in methylammonium lead iodide perovskite. ACS Energy Lett. 1, 880–887 (2016).
Borriello, I., Cantele, G. & Ninno, D. Ab initioinvestigation of hybrid organic-inorganic perovskites based on tin halides. Phys. Rev. B 77, 235214 (2008).
Even, J., Pedesseau, L., Jancu, J.-M. & Katan, C. Importance of spin-orbit coupling in hybrid organic/inorganic perovskites for photovoltaic applications. J. Phys. Chem. Lett. 4, 2999–3005 (2013).
Filip, M. R., Eperon, G. E., Snaith, H. J. & Giustino, F. Steric engineering of metal-halide perovskites with tunable optical band gaps. Nat. Commun. 5, 5757 (2014).
Saliba, M. et al. Incorporation of rubidium cations into perovskite solar cells improves photovoltaic performance. Science 354, 206–209 (2016).
Yin, W.-J., Shi, T. & Yan, Y. Unusual defect physics in CH3NH3PbI3 perovskite solar cell absorber. Appl. Phys. Lett. 104, 063903 (2014).
Quarti, C., Mosconi, E. & Angelis, F. D. Interplay of orientational order and electronic structure in methylammonium lead iodide: implications for solar cell operation. Chem. Mater. 26, 6557–6569 (2014).
Li, X. et al. Improved performance and stability of perovskite solar cells by crystal crosslinking with alkylphosphonic acid ω -ammonium chlorides. Nat. Chem. 7, 703–711 (2015).
Park, M. et al. Critical role of methylammonium librational motion in methylammonium lead iodide (CH3NH3PbI3) perovskite photochemistry. Nano Lett. 17, 4151–4157 (2017).
Comin, R. et al. Lattice dynamics and the nature of structural transitions in organolead halide perovskites. Phys. Rev. B 94, 094301 (2016).
Marronnier, A. et al. Anharmonicity and disorder in the black phases of cesium lead iodide used for stable inorganic perovskite solar cells. ACS Nano 12, 3477–3486 (2018).
Carignano, M. A., Aravindh, S. A., Roqan, I. S., Even, J. & Katan, C. Critical fluctuations and anharmonicity in lead iodide perovskites from molecular dynamics supercell simulations. J. Phys. Chem. C 121, 20729–20738 (2017).
Gold-Parker, A. et al. Acoustic phonon lifetimes limit thermal transport in methylammonium lead iodide. Proc. Natl Acad. Sci. USA 115, 11905–11910 (2018).
Songvilay, M. et al. Lifetime shortened acoustic phonons and static order at the brillouin zone boundary in the organic-inorganic perovskite CH3NH3PbCl3. Phys. Rev. Mater. 2, 123601 (2018).
Li, B. et al. Polar rotor scattering as atomic-level origin of low mobility and thermal conductivity of perovskite CH3NH3PbI3. Nat. Commun. 8, 16086 (2017).
Yaffe, O. et al. Local polar fluctuations in lead halide perovskite crystals. Phys. Rev. Lett. 118, 136001 (2017).
Swainson, I. P. et al. From soft harmonic phonons to fast relaxational dynamics in CH3NH3PbBr3. Phys. Rev. B 92, 100303(R) (2015).
Schuck, G., Lehmann, F., Ollivier, J., Mutka, H. & Schorr, S. Influence of chloride substitution on the rotational dynamics of methylammonium in MAPbI3−x Clx perovskites. J. Phys. Chem. C 213, 11436–11446 (2019).
Guo, Y. et al. Polar rotor scattering as atomic-level origin of low mobility and thermal conductivity of perovskite CH3NH3PbI3. Nat. Commun. 10, 1175 (2019).
Drużbicki, K. et al. Unexpected cation dynamics in the low-temperature phase of methylammonium lead iodide: the need for improved models. J. Phys. Chem. Lett. 7, 4701–4709 (2016).
Zhumekenov, A. A. et al. Formamidinium lead halide perovskite crystals with unprecedented long carrier dynamics and diffusion length. ACS Energy Lett. 1, 32–37 (2016).
Kubicki, D. J. et al. Cation dynamics in mixed-cation (MA)x(FA)1−xPbI3 hybrid perovskites from solid-state NMR. J. Am. Chem. Soc. 139, 10055–10061 (2017).
Poncé, S., Schlipf, M. & Giustino, F. Origin of low carrier mobilities in halide perovskites. ACS Energy Lett. 4, 456–463 (2019).
Pérez-Osorio, M. A. et al. Vibrational properties of the organic-inorganic halide perovskite CH3NH3PbI3 from theory and experiment: factor group analysis, first-principles calculations, and low-temperature infrared spectra. J. Phys. Chem. C 119, 25703–25718 (2015).
Park, B. et al. Resonance raman and excitation energy dependent charge transfer mechanism in halide-substituted hybrid perovskite solar cells. ACS Nano 9, 2088–2101 (2015).
Quarti, C. et al. The raman spectrum of the CH3NH3PbI3 hybrid perovskite: interplay of theory and experiment. J. Phys. Chem. Lett. 5, 279–284 (2013).
Zhou, L. et al. Density of states broadening in CH3NH3PbI3 hybrid perovskites understood from ab initio molecular dynamics simulations. ACS Energy Lett. 3, 787–793 (2018).
Fang, H.-H. et al. Photophysics of organic-inorganic hybrid lead iodide perovskite single crystals. Adv. Funct. Mater. 25, 2378–2385 (2015).
Euchner, H. et al. Phononic filter effect of rattling phonons in the thermoelectric clathrate Ba8Ge40+xNi6+x. Phys. Rev. B 86, 224003 (2012).
Slack, G. A. CRC Handbook of Thermoelectrics (CRC Press, 1995).
Voneshen, D. J. et al. Suppression of thermal conductivity by rattling modes in thermoelectric sodium cobaltate. Nat. Mater. 12, 1028–1032 (2013).
Miyata, K., Atallah, T. L. & Zhu, X.-Y. Lead halide perovskites: crystal-liquid duality, phonon glass electron crystals, and large polaron formation. Sci. Adv. 3, e1701469 (2017).
Bourges, P. et al. Pretransitional dynamics of the structural phase transition in anthracene-TCNB: a comparison of Raman-scattering and inelastic-neutron-scattering experiments. Phys. Rev. B 54, 15002–15015 (1996).
Acknowledgements
This project has received funding from the European Union’s Horizon 2020 programme through a FET Open research and innovation action under the grant agreement No 687008. The open access fee was covered by FILL2030, a European Union project within the European Commission’s Horizon 2020 Research and Innovation programme under grant agreement No. 731096. J.E. is senior member of institut universitaire de France. We wish to thank Marc de Boissieu, Stéphane Pailhès and Yvan Sidis for stimulating discussions and Anna Bourges-Célaries for a proofreading of the manuscript.
Author information
Authors and Affiliations
Contributions
P.B., C.K. and J.E. conceived and supervised the project; A.C.F. and P.B. performed the INS experiments at LLB Saclay and ILL Grenoble with support from A.L.; S.R. and J.O. participated in the INS experiments at ILL as the local contacts for IN12 and IN5, respectively; A.C.F. and P.B. analysed the neutron data; B.H. and B.R. performed the Raman scattering experiments and analysed the Raman data; S.P. synthesized the perovskite single crystal samples with support from S.C.; J.E. contributed to the analysis and discussion of the results. A.C.F., P.B. and J.E. wrote the manuscript with further contributions from all authors. All authors contributed to this work, read the manuscript and agree to its contents.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferreira, A.C., Paofai, S., Létoublon, A. et al. Direct evidence of weakly dispersed and strongly anharmonic optical phonons in hybrid perovskites. Commun Phys 3, 48 (2020). https://doi.org/10.1038/s42005-020-0313-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0313-7
This article is cited by
-
Controlling the electro-optic response of a semiconducting perovskite coupled to a phonon-resonant cavity
Light: Science & Applications (2023)
-
Anharmonic electron-phonon coupling in ultrasoft and locally disordered perovskites
npj Computational Materials (2023)
-
Defect modeling and control in structurally and compositionally complex materials
Nature Computational Science (2023)
-
Electron-phonon interactions in halide perovskites
NPG Asia Materials (2022)
-
Exciton-acoustic phonon coupling revealed by resonant excitation of single perovskite nanocrystals
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.