Abstract
In developing technologies based on superconducting quantum circuits, the need to control and route heating is a significant challenge in the experimental realisation and operation of these devices. One of the more ubiquitous devices in the current quantum computing toolbox is the transmon-type superconducting quantum bit, embedded in a resonator-based architecture. In the study of heat transport in superconducting circuits, a versatile and sensitive thermometer is based on studying the tunnelling characteristics of superconducting probes weakly coupled to a normal-metal island. Here we show that by integrating superconducting quantum bit coupled to two superconducting resonators at different frequencies, each resonator terminated (and thermally populated) by such a mesoscopic thin film metal island, one can experimentally observe magnetic flux-tunable photonic heat rectification between 0 and 10%.
Similar content being viewed by others
Introduction
In miniaturising electrical devices down to nanoscales, heat transfer has not only turned into a serious obstacle, but also a potential resource for future developments in both convention and quantum computing architectures1,2,3. Controlling heat transport in superconducting circuits has thus received increasing attention in engineering microwave environments for circuit quantum electrodynamics (cQED)4,5,6 and circuit quantum thermodynamics (cQTD) experiments7,8. While theoretical proposals for cQTD devices are numerous9,10,11,12,13,14,15, the experimental situation is much less advanced. There exist only relatively few experimental realisations16,17, mostly due to the difficulties in developing the hybrid devices and in interfacing these often technologically contrasting components.
A rectifier is a device in which the transport is directionally impeded, optimally to allow it only in one direction. In the charge regime, the ubiquitous rectifier, or diode, is one of the most fundamental components in electronic circuits and can be realised relatively simplistically, for example, as a device exploiting the depletion zone between electrons and holes in a semiconductor p-type/n-type junction.
The implementation of devices for manipulating charge current is enabled by the discrete and polarised nature of the carrier and their interaction with electromagnetic fields. Heat currents do not have this quality, and manipulating their flow usually relies on precise control of the energy population distributions of the various materials involved in the device18,19,20. In the superconducting regime, it is provided by the superconducting/semiconducting gap in one direction and/or asymmetric couplings of the heat baths to quasiparticle heat carriers, for example, by using metals with differing electron–phonon couplings.
The two-level system of a transmon-type qubit coupled to two unequal resonators is a well-placed tool for studying asymmetric photonic heat transport, each element having engineered resonances and couplings to each other that can be designed for various modes of operation21,22. In particular, it represents a minimal set-up to explore, under well-controlled conditions, the subtle phenomenon of heat rectification, which requires both non-linearities and symmetry breaking23. Hence, we here demonstrate the realisation of a quantum heat rectifier, a thermal equivalent to the electronic diode, utilising a superconducting transmon qubit coupled to two strongly unequal resonators terminated by mesoscopic heat baths, and is the experimental realisation of the spin-boson rectifier proposed by Segal and Nitzan24.
Results
Rectification via an integrated superconducting circuit
By utilising a superconducting quantum interferometer (SQUID) as the non-linear element of the Transmon qubit, the Josephson energy \({E}_{{\rm{J}}}(\Phi )\simeq {E}_{{\rm{J}}0}\left|\cos (\pi \Phi /{\Phi }_{0})\right|\) can be tuned by an incident magnetic flux Φ. Here Φ0 = h/2e is the magnetic flux quantum. This in turn Allows one to control the excitation frequencies of the transmon determined by EJ(Φ) and the charging energy EC with the transition frequencies ωn,n+1 between levels n and n + 1 (n = 0, 1, 2, . . .) given by
where the plasma frequency \({\omega }_{{\rm{p}}}(\Phi )=\sqrt{8{E}_{{\rm{C}}}{E}_{{\rm{J}}}(\Phi )}/\hslash\). The n-dependence in Eq. (1) produces here the necessary non-linearity for rectification; this is the property that in fact makes the transmon a qubit in cQED applications. On the other hand, the symmetry breaking is due to the difference in effective qubit–bath couplings geff,1 and geff,2, via the left and right resonators of clearly different frequencies, ω1 < ω2, respectively. In extension to the set-up considered in ref. 24, here these couplings depend upon the spectral overlap between the corresponding resonator and the transmon and can be controlled by the applied flux25.
Assuming one of the temperatures is T = 1/(kBβ) > 0 and the other one to be equal to 0, or vice versa, the flux-dependent rectification ratio \({\mathcal{R}}\) of power Pi to bath i in the forwards (+) and backwards (−) direction23 is obtained in the two-level approximation for the transmon as
Any value \({\mathcal{R}} \, \ne \, 1\) corresponds to heat rectification while \({\mathcal{R}}=1\) describes completely symmetric heat flux. Note that in order to apply the expression for a bare two-level system to the current situation by introducing effective couplings, we assume that the resonator–bath couplings are sufficiently stronger than the qubit–resonator. By introducing the asymmetry in coupling factors δ = 1 − geff,1/geff,2, this expression can be simplified for ∣δ∣ ≪ 1 to read
A description of rectification in this model for a multi-level system is discussed in Supplementary Note 1.
Experimental realisation
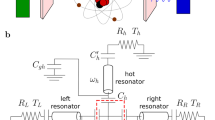
Figure 1 presents a diagram of the realised device, consisting of a transmon qubit coupled to two resonators, designed at 2.8 and 6.7 GHz frequencies, respectively. Each resonator is shunted at the current maximum with a copper thin-film resistor, shown in the left inset as a colourised scanning electron micrograph. This element provides the thermal bath, which is heated and measured by superconducting aluminium probes, grown using an electron beam evaporator with the Dolan bridge technique. The thin insulator is formed by the native oxide of aluminium, grown by an in situ oxidation prior to the deposition of the copper. The SQUID of the transmon qubit is shown on the right inset, utilising a similar fabrication procedure. A simple diagrammatic model for understanding the system is also presented, with the role of the resonator–qubit–resonator structure represented by a diode.
The sample consists of a centrally located Xmon-type superconducting qubit cross-coupled to two superconducting co-planar waveguide resonators at 2.8 and 6.7 GHz, respectively. Each resonator is terminated with a thin-film copper microstrip resistor, acting as a mesoscopic thermal bath, one of which shown in the left inset by a colourised scanning electron micrograph of the copper microstrip resistor (orange), with four superconducting aluminium probes (green) (separated from the copper by an insulator, not visible) for temperature control and readout, and two superconducting aluminium contacts to the co-planar waveguide resonator (blue). The superconducting quantum interferometer is shown similarly on the right inset. The topmost diagram represents a simple model of the system, with the resonator–qubit–resonator structure represented as a diode, and the forward and reverse directions drawn in purple and green, respectively. A third electrode can be seen on the Xmon island, which in non-dissipative variants of the device used for spectroscopy connects the Xmon to a readout resonator.
Owing to the definition of resistance being dissipative, normal metal baths used in this way as terminations to superconducting resonators lead to a substantial decrease in the quality factor of the resonator, from an intrinsic value in the range 104 to a value of order 10, as verified in the measurement in ref. 26. Lower resistance baths would result in higher-quality resonators with larger asymmetry in the qubit–resonator coupling, and thus stronger rectification, but at the expense of lower power transfer.
Temperature differences between the normal metal baths can be controllably achieved by local Joule heating of each bath independently, with the tendency to thermally populate their corresponding resonator. We define the “forward” to be the direction from the low frequency (2.8 GHz) to high frequency (6.7 GHz) resonator and declare the heated bath to be the source with the heat flowing to the target bath. Identical but opposite temperature bias can be applied in the “reverse” direction. The measured power on the target bath is shown in Fig. 2a for various source temperatures between 380 and 420 mK. The horizontal axis depicts the static magnetic flux Φ on the transmon qubit, normalised with respect to the flux quantum Φ0, applied to tune its transition frequency.
a Presented here is the power transmitted between the two baths at three voltage (heating) bias points, with the subplots corresponding to 420 mK (1000 fW), 400 mK (750 fW), and 380 mK (600 fW) source temperatures (powers), in descending order. The bath temperature is kept fixed at 150 mK. Purple is the forward direction, and green the reverse. b Flux-tunable rectification. Rectification ratio of traces from a, with the non-tunable contribution removed.
We observe qualitatively different magnetic flux dependences of the heat transport based on the directionality. Domains of strong differences between forward and backward heat transfer with pronounced sub-structures alternate with those of weak discrepancies and relatively smooth traces. To better understand this directionality, one can extract the rectification by extracting the ratio of transmitted power in the forward direction to the reverse direction, see Fig. 2b. The flux-tunable rectification is isolated by a subtraction of the non-tunable contribution \({{\mathcal{R}}}_{\min }\). The origin for non-zero \({{\mathcal{R}}}_{{\rm{min}}}\) is likely to originate from the uncertainty of the temperature bias, which we estimate to be ±5 mK. This can lead to shifts in the non-flux-dependent heat transport of up to 5 fW.
Apparently, rectification appears to be almost independent of applied power (temperature gradient) but strongly depending on magnetic flux. The first behaviour can be understood from the simple two-state model discussed above. Equation (3) tells us that changes in the rectification coefficient between two different temperature gradients T and T + ΔT with \(\frac{\Delta T}{T}\ll 1\) are suppressed at low temperatures, namely, \({\mathcal{R}}(T)/{\mathcal{R}}(T+\Delta T)\approx 1-\frac{\Delta T}{T}\ \delta \beta \hslash {\omega }_{01}{{\rm{e}}}^{-\beta \hslash {\omega }_{01}}\). This argument also applies to more complex structures. The flux dependence is directly related to the energy levels of the resonator–qubit–resonator compound. In case the resonator–bath coupling prevails against the resonator–qubit coupling, one could think of the resonators as spectral filters for the broadband reservoirs. The effective couplings introduced in Eq. (2) are then given by Lorentzians with maxima around the resonator frequencies ω1 < ω2 (given explicitly in Supplementary Note 2) containing the qubit–resonator couplings and the resonator–bath couplings. At zero flux, the high-frequency oscillator at 7 GHz is close to the transmon transition frequency at 7.2 GHz, while the low-frequency resonator at 2.8 GHz is then far de-tuned. Accordingly, we expect to see resonances in the effective coupling geff,2(Φ) symmetrically around zero flux (ω01 ≈ ω2) as well as for geff,1(Φ) symmetrically around Φ/Φ0 = 1/2 when ω01 ≈ ω1. Experimental spectra of the resonator–qubit–resonator structure in the absence of the resistors by a two-tone measurement are shown in Fig. 3. From the corresponding anti-crossings of the respective modes, we obtain the bare couplings between the resonators and the transmon to be on the same order of 50 MHz. The resonator–bath couplings are estimated from the quality factors of the resonators to be of order 10, based on measurements performed in ref. 26, i.e. on the order of 3 GHz. Given these experimental data, one finds that geff,1(Φ ≈ 0) ≪ geff,2(Φ/Φ0 ≈ 0.5) which implies that, according to Eq. (2), we expect to have pronounced resonances in the rectification coefficient located symmetrically around Φ/Φ0 ≈ 1/2 and much weaker resonances around Φ ≈ 0 (for more information, see Supplementary Note 2).
This readout is performed using a tertiary readout resonator coupled to a third electrode of the qubit. Here the copper terminations are not present. a We observe an anticrossing corresponding to the interaction with the high-frequency resonator at 7.05 GHz. b Qubit–resonator coupling at 5.5 GHz, corresponding to the second mode of the low-frequency resonator, and c qubit–resonator coupling at 2.75 GHz corresponding to the interaction with the first harmonic of the low-frequency resonator. We note, however, that there is broadening of these lines when the copper termination is present, as reported in ref. 26. d Calculated energy spectra. The parameters used are: EJ/h = 45 GHz and EC/h = 0.15 GHz, which give ω01(Φ = 0)/2π = 7.2 GHz.
Discussion
In order to achieve an accurate quantitative description, the effective two-level description must be extended to include the level structure of the entire compound (the level structure is described in Supplementary Note 3); corresponding results will be provided elsewhere. Nevertheless, the simple model already reveals the relevance of resonances in the nonlinear medium so that the variations of the rectification coefficient can also be understood as the opening and closing of photonic transfer channels by varying the magnetic flux.
We have in this experimental realisation of a quantum heat rectifier observed wireless flux-tunable heat rectification up to 10% via the photon channel in a superconducting artificial atom. This phenomenon arises due to anharmonicity of the system and its asymmetric coupling to two microwave resonators, thermally populated by mesoscopic resistive baths. The device can be integrated with existing superconducting circuit architectures, in particular with superconducting qubits and Josephson logic, with potential applications in directionally manipulating heat flow in superconducting devices, for example, in the fast initialisation of a qubit. In addition, this device may be used as a platform for exploring coherent caloritronics and the frontiers of quantum thermodynamics.
Methods
Fabrication protocols
These devices are fabricated on a high-resistivity silicon wafer, upon which a 20-nm-thick alumina film has been grown by atomic layer deposition, followed by a subsequently sputtered 200-nm-thick niobium film. Larger features, namely, the microwave resonators (measured spectroscopically at 2.8 and 6.7 GHz, see Fig. 1), transmon island, and superconducting probe fan-out are patterned by electron beam lithography and then transferred to the niobium by reactive ion etching utilising fluorine chemistry. The coplanar waveguide resonator has characteristic impedance 50 Ω, formed of a 20-μm-wide centreline spaced by 10 μm with respect to the ground plane. The tunnel junction elements in the superconducting probes and interferometer are also patterned by electron beam lithography, then transferred onto the wafer by physical vapour deposition of aluminium in an electron beam evaporator with an in situ oxidation step, resulting in a per junction resistance of 22 ± 3 and 6 ± 3 kΩ for the normal–insulator–superconductor probes and superconducting interferometer, respectively. To ensure sufficient contact between lithographic layers, specifically between the niobium and aluminium features, an in situ Ar ion plasma milling is performed before the aluminium deposition process step. After liftoff in acetone and cleaning in isopropyl alcohol, the substrates are diced to 7 × 7-mm size by diamond-embedded resin blade and wire-bonded to a custom-made brass stage.
Measurements
The measurements are performed in a custom-made plastic dilution refrigerator with the cooling stage set at 150 mK for these measurements. The bonded chip is enclosed by two brass Faraday shields and is readout at room temperature via 1 m of Thermocoax-filtered cryogenic lines, resulting in an effective signal bandwidth of 0–10 kHz, for low-impedance loads. The magnetic-flux tuning of the energy-level spacing of the transmon is achieved by a superconducting solenoid encompassing the entire sample stage assembly, inside of a high-permeability magnetic shield. It is mounted inside the refrigerator at a temperature of 4 K. Electronic characterisation is applied by programmable function generators at room temperature and measured by a low-noise amplification chain (room-temperature low-noise amplifiers FEMTO Messtechnik GmbH DLPVA-100) into a direct current (DC) multimeter (for DC measurements), and additionally into a lock-in amplifier synchronised to the square-wave modulation (22 Hz) of the voltage bias of the heated thermal reservoir, in the configuration shown in Fig. 4. By applying a current bias between the superconducting probes close to the superconducting energy gap, hot electrons from the normal metal can tunnel into the superconducting probes, and a voltage signal can be measured, with a well-characterised dependence on the temperature of the electrons in the metal in the range 100–500 mK, of interest to this experiment. By assuming that the heat is well localised owing to the near-perfect Andreev mirrors at the superconductor–normal metal interface and that the main relaxation channel for the heat is via the electron–phonon coupling, the power can be estimated by \({P}_{{\rm{el}}-{\rm{ph}}}=\Sigma {\mathcal{V}}({T}_{{\rm{el}}}^{5}-{T}_{{\rm{ph}}}^{5})\), where Σ is the material-dependent electron–phonon coupling constant, \({\mathcal{V}}\) is volume of the normal metal bath, and Tel and Tph correspond to the electron temperature and phonon temperature, respectively. As the experiment is performed under steady-state conditions, we can assume that the phonon temperature is in equilibrium with the cryostat base temperature, measured by a ruthenium oxide thermometer that has been calibrated against a Coulomb blockade thermometer. In addition, by voltage biasing the Superconductor-Insulator-Normal Metal-Insulator-Superconductor device structure sufficiently above the superconducting energy gap, Joule heating of the baths can be applied (for small voltage biasing below the gap, evaporative cooling can also occur). Hence, by utilising four superconducting probes, we can both engineer the temperature of the baths and measure this induced temperature in parallel27.
Data availability
The data that support the plots within this article are available from the corresponding author upon reasonable request.
References
Erdman, P. A. et al. Maximum power and corresponding efficiency for two-level quantum heat engines and refrigerators. New J. Phys. 21, 103049 (2019).
Menczel, P. et al. Two-stroke optimization scheme for mesoscopic refrigerators. Phys. Rev. B 99, 224306 (2019).
Karimi, B. & Pekola, J. P. Otto refrigerator based on a superconducting qubit: classical and quantum performance. Phys. Rev. B 94, 184503 (2016).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
Partanen, M. et al. Flux-tunable heat sink for quantum electric circuits. Sci. Rep. 8.1, 6325 (2018).
Tan, K. Y. et al. Quantum-circuit refrigerator. Nat. Commun. 8, 15189 (2017).
Pekola, J. P. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 11, 118 (2015).
Vinjanampathy, S. & Anders, J. Quantum thermodynamics. Contemp. Phys. 57, 545 (2016).
Martínez-Pérez, M. J. & Giazotto, F. The Josephson heat interferometer. Nature 492, 401 (2012).
Hwang, S. Y., Giazotto, F. & Sothmann, B. Phase-coherent heat circulator based on multiterminal Josephson junctions. Phys. Rev. Appl. 10, 044062 (2018).
Ordonez-Miranda, J. et al. Photonic thermal diode based on superconductors. J. Appl. Phs. 122, 093105 (2017).
Pereira, E. Thermal rectification in classical and quantum systems: searching for efficient thermal diodes. EPS 126, 1 (2019).
Barzanjeh, S., Aquilina, M. & Xuereb, A. Manipulating the flow of thermal noise in quantum devices. Phys. Rev. Lett. 120, 060601 (2018).
Li, B. Negative differential thermal resistance and thermal transistor. Appl. Phys. Lett. 88, 143501 (2006).
Kosloff, R. & Levy, A. Quantum heat engines and refrigerators: continuous devices. Annu. Rev. Phys. Chem. 65, 365 (2014).
Ronzani, A. et al. Tunable photonic heat transport in a quantum heat valve. Nat. Phys. 14, 991–995 (2018).
Roßnagel, J. et al. Single atom heat engine. Science 352, 325 (2016).
Chang, C. W. et al. Solid-state thermal rectifier. Science 314, 1121 (2006).
Martínez-Pérez, M. J., Fornieri, A. & Giazotto, F. Rectification of electronic heat current by a hybrid thermal diode. Nature Nanotechnology 10, 303–307 (2015).
Scheibner, R. et al. Quantum dot as thermal rectifier. New J. Phys. 10, 083016 (2008).
Schmidt, D. R., Schoelkopf, R. J. & Cleland, A. N. Photon-mediated thermal relaxation of electrons in nanostructures. Phys. Rev. Lett. 93, 045901 (2004).
Meschke, M., Guichard, W. & Pekola, J. P. Single-mode heat conduction by photons. Nature 444, 187 (2006).
Motz, T. et al. Rectification of heat currents across nonlinear quantum chains: a versatile approach beyond weak thermal contact. New J. Phys. 20, 113020 (2018).
Segal, D. & Nitzan, A. Spin-boson thermal rectifier. Phys. Rev. Lett. 94, 034301 (2005).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Chang, Y.-C. et al. Utilization of the superconducting transition for characterizing low-quality-factor superconducting resonators. Appl. Phys. Lett. 115, 022601 (2019).
Giazotto, F. et al. Opportunities for mesoscopics in thermometry and refrigeration: physics and applications. Rev. Mod. Phys. 78, 217 (2006).
Acknowledgements
This work was funded through the Academy of Finland grant 312057 and from the European Union’s Horizon 2020 research and innovation programme under the European Research Council (ERC) programme and Marie Sklodowska–Curie actions (grant agreements 742559, 766025, and 843706). J.A. acknowledges financial support from the IQST and the German Science Foundation (DFG) under AN336/12-1 (For2724). This work was supported by Quantum Technology Finland (QTF) at Aalto University. We acknowledge the facilities and technical support of Otaniemi research infrastructure for Micro and Nanotechnologies (OtaNano) and VTT technical research centre for sputtered Nb films. We acknowledge L.B. Wang for technical help and thank Y.-C. Chang, A. Ronzani, D. Golubev, G. Thomas, and R. Fazio for useful discussions.
Author information
Authors and Affiliations
Contributions
J.S. and A.G. designed, fabricated, and measured the samples. Modelling of the work, which is detailed in Supplementary Information, was done by B.K., J.A., and J.P.P. Technical support in fabrication, low-temperature set-ups, and measurements were provided by J.T.P. All authors have been involved in the analysis and discussion of scientific results and implications of this work. The manuscript was written by J.S., B.K., J.A., and J.P.P.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Senior, J., Gubaydullin, A., Karimi, B. et al. Heat rectification via a superconducting artificial atom. Commun Phys 3, 40 (2020). https://doi.org/10.1038/s42005-020-0307-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0307-5
This article is cited by
-
Microwave quantum diode
Nature Communications (2024)
-
Non-Fourier heat transport in nanosystems
La Rivista del Nuovo Cimento (2023)
-
Identifying optimal cycles in quantum thermal machines with reinforcement-learning
npj Quantum Information (2022)
-
Photonic heat transport in three terminal superconducting circuit
Nature Communications (2022)
-
Heat current rectification in a single quantum dot system with the presence and absence of the magnetic field
Indian Journal of Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.