Introduction

Solitons (solitary waves) are self-trapped light or matter waves that preserve their speed and shape during propagation through nonlinear media. A typical example is the soliton-like behavior of water waves observed by Russell in a shallow canal1, which was later coined as “soliton” by Zabusky and Kruskal2. Since then, solitons have been brought into focus in various areas of physics, including nonlinear photonics, magnetic matter, semiconductors, superconductors, electronics, and even cosmology3 However, in many cases, experimental observations of solitons have been reported only in effectively 1D settings4. It is practically important to find an efficient way to obtain stable multidimensional solitons which offer the observation of many new phenomena5.

Liquid crystals (LCs) provide especially rich opportunities for the studies of solitons6,7,8. LCs that combine properties of isotropic liquids and crystalline solids are extremely sensitive to a variety of external stimuli, such as electric and magnetic fields, and exhibit fascinating optical behavior9. Studies on solitons in LCs have been carried out for over 5 decades10. Most early studies11,12,13,14,15 were concerned with “walls” in nematics generated by magnetic fields, which actually are transition regions where the LC director smoothly reorients by π. By rotating magnetic fields, a variety of interesting solitary waves were observed16,17,18. The coupling between director orientation and flow in a nematic LC (NLC) introduces a nonlinear term in the director equation of motion, which leads to the possible existence of solitons in a shearing NLC even without external fields6,7,19. Optical solitons in NLCs, called nematicons, represent self-focused, continuous wave light beams, and have received great attention in recent decades due to their promising applications in optical information technology20,21. Topologically structured three-dimensional (3D) solitons in the form of torons or hopfions have been experimentally created by using electric fields22,23 or laser tweezers24,25,26,27 in cholesteric LCs (CLCs). These solitons are basically static (although they can do squirming motions driven by electric fields28). They enable twist in all three spatial dimensions and are stabilized by strong energy barriers associated with nucleation of topological defects24.

Very recently, the so-called (3 + 2)D solitons, where “3” refers to the 3D spatial self-confinement and “2” specifies propagation directions that are either perpendicular or parallel to the alignment direction, were observed in a NLC by Lavrentovich et al.29,30. These formations are nonsingular bow-like director perturbations that propagate rapidly through a slab of a uniformly aligned NLC and survive collisions with each other30,31. It should be noted that a similar phenomenon was earlier observed by Brand et al.32, who reported localized formations in the shape of “butterflies” that could move in the plane of the cell. However, neither the director structure of the formations, nor their motion direction was revealed in their report.

In this work, the generation of such dynamic solitons in CLCs is demonstrated. Their structure and dynamic behavior are investigated and compared with the ones in NLCs. We show that novel soliton-like features are induced by chirality. Unlike the features in NLCs reported before29,30,31, the solitons in CLCs show more complex interactions and behave similar to a wave-particle dualism in so far that they either “pass through” each other without losing identity (solitary wave) or collide with each other and undergo reflection (hard particle). Furthermore, we show that the trajectories of their motion can be controlled by a predesignated alignment pattern allowing the realization of micro-cargo transport by soliton motion.

Results

Generation and structure of solitons

The nematic mixture ZLI-2806 (Merck) with a negative dielectric anisotropy, \(\Delta \varepsilon = \varepsilon _\parallel - \varepsilon _ \bot < \, 0\), and a positive electric conductivity anisotropy, \(\Delta \sigma = \sigma _\parallel - \sigma _ \bot > \, 0\), is used as the soliton medium; the subscripts indicate the directions parallel and perpendicular to the director, n, respectively. To prepare the CLC sample, a small amount of a chiral dopant abbreviated as S811 is added to ZLI-2806. The pitch of the CLC is chosen to P ~ 10 μm, equal to the cell gap. Both NLC and CLC are aligned homogeneously along the alignment direction, m (x-axis), in cells with thickness d = 10.5 ± 0.5 μm. A rectangular alternating current (AC) field E is applied to the cell perpendicular to the xy plane of the sample (Fig. 1a) so that the sandwich cell acts as a plate capacitor.

Fig. 1: Solitons in a nematic and a cholesteric liquid crystal.
figure 1

Polarizing optical textures of solitons in a nematic liquid crystal applied with electric fields a 9 V, 30 Hz and b 11 V, 30 Hz. The widths c and lengths d of the nematic solitons. Polarizing optical textures of solitons in a cholesteric liquid crystal applied with electric fields e 12 V, 50 Hz and f 15 V, 50 Hz. The widths g and lengths h of the cholesteric solitons. The scale bars in a and e are 100 μm. v indicates the velocity of solitons. m indicates the alignment direction. The electric field E is perpendicular to the xy plane of the cell. A and P indicate the analyzer and polarizer, respectively. wN, lN, wC, lC represent the width and length of nematic and cholesteric solitons, respectively. The widths c, g and lengths d, h of the solitons are measured as the widths of the soliton cross-sections normal and parallel to their velocity directions, respectively, as indicated by the yellow symbols in the corresponding polarizing optical textures.

Full size image

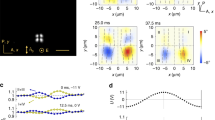
Independent “butterfly-like” solitons (Fig. 1a–d) and “bullet-like” solitons (Fig. 1e–h) are randomly generated in the NLC (Fig. 2a) and the CLC (Fig. 2b) samples, respectively, as the amplitude of the electric field E increases above some frequency-dependent thresholds, Eth (Fig. 2c, d). In both cases the solitons move either parallel to the alignment direction, m, or perpendicular to it by tuning the amplitude and/or frequency of the electric fields (Fig. 2e, f, Supplementary Movie 1). At fixed electric field, the solitons in both the nematic and the cholesteric case preserve their shape during motion. However, when the direction of motion of the solitons changes from parallel to perpendicular to m, the width in the nematic case, wN, shows a slight decrease from ~16 μm to ~13 μm, while its length lN does not change significantly (Fig. 1c, d). On the other hand, in the cholesteric case, the length, lC, increases substantially from ~6 μm to ~13 μm, while the width, wC, shows no distinct change (Fig. 1g, h). The width and length of the solitons are in each case determined by the distance between the two points at which the light intensity of the solitons decreases to its half maximum, i.e., 50% in Fig. 1c, d, and 65% in Fig. 1g, h, respectively. The light intensity is defined by dividing the gray value distribution of solitons by 255. Outside the solitons, n in the mid-plane of samples remains parallel to the alignment direction. Inside the solitons the light intensity increases, indicating azimuthal deviations of n from the initial alignment (Supplementary Fig. 1). To identify the sign of the azimuthal angle, the polarizers are decrossed with an angle β = 20° as shown in Supplementary Fig. 2. By observing the solitons through a higher frame-rate at 50 fps, a periodic modulation of the light intensity is found (Supplementary Figs. 3 and 4). This indicates a time-dependent oscillation of the director inside the solitons induced by the flexoelectric effect (Fig. 2a, b). Such a flexoelectric effect can be further identified from the change of the light intensity transmitted through the soliton and two crossed polarizers. In Supplementary Fig. 2, the intensity of regions 1 and 2 changes in time with the same frequency as the frequency of the AC field. The transmitted light intensity I is dependent on the angle of incidence α, the azimuthal φ and polar θ director angles in the middle plane of the sample, which can be expressed as29,30:

$$I \sim I_0 + \frac{{4\delta ^2}}{{\pi ^2}}G(\delta )\left( {\varphi - \theta \tan \alpha _{LC}} \right)^2$$
(1)

where I0 is the light intensity of the background, δ = 2π∆nd/λ ~ 4.39 is the phase retardation of the undistorted nematic, determined by the wavelength λ ~ 630 nm, and birefringence ∆n = ne – no ~ 0.04428, ne and no are the extraordinary and ordinary refractive indices, respectively. G(δ) is a slowly decaying function depends on δ. αLC = α/no. For α = 0°, the intensity only depends on φ, the periodic change of I at α = 0 in Supplementary Fig. 2b demonstrates that the director of the soliton experiences oscillations in the xy plane. At the same time, the director of the soliton also tilts up and down out of the xy plane by a polar angle. To demonstrate these polar oscillations, we measured I at α = 10°. For such an oblique incidence, the polar oscillations of the director produce different intensity variations for regions 1 and 2 as shown in Supplementary Fig. 2b. It should be noted that the soliton in Supplementary Fig. 2 has a mirror-symmetric structure about x-axis and y-axis and does not move efficiently. By increasing the frequency or amplitude of the field, it loses its symmetry about y-axis (Fig. 1a) or x-axis (Fig. 1b) and then moves quickly. It should be also noted that due to the limited frame rate of our camera (150 fps), to get a better intensity variation curve, the AC field applied here is a sinusoidal wave. Except here, the rest parts throughout the article are applied by rectangular wave AC fields.

Fig. 2: Structures of solitons and their properties as a function of the electric field.
figure 2

The mid-layer director configurations of solitons in the nematic a and the cholesteric b liquid crystal. m and E indicate the alignment direction and the electric field, respectively. d indicates the cell gap. Frequency dependences of thresholds of the amplitude of electric fields, Eth, of solitons and electrohydrodynamics (EHD) in a nematic c and a cholesteric liquid crystal d, respectively. Dependences of velocities of nematic e and cholesteric f solitons on the square of the amplitude of the electric field. The solid and hollow symbols represent the velocities perpendicular and parallel to the alignment direction, respectively. The inset in f represents the velocity distribution of solitons at f = 100 Hz, E2 = 4 V2 μm−2. The error bars in e, f are calculated from the standard deviation of the velocities of different solitons at the same electric fields.

Full size image

The nematic soliton exists in only a narrow range of amplitude and frequency of electric fields (Fig. 2c). In the range of 10–40 Hz, the texture of the nematic phase changes from a homogeneous state via a soliton state to a soliton-electrohydrodynamic (EHD) hybrid state with increasing electric field amplitude. From 40 Hz to 150 Hz, the EHD state appears ahead of the soliton state, and due to the influence of hydrodynamic flow, the motion of the solitons becomes increasingly random with higher field amplitudes and frequencies. Almost no solitons are observed when the frequency is larger than 200 Hz. Note that it is presently unclear whether the solitons will disappear by further increasing the amplitude of electric fields in the range of 10–150 Hz, because in experiments the cells usually experience dielectric breakdown at high voltages. On the other hand, the cholesteric solitons exist in a wider range compared to their nematic counterparts (Fig. 2d). The texture of the CLC changes from a homogeneous state via a soliton state to a soliton-EHD hybrid state in the regime from 10 Hz to 800 Hz. However, when the frequency is larger than 200 Hz, the solitons do not move effectively. Instead, they oscillate locally and form chain-like structures (Supplementary Fig. 5, Supplementary Movie 2). The velocity v of the cholesteric solitons, directed along either the x-axis or y-axis, is dependent on the amplitude and frequency of the applied electric field and increases as v = βE2, where β ≈ 90 ± 10 μm3 V−2 s−1 (Fig. 2f). On the other hand, the amplitude of the velocity v of the nematic solitons only shows a dependence on E2 at 30  Hz and 40  Hz, where β  =  72 and 79  μm3  V−2  s−1, respectively (Fig. 2e). At lower frequencies a saturation behavior is observed. This nonlinear dependence of the velocities of the solitons on the amplitudes of electric fields may originate from the flexoelectricity as well as the ion impurities. According to a very recent theoretical study33, the flexoelectric polarization of the liquid crystal is critical to the formation of the traveling solitons, and the presence of ion impurities as well as the increase of the absolute value of the conductive anisotropy will influence the traveling velocity. In addition, in ref.  31, the authors also claim that the far-field background flow may also contribute to the traveling velocity. However, in our experiments, the convective flow usually occurs at relatively high amplitudes of electric fields and we anticipate that this does not significantly contribute here. On the other hand, ionic impurities as well as flexoelectric contributions can generally not be avoided, so, in our opinion, the origin of the nonlinear traveling behavior of the solitons is most likely caused by a complicated interplay between flexoelectricity and conductivity and needs further investigations to give a clear explanation.

Figure 3 and Supplementary Fig. 6a  show the generation of nematic and cholesteric solitons, respectively. The solitons usually nucleate at the edges of electrodes (Fig. 3a and Supplementary Fig. 6a). Local electroconvection domains (Williams domains) can induce solitons, too, as indicated in Fig. 3b. However, with the nucleation and motion of solitons, these spatially localized domains will subsequently disappear (more details of nucleation of cholesteric solitons can be found in Supplementary Movie 3). In addition, irregularities such as dust particles can also induce the solitons (Fig. 3c and Supplementary Fig. 6). But they can also form at sites where no distinct irregularity is observed (Fig. 3d and Supplementary Fig. 6) which may be attributed to the localization of ions31. Another explanation may be the surface roughness of the indium tin oxide (ITO) electrode layer, leading locally to higher inhomogeneous electric fields. Furthermore, one cholesteric soliton can even split into two or more solitons (Fig. 3e) while the collision of two cholesteric solitons may lead to the eventual creation of four (Fig. 3f, Supplementary Movie 4). Such a proliferation phenomenon usually occurs at Eth and is accompanied with an elongation deformation of the solitons. During the proliferation, the solitons move slowly and obliquely, with a continuous growth of their length. When the soliton length exceeds a specific value, the division occurs (Supplementary Fig. 7).

Fig. 3: Generation of solitons in a cholesteric liquid crystal.
figure 3

a Electrode edges (marked by a dashed line) cause nucleation and reflection of solitons (f = 40 Hz, E = 1.1 V μm−1). b Solitons may also nucleate in a local Williams domain (f = 50 Hz, E = 1.1 V μm−1). Nucleation of solitons at a dust particle is shown in part c (f = 40 Hz, E = 1.4 V μm−1), and at a site where no irregularity is observed d (f = 30 Hz, E = 1.6 V μm−1). e One soliton can split into two (f = 30 Hz, E = 0.8 V μm−1), while f two solitons can collide to create two leaving solitons which in turn split again into the final four soliton system (f = 20 Hz, E = 0.7 V μm−1). The scale bars are 50 μm. m is the alignment direction and v indicates the velocity of the solitons. The analyzer and polarizer are parallel to the x and y axes, respectively.

Full size image

Collisions and interaction of solitons

In a nematic phase, two nematic solitons moving toward each other can collide (overlap spatially and interact nonlinearly) and then “pass through” each other without losing their identity. The collision behavior is slightly different and depends on the degree of offset, ∆xpre (the distance between the centers of the two solitons along the x-axis)29,30,31. But the most frequent scenario is that the two solitons moving along the y-axis coalesce and form a perturbation during the collision. They then split along the x-axis, recover their structure while moving away from each other along the y-axis again at a constant velocity which may be slightly different from the velocity before the collision (Supplementary Fig. 6). The circumstance in CLCs is more complicated. In Fig. 4a, two cholesteric solitons move along the y-axis towards each other and collide. When ∆xpre is very small (<0.5wC), the behavior is somewhat similar to the one observed in nematics, in so far that the solitons reshape during the collision, then recover their structure and move away from each other at a constant velocity along the y-axis (Fig. 4b). The difference with regards to the collision of nematic solitons is that there is no displacement along the x-axis after coalescence, ∆xpost, in the cholesteric case. Otherwise, if the ∆xpre is larger than 0.5wC but smaller than wC, the two cholesteric solitons collide and will reflect at a specific angle which is dependent on ∆xpre and the velocity similar to elastic particles. The solitons will then move away along the y-axis at a constant velocity (Fig. 4c, d). This pseudo-particle behavior may be attributed to the increased mismatch of the director field at the peripheries of the cholesteric solitons due to the helical superstructure or twist (Fig. 2b).

Fig. 4: Collision behavior of cholesteric solitons.
figure 4

a, b shows the trajectory of the collision of cholesteric solitons (s1, s2) in the xy-plane with offset ∆xpre < wC/2 and the corresponding time dependence of the y-coordinates of the solitons, respectively. c, d shows the trajectory of the collision of cholesteric solitons (s1, s2) in the xy-plane with offset ∆xpre > wC/2 and the corresponding time dependence of the y-coordinates of the solitons, respectively. f = 30 Hz, E = 1.2 V μm−1. The insets in a and c are the corresponding polarizing optical textures of the solitons, m indicates the alignment direction, the scale bars are 50 μm. wC indicates the width of the cholesteric solitons. ∆xpre and ∆xpost are the offsets of solitons in x-axis before and after the collision. The analyzer and polarizer are parallel to the x and y axes, respectively.

Full size image

Further interesting phenomena occurs at higher electric fields. In Fig. 5a, two cholesteric solitons are moving along the y-axis towards each other. When they collide, one soliton absorbs the other and then moves away along the y-axis at a constant velocity which is slightly larger than the pre-collision velocity (Fig. 5b). In addition, at a lower frequency, upon the collision, two cholesteric solitons can merge into a single metastable one, which propagates perpendicular to its “parents” at a relatively slow speed for a short duration, and then splits into two solitons again. These then move away from each other along the initial directions (Fig. 5c, d).

Fig. 5: Collisions of cholesteric solitons at higher electric fields.
figure 5

a Trajectories of collision traces of cholesteric solitons (s1, s2, s3) in the xy-plane (f = 40 Hz, E = 1.4 V μm−1) and b the corresponding time dependence of the y-coordinates of the solitons. c Trajectories of collision traces of cholesteric solitons (s1, s2, s3) in the xy-plane (f = 30 Hz, E = 1.4 V μm−1) and d the corresponding time dependence of the y-coordinates of the solitons. The insets in a and c are the corresponding polarizing optical textures of the solitons (scale bars 50 μm. m indicates the alignment direction. The analyzer and polarizer are parallel to the x and y axes, respectively) The inset in d show the time dependence of the x-coordinate of the soliton s3.

Full size image

A distinguishable difference between cholesteric and nematic solitons lies in their collision behavior. When cholesteric solitons move along the alignment direction, m, they behave like hard body elastic particles that they cannot pass through each other. Instead, they collide with each other and then reflect into different directions (Fig. 6a, b). Again, this phenomenon can be attributed to the increased mismatch of the director distortion along the x-axis of cholesteric solitons. Apart from the interaction between solitons introduced above, the solitons can also interact with dust particles (Fig. 6c, d) and the edges of electrodes (Fig. 3a). In both of these cases, the reflection of solitons is observed (more details of interactions of solitons with each other and with dust particles can be found in Supplementary Movie 5).

Fig. 6: Collisions of cholesteric solitons with each other and with a dust particle.
figure 6

a The trajectory and polarizing optical textures (insets) of two solitons (s1, s2) colliding with each other, and b the corresponding time dependence of the x-coordinates of the solitons. (f = 60 Hz, E = 1.3 V μm−1). c The trajectory and polarizing optical textures (insets) of the collision of a cholesteric soliton with a dust particle, and d the corresponding time dependence of the y-coordinate of the soliton. (f = 30 Hz, E = 1.4 V μm−1). The scale bars in the insets of a and c are 50 μm. m indicates the alignment direction. The analyzer and polarizer are parallel to the x and y axes, respectively.

Full size image

Photo-alignment and cargo transport

The most striking feature of the solitons is that their trajectories can be controlled not only by electric fields, but also by the alignment layers. In Supplementary Fig. 8, the sample is divided into three regions with different alignment directions through the photo-alignment technique34,35,36. In each region, the solitons move either parallel or perpendicular to the alignment direction, m, depending on the applied electric field. However, once a soliton crosses the boundaries of different regions, it will continuously change its direction to fit the alignment (Fig. 7a–d). Such a behavior promises a simple and viable method for manipulating soliton motion, in fact along any trajectory and to any destination desired. Furthermore, it has been reported that distorted LC regions can attract colloidal particles9,37. Since these solitons are actually self-confined director deformations, they can even be used to transport micro-cargos. In Fig. 7e, f, a soliton is induced around an impurity once the electric field is turned on, and carries the impurity moving through the bulk of the LC. When the electric field is turned off, it is found that the impurity was transported through a distance a hundred times its size in just a few seconds. More importantly, this process is repeatable and the speed and trajectory of the transport is also controllable by tuning electric fields. By combining this function with photo-alignment techniques, more sophisticated cargo transport can be realized. (More details of photo-alignment induced motions of solitons and cargo transport can be found in Supplementary Movie 6.)

Fig. 7: Manipulation of the trajectories of cholesteric solitons by photo-alignment and cargo-transport.
figure 7

a Trajectory of cholesteric soliton in the xy-plane (f = 40 Hz, E = 1.0 V μm−1) and b the corresponding time dependences of the x- (black) and y- (red) coordinates of the soliton. c Trajectory of cholesteric soliton in the xy-plane (f = 40 Hz, E = 1.6 V μm−1) and d the corresponding time dependences of the x- (black) and y- (red) coordinates of the soliton. Regions I, II and III are the regions in which alignment direction, m is tilted with respect to the x-axis at an angle of 0°, 45°, and 90°, respectively. e Trajectory of the cargo (impurity, indicated in the white square in the inset. Scale bar 10 μm) carried by a nematic soliton (f = 30 Hz, E = 1.2 V μm−1) and f the corresponding time dependence of the displacement D of the cargo. The insets in a, c, and e shows the corresponding optical textures of the solitons (scale bars 50 μm. The analyzer and polarizer are parallel to the x and y axes, respectively. The electric field E is perpendicular to the xy plane.).

Full size image

Discussion

The electrically driven dynamic solitons described above represent a solitary deformation of the director field which is self-trapped in space. They can move either parallel or perpendicular to the alignment direction, depending on applied electric field conditions. In the observations through crossed polarizers, inside the solitons, the light intensity varies spatially in the xy plane according to the director distribution. Along the z axis, the azimuthal deviation of the director field of the solitons show a parabolic-like profile, which reaches a maximum in the middle of the cell, z = d/2, where the boundary conditions are least influential, and diminishes at the boundary surfaces, where the anchoring is strongest, as confirmed by the observation with fluorescence confocal polarizing microscopy (FCPM) in ref. 29. The mid-plane director configuration of nematic solitons can thus be obtained by analyzing their light intensity distribution and optical textures, and the one of cholesteric solitons is deduced by adding the influence of the chirality into the achiral one as shown in Supplementary Fig. 1. The key factor that induces the change of motion direction can be the symmetry-breaking structure of the solitons induced by the background flow31. The solitons propagating along the x-axis lack the symmetry with respect to the y-axis (Supplementary Fig. 1a, c). And the solitons propagating along the y-axis lack the symmetry with respect to the x-axis (Supplementary Fig. 1b, d). The formation and motion of the solitons can be attributed to the flexoelectric effect. The splay and bend of the director field leads to an induced polarization, i.e. flexo-polarization, \({\mathbf{P}}_f = e_1{\mathbf{n}}(\nabla \cdot {\mathbf{n}}) - e_3{\mathbf{n}} \times (\nabla \times {\mathbf{n}})\),where e1 and e3 are the flexoelectric coefficients. By applying an electric field, the flexo-polarization produces a flexoelectric torque on LC molecules, \({\mathbf{\Gamma }}_f = {\mathbf{P}}_f \times {\mathbf{E}}\). This torque is linearly dependent on E and induces periodic oscillations of the director. Such oscillations induced by the flexoelectric effect can be supported by their frequency-dependence behavior (Supplementary Figs. 2–4).

Compared to the “butterfly-like” nematic solitons, which normally behave like propagating solitary waves during the collision (Supplementary Fig. 4b) the “bullet-like” cholesteric solitons behave more like elastic particles in that they reflect each other after collision (Fig. 4c, d and 6a, b). Such a pseudo-particle behavior is also found in the chiral samples with different pitches, 5 μm and 20 μm, representing 4π- and π-twists, in addition to the results reported here for a 2π-twist system. One may attribute this pseudo-particle behavior to the increased mismatch of the director field between cholesteric solitons due to their twist-distorted structures. However, the specific reason of this different behavior of cholesteric solitons from nematic ones is not yet clearly understood and requires further investigations.

The size of nematic solitons is mainly determined by the balance between the elastic energy, the surface anchoring and the sample thickness31. But in the case of the cholesteric solitons, this also depends on the pitch of the CLC. At the same conditions, the larger the pitch, the larger the solitons (Supplementary Figs. 9 and 10). Besides, in the case of the P = 10 μm CLC, the solitons change from a motion parallel to one perpendicular to the alignment direction by increasing electric fields, Fig. 1e, f. This situation is opposite in the case of a P = 20 μm CLC (Supplementary Fig. 9a, b). As confirmed by fluorescent signal measurement19, the structure of solitons is determined by the middle plane of the sample. The increase of pitch from 10 μm to 20 μm in a d = 10 μm cell induces a π/2 rotation of the mid-plane director, thus leading to a π/2 rotation of the soliton propagation direction. However, the situation becomes different in the case of the P = 5 μm CLC. The structure of the solitons is distorted into a “spider-like” shape as indicated in the inset of Supplementary Fig. 9f, and they move randomly without preferred direction. Interestingly, it is found that the solitons absorb “baby solitons” (small bright dots which vibrate locally) and switch their directions subsequently, leading to the irregular motion (Supplementary Movie 7). This exotic phenomenon warrants further investigations. Furthermore, the dependencies of Eth on frequency in all three CLC systems of varying pitch are similar to each other (Fig. 2d, Supplementary Fig. 11).

Previous studies have shown that the generation of the solitons is due to flexoelectric polarization and is dependent on the dielectric and conductive properties of LC29,30,31. Generally, according to de Gennes38, the combination of dielectric properties and conductivity can be classified as (++), (+−), (− −) and (−+), where the plus and minus symbols represent the sign of the dielectric (∆ε) and conductivity (∆σ) anisotropies, respectively. In the experiment, solitons are observed in a (−+) LC in the range where electro-convective patterns are normally observed. This is attributed to the moderately low conductivity anisotropy ~1.3 × 10−8 Ω−1 m−1 of our sample, which is much smaller than the ones usually reported in most studies of electro-convection in (−+) nematics39,40. The significance of this small conductivity anisotropy can be understood by considering the coupling between the electric field E and the space charge Q. According to the classic Carr–Helfrich electro-convection mechanism41,42, the positive conductivity anisotropy and the bend fluctuation in a NLC induces ion segregation and forms Qs which are high and uniformly distributed in space. These Qs produce transverse Coulomb forces which offset the normal elastic and dielectric torques and cause instability, usually in the form of space-filling periodic stripes. However, due to the relatively low conductivity of our samples, there is not sufficient charge accumulation to produce a strong enough dielectric torque to induce a uniform electro-convective effect. Instead, independent solitary structures form at the localization of ions due to the flexoelectric effect31. However, once the applied electric field amplitude is large enough, a uniform electro-convection accompanied with solitons can be observed.

In conclusion, we demonstrate the structure, generation and dynamic behavior of solitons in CLCs and compare them with the ones generated in NLCs. Compared to nematic solitons, cholesteric solitons show more complicated interactions during pair-wise collisions. The helical superstructure (twist) increases the incompatibility between cholesteric solitons and causes them to behave either like elastic particles or like solitary waves. The speed and propagation direction of the solitons can be tuned by electric fields, and their trajectories can be predesignated through photo-alignment. Our work not only provides a feasible method for generating and controlling multidimensional solitons, but also shows that these solitons can be used for targeted 2D delivery of micro-cargos.

Methods

Materials

A commercial nematic LC mixture, ZLI-2806 (Merck), was used. Chiral samples with pitches, P = 5 μm, 10 μm, and 20 μm, were obtained by doping different concentrations of a chiral dopant S811 (ZLI-811) (Xianhua, China) with a helical twisting power of HTP = −8.3 μm−143 into ZLI-2806. The concentrations of S811 were 2.4 wt%, 1.2 wt%, and 0.6 wt%, respectively. For the photo-alignment process, a 0.3% solution of sulfonic azo dye SD1 (Dai-Nippon Ink and Chemicals, Japan) in dimethylformamide (DMF) was used35. The components of dielectric permittivity and conductivity of ZLI-2806 are \(\varepsilon _\parallel \approx {\mathrm{3}}{\mathrm{.0}}\), \(\varepsilon _ \bot \approx {\mathrm{7}}{\mathrm{.6}}\), \(\sigma _\parallel \approx {\mathrm{1}}{\mathrm{.9}} \times {\mathrm{10}}^{ - {\mathrm{8}}}{\mathrm{\Omega }}^{ - 1}\,{\mathrm{m}}^{ - 1}\), \(\sigma _ \bot \approx {\mathrm{6}} \times {\mathrm{10}}^{ - {\mathrm{9}}}\,{\mathrm{\Omega }}^{ - 1}\,{\mathrm{m}}^{ - 1}\), respectively, at 4 kHz and room temperature, measured by use of an LCR meter E4980A (Agilent) using commercial cells with planar and homeotropic alignment, respectively.

Sample preparation

The cell is composed of two glass substrates coated with ITO. The glass substrates were first ultrasonically bathed, plasma cleaned, and then spin-coated with SD1. Afterwards, the empty cell was illuminated by polarized Ultraviolet (UV) light of wavelength λ = 395 nm. Cells were filled by capillary action of either the NLC or the CLC being heated to 80 °C.

Generation of solitons

The sample was kept at 80 °C on a hot stage (LTSE350, Linkam) controlled by a controller (TP 94, Linkam). The AC voltage is applied using a waveform generator (33220 A, Agilent) and a home-built amplifier.

Optical characterization

The sample was observed through a polarizing microscope (Leica OPTIPOL) equipped with a digital camera (UI-3360CP-C-HQ, uEye Gigabit Ethernet) with tunable frame rate from 14.43 fps to 50 fps. The velocity and light intensity distribution of solitons were analyzed by an open-source software ImageJ and its plugin TrackMate.