Introduction

One of the most important questions in the field of quantum materials is the nature of states that emerge from a doped Mott insulator1,2. This is a key prerequisite to understanding the development of high-Tc superconductivity via hole or electron doping from the Mott phase3,4. Furthermore, this helps elucidate why and how the cuprates are different from other doped Mott insulators. With ability to resolve single-particle energy-momentum spectra, angle-resolved photoemission (ARPES) has helped to determine a starting point to modeling cuprates – the doped Hubbard model5. Early on it was shown that strong correlations, in the form of the on-site Hubbard U, lead to an antiferromagnetic (AFM) state from a predominantly Cu 3d9 configuration6. When a single hole is created by photoemission, it disperses from (π/2, π/2) towards the Γ point, which abruptly falls in intensity near the zone center—the so-called "waterfall”7,8,9,10. Rather than dispersing as a free quasiparticle, the low-energy band in a Mott insulator can be well fitted with a velocity on the scale of the spin exchange J ~ 120 meV11,12,13,14. These basic observations of a Mott insulator lie within the framework of the Hubbard model.

In doped Mott insulators, recent experimental and theoretical progress further extends Hubbard model’s descriptiveness. On the experimental side, ARPES and resonant inelastic x-ray scattering (RIXS) have shown evidence of strong correlations15,16,17,18 and collective spin excitations19,20,21,22,23 far beyond the Mott phase, which cannot be addressed using weak-coupling theory. Despite such success, clearly, there are also experimental observations that seem to lie beyond the simple Hubbard and t − J models. An outstanding example is the  ~ 200 meV linewidth of the ARPES spectrum even at (π/2, π/2)7,24, where a single hole described by the t − J model has no phase space to decay11,12. The correct linewidth was obtained only by considering the lattice polaronic effect25,26,27,28, which becomes less dressed at higher dopings due to screening29,30,31. Moreover, in many doped Mott insulators, such as the nickelates32, manganites33, and cobaltates34, doped carriers cause insulating charge structures rather than superconductivity35. While stripe order has also been observed in cuprates, the magnitude is not nearly as strong as in other transition metal oxides36. This difference also led to the consideration of many material-specific degrees of freedom beyond the prototypical Mott insulator, including static and dynamic lattice effects37,38,39,40,41,42,43,44,45. Therefore, both for aspects specific to cuprates and those generic to correlated materials, one may wonder, to what extent exactly can the impact of correlations be captured within such toy models?46,47,48.

To identify universal features resulted from purely electron-electron correlations and their evolution with doping, we systematically study the single-particle spectral function of the doped Hubbard model, with only t, \({t}^{\prime}\) and U and no other external ingredients. By calculating the spectral function at extremely fine doping levels over a wide range of electron and hole dopings, we expect to unbiasedly decipher the doping evolution of the dispersions, weights, and lineshapes of spectral features, and compare with ARPES experiments in cuprates. Though some of these properties have been studied previously at some discrete doping levels49,50, we find that the emergence of quasiparticles and their interplay with the polaronic Mott features cannot be fully addressed without reaching extreme limits of dopings. A detailed understanding of these spectral properties may provide insight on what aspects of experimental photoemission data can or cannot be well represented by the Hubbard model.

Results and discussion

The Hubbard model is presented in the Method section. Historically, a variety of numerical techniques have been used to investigate the single-particle spectrum of the Hubbard model, e.g., exact diagonalization51,52,53, quantum Monte Carlo54,55, density-matrix renormalization group56,57, dynamical mean-field theory58,59,60,61, CPT49,50,62,63,64 and others65,66,67,68,69. To investigate low-temperature spectral features with fine momentum resolution and continuous doping dependence, CPT with superclusters is the most suitable approach.

Overview

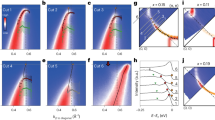
  Fig. 1 shows the calculated spectral function A(k, ω) at two extreme dopings: undoped (half-filling) and heavily doped. At half-filling, a large Mott gap (~4t) separates the lower Hubbard band (LHB) and the upper Hubbard bands (UHB). Within each band, there are two main spectral features (see the markers in Fig. 1a): one at low binding energies, describable within a spin-polaron framework11,14; and a second at higher energies, which results from an effective intra-sublattice hopping70,71. A “waterfall”-like step connects the two features, constituting one of the critical spectral signatures of correlation effects.7,13,70,72 Throughout this paper, we refer to these single-particle these features that exist already at the half-filled Hubbard model as the Mott features. In the other extreme doping limit (see Fig. 1b, c), the spectrum resembles that of non-interacting electrons, although the Hubbard U remains unchanged. A quasiparticle dispersion across EF dominates the spectral function, with indiscernible residual spectral weight on the other side of the Mott gap. This feature, to which we refer as the quasiparticle, follows the tight-binding functional form of the bare band structure, but is subject to a doping-dependent bandwidth renormalization49,50,73.

Fig. 1: Overview of spectral features.
figure 1

Spectral function of the Hubbard model calculated using cluster perturbation theory (CPT): a for the half-filled Mott insulator and b, c for the 87.5% hole- and electron-doped system, respectively. The dotted line in b and c denotes the non-interacting tight-binding dispersion, while the horizontal dashed lines mark EF. The Brillouin zone (BZ) cartoon shows the spectral cut between the Γ, X, and M high-symmetry points for the square lattice. Labels in a denote the “Mott features”.

Full size image

Density of states

Between these two limits, we first investigate the density of states (DOS) evolution with doping (see Fig. 2a–d). We see that a remnant Mott gap exists at all doping levels and well separates the UHB and LHB. Though it is somewhat expected in a single-band Hubbard model, we want to emphasize that the robustness of the charge-transfer gap in doped cuprates has bee recently confirmed through STM experiments74. Moreover, infinitesimal doping leads to the development of spectral weight at EF for both electron- and hole-doping. With increasing doping, the spectral weight transfer gradually depletes the upper (lower) Hubbard band, and the chemical potential smoothly evolves away from half-filling (with a finite linewidth, one can still define a EF at n = 1). In this process, the transferred spectral weight becomes energetically mixed with the lower (upper) Hubbard band upon doping, rather than forming an entirely separate in-gap state25,75.

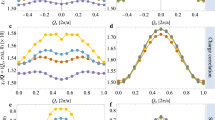
Fig. 2: Doping dependence of density of states.
figure 2

a, d Evolution of the calculated density of states (DOS) with hole and electron doping, respectively. The green regions highlight the doping-induced states above (hole-doping) and below (electron-doping) EF. The gray dashed lines denote the DOS for the non-interacting model, and the brown shades indicate the Mott gap. b The dependence of EF on the electron density n, reflecting the Mott plateau. The solid (open) circles show results from calculations without (with) a supercluster construction. c The integrated weight of panels a and d. The doping-induced and remnant spectral weight in the lower Hubbard band (LHB) and the upper Hubbard bands (UHB) are plotted in green, red and blue, respectively. The solid brown curve denotes their separation at the gap center, while the dashed green curve denotes the separation between doping-induced states and the LHB (UHB), assuming the latter has equal weight with the UHB (LHB).

Full size image

To quantify such spectral weight evolution, we integrate the three regions: residual LHB and UHB (red and blue) and the doping-induced states (green), respectively. Unlike the separations at EF in Fig. 2a, d, we further assume that the residual LHB (UHB) in a hole-doped (electron-doped) system carries the same spectral weight as the UHB (LHB) and, therefore, assign a small portion of spectral weight below (above) EF to the doping-induced states (see Fig. 2c). We believe this assignment gives a better characterization compared to previous studies using small-cluster Hubbard or charge-transfer models49,75,76,77,78,79,80, because we have considered that the doping-induced feature (i.e., quasiparticle) penetrates EF and coexists with the Mott features. As such, with the increasing doping, the rapid growth of it spectral weight involves contributions from both the LHB and UHB via doping. Our analysis shows that initially the spectral weight changes as  ~2x (where x is the concentration of doped carriers), but is reduced to 0.84x starting from roughly optimal doping. This gradual change reflects the unraveling of electronic correlations upon doping.

Spectral function

Taking a closer look in momentum space to identify where and how the quasiparticles emerge via A(k, ω), Fig. 3 shows the doping dependent single-particle spectra along high-symmetry cuts. In contrast to the back-bending spin-polaron at half-filling, doping immediately leads to the appearance of spectral weight near EF (see Fig. 3a), with a heavily renormalized quasiparticle dispersion consistent with ARPES experiments on the underdoped cuprates24,25,28,47. The spectral weight of this quasiparticle grows monotonically with doping: it gradually “fills-in” near the M-point for hole doping, and the Γ-point for electron doping. A clear suppression of the antinodal spectral weight at low hole doping reflects the pseudogap, while a similar suppression of the node at low electron doping indicates the hotspot (see Supplementary Note 1). The appearance of these two distinct phenomena suggests that the major normal-state quasiparticle features at optimal doping may also be qualitatively captured by a single-band Hubbard model.5,81,82 Upon further doping, the renormalization gradually decreases, and the quasiparticle dispersion smoothly evolves into the free dispersion shown in Fig. 1b, c.

Fig. 3: Doping dependence of spectral functions.
figure 3

a Energy distribution curves (EDCs) for calculated spectral functions with 1.4% hole doping. b False-color plot for the spectral function A(k, ω) near EF along high-symmetry cuts, as indicated by the inset, for a fixed energy window and various electron concentrations with hole doping. c, d Same as a, b but for electron doping instead. In a and c, the green arrows denote the quasiparticle features, while the red and blue arrows denote the remnant spin-polaron features at the lower- and upper-Hubbard band, respectively. In all panels, the gray dashed line denotes Fermi level.

Full size image

The difference between the Hubbard model calculation and ARPES spectrum mainly lies in the lineshape near kF. In contrast to a broad peak describable by the strong polaronic dressing at half-filling and light doping25, the renormalized quasiparticle in Fig. 3 is always sharp near (π/2, π/2) for hole doping (also see the Supplementary Note 2). That means the linewidth change in the underdoped regime cannot be attributed simply to the quasiparticle dressed by spin excitations in the doped Hubbard model. Correlation-enhanced phonon polaronic dressing may be required to reproduce the experimental lineshape26. The omission of the phonon dressing also may relate to the shape of the chemical potential jump  ~ t ~ 300meV in Fig. 2b for a small doping out of half-filling, which is observed smoother in cuprate experiments83.

Doping dependence of spectral weights

Besides the qualitative spectral shape, we perform quantitative analysis of the spectral weight doping evolution at two distinct momenta and within reprsentative energy ranges. We first focus on the M-point, where the quasiparticle is most separated from the higher-energy Mott features (see Fig. 1 and Fig. 3b). In Fig. 4a, we observe rapid growth in the spectral weight associated with the quasiparticle (green), overwhelming the remnants of the lower Hubbard band (red) at a moderate hole concentration. Residual spectral weight of the latter features gradually decreases with doping until their disappearance at  ~20% doping (see Fig. 4b). The visibility of these Mott features in doped systems has two interesting implications. On one hand, the coupling between carriers and spin fluctuations is present even in a regime without long-range magnetic order, consistent with several recent experimental observations19,20,21,23. On the other hand, the eventual disappearance of these Mott features may account for the transition to a more metallic phase at  ~20% doping in Bi2Sr2CaCu2O8+x17,18 and YBa2Cu3O6+x48.

Fig. 4: Spectral weight evolution of well-separated features.
figure 4

a Energy distribution curves at the M-point for different hole doping levels. The green shaded region highlights the growth of the quasiparticle, while red marks residual Mott features in the lower Hubbard band. b Integrated spectral weight of features in a. c A similar analysis performed in electron-doped systems at the Γ-point instead, where blue marks the corresponding integrated weight in the upper Hubbard bands.

Full size image

A similar analysis for electron doping, now at the Γ-point, indicates substantial particle-hole asymmetry with respect to doping (see Fig. 4c). The Mott features persist until even higher doping on the electron-doped side. Although the finite cluster size of CPT calculations precludes definitive assessment of long-range order, the correlation effects at heavy doping suggest a substantial impact of spin correlations. This agrees with the recent discovery of Fermi surface reconstruction outside the AFM phase in Nd2−xCexCuO416. Here, the visibility of Mott features at higher doping (up to  ~40%) than the hole-doped side reflects more robust magnetic correlations in the electron-doped Hubbard model84,85,86.

To verify the above dichotomy within occupied states measurable by ARPES experiments, we focus our attention on the spectrum near kF along the nodal direction, where the dispersion crosses EF. Comparing the spectral weight in two momentum-energy windows—one close to EF and a second at higher binding energy—we can quantitatively distinguish the evolution of the quasiparticle spectral weight from the Mott features (specifically spin-polaron in the calculation) at low doping. As shown in Fig. 5a, following a rapid exchange of spectral weight below 2% hole doping, both features begin to saturate and coexist (with comparable spectral intensities). We also observe consistent behavior in experimental spectra for the extremely underdoped regime of La2−xSrxCuO4 (see Fig. 5b–d). After immediate development of the quasiparticle feature at 1% doping, the spectral weight ratio between the quasiparticle and polaronic features saturates in the subsequent large range of doping. Such a saturation has been also observed in optimally doped HgBa2CuO4+δ87 and Nd2−xCexCuO416. This agreement confirms our theoretical prediction that strong correlations continue to play an essential role up to relatively high doping levels. (Note that the two integration windows have different areas: the upper one (red) covers (kF − 0.05Å, kF + 0.05Å) × (−0.05 eV, 0), while the lower one (blue) is (kF−0.23Å, kF + 0.07Å) × (−0.31eV, −0.29eV). Therefore, the ratio in Fig. 5d gives the trend for doping dependence instead of the absolute value of the quasiparticle weight).

Fig. 5: Spectral weight evolution near kF.
figure 5

a The spectral weight ratio between the lower and higher energy windows obtained from calculations (open circles) and experiments (solid squares). The shaded region denotes the antiferromagnetic phase in (La,Sr)2CuO4. b–d Angle-resolved photoemission spectroscopy experiments on underdoped (La,Sr)2CuO4 for half-filling, 1% and 12% doping near kF. The red and blue boxes in c denote the lower and higher energy windows near Fermi momentum kF, corresponding to the quasiparticle and polaronic feature, respectively. Their ratios correspond to the dots in a.

Full size image

In contrast to the agreement of the spectral weight’s doping dependence, the numerically calculated (nodal) spectral features of the Hubbard model are sharper than those found in the ARPES experiment of cuprates (see the comparison between Figs. 3 and 5). While one culprit is the lack of the electron-phonon coupling in the calculations, we cannot completely rule out the possibility that the quasiparticle may become less coherent already within the Hubbard model—but only when explicitly calculated using far larger clusters (which is, as of now, unfeasible due to the exponential growth of the Hilbert space with the cluster size) [see the Methods section].

Conclusion

We have presented a comprehensive benchmark study of the single-particle spectral function of cuprates upon hole and electron doping, from the perspective of the single-band Hubbard model. We have analyzed and dissected the various features of the single-particle spectra, showing their distinct origins by carefully examining their doping dependences. Many of the conclusions drawn from the Hubbard model show good agreement with existing and here reported ARPES experiments. Starting from an extremely underdoped regime, doped carriers induce quasiparticle-like states near the Fermi level. Both the momentum-resolved calculations and ARPES experiments reveal that these itinerant states have no analog in the Mott insulating state at half-filling (i.e., the Mott gap, spin-polaron, and high-energy intra-sublattice features). Instead, an important finding of this work is that these emergent features coexist with the original Mott features in a wide range of doping. Though heavily renormalized with small spectral weight at low doping, this quasiparticle feature gradual emerges from the Mott feature at a rate roughly twice that of the doping. With heavy doping (~20% for hole-doping), the continued presence and electron-hole asymmetry of correlations are consistent with the observations in recent ARPES and RIXS experiments15,16,17,18,19,20,21.

From these aspects, the single-band Hubbard model seems to effectively capture the essence of the emergence of low energy quasiparticles, from the extremely underdoped regime to the overdoped regime. However, in contrast to these qualitative consistencies in spectral weight and dispersion, the almost doping-independent lineshape calculated from the Hubbard model cannot address the observations in parent compounds or lightly doped cuprates; the purely electronic Hubbard model also fails to reproduce the widely observed low-energy kinks in the quasiparticle bands37,38,39. Towards a more comprehensive picture, including lattice polaronic coupling provides another channel to destroy the quasiparticles’ coherence25, contributing to material-specific dependence in various cuprate families as well as other transition metal oxides.

Methods

Hubbard model

The Hamiltonian of the single-band Hubbard model is given by88,89

$${\mathcal{H}}=-{\mathop{\sum }\limits_{{\bf{i}},{\bf{j}},\sigma }}\left({t}_{{\bf{ij}}}{c}_{{\bf{j}}\sigma }^{\dagger }{c}_{{\bf{i}}\sigma }+h.c.\right)+U {\mathop {\sum} \limits_{{\bf{i}}}}\left({n}_{{\bf{i}}\uparrow }-\frac{1}{2}\right)\left({n}_{{\bf{i}}\downarrow }-\frac{1}{2}\right).$$
(1)

Here, \({c}_{{\bf{i}}\sigma }^{\dagger }\) (ciσ) and niσ denote the creation (annihilation) and density operators at site i of spin σ, respectively; U denotes the on-site Coulomb interaction; and tij encodes the electron hopping, restricted here to nearest-neighbors t〈ij〉 = t and next-nearest-neighbors \({t}_{\langle \langle {\bf{ij}}\rangle \rangle }={t}^{\prime}\). We chose parameters U = 8t and \({t}^{\prime}=-0.3t\), common for simulations of cuprates.

Single-particle spectral function and cluster perturbation theory

The single particle spectral function, which corresponds to the ARPES measurement, is defined as:

$$A({\bf{k}},\omega )=-\frac{1}{\pi }{\rm{Im}}{\mathop {\sum} \limits_{\sigma }}\left\langle G\left| {c}_{{\bf{k}}\sigma }^{\dagger }\frac{1}{\omega +{\mathcal{H}}-{E}_{G}+i\delta }{c}_{{\bf{k}}\sigma }\right| G\right\rangle ,$$
(2)

where \({c}_{{\bf{k}}\sigma }={\sum }_{{\bf{i}}}{c}_{{\bf{i}}\sigma }{e}^{-i{\bf{k}}\cdot {{\bf{r}}}_{{\bf{i}}}}/\sqrt{N}\) denotes the electron annihilation operator at momentum space, \(\left|G\right\rangle\) is the ground state with energy EG. We choose a Lorentzian energy broadening of δ = 0.15t throughout this paper.

The idea of cluster perturbation theory (CPT) was invented by Sénéchal et al.63,64 and was demonstrated to be an efficient approach to estimate the A(k, ω) of strongly correlated systems at zero temperature. For completeness, we briefly reiterate the CPT method here, while the readers should refer to Ref. 64 for details. Assuming one divides the infinite plane into clusters, the Hamiltonian can be split into \({\mathcal{H}}={{\mathcal{H}}}_{c}+{{\mathcal{H}}}_{{\rm{int}}}\). Here \({{\mathcal{H}}}_{c}\) contains the (open-boundary) intra-cluster operators, while \({{\mathcal{H}}}_{{\rm{int}}}\) contains the operators with inter-cluster indices (hopping terms for the Hubbard model). Then one can use exact diagonalization to precisely solve the Green’s function Gc(ω) associated with the intra-cluster Hamiltonian \({{\mathcal{H}}}_{c}\). Here, we use the parallel Arnoldi method and the Paradeisos algorithm to determine the equilibrium ground-state wavefunction.90,91

The CPT method then estimate the Green’s function of the infinite plane by treating \({{\mathcal{H}}}_{{\rm{int}}}\) perturbatively, giving

$${\mathcal{G}}({\bf{k}},\omega )=\frac{{G}_{c}(\omega )}{1-V({\bf{k}}){G}_{c}(\omega )}\ .$$
(3)

where \(V({\bf{k}})={\sum }_{{\bf{R}}}{{\mathcal{H}}}_{{\rm{int}}}{e}^{i{\bf{k}}\cdot {\bf{R}}}\) is the inter-cluster interactions projected to the intra-cluster coordinates. Then taking the long-wavelength limit, we obtain

$$A{({\bf{k}},\omega )}_{{\rm{CPT}}}=-\frac{1}{\pi N}{\rm{Im}}{\sum }k_{a,b}{{\mathcal{G}}}_{a,b}({\bf{k}},\omega ){e}^{i{\bf{k}}\cdot ({{\bf{r}}}_{a}-{{\bf{r}}}_{b})},$$
(4)

where a, b are intra-cluster site indices. Although CPT gives corrections to the small-cluster ED calculations and reduces the finite-size effect, the finite-size effect does not entirely disappear in the CPT calculations63,64. With an increase of the system size, the number of poles of the Gc(ω) grows (see Fig. 2 in ref. 63).

The CPT method can be further generalized into superclusters, giving access to any rational doping values. Denoting the Green’s function of a (disconnected) supercluster consisting of M clusters as \({G}_{0}={\oplus }_{m}^{M}{G}_{c}^{(m)}\), where \({G}_{c}^{(m)}\) is the intra-cluster Green’s function of the m-th cluster. Note that these M clusters can be filled by different integer numbers, leading to an averaged rational filling in the supercluster. Then following the CPT philosophy, one can first include the inter-cluster perturbation inside the supercluster, giving

$${G}_{sc}={G}_{0}{\left(1-{{\mathcal{H}}}_{{\rm{int}}}^{(ic)}{G}_{0}\right)}^{-1}$$
(5)

where \({{\mathcal{H}}}_{{\rm{int}}}^{(ic)}\) is the inter-cluster Hamiltonian terms within the supercluster. The CPT correlation of the supercluster Green’s function then gives

$$ A{({\bf{k}},\omega )}_{{\rm{SC}}-{\rm{CPT}}}\\ =-\frac{1}{\pi N}{\rm{Im}}{\mathop{\sum }\limits_{a,b}}{\left[\frac{{G}_{0}(\omega )}{1-\left({{\mathcal{H}}}_{{\rm{int}}}^{(ic)}+{V}_{sc}({\bf{k}})\right){G}_{0}(\omega )}\right]}_{ab}{e}^{i{\bf{k}}\cdot ({{\bf{r}}}_{a}-{{\bf{r}}}_{b})}\ .$$
(6)

Similar to Eq. (3), the Vsc(k) is the inter-supercluster hopping. In the calculations of the main text, we evaluate the 4 × 4 cluster spectral function by an exact solver and 8 × 8 or 12 × 12 by a supercluster solver.64

The density of states (DOS) is calculated through the integration of A(k, ω) over the first Brillium zone:

$${\rm{DOS}}(\omega )=\int_{{\rm{BZ}}}\frac{d{{\bf{k}}}^{2}}{4{\pi }^{2}}A{({\bf{k}},\omega )}_{{\rm{SC-CPT}}}\ .$$
(7)

The Fermi level is then determined by the equality DOS(EF) = n.

Experimental details

High-quality single crystals of La2−xSrxCuO4 (LSCO) are synthesized with traveling solvent floating zone method, and subsequently cut into  ~1 × 1 × 0.5 mm3 pieces along the crystal axes. They are then glued to oxygen-free copper sample holders with alternating layers of conductive silver epoxy and Torr seal resin. Ceramic top posts are then glued to the surface of the single crystals, only to be cleaved under ultrahigh vacuum to expose fresh surfaces for photoemission measurements.

Angle-resolved photoemission spectroscopy on ten different dopings of LSCO is performed at beamline 10.0.1 in the Advanced Light Source at Lawrence Berkeley National Laboratory and beamline 5-4 at Stanford Synchrotron Radiation Lightsource at SLAC National Laboratory. The vacuum is kept at better than 5 × 10−11 Torr throughout the experiments. 55 eV and 20 eV photons are used with the linear polarization parallel to the diagonal Cu-Cu (nodal) direction. All data shown here are collected at 10-15 K except for x = 0 sample, which is measured at 50 K to mitigate static charging effect.