Abstract
Free-space optical communication systems exploit the properties of light beams to transfer information through a free-space link. Indeed such systems provide an exciting alternative for communication. Here we introduce information transfer through free-space using a laser beam having its phase encoded with multiple orthogonal aberration modes. We use Zernike polynomials, which form a complete basis set, to represent the aberration modes. The user information is converted to co-efficients of the Zernike modes which are summed digitally to obtain the resultant phase profile. A single phase modulating device then reads the resultant phase to shape the wavefront of the beam to be transmitted. The receiving station estimates the co-efficients of all modes in the beam from a single measurement of a wavefront sensor, to retrieve the user information. We demonstrate data transfer using multiple modes, each with multiple strengths, and external perturbation compensation using the completeness property of the modes.
Similar content being viewed by others
Introduction
The past couple of decades have seen rapid developments in free-space optical communication (FSO) systems as an alternative mode of communication that can have advantages in terms of speed and security1,2. Such developments are for both outdoor and indoor applications3,4,5,6 of light beams. Light beams with helical wavefronts also known as vortex beams or orbital angular momentum (OAM) beams have been proposed for free-space information transfer, where the information is encoded as OAM states of light7,8,9,10. An OAM mode with l helical phase fronts represented by the complex amplitude \(\exp (il\theta )\), where θ is the azimuthal angle and l is an integer called topological charge, carries OAM per photon equal to lℏ (ref. 7). Therefore, the amount of information to be encoded is decided by the number of l values associated with the light beam. Multiplexing of OAM modes with different l values thus facilitates enhancing the data transfer rate through free-space up to tera bits per second or more11,12, as demonstrated over a propagation distance of ~1 m. In most of the OAM-based FSO systems, first a fixed number of OAM modes are generated and the user data is encoded into each OAM mode by modulating the power (comprising “on” and “off” periods) of the respective mode. Different OAM modes encoded with the user data are then multiplexed often using beam splitters. It is also possible to generate a combination of OAM modes, each with a user-defined power, using a single-phase modulating device13, such as a high-density phase-only liquid crystal spatial light modulator (LCSLM)14. However, the process involves implementing a computationally intensive iterative algorithm to calculate the phase hologram, thereby making the modulation rate slow, if user data is to be encoded by periodically modifying the phase holograms. It is to be noted that different OAM modes suffer different divergences on propagation15,16. It is also well known that in an FSO there exists the possibility of eavesdropping by capturing the radiated power17, since it is always easier to measure modulation in power in a beam than any other modulation of the beam. Therefore, an OAM mode-based FSO system, relying on modulating the power of various OAM modes for encoding, to some extent compromises on its security. However, a major concern for any OAM-based free-space communication system remains the susceptibility of the mode to atmospheric turbulence18. Indeed, it was shown that air turbulence may lead to vortex instability, with a certain OAM mode after propagation breaking into other OAM modes19.
Therefore, a significant amount of efforts in recent times have been aimed at mitigating the effect of air turbulence in the OAM-based FSO systems. Some such efforts are use of modal diversity of different optical modes toward turbulence20, use of auto focusing Airy beams21,22, use of convolutional neural network for adaptive demodulation of the signal at the receiving station23, use of adaptive optics system to compensate for distorted OAM beams24, and exploring the shape invariance property of OAM Bessel beams25. Unfortunately, most of the turbulence compensation schemes lead to an increase in the processing time at the receiving station26, thereby imposing an upper limit on real time decoding.
In this paper, we propose an orthogonal aberration mode-based FSO system. We use Zernike polynomials27, which form a complete set of orthogonal basis functions of two variables, to represent the aberration modes of a single light beam. Multiple Zernike modes whose amplitudes (i.e., co-efficients) are encoded with user information are summed digitally before transmitting the resulting phase profile using a dynamic hologram or a non-holographic phase modulating device, such as a deformable mirror. As the user data is encoded in different modulation cycles by modifying only the phase of the beam, the net power in the beam remains unaltered. The receiving station uses a wavefront sensor to measure the amplitudes of all the Zernike modes constituting the wavefront simultaneously before decoding the user information. The proposed mechanism provides flexibility over the number and types of modes used, and enables compensation of air turbulence utilizing the completeness property of the Zernike modes, without requiring any optical correction of the beam. Moreover, the use of multiple amplitudes of each Zernike mode transmitted enhances the information capacity per modulation cycle for a given number of modes in the beam. In this work, we have demonstrated the proposed free-space information transfer mechanism in a laboratory setup comprising computer-generated holography-based transmission and receiving stations.
Results
Generation of beams using computer-generated holography
Computer-generated holography involves computation of the interference pattern between a plane reference wavefront and a user-defined object beam wavefront. The computed interference pattern describes the transmittance of a hologram, which is fabricated as a phase plate or implemented using a spatial light modulator. The object beam wavefront can be reconstructed in one of the diffracted beams when a plane wave is incident on the hologram. Let us consider that the user-defined beam to be generated has the complex amplitude U(x, y) = eiΦ(x, y), where Φ(x, y) is the phase profile of the beam and (x, y) are the coordinates of the hologram plane. The transmittance function of the hologram can be defined as28
Here, Real(U) represents real part of the function U. t(x, y) can define the amplitude transmittance of the hologram in which case the hologram is termed as binary amplitude hologram. A hologram can also be fabricated with π × t(x, y) as the phase delay introduced by the hologram. Such a hologram is termed as binary phase hologram. Thus, the construction of the hologram does not involve any complex algorithms.
Binary hologram can also be constructed considering a single reference wavefront and a multiple (say, k number of) object beam wavefronts. If Φj(x, y) is the phase in the hologram plane of the jth beam then \(U(x,y)=\sum _{j = 1}^{j = k}{e}^{i{\Phi }_{j}(x,y)}\). The transmittance function of the binary hologram can still be defined by Eq. (1). The hologram to generate a single user-defined beam can be termed as singlex hologram, while the hologram to generate multiple user-defined beams can be termed as multiplex hologram.
In the case of the binary phase or amplitude hologram the plot of t against Φ, at certain location (x, y), is a square wave29. Since the Fourier transform of a square wave contains all the odd harmonics, the binary hologram when illuminated by a plane wave results in odd diffraction orders, such as ±1, ±3, ±5, and so on. In addition, the binary amplitude hologram also results in the undiffracted 0 order. In general the nth order diffracted beam, where n is an integer, carries a phase equal to nΦ and has relative power \(\frac{1}{{n}^{2}}\) with respect to the +1 order beam29. Therefore, out of all the diffracted beams, the +1 order beam carries the user-defined phase Φ and has the highest power. Even though the higher-order beams also carry an integral multiple of the user-defined phase profile, yet for most applications including in the present work the +1 order beam is preferred as it has more power than the higher orders. In order to separate the +1 order beam from the other diffracted beams including the 0 order beam, Φ should also include a wavefront tilt, τ(x, y) = τxx + τyy, where (τx, τy) are wavefront slopes with respect to (x, y) axes. Thus, Φ comprises ϕ representing phase difference relative to a plane perpendicular to the beam propagation direction and the tilt τ(x, y) such that Φ(x, y) = ϕ(x, y) + τxx + τyy. To construct the multiplex hologram, we thus need k number of (ϕ, τx, τy) sets. If the light diffracted from the hologram is focused by a lens, the focal spots corresponding to the ±1, ±3, ±5, ⋯ are located relative to the zero order at τc × ( ±τ, ±3τ, ±5τ ⋯ ), where τc is a constant. Thus, one can use an iris diaphragm to isolate the +1 order from the other orders and re-collimate the isolated +1 order to recover the user-defined phase Φ. Figure 1 illustrates the generation of a user-defined wavefront using a binary amplitude hologram. The diffraction efficiency of the +1 order beam, using Fourier series analysis, in the case of binary amplitude hologram is found to be \(\frac{100}{{\pi }^{2}}\)% and in the case of binary phase hologram is found to be \(\frac{400}{{\pi }^{2}}\)%. The diffraction efficiency in the +1 order beam can be increased to 100% by constructing a phase hologram with t(x, y) = Mod(Φ(x, y), 2π), where the function Mod(Φ(x, y), 2π) returns the remainder after division of Φ by 2π. Such a hologram can be termed as blazed grating hologram.
Generation of user-defined wavefront using computer-generated holography: a collimated laser beam is incident on a binary amplitude hologram kept at the front focal plane of the lens L1. The diffracted beams from the hologram are focused by the lens L1 and the Fourier transform of the hologram transmittance function is obtained in the back focal plane of L1. The back focal plane thus contains three prominent focal spots comprising ±1 and 0 order beams, as seen in the surface plot (along with the colorbar). The separation between the ±1 orders from the 0 order is dependent upon the τ(x, y) used to construct the binary hologram and is chosen in such a way that an iris diaphragm can separate the +1 order from the rest. The user-defined phase profile ϕ is realized at the back focal plane of the collimating lens L2 (seen as a surface plot with colorbar). In this figure, both L1 and L2 are assumed to have the same focal length f.
Figure 2 shows examples of (a) a binary singlex phase hologram, (b) a binary multiplex phase hologram, (c) a binary multiplex blazed grating hologram, and the representative focal spot patterns (d → f), resulting from binary and blazed grating holograms. The phase profile of a single light beam can however also be defined directly or non-holographically by using a device such as a deformable mirror, in which case there is no diffraction and the user-defined phase is carried by the undiffracted zero-order beam. Here, the deformable mirror takes a shape proportional to the desired phase profile ϕ(x, y) and a plane wave is incident on the mirror. The reflected beam from the deformable mirror then carries the user-defined phase profile. One can also use a phase-only LCSLM to directly shape the wavefront in the reflected beam.
Examples of (a) binary singlex phase, (b) binary multiplex phase, and (c) binary multiplex blazed gratings holograms, along with the colorbars indicating the phase in radian. (d–f) Representative focal spot patterns in the back focal plane of the lens if each of the holograms (a–c) is placed in the respective front focal plane. In the case of binary phase holograms both +1 and −1 orders are present, while in the case of the blazed grating hologram only the +1 orders are present.
Zernike polynomials as orthogonal aberration modes
Zernike polynomials provide a complete set of orthogonal basis functions defined over a unit circle. In this work, we use Zernike polynomial Zj(r, θ) as described by Noll27, where r and θ are the radial and azimuthal coordinates, with r varying from 0 to 1. Although OAM modes do not form a complete set, there exists other modes, such as Hermite–Gaussian (HG) and Laguerre–Gaussian (LG) modes30, which also form complete sets of orthogonal functions. However, these are complex functions while the Zernike polynomials are real 2D functions. Therefore, owing to the unique properties of the Zernike modes31 defined over a circular area, they are found suitable in most of the optical systems to represent the phase profile of a light beam, which is also a real 2D function, without much bothering about the amplitude profile of the beam. In fact, a few of the Zernike polynomials represent classical aberrations balanced by lower-order aberrations. For instance, (Z5, Z6) represent primary astigmatism, (Z7, Z8) represent primary coma balanced by tilt, and Z11 represents primary spherical aberration balanced by defocus. More details on Zernike modes is available in the Supplementary Note 1. The expressions of the Zernike polynomials can be converted to Cartesian system using \(x=r\cos \theta\) and \(y=r\sin \theta\). The desired phase profile of a beam can be obtained by simply summing the Zernike modes, such as \({\phi }(x,y)=\sum _{j}a_{j}Z_{j}(x,y)\), where aj is the coefficient as well as root mean square (RMS) amplitude or simply amplitude (referred to as ϕRMS) of the Zernike mode Zj in radian. A beam carrying such a phase profile can thus be generated using computer-generated holography technique or non-holographically.
Multiplexing of Zernike modes to encode user information
In this paper, we use one or more number of Zernike modes and multiple ϕRMS of each Zernike mode to describe the phase profile of a laser beam. Use of multiple ϕRMS of each Zernike mode is possible, since aj in principle can be any finite real number. However, when we consider the presence of more than one Zernike mode in the beam then we should take into account the intermodal cross talk, while the modes are measured at the receiving station. We nevertheless can choose combinations of Zernike modes which have the minimal intermodal cross talk with respect to one another32. If we consider n number of Zernike modes, each having m different ϕRMS values, then there will be mn number of unique linear combinations of n Zernike modes. Thus, the user information can be encoded using these mn unique wavefronts of a laser beam to be transmitted through free space in a sequential manner in equal number of modulation cycles of the beam. To be noted that the net power in the beam between different modulation cycles remains unaltered as only the phase profile, and not the amplitude, of the beam gets modified. The user data which can be text, numbers, image, etc. is first converted to base-mn number system (named as base-mn encoding scheme). Figure 3 depicts an example of the encoding scheme using two Zernike modes each with three values of ϕRMS. Thus, there are 32 = 9 number of unique wavefronts each of which can be mapped to the digits of the user data in base-9 number system using a lookup table, such as Table 1. One may of course use a different lookup table involving same or different Zernike mode and ϕRMS combinations. More examples of such lookup tables for other encoding schemes are provided in the Supplementary Note 2. It is important to note that here the multiplexing of the Zernike modes is done digitally and the scheme uses only one phase modulating device to generate a beam carrying the resultant phase profile. Therefore, the transmission station has the flexibility over the number of the aberration modes and the number of ϕRMS values for each aberration mode without any modification of the setup or without requiring any complex hologram computation. It is worth mentioning here that the optimal number of modes and the optimal number of ϕRMS values is in fact a trade-off between the data transmission rate and the bit error rate (BER). The number of aberration modes possible is primarily decided by the pixel resolution of the phase modulating device or the maximum spatial frequency content in case of deformable mirror. While the number of ϕRMS values for each aberration mode is decided by a number of factors, such as pixel resolution of the phase modulator, length of the free-space link and amount of cross talk among the aberration modes. Therefore, practical limit on the maximum number of modes and ϕRMS levels feasible is decided by the spatial frequency content provided by the phase modulating device, the effect of diffraction due to long distance propagation and the intermodal cross talk. In our proposed scheme, we do not attempt to achieve the optimal information content in the transmitted beam. However, with the use of multiple strengths of each mode for a fixed number of aberration modes to encode the user information, our scheme significantly enhances the information carrying capability of the wavefront relative to the cases where only a fixed strength of each mode is possible.
Schematic of the encoding scheme in the transmission station: user data equal to decimal number 200 is converted to 242 in base-9 number system. Linear combinations of two Zernike modes, say Z6 and Z11, each with multiple values of ϕRMS (say ±0.5 or 0 radian), are used to map to different digits of base-9 number using the lookup Table 1 and the information is sent to a phase modulating device. The device uses the digital data to generate corresponding wavefronts in a beam derived from an incident laser beam. Each wavefront representing a certain base-9 digit is transmitted in a sequential manner through free space in three consecutive time slots. Colorbar shows the false colormap in radian of the phase profiles.
Decoding of user information with a type-K wavefront sensor
The laser beam with the user information encoded wavefront travels the free space and is then incident on a modal wavefront sensor at the receiving station. The modal wavefront sensor should be able to measure simultaneously the ϕRMS of all the Zernike modes present over a range of amplitudes. However, the conventional modal wavefront sensors33,34 can measure only small aberration amplitudes and suffer from intermodal cross talk when multiple aberrations are to be measured. If large aberration amplitudes are to be measured with the same accuracy then the sensing operation is carried out in a loop, thereby lowering the sensing frame rate35,36. In our work, we use a recently proposed type-K modal wavefront sensor37 to measure the multiple Zernike modes (referred to as sensor modes) present in the incident wavefront. The type-K sensor estimates the aberrations from the intensity data captured in a single camera image. It has a large range of linear response that can be more the ten times the linear response range of a conventional modal wavefront sensor and ϕRMS of two or more sensor modes can be measured, with reduced intermodal cross talk. The outputs of the type-K sensor (denoted as SK) representing ϕRMS in radian of the sensor modes undergo a thresholding process to take into account any minor deviation between the ϕRMS used during encoding and ϕRMS as estimated. For instance, if the ϕRMS of a Zernike mode during encoding is −0.5 radian, 0, or 0.5 radian, the estimated ϕRMS is compared with some intermediate value between −0.5 and 0, or 0 and 0.5, say −0.25 or 0.25. If the estimated ϕRMS is 0.4 radian, it becomes 0.5 radian after thresholding. The thresholded ϕRMS of all the sensor modes are then converted to a digit of the corresponding number system, using the appropriate lookup table. Figure 4 presents the schematic of the decoding process for the encoded wavefront shown in Fig. 3. Therefore, in our proposed scheme, the sensor modes employed in the wavefront sensor in the receiving station are same as the aberration modes used for encoding in the transmission station. Although use of Zernike modes in wavefront sensors is very common, our scheme facilitates employing the same Zernike modes as information carrier as well.
Schematic of the decoding scheme at the receiving station: the wavefront from the transmission station is incident on a type-K modal wavefront sensor at the receiving station. The receiving station has a priori the key information regarding the Zernike modes used, such as Z6 and Z11 and their strengths, to design an appropriate type-K hologram (such as the one shown in the inset). For a given incident wavefront the type-K hologram generates a focal spot pattern, such as the one shown in the inset. The focal spot pattern is employed to obtain the sensor outputs for all the Zernike modes used during encoding. The type-K sensor outputs, such as b6 and b11, are first thresholded and then the ϕRMS values after thresholding (such as 0, −0.5, or 0.5 radian) are converted to appropriate base-n digit using the lookup table (such as Table 1 for base-9). Thus, the receiving station a priory needs to have the lookup table. Each wavefront incident on the type-K sensor results in one digit of the base-n number system and base-n digits corresponding to all the wavefronts received at different time slots are converted to the user data.
The type-K modal wavefront sensor comprises primarily a multiplex hologram called the type-K hologram and a camera. The hologram generates a set of +1 order beams for each sensor mode for a given incident wavefront. The hologram effectively adds or subtracts specific amount of the sensor mode to the phase profiles of these +1 order beams. The central intensities of the set of +1 order focal spots are then used to calculate the type-K sensor output SK. Figure 4 inset shows a representative type-K hologram and the resulting +1 order focal spots pattern. The focal spots pattern comprises 30 focal spots, arranged in concentric circles, for three sensor modes with ten focal spots to estimate each sensor mode. There is one more focal spot at the center that corresponds to a +1 order beam without any addition or subtraction of aberration by the hologram. More details of the type-K sensor is available in the Supplementary Note 3.
It is to be noted that for correct decoding of the user information, the receiving station should have two key information, one is the number and types of aberration modes used for encoding (required to design the type-K hologram) and the other is the lookup table (required to connect the sensor outputs to the appropriate base-n digit). As the beam propagates through the free space, it undergoes certain amount of divergence, depending on the distance traveled and to some extent on the types of the orthogonal aberration modes used. Divergence thus suffered by the Zernike modes can effect the orthogonality among the modes, which may result in enhanced cross talk between various modes. Therefore, if such cross talks are to be minimized and the same size of the type-K hologram is to be used for all the distances traveled by the beam, the incident beam is first to be demagnified. Instead one may also image the beam aperture in the transmission station to the receiving station. Besides the type-K sensor output may require to be scaled (normalized) before the same is used for decoding the user data. A demonstration using numerical simulation to show how diffraction affects the light beam carrying Zernike modes after it propagates long distances can be found in Supplementary Note 4. It can be seen that in spite of the diffraction suffered, after the demagnification of the beam aperture, various modes can be detected without any noticeable intermodal cross talk.
Experimental implementation
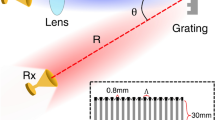
We develop a proof-of-principle setup to demonstrate the working principle of the proposed information transfer. A schematic of the experimental arrangement comprising the transmission station based on a ferroelectric LCSLM (LCSLM1) acting as the binary hologram and a receiving station based on a type-K hologram written on a nematic LCSLM (LCSLM2), separated by a distance of 2.4 m, is seen in Fig. 5(a). Figure 5(b–d) shows some experimental focal spot patterns resulting from the type-K hologram. Instead of using holographic means the transmission station can use a direct (i.e., non-holographic) wavefront shaping device, such as a deformable mirror. A deformable membrane mirror may provide wavefront modulation at frame rates upto tens of KHz. Besides the type-K hologram instead of being implemented using an LCSLM can also be fabricated as a phase plate. The decoding speed can be enhanced significantly by using a set of point photo detectors to record the central intensities of the focal spots instead of the camera.
Schematic of the free-space optical communication system: (a) a collimated laser beam is incident on a reflective ferroelectric LCSLM (LCSLM1). LCSLM1 displays singlex binary holograms sent by PC1 at a rate of 1440 Hz. The user information is encoded as ϕRMS of Zernike modes present in the +1 order beam diffracted from the singlex binary hologram. The beam after traveling the free space is incident on another reflective LCSLM (LCSLM2) that displays an appropriate type-K multiplex hologram via PC2. The resulting +1 order focal spots are captured by a digital camera connected to PC2 that decodes the user information. In this implementation, the two LCSLMs, although not essentially required, are kept in optically conjugate planes. More details of the experimental implementation is found in the “Methods” section. Experimental focal spot patterns (for a plane incident wavefront) of the type-K sensor corresponding to (b) base-9 encoding scheme (using sensor modes Z6 and Z11), (c) base-25 encoding scheme (using sensor modes Z5 and Z11), and (d) base-27 encoding scheme (using sensor modes Z5, Z6, and Z11). (e) Experimental type-K sensor outputs over several camera frames, in the presence of turbulence introduced by a table fan, before external perturbation compensation and (f) after external perturbation compensation. The table fan is positioned at the left of the camera so that the resulting wind affects the information carrying beam over the entire stretch starting from the beam splitter BS to the camera. (g) Screen shot of the oscilloscope showing the display timings of LCSLM1 at 1440 Hz and the timings of user wavefront generation at an interval of tw. Also seen is the schematic of the sequence of reference and information carrying wavefronts from the transmission station, over a duration of 16.67 ms.
External perturbations compensation
We first assess the consistency of accurate decoding of user data over a period of time. We encode the wavefront in the transmission station using three Zernike modes, Z5, Z6, and Z11 and estimate the strengths of the same three modes in the receiving station using the type-K sensor. We notice that owing to the movement and externally caused perturbations in the information carrying beam, the values of ϕRMS at the receiving station fluctuates to some extent over time even though there is no change in the aberration strengths from the transmission station. To be noted that for indoor applications the effect of turbulence will be insignificant, however, for outdoor applications the same will play a very important role. Therefore, to test the effectiveness of our turbulence compensation scheme in the case of outdoor applications, we use a table fan to create instability in the air in between the two stations so as to enhance the fluctuations in SK. The table fan creates a circulating turbulent air with an average speed between 4 and 5 m/s, which introduces random aberrations in the transmitted beam. Introduction of such aberrations leads to the degradation of Strehl ratio from the ideal (i.e., aberration free) value of 1. We estimate the effect of the turbulence for our setup created by the table fan in terms of a Strehl ratio of ~0.3. Figure 5(e) shows such an induced case of sensor output variation over different measurement frames when a fixed combination of ϕRMS = (0, 0.5, 0) of (Z5, Z6, Z11) is transmitted. Figure 5(g) shows the binary pattern display timing of the LCSLM1 at the rate of 1440 Hz. However due to limited frame rate of the camera, we display binary holograms at the rate 360 Hz only with an interval of tw, as seen in the right panel of the same figure. In order to make SK steady against the perturbations, we modify the transmission scheme of the encoded wavefronts, such that each information carrying wavefront is preceded by a reference plane wavefront as depicted in the right panel Fig. 5(g). The reference wavefront when incident on the type-K hologram results in a reference focal spot pattern whose central focal spot location gives a measure of beam movement. The same central focal spot can also be used to get a measure of the intensity fluctuations in the transmitted beam. Since the Zernike modes form a complete set of basis functions, any arbitrary change in the reference phase profile introduced by the perturbation can be expressed as a linear combination of a subset of the Zernike modes31. Therefore, primary effect of perturbation other than the beam movement can be estimated from a measure of the type-K sensor outputs corresponding to the reference wavefront. Since type-K sensor has a linear response range upto several radian of ϕRMS for each sensor mode, corrected SK for each information frame can be obtained, after beam movement compensation, as SK (information frame) – SK (preceding reference frame). Thus, the maximum strength of the perturbation that can be compensated by the scheme is decided by the linear range provided by the type-K sensor, which can be set as per the requirement subject to the spatial resolution available in the type-K hologram37. More details about the perturbation compensation scheme is available in the Supplementary Note 5. On application of the perturbation compensation, the type-K sensor in the receiving station provides a much more consistent measure of the sensor modes, as indicated by the plot in Fig. 5f. The compensation scheme to be effective the nature of the external perturbation should not vary between the reference wavefront and the following information wavefront. In the case of rapid variation in perturbation, the wavefront modulation should take place at a rate at least twice that of the perturbation variation rate.
Therefore, the perturbation compensation scheme addresses the issue of atmospheric turbulence using the same wavefront sensor, which is used for the decoding of the transmitted beam. Moreover the compensation does not involve any optical correction of the beam as is done in an adaptive optics system. However, to be noted that subtraction of the effect of turbulence as proposed in our scheme will not work if the light beam is encoded using modes, which do not form a complete basis set of real orthogonal functions. Hence, such a perturbation compensation scheme can not be adapted to OAM, LG, or HG modes-based FSO systems. We show in Supplementary Note 5 how our scheme utilizes the completeness property of the Zernike modes and why such a scheme will not work with OAM modes.
Discussion
We choose the three Zernike mode combinations (Z5, Z6, Z11) to encode the user data. In our first experiment, we transmit a gray scale image of size 65 × 50 pixels with each pixel as an 8 bit integer. The image pixels are encoded using base-3, 5, 9, 25, and 27 encoding schemes. At the receiving station, the wavefronts are decoded both without perturbation compensation and with perturbation compensation. It can be seen in the Supplementary Note 2 that base-3 and 5 encoding schemes use a single Zernike mode, while base-9 and 25 encoding schemes use two Zernike modes. However due to use of multiple strengths (i.e., amplitudes) for each mode, the information content of m number of wavefronts in the case of base-5 scheme has increased by \(\frac{{5}^{m}-1}{{3}^{m}-1}\times 100\)% relative to base-3 scheme, and the same for base-25 has increased by \(\frac{2{5}^{m}-1}{{9}^{m}-1}\times 100\)% relative to base-9 scheme. In our base-25 encoding scheme, the maximum number of unique information (i.e., the largest integer value) carried by the beam over eight modulation cycles is estimated to be 258 − 1 = 1.5259 × 1011. Instead if we consider OAM mode-based systems using same number (i.e., two) of modes as the base-25 scheme, with different l values, over eight modulation cycles the maximum number is estimated to be 48 − 1 = 65535. Details of this comparison of information content in the beam using fixed number of modes can be found in Supplementary Note 6. The effective rate of data transfer in our proposed scheme is decided by both the encoding scheme and minimum interval (i.e., time period of one modulation cycle) at which the user-defined wavefront can be shaped by the phase modulating device. In our experiment with a modulation frequency of 360 Hz and data transfer using 180 wavefronts per second with perturbation compensation on, the data transmission speed is kept at 4.5 and 4.86 Kbits/s for base-25 and base-27 encoding scheme, respectively.
Figure 6(a) shows the original image transmitted, and Fig. 6(b–f) show the detected images with perturbation compensation when the data is transmitted using different encoding schemes. It is noticed that in the case of base-3 and base-9 encoding schemes the image is detected without a single wrong pixel. Although in the other cases there is an error of maximum one to four pixels, even though there is still no major observable defects in the detected images. In order to further increase the external perturbation, we use the table fan to introduce turbulence in the medium. The directly detected image transmitted as base-25 numbers which travel through the turbulent air is seen in Fig. 6(g) showing several wrong pixels. However on application of perturbation compensation, the number of wrong pixels reduces drastically as seen in Fig. 6(h).
(a) Original image sent by the transmission station. (b–d) Images (experimental) as detected with external perturbation compensation when the user data is transmitted using base-3, base-5, and base-9 encoding schemes, respectively. (e, f) Images (experimental) as detected with external perturbation compensation when the user data is transmitted using base-25 and base-27 encoding schemes, respectively. Images (experimental) as detected (g) without external perturbation compensation and (h) with external perturbation compensation, when the user data is transmitted through turbulent air created by a table fan and using base-25 encoding scheme.
The BERs of image transmissions as presented in Fig. 6 are shown in Table 2. It is observed that BER which is 0.0498 in the case of Fig. 6(g) has improved to 0.0047 in the case of Fig. 6(h).
We then perform yet another experiment to transmit a set of 8 bit integers and alphabets in a similar manner as the above experiment. The results presented in Table 3 confirm that when the user data at the receiving station is decoded with perturbation compensation, the effect of perturbation significantly gets eliminated. Accuracy of the transmission increases when the data is encoded as base-3 and base-5 numbers.
The relatively small number of wrong detections of user data in some of the schemes is attributed to the low modulation frequency of 360 Hz, owing to the limitation of the camera used in the present setup. Even a threefold increase in the modulation frequency should make the perturbation compensation much more effective so as to eliminate wrong detection of user data altogether in all the schemes. Under extreme cases of turbulence, use of an encoding scheme with a smaller base such as base-3 and choosing larger separation between ΦRMS values, such as 0, ±1 instead of 0, ±0.5, will further improve the perturbation compensation. The use of smaller base in combination with blazed grating implementation of the type-K hologram will also improve the signal to noise ratio in the receiving station, in the case of significant drop in signal levels in a long distance free-space link. Further the base-27 scheme due to the use of three different Zernike modes simultaneously can be adapted to error correcting schemes, such as triple-modular redundancy code38. The three modes carrying copies of the same information which pass through the same atmospheric link, however, may get affected differently by turbulence. Therefore triple-modular redundancy code may work efficiently to reduce the BER although at the cost of the transmission speed.
To conclude, we have demonstrated free-space information transfer using a laser beam whose wavefront is encoded with a linear combination of Zernike modes, which form a complete set of orthogonal basis. User information is converted to amplitudes of one or more Zernike modes using multiple amplitude values for each Zernike mode. Multiplexing of modes is done digitally without involving any computationally intensive step and a single-phase modulating device is used to transmit the data, as sequentially transmitted wavefronts of a single beam without affecting the net power in the beam. Use of a complete set of orthogonal functions and multiple amplitudes of a single mode, to encode the wavefront, opens the door toward reaching optimum limit of information content in the beam. The receiving station uses a type-K modal wavefront sensor that provides amplitudes of all the Zernike modes present in the incident wavefront from just one measurement using a camera. The use of the type-K sensor enables measurement of both small, as well as large amplitudes of each Zernike mode with the same accuracy. We have also demonstrated a scheme to compensate for external perturbations, such as turbulence in the air, without requiring any additional optical arrangement, so as to make the information transfer steady. Therefore, in addition to indoor applications where the effect of turbulence is limited, our scheme is expected to be ideal for outdoor applications as well when turbulence is present. The proposed information transfer scheme has a built in security feature against eavesdropping since the receiving station must a priori know the number, types, and amplitudes of the Zernike modes used and the lookup table mapping the Zernike mode amplitudes with the user data. In our scheme, we do not use intensity or power associated with a given mode as a degree of freedom to increase the information content as can be done in the OAM mode-based system. In lieu of the intensity, our scheme uses the amplitude of the Zernike mode as a degree of freedom, which unlike intensity of an OAM mode is less susceptible to external factors due to our compensation scheme and also more secured against eavesdropping. Our experimental arrangement however can be considered as a proof-of-principle setup only and the same was not optimized in the terms of speed, accuracy, information content in the wavefront, and the distance traveled in free space. There is nevertheless an equivalent scope in the proposed scheme, similar to the OAM mode-based systems, to further enhance the information content of the beam by incorporating polarization and wavelength division multiplexing over and above the Zernike mode division multiplexing.
Methods
Construction of binary hologram in the transmission station
Binary hologram to generate the +1 order beam carrying user-defined phase profile ϕ(x, y) with (x, y) = −1 → +1 is constructed over 480 × 480 pixels using τx = 165π and τy = −41π. An appropriate linear combination of Zernike modes Zj(x, y) constitutes ϕ(x, y) and t(x, y) is computed using \(U(x,y)={e}^{i[\phi (x,y)+{\tau }_{x}x+{\tau }_{y}y]}\) in Eq. (1). t(x, y) is multiplied by a unit circle centered at (x, y) = (0, 0) and is then converted to a binary image to be displayed on the ferroelectric LCSLM (ForthDD, SXGA-R3), which has a pixel pitch = 13.62 μm. To be noted that the +1 order beam from the LCSLM has some residual aberrations which may be corrected holographically in order to get a near ideal +1 order beam.
Incident laser beam
The beam incident on the binary hologram on the ferroelectric LCSLM is derived from a He–Ne Laser (wavelength = 632.8 nm, output power = 10 mW). Experiments are performed at ≈50% of the laser power. The +1 order beam carrying the user information has a diameter of ≈6.5 mm.
Construction of the type-K hologram
The type-K multiplex binary holograms are constructed over 750 × 750 pixels and are displayed as binary images on a nematic LCSLM (HoloEye LC-R-1080) that has a pixel pitch = 8.1 μm. t(x, y) is computed using k sets of (ϕ(x, y), τx, τy), where k = 11 for base-3 and 5 encoding schemes, k = 21 for base-9 and 25 encoding schemes, and k = 31 for base-27 encoding scheme. The +1 order beam at the center of the type-K focal spot pattern has τx = 153.8π and τy = 100.9π. For the base-3 encoding scheme, the type-K hologram generates five pairs of bias beams with av = (−1, −0.5, 0, 0.5, 1) radian to detect a single sensor mode. These beams are directed to form a circle using relative tilt with respect to the central beam (defined as Δτ = \(\sqrt{\Delta {\tau }_{x}^{2}+\Delta {\tau }_{y}^{2}}\)) as 21π. For the base-5 encoding scheme, the type-K hologram generates five pairs of bias beams with av = (−1.5, −0.75, 0, 0.75, 1.5) radian to detect a single sensor mode. These beams are also directed to form a circle using Δτ = 21π. Type-K holograms for base-9 and base-25 encoding schemes are designed for two sensor modes using av = (−1, −0.5, 0, 0.5, 1) and av = (−1.5, −0.75, 0, 0.75, 1.5) for each sensor mode, respectively. For both encoding schemes bias beams are directed to form two concentric circles using Δτ = 14π and 24.5π. Type-K hologram for base-27 encoding scheme is designed for three sensor modes using av = (−1, −0.5, 0, 0.5, 1) for each sensor mode and the bias beams are directed to form three concentric circles using Δτ = 11.5π, 21π, and 30π. The bias beams for each type-K hologram use b = 0.7 radian.
Camera used in the type-K wavefront sensor
The focal spot pattern resulting from the type-K hologram is recorded by a CMOS camera (Basler, A504K) having pixel resolution = 1280 × 1024, pixel pitch = 12 μm, bit depth = 8 bit, and a full frame rate = 500 fps.
Data availability
All relevant data are available from the corresponding author upon reasonable request.
References
Chan, V. W. Free-space optical communications. J. Lightwave Technol. 24, 4750–4762 (2006).
Khalighi, M. A. & Uysal, M. Survey on free space optical communication: a communication theory perspective. IEEE Commun. Surv. Tutor. 16, 2231–2258 (2014).
Elgala, H., Mesleh, R. & Haas, H. Indoor optical wireless communication: potential and state-of-the-art. IEEE Commun. Mag. 49, 56–62 (2011).
Liang, T. et al. Secure multiple access for indoor optical wireless communications with time-slot coding and chaotic phase. Opt. Express 25, 22046–22054 (2017).
Wang, G. et al. Highly efficient optical beam steering using an in-fiber diffraction grating for full duplex indoor optical wireless communication. J. Lightwave Technol. 36, 4618–4625 (2018).
Chun, H. et al. A wide-area coverage 35 gb/s visible light communications link for indoor wireless applications. Sci. Rep. 9, 4952 (2019).
Gibson, G. et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 12, 5448–5456 (2004).
Willner, A. E. et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 7, 66–106 (2015).
Padgett, M. J. Orbital angular momentum 25 years on. Opt. Express 25, 11265–11274 (2017).
Willner, A. E. et al. Recent advances in high-capacity free-space optical and radio-frequency communications using orbital angular momentum multiplexing. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 375, 20150439 (2017).
Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 6, 488–496 (2012).
Huang, H. et al. 100 tbit/s free-space data link enabled by three-dimensional multiplexing of orbital angular momentum, polarization, and wavelength. Opt. Lett. 39, 197–200 (2014).
Zhu, L. & Wang, J. Simultaneous generation of multiple orbital angular momentum (oam) modes using a single phase-only element. Opt. Express 23, 26221–26233 (2015).
Fu, S. et al. Experimental demonstration of free-space multi-state orbital angular momentum shift keying. Opt. Express 27, 33111–33119 (2019).
Padgett, M. J., Miatto, F. M., Lavery, M. P., Zeilinger, A. & Boyd, R. W. Divergence of an orbital-angular-momentum-carrying beam upon propagation. N. J. Phys. 17, 023011 (2015).
Saghafi, S. & Sheppard, C. The beam propagation factor for higher order gaussian beams. Opt. Commun. 153, 207–210 (1998).
Boluda-Ruiz, R., García-Zambrana, A., Castillo-Vázquez, B. & Qaraqe, K. Secure communication for fso links in the presence of eavesdropper with generic location and orientation. Opt. Express 27, 34211–34229 (2019).
Paterson, C. Atmospheric turbulence and orbital angular momentum of single photons for optical communication. Phys. Rev. Lett. 94, 153901 (2005).
Lavery, M. P. Vortex instability in turbulent free-space propagation. N. J. Phys. 20, 043023 (2018).
Cox, M. A., Cheng, L., Rosales-Guzmán, C. & Forbes, A. Modal diversity for robust free-space optical communications. Phys. Rev. Appl. 10, 024020 (2018).
Yan, X. et al. Probability density of orbital angular momentum mode of autofocusing airy beam carrying power-exponent-phase vortex through weak anisotropic atmosphere turbulence. Opt. Express 25, 15286–15298 (2017).
Yan, X., Guo, L., Cheng, M. & Li, J. Controlling abruptly autofocusing vortex beams to mitigate crosstalk and vortex splitting in free-space optical communication. Opt. Express 26, 12605–12619 (2018).
Li, J., Zhang, M., Wang, D., Wu, S. & Zhan, Y. Joint atmospheric turbulence detection and adaptive demodulation technique using the cnn for the oam-fso communication. Opt. Express 26, 10494–10508 (2018).
Yin, X. et al. Adaptive turbulence compensation with a hybrid input–output algorithm in orbital angular momentum-based free-space optical communication. Appl. Opt. 57, 7644–7650 (2018).
Mphuthi, N. et al. Free-space optical communication link with shape-invariant orbital angular momentum bessel beams. Appl. Opt. 58, 4258–4264 (2019).
Li, S., Chen, S., Gao, C., Willner, A. E. & Wang, J. Atmospheric turbulence compensation in orbital angular momentum communications: Advances and perspectives. Opt. Commun. 408, 68–81 (2018).
Noll, R. J. Zernike polynomials and atmospheric turbulence. JOSA 66, 207–211 (1976).
Neil, M., Wilson, T. & Juskaitis, R. A wavefront generator for complex pupil function synthesis and point spread function engineering. J. Microsc. 197, 219–223 (2000).
Boruah, B. R. Dynamic manipulation of a laser beam using a liquid crystal spatial light modulator. Am. J. Phys. 77, 331–336 (2009).
Hasegawa, T. & Shimizu, T. Frequency-doubled hermite–gaussian beam and the mode conversion to the laguerre–gaussian beam. Opt. Commun. 160, 103–108 (1999).
Mahajan, V. N. Zernike circle polynomials and optical aberrations of systems with circular pupils. Appl. Opt. 33, 8121–8124 (1994).
Konwar, S. & Boruah, B. R. Estimation of inter-modal cross talk in a modal wavefront sensor. OSA Contin. 1, 78–91 (2018).
Neil, M. A., Booth, M. J. & Wilson, T. New modal wave-front sensor: a theoretical analysis. JOSA A 17, 1098–1107 (2000).
Booth, M. J. Direct measurement of zernike aberration modes with a modal wavefront sensor. Proc. SPIE 5162, 79–91 (2003).
Neil, M. A. A., Booth, M. J. & Wilson, T. Closed-loop aberration correction by use of a modal zernike wave-front sensor. Opt. Lett. 25, 1083–1085 (2000).
Dong, S., Haist, T., Osten, W., Ruppel, T. & Sawodny, O. Response analysis of holography-based modal wavefront sensor. Appl. Opt. 51, 1318–1327 (2012).
Konwar, S. & Boruah, B. R. Improved linear response in a modal wavefront sensor. J. Opt. Soc. Am. A 36, 741–750 (2019).
Lyons, R. E. & Vanderkulk, W. The use of triple-modular redundancy to improve computer reliability. IBM J. Res. Dev. 6, 200–209 (1962).
Acknowledgements
The authors wish to acknowledge the financial support from the Department of Electronics and Information Technology (DeitY), India, vide its letter no. 12(4)/2011-PDD.
Author information
Authors and Affiliations
Contributions
B.R.B. with input from S.K. conceived the experiment. S.K. developed the experimental setup and performed the experiment. Manuscript was prepared with contributions from both the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Konwar, S., Boruah, B.R. Leveraging the orthogonality of Zernike modes for robust free-space optical communication. Commun Phys 3, 203 (2020). https://doi.org/10.1038/s42005-020-00468-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00468-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.