Abstract
Real-time observation of the emergence of coherent structures from noise via instabilities is of particular interest across disciplines ranging from biology to astrophysics. In the context of photonics, ultrafast fibre lasers provide an ideal test-bed for experimental observation of dynamical instabilities and generation of coherent structures of ultrashort pulses. Here we present experimentally obtained switch-on dynamics of counter-propagating ultrashort pulses in a bidirectional mode-locked fibre laser with delayed pulse formation via Q-switched and modulation instabilities, pronounced central wavelength drift, with the multiple-pulse formation. We define a localisation parameter using the round-trip resolved autocorrelation function to quantify the extent of the pulse formation, indicating an energy interchange between coherent features and background radiation. Furthermore, we report the formation of synchronised and unsynchronised dispersion waves. Our results reveal the complexity of the establishment of coherent features and their interaction with background radiation, contributing further towards the understanding of nonlinear systems in general.
Similar content being viewed by others
Introduction
Mode-locked fibre lasers giving rise to stable ultrashort pulses are widely used across scientific disciplines1,2. The pulse characteristics and dynamics are governed by an interplay of gain, loss, nonlinearity, and dispersion, giving rise to self-organised features like solitons. The soliton concept is highly interdisciplinary3 and related to Bose–Einstein condensates4, hydrodynamics and plasmas5. Modern laser systems produce a diversity of soliton-like structures such as self-similar pulses6, noise-like pulses7 and under certain circumstances, coherent bound states8 that operate as soliton molecular complexes9.
The availability of real-time measurement techniques like spatio-temporal dynamics, time lenses10, Dispersive Fourier Transform (DFT)11 and others have enabled the observation of self-organisation of such coherent features12 and their complexes13, soliton interactions14 and soliton explosions15. Such real-time approaches also enable observation of build-up dynamics of various ultrashort pulses. For example, the DFT technique16,17 has confirmed the origination of ultrashort pulses from intensity fluctuations on the noise floor, shaped further via modulation instabilities12 or Q-switched dynamics (modulation of quality factor Q of the laser cavity)18. These studies have shown an essential role of instabilities in pulse formation. The DFT technique helped to detect transitions dynamics of ultrashort processes19,20 and reveal the pulsating nature of ultrashort pulses21 and repetitive soliton explosions22. All this information substantially increases the knowledge of soliton behaviour and dynamics in nonlinear systems.
Bidirectional fibre lasers present unique systems allowing directionally uninhibited generation, resulting in complex dynamics and interactions between counter-propagating beams. In bidirectional lasers, counter-propagating pulses interact in two ways: direct interaction of pulses (colliding) and indirect interactions due to time-dependent parameters of laser cavity components (such as saturable absorber or active media). These interactions and underlying physical processes significantly stand out from interactions of co-propagating pulses23 or, for example, within bound soliton states19. First works on bidirectional generation have presented the technique of colliding mode-locking, where two oppositely directed pulses interacted in a thin saturable absorber24. Further progress in bidirectional ultrafast fibre laser development demonstrated their potential for applications in detecting angular movements25,26,27 and dual-comb spectroscopy28,29. Y. Yu et al. demonstrated the similarity of dissipative solitons build-up dynamics in bidirectional mode-locked laser with normal-net cavity dispersion30. Still, the reports on the fundamentals of bidirectional ultrafast generation are rare.
Here, we present the mutual switch-on dynamics of counter-propagating solitons in a bidirectional hybrid mode-locked Erbium-doped ring fibre laser using spatio-temporal and DFT measurements. We show the formation of Q-switched mode-locked (QML) pulses and their role in further pulse evolution, including the formation of multi-soliton structures. Coherent complexes of two and three solitons are obtained involving complex dynamics such as collisions with the emission of dispersive waves (DWs). For a better understanding, we calculate the pulse-to-pulse energy variations and define a localisation parameter to track shot-to-shot energy redistribution for each of counter-propagating pulses. Strong blue-shift of the central wavelength of up to 9 nm at the pulse stabilisation stage of the less energetic counter-clockwise pulse is also experimentally observed. The final formation of a stable pulse from a QML pulse is also presented. Here, we experimentally observe the existence of synchronised and unsynchronised dispersive wave radiation, which was recently predicted only theoretically31. We demonstrate that redistribution of energy between the counter-propagating directions take a key role in the formation of persistent bidirectional mode-locked generation. Throughout the entire dynamics and stable propagation, except for central wavelength shift, counter-propagating pulses have had identical repetition rates. In contrast, in our previous work32, both pulses had a slight mismatch in repetition rates. Although recorded several dozens of switch-on dynamics demonstrate similar features mentioned above, there has been no preferred sequence of events or single pathway to stable mode-locking generation. The current work presents an extension of our previous efforts of discovering build-up phenomena in bidirectional lasers, where the formation of pulses from continuous-wave radiation by adjustment of polarisation controllers was discussed32. The existence of myriad phenomena and events shows the potential of bidirectional ultrafast laser platform to serve as an efficient test-bed for the investigation of complex dynamics of nonlinear systems in general.
Results
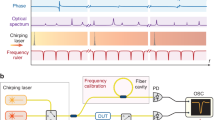
The experimental and measurement setup of bidirectional mode-locked fibre laser is depicted in Fig. 1a. The pump power was set at 97 mW, which was the threshold of colliding mode-locked generation. Summarily, bidirectional ring Er-doped fibre laser, mode-locked by carbon nanotube saturable absorber and nonlinear polarisation evolution, in a steady-state generates near transform-limited 790 and 570-fs soliton pulses at 1555 nm central wavelength and 14.78 MHz repetition rate in both directions33. The phenomenon of identical central wavelengths of counter-propagating solitons refers to the colliding mode-locking34,35. The output power was 1 mW in a clockwise direction, and 0.4 mW in a counter-clockwise direction. However, the direction with the highest energy was governed by adjustment of PCs that highlight the influence of nonlinear polarisation rotation on pulse formation33. One direction always dominated, and no generation with equal pulse energies was obtained in our experiments. Figure 1b, c present the complete picture of the build-up dynamics of the clockwise (CW) and counter-clockwise (CCW) pulses in the bidirectional mode-locked fibre laser recorded via DFT technique (see ‘Methods’ section). Figure 1d, e show optical spectra recorded with an optical spectrum analyser (Yokogawa) and the DFT measurements with sech2-function approximation that show good correlation. Figure 1f shows the evolution of pulse energies over round trips (the spatio-temporal dynamics is shown in Fig. S1 in Supplementary Information). Pulse establishment for both directions took approximately 70 thousand round trips (4.8 ms) with the following events: formation of an unstable mode-locked pulse with experienced spectra blue-shift (Stage ‘Central wavelength drift’), soliton breakup (Supplementary Note S2) with a transition into Q-switched instabilities generation (Stage ‘Q-switched instabilities’), the formation of soliton complexes and soliton collision (Stage ‘Soliton complexes’) and final evolution of stable mode-locked pulse generation from a Q-switched pulse (Stage ‘Final formation and propagation dynamics of stable bidirectional soliton generation’). Similar to unidirectional mode-locked lasers, the pulse formation always initialised through modulation instability12. It should be mentioned that the repetition rates are slightly different during Q-switched instabilities than in a mode-locked generation owing to the effect of the nonlinear refractive index and a slight central wavelength offset of Q-switched instabilities. Although we show only one build-up dynamics in the main manuscript that is the most representative, the following analysis and inferences are applicable to observed build-up dynamics in general.
a The experimental setup of bidirectional mode-locked ring fibre laser for the dispersive Fourier transform (DFT) measurements. SWNT single-walled carbon nanotubes, ISO optical isolator, OC optical coupler, WDM wavelength division multiplexer. Spectral switch-on dynamics in bidirectional mode-locked laser: b clockwise (CW) and c counter-clockwise (CCW) directions. Averaged over 100 round trips DFT spectra with sech2-function approximation (black dashed line), spectra from optical spectrum analyser (OSA) are depicted for d clockwise and e counter-clockwise direction. f Dynamics of the round trip pulse energies.
Central wavelength drift
We have observed the phenomena of central wavelength shift multiple times during the build-up process. The most sustainable shifts have appeared after the first pulse formation from intensity spike (3–10 thousand round trips) and secondly at 45–50 thousand round trips. Figure 2 shows the second central wavelength shift as it was more prominent, though the dynamics remain the same. The shift of the central wavelength always manifested at the early stages of pulse formation only in the less energetic counter-clockwise pulse. The total wavelength blue-shift was 9 nm, which is significantly higher than previously demonstrated16,36. To achieve high precision of measurements of the central wavelength dynamics, we have simultaneously recorded the pulse intensity dynamics in temporal and spectral domains (Fig. 2). For more details of the measurement technique, please, see the ‘Methods’ section.
Initially, before the occurrence of soliton blue-shift, the repetition rates in both directions were the same. Therefore, the counter-propagating pulses always collided at the same two points inside the laser cavity. These interaction points can be derived by a knowledge of the time delay between the counter-propagating pulses. By taking these parameters into account, we can conclude that the counter-propagating pulses have interacted in the carbon nanotube saturable absorber. The central wavelength drift resulted in a difference in the repetition rate of the counter-clockwise pulse and de-synchronisation of the repetition rates. Consequently, the points of soliton collision inside the laser cavity started to change. From the knowledge of the change in the time delay between counter-propagating pulses and their repetition rates, we calculated a total shift of 1.1 m from the original interaction point in the saturable absorber before the counter-clockwise pulse disappeared (see Supplementary Note S1). The counter-propagating generation, obtained after the soliton blue-shift, occurred at wavelengths close to 1555 nm with synchronised repetition rates and collision point in the saturable absorber. These dynamics indicate that colliding mode-locking is a dominant factor over pulse formation and governs the synchronised regime through the steady-state bidirectional generation.
The lack of simulation models of bidirectional mode-locked fibre lasers does not allow an explicit investigation of the underlying phenomena of the observed spectral blue-shift of one of the pulses. It is known, that interaction of co-propagating solitons or soliton with co-propagating continuous-wave radiation can result in soliton deceleration or acceleration23,37,38. Our experiments demonstrate, that the counter-clockwise soliton experiences acceleration (decrease in cavity round-trip time) during blue-shift in net-anomalous dispersion cavity (dn/dω < 0), which can be induced by interacting with counter-propagating soliton and DWs. In addition, the 9-nm-shift in central wavelength can be caused by gain saturation39, gain competition effects and higher gain of Erbium-doped fibre. This effect was accompanied by a loss of pulse energy, while in the counter-propagating direction, the surplus energy increased due to the law of total energy conservation (Fig. 3f). This phenomenon highlights a complex interrelation between energies of counter-propagating beams that is mediated by gain saturation and gain dynamics. We also observed that the phenomena of central wavelength shift always occurs only in the direction with less energy. That makes the less energetic direction more sensitive to soliton perturbation, including central wavelength changes. The central wavelength shift also leads to its inability to maintain nonlinear polarisation rotation condition, eventually leading to a decrease in energy and its dissipation and disappearance. The breakup of the pulse after central wavelength shift (Supplementary Notes S2 and S6) induces excess energy in the counter-propagating direction that was observed to lead to two different scenarios: stage ‘Q-switched instabilities’ formation of Q-switched instabilities or stage ‘Soliton complexes’-formation of multi-soliton.
Q-switched instabilities
Stage ‘Q-switched instabilities’ featuring Q-switch instabilities was observed after the breakup of the mode-locked generation at around the 12 thousandth round trip. The Q-switched instabilities occurred in both directions and lasted for approximately 40 thousand round trips (2.7 ms). The Q-switch repetition rate was 25 kHz (which corresponds to repetition period of 40 μs) with a FWHM duration of 4 μs, i.e. approximately equivalent to 60 round trips of the steady-state mode-locked regime. Here, the laser is operating in Q-switched mode-locking regime, i.e. the radiation had an intensity envelope of a Q-switched pulse with high energy and filled with ultrashort pulses40,41. Part of the energy of instabilities was contained in quasi-continuous-wave radiation (usual Q-switched pulse with a duration much longer than the round-trip time) that preceded the localised ultrashort structures. Typical spectra of ultrashort pulses during Q-switched instability is shown in Fig. 3. In general, Q-switched instabilities are caused by relaxation oscillations of the gain media and due to long upper-state lifetime of Er3+ ions in silica fibre41. The occurrence of such instabilities indicates that the laser was operating close to the lasing threshold42. Unlike the other work36, where the transition from Q-switch to mode-locking was achieved by increasing the pump power, the transition dynamics observed here occurred naturally without any further changes in pump power. Q-switched instabilities are not a necessary step for bidirectional mode-locking operation, but it appears after strong modulation of background radiation (quasi-continuous-wave radiation) or after the breakup of quasi-stable mode-locking generation. Supplementary Note S3 shows more information on presented Q-switched instabilities.
Soliton complexes
Stage ‘Soliton complexes’, corresponding to the formation of soliton complexes, was observed between 42 and 45 thousand round trips. A prerequisite for the multi-soliton formation is excessive energy in the dominant direction after Q-switched burst or intensity spike. In contrast, the counter-propagating pulse lacks enough energy for pulse formation, and it disappears shortly after the central wavelength shift (Supplementary Note S6). The observed dynamics are similar to observations made in unidirectional lasers, where solitons were reported to undergo division and collision12.
For a closer look at pulse characteristics, we exploit the Wiener–Khinchin theorem and calculate round-trip-resolved field autocorrelation function (ACF) from the inverse Fourier transform of the single-shot spectra measured by the DFT technique15,17,43. This approach provides MHz-rate acquisition of the ACF, allowing observation of ultrafast pulse structure changes with high temporal resolution. Figure 3a–c and d–f present the real-time spectra of Q-switched instability, bound solitons, single soliton and corresponding ACFs, respectively. Although real-time field autocorrelation is not sensitive to the spectral phase, it presents the overall dynamics of energy distribution and relative phases. This technique can be used with a high degree of accuracy for almost bandwidth-limited pulses (time-bandwidth products: 0.37 for clockwise, 0.335 for counter-clockwise33, and 0.315 for fundamental solitons). The ACF maximum time delay is inversely proportional to the DFT spectral resolution, while the ACF resolution limited by the DFT frequency span. Here the maximum span is ±400 ps, and the resolution is 560 fs. Note, that FWHM field ACF is 2.5 times broader than actual pulse duration for soliton-shape pulses, which provides appropriate accuracy in order to investigate pulse-to-pulse dynamics. The ACFs for the multi-soliton case (Fig. 3b, e) are seen to be significantly different from the single-soliton case, indicating that these single-shot spectra can provide information about the internal pulse structure and relative phase of the pulse complexes that remains unresolved in the intensity domain measurements9. Figure 4a, b show spectral evolution and the round-trip resolved ACF between 42 and 45 thousand round trips, respectively. These dynamics show the clear formation of multi-soliton structures at different stages. Figure 4 presents the analysis for only the clockwise pulse evolution, as the counter-clockwise pulse is highly attenuated in these round-trips. The observed high-contrast spectral modulation is further indicative of the pulse coherence in multi-soliton complexes (Fig. 3b).
a Dispersion Fourier transform spectra, and b Autocorrelation function traces. c Shot-to-shot variation of the pulse energy normalised to the singe-soliton energy in the steady-state, and d evolution of the localisation parameter. The grey lines show the pulse energy and localisation parameter for mode-locking operation in the steady-state.
Localisation parameter
From Parseval’s theorem by integrating the single-shot spectra from the DFT measurements, one can obtain the data on the pulse energy variation. To confirm the formation of stable solitons and establishment of steady-state mode-locking, it is important to analyse how this energy is distributed across the round-trip span and how much of it is contained in the main pulse. To this end, we define a localisation parameter, L as:
, where
, here E – pulse field, t – time, τ – the ACF time delay and T – the round trip time, tres and τmax – the ACF resolution and maximum time delay, respectively. The ACF at τ = 0 (the overlap of the pulse intensity profiles) is calculated as \({\mathrm{ACF}}(\tau =0)=\mathop{\int}\nolimits_{-T/2}^{T/2}| E(t){| }^{2}dt\) and represents the energy per round trip (see Fig. 4c).
The localisation parameter for each round trip is depicted in Fig. 4d. L equals unity only when all the energy is focused in time scale, shorter than the ACF resolution, and approaches zero if all the energy is equally distributed over a round trip. In other words, the parameter shows the extent to which the energy is accumulated in one specific point in time relative to the total energy. This parameter is normalised and does not depend on the pulse intensity but its duration or shape. Thus, the theoretical value of localisation parameter L for sech2-shaped pulses is 0.4.
Dispersive wave radiation plays a crucial role in the bound-soliton formation44 by providing attractive or repulsive forces between neighbouring solitons45,46. In lasers, these waves manifest in the form of Kelly spectral sidebands47. Here, we use the real-time DFT spectra and ACF to investigate the role of Kelly sidebands in the formation of soliton complexes. We calculated the round-trip resolved pulse energies and L for two cases - when we include the Kelly sidebands in the calculation and when we excluded them. To exclude the Kelly sidebands from energy and the ACF calculation without influence on the ACF time span or resolution, we zero-padded them in DFT data. So the energy variation of Kelly sidebands could be retrieved by the difference of graphs in Fig. 3f. In the spatial domain, Kelly sidebands appear as a quasi-continuous-waves beside the main pulses (Fig. 3f). The Autocorrelation function with excluded Kelly sidebands is depicted in Fig. S5 in Supplementary Note S4.
Firstly, we calculated the localisation parameter and pulse energy corresponding to the mode-locking operation in the steady-state, which are shown by the grey lines in Fig. 4c–d. When the contribution of the Kelly sidebands was removed, the observed localisation parameter L for stable mode-locked pulses was close to the theoretical value of 0.4. In general, we note that when the full DFT spectra were considered, the value of L drops significantly due to the non-localised nature of DWs. Certain round trips show the agreement of values of localisation factor L when they have been estimated with or without consideration of Kelly sidebands. Such dynamics were observed in two cases, such as when the localisation of the pulse itself is low and matches the L value of the sidebands or when the energy of Kelly sidebands is negligible compared to the pulse energy and does not affect the L value.
The ACF in Fig. 4b shows a tendency to form a multi-pulse structure in the clockwise direction. Ref. 48 shows theoretically that collisions of co-propagating solitons can induce a generation of extremely energetic DWs, which we have observed experimentally here in real-time time scale. Each time prior to the formation of the multi-soliton complexes, the total energy and energy in Kelly sidebands had substantially increased. At round-trip numbers near 44 thousand, we observed a two-soliton complex, with decreasing inter-soliton separation over propagation due to unbalanced attraction forces caused by DWs, until they collide. After the pulse collision, the energy localised in Kelly sidebands increased more than 6 times and almost reached the level of the single soliton pulse energy. At the same time, the soliton energy at these round-trips was increased by 15% with the corresponding narrowing of the pulse duration by ~8%. The reduction in pulse duration has been derived from the higher localisation values and in agreement with the soliton area theorem. In other words, the collision of two co-propagating solitons results in the production of one stronger soliton with shorter duration and extra emission of DWs. During these round-trips, we had also noticed higher background radiation which confirms the increase of DWs radiation. After that, starting from 44.4 thousand round trip, the energy of the main pulse continued to rise, while the localisation started decreasing due to the formation of satellite sub-peaks. After 400 round-trips, when the total energy significantly increased, intensity spikes evolved into a pulse, which splits into a 1 + 2 soliton complex9. These dynamics emerge due to the presence of excess energy and soliton energy quantisation effect theoretically described in49,50. The amplitude ratio of solitons in the complex is 4:4:1 with a time separation of 52 and 42 ps. The soliton complex experiences a reduction in energy and decays at 45200 round trip. Right after that, we observe quasi-stable single-soliton generation with a sharp increase of localisation parameter.
Unidirectional generation of multiple pulses arises due to uneven distribution of energies between opposite directions, i.e., when the majority of the intracavity energy is concentrated in one direction. Such a presence of excess energy, after Q-switched instability or intensity spike, tends to operate in multi-soliton regime due to soliton energy quantisation effect49,50. Supplementary Note S6 shows that stable bidirectional mode-locked operation (Stage ‘Final formation and propagation dynamics of stable bidirectional soliton generation’) can be achieved after multi-soliton stage if the energy is more evenly reallocated between both directions.
Final formation and propagation dynamics of stable bidirectional soliton generation
We now consider the final formation of mode-locked pulses from the Q-switched generation and its further propagation. Since at this stage both pulses have experienced dynamics with common features, we show the single-shot spectra (Fig. 5a) and ACF (Fig. 5b) evolution only for the clockwise pulse (see Supplementary Note S5 for the counter-clockwise). At first, the localisation parameter slightly increased during QML pulse with intense continuous-wave radiation and maintained at the same level due to the presence of a low-intensity broad residual pulse. Both directions originated from the residual picosecond pulses and evolved through modulation instability with further spectral broadening and a sharp increase of the localisation. Similar build-up dynamics were observed in ref. 51, where the soliton was formed from subnanosecond intensity spikes on the usual Q-switched envelope via spectral broadening and beating dynamics. Onward both pulses experienced strong beating pattern due to interference between the main pulse and moving aside subordinate intensity spikes (Fig. 5b), which were induced by the nonlinear refractive index and dispersion51. Strong oscillations near the main pulse at the ACF are related to co-propagating DWs. Similar to unidirectional build-up dynamics12,43, we also observed the generation of satellite pulse with more than 10 times lower intensity.
a Dispersion Fourier transform spectra and b Evolution of autocorrelation function during the transition from Q-switched instability into mode-locked generation. Insets: a formation of synchronised and unsynchronised dispersive waves (DWs), b pulse energy and localisation, superimposed on the evolution of autocorrelation function over round trips. c spectra pulsation during stable pulse generation with corresponding energy oscillation in d. e Spectra of pulses with maximum and minimum energies.
Here, we report the experimental observation of the recently theoretically predicted31 synchronised and unsynchronised resonant dispersion waves (see insets in Fig. 5a). Solitons emit DWs due to periodic gain and losses in the laser cavity47. Due to wavelength oscillations, synchronised DWs repeat behaviour of the soliton spectra to maintain phase-matching conditions with the soliton. At the same time, the dynamics of the unsynchronised DWs differs from the oscillation of the central wavelength of the pulse, which prevents the phase-matching conditions31. Insets in Fig. 5a clearly show the synchronisation between the pulse spectra oscillations and DWs at longer wavelengths, while at shorter wavelengths DWs exhibit complex dynamics different from the spectra oscillation. Such dynamics confirm the generation of unsynchronised DWs. During the stable propagation, we have observed the central wavelength oscillations. At the same time, the Kelly sidebands continue to propagate undisturbed, and only a minor amount of energy is travelling between multiple-structured Kelly sidebands. The generation of unsynchronised resonant DWs is observed on both edges of the short-wavelength Kelly sideband with separation of 60 GHz (0.5 nm). As seen in Fig. 5a, unsynchronised DWs have been formed during strong spectra oscillation at the early stage of the soliton formation and continue to propagate further. The energy dissipation from the main pulse seen in the ACF related to the generation of strong unsynchronised DWs. This behaviour of unsynchronised DWs is theoretically described in31. In this work, the unsynchronised DWs were observed only at short-wavelength side. At the same time, the Kelly sidebands at longer wavelength had lower intensity, which may refer to the gain spectrum of the Erbium-doped fibre. The complex multiple-spike DWs structure was also detected by an optical spectrum analyser, as shown in Fig. 1f. In this laser setup, unsynchronised resonant DWs were only observed when the build-up dynamics experienced strong instabilities at certain PC alignment, and the energy of Kelly sidebands was extremely high. When pulses undergo through simpler build-up dynamics shown in ref. 32 no unsynchronised resonant DWs were observed. The results presented here indicate that unsynchronised resonant DWs are dependent on the initial conditions of pulse formation. Since unsynchronised DWs propagate separately from the pulse and do not satisfy phase-matched conditions, they require higher energy and gain compared to synchronised DW. Figure 5c shows DFT spectra obtained when the laser operates in a stable state. The measured DFT spectra demonstrate spectral pulsations in the clockwise direction (the pulse train is demonstrated in Fig. S6 in Supplementary Information). Concisely, clockwise pulse dynamics during the stable propagation is as follows: the energetic pulse is getting broader while moving to the shorter wavelengths by 0.5 nm, a 10%-decrease in energy next the process reverses and repeats periodically within 11 round trips (Fig. 5e, d). According to the soliton area theorem, this leads to the pulse duration oscillations, which are well observed in the ACF and localisation evolution (Fig. 5b). The oscillation range of the central wavelength has matched the spectral separation between multiple-structured Kelly sidebands so that the soliton can maintain the phase-matched condition with complex sidebands.
Soliton pulsations have been theoretically observed for many operation regimes52,53 and recently experimentally observed with the help of the DFT technique21,54. These soliton pulsations are related to period-doubling bifurcations at specific values of the system55. They indicate that the soliton has a strange attractor and cannot be reproduced by one cavity bypass56. Importantly, no pulsations were observed for a bidirectional generation with different pulse repetitions rates for counter-propagating pulses32. The fact, that switching between regimes with equal and different pulse repetitions rates is achieved by adjustment of the PCs, suggests that the bifurcation arises at particular intracavity polarisation state. So, the soliton pulsations could arise to maintain the locking of counter-propagating pulses. The synchronisation of repetition rates of counter-propagating solitons was also observed in microresonators57.
By analysing dozens of build-up dynamics, we have concluded that the energy distribution between both directions is a key factor for stable bidirectional mode-locking formation. If the energy in the dominating direction does not drop by more than 10% after the Q-switched pulse or intensity spike, it will lead to the multi-soliton formation and soliton breakup in the less energetic direction (Supplementary Note S6). In addition, the analysis has not shown a strong correlation between localisation parameter before stable pulse formation. This means that stable bidirectional mode-locking is more reliant on energy distribution between directions than on initial pulse shape. Moreover, counter-propagating pulses eventually evolve into almost identical stable states, even when the preceding dynamics differ.
Discussion
Here we have demonstrated the complex switch-on dynamics experienced by counter-propagating ultrashort pulses during formation in the fibre cavity. Generally, the counter-propagating pulses experienced different build-up dynamics, while their mutual interactions in fibre laser allowed formation of eventually almost identical solitons. After 70 thousand round trips from the first intensity spike observed, a stable bidirectional mode-locked generation, evolving from Q-switched instabilities has been achieved. The obtained bidirectional mode-locked generation was stable with exactly matched repetition rates of counter-propagating pulses for several hours.
The formation dynamics is rich with phenomena and nonlinear processes, which make it stand out when compared to the earlier demonstrated evolution in unidirectional lasers. The demonstrated dynamics highlight the interconnection between both directions. Owing to colliding mode-locking, the pulses have always originated with collision point in saturable absorber that allows saturation at lower intensities. In this work, we have indicated the interrelation and underlying dynamics between different stages. We have revealed that complex interchange of intracavity energy between counter-propagating beams, mediated by active media, plays a vital role in the formation of stable bidirectional mode-locked generation. Deflections in energy allocation lead to different discussed stages such as quasi-stable pulse formation or unidirectional multi-soliton formation in dominated direction. Additional dynamics, presented in Fig. S8–13 in Supplementary Notes S6, S7, feature the same stages and confirm the repeatability of the observations, albeit their sequence and duration substantially varies each time we have switched on the pump power. Such behaviour indicates that complex dynamics arise due to sophisticated operation regime that depends on a variety of underlying parameters.
We have introduced an evaluation parameter of energy localisation for round-trip resolved measurements. The localisation parameter provides the basis for comprehensive analysis of the role of DWs on multi-soliton complexes formation and their interaction. We have demonstrated absolute pulse-to-pulse measurements of central wavelengths deviations and have shown strong blue-shift of the central wavelength during pulse formation. Moreover, these results experimentally reveal the existence of synchronised and unsynchronised dispersion waves and show their origination from complex pulse spectra behaviour. While numerical simulations of bidirectional mode-locked lasers are complicated and out of the scope of the current work, we believe that such simulations can be supported by experimental observations obtained via real-time measurements such as those presented in this paper. Together numerical and experimental studies can help to reveal the true nature of the underlying mechanisms giving rise to the observed phenomena like the wavelength drifts, or even pulse formation from Q-switched instabilities. Compared to the previous studies of bidirectional generations in fibre cavities, we have investigated conventional solitons in all anomalous-net dispersion cavity in details, demonstrating more complex dynamics. These observations open up a great avenue towards versatile manipulation of nonlinear soliton dynamics. We believe the obtained results would constitute a basis for the further investigations of the counter-propagating soliton dynamics and their interactions in complex systems and the role of DWs and Q-switched instabilities on mode-locking generation.
Methods
Experimental setup
The configuration of the laser is the same as described in33. We implement hybrid mode-locking via co-action of single-walled carbon nanotubes (SWNT) and nonlinear polarisation evolution (NPE) which helps to realise mode-lock self-starting. A bent 6-m of polarising fibre with bow-tie geometry was used as a polarisation-sensitive element with an extinction ratio of 30 dB to achieve stable NPE effect for both pulse propagation directions. Two polarisation controllers (PCs) were used for accurate adjustment of operation regime. The total cavity length was 13.4 m with anomalous dispersion. A 2X2 3-dB coupler is used as an out-coupler for the counter-clockwise and clockwise pulses. To record bidirectional onset dynamics simultaneously in spectral and temporal domains we used the following strategy—we combine both outputs from the 3 dB out-coupler via another 3 dB coupler that has one input arm longer than the other. This results in a temporal delay between the clockwise and counter-clockwise pulses allowing their simultaneous recording in a single oscilloscope (Agilent DSOX93204A) channel. Isolators are used as shown to avoid spurious back-reflections into the laser cavity. One of the outputs of the latter 3-dB coupler directly goes to a photodetector for measurement of intensity domain (Fig. 1b). The other output is sent through an 11 km dispersion compensating fibre span (D = −1200 ps/nm) before being made incident on a photodetector. The bandwidth of the photodetectors used was 50 GHz, while the oscilloscope used had a bandwidth of 33 GHz. Using the expressions provided in ref. 11, the calculated resolution of the DFT is 0.025 nm. To record the real-time measurements, we tune PCs to achieve stable self-starting bidirectional mode-locked generation and then switch the power off. By aligning the oscilloscope trigger, we have recorded onset dynamics in both propagation directions by switching the pump power on.
Measurements of the central wavelength dynamics
The DFT method allows measurement of only relative wavelengths, while the central wavelength should be uniquely identified. As a reference, we have used the spectra obtained by an optical spectrum analyser for the steady-state bidirectional mode-locking. However, to estimate the central wavelength shift, one should compare the dynamics in spatial and DFT profiles. We neglect the nonlinear effect on group velocity dispersion (GVD) since the pulse intensity was quite low. Since both the cavity optical length and DFT line are dispersive, it takes different time for different wavelengths to propagate through. The central wavelength drift results in a variation of the cavity round trip time, and also change in the pulse time of flight over the DFT fibre span owing to GVD. Hence, to estimate the central wavelength drift from the DFT measurements, we need to exclude the contribution of the varying cavity round trip time, which can be obtained from the spatio-temporal dynamics. Once this contribution is removed, the wavelength drift can be estimated by using the known value of the dispersion of the DFT fibre span. In our experiments, the DFT line introduces the time delay tDFT of 53.651 μs at 1555 nm wavelength band. The mapping of the position of 1555 nm spectral component back to the recorded DFT is shown as a dark red line in Fig. 2a. Therefore, the time mismatch between spectra and corresponding delayed spatio-temporal intensity evolution trace demonstrates actual central wavelength drift in real-time (Fig. 2b). The obtained mapping confirms that the frequency shift has occurred in the laser cavity rather than in the DFT line.
Data availability
The data that support the presented dynamics in main manuscript are available in figshare with the identifier https://doi.org/10.6084/m9.figshare.12951185.v2. Additional data of other formation dynamics presented in Supplementary Notes are available from the corresponding author upon reasonable request.
References
Grelu, P. & Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photon. 6, 84 (2012).
Fermann, M. E. & Hartl, I. Ultrafast fiber laser technology. IEEE J. Sel. Top. Quantum Electron. 15, 191–206 (2009).
Akhmediev, N. & Ankiewicz, A. Dissipative Solitons: From Optics To Biology And Medicine. Vol. 751 (Springer Science & Business Media, 2008).
Nguyen, J. H., Luo, D. & Hulet, R. G. Formation of matter-wave soliton trains by modulational instability. Science 356, 422–426 (2017).
Kuznetsov, E., Rubenchik, A. & Zakharov, V. E. Soliton stability in plasmas and hydrodynamics. Phys. Rep. 142, 103–165 (1986).
Oktem, B., Ülgüdür, C. & Ilday, F. Ö. Soliton–similariton fibre laser. Nat. Photonics 4, 307 (2010).
Tang, D., Zhao, L. & Zhao, B. Soliton collapse and bunched noise-like pulse generation in a passively mode-locked fiber ring laser. Opt. Express 13, 2289–2294 (2005).
Tang, D., Man, W., Tam, H. & Drummond, P. Observation of bound states of solitons in a passively mode-locked fiber laser. Phys. Rev. A 64, 033814 (2001).
Wang, Z., Nithyanandan, K., Coillet, A., Tchofo-Dinda, P. & Grelu, P. Optical soliton molecular complexes in a passively mode-locked fibre laser. Nat. Commun. 10, 830 (2019).
Azaña, J. Time-to-frequency conversion using a single time lens. Opt. Commun. 217, 205–209 (2003).
Goda, K. & Jalali, B. Dispersive fourier transformation for fast continuous single-shot measurements. Nat. Photon. 7, 102 (2013).
Peng, J. et al. Real-time observation of dissipative soliton formation in nonlinear polarization rotation mode-locked fibre lasers. Commun. Phys. 1, 20 (2018).
Liu, X., Yao, X. & Cui, Y. Real-time observation of the buildup of soliton molecules. Phys. Rev. Lett. 121, 023905 (2018).
Zhou, Y., Ren, Y.-X., Shi, J., Mao, H. & Wong, K. K. Y. Buildup and dissociation dynamics of dissipative optical soliton molecules. Optica 7, 965–972 (2020).
Lapre, C. et al. Real-time characterization of spectral instabilities in a mode-locked fibre laser exhibiting soliton-similariton dynamics. Sci. Rep. 9, 1–12 (2019).
Herink, G., Jalali, B., Ropers, C. & Solli, D. Resolving the build-up of femtosecond mode-locking with single-shot spectroscopy at 90 mhz frame rate. Nat. Photon. 10, 321 (2016).
Ryczkowski, P. et al. Real-time full-field characterization of transient dissipative soliton dynamics in a mode-locked laser. Nat. Photon. 12, 221 (2018).
Wang, X. et al. On the q-switching bunch dynamics in the build-up of stretched-pulse mode-locking. Opt. Express 27, 2747–2753 (2019).
Herink, G., Kurtz, F., Jalali, B., Solli, D. & Ropers, C. Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules. Science 356, 50–54 (2017).
Kurtz, F., Ropers, C. & Herink, G. Resonant excitation and all-optical switching of femtosecond soliton molecules. Nat. Photon. 14, 9–13 (2019).
Wei, Z.-W. et al. Pulsating soliton with chaotic behavior in a fiber laser. Opt. Lett. 43, 5965–5968 (2018).
Peng, J. & Zeng, H. Soliton collision induced explosions in a mode-locked fibre laser. Commun. Phys. 2, 34 (2019).
Wei, Y., Li, B., Wei, X., Yu, Y. & Wong, K. K. Ultrafast spectral dynamics of dual-color-soliton intracavity collision in a mode-locked fiber laser. Appl. Phys. Lett. 112, 081104 (2018).
Fork, R., Greene, B. & Shank, C. V. Generation of optical pulses shorter than 0.1 psec by colliding pulse mode locking. Appl. Phys. Lett. 38, 671–672 (1981).
Krylov, A. A., Chernykh, D. S. & Obraztsova, E. D. Gyroscopic effect detection in the colliding-pulse hybridly mode-locked erbium-doped all-fiber ring soliton laser. Opt. Lett. 42, 2439–2442 (2017).
Chernysheva, M., Sugavanam, S. & Turitsyn, S. Real-time observation of the optical sagnac effect in ultrafast bidirectional fibre lasers. APL Photon. 5, 016104 (2020).
Zhang, W., Zhan, L., Xian, T. & Gao, L. Bidirectional dark-soliton fiber lasers for high-sensitivity gyroscopic application. Opt. Lett. 44, 4008–4011 (2019).
Mehravar, S., Norwood, R. A., Peyghambarian, N. & Kieu, K. Real-time dual-comb spectroscopy with a free-running bidirectionally mode-locked fiber laser. Appl. Phys. Lett. 108, 231104 (2016).
Li, B. et al. Bidirectional mode-locked all-normal dispersion fiber laser. Optica 7, 961–964 (2020).
Yu, Y. et al. Behavioral similarity of dissipative solitons in an ultrafast fiber laser. Opt. Lett. 44, 4813–4816 (2019).
Du, Y., Han, M., Cheng, P. & Shu, X. Pulsating soliton with broadened kelly sidebands in an ultrafast fiber laser. Opt. Lett. 44, 4087–4090 (2019).
Kudelin, I., Sugavanam, S. & Chernysheva, M. Build-up dynamics in bidirectional soliton fiber lasers. Photon. Res. 8, 776–780 (2020).
Chernysheva, M. et al. Isolator-free switchable uni-and bidirectional hybrid mode-locked erbium-doped fiber laser. Opt. Express 24, 15721–15729 (2016).
Kieu, K. & Mansuripur, M. All-fiber bidirectional passively mode-locked ring laser. Opt. Lett. 33, 64–66 (2008).
Afkhamiardakani, H. & Diels, J.-C. Controlling group and phase velocities in bidirectional mode-locked fiber lasers. Opt. Lett. 44, 2903–2906 (2019).
Sun, S., Lin, Z., Li, W., Zhu, N. & Li, M. Time-stretch probing of ultra-fast soliton dynamics related to q-switched instabilities in mode-locked fiber laser. Opt. Express 26, 20888–20901 (2018).
Tartara, L. Frequency shifting of femtosecond pulses by reflection at solitons. IEEE J. Quantum Electron. 48, 1439–1442 (2012).
Gu, J., Guo, H., Wang, S. & Zeng, X. Probe-controlled soliton frequency shift in the regime of optical event horizon. Opt. Express 23, 22285–22290 (2015).
Kalashnikov, V. L., Sorokin, E. & Sorokina, I. T. Mechanisms of spectral shift in ultrashort-pulse laser oscillators. JOSA B 18, 1732–1741 (2001).
Hönninger, C., Paschotta, R., Morier-Genoud, F., Moser, M. & Keller, U. Q-switching stability limits of continuous-wave passive mode locking. JOSA B 16, 46–56 (1999).
Kaertner, F. X. et al. Control of solid state laser dynamics by semiconductor devices. Optical Eng. 34, 2024–2037 (1995).
Schlatter, A., Zeller, S. C., Grange, R., Paschotta, R. & Keller, U. Pulse-energy dynamics of passively mode-locked solid-state lasers above the q-switching threshold. JOSA B 21, 1469–1478 (2004).
Liu, X. & Cui, Y. Revealing the behavior of soliton buildup in a mode-locked laser. Adv. Photon. 1, 016003 (2019).
Pandit, N., Noske, D., Kelly, S. & Taylor, J. Characteristic instability of fibre loop soliton lasers. Electron. Lett. 28, 455–457 (1992).
Loh, W., Grudinin, A., Afanasjev, V. & Payne, D. Soliton interaction in the presence of a weak nonsoliton component. Opt. Lett. 19, 698–700 (1994).
Grudinin, A. & Gray, S. Passive harmonic mode locking in soliton fiber lasers. JOSA B 14, 144–154 (1997).
Kelly, S. Characteristic sideband instability of periodically amplified average soliton. Electron. Lett. 28, 806–807 (1992).
Erkintalo, M., Genty, G. & Dudley, J. Giant dispersive wave generation through soliton collision. Opt. Lett. 35, 658–660 (2010).
Tang, D., Zhao, L.-M., Zhao, B. & Liu, A. Mechanism of multisoliton formation and soliton energy quantization in passively mode-locked fiber lasers. Phys. Rev. A 72, 043816 (2005).
Renninger, W. H., Chong, A. & Wise, F. W. Area theorem and energy quantization for dissipative optical solitons. JOSA B 27, 1978–1982 (2010).
Liu, X., Popa, D. & Akhmediev, N. Revealing the transition dynamics from q switching to mode locking in a soliton laser. Phys. Rev. Lett. 123, 093901 (2019).
Soto-Crespo, J. M., Grapinet, M., Grelu, P. & Akhmediev, N. Bifurcations and multiple-period soliton pulsations in a passively mode-locked fiber laser. Phys. Rev. E 70, 066612 (2004).
Tsoy, E. N. & Akhmediev, N. Bifurcations from stationary to pulsating solitons in the cubic–quintic complex ginzburg–landau equation. Phys. Lett. A 343, 417–422 (2005).
Du, Y., Xu, Z. & Shu, X. Spatio-spectral dynamics of pulsating dissipative solitons in a normal-dispersion fiber laser. Opt. Lett. 43, 3602–3605 (2018).
Akhmediev, N., Soto-Crespo, J. M. & Town, G. Pulsating solitons, chaotic solitons, period doubling, and pulse coexistence in mode-locked lasers: complex ginzburg-landau equation approach. Phys. Rev. E 63, 056602 (2001).
Soto-Crespo, J. M. & Akhmediev, N. Soliton as strange attractor: nonlinear synchronization and chaos. Phys. Rev. Lett. 95, 024101 (2005).
Yang, Q.-F., Yi, X., Yang, K. Y. & Vahala, K. Counter-propagating solitons in microresonators. Nat. Photon. 11, 560 (2017).
Acknowledgements
S.S. would like to acknowledge the support received from H2020-MSCA-COFUND MULTIPLY (GA-713694).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
S.S. and M.C. conceived the experiment. M.C. built the laser, I.K. performed the experiments and analysed the results. All authors contributed towards the analysis of results. I.K. proposed the definition of the localisation parameter and the subsequent analysis based on it. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kudelin, I., Sugavanam, S. & Chernysheva, M. Pulse-onset dynamics in a bidirectional mode-locked fibre laser via instabilities. Commun Phys 3, 202 (2020). https://doi.org/10.1038/s42005-020-00465-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00465-4
This article is cited by
-
Multi-port real-time observation for ultrafast intracavitary evolution dynamics
Communications Physics (2023)
-
Single-shot dynamics of dual-comb generation in a polarization-multiplexing fiber laser
Scientific Reports (2023)
-
Heteronuclear multicolor soliton compounds induced by convex-concave phase in fiber lasers
Communications Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.