Introduction

The field of free-space optical (FSO) communications provides an exciting route forward in wireless information transfer by making use of various multiplexing schemes, including frequency and wavelength division multiplexing, and more recently spatial multiplexing1,2,3,4,5,6. A common method to implement the latter involves making use of orbital angular momentum (OAM), which is a degree of freedom that is in principle unbounded, thus permitting for the application of large alphabets in optical communication schemes. For example, by generating and transmitting various superpositions of OAM states, which result in different “petal pattern” images in the spatial domain, the alphabet size of the communications system may be significantly increased. An integral aspect of any communication protocol, however, is the ability to effectively demodulate the signal at the receiver, which in this case corresponds to determining which OAM superposition was sent and received. In real-world schemes, FSO communication systems comprise of propagation of the beams through random turbulence, attenuation, and non-negligible amount of dark noise at the receiver. As a consequence, the distorted, noisy received signals (images) can result in a lower accuracy, significantly deteriorating their practical implementation7,8.

State-of-the-art generative models have recently been applied to molecular design, radiotherapy, geophysics, speech recognition, and tomography9,10,11,12,13,14. Generative neural networks (GNNs) involve creating a new state at their output, given a noisy or unknown state as the input. One example of the generative learning approach is making use of an autoencoder in a variety of reconstructing scenarios15,16,17. In addition, supervised learning and artificial neural networks as classifiers have been successfully implemented in the context of FSO communications18,19,20,21,22,23,24,25,26. However, in order to train the network as a classifier, all preceding communication set-ups involving only supervised learning schemes require a huge amount of pre-labeled distorted optical profiles at the receiver, which is computationally less efficient and requires more time to generate and process the data. Additionally, in the presence of random distortions, attenuation, and detector noise, it may not be always feasible to tag the optical profiles for supervised learning. This restricts the classification efficiency of the set-up with respect to randomly varying turbulent effects and attenuation in realistic FSO systems.

In this article, we expand significantly upon these works and develop a communication scheme using a generative machine learning approach and demonstrate its robustness and ability to significantly mitigate the effects of turbulence, attenuation, and noise on the accuracy in both simulated and experimental communication settings. This receiver-end system is shown to be effective for a wide range of turbulence and detector noise strengths and requires no feedback to the transmitter of the communication link or any adaptive optics components. Our scheme with the developed generative network first creates new, significantly less distorted optical profiles at the receiver that are later demodulated using a convolutional neural network (CNN) classifier. Note that CNN is solely trained with only undistorted optical modes with added dark noise to simulate a realistic, non-ideal quantum efficiency detector, alone. Additionally, we calculate the cross-talk between the noisy, distorted modes at the receiver and show a significant enhancement when the GNN system is used. Furthermore, our network architecture is portable, cost-effective, and can be pre-trained before performing the communications, which circumvents the general technical issues that are present in adaptive optics.

Results

Model

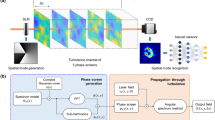
The general experimental set-up is shown schematically in Fig. 1. A laser is incident on a spatial light modulator (SLM) with a given phase mask, such that the resultant optical spatial mode profile is in a desired superposition of OAM values ranging from 0 (Gaussian) to  ±10 (a petal pattern with 20 lobes). The optical profile is then transmitted through turbulence via a second SLM, resulting in a distorted profile, after which it travels through a variable attenuator. Finally, detector dark noise is unavoidably added at the receiver. This noisy, attenuated, distorted image is then fed into the GNN. The GNN generates a new mode profile that may either be used to directly calculate its mean squared error (MSE) from the target or be fed into a CNN that classifies which mode was sent and received (that is, which letter of the communication alphabet). In this work, we produce data in three manners: test and training images both completely simulated (see “Numerical simulation of long distance turbulent propagation” in “Methods”), test and training images both experimentally generated (i.e., with a laser and two SLMs as shown in Fig. 1), and a combination of the two (i.e., simulated training images and experimentally generated test images).

Fig. 1: Experimental set-up.
figure 1

Diagram of the set-up for creating experimental free-space optical communications images as described in the “Experimental results” section. Light from a Ti:Sapp laser tuned to 795 nm travels through an optical fiber and a λ/2 waveplate (WP) before it is incident on the center of two spatial light modulators (SLMs). SLM 1 imparts a specific orbital angular momentum (OAM) superposition on its first reflection order, and the zero-OAM zeroth order is blocked as shown. The phase mask on SLM 2 simulates turbulence of a given \({C}_{n}^{2}\). Finally, a variable attenuator (VA) further reduces the signal-to-noise ratio of the transmitted mode before it is detected on a charged coupled device (CCD) camera. Each captured image is then fed into and corrected by our generative neural network (GNN). Four examples of experimental images are included at appropriate points in the diagram, with orbital angular momentum value l = ±9, turbulence strength \({C}_{n}^{2}=65.6\times 1{0}^{-11}{m}^{-2/3}\), and an attenuation ratio of −1.18 dB.

Full size image

As opposed to the traditional autoencoder27, convolutional denoising autoencoders are able to reconstruct a clean, corrected input from those that are partially distorted28. The idea behind using such a network design is to learn a hidden representation and extract the important features that are robust to noise or distortion present in the inputs. The generative network described here encodes and compresses the extracted crucial features from the input data into a smaller size layer. This smaller dimensional layer is a latent space. The encoded information in the latent space is then forwarded to the decoder, which eventually generates the corrected undistorted, clean modes as shown in Fig. 2a. We have built an encoder with convolutional layers (green blocks in Fig. 2a) with a kernel size of 5 × 5, with zero padding, rectified linear unit (ReLU) activation, stride length of 2, and 3 feature mappings followed by a max-pooling layer (red block) with a pool size of 2 × 2 and fully connected layer (blue circles). After this, the encoder finally stores the features into a latent space using the ReLU activation. Likewise, the decoder is built and starts with a fully connected layer (blue circles), which then forward the information to a convolutional layer with the same parameter settings as described above. Furthermore, in order to regain the original size of the input, a deconvolutional layer (magenta block) is applied, again with the same parameter values. In the end, a convolutional block with a single feature mapping generates a clean, corrected mode profile. Note that we apply a dropout with a rate of 5% after each layer, except at the fully connected layer at the end of the encoder and final convolutional layer of the decoder. We apply the small dropout rate to avoid overfitting, as well as the possible loss of features extracted from the convolution. The size of the fully connected layer is same as that of the latent space. As a classifier, we implement a CNN to demodulate the generated, reconstructed clean mode profiles. The same CNN is also implemented to demodulate the uncorrected detector received profiles at the receiver. This network comprises of a convolutional unit with a kernel of size 5 × 5, zero padding, ReLU activation, stride length of 2, and a single feature mapping followed by a max-pooling with a 2 × 2 filter attached to a fully connected layer (28 × 28 neurons) and an output layer as shown in Fig. 2a. No dropout is employed in this network.

Fig. 2: Network architecture and reconstruction of various orbital angular momentum (OAM) modes.
figure 2

a Architecture of the neural networks consisting of a generative neural network (GNN) and a convolutional neural network (CNN). b–d Example images of various simulated optical modes that are distorted and noisy at the receiver (R) and the generated, corrected modes (C). Decreasing the signal-to-noise ratio, SNR (left:  −0.11 dB, middle:  −3.87 dB, right:  −5.91 dB), is shown in b, increasing the communication link distance (Z) (left: 400 m, middle: 600 m, right: 800 m) is shown in c, and increasing the turbulence strength \({C}_{n}^{2}\) (left: \({C}_{n}^{2}\ =\ 5\, \times 1{0}^{-14}\ {m}^{-2/3}\), middle: \({C}_{n}^{2}\ =\ 7\, \times 1{0}^{-14}\ {m}^{-2/3}\), right: \({C}_{n}^{2}\ =\ 1\,\times 1{0}^{-13}\ {m}^{-2/3}\)) is shown in d. The superposition of OAM degree is increased in each row, from 0 (Gaussian) up to a value of  ±9.

Full size image

Numerical results

Here we describe results from the numerical simulations. Examples of the simulated distorted, noisy images and GNN-generated corrections are shown in Fig. 2b–d, for varying degrees of signal-to-noise ratios (SNRs), communication link distances (Z), and turbulence strengths (\({C}_{n}^{2}\)), respectively. This process is repeated many times for all spatial modes (with random turbulences and noises added), and the accuracy of the system is calculated and compared to the accuracy when the GNN detection system is not used. Note that accuracy measures the ratio of number of correctly classified unknown OAM profiles to the total number of received modes at the receiver. In the first place, we optimize the latent space dimension and evaluate an accuracy for various SNRs of the detected OAM profiles. In order to generate training sets, we simulate 99 random turbulent phase screens with a strength of \({C}_{n}^{2}\) of 5 × 10−14 m−2/3 and transmission distance of 500 m. Note that the 99 simulated phase screens are all different from one another with respect to their phase distributions, such that two different turbulent phase screens produce different scintillation effects on OAM mode propagation even if they have the same turbulence strength. As a result, we have 99 different distorted optical profiles for each superposition OAM mode ranging from ℓ = 0 to  ±10 for a total of 1089 images. The resolution of the images is fixed to 128 × 128 pixels for all of the simulations performed in this paper. Additionally, in order to simulate a transmitter with a fixed transmission intensity, we normalize the total intensity before we propagate the OAM modes into the turbulence. We append random additive Gaussian noise to the distorted, detected optical profiles at the receiver. Then the SNR of the final noisy, distorted optical profiles is measured as discussed in ref. 24. Note that we train the GNN separately for separate SNR image sets (and that the SNR is decreased by increasing the amount of added detector noise, as the transmitter intensity is held constant). Next, in order to train the networks, the set of images is divided into separate training and test sets. As a result, 50 images for each value of ℓ for a total of 550 images are used in training the network, whereas 49 images, again, for each value of ℓ for a total of 539 images are used for testing the networks. Consequently, we optimize the GNN with these training sets with a learning hyper-parameter (rate) set at 0.008. Then unknown test sets are fed to the optimized GNN that generates nearly ideal corrected optical profiles as the output, some examples of which for \({C}_{n}^{2}\ =\ 7\, \times 1{0}^{-14}\ {m}^{-2/3}\) are shown in Fig. 2b. The left, middle, and right columns in Fig. 2b represent the noisy received modes (R) and reconstructed (C) profiles with a GNN when the average SNR of images are 0.11 dB (σ = 20),  −3.87 dB (σ = 50), and  −5.91 dB (σ = 80), respectively. Next, in order to calculate the accuracy, the noisy test optical images (without corrections) and reconstructed/generated images from the GNN are forwarded to a pre-trained CNN and the corresponding accuracies are measured. Note that the pre-trained GNN–CNN networks reconstruct and then classify an optical profile on the order of milliseconds. The accuracy of the test set images with and without the GNN at various SNR levels of 3.11 to  −5.91 dB with respect to different latent sizes of the GNN is shown in Fig. 3a. We find an improvement in accuracy from 0.87 to 0.93 for the image sets with SNR = 3.11 dB even at a small latent size of 4 × 4. As expected, we obtain better reconstructions and more improved accuracies as we increase the latent size up to 32 × 32, after which it begins to saturate. The reconstructed images shown in Fig. 2b are from the GNN with a 32 × 32 latent size. Finally, we achieve an improvement in accuracy from 0.87 to 0.97 at a latent size of 24 × 24, from 0.84 to 0.95 at a latent size of 24 × 24, from 0.77 to 0.92 at a latent size of 24 × 24, and from 0.68 to 0.86 at a latent size of 72 × 72 for the image sets with SNR = 3.11, 0.11,  −3.87, and  −5.91 dB, respectively.

Fig. 3: Results from the numerical simulations.
figure 3

Accuracy versus latent space size a at different levels of signal-to-noise ratio (SNR) with \({C}_{n}^{2}\ =\ 5\,\times 1{0}^{-14}\ {m}^{-2/3}\) and communication link distance (Z)  = 500 m b at various communication link distance with \({C}_{n}^{2}\ =\ 5\,\times 1{0}^{-14}\ {m}^{-2/3}\), and SNR  = −3.87 dB, for the received (noisy and distorted) and corrected (generated) mode profiles. c Accuracy versus \({C}_{n}^{2}\) with various detector noise levels σ at fixed Z = 500 m. The corresponding accuracy at \({C}_{n}^{2}\ =\ 9\,\times 1{0}^{-15}\ {m}^{-2/3}\) and \({C}_{n}^{2}\ =\ 1\,\times 1{0}^{-14}\ {m}^{-2/3}\) are zoomed in and shown in inset. d Accuracy versus latent space size at different turbulent strength \({C}_{n}^{2}\) with fixed σ = 50 and again Z = 500 m. The inset shows the zoomed in accuracy at a latent size of 24 × 24 for \({C}_{n}^{2}\ =\ 1\,\times 1{0}^{-14}\ {m}^{-2/3}\).

Full size image

Next we find the accuracy improvement with respect to different latent sizes over various communication link distances. The same strength of turbulence as described in previous paragraphs is used but again with different, random phase patterns. Here all optical mode profiles are assumed to be detected with an average SNR = −3.87 dB at the receiver. Noisy and reconstructed OAM profiles from the pre-trained GNN for distances of 400, 600, and 800 m are shown in Fig. 2c. The improvement in accuracy with respect to various latent sizes of the GNN at communication link distances from 200 to 800 m is shown in Fig. 3b. Here we find significant improvements in the accuracies from 0.976 to 0.998 at a latent size of 40 × 40, from 0.85 to 0.95 at a latent size of 88 × 88, from 0.72 to 0.88 at a latent size of 40 × 40, and from 0.67 to 0.85 at a latent size of 24 × 24 for the communication link distances of 200, 400, 600, and 800 m, respectively.

Next, we turn to reconstructing severely distorted OAM profiles due to various turbulence strengths in the channel. Turbulence strengths are varied from strong (\({C}_{n}^{2}\ =\ 1\times 1{0}^{-13}\ {m}^{-2/3}\)) to weak (\({C}_{n}^{2}\ =\ 9\times 1{0}^{-15}\ {m}^{-2/3}\)) levels with a fixed Z = 500 m, for a total of 7 different turbulence strength scenarios, with random phase screens for each class and different noise strengths at the receiver. Some examples of simulated received noisy OAM modes and reconstructed corrected modes using the GNN with a latent size of 32 × 32 for \({C}_{n}^{2}\ =\ 5\times 1{0}^{-14}\ {m}^{-2/3}\), \({C}_{n}^{2}\ =\ 7\times 1{0}^{-14}\ {m}^{-2/3}\), and \({C}_{n}^{2}\ =\ 1\times 1{0}^{-13}\ {m}^{-2/3}\) at a dark noise strength of σ = 50 are, respectively, shown in left, middle, and right column of Fig. 2d. Again with the pre-trained GNN with a latent size of 32 × 32, we show a significant improvement in accuracies for various turbulence strengths for noise strengths of σ = 10, σ = 20, σ = 50, and σ = 80 present at the receiver, as seen in Fig. 3c. Significant increase in accuracies are achieved with the GNN, for example, increasing the accuracy from 0.83 to 0.971 at a noise level of σ = 80 and turbulence strength of \({C}_{n}^{2}\ =\ 3\times 1{0}^{-14}\ {m}^{-2/3}\). Furthermore, for an intermediate turbulence strength of \({C}_{n}^{2}\ =\ 1\times 1{0}^{-14}\ {m}^{-2/3}\), we find an uncorrected accuracy of 0.995 and 0.945, respectively, at σ = 50 and σ = 80, which are dramatically enhanced to 1.0 with the GNN. Additionally, the accuracy of 0.989 at σ = 80 for a weak turbulence of \({C}_{n}^{2}\ =\ 9\times 1{0}^{-15}\ {m}^{-2/3}\) has also been corrected to an accuracy of 1.0 with the GNN as shown in the lower inset of Fig. 3c.

Similarly, in order to have a latent size benchmark with respect to different turbulent strengths, we vary the latent size of the GNN and fix the noise strength at σ = 50. Again with the GNN pre-trained for various latent sizes, the enhancements in accuracy with respect to latent sizes are shown in Fig. 3d. We find an improvement in accuracy from 0.995 to 1.0 for every latent size at or above 16 × 16 for \({C}_{n}^{2}\ =\ 1\times 1{0}^{-14}\ {m}^{-2/3}\) (red curve). For example, the accuracy at a latent size of 24 × 24 are zoomed in and shown in the inset. Moreover, we show a significant accuracy enhancement from 0.77 to 0.92 at a latent size of 24 × 24 (blue curve) and from 0.57 to 0.74 at a latent size of 40 × 40 (green curve), respectively, for an intermediate turbulence strength of \({C}_{n}^{2}\ =\ 5\times 1{0}^{-14}\ {m}^{-2/3}\) and strong strength of \({C}_{n}^{2}\ =\ 1\times 1{0}^{-13}\ {m}^{-2/3}\) in Fig. 3d. Note that, from the previous benchmarks of simulated OAM profiles, we set the size of 32 × 32 as the optimized latent space dimension of the GNN for the results discussed in the following paragraphs.

Experimental results

With the network optimized, we now focus on implementing the GNN in the experimental set-up as shown in Fig. 1. Initially, we generate light in OAM superposition modes from  ±l = 0 to 10 on the first spatial light modulator (SLM 1), then mimic propagation through turbulence via a random phase mask on SLM 2 (see Fig. 1) that imparts a turbulence strength from \({C}_{n}^{2}\ =\ 8\times 1{0}^{-11}\) to  80 × 10−11 m−2/3. In order to generate training and test sets, we randomly vary the phase mask on SLM 2 and record the corresponding intensity pattern on a charged coupled device (CCD) camera. For a given \({C}_{n}^{2}\), we record 50 images for each superposition OAM value, for a total of 550 intensity images. We split these 550 images into 495 (45 from each  ±ℓ) for the training set and 55 (5 from each  ±ℓ) for the unknown testing set. Note that, to create a target pattern, we place an empty (zero turbulence) phase mask on SLM 2 for all  ±ℓ. With the pre-trained GNN, we find an efficient reconstruction of the noisy, distorted OAM modes: typically an order-of-magnitude reduction in the MSE, as shown in Fig. 4. Examples of uncorrected noisy/distorted images at the receiver (R) and the corresponding corrected optical profiles (C) for the turbulence strengths of \({C}_{n}^{2}\, =\, 22.4\times 1{0}^{-11}\ {m}^{-2{/}3}\) (left), \({C}_{n}^{2}\, =\, 51.2\times 1{0}^{-11}\, {m}^{-2{/}3}\) (center), and \({C}_{n}^{2}\ =\ 80\times 1{0}^{-11}\ {m}^{-2/3}\) (right) are shown in Fig. 4a. The superposition OAM value in each row is  ±ℓ = 2, 3, 6,  and 9 from top to bottom, respectively. In order to measure the detection success with (blue) and without (tan) the GNN at the receiver, we calculate the MSE between the desired and the corrected or received optical profiles. While there is an expected trend of increasing MSE with increase in turbulence strength, \({C}_{n}^{2}\), the GNN continues to efficiently reconstruct the noisy and distorted OAM modes for all values of \({C}_{n}^{2}\) as shown in Fig. 4b.

Fig. 4: Generative neural network (GNN) in the experimental set-up.
figure 4

Example images of various noisy experimental optical orbital angular momentum (OAM) modes that are uncorrected at the receiver (R) and corrected with the GNN (C). a Various images with increasing turbulence strength (left: \({C}_{n}^{2}\ =\ 22.4\, \times 1{0}^{-11}\ {m}^{-2/3}\), middle: \({C}_{n}^{2}\ =\ 51.2\times 1{0}^{-11}\ {m}^{-2/3}\), right: \({C}_{n}^{2}\ =\ 80\,\times 1{0}^{-11}\ {m}^{-2/3}\)). c Various OAM modes (top–bottom) with increasing attenuation ratio (left:  −0.18 dB, center:  −1.93 dB, right:  −2.43 dB). b Mean square error (MSE) as turbulence strength is varied. The inset shows the dependence of MSE on OAM value at a fixed turbulence strength of \({C}_{n}^{2}\ =\ 51.2\,\times 1{0}^{-11}\ {m}^{-2/3}\). d Dependence of MSE on attenuation ratio in dB. The top-left inset shows the dependence of MSE on OAM value at a fixed attenuation ratio of −1.93 dB. The data between −1.18 and 0 dB are enlarged and included in the right-bottom inset of d for better visibility. The whiskers on all the box plots represent MSE values from Q1 − 1.5 (Q3 − Q1) to Q3 + 1.5 (Q3 − Q1), where Q1 and Q3 represent the first quartile and third quartile of the MSE values. The diamond and notch, respectively, represent the average and median of the MSE for 55 reconstructed unknown noisy-distorted OAM intensity images (5 per each  ±ℓ from 0 to  ±10) at the receiver. The error bars in the top-left insets in b, d represent one standard deviation from the mean.

Full size image

Using the GNN, we demonstrate a significant reduction in mean MSE from 330.2 to 34.2 and from 742.3 to 120.7 for the weak turbulence strength of \({C}_{n}^{2}\ =\ 8\times 1{0}^{-11}\ {m}^{-2/3}\) and strong turbulence of \({C}_{n}^{2}\ =\ 80\times 1{0}^{-11}\ {m}^{-2/3},\) respectively. In order to gain insight into the dependence of our GNN’s performance on OAM value, we show the received (tan) and corresponding corrected (blue) MSE values for each  ±ℓ from 0 to  ±10 with a fixed \({C}_{n}^{2}\) of  51.2 × 10−11 m−2/3 in the inset of Fig. 4b. We reiterate here that the test intensity images (or unknown random turbulence phase masks) are not contained in the training set.

To further mimic the detrimental effect of loss in FSO communications, we fix the turbulence strength at \({C}_{n}^{2}\ =\ 51.2\times 1{0}^{-11}\ {m}^{-2/3}\) and vary the attenuation ratio from −2.52 to 0 dB. Note that we randomly vary the turbulent phase masks on SLM 2 while keeping the strength parameter \({C}_{n}^{2}\) constant. As described in the previous paragraph, we record 50 images for each  ±ℓ from 0 to  ±10 for a total of 550, which is then split between the training and testing sets. With the GNN pre-trained, we successfully reconstruct the unknown noisy, distorted, and attenuated intensity OAM profiles at the receiver. Some examples of noisy-distorted as well as attenuated OAM modes (R) and the corresponding corrected modes (C) for the attenuation ratios of  −0.18 dB (left),  −1.93 dB (center), and  −2.43 dB (right) are shown in Fig. 4c. The superposition OAM value in each row is  ±ℓ = 1, 5, 7,  and 10 from top to bottom, respectively. We find that the GNN successfully reconstructs the lost spatial features of the OAM profiles, even in the presence of strong attenuation. The MSEs between the noisy-attenuated and reconstructed OAM profiles at the receiver with respect to various attenuation ratios are shown in Fig. 4d. Here we show a significant reduction in average MSE, from 1.22 × 104 to 2.5 × 102 and from 9.64 × 102 to 52.8 for attenuation ratios −2.52 and −1.18 dB, respectively. Additionally, we calculate MSE for various OAM values at the attenuation of −1.93 dB, which are shown in left-top inset of Fig. 4d. As expected, the GNN gives an increasing trend of MSE with increasing OAM value. Again, the GNN significantly reduces the MSE in a consistent manner.

Lastly, we train the GNN with only simulated OAM images (see “Methods”) and reconstruct the experimentally distorted and attenuated OAM profiles. Then the reconstructed modes are classified with our CNN, which is again solely pre-trained with the simulated target patterns with Gaussian noise of strength σ = 1. In order to illustrate the success of the GNN in correcting individual OAM profiles and limiting cross-talk with nearby OAM values, we select an experimental test set with moderately strong turbulence \({C}_{n}^{2}\ =\ 51.2\times 1{0}^{-11}\ {m}^{-2/3}\) and an attenuation ratio of −1.93 dB. Here the test set contains 50 distorted experimental optical images for each OAM value of  ±ℓ ranging from 0 to  ±10, for a total of 550. With the optimized GNN trained only with numerically simulated images, we reconstruct 50 unknown experimental images for each OAM mode and predict the corresponding mode value using the CNN. The mode values predicted by the CNN without (a) and with (b) the GNN versus the target OAM value are shown in the cross-talk plot of Fig. 5. We find the majority of the uncorrected optical profiles with OAM mode values ℓ = ±1, ±3, ±4, ±10 are incorrectly demodulated at the receiver as shown in Fig. 5a. However, with GNN reconstruction, the incorrect predictions have been significantly reduced from 18 to 3, from 33 to 9, from 48 to 8, and from 26 to 8 out of 50 test images for each OAM mode value of ℓ = ±1, ±3, ±4, and ±10, respectively, as shown in Fig. 5b.

Fig. 5: Demodulating various orbital angular momentum (OAM) profiles.
figure 5

Cross-talk between experimentally transmitted and demodulated OAM profiles at the receiver for turbulence strength of \({C}_{n}^{2}\ =\ 51.2\,\times 1{0}^{-11}\ {m}^{-2/3}\), and an attenuation ratio of −1.93 dB a before applying generative neural network (GNN) and b after making correction with GNN. The networks GNN and convolutional neural network (CNN) are exclusively pre-trained with simulated OAM profiles.

Full size image

Discussion

In this work, we have developed a GNN and CNN system that efficiently improves received signals in a FSO communication scheme that have been severely deteriorated due to the effects of turbulence, attenuation, and detector noise. We demonstrate the scheme’s ability to significantly improve the accuracy at a receiver and correct for varying levels of distortion, both experimentally and via simulations. We also show such accuracy improvements as the FSO link distance and dark noise at the receiver are varied. By training the GNN solely with simulated images, the system is able to decrease the cross-talk between experimental OAM mode profiles at the receiver. Moreover, by using our GNN, we have significantly improved the classification accuracy of the CNN, which is solely trained with undistorted modes with dark noise at the receiver, allowing for a nontrivial reduction in the training set size as compared to previous CNNs used in FSO communications systems, which require training on an unbounded number of distorted mode profiles. The current system also bypasses the need for active and adaptive optics at the receiver of a FSO communications platform. Furthermore, the addition of this unsupervised learning scheme may be implemented to build an autonomous technique and extended to demodulate more complex optical profiles, which are difficult to label and classify with current supervised techniques. The flexibility and generality of the developed neural networks will allow for the straightforward integration into current FSO communication systems, with the ability to be directly applied to quantum communication systems as well29,30,31,32,33,34,35,36.

Methods

Turbulence simulation

We use a Kolmogorov phase with the Von Karman spectrum effects model37 to simulate the turbulence in the atmosphere, which is given by Eq. (1),

$$\Phi (\kappa )\ =\ 0.023{r}_{0}^{-5/3}{({\kappa }^{2}+{\kappa }_{0}^{2})}^{-11/6}\exp (-{\kappa }^{2}/{\kappa }_{m}^{2}),$$
(1)

where r0 = \({(0.423{k}^{2}{C}_{n}^{2}Z)}^{-3/5}\) is the Fried parameter for a propagation distance Z, and k = 2π/λ is the wave-vector for a given wavelength λ of light. Here κ is the spatial frequency, κm = 5.92/l0, and κ0 = 2π/L0, with inner (l0) and outer (L0) scales of turbulence. Finally, we generate random phase screens using the inverse Fourier transformation as given in Eq. (2),

$$\Phi (x,y)=\Re \left\{{{\mathcal{F}}}^{-1}\left({{\mathbb{C}}}_{NN}\sqrt{{\Phi }_{NN}(\kappa )}\right)\right\},$$
(2)

where ℜ means taking only the real part, \({{\mathcal{F}}}^{-1}\) is the inverse Fourier transformation, \({{\mathbb{C}}}_{NN}\) is a complex random normal number with zero mean and unit variance, and \(\sqrt{{\Phi }_{NN}(\kappa )}\) is the square root of the phase distributions given by Eq. (1) over the sampling grid of size N × N.

Numerical simulation of long-distance turbulent propagation

The turbulent environment is simulated by placing a turbulent phase screen (SLM 2) generated by Eq. (2) a meter away from the SLM 1 plane. Then we propagate the Gaussian beam, G(x, y, w0), through all the phase screens (SLM 1 and SLM 2) and have the intensity profile, \({I}_{r}^{t}\), with additive dark noise, N(0, σ), at the receiver, Z ≥ 200 m away from the SLM 2 plane, using Eq. (3),

$${I}_{r}^{t}={\left|{{\mathcal{F}}}^{-1}\left\{{H}_{2}\times {\mathcal{F}}\left({{\mathcal{F}}}^{-1}\left\{{H}_{1}\times {\mathcal{F}}\big[G(x,y,{w}_{0})\exp \big(i{\Theta }^{(\ell ,-\ell )}\big)\big]\right\}\exp (i\Phi (x,y))\right)\right\}\right|}^{2}+N(0,\sigma )$$
(3)

where \({\Theta }^{({\ell }_{1},{\ell }_{2})}\) represents the OAM phase mask on SLM 1 and H1 and H2 are transfer functions from SLM 1 to SLM 2 plane and from SLM 2 plane to receiver and CCD, respectively. In order to generate the turbulence discussed here, we use w0 = 4 cm, N = 128, λ = 1550 nm, l0 = 1 mm, L0 = 200 m, and \({C}_{n}^{2}\) varies from 9 × 10−15 m−2/3 to 1 × 10−13 m−2/3.

Numerical simulation of laboratory turbulent propagation

In order to simulate various intensity patterns for OAM modes of  ±ℓ = 0–10 to pre-train the GNN as mentioned in the description of Fig. 5 in the text, we first randomly generate 100 turbulent phase mask, again, using Eq. (2) with N = 800, λ = 795 nm, l0 = 1 mm, L0 = 25 m, and \({C}_{n}^{2}\ =\ 36.8\times 1{0}^{-11}\ {m}^{-2/3}\). Then we find the corresponding intensity pattern at the receiver using Eq. (3) with w0 = 0.45 mm, 0.2 m as the distance between SLM 1 to SLM 2, and 0.6 m as the distance between SLM 2 to CCD. After that, we add Gaussian noise with mean 0 and standard deviation of 0.1 and normalize them to 8-bit images. The 100 noisy-distorted images for each OAM mode, as a total of 1100, is split into a training set with 90 images for each OAM, as a total of 990, and a testing set with 10 images for each OAM, as a total of 110 images. Once the GNN is optimized and stored, we feed unknown noisy, distorted, and attenuated experimental OAM images into pre-trained GNN, which finally reconstructs them as its output. Note that we perform the experiment at \({C}_{n}^{2}=\ 51.2\times 1{0}^{-11}\ {m}^{-2/3}\) with an attenuation ratio of −1.93 dB scenario, whereas for numerical simulation we take \({C}_{n}^{2}=\ 36.8\times 1{0}^{-11}\ {m}^{-2/3}\) with dark noise as mentioned above.

Generative convolutional denoising autoencoder

The distorted received optical profiles, \({I}_{r}^{t}\), as given by Eq. (3) are fed to the encoder of the GNN, which compresses them into a latent space S as expressed in Eq. (4),

$${\rm{Encoder}}:\ S\ =\ {f}_{\theta }({I}_{r}^{t})\ =\ \left\{\left(\,{\text{Max}}\,\left({I}_{r}^{t}\star {w}_{1}^{k}+{b}_{1}^{k}\right)\right)\star {w}_{2}^{k}+{b}_{2}^{k}\right\}\times W+B, \\ \theta \in \{{w}_{1}^{k},\ {b}_{1}^{k},\ {w}_{2}^{k},\ {b}_{2}^{k},\ W,\ B\},$$
(4)

where θ represents a parameter space of \({w}_{1}^{k}\), \({w}_{2}^{k}\) (weights) and \({b}_{1}^{k}\), \({b}_{2}^{k}\) (biases) of kth feature mappings of the first and second convolutional layers, respectively, where “Max” corresponds to a max-pooling operation. Also, W and B represent the weight and bias of a fully connected layer, and for convenience “⋆” represents the convolutional/transpose-convolutional operation. Note that we apply the ReLU activation after each convolutional operation. The resulting latent space S is then forwarded to the decoder that maps it to reconstructed pixels I of the input space as given by Eq. (5):

$${\rm{Decoder}}:\ I\ =\ {g}_{{\theta }^{\prime}}(S)=\left\{\left((S\times {W}^{\prime}+{B}^{\prime})\star {{w}^{\prime}}_{1}^{n}+{{b}^{\prime}}_{1}^{n}\right)\star {{w}^{\prime}}_{2}^{n}+{{b}^{\prime}}_{2}^{n}\right\}\star {w}^{\prime}+{b}^{\prime},\\ \quad {\theta }^{\prime}\in \{{{w}^{\prime}}_{1}^{n},\ {{b}^{\prime}}_{1}^{n},\ {{w}^{\prime}}_{2}^{n},\ {{b}^{\prime}}_{2}^{n},\ {w}^{\prime},\ {b}^{\prime},\ {W}^{\prime},\ {B}^{\prime}\},$$
(5)

where primes represent the parameter space of the decoder corresponding to nth feature mappings. Here each training optical profile \({{I}_{r}^{t}}^{(i)}\) is successively mapped into a corresponding latent space S(i) and a generation I(i). After that, a square reconstruction loss L\(({I}^{(i)},{I}_{r}^{(i)})\) is evaluated, where \({I}_{r}^{(i)}\) is an undistorted optical profile at the receiver. Finally, in order to optimize the parameters, we minimize the average reconstruction loss given by Eq. (6) using adamoptimizer of tensorflow38:

$$\theta \ ,{\theta }^{\prime}={\rm{argmin}}_{\theta ,{\theta }^{\prime}}\ \frac{1}{N}\mathop{\sum }\limits_{i}^{N}{\bf{L}}\left({I}^{(i)},\ {I}_{r}^{(i)}\right)\ =\ {\rm{argmin}}_{\theta ,{\theta }^{\prime}}\ \frac{1}{N}\mathop{\sum }\limits_{i}^{N}{\bf{L}}\left({g}_{{\theta }^{\prime}}\left({f}_{\theta }({I}_{r}^{t(i)})\right),\ {I}_{r}^{(i)}\right).$$
(6)

CNN as a demodulator

In order to train a CNN to classify the generated modes, we simulate optical modes at the receiver without any turbulence using Eq. (3) for each OAM superposition value ranging from ℓ = 0 to  ±10. We then manually add random Gaussian noise with σ = 2 (σ = 1 for the result shown in Fig. 5). Here we keep low noise in the training and testing sets of the CNN to estimate how closely the generated modes by the GNN fit with the target mode. Finally, we simulate 150 noisy images for each value of OAM for a total of 16,500 images. The image set is split into a training set with 130 images and a test set with 20 images, again, for each OAM profile. Then the parameter space of the CNN is optimized by minimizing a softmax cross-entropy loss using adamoptimizer. Note that pre-trained CNN network has an unity accuracy with respect to the test images.

Attenuation ratio

We use the following relation in order to calculate the attenuation ratio:

$$\,\text{Attenuation ratio}\,\ =\ 10{{\rm{log}}}_{10}\left(\frac{\,{\text{Total}}\,\, {\text{intensity}}\,\, {\text{with}}\,\, {\text{attenuation}}}{{\text{Total}}\,\, {\text{intensity}}\,\, {\text{without}}\,\, {\text{attenuation}}\,}\right){\rm{dB}}.$$
(7)