Introduction

Copper-based metalloproteins play a major role in biology as electron or dioxygen (\({{\rm{O}}}_{2}\)) transporters. Haemocyanin (Hc) is one of three oxygen transporting proteins found in nature, alongside the iron-based hemerythrin and haemoglobin, and is common to a number of invertebrates, such as molluscs and arthropods. Deoxy-Hc employs two half-spin copper (I) cations, each coordinated by the imidazole rings of three histidine residues, to reversibly bind \({{\rm{O}}}_{2}\). Furthermore, various type 3 copper-based systems possess catalytic properties. Hc can decompose hydrogen peroxide into water and oxygen1 and synthetic analogues have been shown to reversibly cleave the dioxygen bond2 — a mechanism that enables tyrosinase and catechol oxidases to oxidise phenols3.

An accurate understanding of the electronic structure (spin and charge) of the \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) core is essential to clarifying the operation of dioxygen transport and would advance the design of synthetic catalysts that employ dioxygen as a terminal oxidant. There is significant interest in the biomimetic application of naturally occurring metal complexes for use in metallodrug design, with Cu(II) complexes recently employed in cancer therapeutics as artificial DNA metallonucleases4 and tyrosinase mimics5.

However, the formation of oxygenated haemocyanin (oxyHc) via the binding of \({{\rm{O}}}_{2}\) to deoxygenated haemocyanin (Hc) remains a challenging problem. In particular, the binding of \({{\rm{O}}}_{2}\) falls into the category of a spin-forbidden transition. Molecular \({{\rm{O}}}_{2}\) is in a spin triplet configuration, and the Cu ions in deoxyHc are known to be in the Cu(I) \({d}^{10}\) singlet configuration. The combination of triplet \({{\rm{O}}}_{2}\) and singlet deoxyHc, to produce the \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) antiferromagnetic singlet in oxyHc, is believed to occur via a simultaneous charge transfer of one electron from each Cu(I) ion to \({{\rm{O}}}_{2}\) forming a hybrid Cu(II)-peroxy-Cu(II) configuration. A superexchange pathway is hypothesised to form across the two Cu atoms6. This mechanism is supported by superconducting quantum interference device (SQUID) measurements that report a large superexchange coupling7 between the two Cu centres, and a diamagnetic ground state8.

Despite intensive theoretical studies on the nature of the side-on coordinated \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) core, theoretical analysis has so far proved to be challenging for many electronic structure methods including ab initio quantum chemistry, density functional theory (DFT) and mixed quantum/classical (QM/MM) methods due to the complex simultaneous interplay of both the charge and spin, and to the multi-reference character of oxyHc. In particular, DFT and hybrid-DFT do not predict the correct singlet ground state due to the multi-reference nature of the ground state that is not accessible in DFT-based approaches9,10,11. To overcome the limitation of DFT techniques, a spin-projection method (also called spin-mixing) is often applied, whereby the different spin-polarised ground states are calculated individually12, and the entangled singlet is reconstructed by linear combination of the respective Slater determinants (essentially a combination of the spin-broken symmetry state in the up–down, up–up and down–down configurations to extract an effective singlet state). Although this construction yields insights into the energetics, it does not allow for the study of excitations, and limits the scope of comparison with experimental data, such as the optical absorption10, that is a stringent test of any theory. Furthermore, the spin-contamination present in spin-polarised hybrid DFT remains an issue6,11,13,14,15, and typically the broken symmetry state wrongly becomes asymmetric in the oxyHc \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) core10. Finally, experiments have also alluded to the necessity of characterising the oxyHc ground state as a mixed valence state16, which cannot be accessed in the ground state DFT approach.

Meanwhile, multi-reference wave function methods have been used to extensively study the oxyHc core13,14,17,18,19,20,21,22, but these approaches are not feasible for systems containing more than several dozen electrons. Flock and Pierloot18 argue that the inclusion of the imidazole ligands results in steric effects that are critical for a realistic description of oxygen containing dicopper systems, but most multi-reference wave function studies of this core consider a simplified model with ammonia ligands (including CC13,14, CASPT218, MRCI19, RASPT220, and DMRG-CASPT221), while others (such as DMRG22 and DMRG-CT23) are limited to the experimentally inaccessible bare \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\)\({}^{2+}\) core. Furthermore, this system has large active space requirements given that it likely suffers from triplet instability11, and if the number of allowed excitations is too limited, size-extensivity errors arise20. Some of these methods also lack dynamical correlation contributions24,25,26, and others strongly over-correct correlation effects19.

In this work, we apply an alternative strategy: dynamical mean-field theory (DMFT)27. This method belongs to a broad category of embedding approaches and accounts for the limitations discussed above by treating the many-body effects and the superexchange of the di-Cu bridge explicitly (unlike DFT), while limiting this treatment to the correlated subspace of the copper \(3d\) electrons, thereby side-stepping the prohibitive scaling of quantum chemistry methods. DMFT is a sophisticated method that includes quantum dynamical effects, and takes into account charge fluctuations, spin fluctuations, and thermal excitations. Although DMFT is routinely used to describe materials, it was also recently extended to molecular systems28,29, and combined with the linear-scaling DFT software ONETEP to extend the applicability of DFT + DMFT to systems of unprecedented size30,31,32,33,34.

In order to characterise the superexchange mechanism between the Cu\(_{2}\) d-orbitals and intermediate O p-orbitals, we must also use non-local DMFT (or “cluster DMFT”). Single-site DMFT invokes a mean-field approximation across the multiple correlated sites, and thus it can only treat the multiplet structure of each Cu atom separately. This is not the case for cluster DMFT, where all correlated sites are directly treated in a multi-site Anderson impurity model (AIM)—hence our approach might be denoted as DFT + AIM. We also carry out a self-consistency cycle over the charge density, as we work at fixed total number of electrons. This produces a feedback to the solution of the model that is similar in its nature to the mean-field approximation used in DMFT.

Our DMFT + cluster DMFT approach identifies a regime where many-body effects—as characterised by the Hubbard interaction \(U\)—stabilise the singlet for the butterflied Cu\(_{2}\)O\(_{2}\) structure, in line with experiment. We show that a dominant spin singlet state is maximised at \(U=8\,{\mathrm{{eV}}}\) and discuss the validation of the model by optical experiments. The obtained singlet is in the Heitler-London regime (an entangled quantum superposition of two localised magnetic moments), and is associated with incoherent scattering processes that reduce the lifetime of charge excitations.

Results

The spin state of the \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) core

This work presents the first DFT + DMFT simulations on a 58-atom model of the oxyHc functional complex (Fig. 1). While 58 atoms is within the reach of some less accurate quantum chemistry methods, the overhead of extending DFT + DMFT to include much more of the protein environment would come at an insignificant computational cost given our use of linear-scaling DFT.

Fig. 1: The oxyHc functional complex.
figure 1

Structure showing the \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) correlated subsystem, which is treated using dynamical mean field theory, and the surrounding imidazole rings representing the protein environment. Hydrogen, carbon, nitrogen, oxygen and iron atoms are shown in white, green, blue, red, and orange respectively.

Full size image

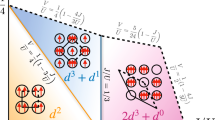
In vivo, the Cu\(_{2}\)O\(_{2}\) core exists in a low-spin (singlet) state, as identified by EPR35. In the model of Metz and Solomon, this low-spin state is stabilised by superexchange via the O\(_{2}\) ligand orbitals, which relies on the Cu\(_{2}\)O\(_{2}\) core being planar (Fig. 2a, b)10. As the peroxide molecule unbinds, the core butterflies (i.e. the dioxygen moves up out of the plane, leaving the core in a bent configuration). Here, each Cu overlaps with a different oxygen \({\pi }^{* }\) orbital on the peroxide (Fig. 2c, d). This removes the superexchange, and the triplet state becomes most favourable. If we measure planarity by \(R=| \frac{1}{2}({{\bf{r}}}_{{\rm{CuA}}}+{{\bf{r}}}_{{\rm{CuB}}})-\frac{1}{2}({{\bf{r}}}_{{\rm{O}}1}+{{\bf{r}}}_{{\rm{O}}2})|\)—that is, the distance between the mean position of the two copper atoms and the mean position of the two oxygen atoms—the singlet-to-triplet transition occurs at R = 0.6 Å using the B3LYP DFT functional10.

Fig. 2: The superexchange model of Metz and Solomon10.
figure 2

The \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) core is depicted from side-on (a, c) and above (b, d). In the planar configuration (a, b), single-ligand orbitals bridge the two copper sites, and superexchange is possible. In a bent configuration (c, d), the copper \(d\) orbitals overlap with different \({\pi }^{* }\) orbitals. As these two sets of orbitals are orthogonal, hopping between the blue and the red subspaces is not possible and the superexchange mechanism breaks down.

Full size image

However, X-ray structures of the \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) core reveal that the bound singlet state is not planar. In oxyHc  R = 0.47 Å, and in oxyTy R = 0.63 Å—beyond the predicted singlet-to-triplet transition36,37. QM/MM studies of the entire oxyHc protein (from which our model complex derives) obtain R = 0.54 to 0.71 Å; evidently, the protein scaffolding around the binding site prevents the core ever reaching the planar structure observed in model complexes11.

With this in mind, we examined the reduced density matrix of our butterflied model (R = 0.68 Å). This provides a detailed picture of the electronic structure of the \(3d\) subspace of the Cu atoms (Fig. 3). Within DMFT, the density matrix is obtained by tracing the Anderson impurity model over the bath degrees of freedom, and gives an effective representation of the quantum states of the two Cu atoms. Note that in our approach, the ground-state wave function is not a pure state with a single allowed value for the spin states (singlet, doublet, triplet, etc.), yet we can describe the fluctuating spin states of the Cu atom by analysing the spin distribution obtained from the dominant configurations.

Fig. 3: Decomposition of the reduced density matrix of the Cu2 dimer in the different quantum sectors.
figure 3

The colours correspond to the respective weights of the different contributions for each value of the Coulomb repulsion \(U\) (if a colour occupies all the vertical axis, for example, it means that all eigenvectors of the density matrix are in that particular quantum sector). Note that the \(d\) occupation is the sum of both Cu sites (e.g., \({d}^{20}\) means both Cu atoms are in the \({d}^{10}\) configuration).

Full size image

DMFT allows us to systematically investigate how many-body and finite-temperature effects alter these results. The Hubbard interaction \(U\) is known to be paramount to capture many-body effects. Several competing and relevant many-body phenomena stem from this term, including charge localisation, exchange of electrons, charge-transfer excitations, and stabilisation of magnetic multiplets. Consequently, the electronic structure of the \(3d\) subspace is highly sensitive to the magnitude of this parameter. Although typical values for \(U\) can be obtained by linear response or constrained RPA38,39, these predictions are typically dependent on the choice of local orbitals and basis representation. In this work we instead consider a range of values for \(U\) (from 0 to 10 eV). By artificially manipulating the magnitude of the local many-body effects, we can systematically investigate their influence on the electronic structure and derived properties.

The effect of \(U\) on the character of the reduced density matrix is shown in Fig. 3. In the weakly correlated regime (U < 2 eV), we obtain a large contribution from the \({d}^{20}\) and \({d}^{19}\) configurations, indicating that the average charge transfer from the Cu to \({{\rm{O}}}_{2}\) involves less than one electron per Cu, thus preventing the formation of a singlet (as the Cu \(3d\) orbitals are nearly full).

As \(U\) increases, the total electronic occupation of the Cu dimer decreases (Fig. 3 and Supplementary Table 1). In the range U = 6 − 8 eV, the \({d}^{18}\) singlet component is maximised, beyond which \({d}^{18}\) triplet excitations begin to contribute. The existence of this singlet is corroborated by the observed local magnetic moment and spin correlation (Supplementary Note 1 and Supplementary Fig. 1). Interestingly, the von Neumann entropy (Supplementary Note 2 and Supplementary Fig. 2) grows as \(U\) increases, pointing to the importance of many low-lying quantum states. Noting that \(U\approx 8-8.5\,{\mathrm{{eV}}}\) in the case of both molecules40 and solids41, it appears that in nature many-body quantum effects stabilise the low-spin singlet in spite of the butterflied structure of the \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) core (Fig. 2c, d).

The superexchange mechanism

Having identified this singlet in the \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) core at \(U\approx 8\, {\mathrm{{eV}}}\), let us establish how it forms. Direct hopping between localised Cu \(d\)-orbitals is very unlikely due to the large distance by which they are separated, and therefore hopping must proceed via an intermediate oxygen \(p\)-orbital (i.e. superexchange)42.

The superexchange process can be pictured in the canonical hydrogen atom dimer system. This system describes a pair of up and down electrons that form a singlet state. In this picture, two different limits are possible: (i) when the H atoms form a bond at short distance, and the up and down electron form a delocalised bound singlet (BS) centred on the bond, with a high degree of double occupancy, (ii) in the dissociated case, known as the Heitler-London (HL) limit, where the H atoms are far apart and the singlet is a true quantum entangled state of the singly occupied H orbitals. In the latter case, the molecular orbital contains only one electron and double occupancy is zero.

In the HL limit, which typically occurs in the limit of dissociation, the charge is localised around the H atoms. However, this effect may also occur in systems where the local Hubbard Coulomb repulsion \(U\) acts as a Coulomb blockade: many-body effects prevent long-lived charge transfer excitations, and the Coulomb repulsion energy is reduced at the expense of the kinetic energy. A signature of the blockade is typically a large increase in the self energy at the Fermi level (pole structure), indicating charge localisation and incoherent scattering associated with a short lifetime of charge excitations.

To investigate the nature of the singlet (BS or HL), we report in Fig. 4a the computed self energy of the Cu \(3d\) subspace, for various values of \(U\). We obtain a qualitative difference between  U = 6 eV and  U = 8 eV, where at  U = 8 eV the self energy develops a pole at \(\omega =0\). The formation of the pole is particular to U = 8 eV (Fig. 4b), and is associated with the regime where excitations are incoherent, which prevents long-lived charge transfer excitations from the Cu \(3d\) orbitals to \({{\rm{O}}}_{2}\). In this limit, the many-body effect acts as a Coulomb blockade and the charge is in turn localised, with weak direct coupling (HL limit). For  U = 6 eV, the singlet is in the BS limit, where charge excitations allow a direct electron transfer across the oxo-bridge. Note that the observation of the BS-HL crossover is not apparent in averaged quantities, such as in the double occupancies (Fig. 4c), which evolve smoothly with the Coulomb repulsion.

Fig. 4: Dynamical mean field self energy.
figure 4

a Imaginary part of the dynamical mean field local self energy \(\Sigma (\omega )\) of the Cu-\(3d\) empty orbital for Hubbard U = 2 eV, 6 eV, and 8 eV. At  U = 8 eV, we obtain incoherent excitations at \(\omega =0\, {\mathrm{{eV}}}\). b The imaginary local self energy at \(\omega =0\) and c the double occupancy of the partially-filled \(3d\) orbitals \(D\) as a function of \(U\). Note that although the double occupancy is evolving smoothly with the Coulomb interaction \(U\), \(\Sigma (\omega =0)\) shows a sharp increase near \(U=8\), associated with the stabilisation of a localised singlet.

Full size image

Turning back to the physical system, superexchange relies on a single-ligand orbital linking the two copper sites. (Superexchange pathways via two \(p\) orbitals are possible, but they give rise to ferromagnetic coupling that is significantly weaker than antiferromagnetic coupling from single-ligand orbital pathways43.) Examination of the molecular orbitals near the Fermi level (Fig. 5) reveals that, for the HOMO of the bent \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) structure, electronic density of the oxygen ligand is directed into the copper plane, thus providing a pathway for the antiferromagnetic superexchange that we observe.

Fig. 5: Molecular orbital isosurfaces.
figure 5

The isosurface for the highest occupied molecular orbital (a, c) and lowest unoccupied molecular orbital (b, d) densities for  U = 8 eV, as viewed side-on (a, b) and above (c, d). Note that because these are extracted from the Green's function via the spectral density, the phase of the orbitals is inaccessible.

Full size image

Interestingly, we note that these molecular orbitals differ in their energetic ordering compared to those from DFT studies of planar model complexes8. In particular, the HOMO involves hybridisation with oxygen \({\pi }^{* }\) rather than \({\sigma }^{* }\) orbitals (with the \({\sigma }^{* }\) oxygen orbital featuring approximately 3 eV above the Fermi level). This reordering will have substantial ramifications for the potential catalytic pathways, especially considering the importance of the \({\sigma }^{* }\) orbital to bond-breaking. This picture is confirmed by natural bond orbital (NBO) analysis, the results of which are presented in Supplementary Note 3.

Optical transitions

As a validation of the DFT + DMFT computational model, and to identify the strength of correlations in oxyHc, we extracted the optical absorption spectrum of ligated haemocyanin (Fig. 6).

Fig. 6: Theoretical optical absorption of the Cu2O2 core and imidazole rings obtained by dynamical mean field theory for values of the Coulomb repulsion U = 6 − 10 eV.
figure 6

For comparison, we show the experimental optical absorption44 in a wide range of wavelengths (infrared to UV). There are several smaller peaks in the experimental spectra that are not visible at this scale (indicated with arrows).

Full size image

As experiments are performed in the gaseous phase and not in a single crystal, we have calculated the isotropic and anisotropic components of the dielectric tensor. The former involves only pair correlators along the same spatial directions, whereas the latter also incorporates non-diagonal terms (note that both are causal quantities), which are important in oxyHc as the local coordination axes of the Cu atoms are not aligned. Remarkable agreement is obtained for U = 8 eV, with however a blue shift at high frequency (\(\omega\, > \, 4\,{\mathrm{{eV}}}\)), and a concomitant transfer of optical weight to lower energies (\(\omega\, <\, 3\, {\mathrm{{eV}}}\)). The position of the peak at approximately  3.5 eV is in excellent agreement. The experimental features at 3 eV (see arrow) are also visible in the theoretical calculations. The peaks at  1.8 and  2.2 eV contribute to the long infrared tail of the optical weight down to  1.5 eV. We note that the main difference between the BS (\(U\le 6\,{\mathrm{{eV}}}\)) and the HL singlet (U = 8 eV) is the presence of several large peaks associated with charge transfer from ligand to Cu \(3d\) orbitals below  2.5 eV, which are significantly smaller/absent in experiment45,46. The suppression of the optical weight at  2 eV is due to a large increase in incoherent scattering at \(\omega =0\, {\mathrm{{eV}}}\) at  U = 8 eV (Fig. 4), associated with the localisation of the holes in the Cu \(3d\) shell at  U = 8 eV. The strong suppression of the optical weight in the near infrared regime and the consistent agreement with our calculations shows that the di-Cu singlet is in the HL regime. In comparison, DFT, without extensions, puts a strong emphasis on the near infrared peak in the optical absorption10 because the aforementioned scattering processes are absent at this level of theory. (See also the very small HOMO-LUMO gap in Supplementary Fig. 4 for small values of \(U\).)

The absorption spectrum of this protein has been reported experimentally to be qualitatively dependent on its ligation state. In its oxygenated form, a weak peak at 570 nm (approximately 2.2 eV, see arrow) is attributed to ligand-to-metal charge transfer45,46 from the \({{\rm{O}}}_{2}\)\(\pi\) anti-bond with lobes oriented perpendicular to the metal atoms. This orbital is denoted “\({\pi }_{v}^{* }\)”; the \(\pi\) anti-bond with lobes directed towards the copper atoms is denoted \({\pi }_{\sigma }^{* }\) and is responsible for an experimentally observed (and much larger) peak at approximately 3.6 eV. Our calculations accurately reproduce this large peak, associating it with a transition from the weight at −1 eV in the density of states (Supplementary Fig. 4), which is localised on CuA/CuB/imidazole, to the LUMO, which in our calculations is a hybridised state between the Cu and the \({\pi }_{\sigma }^{* }\) O\(_{2}\), with dominant Cu \(3d\) character (Fig. 5b, d). Meanwhile, a small peak at 2  eV exists corresponding to the HOMO-to-LUMO transition (\({\pi }_{v}^{* }\) to Cu charge transfer). Overall, comparison with the experimental spectrum suggests \(U\ge 8\, {\mathrm{{eV}}}\) which is compatible with the value of \(U\) that gives rise to the singlet. We note that time-dependent density functional theory (TDDFT) calculations reproduce the absorption peak at 3.6 eV, but not the peak at 4.5 eV. More importantly, the ground state electronic structure at this level of theory is not the antiferromagnetic singlet state observed experimentally; thus, agreement between TDDFT and experiment likely involves some cancellation of errors.

Discussion

We have presented the application of a DFT + cluster DMFT approach, designed to treat strong electronic interaction and multi-reference effects, to oxyHc, a molecule of important biological function. The reduced density matrix of the \(3d\) subspace of the two Cu atoms revealed the presence of fluctuating spin-states, in which a Cu\(_{2}\)\({d}^{18}\) singlet component is maximised at U = 8 eV in spite of the butterfly distortion of the \({{\rm{Cu}}}_{2}{{\rm{O}}}_{2}\) core. The Hubbard \(U\) is necessary to capture the multi-reference character of the ground-state, placing oxyHc in the limit of a true quantum entangled singlet in the limit of the Heitler-London model, while the highest occupied molecular orbital has been shown to provide a pathway for antiferromagnetic superexchange. This work provides a starting point for studying biological activity of oxyHc and related type 3 Cu-based enzymes by (a) establishing that the singlet can survive the butterfly distortion, thereby resolving a prior inconsistency between structural data, spectroscopy, and first-principles calculations, and (b) by providing a framework for subsequent studies to account for the effect of the protein “scaffolding” in which the active site sits, as well as the effects of strong electronic correlation. Our approach reproduced the experimentally observed peaks in the absorption spectrum at around 2.2, 3.7, and 4.5 eV.

The DFT + DMFT method provides a useful middle-ground between (a) density-functional theory-based simulations of metalloproteins, which depend heavily on the choice of functional and incorrectly describe multi-reference effects, and (b) single- or multi-reference quantum chemistry approaches, whose unfavourable scaling prevents studies on models of realistic size. More generally, our particular implementation of DMFT within linear-scaling DFT software32 can account for strongly correlated electronic behaviour while simultaneously including the effects of protein environments, making it ideally suited for studying biological activity in a wide range of transition metal-containing proteins47,48.

Methods

Geometry

The geometry of the 58-atom system was obtained from the literature11. This had been optimised using the B3LYP hybrid functional and closely matches the experimentally observed structure11,36. The coordinates of this structure are provided in Supplementary Note 4.

DFT

The DFT ground-state was obtained using ONETEP30, which is a linear-scaling DFT code that is formally equivalent to a plane-wave method. Linear-scaling is achieved by the in situ variational optimisation of its atom-centred basis set (spatially truncated nonorthogonal generalised Wannier functions, or NGWFs)49. The total energy is directly minimised with respect to the NGWFs and the single-particle density matrix. The use of a minimal, optimised Wannier function representation of the density-matrix allows for the DFT ground state to be solved with relative ease in large systems. This is particularly useful in molecules, since explicit truncation of the basis functions ensures that the addition of vacuum does not increase the computational cost50.

The DFT calculations of the oxyHc system were run with an energy cut-off of 897  eV, using the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional51. Nine NGWFs were employed on the copper atoms, four on each carbon/nitrogen/oxygen, and one on each hydrogen. Spin symmetry was imposed. NGWFs were truncated using 7 Å cut-off radii. Open boundary conditions were achieved via a padded cell and a Coulomb cut-off52. The Hubbard projectors were constructed from the Kohn–Sham solutions to an isolated copper pseudopotential53. The pseudopotentials were generated with the OPIUM pseudopotential generation project54. These pseudopotentials partially account for scalar relativistic effects. (Studies have demonstrated that relativistic effects can play a role in the electronic structure of the Cu\(_{2}\)O\(_{2}\) core55.)

DMFT

We refined our DFT calculations using the DFT + DMFT method27,56 in order to obtain a more accurate treatment of strong electronic correlation effects. The oxyHc model was mapped, within DMFT, to an Anderson impurity model (AIM) Hamiltonian57, and we used a recently developed extended Lanczos solver58 to obtain the DMFT self energy. The convergence of the mapping is shown in Supplementary Fig. 5 and discussed in Supplementary Note 5.

To identify the best spatial representation of the local \(d\)-space in the projected Anderson impurity model, we first identified the orthogonal transformation that reduces the off-diagonal elements of the local Green’s function, for respectively the CuA and CuB sites. Then, we implemented a minimisation procedure that finds the closest corresponding real space \(SO(3)\) rotation of the local Cartesian axis corresponding to the \(O(5)\) orthonormal transformation in \(d\)-space. This provides a set of local axes, different on each Cu atom, which make the local Green’s function nearly diagonal in frequency space. These axes are plotted in Supplementary Fig. 6 and discussed in Supplementary Note 6. As a result, we observed that the CuA and CuB holes are of pure orbital character within this local axis representation. The validity of this approach was vindicated by the NBO analysis, which when performed on the DMFT density revealed a hole in one \(3d\) orbital for each Cu atom, confirming the expected Cu(II) oxidation state 3\({d}^{9}\)4\({s}^{0}\) (see Supplementary Note 3 for details).

Since only a single impurity site (\(3d\) orbital subspace) is present, the system becomes crystal momentum independent in the molecular limit, and since the Kohn–Sham Green’s function is computed in full before projection onto the impurity subspace, the Anderson impurity mapping is effectively exact, and the necessity of invoking the DMFT self-consistency is not required. However, in DFT + DMFT there is also a charge self-consistency cycle, where (i) the chemical potential can be updated to ensure particle conservation and/or (ii) the DFT + DMFT density kernel can be used to generate a new Kohn–Sham Hamiltonian, which in turn provides a new input to DMFT; the procedure being repeated until convergence is achieved59,60,61. In this work, we updated the chemical potential but not the Hamiltonian due to computational cost.

To obtain the Kohn–Sham Green’s function, we performed the matrix inversion, as well as all matrix multiplications involved in the DMFT algorithm, on graphical processing units (GPUs) using a tailor-made parallel implementation of the Cholesky decomposition written in the CUDA programming language. Electronic correlation effects are described within the localised subspace by the Slater−Kanamori form of the Anderson impurity Hamiltonian62,63, specifically:

$$\begin{array}{ll}{{\mathcal{H}}}_{U}=\,&U\sum _{{{m}}}{n}_{{{m}}\uparrow }{n}_{{{m}}\downarrow }+\left(U^{\prime} -\frac{J}{2}\right)\sum _{{{m}}> {{m}}^{\prime} }{n}_{{{m}}}{n}_{{{m}}^{\prime} }\\ &-J\sum _{{{m}}> {{m}}^{\prime} }\left(2{{\bf{S}}}_{{{m}}}{{\bf{S}}}_{{{m}}^{\prime} }+\left({d}_{{{m}}\uparrow }^{\dagger }{d}_{{{m}}\downarrow }^{\dagger }{d}_{{{m}}^{\prime} \uparrow }{d}_{{{m}}^{\prime} \downarrow }\right)\right),\end{array}$$
(1)

where \(m,m^{\prime}\) are orbital indices, \({d}_{{{m}}\sigma }\) (\({d}_{{{m}}\sigma }^{\dagger }\)) annihilates (creates) an electron with spin \(\sigma\) in the orbital \(m\), and \({n}_{m}\) is the orbital occupation operator.

The first term describes the effect of intra-orbital Coulomb repulsion, parameterised by \({S}_{{{m}}}=\frac{1}{2}{d}_{{{m}}s}^{\dagger }{\overrightarrow{\sigma }}_{ss^{\prime} }{d}_{{{m}}s^{\prime} }\), and the second term describes the inter-orbital repulsion, proportional to \(U^{\prime} =U-2J\), which is renormalised by the Hund’s exchange coupling parameter \(J\) in order to ensure a fully rotationally invariant Hamiltonian (for further information on this topic, we refer the reader to Imada et al.64) The third term is the Hund’s rule exchange coupling, described by a spin exchange coupling of amplitude \(J\). \({{\bf{S}}}_{m}\) denotes the spin corresponding to orbital \(m\), so that \({S}_{{\rm{m}}}=\frac{1}{2}{d}_{{\rm{m}}s}^{\dagger }{\overrightarrow{\sigma }}_{ss^{\prime} }{d}_{{\rm{m}}s^{\prime} }\), where \(\overrightarrow{\sigma }\) is the vector of Pauli matrices.

Our DMFT calculations were carried out at room temperature,  T = 293 K and the Hubbard \(U\) was varied in the range 0–10 eV, with a fixed Hund’s coupling  J = 0.8 eV. The theoretical optical absorption was obtained in DFT + DMFT within the linear-response regime (Kubo formalism), in the no-vertex-corrections approximation65, which is given by:

$$\begin{array}{ll}\sigma (\omega )=\,&\frac{2\pi {e}^{2}\hslash }{\Omega }\int {\mathrm{d}}\omega ^{\prime} \ \frac{f(\omega ^{\prime} -\omega )-f(\omega ^{\prime} )}{\omega }\\ &\times ({\rho }^{\alpha \beta }(\omega ^{\prime} -\omega ){{\bf{v}}}_{\beta \gamma }{\rho }^{\gamma \delta }(\omega ^{\prime} )\cdot {{\bf{v}}}_{\delta \alpha }),\end{array}$$
(2)

where the factor of two accounts for spin-degeneracy, \(\Omega\) is the simulation-cell volume, \(e\) is the electron charge, \(\hslash\) is the reduced Planck constant, \(f\left(\omega \right)\) is the Fermi-Dirac distribution, and \({\rho }^{\alpha \beta }\) is the density-matrix given by the frequency-integral of the interacting DFT + DMFT Green’s function. The matrix elements of the velocity operator, \({{\bf{v}}}_{\alpha \beta }\), noting that we do not invoke the Peierls substitution65, are given by:

$${{\bf{v}}}_{\alpha \beta }=-\frac{i\hslash }{{m}_{e}}\langle {\phi }_{\alpha }| {\boldsymbol{\nabla }}| {\phi }_{\beta }\rangle +\frac{i}{\hslash }\langle {\phi }_{\alpha }| \left[{\hat{V}}_{nl},{\bf{r}}\right]| {\phi }_{\beta }\rangle .$$
(3)

This expression is general to the NGWF representation used in this work66, where the contribution to the non-interacting Hamiltonian due to the non-local part of the norm-conserving pseudopotentials67,68, represented by \({\hat{V}}_{nl}\), is included.

Finally, the double-counting correction \({E}_{{\mathrm{{dc}}}}\) must be introduced, since the contribution of interactions between the correlated orbitals to the total energy is already partially included in the exchange-correlation potential derived from DFT. The most commonly used form of the double-counting term is69

$${E}_{{\rm{dc}}}=\frac{{U}^{{\rm{av}}}}{2}{n}_{d}\left({n}_{d}-1\right)-\frac{J}{2}\sum _{\sigma }{n}_{d\sigma }\left({n}_{d\sigma }-1\right),$$
(4)

where

$${U}^{{\rm{av}}}=\frac{U+2(N-1)U^{\prime} }{2N-1}$$
(5)

with \(N\) being the number of orbitals spanning the correlated subspace (and recall that \(U^{\prime} =U-2J\)). This double-counting is derived by attempting to subtract the DFT contributions in an average way; \({U}^{{\mathrm{{av}}}}\) is the average of the intra- and inter-orbital Coulomb parameters.