Abstract
Electrical tunability of the \(g\)-factor of a confined spin is a long-time goal of the spin qubit field. Here we utilize the electric dipole spin resonance (EDSR) to demonstrate it in a gated GaAs double-dot device confining a hole. This tunability is a consequence of the strong spin-orbit interaction (SOI) in the GaAs valence band. The SOI enables a spin-flip interdot tunneling, which, in combination with the simple spin-conserving charge transport leads to the formation of tunable hybrid spin-orbit molecular states. EDSR is used to demonstrate that the gap separating the two lowest energy states changes its character from a charge-like to a spin-like excitation as a function of interdot detuning or magnetic field. In the spin-like regime, the gap can be characterized by the effective \(g\)-factor, which differs from the bulk value owing to spin-charge hybridization, and can be tuned smoothly and sensitively by gate voltages.
Similar content being viewed by others
Introduction
In semiconductor spintronics, spin rotation is an essential element of coherent control1,2. The most direct method of achieving spin rotation involves a pulsed magnetic field. This technique, however, produces slow rotations and leads to qubit addressability difficulties3,4. Therefore, the preferred approach is electric dipole spin resonance (EDSR), involving an electrical microwave modulation of the system5,6. The EDSR frequency is defined by the Zeeman energy \({E}_{{\rm{Z}}}\) (spin splitting), which is set by the static external magnetic field. \({E}_{{\rm{Z}}}\) depends on the effective \(g\)-factor of the host material, and therefore addressing individual spins in a multi-qubit device would benefit from the ability to tune the \(g\)-factor in a spatially selective manner7.
In EDSR, the spin-flip results from electrical modulation of the particle’s position, and thus a mechanism coupling these two degrees of freedom is required. Such a mechanism can be engineered by creating position-dependent magnetic interactions with micromagnets7,8,9 or nuclei of the host material10. In gated GaAs or Si devices confining electrons, the spin–orbit interaction (SOI) inherent in the semiconductor material has also been exploited5,6,11; however, the resulting coupling is weak so coherent control of the spin is possible only on timescales comparable to the spin decoherence time6. The SOI strength can be increased by confining electrons in InAs12,13 or InSb dots14; however, switching the carrier type to holes that can deliver strong SOI holds the greatest promise. EDSR in hole systems has been described theoretically15,16 but to date demonstrated only in dots defined in silicon17,18 or germanium19, for which the SOI is relatively weak owing to the inversion symmetry of the crystal lattice. However, a side effect of the increased SOI may result in a shorter hole spin relaxation time \({T}_{1}\), as this process is brought about by phonon-assisted SOI. Recently, \({T}_{1}\) in the GaAs gated hole device was measured and shown to be somewhat shorter than that in electron-based GaAs devices20. Nonetheless, the advantage of hole-based devices lies in the fact that holes interact more weakly with nuclear spins than electrons21,22. This hyperfine interaction severely limits the \({T}_{1}\) of the electron spin at low magnetic fields, while the hole spin \({T}_{1}\) remains limited by the phonon-assisted SOI and therefore may become much longer23,24. Moreover, the hole spin \({T}_{1}\) could be further extended by engineering the phonon density of states to eliminate the phonon modes mediating the spin-flip transitions. Preliminary work toward that end has already been demonstrated for electronic dots in nanowires25.
Being a perturbative effect, the SOI in devices confining electrons is too weak to renormalize the Zeeman gap noticeably. This is why local electrostatic tuning of the \(g\)-factor for electrons has been attempted by other methods, e.g., by engineering of materials with composition gradients26,27, exploiting interactions with magnetic impurities28 or nuclear spins29, or utilizing a combination of SOI and the Stark shift30. In silicon and germanium devices confining holes, weak SOI permits only a small degree of electrical control of the \(g\)-factor via engineering of valence subband mixing17.
Here we demonstrate an electrically tunable effective \(g\)-factor, \({g}_{{\rm{eff}}}\), in a lateral gated GaAs double quantum dot (DQD) confining one hole20,31,32,33 in the strong interdot coupling regime. In this system, the spin-flip tunneling due to strong SOI20,33 introduces orbital (charge-transfer) effects. Consequences of strong level hybridization have been investigated previously in electron devices, where spin relaxation hotspots were detected in Si-based single dots34 and GaAs double dots35, and valley orbit mixing effects were explored in Si dots36. Here we demonstrate that the SOI-induced level hybridization alters the energy gap separating the levels involved in the microwave absorption (the EDSR gap), making \({g}_{{\rm{eff}}}\) voltage dependent. Moreover, the SOI is sufficiently strong that one can utilize EDSR as a spectroscopic tool to map out the level structure of the DQD over a broad range of magnetic fields and gate voltages, which we carry out by electrical transport measurements. We engineer both the spectral content of the states and the effective \(g\)-factor by controlling the amount of mixing between different orbitals of the DQD. This is accomplished by adjusting the coupling and detuning between dots and the external magnetic field. The voltage dependence of \({g}_{{\rm{eff}}}\) paves the way toward protocols for coherent control of single-hole spins involving fast voltage tuning of the EDSR gap character: from purely spin-like, conducive for long spin relaxation times, to a spin-charge hybrid, enabling fast coherent rotations in a constant magnetic field and under continuous microwave modulation.
Results
The system
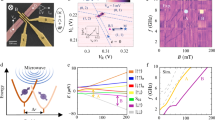
The gate layout of the device is shown in Fig. 1a (see “Methods” for device details). Unlike in our previous studies32,33, the system is tuned to exhibit a much stronger interdot tunnel coupling leading to the formation of quantum molecular states. Signatures of this coupling are found in the charging diagram, mapped out by low source-drain bias transport (Fig. 1b) and by charge detection (Fig. 1c) at \(B=0\) T. In this report, we focus on the region where \(({n}_{L},{n}_{R})=(0,0)\), \((1,0)\), and \((0,1)\) charge configurations are close in energy (dashed rectangle in Fig. 1b), with \({n}_{L}\) (\({n}_{R}\)) denoting the number of holes in the left (right) dot. The strong coupling results in a curved single-hole charge addition line, as well as an extended transport region along this line. This is in contrast to the weak interdot tunneling case, in which the transport signature consists typically only of a so-called triple point, occurring at gate voltages corresponding to the exact energy resonance of the single-hole levels of individual dots.
The layout of the gates defining the device is shown in a. The crossed boxes represent the Ohmic contacts used to measure the current through the DQD \({I}_{{\rm{DOT}}}\) and the quantum point contact charge sensor \({I}_{{\rm{CS}}}\). Microwave (MW) modulation is applied to gate R. The charge stability diagram is measured by transport at low source-drain voltage \({V}_{{\rm{SD}}}=50\) μV (b) and by charge detection with the quantum point contact (c) as a function of the voltages \({V}_{L}\) and \({V}_{R}\) on the gates \(L\) and \(R\), respectively. d, e show, respectively, the transport in the derivative \({\rm{d}}{I}_{{\rm{DOT}}}/{\rm{d}}{V}_{L}\) at \(B=0\) T and \(B=2\) T. The transport features in the single-hole current stripe marked by white arrows arise from the four-level system (GS, ES1, ES2, ES3) probed by a single hole, shown schematically in f. The hole tunnels from the source, through the quantum molecular levels available in the conduction window at high source-drain voltage (\({V}_{{\rm{SD}}}=1\) mV), into the drain. In this schematic, GS, ES1 (ES2, ES3) levels have large contributions of the left-dot (right-dot) orbitals, as denoted by solid lines.
The system is further characterized by transport measurements in the high source-drain bias regime (\({V}_{{\rm{SD}}}=1\) mV) at \(B=0\) T (Fig. 1d) and \(B=2\) T (Fig. 1e). In both cases, the strong interdot coupling leads to distinct curvature of the single-hole ground and excited state (GS and ES, respectively) addition lines denoted by white arrows. For \(B=0\) T, the hole can tunnel from the source to the drain via either of the two Kramers degenerate DQD quantum molecular levels, bonding (upper arrow) or antibonding (lower arrow). The magnetic field removes the Kramers degeneracy and for \(B=2\) T we find four lines, marked with four arrows in Fig. 1e, indicating contributions of each of the four lowest-energy DQD states when they enter the transport window.
Our system is modeled by the two-site single-hole Hubbard Hamiltonian with spin:
It is written on the basis of the four spin states of the DQD, \(\left|L\Uparrow \right\rangle\), \(\left|L\Downarrow \right\rangle\), \(\left|R\Uparrow \right\rangle\), and \(\left|R\Downarrow \right\rangle\), i.e., the left (\(L\)) and right (\(R\)) dot orbitals with spin up (\(\Uparrow\)) and down (\(\Downarrow\)). The interdot coupling is accounted for by the tunneling matrix elements \({t}_{N}\) (spin conserving) and \({t}_{F}\) (spin flipping, resulting from the SOIs)20,32,33. The diagonal terms represent the onsite energies, determined by gate voltages and the magnetic field through the Zeeman energy \({E}_{{\rm{Z}}}={g}^{* }{\mu }_{{\rm{B}}}B\), where \({g}^{* }\) is the bulk \(g\)-factor and \({\mu }_{{\rm{B}}}\) is the Bohr magneton. The four quantum molecular states are obtained by diagonalizing this Hamiltonian and are shown schematically in Fig. 1f. We note that in all energy diagrams henceforth we measure the hole energy from the valence band edge, i.e., the positive direction of the energy axis corresponds to increasing hole energies. Owing to the strong interdot coupling, the molecular orbitals are spinors, expressed as superpositions of single-dot states with either spin. Further model details, including the dependence of the energies of the four states on the interdot detuning and the magnetic field are presented in Supplementary Notes 1 and 2.
Resonant microwave absorption
Figure 2a shows a derivative of the single-hole high-bias transport triangle in the presence of monochromatic microwave modulation with frequency \(f=37.12\) GHz applied to the right-dot gate R at \(B=2.5\) T. Compared with Fig. 1e, we detect two new resonance lines (labeled I and II) resulting from the EDSR process, whereby microwaves are resonantly absorbed and the hole is promoted from GS to ES1. The arrangement of levels occurring at point b on the resonance line I is shown in Fig. 2b. Here the GS lies below the Fermi energy of the drain, i.e., the system is in the Coulomb blockade regime. Indeed, point b lies outside the transport triangle, where the current in the absence of microwaves is blocked. However, as ES1 lies above the Fermi energy of the drain, resonant microwave absorption lifts the Coulomb blockade resulting in current flow. This alignment of levels is analogous to that in the spin readout technique of Elzerman et al.37. Without SOI, the microwave frequency \(f\) at which the EDSR signal occurs would correspond to the Zeeman energy \({E}_{{\rm{Z}}}={g}^{* }{\mu }_{{\rm{B}}}B\), with \({g}^{* }\) being the bulk effective \(g\)-factor and \({\mu }_{{\rm{B}}}\) being the Bohr magneton. However, the presence of strong SOI leads to noticeable repulsion of levels ES1 and ES2. As a result, the spin gap is renormalized and can be characterized by an effective \(g\)-factor defined as \({g}_{{\rm{eff}}}=hf/{\mu }_{{\rm{B}}}B\), with \(h\) being Planck’s constant. The degree of renormalization clearly depends on the energy separation between ES1 and ES2, which can be controlled by adjusting the detuning, hence \({g}_{{\rm{eff}}}\) becomes voltage tunable. Figure 2a also reveals the second resonance line (II) parallel to I and equidistant from the charge transfer line \(\varepsilon =0\) but located at opposite (negative) detuning. The alignment of DQD levels at point c on that line is shown in Fig. 2c. At this detuning, without strong hybridization the energies of the left-dot orbitals of each spin would be higher than their right-dot counterparts, making it an energy blockade condition, and no current could flow. It should be noted that in our previous study20 we found that the rate of tunneling from GS into the drain (dashed arrow) is smaller than that from ES1 (solid arrow). This is because the tunneling barrier is not rectangular but is wider (narrower) at lower (higher) energies. The absorption of microwaves results in the hole being promoted from GS to ES1 and therefore in an enhancement of the tunneling current. This difference in the tunneling rates is necessary to observe current enhancement along resonance line II at the EDSR condition.
a shows the single-hole high-bias transport triangle at \(B=2.5\) T, plotted as the derivative \({\rm{d}}{I}_{{\rm{DOT}}}/{\rm{d}}{V}_{L}\). The alignment of levels at two selected points is depicted in b, c: the former corresponds to the line I, and the latter to the line II in a. In either case, along the EDSR lines I and II, the hole finds its way onto the ground state GS of the system, which is energy blockaded (b) or weakly connected to the drain (c), resulting in zero or weak current, respectively. In both panels, microwave modulation leads to the promotion of the hole onto the excited state ES1, better connected to the drain, which is detected as a resonant EDSR peak.
Charge-like and spin-like regimes
The central observation in Fig. 2 is that the EDSR signal occurs for specific detuning conditions set by the gate voltages. If the gap probed by microwaves were purely related to spin, i.e., defined only by a constant bulk \(g\)-factor, the resonance condition would depend only on the magnetic field and be voltage independent. To explore the voltage tuning of the EDSR, we follow the position of resonance line in the Coulomb blockade region, along the dashed yellow line in Fig. 3a, where we plot \({I}_{{\rm{DOT}}}\) at \(B=2.5\) T and microwave frequency \(f=40.62\) GHz. This line is equivalent to the line I in Fig. 2a. Figure 3b shows the magnetic field dependence of the detuning corresponding to the EDSR signal observed on scanning the gate voltages along the yellow dashed line in Fig. 3a, moving toward the \(\varepsilon =0\) charge transfer line denoted by the white dashed line. This procedure changes the detuning between the dots, keeping GS below the Fermi energy of the drain and ES1 above it. For a voltage-independent EDSR signal, we would expect the peak to occur only for one value of B. However, we recover the EDSR peak at other magnetic fields, and the corresponding detuning position is magnetic field dependent. We analyze this dependence in detail in Supplementary Note 3. As examples, here we plot for \(B=2.4\) T and \(B=3.0\) T the calculated eigenenergies of the system with solid lines as a function of the detuning (Fig. 3c, d, respectively) with system parameters obtained from the experimental data (see “Methods”). The Hamiltonian parameters in Fig. 3c are \({t}_{N}=62.7\) μeV, \({t}_{F}=42.0\) μeV, and \({g}^{* }=1.24\), while in Fig. 3d we use \({t}_{N}=54.5\) μeV, \({t}_{F}=12.9\) μeV, and \({g}^{* }=1.18\). These two cases correspond to the two points, c and d, identified in Fig. 3b. In each diagram, for positive detuning, we find a unique match of the microwave energy (green bar) to the GS–ES1 gap, at the detuning \(425\) and \(130\) μeV, respectively, which accurately corresponds to the experimental resonance position in Fig. 3b. Here the crucial feature is the anticrossing of energies of ES1 and ES2 caused by the spin-flip tunneling process. If this tunneling is switched off, the energy levels correspond to bonding and antibonding quantum molecular states with definite spin: down (blue dashed lines) and up (red dashed lines). However, in the presence of the spin-flip tunneling the ES1 and ES2 anticross with the corresponding mixing of spin states. The anticrossing defines two clear regimes for EDSR. For sufficiently high detuning, as in Fig. 3c, the resonance is spin-like, as it connects GS and ES1 characterized predominantly by opposite spins. For small detuning, as in Fig. 3d, the excitation is charge-like, as the resonance connects GS and ES1 mostly with the same spin but differing by hole charge distribution. Interestingly, in the small detuning limit, at large magnetic field, the signal observed is essentially driven by photon-assisted tunneling rather than EDSR38. At intermediate detuning, the excitation is of a hybrid (spin-charge) nature. The effective factor \({g}_{{\rm{eff}}}\) is therefore a three-dimensional parameter being both voltage and magnetic field dependent. The top axis in Fig. 3b shows the value of \({g}_{{\rm{eff}}}\) corresponding to the observed EDSR signal at different magnetic fields. We find that in this experiment we are able to tune \({g}_{{\rm{eff}}}\) by 30% by simultaneous adjustment of the gate voltages and the magnetic field.
a The high-bias transport triangle (\({V}_{{\rm{SD}}}=+1\) mV) for a single hole with the electric dipole spin resonance (EDSR) feature at \(B=2.5\) T and microwave frequency \(f=40.62\) GHz. The detuning \(\varepsilon\) of the dots is swept along the yellow dashed line toward the charge transfer line \(\varepsilon =0\) (white dashed line). b The detuning position of the EDSR peak and the smooth transition from a spin-like to a charge-like character as a function of the magnetic field (note smaller detuning is toward the top of the plot). Since the frequency is kept constant, the presence of an EDSR signal for different magnetic fields indicates an effective \(g\)-factor \({g}_{{\rm{eff}}}=hf/{\mu }_{{\rm{B}}}B\) (see top axis) that is voltage tunable. c, d The energies of the four levels GS, ES1, ES2, and ES3 as a function of detuning at \(B=2.4\) and \(B=3\) T, respectively. The energy gap of \(168.0\) μeV, corresponding to \(f=40.62\) GHz, is marked in each panel with a green bar. The EDSR signal at the two green dots marked in b occurs for the cases depicted in c, d. In the two lower panels, the minimal gap corresponding to zero detuning is marked by a black double arrow. The dashed lines show energies of spin-down (blue) and spin-up (red) states calculated for the case when spin-flip tunneling is absent. For each spin projection, the low-energy (high-energy) state can be identified as the bonding (antibonding) quantum molecular orbital. The black solid lines denote energies in the presence of spin-flip tunneling.
Voltage tuning of the effective \(g\)-factor
In Fig. 4, we present examples of the voltage tunability of the EDSR signal by tracking the peak position in \({V}_{L}\) as a function of microwave frequency at \(B=1.5\) T (Fig. 4a), and \(B=1.75\) T (Fig. 4b). The smallest gap corresponds to zero detuning (see black double arrows in Fig. 3c, d). In Fig. 4c, we show the microwave frequency corresponding to this minimal gap (see green symbols in Fig. 4a, b) as a function of magnetic field. With the EDSR bridging the pure Zeeman gap, we would expect this dependence to be purely linear, with the slope corresponding to the material bulk \(g\)-factor, \({g}^{* }\). This linearity is clear for small magnetic field (region (1)). However, from its slope we extract \({g}_{{\rm{eff}}}=0.85\), which is 30% lower than the bulk value \({g}^{* }=1.35\) measured by us previously32, reflecting the strong spin-gap renormalization. As the magnetic field grows, the relationship becomes nonlinear, and at point (2) it reaches a maximum, corresponding to the onset of the anticrossing of ES1 and ES2 levels. Here the interpretation in terms of a renormalized spin gap reaches its limit even though \({t}_{F}\) is finite. From Fig. 3d, one might expect that at even higher magnetic field the EDSR bridges the gap between states of the same spin, i.e., it is a charge-like excitation, and that the dependence in Fig. 4c should become magnetic field independent. However, in region (3) we find that the GS–ES1 gap decreases with increase of magnetic field. This is due to the decrease of both tunneling matrix elements resulting from diamagnetic effects as described in our previous work for much weaker interdot coupling33. In Fig. 4d, we measure the dependence of the EDSR frequency on magnetic field, however, now at large detuning, i.e., in spin-like regime. Here the dependence appears to be linear: at large detuning the ES1–ES2 anticrossing is expected only at much higher magnetic field. Owing to a much weaker renormalization by ES2, the extracted value of \({g}_{{\rm{eff}}}=1.25\pm 0.03\) is much closer to the bulk value of \({g}^{* }\). We stress that \({g}_{{\rm{eff}}}\) here is not determined from the slope of the dependence but by calculating it as \({g}_{{\rm{eff}}}=hf/{\mu }_{{\rm{B}}}B\) at a number of points. We note that in Fig. 4a, b we track the EDSR peaks on both sides of the charge transfer line in Fig. 2a, i.e., we observe a response at both positive and negative detuning (resonance lines I and II). This allows us to fit the experimental data (symbols) to the four-level model (Fig. 4e, solid lines) as a function of the microwave frequency and magnetic field and extract the system parameters (see “Methods” for details). The dependence of the tunneling matrix elements \({t}_{N}\) (spin conserving) and \({t}_{F}\) (spin flipping) on the magnetic field shown in Fig. 4f indicates a clear decrease in their magnitude due to the diamagnetic squeezing of the single-dot orbitals.
a, b The left gate voltage \({V}_{L}\) dependence of the EDSR signal as a function of the microwave frequency for \(B=1.5\) and \(1.75\) T, respectively. Note \({V}_{L}\) and \({V}_{R}\) are covaried to cut through resonance lines I and II. The characteristic minimum, marked with the green circle, corresponds to the condition of zero detuning. c The resonance frequency at zero detuning as a function of magnetic field, with (1), (2), and (3) denoting the spin-like, mixed, and charge-like regions, respectively. The slope of the relationship in region (1) is proportional to the renormalized effective \(g\)-factor \({g}_{{\rm{eff}}}\), and we extract \({g}_{{\rm{eff}}}=0.85\). d The measured dependence of resonance frequency \(f\) on magnetic field at large detuning. Here the extracted \({g}_{{\rm{eff}}}=1.25\). Fitting of the experimental EDSR traces for \(B=0.8\), \(1.25\), \(1.5\), \(1.75\), \(2\), and \(2.4\) T (e, symbols) with the theoretical model (solid lines) allowing us to extract the model tunneling matrix elements \({t}_{N}\) and \({t}_{F}\) as a function of magnetic field (f).
Discussion
Our work demonstrates that the single-hole GS–ES1 gap is tunable on adjusting the detuning between the dots and, in addition, is sensitive to the magnetic field through the Zeeman energy. Importantly, this gap can be probed by EDSR across the regimes of charge, spin, and hybrid excitations at a constant magnetic field by tuning the microwave frequency. The physics can be described in terms of a voltage-tunable \(g\)-factor, \({g}_{{\rm{eff}}}\). The identification of different EDSR regimes also enables electrical control of the spin relaxation time \({T}_{1}\), which may be useful, for example, for spin state initialization. Indeed, in the spin-like regime (region (1) in Fig. 4c) relaxation requires a higher-order process involving the SOI and phonons, and thus relaxation here has a longer timescale compared to that in the charge-like regime (region (3)) in which it is only mediated by the phonons. Spin qubit manipulation during the coherent control phase of a quantum algorithm should be undertaken with the longest possible \({T}_{1}\). Moreover, we expect shorter values of the decoherence time \({T}_{2}^{* }\) in the charge-like regime owing to a strong dependence of the gap on the detuning, while in the spin-like regime the gap becomes voltage independent and is therefore less susceptible to the charge noise. This expectation follows from the gap behavior in the energy diagrams in Fig. 3c, d and is reflected by the EDSR signal position approaching a vertical asymptote in Fig. 4a, b, e.
The voltage dependence of the \(g\)-factor paves the way for local addressability of spin qubits in multi-qubit systems required for fast single-qubit addressability. This property removes the need of strongly focused and pulsed magnetic fields for single-qubit rotations or local nonuniform magnetic fields created by micromagnets. These magnetic techniques for implementing single-qubit operations are typically slow, with characteristic times comparable to the spin relaxation time \({T}_{1}\), and require complex material engineering. A system with a voltage-tunable \(g\)-factor may be manipulated at a constant magnetic field and with small, monochromatic, global microwave modulation by tuning the transition in and out of resonance through adjustment of the detuning, which can be fast. An optimal qubit design combining the advantages of the different regimes identified in our work and with optimized decoherence times would be a two-level system placed deep in the spin-like regime at high detuning, which could then be brought to the EDSR condition for fast manipulations by suitable pulsing of gate voltages. This could greatly simplify the geometry and the coherent control protocol of the double-dot system for the recently demonstrated controlled-NOT and controlled-Z operations39,40 and therefore facilitate the scaling of the spin-based quantum processors beyond the demonstrated two-qubit systems. Furthermore, the strong EDSR response of the hole-based device makes it an ideal candidate for the long-range qubit coupling design, in which the two-qubit operations are carried out via a superconducting microwave cavity. Strong coupling between the qubit and the cavity photon was recently demonstrated for the charge qubit in Si41, where the cavity-mediated interaction naturally couples to the charge degree of freedom of the single electron confined in a double-dot potential. However, achieving a coupling between the cavity photon and the spin qubit again requires the use of micromagnets42, which makes the precise tuning of the device difficult, and the coupling strength is not yet sufficiently strong to demonstrate the two-qubit operations in the time domain. The hole-based spin qubits, on the other hand, will exhibit a stronger coupling to the cavity photons along the mechanism discussed in this work and with an additional benefit of precise, electrostatic tuning of the EDSR to the cavity mode. In a broader context, our work constitutes a step toward utilization of the hole-based spin devices in photon-to-spin conversion and quantum repeaters for quantum communication43. Indeed, the voltage-tunable coherent control, together with the direct bandgap of the GaAs host and the anisotropy of the \(g\)-factor33, allow for a straightforward coupling between the photons (flying qubits) and spins (stationary qubits), opening the way toward spin–photon hybrid quantum devices.
Methods
Device details
The experiments were performed on a DQD device fabricated from an undoped GaAs/Al\({}_{x}\)Ga\({}_{1-x}\)As (x = 50%) heterostructure employing lateral split-gate technology20,31,32,33. A suitable DQD potential profile was defined by lateral surface Ti/Au gates. The two-dimensional hole gas (2DHG) was created by a global gate deposited above the structure separated by a 110-nm-thick Al\({}_{2}\)O\({}_{3}\) dielectric layer grown by atomic layer deposition. Left and right plunger gates, labeled in Fig. 1a as L and R, respectively, were used to tune the hole energy levels in each dot, while the gate C was used to adjust the interdot tunneling barrier. The device was cooled down in a dilution refrigerator. The nominal lattice temperature was \(60\) mK. The charge state of the DQD was probed using the quantum point contact charge sensor with a constant source-drain bias voltage of 100 μV. The magnetic field was applied in the direction normal to the plane of the 2DHG. An Anritsu microwave signal generator Model 69377B was used and the nominal microwave power at source was typically between \(-20\) and \(-10\) dBm. In addition, the microwave signal was attenuated by \(-20\) dB at the 1K stage20.
Fitting to experimental data
The EDSR data presented in the main text allow us to map out the gap between the two lowest-energy spinor states as a function of the magnetic field \(B\), the microwave frequency \(f\), and the detuning defined by voltages \({V}_{L}\) and \({V}_{R}\) (yellow dashed line in Fig. 3a). We convert the microwave frequency into energy \({E}_{{\rm{MW}}}=hf\), where \(h\) is Planck’s constant. However, to establish a link between our theoretical model and the experimental data we need to express the onsite energies \({\varepsilon }_{L}\) and \({\varepsilon }_{R}\) of the dots in terms of the gate voltages. We do this by utilizing lever arm parameters extracted from Coulomb diamond measurements (data not shown). \({\varepsilon }_{L}\) and \({\varepsilon }_{R}\) can be expressed as
with the lever-arm parameters \({\alpha }_{L,L}=63.4\) μeV\(/\)mV, \({\alpha }_{L,R}=39.3\) μeV\(/\)mV, \({\alpha }_{R,L}=46.7\) μeV\(/\)mV, and \({\alpha }_{R,R}=62.2\) μeV\(/\)mV. The goal is to determine the tunneling matrix elements \({t}_{N}\), \({t}_{F}\), and the bulk \(g\)-factor \({g}^{* }\) (which is the limit of experimentally measured \({g}_{{\rm{eff}}}\) at large detuning) by fitting experimental results to the theoretical model. Bearing in mind that \({t}_{N}\) and \({t}_{F}\) may depend on the magnetic field, we focus on the datasets showing the position of the EDSR peak as a function of the microwave frequency (see Fig. 4a, b) as they are recorded at constant \(B\). For each dataset, we (i) extract the voltages \({V}_{L}\), \({V}_{R}\), and frequency \(f\) at which we observe EDSR peaks, (ii) translate these values into energy units as described above, and (iii) fit all the data points with the calculated gap between the GS and ES1 in our model parametrized with a single set of parameters \({t}_{N}\), \({t}_{F}\), and \({g}^{* }\). We adjust the values of these parameters using a genetic algorithm to optimize the quality of the fit. We repeat this procedure for several magnetic fields and allow the parameters to vary from one magnetic field to another. The results of the fitting procedure are presented in Fig. 4e of the main text and show extracted values of \({t}_{N}\) and \({t}_{F}\) in Fig. 4f of the main text. We observe a clear decrease of both tunneling matrix elements as a function of magnetic field. This decrease is due to the diamagnetic effects as described in our previous work but for much weaker interdot coupling33 (\({t}_{N}\), \({t}_{F} \sim 0.2\) μeV). As for the bulk \(g\)-factor \({g}^{* }\), the fitted values are found to lie within \(\pm 5\)% of \({g}^{* }=1.2\). This value is somewhat smaller than the value of \({g}^{* }=1.35\) obtained by a magneto-transport tunneling measurement in our earlier study32,33. This difference may be due to details of sample tuning as well as the model not accounting for higher-order effects such as a small difference in the \({g}^{* }\) of the two dots or dependence of the tunneling matrix elements \({t}_{F}\) and \({t}_{N}\) on the detuning.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge University Press, New York, NY, 2011).
Hanson, R., Kouwenhoven, L. P., Petta, J. R., Tarucha, S. & Vandersypen, L. M. K. Spins in few-electron quantum dots. Rev. Mod. Phys. 79, 1217–1265 (2007).
Koppens, F. H. L. et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766–771 (2006).
Pla, J. J. et al. A single-atom electron spin qubit in silicon. Nature 489, 541–545 (2012).
Golovach, V. N., Borhani, M. & Loss, D. Electric-dipole-induced spin resonance in quantum dots. Phys. Rev. B 74, 165319 (2006).
Nowack, K. C., Koppens, F. H. L., Nazarov, Y. V. & Vandersypen, L. M. K. Coherent control of a single electron spin with electric fields. Science 318, 1430–1433 (2007).
Zajac, D. M. et al. Resonantly driven CNOT gate for electron spins. Science 359, 439–442 (2018).
Pioro-Ladrière, M., Tokura, Y., Obata, T., Kubo, T. & Tarucha, S. Micromagnets for coherent control of spin-charge qubit in lateral quantum dots. Appl. Phys. Lett. 90, 024105 (2007).
Pioro-Ladrière, M. et al. Electrically driven single-electron spin resonance in a slanting Zeeman field. Nat. Phys. 4, 776–779 (2008).
Laird, E. A. et al. Hyperfine-mediated gate-driven electron spin resonance. Phys. Rev. Lett. 99, 246601 (2007).
Corna, A. et al. Electrically driven electron spin resonance mediated by spin-valley-orbit coupling in a silicon quantum dot. npj Quant. Inf. 4, 6 (2018).
Klotz, F. et al. Observation of an electrically tunable exciton g factor in InGaAs/GaAs quantum dots. Appl. Phys. Lett. 96, 053113 (2010).
Schroer, M. D., Petersson, K. D., Jung, M. & Petta, J. R. Field tuning the g factor in InAs nanowire double quantum dots. Phys. Rev. Lett. 107, 176811 (2011).
Liu, Z.-H., Li, R., Hu, X. & You, J. Q. Spin-orbit coupling and electric-dipole spin resonance in a nanowire double quantum dot. Sci. Rep. 8, 2302 (2018).
Bulaev, D. V. & Loss, D. Electric dipole spin resonance for heavy holes in quantum dots. Phys. Rev. Lett. 98, 097202 (2007).
Venitucci, B. & Niquet, Y.-M. Simple model for electrical hole spin manipulation in semiconductor quantum dots: Impact of dot material and orientation. Phys. Rev. B 99, 115317 (2019).
Voisin, B. et al. Electrical control of g-factor in a few-hole silicon nanowire MOSFET. Nano Lett. 16, 88–92 (2016).
Maurand, R. et al. A CMOS silicon spin qubit. Nat. Commun. 7, 13575 (2016).
Watzinger, H. et al. A germanium hole spin qubit. Nat. Commun. 9, 3902 (2018).
Bogan, A. et al. Single hole spin relaxation probed by fast single-shot latched charge sensing. Commun. Phys. 2, 17 (2019).
Burkard, G. Positively spin coherent. Nat. Mater. 7, 100–101 (2008).
Fischer, J., Coish, W. A., Bulaev, D. V. & Loss, D. Spin decoherence of a heavy hole coupled to nuclear spins in a quantum dot. Phys. Rev. B 78, 155329 (2008).
Gerardot, B. D. et al. Optical pumping of a single hole spin in a quantum dot. Nature 451, 441–444 (2008).
Greilich, A., Carter, S. G., Kim, D., Bracker, A. S. & Gammon, D. Optical control of one and two hole spins in interacting quantum dots. Nat. Photon. 5, 702–708 (2011).
Wang, M., Yin, Y. & Wu, M. W. Electric manipulation of electron spin relaxation induced by confined phonons in nanowire-based double quantum dots. J. Appl. Phys. 109, 103713 (2011).
Salis, G. et al. Electrical control of spin coherence in semiconductor nanostructures. Nature 414, 619–622 (2001).
Doty, M. F. et al. Electrically tunable g factors in quantum dot molecular spin states. Phys. Rev. Lett. 97, 197202 (2006).
Lyanda-Geller, Y., Reinecke, T. L. & Bacher, G. Electric field tuning of spin splitting in a quantum dot coupled to a semimagnetic quantum dot. J. Appl. Phys. 111, 093705 (2012).
Laucht, A. et al. Electrically controlling single-spin qubits in a continuous microwave field. Sci. Adv. 1, e1500022 (2015).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 9, 981–985 (2014).
Tracy, L. A., Hargett, T. W. & Reno, J. L. Few-hole double quantum dot in an undoped GaAs/AlGaAs heterostructure. Appl. Phys. Lett. 104, 123101 (2014).
Bogan, A. et al. Consequences of spin-orbit coupling at the single hole level: spin-flip tunneling and the anisotropic g factor. Phys. Rev. Lett. 118, 167701 (2017).
Bogan, A. et al. Landau-Zener-Stückelberg-Majorana interferometry of a single hole. Phys. Rev. Lett. 120, 207701 (2018).
Yang, C. H. et al. Spin-valley lifetimes in a silicon quantum dot with tunable valley splitting. Nat. Commun. 4, 2069 (2013).
Srinivasa, V., Nowack, K. C., Shafiei, M., Vandersypen, L. M. K. & Taylor, J. M. Simultaneous spin-charge relaxation in double quantum dots. Phys. Rev. Lett. 110, 196803 (2013).
Ferdous, R. et al. Valley dependent anisotropic spin splitting in silicon quantum dots. npj Quant. Inf. 4, 26 (2018).
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004).
Oosterkamp, T. H. et al. Microwave spectroscopy of a quantum-dot molecule. Nature 395, 873–876 (1998).
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015).
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).
Mi, X., Cady, J. V., Zajac, D. M., Deelman, P. W. & Petta, J. R. Strong coupling of a single electron in silicon to a microwave photon. Science 355, 156–158 (2017).
Borjans, F., Croot, X. G., Mi, X., Gullans, M. J. & Petta, J. R. Long-range microwave mediated interactions between electron spins. Preprint at https://arxiv.org/abs/1905.00776 (2019).
Gaudreau, L. et al. Entanglement distribution schemes employing coherent photon-to-spin conversion in semiconductor quantum dot circuits. Semiconductor Sci. Technol. 32, 093001 (2017).
Acknowledgements
S.S. and A.B. thank the Natural Sciences and Engineering Research Council of Canada for financial support. M.T and Y.H. thank Tohoku University GP-Spin program for support. This work was performed in part at the Center for Integrated Nanotechnologies, a U.S. DOE, Office of Basic Energy Sciences user facility, and Sandia National Laboratories, a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA-0003525. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.
Author information
Authors and Affiliations
Contributions
M.T. and S.S. performed the measurements; M.T., S.S., M.K., D.G.A., L.G., J.D., A.P.-B., A.B., A.S., and Y.H. analyzed and discussed the data; S.S., M.K., D.G.A., and A.S. wrote the paper; P.Z. provided maintenance of the cryogenic and measurement equipment; L.T., J.R., and T.H. fabricated and characterized the device.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Studenikin, S., Korkusinski, M., Takahashi, M. et al. Electrically tunable effective g-factor of a single hole in a lateral GaAs/AlGaAs quantum dot. Commun Phys 2, 159 (2019). https://doi.org/10.1038/s42005-019-0262-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0262-1
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.