Introduction

Bolometers for astrophysical applications and especially for balloon and space missions are under intense development thanks to challenging, new tasks such as measurement of the primordial B-mode polarization left after the inflation stage of the evolution of the universe1,2.

The trend in bolometer development is such that sensitivity, defined as the noise equivalent power (NEP), is increased by lowering the operating temperature of the bolometer. This is true for both types of the most commonly developed bolometers: the transition edge sensor (TES)3,4,5 and the kinetic inductance detector (KID)6.

We have developed a cold-electron bolometer (CEB)7,8,9,10 with a normal metal absorber whose working body is the electron gas. The maximal responsivity in current-bias mode8 at temperatures \({k}_{{\rm{B}}}{T}_{{\rm{e}}}\ll\Delta\) and voltages \({k}_{{\rm{B}}}{T}_{{\rm{e}}}< \ \Delta -{k}_{{\rm{B}}}{T}_{{\rm{e}}}\) depends on the temperature \({T}_{e}\) of the electron gas as

$${S}_{{\rm{V}}}^{{\mathrm{max}}}=1-2\frac{{k}_{{\rm{B}}}}{e\Sigma {V}_{{\rm{N}}}{T}_{{\rm{e}}}^{4}}.$$
(1)

where \({k}_{{\rm{B}}}\) is the Boltzmann constant, \(e\) is the electron charge, \(\Sigma\) is the experimentally determined electron–phonon coupling constant11 and \({V}_{{\rm{N}}}\) is the volume of the normal absorber. As one can see from Eq. (1), the responsivity can be increased by decreasing the volume or by lowering the electron temperature, while the phonon temperature \({T}_{{\rm{ph}}}\) can be higher than \({T}_{{\rm{e}}}\). This is the major difference between our bolometer and other types, that require cooling of the entire sample.

The presented here concept of a bolometer9,12 avoids the need to cool the entire detector. We use the cooling power of NIS (normal metal—insulator—superconductor) junctions to cool the electron gas in the absorber13,14,15,16. NIS junction-based cooling is provided by the tunneling current that flows from N to S. This consists primarily of high-energy electrons, whose removal from the absorber causes the average electron temperature in it to be reduced. As the voltage increases, the high-energy electrons gain ability to tunnel early because there are available states in the superconductor for them above the gap. Electron cooling serves as strong electrothermal feedback in CEBs, just as it does in TES17,18. However, there is one principle difference: the artificial heating that occurs within a TES is replaced by effective electron cooling.

We demonstrate experimentally that the cooling efficiency of our samples is high enough to ensure that the electrons in the absorber remain below the bath temperature even at high power loads. Furthermore, we investigate the possibility of using this effect to reach the record sensitivities of other detectors, but at higher bath temperatures. We also show that cold-electron bolometers can be a potential replacement of expensive adiabatic demagnetization refrigerators and the cooling platforms (CP). This technology can significantly reduce the cost of future space missions.

Results

Single bolometer

Here we demonstrate the potential of CEB, using a receiving pixel that is designed according to the requirements of the balloon mission OLIMPO (Osservatorio per il Lontano Infrarosso e le Microonde su Pallone Orientabile, in Italian)19. This system is aimed at precision measurement of the spectral distortion of the cosmic microwave background (CMB) near rich galaxy clusters (the Sunyaev-Zeldovich effect) and the power spectra of diffuse sky radiation simultaneously in four frequency bands: 150, 210, 350, and 480 GHz. In space missions the power load can be rather low (on the order of 0.1 pW per pixel) due to the absence of atmosphere and clouds. However, balloon-borne missions can impose a power load of 30–60 pW for one pixel in the 350 GHz channel, depending on the operating mode. The accepted efficiency of absorbtion is 50%, i.e. with regard to absorbed power, photon-noise-limited operation must be in the range of 15–30 pW. Below, we show how to design a CEB-based pixel for any desired power load.

The cold-electron-bolometer consists of a normal metal absorber, a tunnel barrier and two superconducting leads that form NIS junctions from both sides of the absorber. Coupling of external radiation occurs through the antenna, which is connected to superconducting leads7,9. Radiation is absorbed in a normal absorber.

As follows from Eq. (1) the responsivity is inversely proportional to the absorber volume. We have fabricated bolometers with \({V}_{{\rm{N}}}\) of just \(0.02\ {\mathrm{\mu}} {{\rm{m}}}^{3}\). The small absorber volume means that the electron gas is thermally decoupled from the phonon system, since the heat flow \({P}_{{\rm{e-ph}}}\) between electron and phonon subsystems in normal metal is described by the following dependence20,21,22,23:

$${P}_{{\rm{e-ph}}}=\Sigma {V}_{{\rm{N}}}({T}_{{\rm{e}}}^{5}-{T}_{{\rm{ph}}}^{5}).$$
(2)

The smaller the volume, the more decoupled the two subsystems. This allows one to manipulate the electron temperature in the normal absorber without affecting the phonon system. We note that the coupling constant \(\Sigma\) and the power law (2) vary by materials. For example in24 a CEB was made using a doped silicon absorber, which has a power 6 in temperature dependence of \({P}_{{\rm{e-ph}}}\)(2).

Discovery of the electron cooling effect in NIS tunnel junctions13 has initiated a new era of on-chip cooling systems with the potential to cool from 300 to 100 mK. Two NIS tunnel junctions, connected in SINIS (superconductor-insulator-normal metal-insulatior-superconductor) structure, provide twice more efficient cooling than a single junction14. This property of NIS junctions is used in CEBs with one important addition: besides cooling, these junctions are used for read-out and coupling with the antenna. Such easy coupling with the antenna is possible due to one more advantage of CEB—its micron size. This allows CEB integration into various planar antennas with frequency bands from 1 GHz to above 1 THz without external feed lines.

The effect of electron cooling is explained using the energy diagram in Fig. 1a. When the voltage applied to the NIS junction is much less than the superconductor gap, the current is suppressed. When the voltage approaches the gap, the hottest electrons above the Fermi level in the normal metal get a probability of tunneling to the superconductor. The closer the voltage is to the gap, the more cooling power is available.

Fig. 1
figure 1

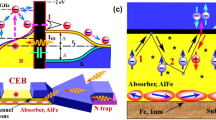
A single cold-electron-bolometer (CEB). a Simplified scheme showing a CEB in current-bias mode and an energy diagram that shows the main heat flow processes: absorption of a photon by an electron in a normal absorber, thermalization of electrons, tunneling of hot electrons, and dissipation of heat in the phonon system. The read-out scheme is shown in current-bias mode. b 3D-model of a CEB, fabricated by the shadow evaporation technique. Superconducting electrods are shown for the top junction only. c A scanning electron microscope image of fabricated CEB integrated into a gold antenna. The color legend applies to the entire figure

Full size image

A schematic representation of a CEB can be seen in Fig. 1a, where the main quasiparticle processes are shown in dc current-biased mode. The initial process is the absorbtion of a photon by an electron in the absorber. Then, the equilibrium temperature of the electron subsystem increases due to thermalization with other electrons. The hottest electrons tunnel to the superconductor under an applied dc bias current, cooling the absorber. In addition, there is a heat flow from electrons to phonons in the absorber (see the characteristic times of both processes in Supplementary Note 1 and Fig. 1). But, this heat flow is much smaller than NIS cooling, because the electrons are thermally decoupled from the phonon bath due to the tiny absorber volume.

Figure 1b, c show a 3D model of a CEB and a SEM image of the fabricated sample. The normal absorber is made of aluminum with a thin (0.7 nm) underlayer of Fe, which destroys the superconductivity in aluminum. The gold antenna is fabricated in the first layer (yellow). The bolometer itself is fabricated in the final step. We deposite the absorber before the superconducting electrodes as in25, thus minimizing the absorber volume and maximizing the bolometer sensitivity. Further fabrication details are given in Methods.

Array development

A single CEB can receive up to 0.5 pW without saturating26. For higher power loads we combine several bolometers in one pixel in order to divide the power between them, so that each bolometer works at its highest sensitivity27. According to our calculations, 100–200 bolometers would be optimal for typical OLIMPO power loads. In the current design we use 192 bolometers in one pixel. In all, 350-GHz radiation goes through the standard band-pass and low-pass filters to the back-to-back horn and through the substrate to bolometers integrated into dipole antennas (see Fig. 2a).

Fig. 2
figure 2

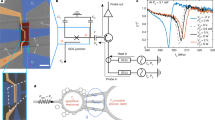
An array of cold-electron-bolometers (CEBs). a Band-pass and low-pass filter transmission for the 350 GHz channel. b 2D electrical field distribution based on numerical simulation of a Si substrate with bolometers. c An overall view of a CEB array with dc connections, an optical image of one antenna element and a scanning electron microscope image of a CEB in the antenna port

Full size image

We have developed an array of dipole antennas in the shape of a corner for the purpose of receiving both polarizations. CST Microwave Studio was used to tune the antennas to match the bolometer impedance and the OLIMPO optical system beam shape, Fig. 2b. The shapes of the fabricated antennas are shown in Fig. 2c. Two dipole antennas are joined together at \(9{0}^{\circ }\) angle to make an element sensitive to both vertical and horizontal polarizations. Each angular element is connected by dc-lines to its neighboring elements. The entire array is fed by only one bias current channel.

The antennas are distributed on the substrate to cover an entire Airy disc, formed by a back-to-back horn. We use multi-mode horn for three modes (first and third modes with two orthogonal polarizations). The electrical field on the substrate for vertical polarization of modes 1 and 2 (bottom) is presented from bolometer side in Fig. 2b. Mode 1 has its maximum electric field in the center of the array, while mode 2 has its maximum intensity closer to the side. Thus, all three modes cover the Airy spot with similar intensities and different bolometers absorb similar portions of the available power. From the bolometer side of the substrate, a backshort is placed at a distance of 213 \({\mathrm{\mu}}\)m.

Experiment

The fabricated samples were measured in a Triton 200 dry dilution cryostat under optical load from a black body (BB). The scheme of experiment is shown in Supplementary Fig. 2. The photon-noise-limited mode of operation of the array has been observed at phonon temperatures of 200 mK and 310 mK.

We have measured the bolometer array voltage response and the voltage noise at several bias points and various BB temperatures (\({T}_{{\rm{bb}}}\)). With our experimental apparatus, the black body source is attached to a 4 K plate and can be heated up to 35 K while keeping coldest plate with bolometers at 200 mK. It can also be heated to 46 K while keeping the bolometer plate at 310 mK.

In the optical experiment the phonon temperature of the cryostat plate \({T}_{0}\) is not always equal to that of the attached chip with bolometers. As the black body continues to be heated, microwave radiation heats the chip above \({T}_{0}\), despite the band-pass and low-pass quasi-optical filters between the black body and the bolometers. We monitor the chip temperature with the help of an on-chip thermometer, made in the same technological cycle as the bolometers (see the Supplementary Note 2 for more details). The overheating effect becomes visible above \({T}_{{\rm{bb}}}=20\ K\) (Supplementary Fig. 3). Thus, we see a mixed response to the microwave power load and temperature increase at high \({T}_{{\rm{bb}}}\). The phonon temperature of the chip is given in the legend of Fig. 3a and b together with the absorbed power \({P}_{0}\).

Fig. 3
figure 3

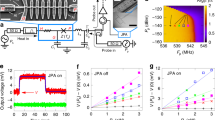
Experimental and fitting results. a Current (dots - experiment, red solid curves—fit) and electron temperature (blue curves) versus voltage for various absorbed power levels and chip phonon temperatures. b Responsivity versus voltage at various power loads and phonon temperatures. c Components of noise equivalent power (NEP): total, bolometer, and photon NEPs versus absorbed power for a cryostat temperature of 200 mK. Right axis - \({T}_{e}\) and \({T}_{ph}\). The error bars of the NEP come from the noise measurements and are calculated as a standard deviation of the mean noise value in the frequency band (105–135) Hz. d NEP versus voltage. Cryostat temperature 200 mK, black body temperature 35 K, chip phonon temperature 235 mK, absorbed power 28 pW. The error bars are obtained as in c. e Voltage noise versus voltage under optical load and cryostat heating. The chip phonon temperature and absorbed power are indicated in the legend. Both noise curves are obtained for identical IV-curves. The error bars are calculated as a standard deviation of the mean noise value in the frequency band (105–135) Hz. f Total, bolometer, and photon NEPs versus absorbed power at a cryostat temperature of 310 mK. The error bars are obtained as in c

Full size image

Experimental IV-curves were fitted to the theoretical model16,8 in order to determine the absorbed power (Fig. 3a, see details in Methods). We found that the array absorbs \({P}_{0}=28\) pW at a maximum BB temperature of 35 K and \({T}_{0}=200\) mK, and 32 pW at \({T}_{{\rm{bb}}}=46\ {\rm{K}}\) and \({T}_{0}=310\ {\rm{mK}}\). Thus, the array absorbtion efficiency is ~ \(60 \%\). The electron temperature, responsivity (\({S}_{{\rm{V}}}\)) versus bolometer voltage and NEP versus absorbed power were deduced via fitting and are shown in Fig. 3a, b, and c, respectively, for a cryostat temperature of 200 mK. The top IV-curve corresponds to the top \({T}_{{\rm{e}}}\) curve, etc.

In Fig. 3a we plot two IV-curves, obtained at \({T}_{0}=200\ mK\), and the other at \({T}_{0}=310\ mK\). The electron temperature is shown using blue curves in the (0–15) mV voltage range within Fig. 3a. Solid curves are used when the theoretical fit and experiment agree well and dashed curves are applied when the theory may not work. It is impossible to predict the electron temperature within our quasi-equilibrium theory correctly near the gap due to overheating. Fig. 3a shows, that at 13 mV (operating point) the electron temperature of the absorber is below the base temperature of 200 mK even at the highest absorbed power of 28 pW and below the base temperature of 310 mK at an absorbed power 32 pW. Despite high power loads, the CEBs work at electron temperatures that are less than the phonon temperature. This is the first demonstration of effective electron cooling under high power loads. One can compare this to ref. 28, where a bolometer was cooled from 300 to 255 mK without power load.

Noise equivalent power

The noise equivalent power is the ratio of the measured voltage noise density (\(\delta V\)) to the responsivity \({S}_{{\rm{V}}}\). The bolometer NEP consists of three components8:

$$\begin{array}{l}{{\rm{NEP}}}_{{\rm{e-ph}}}^{2}=10{k}_{{\rm{B}}}\Sigma {V}_{{\rm{N}}}({T}_{{\rm{e}}}^{6}+{T}_{{\rm{ph}}}^{6}),\\ {{\rm{NEP}}}_{{\rm{NIS}}}^{2}=\partial {P}_{0}^{2}+\frac{\partial {I}^{2}}{{(\partial I/\partial V\cdot {S}_{{\rm{V}}})}^{2}}-2\frac{\partial {P}_{0}\partial I}{\partial I/\partial V\cdot {S}_{{\rm{V}}}},\\ {{\rm{NEP}}}_{{\rm{amp}}}^{2}=\frac{\delta {V}^{2}+{(R\delta I)}^{2}}{{S}_{{\rm{V}}}^{2}}.\end{array}$$
(3)

where \(V\) and \(I\) are the voltage and current through the bolometer, \(R\) is its differential resistance and \(\delta I\) is the current noise of the amplifier. The \({{\rm{NEP}}}_{{\rm{e-ph}}}\) is the noise due to electron–phonon interaction. \({{\rm{NEP}}}_{{\rm{NIS}}}\) is the noise of NIS contacts, composed of heat flow noise, shot noise and their correlation. The \({{\rm{NEP}}}_{{\rm{e-ph}}}\) and \({{\rm{NEP}}}_{{\rm{NIS}}}\) terms are the undiminished intrinsic noise terms of the bolometer. Therefore we refer to their sum as “self-noise”. The amplifier noise \({{\rm{NEP}}}_{{\rm{amp}}}\) depends on the read-out type. For our room temperature amplifiers it has current and voltage noise terms. The “total NEP” comprises the sum of the bolometer NEP and photon NEP.

The internal signal noise (the photon noise) increases as \({{\rm{NEP}}}_{{\rm{ph}}}=\sqrt{{P}_{0}hf+{P}_{0}^{2}/\delta f}\), where \({P}_{0}\) is the absorbed signal power, \(f\) is the signal frequency, \(\delta f\) is the frequency band and \(h\) is the Planck constant32. Two terms account for the wave-particle duality of BB radiation: shot noise \(\sim \sqrt{{P}_{0}}\) and bunching noise \(\sim {P}_{0}\).

In Fig. 3d we show the different components of noise equivalent power as functions of the bolometer voltage alongside the experimental NEP. There is good agreement between the experimental and theoretical NEPs. The photon NEP (independent of bolometer voltage) is almost twice as high as the bolometer NEP in the 6–15 mV voltage range. This indicates that the bolometer is limited by the photon noise. This plot also demonstrates how to choose the operation point for current-biased CEBs. The desired operating point occurs at approximately 3/4 of the gap (13 mV in this plot), where the bolometer NEP is minimized.

Good agreement with the theoretical model is necessary but not sufficient to prove that the measured noise has a photon component and that this component is significant relative to the other components. Thus, we performed an additional experiment to expose the noise increase that occurs when optical power is applied.

In this experiment the cryostat temperature was regulated such that the IV-curves with and without an optical load nearly coincided. It is clear that the cryostat temperature must be higher without an optical load. The voltage noise levels, measured in the two cases appear to be different (Fig. 3e). Due to the similarity of the IV-curves, the amplifier and NIS noises are nearly the same. The electron–phonon noise is small enough to be excluded from consideration. Therefore, the additional noise, which we see with an optical load, can come only from absorbed photons.

The detectors presented here are photon noise-limited. This means that the noise of the absorbed signal is higher than the total internal noise of the detector, including the amplifier noise. This is demonstrated in Fig. 3c, where the photon and bolometer NEPs are shown versus the absorbed power. The graph starts at a low power load of 0.3 pW. At this power the responsivity is high (Fig. 3b) but the photon noise of the incoming signal is too low and thus the total NEP is equal to the bolometer noise. At higher power loads, the bolometer NEP increases but the photon NEP increases faster. Above 1 pW, the total NEP is determined mainly by the photon noise. We note that there are no signs of saturation at 28 pW, which means that photon noise-limited operation continues at higher power loads than we can provide in our experimental setup.

In Fig. 3–f we show a plot similar to that in Fig. 3c, but for a cryostat temperature of 310 mK. The photon noise-limited mode starts at 10 pW of absorbed power and continues at least up to 32 pW. As can be seen in Fig. 3c and f, the phonon temperature also increases, presumably due to absorption of the out-of-band radiation by Si chip that leaks through the filter system at high black body temperature. If sample overheating is decreased, photon noise-limited operation continues even at higher power loads.

Discussion

High-performance photon sensors for future astronomical instruments are typically cooled to 100 mK or below in a dilution cryostat33,34. However, the cost and complexity of these units are an obstacle to the widespread use of 100 mK sensors. The real problem is the design of dilution cryostats for space applications that occur in the absence of gravity. The most effective current solutions are applicable only at a temperature of 0.3 K. Our goal is to show that cold-electron bolometers can reach the photon NEPs required for space mission optical power loads, even with 300 mK cryostats.

We have designed a pixel with 192 bolometers that achieves the best performance at power levels of 10–30 pW at 300 mK and a corresponding photon NEP of \(8\cdot 1{0}^{-17}-2\cdot 1{0}^{-16}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\). If we take one bolometer from this array, can its NEP go beyond \({{\rm{NEP}}}_{{\rm{ph}}}=6.8\cdot 1{0}^{-18}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\), corresponding to a power load of 100 fW at 350 GHz? In Fig. 4a the calculated NEP of a single bolometer is shown with all parameters exactly as in the array. The dark NEP of one CEB is \(8\cdot 1{0}^{-18}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\) and the best performance occurs at 150 fW, where the bolometer NEP appears to be \(1.7\) times larger than the photon noise.

Fig. 4
figure 4

Components of the noise equivalent power (NEP) of a single cold-electron bolometer versus absorbed power. a Room temperature amplifier AD745 and a plate temperature of 300 mK. The bias-voltage is \(190\ {\mathrm{\mu}} {\rm{V}}\). b Cooled amplifier and a plate temperature of 260 mK. The bias-voltage is \(300\ {\mathrm{\mu}} {\rm{V}}\)

Full size image

One can see that the largest NEP component in Fig. 4a, which prevents us from reaching photon-noise-limited operation, is the amplifier noise. This is because we use an AD745 room-temperature amplifier with a high current noise of \(9\ {\rm{fA}}\ {{\rm{Hz}}}^{-1/2}\) at 120 Hz. This term depends on the read-out type and can be lowered significantly using cold amplifiers35 or SQUIDs36. Thus, it is a technical issue that can be solved via ordinary means. We prefer to focus on the electron–phonon and NIS noises since they are fundamental and define the real CEB sensitivity limit.

We calculate these two components separately as functions of the bolometer voltage at several power loads (see Supplementary Note 3 and Supplementary Fig. 5). We plot their minima at a voltage of \(250\ \mu {\rm{V}}\) versus power in comparison with the photon noise term in Fig. 4b. We also add the NEP component of the cold amplifier to this plot. Its voltage noise of \(1.5\ {\rm{nV}}\ {{\rm{Hz}}}^{-1/2}\) and current noise of \(1{0}^{-16}\ {\rm{A}}\ {{\rm{Hz}}}^{-1/2}\) are taken from35 as typical values. Furthermore, advanced sorption pump technology (for example, from Cryo Industries) can help He3 cryostats reach 260 mK with a cooling power 5 pW. Therefore, we calculate the NEP in Fig. 4b and Supplementary Fig. 5 for a phonon temperature of 260 mK. Thus the difference between A and B of Fig. 4 represents the amplifier noise and the cryostat phonon temperature. For such parameters, the dark NEP of the CEB is \(2.5\cdot 1{0}^{-18}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\) and photon-limited operation starts from 15 fW. This is the minimal NEP of a cold-electron bolometer with the current design, and can be reached in He3 cryostats with low-temperature amplifiers. We are currently working on such a readout, whose noise is less than two natural non-decreasable noise components. Further, the sensitivity can be increased by decreasing the absorber volume to \(0.01\ \mu {{\rm{m}}}^{3}\) or even to \(0.005\ \mu {{\rm{m}}}^{3}\), potentially reaching the spectacular level of \(1.2\cdot 1{0}^{-18}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\).

We can compare this result with those from TES and KID bolometers at similar temperatures and frequency ranges. Researchers typically calculate the photon NEP from the incoming power, while we calculate the photon NEP from the power accepted by the bolometer, which can be 50% smaller. The TES detector array, which was developed for 280 GHz37 at 300 mK has an NEP of \(2.6\cdot 1{0}^{-17}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\). A KID at 150 GHz38 has a dark NEP of \(2\cdot 1{0}^{-17}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\) at 120 mK with photon limited operation from 1 pW. A similar KID designed for \(80-120\) GHz and presented in ref. 39 has a dark NEP of \(2\cdot 1{0}^{-17}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\) at a bath temperature of 100 mK.

In addition, while KIDs have become more popular, the most prominent NEP values are typically reported for frequencies on the order of 1.5 THz and low power loads because superconductive absorbing elements impose limitations on low frequencies. See for example ref. 6. Unlike with KIDs, the radio frequency signal is absorbed by the normal metal in CEBs. This allows a broad frequency range of operation, from several GHz to substantially above 1 THz.

Other shortcomings of both TESs and KIDs is their large surface and ability to couple to a substrate/spider-web, which is important for balloon and space applications. It is known that a large fraction of Planck data is unusable due to cosmic rays that result in noisy glitches. For example, in a TES with a spider-web membrane, the absorber volume is usually on the order of \(0.01\ {{\rm{mm}}}^{3}\), while the CEB absorber volume is only \(0.02\ \mu {{\rm{m}}}^{3}\). The combination of a large volume difference and a weak electron–phonon coupling results in CEB cosmic rays immunity40 that is outstanding in comparison to TESs and KIDs. Cosmic rays that hit the substrate do not reach the absorber, which is the only sensitive element of the CEB.

Thus, a cold-electron bolometer with a dark NEP of \(2.5\cdot 1{0}^{-18}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\) at 260 mK and a proper read-out system reaches sensitivities not available with KID or TES devices. Thus, it can satisfy modern requirements and balance the three main concerns of future space and balloon missions: cooling system, detectors and cost.

We should note that there is an alternative method of developing cryogenic detectors. One can decrease the phonon temperature of the receiver using the electron cooling effect, producing a cooling platform (CP)15,41,42. However, this concept has several disadvantages and cooling becomes significantly less effective as the temperature decreases43. This results in a minimum cooling temperature of ~200 mK from a 300 mK base temperature.

Now let us discuss the difference between CPs and CEBs. CP-based electron cooling is not effective because the system must overcome the small electron–phonon thermal conductance and Kapitsa resistance twice. One must cool membrane electrons, membrane phonons (weakly coupled to the electrons), detector phonons, and detector electrons. In this case, the cooling efficiency decreases significantly by the second cooling stage, during which the membrane electrons cool phonons as they are thermally decoupled. Moreover, the e-ph conductivity weakens with \({T}^{4}\) as the temperature decreases, making further cooling more difficult. The CP efficiency (the ratio of cooling power to dissipated power \({P}_{{\rm{COOL}}}/IV\)) is considerably less than \(1 \%\). The data used to estimate the cooling efficiency is taken from43: the cooling power of one pair of NIS junctions is 1 nW, the input power of the cooler is about 100 nW and the total power dissipated in the membrane surroundings is \(1\ \mu {\rm{W}}\).

Unlike with CP, CEB uses weak e-ph thermal conductance to protect the absorber from leakage of heat to phonons. Therefore, direct electron cooling of the absorber through the tunnel junctions is highly effective and any cooling leads to a decreased e-ph thermal conductance and improved absorber thermal isolation. The efficiency of CEB cooling is ~\(40 \%\).

In addition, the thin-legged suspended membrane used to achieve thermal isolation of the cooler from a substrate in CP is fragile. In contrast, CEB is a rigid structure on a planar Si substrate.

Furthermore, CP commonly uses a large cooling current to maximaze the cooling power. This creates problems with hot quasiparticles in the superconductor and consequently leads to lower cooling efficiencies. A CEB has fewer hot quasiparticles due to its smaller cooling current because the cooling power need not be maximized since the system cools only electrons in a small absorber.

Therefore, the CEB represents an effective solution that is scalable to the desired power level and able to reach low NEP values even at a working temperature of 0.3 K. It also offers high cosmic ray immunity, which is crucial for space applications.

Thus, a mm/IR bolometer that operates at an electron temperature that is less than the phonon temperature under a high power load is presented for the first time. Electron cooling provides strong electrothermal feedback as in TES but with substantial difference: the artificial heating of TES is replaced with strong electron cooling. Due to effective electron self-cooling of the absorber, photon-noise-limited operation of a 2D array of CEBs has been achieved at 310 mK. The resulting 2D array of CEBs represents a single pixel for 350 GHz channel of the OLIMPO balloon experiment.

We have shown that electron temperature in a CEB array can go from 310 to 120 mK. This study suggests that CEBs with internal self-cooling are potential candidates to form the basis of a core technology with ultimate parameters for advanced radio astronomy projects that must avoid dilution refrigerators. With a proper readout, they could potentially reach the spectacular NEP of \(1.2\cdot 1{0}^{-18}\ {\rm{W}}\ {{\rm{Hz}}}^{-1/2}\) at 260 mK. Therefore, this can solve the main problem of the COrE space mission that was not accepted by the European Space Agency from 2007 due to necessity to find compromise between sensitivity, cryogenics and cost.

Methods

Technology and materials

Samples were fabricated on silicon wafers using three steps: Si wafer etching, antenna fabrication and bolometer fabrication.

Numerical simulations have shown that absorption is maximized with a substrate thickness of \(127\ \mu {\rm{m}}\). We chose \(350\ \mu {\rm{m}}\) substrates and etched the area covered by Airy spot down to the required \(127\ \mu {\rm{m}}\) from the back side.

The antennas and bolometers were fabricated on the front side of the wafer. The antennas were fabricated using optical lithography and electron beam evaporation of three metals: 10 nm of Ti for adhesion, 200 nm of Au and 20 nm of Pd for good contact with Al.

The bolometer mask was formed via electron beam lithography. The bolometers were made using a self-aligned shadow evaporation technique. First a normal absorber made from 14 nm of Al with a 1 nm underlayer of Fe was evaporated at zero angle. Then, the tunnel barrier was formed via oxidation at 10 mbar. Next, 60 nm and 70 nm thick superconducting Al electrods were evaporated at angles of +45 and −45 degrees, respectively. This method differed from that provided by ref. 25 with regard to fabricating normal Al from superconducting Al.

Heat balance model and fitting of experimental results

Fitting was achieved by solving heat balance equations with parameters that described the experimental IV-curves well. The absorptive element in the CEB, the electron gas of a normal metal, was described well by the heat balance equation

$${P}_{{\rm{N}}}+{P}_{0}+2\beta {P}_{{\rm{S}}}={P}_{{\rm{e-ph}}}+2{P}_{{\rm{COOL}}}.$$
(4)

There were three heating sources in the normal absorber: Joule heat \({P}_{{\rm{N}}}\) in the absorber due to its finite resistivity, absorbed radiation power \({P}_{0}\), and \({P}_{{\rm{S}}}\) – the net power dissipated in the superconducting electrode. The power flow from backtunneling of quasiparticles in the superconducting electrode to the normal absorber through the absorption of phonons emitted by quasiparticle recombination was represented by \(2\beta {P}_{{\rm{S}}}\). There was also one cooling source, the cooling power of the NIS junction \({P}_{{\rm{COOL}}}\). The electron–phonon heat exchange \({P}_{{\rm{e-ph}}}\) can either be cooling or heating source depending on whether \({T}_{{\rm{e}}}\) is larger than \({T}_{{\rm{ph}}}\) or smaller.

To increase the accuracy of the model, we also used the equation for quasiparticles in superconducting electrodes, which exchange the heat with phonons and normal metal electrons

$$\epsilon (1-\beta){P}_{{\rm{S}}}={P}_{{\rm{e-ph,S}}}.$$
(5)

The superconductor quasiparticles were heated by the power, transferred from the normal metal \((1-\beta){P}_{{\rm{S}}}\). Part of this power was moved away from the tunnel junction or dissipated in the phonon system21, but some fraction \(\epsilon\) of this power stayed in the quasiparticle system (\(\epsilon < 1\) is a fitting parameter). \({P}_{{\rm{e-ph,S}}}=0.98{\Sigma }_{{\rm{S}}}{V}_{{\rm{S}}}({T}_{{\rm{S}}}^{5}-{T}_{{\rm{ph}}}^{5}){e}^{-\Delta ({T}_{{\rm{S}}})/{k}_{{\rm{B}}}{T}_{{\rm{S}}}}\) was the electron–phonon coupling in the superconductor22. The problem of superconducting electrodes overheating arose at high voltages (near the gap), where our model is not particularly accurate. The accuracy (and the complexity) of the model could be increased by considering the spatial dependence of the temperature in the superconducting electrodes. However, we did not use this approach since we worked below the gap.

The phonons in both normal metal and the superconductor were intended to remain at the bath temperature at all times.

The phenomenological parameter \(\beta\) reflected the fact that the heat removed from the absorber via electron tunneling can typically return to the absorber through the phonons, and in an ideal case \(\beta =0\). In order to prevent this heat from returning, the hot electrons in superconductor must be moved away from the tunnel barrier efficiently. For this purpose we designed a double stock at both sides of the tunnel junction and increased the superconducting electrode thickness and width16 to provide more volume for quasiparticle dissipation. Thus, we managed to decrease \(\beta\) from 0.35 in ref. 29 to 0.06. A further decrease can be achieved via implementation of normal metal traps30,31, that require one additional technological layer.

The investigated sample represented an \({\rm{Al}}-{{\rm{Al}}}_{2}{{\rm{O}}}_{3}-{\rm{AlFe}}-{{\rm{Al}}}_{2}{{\rm{O}}}_{3}-{\rm{Al}}\) SINIS structure, where the superconductivity of the Al absorber was suppressed by a thin Fe layer underneath Al. The following parameters were measured directly: normal array resistance \({R}_{{\rm{n}}}\) = 37.6 kOhm (Supplementary Fig. 4), volume of the absorber in one bolometer \(0.02\ \mu {{\rm{m}}}^{3}\), critical temperature of the Al electrodes 1.244 K, absorber resistance 50 Ohm. The phonon temperature of the chip was measured using an on-chip thermometer, made of NIS tunnel junctions.

The fitting parameters were: \(\Sigma =1.3\ {\rm{nW}}\ {{\rm{K}}}^{-5}\mu {{\rm{m}}}^{-3}\), effective volume of the superconducting electrode \(2.5\ \mu {{\rm{m}}}^{3}\), \({\Sigma }_{{\rm{S}}}=0.45\ {\rm{nW}}\ {{\rm{K}}}^{-5}\mu {{\rm{m}}}^{-3}\), \(\beta =0.06\), leakage resistance of the array 300 MOhm, and \(\epsilon =0.003\). The absorbed power varied from 0.3 to 32 pW depending on the black body temperature.

Electro-magnetic simulations

Electro-magnetic simulations of the entire system were performed to maximize the absorption efficiency. The system consisted of a substrate with an array of dipole antennas with bolometers, a backshort from the front side of the wafer, and a triple-mode waveguide horn designed to form a beam matched with a telescope beam. The source of excitation was a waveguide port at the far end of the horn. First, the radiation went through the horn and the half-wavelength substrate to the bolometers, where part of it was absorbed and part went to the backshort to be reflected back to the bolometers. The substrate thickness and distance to the backshort were tuned so that the transmitted and reflected waves formed a standing wave. Thus, the wave energy stayed near the bolometers until it was absorbed. We used 192 antennas to cover the 3 mm diameter Airy spot: 96 for vertical and 96 for horizontal polarizations. The length of one dipole was \(130\ \mu {\rm{m}}\). The impedance of each dipole was 50 Ohms. With such parameters, we achieved the absorption efficiencies of 70\(\%\) in simulations and 60\(\%\) in experiments.

We started by simulating of the noise properties of the CEB array in the framework of the heat balance model developed in16,21 and 8. In this model, electron subsystem thermal equilibrium was assumed so that the Fermi-Dirac distribution could be used. The model is valid for a broad range of parameters, until operating conditions become highly non-equilibrium (low temperatures or high currents). In the present article, the operating point is always in a region where the Fermi-Dirac distribution is a good approximation.

Noise from readout electronics

The pixel impedance at the operating point must be below the input impedance of the amplifiers to minimize the noise introduced by the readout electronics. We use the JFET room temperature amplifiers AD745. They have voltage noise \(5\ {\rm{nV}}\ {{\rm{Hz}}}^{-1/2}\) and current noise \(9\ {\rm{fA}}\ {{\rm{Hz}}}^{-1/2}\) at 120 Hz, making the input resistance around 500 MOhm.

The power load in the OLIMPO mission per pixel is 10 pW - 60 pW, which significantly exceeds the power that one CEB can accept without going into saturation. Therefore, we use several bolometers in one pixel, distributing the power load so that each bolometer receives no more than 0.3 pW. In total, 192 bolometers are used in the array. A single bolometer of the considered design has a resistance of 88 kOhm at the operating point at 300 mK without power load and 26 kOhm at maximum power load of \({P}_{{\rm{in}}}=0.3\ {\rm{pW}}\). In order to match the impedance of the array with 500 MOhm, we connect the bolometers with each other both sequentially and parallelly. For this project, 48 serial connections and four parallel connections are used.

A complete analysis of noise properties was performed in the heat balance model. Along with the amplifier noise we accounted for intrinsic noise from bolometers and external photon noise.