Ultra compact electrochemical metallization cells offering reproducible atomic scale memristive switching

Abstract

Here we show electrochemical metallization cells with compact dimensions, excellent electrical performance, and reproducible characteristics. An advanced technology platform has been developed to obtain Ag/SiO₂/Pt devices with ultra-scaled footprints (15 × 15 nm²), inter-electrode distances down to 1 nm, and a transition from the OFF to ON resistance state relying on the relocation of only few atoms. This technology permits a well-controlled metallic filament formation in a highly confined field at the apex of an atomic scale tip. As a consequence of this miniaturization process, we achieve set voltages around 100 mV, ultra-fast switching times of 7.5 ns, and write energies of 18 fJ. Furthermore, we demonstrate very good cell-to-cell uniformity and a resistance extinction ratio as high as 6 · 10⁵. Combined ab-initio quantum transport simulations and experiments suggest that the manufactured structures exhibit reduced self-heating effects due to their lower dimensions, making them very promising candidates as next-generation (non-)volatile memory components.

Introduction

Non-volatile and volatile memristive devices hold promise for offering high-density, energy-efficient operation, and high-speed. All of which is needed in light of the high demand for sharing, analyzing, and storing information in everyday life. In this regard, memristive devices might play an essential role toward the further development of large-scale neuromorphic computer systems as well as energy-efficient memory devices for the Internet of Things (IoT). Already, non-volatile memristive devices have attracted attention for various applications such as high-density storage units^1,2, logical circuits^3,4, photonic systems^5,6, or neuromorphic computing elements^7,8. Also, volatile memristive devices have shown many applications related to low refresh dynamic memories⁹, short-term-memories (STM)¹⁰, selectors for crossbar arrays^11,12, and steep threshold slope transistors¹¹. Yet, such devices should not only operate at lowest power but also operate reliably with complementary metal-oxide semiconductor (CMOS) compatible materials and offer an atomic scale footprint.

Different memristive technologies have been proposed so far¹³, e.g., phase change material¹⁴ or oxide-based random access memory (RAM)¹⁵. Of particular interest are the electrochemical metallization (ECM) cells, also known as conductive bridging random access memory (CBRAM). Typical ECM cells consist of metal-insulator-metal layer stacks. Their switching is achieved by the electrochemical growth and dissolution of a tiny metal filament between an inert and active electrode¹⁶. Indeed, ECM cells exhibit particularly attractive storage features, either comparable or better than state-of-the-art memristive technologies. For instance, they offer low power consumptions, fast switching speeds, and high integration densities through multiple bits per cell¹⁷. Even more importantly, the ECM technology can scale to the size of few atoms when the electrodes are arranged in liquid¹⁸ or in a solid Ag₂S electrolytes¹⁹ featuring quantum conductance and switching voltages of 30 and 100 mV, respectively. However, the industry would prefer stable CMOS compatible dielectrics as a matrix material between the metallic electrodes such as, e.g., SiO₂, TiO₂, HfO₂ or Ta₂O₅, and others¹. Beyond, the fabrication methods of most atomic scale devices require sophisticated conditioning procedures to reach quantum conductance. To make atomic scale devices practical, a path toward a more reproducible technology providing devices with a high endurance is needed. And indeed, geometry engineering has already shown promise toward this goal^20,21,22,23. Researchers already demonstrated that they could lower the mean switching voltages from 1.11 to 0.27 V and improve the cycle-to-cycle variance when transitioning from a flat to a tip-like electrode shape²¹. It was also found that decreasing the oxide layer thickness from 74 to 10 nm reduced the switching voltage from 0.5 to around 0.2 V, at the cost of decreasing the on–off ratio to around 50 at 10 nm thickness. In addition, due to the limits imposed by e-beam and other lithography tools, the tip size was limited to tens of nanometers. Moreover, to prevent leakage current through the insulating layer, the thickness of the latter was typically limited to about 10 nm. As a result, the benefit of geometry engineering at atomic scale remains elusive.

In this paper, we introduce a new technology relying on sharp three-dimensional (3D) metal tips that allows for the reliable relocation of few atoms in both volatile and non-volatile ECM Cells. The chosen technique leverages 3D sharp tip capabilities enabled by thermal probe lithography^24,25,26. Using this advanced technology, we show excellent ECM device performance: a combination of switching voltages around 100 mV, an ultrafast switching speed 7.5 nanoseconds with write energies of 18 fJ, a resistance extinction ratio as high as 6 × 10⁵, an endurance way beyond thousands of cycles, and a reliable operation up to high currents (200 μA). The combination of these unique features can be attributed to highly localized electric fields offered by properly engineered device geometries, namely the presence of a sharp nanometer-sized metal tip at one of the two metallic electrodes that form the ECM device. Ab-initio quantum transport calculations further highlight the advantages of the proposed ultra-short and narrow metallic filaments when it comes to power consumption and heat dissipation within the filament.

Results

Development of sharp tip fabrication technology

An illustration of the device consisting of an Ag-amorphous SiO₂-Pt layer structure is presented in Fig. 1a. A finite element method (FEM) electric field simulation is shown in Fig. 1b with the computer simulation technology (CST) Studio Suite. A strong electric field confined to the apex of the tip can be seen. In fact, the electrical field peaks around the tip and drops off to 50% within a radius of about 4 nm. Additionally, an ab-initio simulation of the electrical field by means of a real-time time-dependent-density functional theory (RT-TDDFT) calculation and its result is presented in Fig. 1c. The simulation confirms the strong field confinement at the apex of the tip. Simulation details are given in the Supplementary Note 1. Since the filament formation strongly depends on the magnitude of the field, the filament is expected to be formed preferably at the apex of the tip. A top- and cross-section view of the atomic scale ECM cell is depicted in Fig. 1d, e, respectively. The ultra-sharp tip of Ag is patterned with the help of thermal-scanning probe lithography^24,25,26 (t-SPL). The thermal-scanning tip typically has a 3 nm radius²⁷. The thermal lithography transfers the 3D profile of the ultra-sharp thermal-scanning tip into the pattern transfer layer of PPA (polyphthalaldehyde) and subsequently into SiO₂. In a final step, the thin switching matrix layer and top Ag electrode are deposited subsequently on top of the 3D structure to fill the hole and form an ultra-sharp tip. A more detailed description of the fabrication technology is given in the methods section.

Fig. 1

Sharp-shaped tip electrochemical metallization (ECM) devices. a Schematic illustration of the sharp tip ECM cell. b Simulation of the electric field inside the SiO₂ layer. c A visualization of the electric field as obtained through a real-time time-dependent density functional theory (RT-TDDFT) simulation of the system in CP2K⁵¹. d Scanning electron microscope (SEM) image showing the top view of the atomic scale ECM cell. The dashed area indicates the location of the sharp tip, which is beneath the center area with the darker contrast. Scale bar, 200 nm. e Atomic force microscope (AFM) measured surface topology. f Transmission electron microscope (TEM) image of the device cross-section. The tip radius is 10 nm, marked by the red dashed line. Scale bar, 10 nm

The thermal-scanning probe lithography fabrication method is attractive as it can be extended toward a large-scale high-throughput technology, which is essential for mass production²⁸. The small recession between the Pt and Ag layers in Fig. 1d indicates the location of the active area with the atomic scale tip. Figure 1e shows the topology of the sharp tip, measured by an atomic force microscope (AFM). Figure 1f shows the image obtained by transmission electron microscopy (TEM) of the cross-section of the final tip-like ECM cell. The radius of the tip is determined to be 10 nm, as marked by the red dashed line. For the sake of a better image contrast, we have deposited a sample with a 4 nm thick SiO₂ rather than a 1 nm SiO₂ layer. For thinner SiO₂ layers the tip radius supposedly would be even smaller. The AFM measurement agrees well with the TEM cross-section image. According to the AFM measured topology, the full width half maximum (FWHM) of the tip is ~15 nm. It is worth mentioning that with this technology the matrix material is not limited to SiO₂. Other materials such as HfO₂¹⁰, Ta₂O₅²⁹, and TiO₂³⁰ can also be implemented.

Performance enhancement with ultra-thin oxide

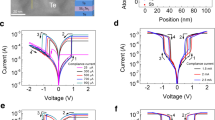
The results depicted in Fig. 2 show that a reduction of the oxide gap thickness d within the sharp tip devices. The combination of sharp tip and thin oxide confines the location of a conductive filament to an ultra-small volume (see Fig. 1b, c). Smaller switching voltages, a more reliable switching operation and a lower heat dissipation across the junction have been achieved.

Fig. 2

Performance enhancement with ultra-thin oxide gap. a Statistics of the switching voltage for different devices. The dot indicates the median switching voltage and the error bar indicates the 25th and 75th percentiles from multiple measurement. To properly investigate and compare the performance we measured around ten devices with many switching cycles for each gap thickness. b Histogram of switching voltage for various gap thicknesses. c Cumulative plot of the on-state and off-state resistances for ten devices with a gap thickness of 1 nm. d Maximum current achieved before device breakdown. e Ab-initio simulation of self-heating obtained from density functional theory non-equilibriums Green’s function (DFT-NEGF) simulations for different gap thicknesses. The temperature of the filament atoms (diamonds) and average (solid lines) is derived from the non-equilibrium phonon population. The corresponding constructed atomic geometries are depicted at the bottom

The relation between the oxide gap thickness d and the switching voltage can be seen in Fig. 2a, where the median switching voltage has been plotted for different gap thickness, d. To determine the switching voltage, a bias has been applied to the Ag electrode while the Pt one is grounded. The bias has then been gradually increased at a rate of ~20 mV per 20 ms. It can be seen that the switching voltage reduces as d decreases. Such a trend has also been reported in the literature^21,31,32. In particular, our work shows that ultra-small gaps in the order of d = 1 nm (which are among the smallest ever reported) can be realized while high on–off ratios are still preserved and excessive tunneling leakage can be suppressed.

A massive reduction of the switching voltage variances for smaller insulator gaps can be derived from Fig. 2b. Here, the statistics of more than 1000 switching cycles of around 30 devices have been collected. The small variability of switching voltages found here appears in ultra-thin devices only and is very beneficial, especially for large-scale integration. For devices with a 1 nm gap, ~85% of the switchings occur at voltages <0.5 V and more than 50% of the devices feature switching voltages below 0.2 V. Figure 2c shows the distribution of the resistance states, including the off-state and on-state resistances for 10 devices with a 1 nm gap size at a compliance current of 10 μA. For all switching cycles, both states show narrow distributions. Approximately 80% of the switching remains within 1 order of magnitude. The reasons behind the better performance and lower variability with smaller insulating thicknesses can be explained as follow: (a) The gap thickness has a strong influence on the intensity and the distribution of the E-field^33,34. The smaller the gap thickness, the stronger the field confinement, which promotes a more controllable and uniform filament formation at the apex of the nanometer size tip; (b) Since the formation of a conductive bridge is a stochastic process^13,35, the smaller the insulating thickness, the higher the probability to form a single conductive filament; (c) It is known that the insulating film is driven by a soft breakdown during the forming process of the device, leaving behind a localized spot of permanent high ion conductivity. So for our device, the small gap thickness and sharp tip limit the switching filamentary volume and thus lead to a better controllability and reliability. To the best of our knowledge, this is the smallest switching voltage below 3 nm gap thickness^31,32. Such a thin insulating thickness within Ag/SiO₂/Pt structure has only become feasible because of the development of the 3D sharp tip technology mentioned above that confine the location of a conductive filament to an ultra-small volume. This reduces the probability of finding a defect that could lead to a destruction of the device. In fact, for gap thickness d = 1 nm we fabricated devices without sharp tips and observed that they all fail. Also, we have compared conventional flat and sharp tip ECM cells at a thickness of d = 1.5 nm. The flat ECM cells show a larger cycle-to-cycle variance (see Supplementary Note 2 and Supplementary Fig. 2).

Joule heating during switching operations can lead to instability^36,37 and even destruction of the device^38,39. This will limit the possibility of scaling up devices. The effect of the gap thickness on the Joule heating has been explored by experiment and is supported by simulations. From Fig. 2d it can be seen how the cells with 1 nm gap thickness work stably up to highest compliance currents of 200 µA. By increasing the gap thickness, the maximum current decreases.

To understand why devices with shorter gap thickness support higher currents, we performed ab-initio quantum transport simulations of ultra-scaled ECM cells in the presence of electron-phonon scattering. Simulation provides a hypothesis that structures with a thinner oxide suffer distinctly less from resistive heating effects. As a result, ultra-thin structure could potentially benefit from more stable and reliable switching at even higher currents. The ab-initio simulation takes into consideration of electro-thermal phenomena such as Joule heating at the atomic scale. We investigated the impact of self-heating through power dissipation in realistic devices. The modeled geometries feature insulator thicknesses ranging from 1.6 to 3.5 nm. The contacts and the filament consist of Cu atoms, while amorphous SiO₂ forms the insulator. The density functional theory (DFT) module of the CP2K tool^40,41 was used to compute the electronic properties of the constructed cells, whereas a valence-force-field method⁴² was employed to obtain the phonon properties. The resulting Hamiltonian, overlap, and dynamical matrices were imported into a quantum transport simulator based on the non-equilibriums green’s function (NEGF) formalism and capable of accounting for electro-thermal and self-heating effects⁴³. More details about the simulation approach are given in the Supplementary Note 3. Such ultra-thin devices operate close to their ballistic limit so that only a fraction, namely α, of the overall power dissipation occurs in the device itself, the rest is dissipated in the metallic electrodes. This internal power dissipation has the form P_in= αRI², where R is the device resistance and I the electrical current. The origin of excessive heating in longer devices is twofold. The thicker the device, the larger α is because the probability for electrons to emit phonons increases with the oxide thickness. Furthermore, thick devices exhibit a larger thermal resistance R_th, hindering efficient removal of excess thermal energy. The combination of these effects causes much higher temperatures in thick devices, thus leading to more pronounced thermal instabilities and potentially device failures⁴⁴. This is confirmed in Fig. 2e, where it shows the temperature of each individual metallic atom (diamonds) constituting the filament as well as the average temperature (solid lines) through devices of different oxide lengths for an applied voltage of 0.2 V and current of ~ 3.6 µA. These simulation results agree well with the experimental findings that thinner devices suffer distinctly less from resistive heating effects shown in Fig. 2d.

Highly reproducible and reliable switching

The low switching voltages at 120 mV of the memristive switch are shown in Fig. 3a. The device current (top panel) and resistance (bottom panel) are plotted for the voltages that are ramped at a rate of ~10 mV per 10 ms between −0.01 V and 0.25 V. The result of these 100 consecutive volatile switching cycles demonstrates the excellent cycle-to-cycle variance in terms of switching voltage and on/off switching resistance despite of small, atomic scale dimensions. The averaged switching voltage is 121.2 mV with a standard deviation of only 3.8 mV. The reliability of the device after several cycles is further reflected by the small variation of the “on” and “off” resistances (see Supplementary Note 4 and Supplementary Fig. 4). During the operation, the compliance current has been set to 200 nA.

Fig. 3

Switching results of the sharp tip electrochemical metallization (ECM) cell. a Reproducibility of resistive switching (100 consecutive cycles). The current (upper) and resistance (lower) is measured as a function of the applied voltage and demonstrate an excellent cycle-to-cycle variance. b Resistance of the on and off states for 50,000 cycles. To keep the plot as legible as possible, we have always plotted the first resistance in a group of consecutive 100 cycles. The inset shows the voltage sequence applied to the device. c The off-state and on-state resistance as a function of compliance current. The dot indicates the median and the error bar indicates the 10th and 90th percentiles. d The on-state resistance histogram at a compliance current of 12, 25, and 35 µA, indicating that the on-state resistance is quantized

The reliability of the device is further confirmed by endurance measurements of on-state and off-state resistance. The endurance measurement was performed as follows: The device was set to its on-state with a 0.5 V, 200 ms pulse and reset by a −100 mV pulse of 200 ms duration. In-between we had a hold time of 200 ms at a 50 mV voltage. The resistance was measured at the beginning of the first hold time and the end of the second hold time. The voltage sequence is shown in the inset of Fig. 3b. The plot shown in Fig. 3b highlights the small variance within 50,000 consecutive switching cycles. The switching success rate is 100%. In addition, the on–off ratio remains larger than 2,000 in all instances. This high on–off ratio is good enough for practical applications. The on-state resistance shows some fluctuations—yet there was not a single instance with a resistance above 4 × 10⁵ Ω. These fluctuations may be attributed to the stochastic operation of the device.

The large on–off resistance ratio is documented by the plots in Fig. 3c. The plot shows how the on-state resistance reliably decreases as the compliance current increases, while the off-state resistance barely changes. At a compliance current of 50 µA, we achieve a large on–off ratio of 6 × 10⁵. Below 10 µA, multiple resistances are reached, this could be explained as the tunneling gap is tuned by adjusting the compliance current⁴⁵. At around 10 µA the conductance becomes discretized (a zoomed-in plot of conductance at high compliance current is shown in Supplementary Fig. 5 and further discussed in Supplementary Note 5). In fact, this reflects the fact that we are approaching the quantum conductance level G₀. By further increasing the compliance current above 10 µA we reach multiple G₀ levels. The experiments clearly reveal that the states can be controlled by single atoms.

To better reveal the distinct quantum states, we have plotted the occurrences of the different quantum conductance events in a histogram when increasing the compliance current in Fig. 3d. It is observed that events cumulate around the discrete quantum conductance levels. This implies that the atomic relocation can be well-controlled with the compliance current.

Volatile and non-volatile switching

It has been demonstrated that the stability of the filament is dependent on the compliance current^11,46. Following this, we measured the relationship between the retention time and the compliance current. A ~4 s, 1 V pulse with compliance currents of 1, 100, and 200 µA were applied to the same device to set it into its low resistance state. After applying the set pulse, we measured the resistance continuously as a function of time, as shown in Fig. 4a. The resistance is measured at 20 mV, minimizing the influence of the read voltage on the retention time. We observed that with a higher compliance current, the on-state resistance becomes smaller and the retention time longer. This can be explained by the fact that a high set current results in more stable filaments in terms of retention time that makes it more difficult to rupture them¹¹. Particularly, for the specifically investigated device, I_cc = 200 µA the retention time is above 6 weeks without significant resistance variations, which is a non-volatile operation. This indicates the device can be used for both volatile and non-volatile applications by selecting corresponding compliance currents. The R–V characteristics of volatile and non-volatile switching within the same device are shown in Fig. 4b.

Fig. 4

Volatile and non-volatile operation of electrochemical metallization (ECM) cell. a Device retention time at various compliance current. The legend shows the on-state resistance of the devices at I_cc = 1, 10, and 200 µA are 580, 5.5, and 1.3 kΩ, respectively. At I_cc = 200 µA the device becomes non-volatile. b R–V characteristics of memristive devices with different compliance currents. When operating the device with a compliance current of 1 µA it clearly features volatile characteristics. When increasing the compliance current to 200 µA the device becomes non-volatile. The embedded plot shows the non-volatile characteristics with both the Set and Reset phase at I_cc = 200 µA

High-speed operation

To further reveal the switching dynamics of the atomic scale memory we performed pulse measurements, see Fig. 5. A switching time of 7.5 ns can be observed, which is among the fastest for Ag/SiO₂/Pt ECM Cells^47,48. The set-up used for this experiment is shown in Fig. 5a. We used a Keysight 33500B and Keysight M8190A Arbitrary Waveform Generator (AWG). At Channel 1 we monitored the voltage output. At Channel 2 we used an active probe with R_L = 100 kΩ to limit the current to ~10 µA and to operate around the single conductance quantum regime. Figure 5b demonstrates the switching behavior. Before t = 0 the device is in the high resistance state. This can be seen as with a small read voltage, the current (plotted in red on right axis) through the device is close to 0 μA at t = −250 ns. The 1 V, 20 ns set pulse was applied at t = 0. After a delay, the device is switched on and we observe an abrupt increase in current. The device remains in its low resistance state that is determined as R_on = 9.5 ± 1.4 kΩ at t = 220 ns. Figure 5c shows the details of the set process. The time difference between the applied set voltage and an abrupt increase of current was measured and indicated by the double arrow. A switching time of 7.5 ns can be observed. It is worth noting that the measurement set-up has been calibrated to cancel the delay between channel 1 and channel 2 with a dummy non-switching device of ~50 Ohm resistance. The capacitance of the active probe is C_L = 0.6 pF. We calculate τ = R_onC_L = 5.7 ns, which corresponds well to the slope of the current in Fig. 5c. We also calculate the energy consumption during the switching as $E_{{\mathrm{Switch}}} = \mathop {\int }\nolimits_0^{20\,{\mathrm{ns}}} U\left( t \right) \cdot I\left( t \right){\mathrm{d}}t = 17.8\,{\mathrm{fJ}}$, which is the lowest for such a high-speed ECM Cell. Figure 5d reports three complete cycles with both set and reset processes. At t = 0, t = 5 ms and t = 10 ms, the turn-on process is initiated by a positive voltage, which switches the device within a few nanoseconds as described above. The reset process is initiated by a negative pulse voltage of −0.1 V applied at t = 3 ms, t = 7 ms, and t = 12 ms. It can be seen in Fig. 5e that it takes 40 µs until the negative current abruptly switches to zero, which indicates that the device is switched off. The reset voltage was kept at −0.1 V to prevent excess negative current flowing through the ECM cells during the test. By applying a larger reset voltage, the reset time potentially could be significantly reduced^10,47. It is well known that the switching speed exponentially increases with the voltage^30,47,49.

Fig. 5

Short pulse measurements. a Experimental set-up to test the dynamics of the memristive switch. b A single switching cycle with a set pulse and two read pulse before and after the set pulse. c Blow-up of the set dynamics of the memristive cycle given in Fig. 5b. A delay of about 7.5 ns is found between the setting of the voltage and the response of the device. d Three complete switch cycles consisting of set and reset procedures. e Blow-up of the reset dynamics given in Fig. 5d upon applying a negative pulse. It takes 40 µs until the device is switched off and currents drop to zero

Discussion

To summarize, we experimentally demonstrated a new technology with the potential to scale ECM cell’s dimensions to a few tens of atoms. The fabrication technique is based on an ultra-sharp 3D metal tip that patterned by a thermal nanoscale lithography tool. The reported devices benefit from a highly confined electric field at nanometer size and feature low switching voltage around 100 mV, operation speed in the nanosecond range, extinction resistance ratio as high as 6 × 10⁵, reliable operations despite its atomic scale dimensions, and the possibility to a achieve multi-level behavior. It was also shown by experiments and supported by ab-initio simulations that the ultra-short oxide gap thickness reduces the temperature of the filament and thus the device failure probability. The optimization of such a technology platform could lead to the demonstration of memory crossbar arrays with ultra-high ECM cell densities and few-atom operations.

Methods

Device fabrication

Figure 6 depicts the fabrication steps for the reliable fabrication of a sharp atomic metallic tip. Figure 6a shows the device after the Pt metallization. The Pt electrode was patterned by a standard electron beam lithography technique and deposited by electron beam evaporation. Figure 6b shows the preparation for patterning. A 15 nm layer of SiO₂ was deposited on top of the Pt electrode by using atomic layer deposition (ALD). On top of SiO₂, a double layer of 2 nm polymethylmethacrylate (PMMA) and 20 nm PPA was spin coated. The 2 nm PMMA thereby serves as a buffer layer and prevents the scanning tip from getting blunt. Figure 6c shows the sharp tip shape patterned using thermal-scanning probe lithography^24,25,26 (t-SPL). The ultra-sharp scanning tip’s radius is in the range of 2.5 to 3.5 nm with a 1–2 nm thin native oxide covering the crystalline silicon²⁷. The resulting patterning creates sharp holes into the PPA layer. Figure 6d shows the tip transferred into SiO₂ by using CHF₃ reactive ion etching (RIE). The recipe was optimized so that physical etching is dominant and the sharp sidewall is preserved. We etched up to the point where Pt is exposed at the tip. Figure 6e shows a SiO₂ layer of thickness d deposited by ALD on the chip after the RIE etching. It is reported that for ALD deposition thickness uniformity in the range 0.3–4% (standard deviation, 1 sigma) over a 300 mm wafer can be obtained⁵⁰. This basically means a deviation of less than one atomic layer in 1 and 1.5 nm gap sizes within our entire chip of 1× 1 cm². This insulating layer serves as the switching matrix for the device and it accurately determines the SiO₂ gap thickness d of the switching area. Finally, the Ag metallization is performed by using e-beam lithography and standard lift off process, see Fig. 6f.

Fig. 6

Illustration of fabrication steps. a Pt metal deposition. b Chip preparation for thermal-scanning probe lithography (t-SPL). c Writing sharp holes into the top polyphthalaldehyde (PPA) layer with t-SPL. d Reactive ion etching (RIE) to transfer the pattern into SiO₂. e Atomic layer deposition (ALD) of a thin layer of SiO₂ (thickness d) as switching matrix. f Deposition of top metal and finalize the device

Transmission electron microscopy

Cross-sectional TEM samples were prepared using FEI Helios dual beam FIB/SEM system with a protective Pt layer. In-situ focused ion beam (FIB) lift-out method was used to prepare the lamella. The lamella was further thinned down with low-energy Ga⁺ ion milling. FEI Talos F200X was used for TEM imaging.

Scanning electron microscopy

SEM was carried out with Hitachi’s SU8200 Series Cold Field Emission SEM. A low acceleration voltage of 5 keV was used in order to minimize charging of the sample and give enough contrast to reveal the location of the tip shown in Fig. 1d.

Finite element method simulation

Simulation of the electric field distribution of the tip-like memristor in Fig. 1b was performed with the 3D electro-static solver from CST Studio. Both metallic contacts were assumed to be silver. The insulator material between the metal electrode and the tip is silicon dioxide with a permittivity of 3.9.A potential of 1 V applied between the two electrical contacts. The tip is 5 nm height with a radius at the tip of 6 and 24 nm at the base. The simulation domain is 50 nm squared.