Joule overheating poisons the fractional ac Josephson effect in topological Josephson junctions

Abstract

Topological Josephson junctions designed on the surface of a 3D-topological insulator harbor Majorana bound states among a continuum of conventional Andreev bound states. The distinct feature of these Majorana bound states lies in the 4π-periodicity of their energy-phase relation that yields a fractional ac Josephson effect and a suppression of odd Shapiro steps under radio-frequency irradiation. Yet, recent experiments showed that a few, or only the first, odd Shapiro steps are missing, casting doubts on the interpretation. Here we show that Josephson junctions tailored on the large bandgap 3D-topological insulator Bi₂Se₃ exhibit a fractional ac Josephson effect acting on the first Shapiro step only. With a modified resistively shunted junction model, we demonstrate that the resilience of higher order odd Shapiro steps can be accounted for by thermal poisoning driven by Joule overheating. Furthermore, we uncover a residual supercurrent at the nodes between Shapiro lobes, which provides a direct and novel signature of the current carried by the Majorana bound states. Our findings showcase the crucial role of thermal effects in topological Josephson junctions and lend support to the Majorana origin of the partial suppression of odd Shapiro steps.

Introduction

Topological superconductivity engineered by coupling superconducting electrodes to topological states of matter has attracted considerable attention due to the prospect of manipulating Majorana states for topological quantum computing^1,2,3. Intense experimental efforts have focused on spectroscopic signatures of Majorana bound states (MBSs) in various superconductivity-proximitized systems, including semiconducting nanowires^4,5,6,7,8, atomic chains^9,10 or islands¹¹ of magnetic atoms, and vortices at the surface of 3D-topological insulators (TIs)¹².

Another key approach to substantiate the very existence of MBS relies on the fractional AC Josephson effect^13,14,15 that develops in topological Josephson junctions^3,15. Theory predicts that MBSs shall emerge in such junctions as a peculiar, spinless Andreev bound state (ABS). Contrary to the conventional ABSs whose energy level varies 2π-periodically with the phase difference ϕ between the junction electrodes, the MBS is 4π-periodic and crosses zero-energy for a phase π (see Fig. 1a), yielding a fractional AC Josephson effect at frequency f_J/2 = eV/h (e is the electron charge, V the voltage drop across the junction and h the Planck constant), that is, half the Josephson frequency f_J^3,15.

Fig. 1

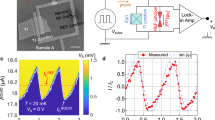
Topological Josephson junction on Bi₂Se₃. a Energy-phase spectrum of the Andreev bound states for a topological Josephson junction at the surface of a 3D-topological insulator. 4π-periodic, spinless, Majorana bound states coexist with conventional 2π-periodic Andreev bound states (ABS). The maximum energy E_ABS is lower than the quasiparticle continuum at Δ in case of imperfect interface transparency or the presence of a magnetic barrier^3,15,43. b Optical image of device. Scale bar is 9 μm. c Schematic of the Josephson junction geometry showing the superconducting electrodes (S) in orange that contact the top of the Bi₂Se₃ flake (in blue). d Current-voltage characteristic of the junction indicated by the arrow in c. Measurements were carried out at 0.05 K

Yet, revealing such a 4π-periodic contribution has proven challenging in dc transport experiments due to the presence of often prevailing, conventional ABSs^16,17,18. Moreover, poisoning processes—stochastic parity-changes of the quasiparticle occupation number—may obscure the MBS contribution by limiting its lifetime^19,20. Measurement schemes probing at time scales shorter than this lifetime are thus essential. The Shapiro effect comes forth with the combined advantages of a radio-frequency (f_rf) excitation of the phase that can be faster than the poisoning dynamics^15,21,22, and the ease of dc current-voltage (I-Vs) characteristics measurements.

The immediate consequence of the fractional AC Josephson effect is an unusual sequence of Shapiro voltage steps ${\mathrm{\Delta }}V = \frac{{hf_{{\mathrm{rf}}}}}{e}$ in the I-V characteristics, twice of that of conventional Shapiro steps $\left( {\frac{{hf_{{\mathrm{rf}}}}}{{2e}}} \right)$^{13,21,22,23,24,25,26}, providing direct evidence for the MBS 4π-periodicity. First experiments performed on InSb nanowires²⁷, on strained HgTe 3D TI²⁸, and on Bi_1−xSb_x²⁹ junctions however showed surprises in the sequences of Shapiro steps. In all these cases, only the n = ±1 steps were absent in a given range of radio-frequency (rf) power and frequency (n is the integer index of the Shapiro steps), an absence which was described as an (incomplete) signature of the fractional a.c. Josephson effect. More recent measurements on 2D HgTe quantum wells showed the absence of odd steps up to n = 9³⁰ and Josephson radiation at half the Josephson frequency³¹, though without the demonstration of time-reversal symmetry breaking that is required to induce MBSs in quantum spin-Hall edge channels^15,32. While the latter observations advocate more clearly for the existence of 4π-periodic Andreev modes, the fact that the fractional AC Josephson effect acts only on some odd Shapiro steps depending on the system remains unclear. Whether it provides a signature of the Majorana mode is a central question for identifying topological superconductivity in a variety of implementations.

In this work we report on the observation and understanding of the partial fractional AC Josephson effect in Josephson junctions designed on exfoliated flakes of the 3D-topological insulator Bi₂Se₃. Our devices exhibit an anomalous sequence of Shapiro steps with (only) the first step absent at low rf power and frequency. The 4π-periodic contribution to the supercurrent is directly identified as a residual supercurrent at the first node of the critical current when the rf power is increased. To shed light on our findings, we develop a two-channel resistively shunted junction (RSJ) model that includes the quasiparticle overheating induced by Joule effect^33,34,35, and a thermally activated poisoning of the MBS. We show that Joule overheating suppresses the parity lifetime of the MBS and thus terminates the 4π-periodic contribution to any higher index Shapiro steps, accounting for the observed suppression of the first Shapiro step only.

Results

Partial even-odd effect in Bi₂Se₃ Josephson junctions

Our samples are based on flakes of Bi₂Se₃ crystals exfoliated with the scotch tape technique. Figure 1b shows a 30 nm thick flake of Bi₂Se₃ contacted with multiple electrodes of vanadium enabling both magneto-transport and Josephson junction measurements on the same Bi₂Se₃ crystal (see Appendix for fabrication and measurement details). Analysis of Shubnikov-de-Haas oscillations and Hall effect enable identification of three electronic populations contributing to the sample conductance: Bulk states with a charge carrier density of 4.5 × 10¹⁹ cm⁻³, and the top and bottom surface states with densities of 1 × 10¹² and 4 × 10¹² cm⁻² respectively (see Supplementary Note 1). All three channels may thus carry supercurrent by proximity effect³⁶.

We focus here our discussion on the Josephson junction of length L = 125 nm and width W = 2.25 μm (see geometry in Fig. 1c) indicated by the white arrow in Fig. 1c. Below the superconducting transition temperature of the electrodes (T_c = 5 K), the proximity effect develops in the TI, leading to a dissipationless supercurrent in the I-Vs as shown in Fig. 1d (see Supplementary Note 2 for I-Vs at higher current bias showing an excess current due to Andreev reflections). The transition to the resistive state of the junction (R = 7.5 Ω) is hysteretic at 0.05 K with switching and retrapping currents of I_sw = 7.3 μA and I_r = 5.0 μA, respectively. Such a hysteresis is a common feature of most Josephson junctions made with metallic weak links and results from a quasiparticle overheating in the normal section of the junction³⁴. As we will show below, the ensuing quasiparticle overheating is key for understanding the suppression of the n = ±1 Shapiro steps only.

The dc response of the Josephson junction to an rf irradiation is shown in the Shapiro maps of Fig. 2a, b that display the color-coded differential resistance dV/dI versus rf power P_rf and dc current I. For an rf frequency of 3.5 GHz, Fig. 2a, well-defined Shapiro steps develop in the I − V curves, two of which are shown in Fig. 2c, with voltage steps that match the standard value $V_n = \pm n\frac{hf_{\mathrm{rf}}}{2e} = n \,\times 7.2\,{\kern 1pt} {{\upmu}} {\mathrm{V}}$ expected for a 2π-periodic current-phase relation. In the Shapiro map, the black areas indicate dV/dI = 0 and hence the position and amplitude of the Shapiro steps in the P_rf − I plane. Two features standard for a usual Shapiro map are visible. First, on increasing P_rf, the critical current continuously decreases till nearly full suppression at P_rf = 9 dBm and then oscillates at higher P_rf. Second, the sequence of appearance of the Shapiro steps with P_rf is sorted by the Shapiro step index n, and, importantly, starts with the step n = 1.

Fig. 2

Partial fractional AC Josephson effect. a, b Shapiro maps displaying the differential resistance dV/dI versus rf power P_rf applied to the antenna and dc current I measured at f_rf = 3.5 GHz in (a) and 1 GHz in (b). White numbers indicate the Shapiro steps index. c, d Voltage V in units of f_rfh/2e versus I extracted from the Shapiro map in (a, b) respectively at two different P_rf values. The corresponding P_rf values are indicated by the black arrows in (a, b). e Shapiro map displaying dV/dI versus P_rf and I, measured at a different frequency f_rf = 0.953 GHz during a second cooling of the sample, and zoomed on the first resistive node. The white arrow indicates twice the residual supercurrent $\left( {2 \times I_0^{k = 1}} \right)$ at the first resistive node

The central experimental result of this work is displayed in Fig. 2b, where we show the rf response of the same junction at a lower frequency of 1 GHz. This Shapiro map exhibits distinct features that markedly differentiate it from the higher frequency map. On increasing P_rf, the first Shapiro step n = 1 sets in at high P_rf after the steps of higher index for both switching and retrapping currents. This anomaly, sometimes termed even-odd effect^21,22, results in the conspicuous absence of the first Shapiro step in I–Vs picked out at low P_rf, while steps of higher indexes already appears, see Fig. 2d (similar results obtained on another sample are shown in Supplementary Note 3). Our findings match those recently obtained on InSb nanowires²⁷, strained HgTe 3D TI²⁸ and Bi_1−xSb_x alloy²⁹, which were interpreted as a signature of a 4π-periodic MBS contribution.

A second and new feature emerges at the first minimum of the critical current when the rf power is increased, i.e., at P_rf ≃ 10.7 dBm. Contrary to a conventional Shapiro map where a complete supercurrent suppression is expected at what can be called a resistive node, a small supercurrent I_c ~ 190 nA remains. This appears clearly in the individual I-Vs of Fig. 2d, see for instance the blue curve there. Figure 2e displays a similar Shapiro map obtained at a slightly different f_rf in the low-frequency regime, but zoomed on the resistive node where the critical current is expected to vanish but does not. We shall see in the following that this residual supercurrent provides a direct signature of the presence of a 4π-periodic mode in the junction.

Determination of the coherent transport regimes

Capturing the ABS spectrum of a Josephson junction on 3D TIs remains difficult as several conduction channels, including bulk and surfaces, intervene. Should all channels carry supercurrent, the nature of charge carriers in them may lead to virtually different regimes of coherent transport that we assess in the following. For bulk carriers, a rough estimate of the mean-free path (see Supplementary Note 1) gives a Thouless energy E_th = ħD/L² ≃ 417 μeV, smaller than the superconducting gap of the vanadium electrodes Δ = 800 μeV. This channel thus belong to the class of long diffusive Josephson junctions³⁷. In contrast, for the topological surface states, the spin texture of the Dirac electrons stemming from the spin-momentum locking leads to a very strong scattering anisotropy which promotes forward scattering. As a result, the transport time τ_tr is expected to be significantly enhanced with respect to the elastic scattering time τ_e, with ratio τ_tr/τ_e up to 60 depending on the disorder source³⁸. Recent experiments on Bi₂Se₃ flakes combining field effect mobility and quantum oscillations assessed a ratio τ_tr/τ_e ≳ 8³⁹. Taking the latter value as a conservative estimate and the surface state elastic mean-free path l_e ≃ 28 nm of our sample (see Supplementary Note 1) leads to a transport length l_tr ≳ 225 nm. These considerations suggest that surface transport is ballistic with, importantly, a non-zero probability for straight electronic trajectories impinging both electrodes. This is also consistent with signatures of ballistic transport over 300 nm evidenced in Bi₂Se₃ nanowires^40,41.

Consequently, we consider the topological surface state channel as ballistic. As such, the relevant energy scale for the ABSs is ħv_F/L = 2.8 meV with v_F = 5.4 × 10⁵ m/s the Fermi velocity⁴². It is greater than Δ, which shall lead to ABSs in the short ballistic limit. Theory then predicts that a 4π-periodic MBS exists, even in the case where the Fermi level is far from the Dirac point of the surface states, which is here the experimentally relevant regime⁴³. This MBS corresponds to ballistic trajectories impinging perpendicularly the superconducting electrodes, all other incidence angles yielding conventional 2π-periodic ABSs^3,43.

Eventually, observability of the 4π-periodicity theoretically implies a strong constraint on the Andreev spectrum: The MBSs must be decoupled from the quasiparticle continuum at ϕ = 0 and 2π to avoid direct transfer of quasiparticles into or from the continuum. Such a transition would indeed occur from the excited to the ground state every 2π, restoring an effective 2π-periodicity for the MBS. This detrimental effect can be remedied by adding a magnetic layer or magnetic field that break time-reversal symmetry, and thus open a gap between the MBS and the quasiparticle continuum^{15,21,23,43,44}, as sketched in Fig. 1a. In our samples, the vanadium that we use as superconducting electrodes is known to form magnetic dopants in Bi₂Se₃ and eventually a ferromagnetic phase at large concentration⁴⁵. Given that a smooth ion milling of the Bi₂Se₃ surface is processed before vanadium deposition, favoring vanadium diffusion into the Bi₂Se₃ crystal, there is presumably a magnetic layer or local magnetic moments at the superconducting interface as well as magnetic moments on the oxidized vanadium side surfaces of the electrodes. This singular configuration is likely to break time-reversal symmetry on the scale of the junction, thus leading to the decoupling of the MBS from the continuum and to the ensuing observability of 4π-periodicity in our Shapiro maps.

Two-channel RSJ model

To understand our experimental findings, we consider a RSJ model comprising a pure Josephson junction in parallel with a shunt resistor R. In the usual scheme of a single Josephson channel with a critical current I_c, the key parameter for the phase dynamics is the phase relaxation time $\tau _{\mathrm{J}} = \frac{\hbar }{{2eRI_{\mathrm{c}}}}$ which sets the typical time scale for the phase to adapt to a drive current change³³. With a rf drive, the RSJ model thus acts on the phase as a low pass filter of cutoff frequency 1/τ_J (see Supplementary Note 4). The regime of visibility of Shapiro steps is thus defined by f_rfτ_J < 1.

To phenomenologically capture the complex dynamics of a topological Josephson junction where a MBS lies within (a majority of) ABSs, we include two different Josephson junctions J1 and J2 in the RSJ model (see Fig. 3a)^24,26. The first junction J1 stands for the conventional ABSs with a 2π-periodic current-phase relation, and the second one J2 represents the 4π-periodic MBSs.

Having both 2π and 4π-periodic contributions in the total supercurrent $I_{\mathrm{s}}(\phi ) = I_{\mathrm{c}}^{2\pi }{\kern 1pt} {\mathrm{sin}}(\phi ) + I_{\mathrm{c}}^{4\pi }{\kern 1pt} {\mathrm{sin}}(\phi {\mathrm{/}}2)$ drastically changes the Shapiro steps sequence. The dynamics is now ruled by two different phase relaxation times $\tau _{\mathrm{J}}^{2\pi } = \frac{\hbar }{{2eRI_{\mathrm{c}}^{2\pi }}}$ and $\tau _{\mathrm{J}}^{4\pi } = \frac{\hbar }{{eRI_{\mathrm{c}}^{4\pi }}}$ set by the respective critical current amplitudes $I_{\mathrm{c}}^{2\pi }$ and $I_{\mathrm{c}}^{4\pi }$. Consequently, the 4π-periodic contribution will impact the junction dynamics only for drive frequencies $f_{{\mathrm{rf}}} \,< \,1{\mathrm{/}}\tau _{\mathrm{J}}^{4\pi }$. This can be straightforwardly seen in the Shapiro maps that we obtained by numerically solving the RSJ equation together with the Josephson relation $V = \frac{\hbar }{{2e}}\left\langle {\frac{{{\mathrm{d}}\phi }}{{{\mathrm{d}}t}}} \right\rangle$. In the low-frequency limit $f_{{\mathrm{rf}}}\tau _{\mathrm{J}}^{2\pi } \,< \, f_{{\mathrm{rf}}}\tau _{\mathrm{J}}^{4\pi } \, < \,1$, all even Shapiro steps develop at rf power P_rf lower than their neighboring odd steps, leading to the following appearance sequence |n| = {2, 1, 4, 3, 6, 5…} on increasing P_rf (see Fig. 3b). Lowering f_rf would enhance this even-odd effect and result ultimately in a quasi-suppression of odd Shapiro steps. Conversely, when the drive frequency is faster than $1{\mathrm{/}}\tau _{\mathrm{J}}^{4\pi }$ but still lower than $1{\mathrm{/}}\tau _{\mathrm{J}}^{2\pi }$, that is, $f_{{\mathrm{rf}}}\tau _{\mathrm{J}}^{2\pi } \, < \, 1 \, < \, f_{{\mathrm{rf}}}\tau _{\mathrm{J}}^{4\pi }$, the 4π-periodic contribution is suppressed, restoring the regular sequence of Shapiro steps appearance |n| = {1, 2, 3, 4…} on increasing P_rf, as shown in Fig. 3c. In a 2D space (f_rf, P_rf), the ranges of existence of the even and odd Shapiro steps are sketched in Fig. 3d. Importantly, the even-odd effect is robust even if $I_{\mathrm{c}}^{4\pi }$ sounds negligible compared to $I_{\mathrm{c}}^{2\pi }$, since the even-odd effect will always be present at low enough frequency as soon as $f_{{\mathrm{rf}}} \, < \,1{\mathrm{/}}\tau _{\mathrm{J}}^{4\pi }$. This low-frequency observability of the even-odd effect furthermore excludes an explanation for the existence 4π-periodic contribution based on Landau-Zener transitions at a soft gap, which should be otherwise enhanced at high frequencies.

Fig. 3

Two-channel resistively shunted junction model. a Equivalent circuit of the two-channel resistively shunted junction (RSJ) model comprising two Josephson junctions J1 and J2 of different critical current and current-phase periodicity, that is, $I_{\mathrm{s}} = I_{\mathrm{c}}^{2\pi }{\mathrm{sin}}(\phi )$ and $I_{\mathrm{s}} = I_{\mathrm{c}}^{4\pi }{\mathrm{sin}}(\phi {\mathrm{/}}2)$ respectively, in parallel with the shunt resistor R. b, c Computed Shapiro maps for the two-channel RSJ model displaying the differential resistance dV/dI versus normalized current I/I_c and P_rf. The model parameters are presented in the Supplementary Note 8. The product $f_{{\mathrm{rf}}}\tau _{\mathrm{J}}^{4\pi } = 0.4$ and 1.5 in (b, c) respectively. d Range of existence of the even and odd Shapiro steps versus radio-frequency (rf) f_rf and rf power P_rf. The phase relaxation times $1{\mathrm{/}}\tau _{\mathrm{J}}^{2\pi }$ and $1{\mathrm{/}}\tau _{\mathrm{J}}^{4\pi }$ indicate the cutoff frequency above which the contribution to the Shapiro steps of their respective channel is strongly suppressed

Let us now consider in the same computed maps the P_rf-dependence of the Shapiro steps amplitude. In contrast with the standard oscillatory behavior with a complete suppression at the resistive nodes, the even steps, including the supercurrent branch (n = 0), exhibit a non-vanishing amplitude at every two resistive node on increasing P_rf, see Fig. 3b, c. This unusual feature has been predicted in a recent paper by Domínguez et al.²⁶. It is a direct consequence of the presence of the 4π-periodic channel. It also conspicuously matches the residual supercurrent at the first node of the supercurrent branch in the experimental data of Fig. 2b, e.

We demonstrate below that the amplitude of this residual supercurrent can be quantitatively related to the 4π-periodic critical current $I_{\mathrm{c}}^{4\pi }$. Figure 4a displays the computed switching current I₀ of the Shapiro step n = 0, extracted from Fig. 3b as a function of P_rf. This plot both highlights the oscillatory behavior of I₀ with P_rf and enables us to identify the residual supercurrent of the first node that we note $I_0^{k = 1}$, with k the node index. To demonstrate the correlation between $I_0^{k = 1}$ and $I_{\mathrm{c}}^{4\pi }$, we performed a numerical study of the dependence of $I_0^{k = 1}$ on the relevant parameters $I_{\mathrm{c}}^{4\pi }$ and f_rf by systematically computing Shapiro maps for different sets of parameters. Figure 4b displays the calculated $I_0^{k = 1}{\mathrm{/}}I_{\mathrm{c}}^{4\pi }$ versus $f_{{\mathrm{rf}}}{\kern 1pt} \tau _{\mathrm{J}}^{4\pi }$ for different $I_{\mathrm{c}}^{4\pi }{\mathrm{/}}I_{\mathrm{c}}$ ratios (we define here the total critical current $I_{\mathrm{c}} = I_{\mathrm{c}}^{2\pi } + I_{\mathrm{c}}^{4\pi }$). All $I_0^{k = 1}{\mathrm{/}}I_{\mathrm{c}}^{4\pi }$ values collapse on a single curve which tends to saturate to ~0.7 in the limit $f_{{\mathrm{rf}}}{\kern 1pt} \tau _{\mathrm{J}}^{4\pi } \ll 1$. Conversely, $I_0^{k = 1}$ vanishes when $f_{{\mathrm{rf}}}{\kern 1pt} \tau _{\mathrm{J}}^{4\pi }\sim 16$, indicating that this residual supercurrent is visible at higher frequencies than the even-odd effect on the step appearance order.

Fig. 4

Residual supercurrent. a Switching current of the Shapiro step n = 0 (supercurrent branch) I₀ normalized to the zero-power critical current I_c versus rf power P_rf. I₀ is extracted from Fig. 3b. The residual supercurrent that remains at the first node k = 1 is noted $I_0^{k = 1}$. b Evolution of $I_0^{k = 1}$ normalized to $I_{\mathrm{c}}^{4\pi }$ versus $f_{{\mathrm{rf}}}{\kern 1pt} \tau _{\mathrm{J}}^{4\pi } = f_{{\mathrm{rf}}}\hbar {\mathrm{/}}eRI_{\mathrm{c}}^{4\pi }$ computed for various $I_{\mathrm{c}}^{4\pi }{\mathrm{/}}I_{\mathrm{c}}$ ratios. All points collapse on a single curve. The black dashed line is a polynomial fit that enables to extract $I_{\mathrm{c}}^{4\pi }$ from experimental parameters. Note that fluctuations of $I_0^{k = 1}{\mathrm{/}}I_{\mathrm{c}}^{4\pi }$ around this dashed line stem from the limited sampling of the Shapiro maps computed

The remarkable consequence of the collapse is that $I_{\mathrm{c}}^{4\pi }$ is uniquely defined for a fixed set of parameters $I_0^{k = 1}$, R and f_rf. Using a polynomial fit of the data points in Fig. 4b (black dashed line), we can thus directly determine $I_{\mathrm{c}}^{4\pi }$ from the measured value of the residual supercurrent $I_0^{k = 1}$ at a given frequency f_rf (see Supplementary Note 5). With the experimental parameters of Fig. 2b, that is, R = 7.5 Ω, $I_0^{k = 1} = 190\,{\mathrm{nA}}$ and f_rf = 1 GHz, we obtain $I_{\mathrm{c}}^{4\pi } = 290{\kern 1pt} \,{\mathrm{nA}}$ and thus a ratio $I_{\mathrm{c}}^{4\pi }{\mathrm{/}}I_{\mathrm{c}}\sim 4\%$. This value of $I_{\mathrm{c}}^{4\pi }$ is close to the theoretical value of the supercurrent carried by a single mode eΔ/ħ = 195 nA with Δ = 0.8 meV being the superconducting gap of the vanadium electrodes⁴⁶, although the exact value of the induced gap is most likely smaller than Δ due to non-perfect interface transparency. Furthermore, the resulting values $f_{{\mathrm{rf}}}{\kern 1pt} \tau _{\mathrm{J}}^{4\pi } \simeq 0.3$ and 1 for the 1 and 3.5 GHz Shapiro maps of Fig. 2b and a respectively are in agreement with the presence (absence) of even-odd effect in the data, confirming the consistency of the analysis. Note that our estimate of $I_{\mathrm{c}}^{4\pi }$ is close those found on strained HgTe²⁸ and Bi_1−xSb_x²⁹ systems, which were based on the frequency cut-off criterion.

Joule-induced poisoning of the MBS

The two-channel RSJ model, however, does not account for the experimental absence of the first Shapiro step only. Inclusion of a junction capacitance geometric (or instrinsic⁴⁷) through a two-channel RSCJ model mitigates the suppression of the n ≥ 3 odd steps⁴⁸, but is however not relevant for our strongly overdamped Bi₂Se₃-based Josephson junctions (With a geometrical capacitance of the order of 10 aF estimated with a planar capacitor approximation for the superconducting electrodes, we obtain a damping parameter $\sigma = \sqrt {\hbar {\mathrm{/2}}eI_{\mathrm{c}}R^2C} \sim 260$. We also estimate an intrinsic capacitance C^* ~ 0.1 pF predicted in ref. ⁴⁷ which leads to σ = 2.5. This overdamped regime is in contradiction with the hysteresis seen in the I-Vs, consequently bearing out the electron overheating scenario.). Furthermore, in the case of strongly underdamped, hysteresis should also be sizable in the Shapiro steps⁴⁹, which is not observed in our experiment.

We propose instead that the absence of the first step can be explained by including thermal effects resulting from Joule heating, and their impact on the 4π-periodic mode. Some of us recently showed that electron overheating must be taken into account with the RSJ model to capture Shapiro maps in conventional metallic Josephson junctions³⁵. Assuming that quasiparticles in the junction form a thermal distribution with an effective temperature T_qp different from the phonon bath temperature T_ph, we included the temperature dependence of the critical current, I_c(T_qp), and solved the RSJ equation self-consistently together with the heat balance equation $P = \left\langle {I(t)V(t)} \right\rangle = {\mathrm{\Sigma}} {\mathrm{\Omega }}\left( {T_{{\mathrm{qp}}}^5 - T_{{\mathrm{ph}}}^5} \right)$ (Σ is the electron-phonon coupling constant and Ω the volume of the normal part, see Supplementary Note 6 for values) to extract T_qp for each dc current. Solving such a thermal RSJ model (tRSJ), we obtain a significant raise of T_qp, when a dc voltage drop sets in on the firstly developed Shapiro step³⁵.

We then conjecture that the ensuing excess of non-equilibrium quasiparticles that we express in terms of an effective quasiparticle temperature poisons the 4π-periodic mode. Note that any non-thermal distribution would have the same consequences. Acting on a single mode, poisoning causes a stochastic parity-change^{15,21,22,31,44} that switches in time the quasiparticle occupation from the excited to the ground state, as illustrated in Fig. 1a by the black dotted arrow. Within the two-channel RSJ model, we model this parity-change of the 4π-periodic contribution to the supercurrent as

$$I_{\mathrm{s}}^{4\pi }(t) = ( - 1)^{n_{sw}(t)}I_{\mathrm{c}}^{4\pi }{\mathrm{sin}}\left( {\frac{{\phi (t)}}{2}} \right),$$

(1)

where n_sw(t) is a random occupation number of characteristic time scale determined by a switching parity lifetime τ_sw (see Supplementary Note 7). The exact microscopic processes that yield such a diabatic event can involve several transitions, including pair breaking, quasiparticle recombination with various rates, and possible coupling to the bulk states. Phenomenologically, but without loosing the generality of the foregoing, we follow the approach of Fu and Kane¹⁵ and consider a thermally activated switching parity lifetime τ_sw for the 4π-periodic mode:

$$\tau _{{\mathrm{sw}}} = \tau _0\,{\mathrm{exp}}\left( {\frac{{{\mathrm{\Delta }} - E_{{\mathrm{MBS}}}}}{{k_{\mathrm{B}}T_{{\mathrm{qp}}}}}} \right),$$

(2)

where Δ − E_MBS is the minimal energy gap separating the 4π-periodic mode to the continuum (see Fig. 1b), τ₀ the characteristic time scale for the activation process, and k_B the Boltzmann constant. When the quasiparticle effective temperature T_qp is high, the switching time is small τ_sw ≲ τ_J and poisoning suppresses the 4π-periodic Josephson effect, and hence the even-odd effect, by switching frequently the current-phase relation (see Supplementary Note 7). For the opposite limit $\tau _{{\mathrm{sw}}} \gg \tau _{\mathrm{J}}$, poisoning is irrelevant.

We thus claim that understanding the partial even-odd effect in topological Josephson junctions relies on the interplay between activated poisoning and thermal effects in the two-channel tRSJ model. We show in Fig. 5a, b two Shapiro maps computed for the same rf frequency and junction parameters as those in Fig. 3b. Figure 5a is the result of the tRSJ model that includes a T-dependence of $I_{\mathrm{c}}^{2\pi }(T)$ given by the measured I_sw(T)³⁵ and realistic parameters for the heat balance equation (see Supplementary Note 6 for an estimate of ΣΩ in our junctions). We assume here that most of the T-dependence of I_sw(T) comes from the 2π-periodic modes. Compared to Fig. 3b, the electron overheating leads to a broadening of the resistive transitions at high P_rf between the periodic oscillations of the Shapiro steps. Nevertheless, the full even-odd effect acting on all odd steps remains as in the absence of thermal effect, see Fig. 3b.

Fig. 5

Poisoning of the even-odd effect. a Shapiro map computed with the two-channel thermal resistively shunted junction (RSJ) model displaying the differential resistance dV/dI versus dc current I normalized to the critical current I_c and radio-frequency power P_rf. For the sake of clarity, we took the same parameters as in Fig. 3b, that is, $f_{{\mathrm{rf}}}\tau _{\mathrm{J}}^{4\pi } = 0.4$ (see Supplementary Note 8), with a phonon bath temperature T_ph = 0.1 K. The model includes the experimental T-dependence for $I_{\mathrm{c}}^{2\pi }(T)$ and an estimate of the electron-phonon coupling in Bi₂Se₃ (see Supplementary Note 6). On each point a recursive algorithm solves successively the RSJ equation, the ensuing time dependent voltage and dissipated power, the raise of the quasiparticle temperature T_qp, and then re-solves the RSJ equation with the new $I_{\mathrm{c}}^{2\pi }\left( {T_{{\mathrm{qp}}}} \right)$ till convergence. b Shapiro map computed with the two-channel thermal RSJ model as in a but including the thermal poisoning. The implementation of a thermally activated poisoning suppresses the even-odd effect for the Shapiro step of indexes n ≥ 3

Figure 5b is the main result of our theoretical analysis. It displays a Shapiro map computed with the same tRSJ than Fig. 5a, but including thermally activated poisoning of the 4π-periodic channel defined by Eqs. (1) and (2) which ensues from Joule overheating. The 4π-periodic channel now impacts only the steps n = ±2 by enhancing their amplitude, therefore inverting the appearance order on increasing P_rf between step n = 1 and 2. The sequence of appearance of all higher order steps turns out to be regularized due to the suppression of the 4π-periodic contribution by poisoning. This finding, that is, the even-odd effect limited to the first Shapiro step only, is in full agreement with our experiment shown in Fig. 2b and with works on other systems^27,28,29.

The thermally activated poisoning can be captured by inspecting the computed T_qp and τ_sw for two different P_rf. Figure 6a displays the I-V curves corresponding to the black arrows in Fig. 5b. In Fig. 6b, we show the corresponding T_qp versus I, which raises linearly once a dissipative voltage sets in. Accordingly, τ_sw is exponentially suppressed, and becomes inferior to τ_J on the Shapiro steps n ≥ 2 (Fig. 6c). This explains why the 4π-periodic component acts only on the appearance order of the n = 1 and 2 steps, leaving all other steps unaffected.

Fig. 6

Thermally suppressed parity lifetime. Data extracted from Fig. 5b at two different radio-frequency powers P_rf indicated by the black arrows in Fig. 5b, showing the voltage V normalized to hf_rf/2e (a), Quasiparticle temperature T_qp (b), and the switching time τ_sw (c) versus current I normalized to the critical current I_c. At P_rf = −112 dBm, the first Shapiro step is absent in the I − V. The increase of T_qp when a voltage sets in on Shapiro steps leads to an exponential suppression of τ_sw. When $\tau _{{\mathrm{sw}}} \, < \, \tau _{\mathrm{J}}^{4\pi }$ (the phase relaxation time $\tau _{\mathrm{J}}^{4\pi }$ is indicated by the black dotted line in c), poisoning suppresses the contribution of the 4π-periodic channel to the Shapiro steps n > 2, and all odd Shapiro steps are present in the I − V, see blue curve in (a)

Furthermore, inspecting Fig. 5b we see that the residual supercurrent of only the first resistive node $I_0^{k = 1}$ remains in presence of poisoning, as observed in the data of Fig. 2b. This confirms that the residual supercurrent $I_0^{k = 1}$ is a robust feature that provides a new indicator for the presence of 4π-periodic modes, and enables a direct and quantitative determination of the corresponding 4π-periodic critical current as discussed above.

Within this approach of thermal poisoning by Joule overheating, it is interesting to compare the power dissipated between the available experiments on different TI systems. For instance, estimates of the dissipated power on the n = 2 Shapiro step give two orders of magnitude difference between different TI materials: $P \simeq 2\frac{{hf_{{\mathrm{rf}}}}}{{2e}}I\sim 25\,{\mathrm{pW}}$ for our data and 17 pW for strained HgTe²⁸. For InAs nanowires²⁷ and Bi_1−xSb_x²⁹, P ~ 2 pW. For HgTe quantum wells³⁰, the dissipated power is the smallest P ~ 0.2 pW. Comparing the strained HgTe to the HgTe quantum wells that share the same electron-phonon coupling constant, we estimate a power per unit of volume of ~80 fW μm⁻³ and ~2 fW μm⁻³, respectively (~300 fW μm⁻³ in our Bi₂Se₃ samples). Such a small dissipated power density in the experiment on HgTe quantum wells should result in a minimized amount of non-equilibrium quasiparticles and limited poisoning, therefore explaining the observed full suppression of not only the first but of several odd Shapiro steps in this system.

Discussion

Our theoretical approach, combining two Josephson channels in parallel, electronic overheating and quasiparticle poisoning, can be extended to more elaborate situations. For instance, recent theory works predict for the case of the quantum spin Hall regime an 8π-periodicicity due to either interactions⁵⁰ or quantum magnetic impurities^51,52. Although this has not been reported so far in experiments, it would be interesting to study how multiple periodicities mix in the Shapiro response. Given the understanding of the two-channel RSJ model, we expect the 8π-periodicity to enhance every steps of index ±4n and significantly modify the beating pattern at high P_rf. Other effects such as the voltage dependence of the phase relaxation time²¹ could be included in our model and should enhance the effect of thermal poisoning on the partial suppression of the even-odd effect.

To conclude, our work elucidates the origin of the puzzling suppression of only the first Shapiro step in topological Josephson junctions. In our Bi₂Se₃ Josephson junctions, this suppression is accompanied by a residual supercurrent that provides a new indicator of the 4π-periodic contribution to the supercurrent. Together, these observations can be captured by a two-channel thermal RSJ model in which Joule overheating activates poisoning of the 4π-periodic mode. The even-odd effect restricted to the first Shapiro step and the residual supercurrent do provide a clear signature of a 4π-periodic mode in the Andreev spectrum, conspicuously pointing to MBSs. Our phenomenological model illustrates a direct consequence of thermal poisoning on MBSs, signaling that dissipation must be scrutinized with attention in dc-biased measurements. Addressing a microscopic description of the enhanced poisoning in such non-equilibrium measurement schemes is a challenging task for theory that should lead to significant progress towards new devices for Majorana physics and possible MBS qubits.

Methods

Bi₂Se₃ crystals were synthesized by melting growth method with high purity (5N) Bi and Se in an evacuated quartz tube. Crystals were analyzed by X-rays diffraction, and angle-resolved photoemission spectroscopy. Flakes of Bi₂Se₃ were exfoliated from the bulk crystal on silicon wafer and systematically inspected by atomic force microscopy to ensure crystal quality. V/Au superconducting electrodes were patterned by e-beam lithography and deposited by e-gun evaporation after a soft ion beam etching.

Measurements were performed in a dilution refrigerator equipped with highly filtered dc lines that comprise room temperature feed-through Pi-filters, lossy custom-made coaxial cables and capacitors to ground on the sample holder. Radio-frequency are fed through a dedicated coaxial cable ending as an antenna that were adjusted in the vicinity of the devices. Shapiro map measurements were performed with standard lock-in amplifier technique.