Introduction

Recent progress of X-ray scattering techniques revealed a short-range charge order in hole-doped cuprates (h-cuprates)1,2,3,4,5,6,7,8,9,10,11 as well as in electron-doped cuprates (e-cuprates)12,13,14. To investigate the energy-resolved charge-excitation spectrum, resonant inelastic X-ray scattering (RIXS) is the most powerful tool15,16,17. RIXS measurements were performed to explore the high-energy region in both e-cuprates18,19,20 and h-cuprates21,22. For e-cuprates, Lee et al.18 uncovered that the high-energy charge excitations form a steep dispersion around q|| = (0, 0), where q|| is the in-plane momentum, with an excitation gap about 300 meV at q|| = (0, 0). On the other hand, Ishii et al.19,20 measured charge excitations in a wider q|| region than Lee et al.18. The spectrum was found to be typically broad and to become broader toward the Brillouin zone (BZ) boundary. In contrast to Lee et al.18, a gap feature around q|| = (0, 0) was not resolved. The observed charge excitations were thus interpreted differently: they may be related to a certain mode near a quantum critical point associated with a symmetry-broken state in Lee et al.18, whereas they can be intraband particle-hole excitations with strong incoherent character in Ishii et al.19,20. The situation in h-cuprates is more controversial. Ishii et al.21 showed that high-energy charge excitations similar to the ones in e-cuprates occur also in h-cuprates, while Dellea et al.22 emphasized that the high-energy charge excitations are a unique feature in e-cuprates and do not occur in h-cuprates.

Recently, a theoretical study of the layered t–J model with the long-range Coulomb interaction implied that the charge excitation spectrum of cuprates is characterized by a dual structure in the energy space23. The low-energy charge excitations correspond to various types of bond-charge fluctuations driven by the exchange term (J-term), whereas the high-energy charge excitations are essentially independent of the J-term and come from usual on-site charge fluctuations. In this scenario, the high-energy spectrum is dominated by plasmonic excitations with a finite out-of-plane momentum qz. The plasmon mode has a gap at q|| = (0, 0) and its magnitude is proportional to the interlayer hopping tz (Greco et al.24). This theoretical proposal provides a third idea to understand the high-energy charge excitations.

Therefore three different ideas are proposed for the origin of the high-energy charge excitations: (i) a certain collective mode near a quantum critical point associated with a symmetry-broken state, which should be specific to e-cuprates18,22, (ii) intraband particle-hole excitations (not plasmons) present in both e- and h-cuprates19,20,21, and (iii) a plasmon mode with a finite qz (Greco et al.24). In this paper, we show that the plasmon scenario yields results consistent with the experimental observations. We propose several experimental tests to distinguish different scenarios.

Results

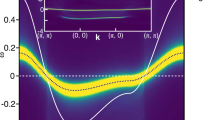
We compute the imaginary part of the usual charge susceptibility Imχc(q, ω) in the layered t–J model with the long-range Coulomb interaction in a large-N scheme (see Methods and Supplementary Note 1). We show in Fig. 1 the high-energy collective dispersions, namely the peak positions of Imχc(q, ω), for e-cuprates with doping x = 0.15 (black line), and for h-cuprates with x = 0.125 (green line) and x = 0.25 (purple line). These excitations correspond to plasmons realized in the layered system with a gap at q|| = (0, 0). For comparison, we include in Fig. 1 the peak position of the charge excitations obtained in the experiments18,19,20,21. The agreement with the experimental data is very good in \({|{\mathbf{q}}_{||}| \,\lesssim \,0.5\pi }\) for both e- and h-cuprates.

Fig. 1
figure 1

Plasmon dispersion. Our theoretical results are denoted by the black line for e-cuprates with x = 0.15, and green and purple lines for h-cuprates with x = 0.125 and x = 0.25, respectively, along the (π, π)–(0, 0)–(0, π) direction. For comparison, experimental data are plotted: Black up-triangles and black circles for Nd2−xCexCuO4 with x = 0.15 reported in Lee et al.18 and Ishii et al.19,20, respectively, and green circles and purple squares for La2−x(Br,Sr)xCuO4 with x = 0.125 and x = 0.25, respectively21. The dashed line is the dispersion proposed in Lee et al.18. (qx, qy) is the in-plane momentum. Error bars are defined in the corresponding references

Full size image

Our obtained dispersion for x = 0.25 has higher energy than that for x = 0.125. This feature captures the experimental data shown in Fig. 1. In fact, the analysis in Ishii et al.21 finds that the energy at q|| = (0.46π, 0) increases by a factor of 1.16 when doping is increased from x = 0.125 to x = 0.25. In the present theory, we obtain a factor of 1.30. Similar results were also obtained in the density-matrix renormalization-group calculations in the three-band Hubbard model21.

For x = 0.15 in e-cuprates in the large q|| region, i.e., (0.5π, 0)–(π, 0), the experimental data deviate downward from the dispersion proposed in Lee et al.18 (dashed line in Fig. 1) and tend to be closer to our obtained dispersion. Still, the deviation between the experimental data and our results seems substantial, compared with the agreement in the small q|| region. However, we think that such a deviation could be related to, as we shall discuss later, the broad spectrum observed in the experiments especially in a large q|| region.

In addition to the agreement with the experimental data in Fig. 1, the present theory implies the following: (i) The high-energy charge excitations correspond to a plasmon mode with a gap at q|| = (0, 0); the gap is proportional to tz (Greco et al.24). (ii) Our high-energy charge excitations are present in both e- and h-cuprates. (iii) The dispersion around q|| = (0, 0) has a larger slope in e-cuprates than h-cuprates, consistent with the observation in Ishii et al.21. (iv) The dispersion is rather symmetric between the direction (0, 0)–(π, 0) and (0, 0)–(π, π).

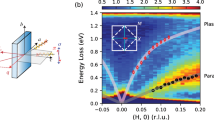
Since the plasmon is a collective mode, it can form a very sharp peak in q||−ω space as shown in Fig. 2a. On the other hand, the experiments in Ishii et al.19,20,21 do not show a peak signal at q|| = (0, 0) and in addition, the spectrum is broad and becomes broader with increasing q|| toward the BZ boundary (Fig. 2b). These features are not seen in Fig. 2a because it was computed in an ideal situation by taking Γ = 0.001t, i.e., the damping is assumed to be very small (see Methods for the definition of Γ). Considering a realistic situation, we compute the charge-excitation spectrum by employing a large Γ. In principle, Γ would depend on momentum and energy, but we take a constant Γ = 0.7t as the simplest case. As shown in Fig. 2c, the spectrum is substantially broadened and becomes broader with increasing q||. In addition, the spectrum near q|| = (0, 0) becomes poorly resolved. These features are very similar to the experimental results (Fig. 2b). In Fig. 2b, there is strong intensity around q|| = (0, 0) and ω = 2 eV, which comes from the charge transfer excitations between oxygens and coppers, namely interband excitations. This feature is beyond the scope of the analysis of the present one-band model.

Fig. 2
figure 2

Charge excitations for e-cuprates with x = 0.15. a, c q|| − ω spectral weight for Γ = 0.001t (a) and Γ = 0.7t (c). In (a), the sharp spectrum (red) comes from plasmons whereas weak intensity around 0.5 eV (green and yellow) is due to individual particle-hole excitations. The experimental result of figure 2d in Ishii et al.20 is reproduced in (b) for comparison with (c). d q|| dependence of the peak area obtained from (c). Red circles are the experimental results for Nd2−xCexCuO4 with x = 0.15 (Ishii et al.20). (qx, qy) is the in-plane momentum. Error bars are defined in the corresponding reference

Full size image

The inclusion of a large Γ is actually invoked theoretically when the spectral line shape is compared with experiments21. In Greco et al.24 a finite Γ was also used to discuss the temperature dependence of spectral weight18. Physically there should be two different broadenings, intrinsic and extrinsic ones. The extrinsic broadening is due to the instrumental resolution, which is about 250 meV (Γ  ~  0.35t) in Ishii et al.19, and 130 meV (Γ  ~  0.2t) in Lee et al.18. Because of this difference in the instrumental resolution, it is possible that the charge excitation around q|| = (0, 0) is resolved in Lee et al.18, but not in Ishii et al.19. In addition, in the low q|| region studied in Lee et al.18 the peak width seems to become broader with increasing q||, consistent with Ishii et al.19,20. The intrinsic broadening comes from incoherent features of high-energy charge excitations due to electron correlation effects as demonstrated in various numerical calculations in the t–J (Prelovšek et al.25 and Tohyama et al.26) and Hubbard19,21 models.

We have also calculated the peak area at a given q|| along the (π, π)−(0, 0)−(0, π) direction and compare it with the experimental results in Fig. 2d. This agreement with the experiment reinforces the idea that the high-energy charge excitations are plasmons.

Our plasmon mode should not be confused with usual optical plasmons, which are actually observed in optical measurements27 and electron energy-loss spectroscopy28,29 in cuprate superconductors. The optical plasmon mode is in fact reproduced in our theory by invoking qz = 0 (Greco et al.24). However, qz is usually finite in RIXS. Once qz becomes finite, the optical plasmon energy is substantially suppressed to be proportional to the interlayer hopping tz, yielding acoustic-like plasmons as shown in Fig. 1. While this strong qz dependence was, in part, already discussed in Greco et al.24, as well as in early theoretical works where tz = 0 was assumed in a layered model30,31,32, we present further results. Figure 3 shows a map of the spectral weight of plasmons in the plane of qz and ω for several choices of Γ at a small q||. The plasmon energy rapidly decreases with increasing qz and stays almost constant in qz > π/3; this rapid change is more pronounced when a smaller q|| is chosen. The plasmon intensity, on the other hand, increases with increasing qz, following nearly a \(q_z^2\) dependence at small qz. Those qualitative features are independent of the broadening Γ. However, the peak intensity at a small q|| is suppressed substantially with increasing Γ (see also Fig. 2c). Hence the qz dependence of plasmons may be well observed for a small Γ. Although the importance of the qz dependence of plasmons was not recognized in experimental papers18,19,20,21,22, we have learned that results similar to Fig. 3 are recently obtained in RIXS33.

Fig. 3
figure 3

Intensity maps of plasmons in the plane of qz and ω. The in-plane momentum q|| is set to (0.05π, 0.05π) and open circles denotes the peak position at each out-of-plane momentum qz. Each panel has a different value of broadening Γ: Γ = 0.01t in (a), Γ = 0.1t in (b), Γ = 0.3t in (c), and Γ = 0.7t in (d)

Full size image

The reason why plasmons show a strong qz dependence is easily understood by recalling that plasmons originate from the singularity of the long-range Coulomb interaction in the limit of long wavelength. A special feature of the present layered model lies in the anisotropy of the momentum dependence of the long-range Coulomb interaction V(q) [see Eq. (2)]. When qz = 0, V(q) is singular at q|| = (0, 0), which leads to usual optical plasmons. However, due to the anisotropy between q|| and qz, the plasmon energy becomes different when qz is reduced to zero at q|| = (0, 0). In particular, the plasmon energy would become zero if the interlayer hopping is neglected. This is the reason why the plasmon energy becomes sensitive to the value of qz, especially in a region of a small q||.

Discussion

We have shown that acoustic-like plasmon excitations with a gap at q|| = (0, 0) due to a finite interlayer hopping describe the main features observed by different experimental groups18,19,20,21 in a consistent way. How about other scenarios?

The scenario proposed in Lee et al.18 and Dellea et al.22 invokes a collective mode associated with a certain symmetry-broken state to understand the high-energy charge excitations around q|| = (0, 0). The crucial point of this scenario is that their hypothetical order should be specific to e-cuprates, because Lee et al.18 and Dellea et al.22 claim that similar charge excitations around q|| = (0, 0) are not present in h-cuprates at least from their RIXS measurements using the Cu L3-edge. However, both spin and charge excitations are detected in the Cu L3-edge and the intensity from the later can be lower than the former. In fact, recently Ishii et al.21 successfully detect the high-energy charge excitations also in h-cuprates by using the oxygen K-edge RIXS, which can probe directly the charge dynamics of doped holes. This recent experimental data is not reconciled with the scenario proposed in Lee et al.18 and Dellea et al.22. Thus, in order to discriminate the scenario of Lee et al.18 and Dellea et al.22 from the others, it is crucial to test the presence of high-energy charge excitations in h-cuprates by different experimental groups.

Ishii et al.19,20,21 propose intraband charge excitations and emphasize their incoherent character. This scenario can be interpreted in two different ways. On one hand, our acoustic-like plasmons are also from intraband particle-hole excitations and their experimental data (Figs. 1 and 2b, d) are well captured by introducing a large Γ (Fig. 2c, d). Therefore their scenario can be understood in terms of plasmons with a large damping, although this possibility was not discussed in Ishii et al.19,20,21. On the other hand, incoherent intraband excitations occur also as individual charge excitations, which form the continuum spectrum below the plasmon energy. In this case, two predictions are possible. First, charge excitations should be gapless at q|| = (0, 0). Although a region around q|| = (0, 0) was not resolved below 2 eV in their measurements (see Fig. 2b), Lee et al.18 reports a gap feature (see also Fig. 1). Therefore, besides Lee et al.18, it is decisively important to confirm the presence of a charge gap at q|| = (0, 0) by different experimental groups. The second prediction concerns the qz dependence of the charge excitations. We have computed the qz dependence of individual charge excitations in our model as shown in Fig. 4 (see Supplementary Note 2 for details). While the peak position depends on choices of Γ, its qz dependence is almost negligible. This feature is qualitatively different from plasmons shown in Fig. 3 and thus serves to clarify the underlying physics of the high-energy charge excitations.

Fig. 4
figure 4

Intensity maps of individual particle-hole excitations in the plane of qz and ω. The in-plane momentum q|| is set to (0.05π, 0.05π) and open circles denotes the peak position at each out-of-plane momentum qz. Each panel has a different value of broadening Γ: Γ = 0.01t in (a), Γ = 0.1t in (b), Γ = 0.3t in (c), and Γ = 0.7t in (d)

Full size image

One may wish to consider a scenario without the long-range Coulomb interaction, which may replace plasmons with a zero-sound mode in the t–J model. To demonstrate this, we have computed charge excitations in our model by using the short-range Coulomb interaction instead of the long-range one (see Supplementary Note 3). Our obtained spectrum is shown in Fig. 5a, which is qualitatively similar to Fig. 2a. While it is clear theoretically that the zero-sound mode is fundamentally different from plasmons34, their distinction is less clear from an experimental point of view. Hence, we have computed the qz dependence of the zero-sound mode for a small q|| in Fig. 5b. The zero-sound energy increases with increasing qz in a small qz region, which is qualitatively different from the plasmon case shown in Fig. 3. This is because the zero-sound mode becomes gapless at q|| = (0, 0) and qz = 0 as shown in the inset of Fig. 5a. Therefore, besides Hepting et al.33, additional experimental data about the qz dependence of the high-energy charge excitations may confirm the importance of the long-range Coulomb interaction in the charge dynamics in cuprates.

Fig. 5
figure 5

Intensity maps of charge excitations without the long-range Coulomb interaction. a q||-ω spectral weight for qz = π; Γ = 0.01t is taken for numerical convenience. The sharp spectrum describes a zero-sound mode. Inset: zero-sound dispersion for qz = π and 0 around q|| = (0, 0). q|| = (qx, qy) is the in-plane momentum. b Intensity map of the spectral weight in the plane of out-of-plane momentum qz and energy ω at \({\mathbf{q}}_{||} = (0.02\pi ,0.02\pi )\). Open circles denotes the peak position at each qz

Full size image

We have demonstrated that acoustic-like plasmon excitations can consistently explain experimental data obtained by different groups18,19,20,21. Conceptually, plasmons are well known in solids, but the presence of the acoustic-like plasmon mode in cuprates has not been recognized yet in experiments. Thus, our theoretical recognition of the acoustic-like plasmons in cuprates highlights the importance of charge dynamics in cuprates. Recalling that cuprates have been studied largely by focusing on spin degrees of freedom, it is worth exploring unresolved issues in cuprates such as the origin of the pseudogap and the mechanism of high-Tc superconductivity in terms of charge degrees of freedom, including the present acoustic-like plasmons.

Methods

We employ the three-dimensional extended t–J model:

$$H = - \mathop {\sum}\limits_{i,j,\sigma } t_{ij}\tilde c_{i\sigma }^\dagger \tilde c_{j\sigma } + \mathop {\sum}\limits_{\langle i,j\rangle } J_{ij}\left( {{\mathbf{S}}_i \cdot {\mathbf{S}}_j - \frac{1}{4}n_in_j} \right) + \frac{1}{2}\mathop {\sum}\limits_{i,j} V_{ij}n_in_j$$
(1)

where (a) the hopping tij takes a value t (t′) between the first (second) nearest-neighbors sites on the square lattice and tz between the layers, (b) the magnetic exchange interaction Jij is considered only in the plane and we neglect the magnetic exchange interaction between the planes, which is much smaller than the in-plane J (Thio et al.35), (c) Vij is the long-range Coulomb interaction. \(\tilde c_{i\sigma }^\dagger\) and \(\tilde c_{i\sigma }\) are the creation and annihilation operators of electrons with spin σ in the Fock space without double occupancy, \(n_i = \mathop {\sum}\nolimits_\sigma \tilde c_{i\sigma }^\dagger \tilde c_{i\sigma }\) is the electron density operator, Si is the spin operator, and 〈i, j〉 denotes a nearest-neighbor pair of sites.

The long-range Coulomb interaction in the momentum space is written as36

$$V({\mathbf{q}}) = \frac{{V_{\mathrm{c}}}}{{A(q_x,q_y) - {\mathrm{cos}}q_z}}$$
(2)

and A(qx, qy) = α(2 − cosqx − cosqy) + 1. The constants Vc and α are given by Vc = e2d(2ε⊥a2)−1 and \(\alpha = (d/a)^2\varepsilon _{||}/\varepsilon _ \bot\), respectively. Here e is the electric charge of electrons, a (d) is the lattice constant in the plane (between the planes), and \(\varepsilon _{||}\) and ε⊥ are the dielectric constants parallel and perpendicular to the planes, respectively; \({\mathbf{q}}_{||} = (q_x,q_y)\) is measured in units of a−1, and qz in units of d−1.

Since the Hamiltonian (1) is defined in the Fock space without double occupancy, its analysis is not straightforward. Here we use a large-N technique based on path integral representation of the Hubbard X operators37,38, which was extended to a layered model in Greco et al.24. In the Supplementary Note 1, we present the essential part of our formalism.

The model Hamiltonian (1) contains several parameters, which may depend on materials. Fixing a value of J and the long-range Coulomb interaction V(q) as J/t = 0.3 (Hybertsen et al.39), and Vc/t = 17 and α = 4.5 (Greco et al.24), respectively, we allow a material dependence of the other parameters: t′/t = 0.30 and tz/t = 0.1 for Nd2−xCexCuO4 (Greco et al.24), and t′/t = −0.20 and tz/t = 0.05 (Horio et al.40) for La2−x(Br,Sr)xCuO4. It would also be possible to assume a similar value of tz between them and to take a slightly different values of Vc and α. However, we do not attempt such a tuning. Instead we aim to capture the major features of charge-excitation spectrum with a minimal change of the parameters. We take the number of layers as Nz = 30, which should be large enough. To address the high-energy charge-excitation spectrum, we compute the imaginary part of the usual charge susceptibility χc(q, iωn) after analytical continuation iωn→ω + iΓ in Eq. (S9) in Supplementary Note 1, where Γ is positive and, in principle, infinitesimally small. In RIXS, the interlayer momentum transfer qz is usually finite. We thus first present results for qz = π as representative ones in Figs. 1 and 2, and then study their qz dependence. The temperature is set to zero.

In the comparison with the experimental data in Fig. 1, we have used t = 750 meV for Nd2−xCexCuO4 and t = 500 meV for La2−x(Br,Sr)xCuO4. The value of t for the former is somewhat larger than the accepted value39. A possible reason lies in the renormalization of the bare hopping t in the large-N scheme, i.e., \(t \to t\frac{x}{2}\) [see Eqs. (S7) and (S8) in Supplementary Note 1], which is simply reduced by x and thus can be simple quantitatively.