Abstract
Heralded single-photon sources with on-demand readout are a key enabling technology for distributed photonic networks. Such sources have been demonstrated in both cryogenic solid-state and cold-atoms systems. Practical long-distance quantum communication may benefit from using technologically simple systems such as room-temperature atomic vapours. However, atomic motion has so far limited the single-excitation lifetime in such systems to the microsecond range. Here we demonstrate efficient heralding and readout of single collective excitations created in warm caesium vapour. Using the principle of motional averaging we achieve a collective excitation lifetime of 0.27 ± 0.04 ms, two orders of magnitude larger than previously achieved for single excitations in room-temperature sources. We experimentally verify non-classicality of the light-matter correlations by observing a violation of the Cauchy-Schwarz inequality with R = 1.4 ± 0.1 > 1. Through spectral and temporal analysis we investigate the readout noise that limits single-photon operation of the source.
Similar content being viewed by others
Introduction
The deployment of photonic quantum networks over large distances introduces losses that eventually hamper the network usefulness for quantum computation1 or secure quantum communication2. Implementing quantum memory in the network allows for synchronization between operations with low success probabilities (such as single-photon generation, entanglement generation and swapping) drastically improving the overall success rate of the network operation. For short-distance networks, the crucial figure of merit is the memory time-bandwidth product3. While this remains important for longer distances, the main limitation for the range of the network is the memory lifetime since the coherence needs to be maintained as the photons propagate between the nodes of the network4.
The realization of quantum memories for quantum repeater (QR) schemes has been studied extensively4. QRs can alleviate the losses in the optical fibres used to distribute quantum information over long distances, thereby increasing the distance over which entanglement can be efficiently distributed by means of entanglement swapping5.
Many attempts to realize such schemes are based on the Duan-Lukin-Cirac-Zoller (DLCZ) protocol for atomic ensembles6, where quantum information is stored in collective degrees of freedom of the ensembles. Since the first experimental realizations of the DLCZ protocol7,8 more than a decade ago, frequent improvements in cold atomic ensembles have been reported9,10,11,12,13,14,15,16,17,18,19,20 with memory times reaching 0.22 s19 and retrieval efficiencies up to 84%18. Progress has recently also been shown in solid-state systems, particularly in rare-earth-doped crystals21,22,23,24. However, cryogenic cooling is required for these platforms. Room-temperature systems offer reliability and scalability, as they do not need cooling apparatus. Spin coherence with timescales of seconds in nitrogen-vacancy (NV) centres in diamond25, and minutes with atomic vapour in anti-relaxation-coated glass containers26, has been demonstrated at room temperature. Still, coherent optical interaction with NV centres at room temperature remains a challenge27 due to severely broadened optical transitions. These memories can therefore not directly be employed for quantum communication. Broadband, short-lived quantum memories have been demonstrated in warm vapours28,29, but thermal atomic motion impedes long life spans of the generated collective excitations or stored light30,31,32 since atoms rapidly leave the interaction region due to thermal motion. The utilization of buffer gas to slow down atomic diffusion has allowed to extend the light storage duration at the few-photon level to 20 μs33. At the single-photon level, non-classical DLCZ-type correlations have been reported with buffer gas34,35,36,37, but with a lifetime limited to a few microseconds. Anti-relaxation coating of the container walls has enabled continuous-variable quantum memory of a few milliseconds38 and classical light storage up to 0.43 s39, but non-classical correlations for single excitations on such time scale remain to be observed.
To extend the storage time, the principle of motional averaging was introduced in ref. 40. As opposed to the previous studies, which operated in the regime where atoms remain in the interaction region throughout the experiment, the motional-averaging scheme operates in the complete opposite regime, where atoms rapidly leave. By extending the interaction time so that atoms traverse the interaction region multiple times, however, the average interaction of each atom with the light is the same, enabling coherent interaction with the symmetric collective atomic mode used for storage.
In this work, we use motional averaging to demonstrate a lifetime of 0.27 ± 0.04 ms by observation of a slowly decaying retrieval efficiency as the readout delay is increased. We confirm the non-classicality by observing the violation of the Cauchy–Schwarz inequality for field intensities41. The readout fidelity in our system is limited by the excess noise in the readout process leading to a high probability for detection events which do not originate from conversion of the collective excitation. We identify part of this noise as four-wave mixing (FWM)32,42,43,44. The motional-averaging approach could serve as a solution toward the implementation of scalable quantum memories for applications such as spatially multiplexed quantum networks, or deterministic single-photon sources for quantum information processing45,46,47. To the best of our knowledge, it constitutes the only viable solution to a room-temperature QR without any need for cooling.
Results
Experimental setup
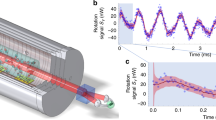
A vapour cell filled with caesium atoms, placed in a homogeneous magnetic field, is the basis for our experiment (Fig. 1a). Paraffin coating of the cell walls preserves the atomic spin coherence upon hundreds of wall collisions. The cell is aligned within a low finesse (\({\cal F} \approx 18\)) asymmetric cell cavity, enhancing light-atom interaction. The light leaving the cell cavity passes through polarization and spectral filtering stages before detection by a single-photon counter (Methods section). We initialize the caesium atoms via optical pumping into \(\left| g \right\rangle \equiv \left| {F = 4,m_{\rm{F}} = 4} \right\rangle\). A far-detuned, weak excitation pulse, linearly polarized perpendicular to the magnetic field, randomly scatters a photon via spontaneous Raman scattering (Fig. 1b). We herald the creation of a long-lived symmetric Dicke state48 in \(\left| s \right\rangle \equiv \left| {F = 4,m_{\rm{F}} = 3} \right\rangle\) upon detection of such a photon scattered into the cell cavity mode. Since the transverse Gaussian profile of the cavity mode is narrower than the cell width, such detection events tend to be associated with asymmetric collective excitations distributed only on the atoms inside the beam at the time of detection. These collective excitations have a very limited lifetime due to atoms moving and leaving the beam. We overcome this by using motional averaging40, extending the duration of the single photon wave packet, thus allowing for the atoms to cross the excitation beam several times. This is achieved by a narrow-band spectral filter, consisting of two optical cavities. The spectral filter adds a random delay to the heralding photon, thus erasing “which path” information and ensuring that a detection event is equally likely to originate from any of the atoms, resulting in a long-lived symmetric collective excitation. The other purpose of the filtering cavities is to separate the excitation light from the scattered photon.
Experimental setup, sequence and level scheme (only main elements are shown). a The caesium vapour cell is aligned with the Gaussian mode of the cell cavity. Optical pumping along the homogeneous magnetic field B prepares the atoms in the \(\left| g \right\rangle\) state. The excitation beam is coupled into the cell cavity. Forward-scattered photons passing through the two filtering cavities are detected with a single-photon detector, while the excitation light is filtered out by the cavities and a Glan–Thompson polarizer. b The write excitation pulse (solid line) acts on the atomic ensemble initially prepared in \(\left| g \right\rangle\) and creates a single-collective excitation in the Zeeman level \(\left| s \right\rangle\). It also couples to the \(\left| {F^\prime = 5,m^{\prime}_{\rm{F}} = 5} \right\rangle\) excited state (dashed line) which has a slight influence on the collective excitation state. c The read excitation pulse converts the collective excitation back into a photon. Simultaneously it acts on the initial state \(\left| g \right\rangle\) (dashed line) creating more excitations, thus leading to spurious four-wave-mixing noise. d The experimental sequence includes up to 55 cycles comprising pump, write and read pulses after each cavity locking period. The delay is defined as the difference between the on (off) times at half maximum for the read (write) pulses
The size of the vapour cell is thus subject to a trade-off between lifetime and motional-averaging time. For a larger cross-section, the atomic coherence time T2 is longer due to the lower rate of wall collisions. On the other hand, to achieve motional averaging, atoms must return to the beam many times. Thus, the time needed for motional averaging increases with the cross-section, introducing technical difficulty as the spectral filter must be even narrower.
After a controllable delay τD, the collective excitation is converted into a readout photon by a second, far-detuned pulse (Fig. 1c). Creating the collective excitation between Zeeman levels allows us to profit from their long coherence times. However, the small Zeeman splitting of νZ = 2.4 MHz presents a challenge for filtering out the excitation light. With our setup we achieve a suppression of the excitation light relative to the desired photon transmission by nine orders of magnitude. The read excitation light is chosen such that the readout photon is similar to the heralding photon in frequency and polarization. Thus only a single filtering and detection setup is required for both heralding and readout.
We start our experimental sequence by locking all cavities and initially optically pumping the atoms (Fig. 1d). The following cycle comprising optical pumping for state re-initialization followed by write and read excitation pulses with controllable delay, is repeated up to 55 times before the sequence restarts, resulting in an average experimental repetition rate of up to 1 kHz.
Spectrum of scattered photons
First, we analyse the spectrum of the scattered photons by varying the resonance frequency of the spectral filter. A weak write excitation pulse with a duration of about 33 μs is sent, and the photons transmitted through the filtering stages are detected (Fig. 2a). The frequency of the scattered photons is blue-detuned by νZ with respect to the write excitation. We observe a narrow-band component associated with the symmetric Dicke state, above a broad background which is due to scattering associated with short-lived asymmetric excitations of the atoms. The width of the narrow peak is determined by the width of the spectral filter. We define the write efficiency to be the ratio of these contributions, which is ηW = (63 ± 1)%. It corresponds to the probability of having created a symmetric Dicke state upon detection of a scattered photon during the write process. The mean number of counts per pulse at zero detuning of 0.014 leads to 0.23 scattered photons per pulse in the cell cavity mode after correction for the detection efficiency and the escape efficiency out of the cell cavity. Counts from leakage of the excitation pulse are completely suppressed by polarization and spectral filtering. Further background counts are negligible during the write pulse.
Detected counts per pulse versus detuning of the filter resonance. Zero detuning is one Zeeman splitting above (below) the write (read) excitation frequency. Each point represents around 1000 experiments with 55 repetitions each. The points on resonance with the write pulse include 60 times as many experiments. a Heralding photon detection. b Unconditional photon detection in the readout, considering only the first 40 μs. Blue crosses show data with write pulse present, magenta circles with write pulse off. The solid (dashed) lines show a fit with (without) write, containing scattered photons (blue, red), contribution from asymmetric excitations (grey), leakage (yellow), and background (unfilled). Error bars are standard error of the mean
A read pulse is sent after the end of the write pulse, with τD = 30 μs and a similar energy. The frequency of the read pulse is blue-detuned by 2 × νZ from the write pulse such that the desired readout photons have the same frequency as the heralding photons. Scanning the filter resonance we observe a narrow peak above a broad background and an extra noise component (Fig. 2b). The narrow peak contains the retrieved photons, while the extra noise is due to the read excitation light leaking through the spectral filter. The leakage rate depends on the filter detuning from excitation light frequency resonance at ΔFC = +νZ. This leads to an asymmetry in the spectrum. Due to linear birefringence caused by detuning-dependent atom–light interaction, and different phase shifts for the write and read excitation pulses arising from the temporal decay of the initial atomic state, the polarization filtering cannot be optimized for write and read excitation light simultaneously. We chose to optimize it for the write process leading to stronger leakage noise for the readout.
When repeating the same experiment without a write excitation pulse, we only detect background counts during the write detection window while we still observe a significant contribution in the number of read detection events. This is partly because the splitting of the two ground states is small compared to the detuning from the excited states, such that the read excitation field couples \(\left| g \right\rangle\) and \(\left| s \right\rangle\) via both the \(\left| {m_{\rm{F}}^\prime = 3} \right\rangle\) (dashed transition in Fig. 1c) and \(\left| {m_{\rm{F}}^\prime = 4} \right\rangle\) excited manifolds with comparable strength. The read excitation thus creates atomic excitations through transitions from \(\left| {m_{\rm{F}} = 4} \right\rangle\) to \(\left| {m_{\rm{F}} = 3} \right\rangle\) and simultaneously reads them out by driving them back. This FWM process leads to short-term non-classical correlations, which, however, cannot be resolved with our setup and are mixed with the long-lived correlations generated by the write pulse. Hence, those otherwise interesting correlations49,50 have to be considered as noise here. When we include the write excitation pulse, we observe an increase in detection events from the readout of the excitation generated in the write step. We observe that this desired readout and the FWM noise are spectrally indistinguishable. Due to the large background only approximately 1 in 5 counts are due to the desired readout of write excitations. When conditioning on the detection of a write photon, however, the ratio increases to approximately half for the first few tens of microseconds (see below for detailed analysis), indicating a strong correlation between read and write processes. As we will now show these correlations are non-classical.
Long-lived non-classical correlations
In order to verify the quantum nature of the scheme we test for a violation of the Cauchy–Schwarz inequality \(R\) = \(( {g_{{\mathrm{wr}}}^{(2)}} )^2{\mathrm{/}}( {g_{{\mathrm{ww}}}^{(2)}g_{{\mathrm{rr}}}^{(2)}} ) < 1\) where subscripts ww, rr refer to normalized second order auto-correlation functions for write and read fields and subscript wr to cross-correlation between the write field and the following read field7. A nice feature of our system is that the single-photon wave packets have a long duration set by the inverse bandwidth of the filter cavity, which is much longer than the detector dead time. This makes it possible to distinguish photon number states with a single detector. The correlation functions are then calculated from the average number of counts according to \(g_{ij}^{(2)}\) = \(\langle {n_i( {n_j - \delta _{ij}} )} \rangle {\mathrm{/}}( {\langle {n_i} \rangle \langle {n_j} \rangle } )\) with i, j ∈ {w, r} and nw (nr) is the number of detector clicks during the write (read) process. δij is the Kronecker delta accounting for the non-commuting annihilation operators appearing in the auto-correlation functions.
In the experiment we send read pulses with a 200 μs duration, and vary the integration time τR for the read detection window. We define the retrieval efficiency as ηR = 〈nr|w〉 − 〈nr〉, the heralded readout probability subtracted by the unconditional readout probability. Figure 2a shows how the trade-off between R and ηR varies with τR.
In the following, we set τR to only 40 μs in order to increase the signal-to-noise ratio. At ΔFC = 0 and for τD = 30 μs, we observe R = 1.4 ± 0.1, confirming the non-classicality of the scheme within four standard deviations. For the same parameters, we measure ηR = (1.55 ± 0.08)%, leading to an intrinsic retrieval efficiency \(\eta _{\mathrm{R}}^{\mathrm{i}}\) = (16.1 ± 0.9)% at the cell cavity output when correcting for the transmission loss and detector quantum efficiency. For a pure two-mode squeezed state, expected in this type of protocols in the absence of noise, theory predicts thermal auto-correlation functions \(( {g_{ii}^{(2)} = 2})\), hence \(g_{{\mathrm{wr}}}^{(2)} > 2\) is required to violate the Cauchy–Schwarz inequality7. We find significantly lower auto-correlation values, \(g_{{\mathrm{ww}}}^{(2)}\) = 1.86 ± 0.07 and \(g_{{\mathrm{rr}}}^{(2)}\) = 1.45 ± 0.05, allowing us to achieve non-classicality with our measured value \(g_{{\mathrm{wr}}}^{(2)}\) = 1.97 ± 0.05. We attribute the reduced auto-correlations to leakage of the read drive pulse and mixing of two independent thermal processes in the write step.
We observe an increased value for the cross-correlation function \(\tilde g_{{\mathrm{wr}}}^{(2)}\) = 2.08 ± 0.07 when using only the last 20 μs of the write pulse. We attribute this to the shorter effective delay between write and readout photons. However, the reduced photon statistics in this case does not allow us to extend this analysis to all of our data.
In Fig. 3b we show the decay of the retrieval efficiency as the write–read delay τD increases. From an exponential fit we extract a memory lifetime of τ = 0.27 ± 0.04 ms, which by far exceeds previously reported memory times at the single-photon level for room-temperature atomic vapour memories36,37. The collective excitation lifetime is expected to be half of the transverse macroscopic spin amplitude decay time, separately measured to be T2 = 0.8 ms (Methods section) and to be governed by spin relaxation due to wall collisions.
Temporal dynamics of the readout. a Cauchy–Schwarz parameter (blue asterisks, left axis) and retrieval efficiency (red circles, right axis) versus read detection integration time for τD = 30 μs. We observe violation of the Cauchy–Schwarz inequality for τR < 140 μs while the retrieval efficiency increases throughout the read pulse. To limit the influence of noise we choose τR = 40 μs for our correlation analysis. b Retrieval efficiency versus write–read delay, for τR = 40 μs. An exponential fit (line) yields a 1/e collective excitation lifetime of τ = 0.27 ± 0.04 ms. We observe non-classical correlations for τD < 80 μs (see Supplementary Note 1). The plotted values in the two graphs originate from different data sets hence the points at τD = 30 μs and τR = 40 μs are not identical. The top graph data set corresponds to ΔFC = 0 in Fig. 2. Error bars for ηR are standard deviation and error bars for R represent statistical uncertainty for the correlations (Methods section)
It should be duly noted that our implementation does not represent a single-photon source due to the excessive photon counts from FWM during the read pulse. When conditioning on detected heralding we observe a readout auto-correlation \(g_{{\mathrm{rr}}|{\mathrm{w}}}^{(2)}\) = 1.3 ± 0.2.
Temporal shape of the readout photons
To determine the nature and weight of the undesirable components limiting the fidelity of the readout photons, we fit their temporal shape using a model adapted from ref. 51. According to the model, the detected readout photons have two contributions: a desired part from the readout of the atomic excitations created during the write process, and the unwanted result of the FWM process depicted in Fig. 1c, present even in the absence of the write step. The photons scattered from \(\left| {F^\prime ,m_{\rm{F}}^\prime = 3} \right\rangle\) to \(\left| s \right\rangle\) are not resonant with the filtering cavities and are thus not detected. The photons scattered on the \(\left| {F^\prime ,m_{\rm{F}}^\prime = 4} \right\rangle\) to \(\left| g \right\rangle\) transition, however, are indistinguishable from the desired read photons and lead to spurious detection events spoiling the fidelity of the readout. The model includes a noise offset comprising a constant term accounting for background and dark counts, and a power-dependent and time-dependent term accounting for contamination from the drive leaking through the polarization and spectral filtering stages (see Supplementary Methods).
The temporal shape of the detected readout photons is shown in Fig. 4, together with the model. Figure 4a represents the unconditional detection events, while Fig. 4b represents the heralded detection events conditioned on one or more write detection events, for the same data set. The values are normalized by the duration of the time bins, and by the total number of pulses in Fig. 4a and by the number of trials with one or more write detection events in Fig. 4b. The total number of trials is 3,248,135, and the total number of heralding events is 45,774. In both graphs, we use common parameters except for the mean number of collective excitations created during the write step, which we estimate from the number of write detection events and the total detection efficiency. We note that the model agrees well with the data if we add a constant term (blue line). The origin of this spectrally narrow contribution C is not fully understood. Its relative fraction compared to the broadband noise contribution B is similar to the fraction during the write process with ηW ≈ C/(B + C). This suggests a common origin of the narrow-band and broadband noise during the read and could be explained by scattering from atoms residing in Zeeman states other than mF = 4. However, for the state initialization we achieve, we would expect a contribution which is about a quarter of what is observed, suggesting that modifications to the FWM model are needed. See Supplementary Methods for a detailed description of the model.
Temporal shape of the detected readout photons. a Unconditional detection events. b Heralded detection events. The red bar graphs represent the detection events after a preceding write pulse with a 5 μs (a), and 10 μs (b) binning. The black-framed bar graphs show the detection events without preceding write pulse in 10 μs binning. In both plots the leakage (yellow) and broad (grey) contributions have been extrapolated from fits to the spectrum obtained for segments of the detection window. The blue line represents an added constant offset. The green and cyan lines are the model predictions for readout and four-wave mixing noise contribution, respectively. The data presented correspond to the point at zero detuning in Fig. 2. The origin of the horizontal axes is defined from the beginning of the detection window
Discussion
We have realized an efficient heralded light source based on an atomic ensemble at room temperature, demonstrating a long single-collective excitations lifetime of 0.27 ± 0.04 ms and a generation efficiency of (63 ± 1)%. This lifetime could be extended significantly by employing a cell displaying a longer T2 time. We have demonstrated non-classicality of the light–matter correlations by observing a violation of the Cauchy–Schwarz inequality with four standard deviations. Even though the utility of those results is so far limited by excess noise from the leakage of the excitation light, FWM and other noise sources, we highlight that there are possible routes to suppress FWM by modifying the excitation scheme as suggested in the following. The FWM contribution can be greatly reduced by using hyperfine instead of Zeeman storage, or suppressed by elaborate cavity design29,52. Alternatively, the FWM can be eliminated in our setup by exciting the ensemble with circularly polarized light propagating along the magnetic field and storing the collective excitation in \(\left| {F = 4,m_{\rm{F}} = 2} \right\rangle\). The suppression of this two-photon transition for large detunings43 can be mitigated by using the caesium D1 line and an appropriate choice of detuning on the order of the excited state hyperfine splitting. For the unexplained noise source, further investigation is required to determine to what extent it can be reduced. Further reduction of the remaining leakage will be possible by adding another filter cavity or by narrowing the filtering bandwidth. This narrowing will at the same time further improve the write efficiency. Finally, an active control of the polarization of the light at the cavity output could allow us to maximize the extinction of the polarization filter at all times. Even in the absence of the noise suppression, our work demonstrates that long-lived collective excitations can be efficiently heralded and retrieved. With such improvements, our system could form the basis for scalable room-temperature quantum repeaters.
Methods
Light
We use a home-built external cavity diode laser at 852 nm that is locked to and narrowed in linewidth (≤10 kHz) by optical feedback from a triangular locking cavity. A slow feedback (<Hz) from a beatnote measurement of this excitation laser with a reference laser stabilized by atomic spectroscopy keeps the locking cavity resonance at a fixed detuning of 925 MHz from the 4–5′ transition of the D2 line of caesium. We send the excitation laser light through an acousto-optic modulator to pulse the light and choose the individual frequencies of the write and read pulses.
Vapour cell
The caesium vapour cell has a square cross-section of 300×300 μm and a length of 10 mm. It is coated with a spin-preserving anti-relaxation layer of paraffin (alkane). It is aligned along the optical axis of a low finesse (\({\cal F} \approx 18\)) cavity to enhance the light interaction. The losses of this “cell cavity” are dominated by the output coupler transmission. The vapour cell is inserted in a magnetic shield with internal coils that produce a homogeneous magnetic field perpendicular to the optical axis. We work at a Zeeman splitting frequency of νZ ≈ 2.4 MHz where the dissipated power in the coils heats up the vapour cell to around 43 °C. Under these conditions we identify a coherence time of the ground state Zeeman levels of T2 ≈ 0.8 ms, by performing a magneto-optical resonance spectroscopy measurement53.
Cavity stabilization
To stabilize the cell cavity length we input frequency-modulated light from the reference laser and derive an error signal from the transmitted signal. The error signal for the filter cavities are acquired from the transmission of frequency-modulated light from the excitation laser in the counter-propagating direction. The length of each cavity is then stabilized by a feedback acting on the respective piezo-actuated mirror mount. The lock light for the filter cavities is blocked by a chopper during the optical pumping and experiment periods.
Pumping
The atoms are initialized by circularly polarized pump and repump elliptical beams aligned along the magnetic field direction. The repump laser is locked on the F = 3 to F′ = 2, 3 crossover of the D2 line, the pump laser is locked on the F = 4 to F′ = 4 transition of the D1 line. We typically observe an atomic orientation of >98.5%.
Filtering
We compensate for birefringence with a quarter wave plate and a half wave plate after the cell cavity and achieve a polarization filtering on the order of 10−4 with a Glan–Thompson polarizer. Spectral filtering is achieved by two concatenated triangular cavities. The first filter cavity is a narrow bandwidth cavity with a full width at half maximum (FWHM) of 66 kHz with an on resonance transmission of 66%. The second filter cavity has an on resonance transmission of 90% and a FWHM of 900 kHz. Both cavities together yield a spectral filtering of 7 × 10−6 at a detuning of 2.4 MHz. The cavities do not only provide filtering but also enable the motional averaging40. They erase the 'which-atom' information by introducing a random delay due to the cavity photon lifetime.
Detection efficiency
We measure the detection efficiency of the setup by sending a well-calibrated attenuated light pulse with the same polarization and frequency as the scattered photons through the system, and calculating the ratio of the count-rate versus the input rate obtained from the known power. We obtain a mean value of about 9.6% from the output of the cell cavity onto the single-photon detector (model COUNT-10C from LASER COMPONENTS), including the detector's quantum efficiency.
Cell cavity escape efficiency
We estimate the escape efficiency through the output coupler of the cell cavity from the transmission of this coupler (~20%) and the losses obtained from the finesse measurement. The obtained value is ~62%.
Uncertainty estimation
To estimate the uncertainty of correlation functions we implement a bootstrapping technique. For a set of write and read pulses we obtain a distribution of the number of write and read counts in each write–read sequence. We then draw samples of the same size as the data set from a probability distribution given by the data set. For each sample we calculate the value of the correlation functions and as the number of samples increases, the variances of these bootstrap correlations converges. We find that the bootstrap correlations are close to normally distributed and the uncertainty estimates are given by the square root of the convergence values for the variances.
Data availability
The data sets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Nunn, J. et al. Enhancing multiphoton rates with quantum memories. Phys. Rev. Lett. 110, 133601 (2013).
Sangouard, N., Simon, C., de Riedmatten, H. & Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80 (2011).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Duan, L. M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Kuzmich, A. et al. Generation of nonclassical photon pairs for scalable quantum communication with atomic ensembles. Nature 423, 731–734 (2003).
van der Wal, C. H. et al. Atomic memory for correlated photon states. Science 301, 196–200 (2003).
Bao, X.-H. et al. Efficient and long-lived quantum memory with cold atoms inside a ring cavity. Nat. Phys. 8, 517–521 (2012).
Bimbard, E. et al. Homodyne tomography of a single photon retrieved on demand from a cavity-enhanced cold atom memory. Phys. Rev. Lett. 112, 033601 (2014).
Chen, S. et al. Deterministic and storable single-photon source based on a quantum memory. Phys. Rev. Lett. 97, 173004 (2006).
Choi, K. S., Goban, a, Papp, S. B., van Enk, S. J. & Kimble, H. J. Entanglement of spin waves among four quantum memories. Nature 468, 412–416 (2010).
Farrera, P. et al. Generation of single photons with highly tunable wave shape from a cold atomic ensemble. Nat. Commun. 7, 13556 (2016).
Inoue, R., Yonehara, T., Miyamoto, Y., Koashi, M. & Kozuma, M. Measuring qutrit-qutrit entanglement of orbital angular momentum states of an atomic ensemble and a photon. Phys. Rev. Lett. 103, 110503 (2009).
Jiang, Y., Rui, J., Bao, X. H. & Pan, J. W. Dynamical zeroing of spin-wave momentum to suppress motional dephasing in an atomic-ensemble quantum memory. Phys. Rev. A. 93, 063819 (2016).
Laurat, J. et al. Efficient retrieval of a single excitation stored in an atomic ensemble. Opt. Exp. 14, 6912–6918 (2006).
Radnaev, A. G. et al. A quantum memory with telecom-wavelength conversion. Nat. Phys. 6, 894–899 (2010).
Simon, J., Tanji, H., Thompson, J. K. & Vuletić, V. Interfacing collective atomic excitations and single photons. Phys. Rev. Lett. 98, 183601 (2007).
Yang, S.-J., Wang, X.-J., Bao, X.-H. & Pan, J.-W. An efficient quantum light-matter interface with sub-second lifetime. Nat. Photon. 10, 381–384 (2016).
Zhao, R. et al. Long-lived quantum memory. Nat. Phys. 5, 100–104 (2008).
Sinclair, N. et al. Spectral multiplexing for scalable quantum photonics using an atomic frequency comb quantum memory and feed-forward control. Phys. Rev. Lett. 113, 053603 (2014).
Zhong, M. et al. Optically addressable nuclear spins in a solid with a six-hour coherence time. Nature 517, 177–180 (2015).
Kutluer, K., Mazzera, M. & de Riedmatten, H. Solid-state source of nonclassical photon pairs with embedded multimode quantum memory. Phys. Rev. Lett. 118, 210502 (2017).
Laplane, C., Jobez, P., Etesse, J., Gisin, N. & Afzelius, M. Multimode and long-lived quantum correlations between photons and spins in a crystal. Phys. Rev. Lett. 118, 210501 (2017).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
Balabas, M. V., Karaulanov, T., Ledbetter, M. P. & Budker, D. Polarized alkali-metal vapor with minute-long transverse spin-relaxation time. Phys. Rev. Lett. 105, 070801 (2010).
Ghobadi, R., Wein, S., Kaviani, H., Barclay, P. & Simon, C. Towards a room-temperature spin-photon interface based on nitrogen-vacancy centers and optomechanics. Preprint at http://arxiv.org/abs/1711.02027 (2017).
Hosseini, M., Campbell, G., Sparkes, B. M., Lam, P. K. & Buchler, B. C. Unconditional room-temperature quantum memory. Nat. Phys. 7, 794–798 (2011).
Saunders, D. J. et al. Cavity-enhanced room-temperature broadband Raman memory. Phys. Rev. Lett. 116, 090501 (2016).
Höckel, D. & Benson, O. Electromagnetically induced transparency in cesium vapor with probe pulses on the single-photon level. Phys. Rev. Lett. 105, 153605 (2010).
Ma, L., Slattery, O., Kuo, P. & Tang, X. EIT quantum memory with Cs atomic vapor for quantum communication. Proc. SPIE 9615, 96150D (2015).
Phillips, N. B., Gorshkov, A. V. & Novikova, I. Optimal light storage in atomic vapor. Phys. Rev. A. 78, 023801 (2008).
Namazi, M., Kupchak, C., Jordaan, B., Shahrokhshahi, R. & Figueroa, E. Ultralow-noise room-temperature quantum memory for polarization qubits. Phys. Rev. Appl. 8, 034023 (2017).
Eisaman, M. D. et al. Electromagnetically induced transparency with tunable single-photon pulses. Nature 438, 837–841 (2005).
Manz, S., Fernholz, T., Schmiedmayer, J. & Pan, J.-W. Collisional decoherence during writing and reading quantum states. Phys. Rev. A. 75, 040101 (2007).
Bashkansky, M., Fatemi, F. K. & Vurgaftman, I. Quantum memory in warm rubidium vapor with buffer gas. Opt. Lett. 37, 142–144 (2012).
Dou, J.-P. et al. A broadband DLCZ quantum memory in room-temperature atoms. Comms. Phys. 1, 55 (2018).
Hammerer, K., Sørensen, A. S. & Polzik, E. S. Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 82, 1041–1093 (2010).
Katz, O. & Firstenberg, O. Light storage for one second in room-temperature alkali vapor. Nat. Commun. 9, 2074 (2018).
Borregaard, J. et al. Scalable photonic network architecture based on motional averaging in room temperature gas. Nat. Commun. 7, 11356 (2016).
Clauser, J. F. Experimental distinction between the quantum and classical field-theoretic predictions for the photoelectric effect. Phys. Rev. D. 9, 853–860 (1974).
Lauk, N., O'Brien, C. & Fleischhauer, M. Fidelity of photon propagation in electromagnetically induced transparency in the presence of four-wave mixing. Phys. Rev. A. 88, 013823 (2013).
Vurgaftman, I. & Bashkansky, M. Suppressing four-wave mixing in warm-atomic-vapor quantum memory. Phys. Rev. A. 87, 063836 (2013).
Michelberger, P. S. et al. Interfacing GHz-bandwidth heralded single photons with a warm vapour Raman memory. New J. Phys. 17, 043006 (2015).
Aspuru-Guzik, A. & Walther, P. Photonic quantum simulators. Nat. Phys. 8, 285–291 (2012).
Aaronson, S. & Arkhipov, A. In Proc. 43rd Annual ACM Symposium on Theory of Computing - STOC '11. 333–342 (ACM Press, New York, NY, 2011).
Tillmann, M. et al. Experimental boson sampling. Nat. Photon. 7, 540–544 (2013).
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954).
Podhora, L., Obšil, P., Straka, I., Ježek, M. & Slodička, L. Nonclassical photon pairs from warm atomic vapor using a single driving laser. Opt. Exp. 25, 31230 (2017).
Zhu, L., Guo, X., Shu, C., Jeong, H. & Du, S. Bright narrowband biphoton generation from a hot rubidium atomic vapor cell. Appl. Phys. Lett. 110, 161101 (2017).
Dabrowski, M., Chrapkiewicz, R. & Wasilewski, W. Hamiltonian design in readout from room-temperature Raman atomic memory. Opt. Exp. 22, 26076 (2014).
Nunn, J. et al. Theory of noise suppression in Λ-type quantum memories by means of a cavity. Phys. Rev. A. 96, 012338 (2017).
Julsgaard, B., Sherson, J., Sørensen, J. L. & Polzik, E. S. Characterizing the spin state of an atomic ensemble using the magneto-optical resonance method. J. Opt. B 6, 5–14 (2004).
Acknowledgements
We would like to thank M. Balabas for fabricating the cell used for this experiment. We would also like to thank J. Borregaard for helpful discussions, and acknowledge J. Appel and G. Vasilakis for their contributions at the early stages of the project. Funding has been provided by the ERC AdG Interface, ERC AdG Quantum-N, ERC consolidator QIOS, ARO grant W911NF and by John Templeton Foundation.
Author information
Authors and Affiliations
Contributions
M.Z., K.B.D. and B.A. have contributed equally to the work, setting up and performing the experiment, analysing the data and writing the paper. A.S.S. and E.S.P. conceived the project. E.S.P. supervised the project. All authors contributed in the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zugenmaier, M., Dideriksen, K.B., Sørensen, A.S. et al. Long-lived non-classical correlations towards quantum communication at room temperature. Commun Phys 1, 76 (2018). https://doi.org/10.1038/s42005-018-0080-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0080-x
This article is cited by
-
Entangling motional atoms and an optical loop at ambient condition
npj Quantum Information (2023)
-
Single-mode quantum non-Gaussian light from warm atoms
npj Quantum Information (2022)
-
Enhancing photon generation rate with broadband room-temperature quantum memory
Scientific Reports (2022)
-
Lifetime reductions and read-out oscillations due to imperfect initial level preparations of atoms in a long-lived DLCZ-like quantum memory
Applied Physics B (2022)
-
Multipartite entanglement of billions of motional atoms heralded by single photon
npj Quantum Information (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.