Machine learning inverse problem for topological photonics

Abstract

Topology opens many new horizons for photonics, from integrated optics to lasers. The complexity of large-scale devices asks for an effective solution of the inverse problem: how best to engineer the topology for a specific application? We introduce a machine-learning approach applicable in general to numerous topological problems. As a toy model, we train a neural network with the Aubry–Andre–Harper band structure model and then adopt the network for solving the inverse problem. Our application is able to identify the parameters of a complex topological insulator in order to obtain protected edge states at target frequencies. One challenging aspect is handling the multivalued branches of the direct problem and discarding unphysical solutions. We overcome this problem by adopting a self-consistent method to only select physically relevant solutions. We demonstrate our technique in a realistic design and by resorting to the widely available open-source TensorFlow library.

Introduction

The rapidly growing interest in topological photonics^1,2 is leading to the design of complex structures for many applications of optical topological insulators³. One leading goal of topological photonics is photon transport protected from unwanted random scattering. This is achieved by realizing analogs of the quantum Hall effect^4,5,6 through magnetic-like Hamiltonians in photonic systems⁷. In the optical domain, topological insulators⁸ have been implemented in modulated honeycomb lattices⁷, in arrays of coupled optical-ring resonators⁹, and optical quantum walks¹⁰. Geometry-independent topological structures have been proposed to obtain nonreciprocal single mode lasing^11,12,13,14 as well as systems with balanced gain and loss for parity-time symmetric structures with topological order^15,16. Emulations of four-dimensional (4D) physics have also been reported^17,18. By using one-dimensional (1D) Harper modulations, it is possible to simulate two-dimensional (2D) topological systems. Similarly, by 2D topological systems, one can simulate 4D ones, as recently investigated in refs.^17,18.

One challenge in this field is to find an effective methodology for the inverse problem in which the target optical properties result from topological characteristics. Although various computational techniques are available, these require specific implementations tailored to the task at hand. Machine learning (ML)^19,20,21 has recently been proposed as an encompassing technology for dealing with greatly differing problems through a unified approach. ML techniques have shown a remarkable growth in sophistication and application scope in multiple fields^22,23,24; ML offers exciting perspectives in topological photonics. ML is applied in two main classes of problems: (i) classification for categorizing information and (ii) regression to predict continuous values, both typically performed by supervised training. Unlike parametric regression—in which a best fit of the data is determined on the basis of a specific function—ML regression employs a neural network (NN) emulating the behavior of the data on which it has been trained: “the NN learns the model”.

In this paper, we employ ML regression for solving the inverse problem in topological photonics. We apply advanced ML techniques to design photonic topological insulators enabling innovative applications through custom tailoring of desired optical parameters. In our approach, we introduce a twist in order to ensure that only physically possible solutions are found. This twist is based on a self-consistent cycle in which a tentative solution obtained from the inverse problem NN is run through the direct problem NN in order to ensure that the solution obtained is indeed viable. This has the added benefit of checking that multivalued degeneracy has been effectively removed.

Results

We consider one of the simplest structures that support nontrivial topological properties. In 1D systems, synthetic magnetic fields occur by lattice modulation²⁵ of the optical structure. In the Aubry–Andre–Harper (AAH) model^26,27, identical sites—resonators, two-level atoms, waveguides, etc.—are centered at positions $z_n = d_{\rm o}\left( {n + \eta \delta _n^H} \right)$, with n an integer label, d_o the primary lattice period, η the modulation strength, and $\delta _n^H = {\mathrm{cos}}\left( {2\pi \beta n + \phi } \right)$ the Harper modulation²⁷. The parameter β is the frequency of the Harper modulation. Together, β and the phase shift ϕ furnish the topological properties by a “2D ancestor” mapping²⁸. The 2D ancestor is characterized by the dependence of the dielectric function on the coordinate z and on the parameter ϕ, which acts as a periodic artificial coordinate. Hence, the phase ϕ can be treated as a wave vector in a fictitious auxiliary direction²⁸. For β = p/q with p > 0 and q > 0 integers, the lattice displays two commensurate periods with q sites z_n in the unit-cell. Properly chosen parameters give rise to nontrivial topological phases with protected states at the border of the structure. These “edge-states” are hallmarks of topological insulators. The phase ϕ tunes edge-state eigenfrequency in the photonic band-gaps.

Our photonic topological insulator is an array of layers A of normalized thickness ξ = L_A/d_o, centered in z_n, in an homogeneous bulk of material B. This kind of structure can be effectively modeled by the transfer matrix technique^16,29, as reported in Fig. 1a. In this figure A₀ and A_n are the initial and final amplitudes of the right-traveling waves; while B₀ and B_n are their equivalent for the left-traveling wave amplitudes. As detailed in Methods, we obtain the transfer matrix for the single period T⁽¹⁾(ω, ϕ, ξ) with elements $T_{11}^{(1)}$, $T_{12}^{(1)}$, $T_{21}^{(1)}$, and $T_{22}^{(1)}$. Figure 1a shows the final wave amplitudes A_n, B_n by the n-fold repeated action of T⁽¹⁾(ω, ϕ, ξ) on A₀, B₀. The dielectric constant profile - for the case β = 1/3 is schematically illustrated in Fig. 1b.

Fig. 1

Multilayer system with Harper modulation. a Scheme of the topological optical structure. b Dielectric function profile for an Aubry–Andre–Harper (AAH) chain with β = 1/3, with s_i = [z_i+1 − z_i − L_A]/d_o. c Band diagram with χ = ϕ + π(2β − 1)/2. For |χ/π| > 1, one can identify the gaps of the unmodulated structure (blue regions). The range |χ/π| < 1 shows the gaps with Harper modulation: each gap of the unmodulated structures (|χ/π| > 1) splits into q bands. d Orange and green regions correspond to gaps. White areas indicate the regions where Q(ω, χ, ξ) > 0, blue the regions where Q(ω,χ,ξ) < 0. Edge states are possible only in the regions with crosses in orange and green gaps

For η = 0, we have a periodical unmodulated structure with frequency bandgaps labeled by an integer i. For η ≠ 0, each gap of the unmodulated structure splits into q gaps, each one labeled by indices (i, j) (j = 1, …, q)³⁰. This splitting is shown in Fig. 1c for β = 1/3 with respect to the variable χ = ϕ + π(2β − 1)/2.

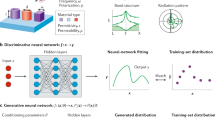
As detailed in Methods and illustrated in Fig. 1d, enforcing boundary conditions at the left edge^31,32 and defining the function Q(ω, ϕ, ξ) enables one to establish the presence of edge states corresponding to poles ω_t of the reflection coefficient. However, the function ω_t = ω(χ, ξ) cannot be analytically inverted to express the geometrical parameters χ and ξ in terms of the variable ω_t. Exploiting ML techniques, we solve this inverse problem and design topological insulators with target edge modes. The inverse problem in artificial NN theory—and therefore in ML—is widely discussed in numerical modeling, engineering, and other fields^{33,34,35,36,37}. Regression in ML optimizes an NN so that a given vector input (${\Bbb R}^n$) will result in a scalar (${\Bbb R}$) output, emulating the behavior of the training data. A regressive NN is a configuration of computational layers such that a specific set of input nodes $\underline I$ is connected to a single output node, through a configurable set of N_h hidden layers each containing n_i nodes h_ij, where i = 1, …. N_h and j = 1, …. n_i. Examples of such regressive NNs are shown in Fig. 2a, b. A generic node k + 1, j, shown in Fig. 2c, receiving as inputs h_ki, with i = 1, …. n_k, yields on output $h_{k \,+\, 1j} = g\left( {\mathop {\sum}\nolimits_l {\kern 1pt} w_{k \,+ \, 1jkl}h_{kl} + b_{k \,+\, 1j}} \right)$, with g(x) being a nonlinear activation function, w_{k + 1jkl} the weight of h_kl on h_k+1j with a bias term b_{k + 1j}. Following accepted practice, our activation function is g(x) = tanh(x).

Fig. 2

Architecture of fully connected feed-forward neural networks. Orange and green circles are the input and output units, respectively. Blue ones represent the nodes of the hidden layers. Interconnections among the units are given by arrows. The networks in the background are specific to the unfolded problem; in the foreground, we show the networks with extra mode and trend inputs. a Inverse problem network. b Direct problem network. c Single unit scheme. The node performs a linear combination of its inputs followed by a nonlinear activation function

Optimization of the NN is performed by minimizing a cost function by a gradient descent method that updates weights and biases. In the initial state, weights w_ijkl are selected from a truncated normal and biases are set to zero. Training applies this procedure to a dataset randomly split into two separate classes: (i) an actual training set and (ii) a validation set. The network is iteratively updated until the error on the validating dataset converges to a given rate.

The inverse topological problem at hand is to obtain the desired optical behavior: a target edge-state at frequency ω_t, which is an input to the design (Fig. 2a). ML techniques achieve this result by modeling the multidimensional nonlinear relationships among all the structure parameters ω_t, χ, β, $\epsilon _{\rm A}$, $\epsilon _{\rm B}$, and ξ. In our specific case, the dataset fixes $\epsilon _{\rm A}$, $\epsilon _{\rm B}$, β at the values $\epsilon _{\rm A} = 9$, $\epsilon _{\rm B} = 4$ and β = 1/3.

First, we generate a dataset to train our NNs by numerically computing the complex roots of $T_{12}^{(1)}(\omega ,\chi ,\xi )$ covering the region of interest for parameters χ and ξ. The real part of these roots, shown in Fig. 3a, represents the edge states dispersion. Interestingly the same dataset can be used both for the inverse and direct NN training phase, by suitably selecting the features and target fields. The inverse problem NN (Fig. 2a) targets a value χ = χ_o, a topological parameter on the basis of features including ω_t. For a direct problem (Fig. 2b), the mode frequency ω_t would be the target of a network whose features include the topological parameters (χ, ξ).

Fig. 3

Edge modes dispersion. a The training dataset. Points are the real component (mode frequencies) of the complex roots of the function $T_{12}^{(1)}(\omega ,\chi ,\xi )$. b Edge state dispersion for a specific mode and ξ value, exhibiting a positive s₊ (green) and negative s₋ (red) trend. c Multivalued relationship of features and targets for the same edge mode dispersion. The s_± labels are used for training the inverse model

The dataset contains various branches since there exist an edge state for each band gap (i, j) with j ≠ 3, as results by Eq. (2) in Methods. Due to the folding of the Brillouin zones, the edge state frequency ω(χ, ξ) is then a multi-mode function, which we unfold by introducing a label $m_{ij}^ \pm$ for each mode; here i = 1, …∞ and j = 1, …q, while the sign ± indicates modes in the positive/negative χ domain. In Fig. 3a, data points with different ij values are identified with different colors, and solving the inverse problem is a matter of determining when these surfaces intercept a specific target value of the ω axis. Three outcomes are possible: a single value for χ and ξ when a monotonic mode surface is intercepted, no solution for values of ω laying between surfaces, and multiple solutions in other cases. This implies that the feature set (χ, ξ, $m_{ij}^ \pm$) is insufficient. To tackle this problem, we take into account the trend s_± = sgn(dω_t/dχ) as an additional variable. The NNs with this enlarged feature set are illustrated in Fig. 2a, b.

In the terminology used in ML, the mode index $m_{ij}^ \pm$ and trend s_± labels are "categorical features'' and lead to two possible courses of action for the actual implementation of the NNs used in our problem. One in which a single NN is constructed in a hybrid feature space with both continuous variables (real valued ξ's and χ's) and categorical features, as illustrated in Fig. 2b. Another course is to adopt multiple independent NNs, one NN for each mode and each trend.

The single NN approach is hindered by the presence of discontinuities in the features domain: with respect to the ω variable they are a consequence of the fact that edge states fall within the bulk energy gaps; with respect to the χ variable these arise from considering only the left-edge states. Figure 3a clarifies this aspect. Due to these discontinuities, we have chosen to use multiple independent NNs.

Moreover, when considering the solution provided by the inverse NNs, we identify a specific problem in the use of ML as they may furnish solutions that are not physical. An example of this issue is given in Fig. 3b where—for a fixed band and a fixed ξ—the curve representing ω as a function of χ is shown together with its inverse (Fig. 3c). Inverting the function ω(χ), we consider an interval of values for ω spanning from its minimum ω_min to the maximum ω_max, but for the two branches of the inverse function χ(ω)—identified by colors in Fig. 3c—the range of ω is different. For example, for the red branch, the maximal value of ω is ${\omega{\prime}} _{{\rm max}} < \omega _{{\rm max}}$. When the target frequency is outside of this range, the NN produces an output outside of the physically acceptable range for χ (see details in Supplementary Information: Supplementary Figs. 1–3). The inverse NN can furnish spurious nonphysical solutions.

Our approach tackles this issue by a two-step self-consistent cycle, detailed in the Supplementary Information (Supplementary Fig. 4): (i) in the first stage, a desired input ω_t forms part of the feature set $\left( {\omega _t,m_{ij}^ \pm ,s_ \pm } \right)$ resulting in the output χ_o of the inverse NN; this set is used as input $\left( {\chi _{\rm o},m_{ij}^ \pm ,s_ \pm } \right)$ to a direct problem network; (ii) in the second stage, the target of this direct network ω_sc is compared with the input value ω_t and χ_o is retained as a solution of the inverse model if $\left| {\omega _{sc} - \omega _t} \right| < \delta$ with δ a user-defined small positive quantity. The value of δ affects the model accuracy (see Supplementary Fig. 5 and related comments). A reasonable choice can be $\delta \sim E_j^{{\rm max}}$ (with j = I,D), i.e., the maximum value of the squared error functions for the inverse (I) and the direct (D) networks.

The training dataset was generated with 11 sets of ξ ranging from 0.10 to 0.20 in steps of 0.01 and for each set χ spans −π to π with 997 equally spaced values. Results based on using an array of NNs each composed of 5 hidden layer of 131 nodes are shown in Fig. 4 together with its training set (colored lines). The model was developed using 80% of the dataset randomly chosen, the rest being used for validation and comprising of 250,000 steps. Training each model takes about 8 min on our hardware using a single Nvidia GP-GPU Tesla K20c. The purple dots in Fig. 4 are based on 100 values of ξ while exploring the ω domain with a resolution of 10⁻⁵. Each array element is trained for a specific value of the categorical features and pertains to either the positive or the negative χ domain.

Fig. 4

Reconstruction of edge states dispersion by neural network (NN) models. a Direct problem solution as reproduce by our self-consistent cycle. b Inverse problem solution (see also Supplementary Information: Supplementary Fig. 6); ω is in units of d₀/c

The results of applying the direct and inverse NNs, portrayed in Fig. 4a, b, respectively, show that the proposed method gives accurate solutions matching the original data in the whole range of interest. Figure 4 clearly shows that our ML strategy solves the inverse topological design problem.

Discussion

The inverse problem in topological design is solved by a supervised ML regression technique. We employ a self-consistent procedure to rule out unphysical solutions enabling tailored engineering of protected edge-states. We successfully tackle multivalued functions introducing categorical features, as the trend, which tags training data according to their gradient’s sign. Discontinuous domains are effectively treated by adopting multiple independent NNs each one specific to its domain. Our general method can be extensively applied—well beyond the example considered in this work—and may also be exploited for other physical systems in topological science, as polaritonics^38,39, quantum technologies and ultra-cold atoms^40,41. The method is scalable to very complex structures involving hundreds of topological devices, as those recently considered for large scale synchronization⁴², and frequency comb generation⁴³, eventually including non-Hermitian systems^44,45. Further applications include 2D and 3D topological systems¹¹ and quantum sources and simulations^17,18.

Methods

TensorFlow

Tensorflow is Google’s versatile open-source multiplatform dataflow library capable of efficiently performing ML tasks such as implementing NNs (https://tensorflow.org). Multidimensional data arrays, referred to as “tensors” are executed on the basis of stateful dataflow graphs, hence the name TensorFlow. For our final code implementation, Tensorflow version 1.3 with python API bindings was used.

The nature of our problem is such that there is a discontinuity in ξ = 0 which cannot be correctly handled by a single NN bridging this point; this is relevant to both the inverse and direct cases. Breaking up the dataset into two parts to be used for two separate NNs is the simplest solution to this problem.

Another interesting aspect is related to the fact that the feature set in our inverse and direct NNs contain both continuous and discrete variables. The discrete variables can either be treated as such or handled by constructing multiple NNs each relative to a specific value of the discrete variable. The trend variable which has two possible values is one such case as is the mode number. In our code, we have implemented a flexible system which allows one to decide which discrete variables are to be included in each NN, the others being broken up into arrays of NNs one for each value of the variable. Once the bookkeeping issues have been tackled, this generalized approach allows one to tailor the problem to the given dataset.

Transfer matrix

Given the stepped and periodic dielectric function of period D = qd_o:

$$\varepsilon _\phi (z) = \left\{ {\begin{array}{*{20}{l}} {\varepsilon _{\rm A}\quad z_n - L_{\rm A}{\mathrm{/}}2 \le z \le z_n + L_{\rm A}{\mathrm{/}}2} \hfill \\ {\varepsilon _{\rm B}\quad z_n + L_{\rm A}{\mathrm{/}}2 \le z \le z_{n + 1} - L_{\rm A}{\mathrm{/}}2} \hfill \end{array}} \right.;$$

in each layer, the electric field can be represented as the superposition of a left- and a right-traveling wave. Applying the boundary conditions, the matrices

$$M_{\alpha \gamma } = \frac{{q_\gamma + q_\alpha }}{{2q_\gamma }}\left( {\begin{array}{*{20}{c}} 1 & {r_{\alpha \gamma }} \\ {r_{\alpha \gamma }} & 1 \end{array}} \right)$$

with α, γ = A or B and $r_{\alpha \gamma } = {\textstyle{{q_\gamma - q_\alpha } \over {q_\gamma + q_\alpha }}}$, describe the light propagation through the interfaces, having introduced $q_\alpha = (\omega {\mathrm{/}}c)\sqrt {\epsilon _\alpha }$, while the propagation within each layer A and B is given by:

$$\begin{array}{l}T_{\rm A} = \left( {\begin{array}{*{20}{c}} {{\rm e}^{iq_{\rm A}d_o\xi }} & 0 \\ 0 & {{\rm e}^{ - iq_{\rm A}d_o\xi }} \end{array}} \right),\\ T_{{\rm B}_n} = \left( {\begin{array}{*{20}{c}} {{\rm e}^{iq_{\rm B}d_os_n}} & 0 \\ 0 & {{\rm e}^{ - iq_{\rm B}d_os_n}} \end{array}} \right)\end{array},$$

where s_n = [z_n+1 − z_n − L_A]/d_o are the normalized thicknesses of the B layers.

From these, we obtain the transfer matrix for the single period T⁽¹⁾(ω), the matrix connecting the fields in the left side of the elementary cell to the ones in the right side:

$$T^{(1)} = \mathop {\prod}\limits_{i = 0}^{q - 1} {\kern 1pt} T_{{\rm B}(q - i)}M$$

with M = M_ABT_AM_BA. The quantity $\rho = - \frac{1}{2}TrT^{(1)}(\omega ,\phi ,\xi )$ allows one to locate bulk bands in the regions where $\rho ^2\leqslant 1$, and gaps where ρ² > 1. Alternatively, the amplitude $\left| {r_\infty (\omega ,\phi ,\xi )} \right|^2$ of the reflection coefficient of the structure²⁸

$$r_\infty (\omega ,\phi ,\xi ) = \frac{{{\rm e}^{ik(\omega )D} - T_{11}^{(1)}(\omega ,\phi ,\xi )}}{{T_{12}^{(1)}(\omega ,\phi ,\xi )}},$$

(1)

where e^ik(ω)D is an eigenvalue of the matrix T⁽¹⁾(ω, ϕ, ξ), can also be used to locate the gaps of the system.

Band structure of the unmodulated system

The unmodulated structure (η = 0) features stopbands at $\tilde \omega _0$ = $\omega _0d_0{\mathrm{/}}c$ = $\pi {\mathrm{/}}\left( {\sqrt {\varepsilon _{\rm A}} + (1 - \xi )\sqrt {\varepsilon _{\rm B}} } \right)$, where ξ = L_A/d_o is the characteristic size ratio.

Q(ω, ϕ, ξ) function

To determine the existence of the edge states, one needs to specify the boundary conditions on each edge of the structure. For the left edge, this condition is given by:

$$0 = \left( {q_b + q_a} \right)A_1 + \left( {q_b - q_a} \right)B_1,$$

where A₁ and B₁ are the amplitudes of the right and left-traveling waves in the first layer of the structure. This condition can be reformulated as

$$det\left( {b_1,a_1} \right) = 0$$

with b₁ = ((q_a − q_b), (q_a + q_b))^T and a₁ = (A₁, B₁)^T, and together with the eigenvalues λ_± and eigenvectors $v_ \pm = \left( {T_{12}^{(1)},\lambda _ \pm - T_{11}^{(1)}} \right)$ of the transfer matrix T⁽¹⁾, it is possible to determine the existence and dispersion of edge states.

Following refs.^31,32, it can be in fact shown that a proportionality relation exists between the boundary vector b₁ and the eigenvectors v_± of the transfer matrix. So the condition for the existence of the edge states is given by det(b₁, v_±) = 0 in a gap where $\left| {\lambda _ \pm } \right| < 1$. This entails searching for the zeros of the function F_l,± = $\left( {q_{\rm A}- q_{\rm B}} \right)\left( {\lambda _ \pm - T_{11}^{(1)}} \right)$ − $T_{12}^{(1)}\left( {q_{\rm A} + q_{\rm B}} \right)$.

Specifically, the real part of F_l,± = 0 yields the function Q(ω, ϕ, ξ) = ${\rm Re}\left\{ {T_{12}^{(1)}\left( {q_{\rm A} + q_{\rm B}} \right)} \right.$ − $\left. {\left( {q_{\rm A} - q_{\rm B}} \right)\left( {T_{22}^{(1)} - T_{11}^{(1)}} \right){\mathrm{/}}2} \right\}$ and, as shown in Fig. 1c, this implies that edge states exist only in the gaps where |ρ| > 1 and Q(ω, ϕ, ξ) · ρ > 0. At the same time, edge states cannot exist in gaps where Q(ω, ϕ, ξ) does not change sign. Moreover, due to a bulk-boundary correspondence⁴⁶, the number of these edge modes is equal to the modulus of the associated topological invariant |ν_ij|, given by the winding number of the reflection coefficient:

$$\nu _{ij} = \frac{1}{{2\pi i}}\mathop {\int}\limits_{ - \pi }^\pi {\kern 1pt} d\chi \frac{{\partial {\rm ln}(r_\infty (\omega ,\chi ))}}{{\partial \chi }},$$

(2)

i.e., the extra phase (divided by 2π) of r_∞ (ω, χ) when χ varies in the range (−π, π) with ω in the stop band⁴⁷.

By relying on the transfer matrix method, our approach can be applied to a general class of problems and thus makes it suitable for a wide range of systems beyond our baseline AAH model. Specifically, it can be extended to many physical systems whose behavior is described by a gapped unitary operator, e.g., photonic Floquet topological insulators^7,48 and photonic topological quantum walks¹⁰. Analogously to the AAH model, the edge states of these systems can be defined with an equivalent F_l,±(ω, p₁, ..p_n) function, where (p₁, ..p_n) are relevant parameters describing the structure. The imaginary component of F_l,±(ω, p₁, ..p_n) = 0 furnishes the dispersion relations of the edge modes and hence the training dataset of our ML inverse problem.

Code availability

The code developed for the present study is available from the corresponding author on reasonable request.