Introduction

The potential vulnerabilities of widely employed public-key encryption systems1 have led to the development of alternative communications protocols, such as quantum key distribution (QKD)2,3 and quantum digital signatures4,5, that employ the laws of quantum mechanics and can, with the correct implementation, achieve unconditional security6. Early protocols proposed using single photons to encode information7, but the challenges associated with generating single photons on demand8,9 mean that practical implementations typically use low-intensity laser pulses, modeled as weak coherent states, as the information carriers10. Quantum communication protocols are, in general, much easier to implement experimentally if they use coherent states as the information carriers. The coherent states are attenuated such that the mean number of photons in a pulse is much less than one. The photon statistics of a coherent state are Poissonian, so the probability of a pulse being devoid of photons is high in this regime. An attempt to amplify these weak coherent states using deterministic methods introduces noise that destroys any quantum properties of the signal11,12. Therefore, communications protocols have been limited to transmission distances of less than 400 km in optical fiber13,14. The global optical fiber telecommunications network relies heavily on the presence of optical amplifiers in order to amplify signals deterministically with low noise to allow transmission over intercontinental distances15. A quantum internet with global capabilities will require either quantum specific amplifiers, repeater devices, or even the implementation of quantum satellites as nodes in orbit16,17,18,19,20,21.

Non-deterministic noiseless amplification is a research area of growing importance, with new experimental approaches generating significant interest22. Amplifier systems have already been proposed for device-independent QKD23,24 and experimentally demonstrated for entanglement-based continuous variable QKD25. Non-deterministic amplifiers amplify quantum states probabilistically based on a set of heralding conditions, which are typically a certain set of detection outcomes26,27. Non-deterministic amplification was predicted and demonstrated for amplification of states without a local phase reference, by addition of thermal (uncorrelated) noise28,29. Other approaches include heralded scissor devices30, and qubit amplifiers23. These amplifiers typically rely on “quantum” resources, such as heralded single-photon sources, or photon number resolving detectors, which are often difficult to implement in practice using current technology31. Amplification without quantum resources has also been successfully implemented in ref. 32, which is a similar amplification method to the one presented in this paper. More recently a new type of postselecting amplifier based on both deterministic and probabilistic scissors-type amplification and phase-dependent homodyne detection has been implemented to produce multiple clones of input states33.

In this paper, we consider the comparatively simple state comparison amplifier (SCAMP)34. Operation of this amplifier requires only coherent state sources (such as an attenuated laser), linear-optical components (primarily beamsplitters and phase modulators), and single-photon avalanche diode (SPAD) detectors operating in Geiger-mode35, making the SCAMP approach considerably easier to implement than other proposed schemes for quantum amplification. Altering the beamsplitter ratios of the SCAMP allows us to alter the properties of the amplifier. Typically postselecting amplifiers work with high fidelity only in either the low mean photon number regime or with low gain. The amplifier presented here is not limited by these restrictions. We have also demonstrated increased output fidelity, at some cost to the gain, by introducing a second subtraction stage.

Results

State comparison amplification

As shown in Fig. 1, a SCAMP has two individual modular stages: a state comparison stage, and a photon subtraction stage. The state comparison stage interferes two weak coherent states on a beamsplitter. One state is the signal state which has unknown phase encoding but a known mean photon number per pulse (or |α|2—where α is the coherent state amplitude), possibly transmitted from a remote source, such as Alice in a QKD scenario. The other is a second state phase encoded with a random guess as to the possible phase of the signal. Although the discrete alphabet of possible phase encodings defined by {exp(2mπi/N)}, where m = 0, …, N − 1 is common to both sender and amplifier, the actual phase encodings of each of the signal and guess states are chosen independently at random from within the alphabet. The use of such a randomized discrete phase alphabet in amplification was first suggested in ref. 29 and used in refs. 32,34. This discretization of the phase alphabet is a common feature of many quantum communications protocols36 (N = 4) and if we are to work with such communication schemes then tailoring the amplifier to these restricted alphabets is sensible.

Fig. 1
figure 1

The state comparison amplifier with a state comparison stage and two photon subtraction stages. The state comparison stage interferes two quantum coherent states, referred to as the signal and guess, which are independently selected from a commonly known discrete phase alphabet. If both quantum coherent states are indistinguishable, all light intensity will be routed through the amplifier device to the output. For all other cases, some light is routed to the D0 detector, resulting in a finite probability of a detection event. The second and third beam splitters are used for photon subtraction. The photon subtraction stages are highly transmissivity beamsplitters used to increase the amplified state fidelity. The detection events at each detector are processed in post-selection to determine if an input signal state was successfully amplified. The secondary subtraction stage (shown in faint) is used only for the extra subtraction stage experiment

Full size image

The interference at the state comparison stage is monitored using a SPAD, D0, whose output becomes one of the post-selection conditions for the amplifier. In the case of the guess state being correct, then no light exits to the D0 arm, and all of the light is routed to the output arm. Therefore, the first post-selection condition for the SCAMP is “no counts at the state comparison stage detector D0”. However, the comparison detector is only an imperfect indication that the guess was right and that the output contains the correct amplified state due to several factors: the non-zero loss in optical components; non-unity detection efficiency; and the finite probability that a pulse contains no photons. Conditioning the output of the non-deterministic amplifier solely on this first condition will lead to a low-fidelity output (fidelity is a measure of the output quality, see the Methods section), which can be improved by adding a photon subtraction stage.

The photon subtraction stage can be implemented via a low reflectivity beamsplitter monitored on reflection by a second SPAD, D1 as shown in Fig. 1. An event recorded at this detector corresponds to the approximate implementation of the annihilation operator of the electro-magnetic field mode of which a coherent state is an eigenstate37. The post-selection condition for this stage is that a detection event at D1 indicates successful amplification. This is because a correctly guessed input state provides an output at the comparison stage with an amplitude larger than that provided by an incorrectly guessed input state and is therefore more likely to trigger a photo-detection event at the second stage—thus, resulting in an increased fidelity compared to only conditioning on the comparison stage. While this increases the amplified state fidelity, it reduces the overall intensity, gain, and success probability of the amplifier.

The successful events are those for which D0 does not trigger while D1 does trigger and these constitute an imperfect indication that the SCAMP’s output contains the correct amplified state. The modular nature of the SCAMP configuration means that comparison and subtraction stages can be introduced, removed, or tuned (in terms of transmission and reflection coefficients) as required to modify key parameters such as gain, fidelity, and success rate. A previous demonstration of a SCAMP configuration has shown low gain with a high output fidelity38. Here a revised configuration is shown that offers high gain, which can be then adapted with the addition of further subtraction stage that further enhances the correct state fraction and the fidelity. The ease with which another stage can be incorporated demonstrates the modular features of the SCAMP approach.

In a real application, where the SCAMP would act as a trusted node station in a quantum communication network, continuous noise will be present—introduced by various sources not under the user’s control. This noise could originate from, for example, ambient light or non-linear Raman scattering in the optical fiber39, or even detectors with much higher dark count rates than those used in these experiments35. Detector properties, such as the non-linear response with overall count rate, will be affected by the continuous noise, and this will have a direct effect on the amplification process. Therefore, it is important to examine how post-selected correlations in SCAMP are affected by the addition of continuous noise. For this reason, noise was deliberately introduced into the SCAMP at varying levels and the effect on the output studied.

Six parameters are of interest to characterize the amplifier: fidelity, effective gain, correct state fraction, interferometer visibility, success rate, and success probability. Fidelity describes the effectiveness of the SCAMP process in amplifying the input state correctly. The effective gain is simply the ratio of output to input mean photon number. The correct state fraction is the probability of having a correct output given declaration of success—as defined by the post-selection conditions. Interferometer visibility, allows us to gauge how accurate the phase matching is between guess and signal phase alphabets. Success rate is the number of correlations between D0 not triggering and D1 triggering, measured per second, and here we demonstrate a particularly high success rate compared to alternative quantum amplifiers. For SCAMP the success rate will be linearly proportional to the repetition frequency of the laser and hence we can obtain higher rates in future demonstrations by using sources with much higher repetition frequencies, e.g., in the GHz region. Finally, the success probability of the amplifier is defined as the rate of successful correlated post-selected events divided by the pulse repetition frequency, which is 1 MHz for all experiments reported in this paper.

Results from the enhanced gain SCAMP configuration using only a single subtraction stage are presented first to establish the base characteristics of the amplifier. Subsequently, the robustness to noise of this base configuration of amplifier is shown. Finally, a comparison is given showing the improvement in fidelity provided by the introduction of an extra subtraction stage device.

Single subtraction stage

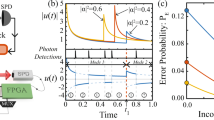
Figure 2 shows the results from the enhanced gain SCAMP configuration using a 90:10 comparison beamsplitter. Figure 2a shows how the fidelity of the amplified output varies with the mean photon number per pulse. The fidelity curves exhibit a characteristic shape corresponding to competition between two effects. The first effect is the rapidly decreasing overlap between the incorrect amplifier output and the reference state as the mean photon number increases, which decreases the amplifier output fidelity at higher mean photon numbers. The second effect counteracts the first by excluding those incorrect outputs at higher input mean photon numbers through post-selection. The increase in correct state fraction confirms this in Fig. 2b. As the correct state fraction increases, there are fewer incorrectly amplified states post-selected, therefore the overlap between the amplified output and the correct reference state is larger on average. In all of the examined cases, N = 2, 4, and 8, the correct state fraction is significantly larger than the 1/N that can be achieved with a random guess of the input, thus illustrating the effectiveness of the device23,24,25,26,28,30.

Fig. 2
figure 2

Experimental estimations computed from the experimental model at the tomography stage, illustrating the output state fidelity, correct state fraction, effective gain, and success rate as a function of mean photon number for N = 2, 4, and 8. The lines shown in a and b correspond to the output of the theoretical model for each phase state tested. The line in c corresponds to the theoretical gain value for this configuration. The lines shown in d correspond to optimal unambiguous state discrimination for the N = 2, 4, and 8. The uncertainty in the mean photon number per pulse is 1.5%, due to a small drift in coherent source power. The y-axis errors were found to be less than 2% and are therefore hidden by the data points

Full size image

The effective gain of the output intensity, shown in Fig. 2c, is reasonably constant over a large range of different mean photon numbers per pulse. An apparent decrease can be seen for higher mean photon numbers per pulse, due to the high photon detection rates causing a different non-linear response at each detector. The average intensity gain for data points with mean photon numbers less than 0.1, where the non-linear response of the detectors is negligible, was found to be 8.26 ± 0.14, which is close to the expected nominal gain of 8.35, presented in the Methods section. When the whole range of mean photon numbers per pulse are included, the average intensity gain was found to be 8.04 ± 0.29, which is lower than the expected value. This reduction in gain results from difficulty in correcting for the individual non-linear responses of each SPAD at this high count rate regime, as will be discussed in more detail in the Methods section.

Figure 2d shows the success rate of the amplifier. As can be seen, this increases almost exponentially with mean photon number per pulse because there is a greater likelihood of triggering the subtraction stage detector with higher intensity coherent states. The exponential trend comes directly from the Kelley–Kleiner formula40. The highest achieved success rate of 220 kHz at the operational pulse repetition rate of 1 MHz corresponds to a success probability of 22%. For a mean photon number per pulse of 1, the device has a success probability of approximately 10% (corresponding to a rate of 100 kHz in this case), an order of magnitude increase on the previous reported value for a SCAMP of 1%38—a value which already offered several orders of magnitude improvement in the success rate over other quantum amplifier experiments23,24,25,26,28,30.

In Fig. 2d, we also compare the success rate of the SCAMP with that of optimal unambiguous state discrimination (USD)27. This figure highlights that our implementation has a lower success probability (and hence success rate) than USD for N = 2 for all mean photon numbers examined.This is partially due to the quantum efficiency of our detectors at the state comparison and photon subtraction stages. However, for mean photon numbers less than approximately 0.8, the SCAMP outperforms USD for N = 4 and 8. It is worth noting that for these two phase alphabets there is no linear optical implementation that achieves the optimal bounds on USD measurement of the phase, only suboptimal cases. Unambiguously identifying states from these larger sets has a low success probability due to many states having to be eliminated by measurement. The fidelity of any output state regenerated after USD is, of course, perfect, provided that the system only generates an output state in the event of a successful USD measurement and is not forced to produce an output state for each input or ambiguous measurements.

The success rate, the correct state fraction, and the fidelity of the amplifier could be improved further by increasing the quantum efficiency of the detectors are the state comparison, and photon subtraction stage. The higher probability of detection allows better identification of wrong guesses at the comparison stage improving overall the system performance of the SCAMP.

Added channel noise with single subtraction stage

Measuring the effect of ambient light, or higher detector dark count rates, on the fidelity allows us to gauge how the amplifier would perform in a real communications channel where amplification has to take place against a noise background. We mimic this by adding temporally uncorrelated light to the system directly using a continuous spectrally broadband light-emitting diode (LED) as the source of thermal noise. Three levels of added noise were tested, corresponding to an ungated background level of 0.16, 0.6, and 0.8 mega-counts per second, respectively. This corresponds to a probability of a photon arriving during an individual gating window on the D0 (state comparison) detector of 0.8 × 10−3, 3 × 10−3, and 4 × 10−3. These values can be compared to the probability of detector dark noise alone, in the gated region, of approximately 2.1 × 10−6, corresponding to a dark count rate of 420 counts per second.

Figure 3a–d shows the results for output state fidelity, correct state fraction, success rate, and visibility of the state comparison stage (see Methods) with different noise levels applied. For Fig. 3a, b, N = 2, 4, and 8 are presented and, for clarity, only the no additional noise, and high level of noise data points are plotted. There is an exception for N = 8, where the highest level of noise recorded was 0.4 mega-counts per second, equivalent to the medium noise level for N = 2, and 4. This was due to a pre-conditioning threshold in the custom real-time data acquisition software which required a threshold interferometric visibility to be reached at the state comparison stage, and tomography stage before data was recorded. For no additional noise measurements the visibility threshold was set to >90%. This was reduced as required as the noise added was increased in order for measurements to be made. In all cases the other levels of noise measured bridge the gap between the no noise and high level noise data points presented. Figure 3c and d only shows the results for N = 4, this again is for clarity since N = 2, and 8 also exhibit the same trends. This shows the full range of noise measurements made. The visibility drop at low values of mean photon number is due to the decrease in the signal-to-noise ratio with increased background noise.

Fig. 3
figure 3

Experiments carried out with additional channel noise. In a and b, the filled data points refer to experiments performed without added noise. The solid lines correspond to the theory for a particular N. For c and d, the results are only for N = 4, for clarity, as the trend for N = 2, and 8 are the same. d The gated visibility of the state comparison stage for different levels of noise. The uncertainty in the mean photon number per pulse is 1.5%, due to a small drift in coherent source power. The y-axis errors were found to be less than 2% and are therefore hidden by the data points

Full size image

The effect of injecting thermal noise is to decrease the correct state fraction and, in turn, the fidelity. Even when the guess is right, thermal light will “leak” through to the comparison detector making it more likely to fire with respect to the no noise case. Furthermore, the presence of thermal light at the subtraction stage makes an incorrectly amplified state more likely to trigger the subtraction detector. Overall, due to the injection of thermal light, a correct guess is less likely to meet the success criteria while the incorrect one is more likely. Consequently, the overall success probability is expected to be higher for input mean photon numbers per pulse smaller compared to the thermal contribution.

The decrease of fidelity and correct state fraction and the increase of the success rate for mean photon number per pulse smaller than 0.2 are shown in Fig. 3a–c, respectively, where the case N = 4 is considered, other state space dimensions (values of N) follow the same trend.

From Fig. 3c, it is apparent that as the level of noise in the channel is increased, measurements at low mean photon number per pulse were not recorded. This was due to the real-time acquisition code failing to meet the pre-determined threshold requirements of visibility on the state comparison and tomography stages. The corresponding visibility of the state comparison stage is shown in Fig. 3d, and it can be seen that the additional noise has a significant effect when compared to the channel with no additional noise. It also highlights why no measurements were recorded for a mean photon number per pulse of below 0.01 at medium and high levels of noise—because the visibility would be less than 20% and was therefore deemed too low to be usable in an interference experiment.

Increasing the mean photon number per pulse allows the visibility to be recovered (as would be expected, since the input signal-to-noise ratio increases), but this is not ideal for quantum experiments which typically rely on values of mean photon number per pulse of lower than 0.5. Monitoring the visibility is not only a useful means of monitoring the level of noise being coupled into the quantum channel, but also may indicate whether a malevolent party is attempting a Trojan horse or detector blinding attack as this is likely to alter the background level seen41,42. Overall these results shows that SCAMP has a robustness to channel noise that exhibits a dependence on mean photon number per pulse.

Extra subtraction stage

Figure 4 shows the performance of the SCAMP with an extra subtraction stage system for N = 2, and 4. No additional noise was added in these measurements. The addition of further subtraction stage introduces a further post-selection condition and successful amplification is now conditioned on the case of no photon event at D0, and photon events at both D1 and D2. Since each subtraction stage uses a highly transmitting/low-reflectivity beamsplitter, it is unlikely that a low-intensity coherent state will be able to trigger the detectors at both subtraction stages. Hence the revised system will demonstrate a higher output state fidelity and correct state fraction. This advantage does come at a cost—a lower nominal and effective gain and success rate than the system with only one subtraction stage.

Fig. 4
figure 4

Experiments carried out with an extra subtraction stage. Dashed lines in a and b are theoretical lines for the extra subtraction stage which are shown in comparison with the theoretical lines for state comparison amplifier with one subtraction stage which are represented by solid lines, as shown in Fig. 2. The dashed line in c is the nominal gain value for the extra subtraction stage, having a value of 6.50. As the success rate for other N follow the same trend only N = 4 is presented in d, the drop in success rate highlights the cost for implementing a second subtraction stage.The uncertainty in the mean photon number per pulse is 1.5%, due to a small drift in coherent source power. The y-axis errors were found to be less than 2% and are therefore hidden by the data points

Full size image

In Fig. 4 which has some data points that are common with Fig. 2, all solid filled data points are for a single subtraction stage. The solid lines in Fig. 4 are theory for the single subtraction stage. The dashed lines are theoretical curves for the extra subtraction stage set-up, and the data points denoted by squares with vertical crosses refer to extra subtraction stage experimental results. Black squares denote N = 2, while red circles are N = 4.

Figure 4a and b shows direct comparisons between the single subtraction stage and double subtraction stage SCAMP experiments for fidelity and correct state fraction, respectively. The advantage over the single subtraction stage can be clearly observed by the significant improvement in output state fidelity at mean photon number per pulse values less than 0.4, after which the theory and data converge. The same effect can be seen at mean photon number per pulse values less than 0.02.

The correct state fraction presented in Fig. 4b shows a similar trend in advantage at mean photon number per pulse values lower than 0.4. Above this the correct state fraction converges to that of the single subtraction stage.

The effective gain for the extra subtraction stage system, shown in Fig. 4c, is lower than the previous experiment with a single subtraction stage, due to the extra loss introduced by the additional stage. Taking into account inherent beamsplitter losses, the estimated effective gain was found to be 5.90 ± 0.48, only slightly lower than the nominal value of 6.50 represented by the dashed line. This discrepancy is consistent with the expected optical loss from fiber splices between the beamsplitters and individual saturation effects at the detectors.

The success rates for N = 4 are compared in Fig. 4d for a single and extra subtraction stage. N = 2 and 4 follow the same trend, hence only N = 4 is shown for clarity. The filled data points are for the single subtraction stage, and it can be seen that there is a lower success probability for the SCAMP with an extra subtraction stage. This reduction is approximately a factor of 0.1 at a mean photon number of 1 due to the 10% splitting of the second subtraction stage. However, it can be seen from Fig. 4d that the reduction factor varies over the mean photon number range presented. At the largest mean photon number per pulse of 2.93, the success rate was found to be 238 kilo-correlations per second corresponding to a success probability of 23.8% at the operational pulse repetition rate of 1 MHz.

Figure 4 shows that the fidelity and correct state fraction can be significantly improved for a range of mean photon numbers per pulse by adding an extra subtraction stage. This advantage does reduce above a mean photon number per pulse of greater than 0.4, and for very low mean photon number per pulse values of less than 0.02. This benefit does come at the expense of reducing the effective gain and the success probability compared to the configuration with a single subtraction stage. Figure 5a and b highlights that additional subtraction stages can be used to increase the correct state fraction further for phase alphabets N = 2 and 4, respectively.

Fig. 5
figure 5

The effect of multiple subtractions: each subtraction increases the correct state fraction toward the theoretical limit of unity. a represents a phase alphabet of N = 2, while b represents N = 4. Although each additional photon subtraction stage increases the correct state fraction, this will decrease the success probability of the amplifier

Full size image

Discussion

We have presented three experiments for state comparison amplification using two experimental configurations. A detailed theoretical model of the experiment allowed an estimation of quantities despite experimental imperfections. The model showed excellent agreement with the experimental results over the range of input mean photon numbers and system configurations examined in this work. In the first experiment we show an high gain single subtraction system that amplifies with high fidelity, rate and gain. Noise introduced to the signal channel was used to examine the robustness of the amplifier to the addition of ambient light, crosstalk from other co-propagating signal channels, or detectors with significantly greater dark count rates. The results presented here indicate that it is possible to time-gate away noise which has a temporally uniform profile and subsequently monitor characteristics, such as visibility with a reference state, to determine the noise level in the channel, and monitor change in noise levels over time. This shows resilience against attacks on the amplifier, such as the Trojan horse attack.

The final experiment added a second subtraction stage to the previously examined SCAMP designs. This significantly improved the fidelity and correct state fraction, for the mean photon number per pulse range of 0.02–0.4, by adding a third post-selection condition. The benefit was less significant outside of this range where the data converged with that from a single stage amplifier. The benefit did come at the cost of a decreased success probability (and therefore success rate), and lower effective gain through increased loss in the SCAMP system. Additionally, the ease with which such a modification could be implemented highlighted that the SCAMP offers a modular approach that can be tailored to the specific application.

The fidelity and correct state fraction could be improved further by introducing another subtraction stage, a photon number resolving detector to condition the number of photons received28, or by introducing a feed-forward mechanism to correct for incorrect guesses. The feed-forward system, in particular, could be used operate as a quantum repeater in non-entanglement-based quantum communications systems with known phase alphabets.

Methods

Experimental system

The experimental system is shown in schematic form in Fig. 6, and was comprised of an outer tomography interferometer, used to measure the fidelity of the amplified output, with a smaller state comparison amplifier interferometer forming part of one of the larger interferometer’s paths. Light propagating through path 1 was not altered in phase, and provided the reference copy of the unamplified signal used for the final tomography measurement. Light in path 2 was used for the SCAMP process.

Fig. 6
figure 6

The optical set-up for the state comparison experiments. A coherent laser source is coupled into a single-mode optical-fiber, then attenuated down to single-photon level. The experiment interferometers are constructed of polarization maintaining fiber, therefore the polarization of the coherent light is aligned with the fast axis of the polarization maintaining fiber. The initial 50:50 beamsplitter splits the light intensity into two paths. Path 1 is a reference copy of the quantum coherent state, used to perform state tomography of the amplified state on the final beamsplitter. The signal and guess quantum coherent states, required for state comparison amplification, are created by splitting Path 2 into a further two paths. One path remains unchanged, simulating the unknown signal state, while the guess state is modified using a phase modulator, simulating a guess state from the amplifier. Gray beamsplitter cubes denote 50:50 splitting ratios, while the red denote 90:10 ratios (90% transmission). The faint beamsplitter is the second subtraction stage. The additional channel noise used in some of the experiments was provided by a light-emitting diode (LED) coupled into the signal arm

Full size image

The coherent light source for the experiment was a gain-switched pulsed free-space vertical-cavity surface-emitting laser (VCSEL) diode, which emitted at a central wavelength of 850 nm. This wavelength was chosen43 as it offers compatibility with commercial silicon SPADs35 while balancing the increasing loss of silica optical fibers at shorter wavelengths44. The free-space VCSEL was coupled into 4.5 μm core diameter “panda-eye” structure single-mode polarization-maintaining optical-fiber, necessitating careful rotational alignment of the linear polarization of the light emitted by the VCSEL with one birefringent axis of the fiber. The mean photon number per pulse was defined at the input to the state comparison beamsplitter at “Point A” but was set using a motorized attenuator prior the first beamsplitter input.

The light from Path 2 that was used for the SCAMP process was initially split into two separate optical paths. Each optical path provided a separate coherent state source for the signal and guess states (respectively), which were subsequently recombined on a 90:10 beamsplitter at the state comparison stage. The phase-encoding of the guess state was generated by a lithium-niobate phase-modulator, which chose one of the phases from the limited discrete-phase alphabet. After the state comparison stage, photon subtraction was performed by a highly transmitting (nominally 90:10) beamsplitter, where a single photon detector D1 was placed on the low reflectance output. A second photon subtraction (shown faint in Fig. 6), also consisting of a nominally 90:10 beamsplitter and detector, was added for subsequent experiments in order to evaluate performance with additional post-selection conditions. The output of the amplifier was then recombined with the reference state from Path 1 at the tomography stage, to allow for an estimation of the performance parameters of the amplifier, such as output state fidelity.

The time of the electrical output events for each of the SPADs were recorded using a picosecond resolution time-stamping module45 and partially processed in approximate real time using custom software written using a commercial data analysis toolkit (MATLAB 2016a (9.0.0.341360)), to allow ongoing observation of the SCAMP experiment and an initial estimation of interferometric visibility of both the SCAMP and tomography systems. Following completion of the experimental data recording process, further custom software post-processed the time stamps to identify correlations between detectors. The time stamps of the recorded events were temporally filtered (post-gated) in software with a window of duration ±2.5 ns around the expected arrival times for the photons and the same window also served as a bracketing condition for the coincidence and anti-coincidence count matching. Hundred sets of measurements were taken at each mean photon number per pulse and the average rates calculated along with the standard deviation. This analysis gave the raw experimental parameters for the SCAMP experiment which were then processed using the theoretical model of the experiment (discussed in the next section) to give estimations of the true parameters once component induced optical loss, mismatches in the interferometer arms’ parameters, non-unity detection efficiency, and non-linear detector performance with count-rate had been compensated for.

The source of the additional noise was a LED with a central wavelength of 869.5 nm and a spectral bandwidth of 31.5 nm. This was evanescently coupled into an exposed fiber splice in the smaller interferometer, as shown in Fig. 6. The LED produced continuous wave emission giving constant probabilities per unit of time of photons arriving during the gating window at the D0 detector. Three levels of additional noise were tested, hereafter referred to as low, medium, and high. The probability of a noise photon per individual detection gate at D0 for low, medium, and high were 0.8 × 10−3, 3 × 10−3, and 4 × 10−3, corresponding to ungated raw count rates of 0.16, 0.4, and 0.8 mega-counts per second, respectively. These probabilities are three orders of magnitude larger than the gated dark count rate contribution which is 2.1 × 10−6, which corresponds to an ungated dark count rate of 420 counts per second.

Theoretical analysis

A theoretical model of the experiment was used to analyze the recorded measurements. This was based on Eleftheriadou et al.34, and extended in order to consider experimental imperfections. The model provided estimations for various quantities useful for characterizing the experiment, such as effective gain (gT), the fraction of correct amplified states, and the amplified state fidelity. The data points in the graphs presented in this paper have been analyzed using the model. The coherent amplitude of Bob’s guess is given by t1αeiϕ/r1, where ϕ represent a phase mismatch given by the difference of the optical paths in the interferometers arms. The nominal gain, g2, of the amplifier with one subtraction stage was defined in ref. 34 as \(g^2 = t_2^2{\mathrm{/}}r_1^2,\) where \(t_2^2\) refers to the transmissivity of the subtraction stage and \(r_1^2\) the reflectivity of the state comparison stage, has been altered to include the unbalanced beamsplitting ratios of the components actually used in the experiment to give:

$$g^2 = \left( {t_{{\mathrm{g}},1}^2t_{{\mathrm{s}},1}^2 + r_{{\mathrm{g}},1}^2r_{{\mathrm{s}},1}^2 + 2t_{{\mathrm{g}},1}t_{{\mathrm{s}},1}r_{{\mathrm{g}},1}r_{{\mathrm{s}},1}} \right)\frac{{t_2^2}}{{r_{{\mathrm{g}},1}^2}},$$
(1)

where \(t_{{\mathrm{g}},1}^2\), \(t_{{\mathrm{s}},1}^2\), \(r_{{\mathrm{g}},1}^2\), and \(r_{{\mathrm{s}},1}^2\), refer to the transmission and reflection coefficients with respect to the input ports for the guess and signal. \(t_2^2\) refers to the transmission of the subtraction stage. The value of g2 for the amplifier with a single subtraction stage was calculated to be 8.35. Calculation of the nominal gain for the case with the secondary subtraction stage simply requires Eq. (1) to be multiplied by the experimentally measured value of the secondary subtraction stage transmission \(t_3^2\), which gave a value of 6.50.

The probability that a photon causes a SPAD to fire is given by its detection efficiency, η. However, these detectors exhibit a non-linear count rate response which is dependent on the rate of incident photons on the SPAD. This effect can be quantified, according to the generic detector specification sheet, as a multiplicative correction on the recorded counts given by \(c = N \cdot 10^{ - 7}{\kern 1pt} n_{{\mathrm{exp}}}^{\mathrm{i}} + 1\), where N is the state space dimension and \(n_{{\mathrm{exp}}}^{\mathrm{i}}\) is the raw photon count rate on a given detector. Each detector in the experiment has a slightly different detection efficiency, ηi, whose values were measured at low detector count rates where the non-linearity in the responses are negligible. The relation between the recorded raw counts and the incident mean photon number per pulse is thus obtained by the Kelley–Kleiner formula:40

$$\frac{{cn_{{\mathrm{exp}}}^{\mathrm{i}}}}{n} = 1 - {\mathrm{e}}^{ - \eta _{\mathrm{i}}|\alpha |^2},$$
(2)

where n is the number of generated pulses per second at the source (1 million pulses at our pulse repetition frequency of 1 MHz). To ease the comparison of data from different detectors, we can relate the raw counts from different detectors to those that the same coherent signal would cause at an ideal detector, \(\tilde n\). Similarly to before, the value of \(\tilde n\) is linked to the mean photon number per pulse by the Kelley–Kleiner formula:

$$\frac{{\tilde n}}{n} = 1 - {\mathrm{e}}^{ - |\alpha |^2},$$
(3)

we can combine the previous formulae to relate \(\tilde n\) to \(n_{{\mathrm{exp}}}^{\mathrm{i}}\) obtaining:

$$\tilde n = n\left( {1 - \left( {\frac{{n - cn_{{\mathrm{exp}}}}}{n}} \right)} \right)^{\frac{1}{\eta }}.$$
(4)

The different, non-zero loss of each beamsplitter was measured and is considered in the theoretical model. The model allows for two separate estimations of the relevant quantities, one based on results from the amplification system detectors D0 and D1 (which represents an estimation made at the SCAMP) and one from the tomography detectors DA and DB that represents the point of view of the receiver. The phase mismatch, ϕ, is linked to the visibility as follows:

$${\mathrm{cos}}{\kern 1pt} \phi = \frac{{\left| {D_0^{\mathrm{W}}} \right|^2 - \left| {D_0^{\mathrm{R}}} \right|^2}}{{\left| {D_0^{\mathrm{W}}} \right|^2 + \left| {D_0^{\mathrm{R}}} \right|^2}} = {\mathrm{Visibility}},$$
(5)

where \(\left| {D_0^{\mathrm{W}}} \right|^2\) \(\left( {\left| {D_0^{\mathrm{R}}} \right|^2} \right)\) refers to the intensity reaching the state comparison detector in the wrong (right) guess.

The estimated effective gain can be calculated from the ratio of the intensity at the final tomography stage to that of the signal incident on the state comparison stage:

$$g_{\mathrm{T}}^2 = \frac{{\left| {D_{\mathrm{A}}^{\mathrm{R}}} \right|^2 - \left| {D_{\mathrm{B}}^{\mathrm{R}}} \right|^2}}{{2L\left| \alpha \right|^2}},$$
(6)

where \(\left| {D_{\mathrm{A}}^{\mathrm{R}}} \right|^2\left( {\left| {D_{\mathrm{B}}^{\mathrm{R}}} \right|^2} \right)\) is the estimated intensity from the DA (DB) tomography stage detectors in the event of a correct guess. L is the accumulated losses through the SCAMP from the point A in Fig. 1 to the tomography detectors, and is mainly composed of beamsplitter coupling losses. |α|2 is the mean photon number per pulse, where α is the electric field amplitude.

As well as performing amplification, a SCAMP will also skew the output probability distribution toward the correct amplified state if the output is conditioned on the successful events. The correct state fraction at the output can be expressed as a function of the success probability via the Bayes Theorem:

$$P_{{\mathrm{R}}|{\mathrm{S}}} = \frac{{P_{{\mathrm{S}}|{\mathrm{R}}}}}{{P_{{\mathrm{S}}|{\mathrm{R}}} + P_{{\mathrm{S}}|{\mathrm{W}}}}} = \frac{{n_{\mathrm{R}}}}{{n_{\mathrm{R}} + n_{\mathrm{W}}}},$$
(7)

where PS|R and PS|W are the probabilities for the output to satisfy the post-selection conditions successfully given that the guess made in the SCAMP was right and wrong, respectively. nR (nW) is the actual number of correct (wrong) amplified states recorded. PR|S is therefore the probability that an output state with successful post-selection conditioning correlations (i.e., no detection at the state comparison, and a detection at the subtraction stage) is actually the correct amplified state.

To estimate the correct state fraction at the tomography detector the approach adopted previously by Donaldson et al.38 has been generalized. In the previous work, the count rates at detectors DA and DB when success is declared were related to the actual number of correct and wrong amplified states via a perturbative expansion. In the current experiment it is assumed that the count rates at detector DB when the guess is right are much smaller than all the other count rates at the tomography stage and this is used as a perturbation parameter.

The fidelity F, which quantifies how close the amplified output is to a reference copy of the amplified signal, can thus be calculated from the results obtained at the tomography stage38:

$$F\left( {\rho _{{\mathrm{out}}}||O^{\mathrm{R}}} \right) = P_{{\mathrm{R}}|{\mathrm{S}}} + P_{{\mathrm{W}}|{\mathrm{S}}}{\kern 1pt} {\mathrm{exp}}\left( { - \frac{2}{L}\left( {\left| {D_{\mathrm{B}}^{\mathrm{W}}} \right|^2 - \left| {D_{\mathrm{B}}^{\mathrm{R}}} \right|^2} \right)} \right).$$
(8)

Inevitably the tomography stage adds further loss and slightly degrades the measured performance due to a non-ideal visibility in the tomography process itself. In an actual implementation the degradation from the tomography stage may not be present as a third party might perform operations directly on the output from the amplifier. Experimental errors for the data points presented in the figures were found to be less than 2%, and are therefore hidden by the data points. The small magnitude of this error, computed through standard error propagation through the analytical model, was due to the large sample size of the data.