Abstract
Low-frequency noise generated by a fluctuation of current is a key issue for integrating electronic elements into a high-density circuit. Investigation of the noise in organic field-effect transistors is now sharing the spotlight with development of printed integrated circuits. The recent improvement of field-effect mobility (up to 15 cm2 V−1 s−1) has allowed for organic integrated circuits with a relatively high-speed operation (~50 kHz). Therefore, an in-depth understanding of the noise feature will be indispensable to further improve the circuit stability and durability. Here we performed noise measurements in solution-processed organic single crystal transistors, and discovered that a low trap density-of-states due to the absence of structural disorder in combination with coherent band-like transport gives rise to an unprecedentedly low flicker noise. The excellent noise property in organic single crystals will allow their potential to be fully exploited for high-speed communication and sensing applications.
Similar content being viewed by others
Introduction
The recent development in synthetic chemistry together with nanotechnology leads to a revolution of π-conjugated semiconducting compounds. Their potential as an electronic element is recently rediscovered not only for their unique processability, but also for their excellent performance1,2,3. Particularly, an improvement of field-effect mobility of single-crystalline organic semiconductors (up to 15 cm2 V−1 s−1) allows for a large-scale production of high-density integrated circuits such as multi-bit logic circuits4,5, analog-to-digital (AD) converters6,7, radio-frequency identification (RF-ID) tags8,9,10.
Low-frequency electronic noise, which is generated inherently by a fluctuation of current passing through an individual transistor, is a key issue for integrated circuit applications11. Among various sources of electronic noise, flicker noise, which is often referred to as 1/f (the low-frequency noise with a spectral density that decreases inversely with frequency f), plays an important role12,13. Because the electronic noise is likely to be amplified during its propagation, it can hamper the operational stability when numerous devices and circuits are integrated. Particularly in view of the Internet of Things technology, high-density integrated circuit composed of organic semiconductors are now being intensively studied. For example, the cutoff frequency of the best performing organic field-effect transistor (OFET) approaches 30 MHz8, and operation frequencies of organic integrated circuits are on the order of 0.1–1 MHz4,14. It is known that jitter, which are variations of the edge of a digital signal from true periodicity, often impairs the bit error rate in digital logic, which becomes more predominant in nanoscale devices and sensing applications15,16. Recent investigations of the 1/f noise in organic field- effect transistors based on π-conjugated polymers17,18,19, amorphous or polycrystalline small molecules20,21,22,23,24,25,26 were mainly focusing on device degradation under ambient and/or irradiated conditions, and on the contact resistance effect. Unfortunately, these organic compounds typically have unavoidable structural disorder and their mobility is not sufficient for high-speed circuit operation. In addition, hopping transport, which is an inherent charge transport mechanism in such disordered systems, can be a significant impediment to the development of practical applications. In striking contrast to such disordered organic compounds, solution-processed single crystals composed of organic molecules exhibit an excellent mobility of up to 15 cm2 V−1 s−1 ref. 1,2,3,8, which has motivated intensive research to explore not only the coherent (band-like) charge transport physics27,28, but also functionalities for next-generation (opto)electronic applications29,30. However, a subject under consideration still remains: how the charge carrier transport mechanism correlates to the 1/f noise, and to what extent the noise level can be reduced in a practical electronic circuit. In this paper, we demonstrate noise measurements with wide frequency bands up to 1 MHz in an ideal, single crystal organic semiconductor. Thanks to its low trap density-of-states (DOS), and the coherent (band-like) transport nature, the amplitude of 1/f is found to be remarkably low, comparable to solution-processable, inorganic oxide semiconductors.
Results
Transistor characteristics and noise measurements
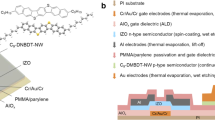
The single-crystalline thin film of our benchmarked organic semiconductor, 3,11-dioctyldinaphtho[2,3-d:2′,3′-d′]benzo[1,2-b:4,5-b′]dithiophene (C8–DNBDT–NW), was formed by edge casting, a simple one-shot solution crystallization method3 developed in our group (Fig. 1a and Supplementary Fig. 1. Further details are available in Supplementary Note 1). Edge casting allows for an ideal deposition of a single-crystalline thin film with large areal coverage and uniformity31. An OFET with a top-contact/bottom-gate architecture was fabricated on a Si/SiO2 wafer with Au source/drain electrodes (Fig. 1b). The single-crystalline thin film of C8–DNBDT–NW was successfully formed over a 300 × 300 μm channel, which is confirmed by a polarized optical microscope image (Fig. 1c). The fabricated transistor shows a textbook-like behavior with near-zero turn-on voltage and the mobility of μ = 13.6 cm2 V−1 s−1 (Fig. 1d, e). Note that a non-ideal behavior of the transfer characteristics often causes significant overestimation of the mobility. Recently, the measurement reliable factor r, which provides an indication of effective mobility, has been introduced32. Given the similar expression32, r was estimated to be 88 and 89% in the linear and saturation regimes from Supplementary Fig. 2c, d, respectively. Linear and saturation mobilities are found to be identical and show a clear plateau at high gate voltage (VG) regime (see Supplementary Fig. 2), which is an indicative of coherent band-like transport8,33,34.
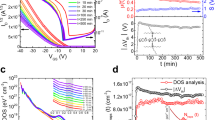
Transistor characteristics and noise measurements. Schematic images of a the crystal growth method (namely edge-casting) and b the fabricated OFET. The channel length (L) and width (W) were 200 and 300 μm, and the gate channel capacitance per area (Ci) was 34.5 nF cm−2. c Cross-polarized optical microscopy image of the fabricated C8–DNBDT–NW single crystal. d Transfer characteristics (ID vs. VG) at linear (VD = −1 V; blue) and saturation regimes (VD = −20 V; red). A typical gate leakage current, IG, is also shown (gray). e Output characteristics (ID vs. VD) with various VG. The transistor shown in this figure exhibits a mobility of μ = 13.6 cm2 V−1 s−1 with the measurement reliable factor32 of 88% (see more details in Supplementary Note 2). f A current fluctuation of C8–DNBDT–NW FETs in time domain, where constant VD, and VG were applied. Over 106 points were recorded within 10 s. The inset shows the magnified data set. The scale bar indicates 1 nA. The relative error in ID is approximately 50 pA, estimated from the intrinsic current measurement error of the semiconductor parameter analyzer Agilent B1500A. g Typical power spectral density of drain current fluctuations, \(S_{I_{\mathrm{D}}}\), obtained by fast Fourier transform of (f)
For the noise measurements, a semiconductor parameter analyzer with a waveform generator module was employed. To reduce any extrinsic contribution to the noise, the fabricated OFET was mounted on a custom made circuit board (see more details in Supplementary Figs 3–5 and Supplementary Note 2). An example of time domain profile of the drain current (ID) under constant drain (VD) and gate voltages (VG) is shown in Fig. 1f, where ~106 data points were recorded within 10 s. The power spectral density in ID noise \(\left( {S_{I_{\mathrm{D}}}} \right)\) as a function of the frequency (f) was then obtained by a fast Fourier transform of ID (Fig. 1g). The first attempt in this work is to identify the origin of noise in the state-of-the-art organic single-crystalline semiconductor C8–DNBDT–NW, where the charge carrier undergoes coherent band-like transport. The band-like carrier transport in the present single crystal form of C8–DNBDT–NW was unambiguously verified by the Hall effect measurements and electron spin resonance spectroscopy33,34. Previous studies about the 1/f noise in disordered organic semiconductors have revealed that the 1/f noise in ID originates mainly from carrier number fluctuation (δn), i.e., δI ∝ e(δn)μ23,24,25,26, which is referred to as McWhorter’s model (see “Methods” section)35,36. McWhorter’s model, which is widely adapted to the 1/f noise in inorganic semiconductors, accounts for carrier capture/emission processes at the transistor’s gate dielectric interface and describes the resulting current fluctuations. Empirically, the amplitude of the power spectral density \(S_{I_{\mathrm{D}}}\) is known to scale with the trap DOS. It should be natural that in disordered organic materials, carriers are likely to be localized, and that multiple-trap-and-release process dominates the net modulation of ID in the FET channel. The question remains whether the model can be applied to coherent band-like transport system realized in organic single-crystal semiconductors.
To assess the origin of 1/f noise in C8–DNBDT–NW FETs, we first investigated \(S_{I_{\mathrm{D}}}\) as a function of f, while the population of band-like carriers and thus ID is effectively modulated by the gate voltage VG. The ID -normalized power spectral density \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) as a function of f is plotted in Fig. 2a, at various VG (VG = −2 to −10 V with an increment of −1 V). The observed low-frequency noise in the organic single crystal agrees with 1/f spectral dependence in the range of 0.4 Hz–1 kHz. \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) is significantly lower for more negative VG (the channel is more accumulated), which is qualitatively interpreted as a suppression of the carrier number fluctuation δn upon accumulating more carriers in the channel. To clarify this, \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) is plotted as a function of ID (Fig. 2b), where the frequencies of the analysis are f = 10 Hz (red) and 100 Hz (blue). Black curves in Fig. 2b represents computed fit based on the McWhorter’s model (Eq. (2))35. The good agreement between experiments and the model strongly verifies that the McWhorter’s model can be applied to C8–DNBDT–NW FETs. The validity of the McWhorter’s model is further confirmed by the channel-size dependence of 1/f noise (see Supplementary Fig. 6 and Supplementary Note 3).
Frequency f and drain current ID dependences of normalized power spectral density \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^{\mathrm{2}}\). a The ID normalized power spectral density, \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\), as a function of VG. The dashed line represents 1/f. b ID dependence of \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\). The frequencies of the analysis are f = 10 Hz (red), and 100 (Hz). The error bars, shown separately from the symbols, represent compound errors that result from propagation of the uncertainties by the current measurement and by a fast Fourier transform. Black curves are the recalculation of the transfer curve based on the McWhorter model, where the fitting variant was only the energy-independent trap DOS (N = 8.3 × 1018 eV−1 cm−3). The small deviation of this fit are the corrections for the density of traps at the specific current and therefore Fermi level. The result the energy-dependent trap density calculation is shown in Fig. 5
In this first straightforward approach of fitting the measured noise with McWorther’s model, the density of trap states as the only fitting parameter (N = 8.3 × 1018 eV−1 cm−3) was assumed to be energy-independent. In organic semiconductors, however, the trap DOS typically increases towards the transport level37. To further investigate the effect of an energy-dependent trap distribution on the 1/f noise, we have conducted a temperature-dependent noise analysis of an C8–DNBDT–NW single-crystal FET from T = 295 to 115 K (see more details in “Methods” section). As a result of the narrowing of the Fermi Dirac statistics towards lower T, the Fermi energy EF at a given VG is shifted closer to the transport level, where the trap density is generally increasing. Therefore, upon cooling a raise of the trapping/detrapping is expected, expressed in an increasing noise signal.
Temperature dependence of noise characteristics
The measured \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) vs. f at various temperatures are shown in Fig. 3a–c and in Supplementary Fig. 7. 1/f noise is confirmed in the entire temperature range (115–295 K). Although according to Eq. (2), the power spectral density is expected to scale with T, the amplitude of the measured \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) is almost constant from 235–295 K, which is interpreted as a direct result of the increasing trap density towards the transport level. In this temperature regime, the mobility notably increases with decreasing T (Fig. 3d, e). Note that the exponent q in the power law of temperature dependence, μ ∝ Tq, is estimated to be q = −0.83 ± 0.04, which is almost identical to that previously observed for C8–DNBDT–NW34. This gives confidence that at least in this temperature regime, band-like transport is realized33,34. At temperatures down from 215 K, the noise amplitude increases remarkably, while the mobility rapidly diminishes (Fig. 3e), reminiscent of a thermally activated transport regime (see more details in Supplementary Note 4). Further lowering T decreases the population of coherent, mobile charges, hence charge carriers are more likely to be captured by trap sites which are likely to be induced by unavoidable cracking in the organic single crystal due to the mismatch of thermal expansion coefficients between organic semiconductor and solid-state gate dielectric38. This noise level increase below the transition of the two transport regimes demonstrates that the transport mechanism itself is a key factor in reducing the 1/f noise.
Temperature dependence of noise characteristics. Examples of \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) at various temperatures T; a T = 295 K, b T = 215 K, and c T = 115 K. d Transfer characteristics at various T. e T dependences of field-effect mobility μ (red) and the normalized power spectral density \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) (blue). The error bars in μ and \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) are determined from the uncertainty by the current measurement. The transition from band-like to activated transport leads to a large increase of the noise level. f The distribution of trap DOS with respect to the energy above HOMO level calculated from McWhorter’s model. The error bars represent compound errors that result from propagation of the uncertainties in \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) and transconductance
By combining McWorther’s model with an estimation of the Fermi energy for each measured point in the transfer curve (Eq. (5) in “Methods” section), we can directly extract the energy distribution of traps from the measured noise data. As shown in Fig. 3f, the data taken at various temperatures smoothly join and yield a trap DOS that is exponentially increasing towards the transport level. This trap distribution is in good agreement with determined distribution of trap DOS independently derived from the FET transfer characteristics by numerical simulation, as will be discussed later.
Comparison in noise level with various solution-processed semiconductors
In the last part of this work, the amplitude of \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) is compared among various solution-processed semiconductors. We have selected four different classes of semiconductors: (i) single-crystalline small molecule C8–DNBDT– NW with the best mobility of up to 13 cm2 V−1 s−1, (ii) C8–DNBDT–NW with the intermediate mobility ~4 cm2 V−1 s−1 and intentionally induced traps, (iii) polymeric semiconductor poly(2,5-bis(3-tetradecylthiophen-2-yl)thieno[3.2-b]thiophenes) (PBTTT), and (iv) amorphous oxide semiconductor Indium-Zinc-Oxide (IZO). Details of the device fabrication are given in “Methods” section. The logarithmic FET transfer characteristics for the four semiconductors are shown in Fig. 4a–d, where mobilities are estimated to be 13.6 cm2 V−1 s−1 for the best C8–DNBDT–NW, 3.4 cm2 V−1 s−1 for C8–DNBDT–NW with intentionally reduced mobility, 0.03 cm2 V−1 s−1 for PBTTT, and 5.7 cm2 V−1 s−1 for IZO. Note that, for comparison, the C8–DNBDT–NW OFET (ii) with relatively low mobility was fabricated with an intentional introduction of imperfections in the self-assembled monolayer film (see “Methods” section). Together with transfer characteristics, the channel size normalized \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) (\(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) × W × L) are plotted in Fig. 4e–h, such that the amplitude of noise can be compared directly regardless of the channel dimension. The 1/f noise is seen in the entire frequency bands for C8–DNBDT–NW and IZO, whereas for PBTTT a significant deviation from 1/f is found particularly in the high frequency regime, which is attributed to thermal noise (white noise). We further investigated the \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) at higher-frequency regimes (see more details in Supplementary Fig. 8 and Supplementary Note 5). As a result, it can be concluded that the 1/f noise in C8–DNBDT–NW is remarkably lower compared to PBTTT and IZO, which is unambiguously because the trap DOS for C8–DNBDT–NW is low thanks to the vanishingly small structural disorder. Figure 5 summarizes the energy-dependent trap DOS for the four different semiconductors, where symbols correspond to the trap DOS determined experimentally from noise measurements (Fig. 4) and the black lines represent the trap distribution derived from the transfer characteristics via numerical modeling37,39,40 (see details in Supplementary Fig. 9 and Supplementary Note 6). The magnitudes of the trap DOS derived from two separate measurements are in reasonable agreement. Particularly, for organic single-crystals the energy distribution of trap DOS typically found in OFETs, that is, trap DOS increases as EF approaches the edge of valence band, is verified. The observed deviation for the other two materials (PBTTT and IZO) may arise from an unavoidable bias stress effect (see time domain profiles in Supplementary Fig. 4). The good agreement of the two trap density extraction methods is a clear evidence, that the trap states influencing the steady state I − V curves and the trap states giving rise to the 1/f noise are essentially the same ones. We do not speculate, but merely comment on the possible origin of traps in the present C8–DNBDT–NW single crystal. Judging from the comparison between C8–DNBDT–NW OFETs situated with (i) and (ii), trap DOS is apparently influenced by the quality of semiconductor/dielectric interface; random potential, which may be induced by imperfection of surface treatment of dielectric interface, can be a major impediment not only for solution crystallization, but also for charge transport. Given the fact that the trap DOS for rubrene single crystals grown by physical vapor transport is measured to be significantly lower41, residual solvent may induce additional traps in our solution-processed crystalline films. However, in recent synchrotron X-ray diffraction measurements, we do not see any trapped solvent molecules in the bulk crystal structure of C8–DNBDT–NW8. We therefore assume the trapped solvent effect to be more significant in polymeric semiconductors because they may have free space to capture the solvent molecules42. Overall, the present results manifest that noise spectroscopy will be a powerful tool to extract the trap DOS in organic semiconductors, and the usage of single-crystal form of organic semiconductors is highly advantageous not only in terms of mobility, but in particular for achieving remarkably low 1/f noise levels.
Comparison of noise level for various solution-processed semiconductors. Transfer and \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) characteristics of (a, e) the best C8–DNBDT–NW, (b, f) the C8–DNBDT–NW with intermediate mobility by intentionally induced SAM imperfection, (c, g) polymeric semiconductor PBTTT, and (d, h) oxide semiconductor IZO. The steeper the subthreshold regime the lower the noise level
Consistent results from two different trap DOS calculations using the noise or the transfer curves. Trap DOS for the best C8–DNBDT–NW (red), the C8–DNBDT–NW with intermediate mobility by intentionally induced SAM imperfection (orange), polymeric semiconductor PBTTT (green), and oxide semiconductor IZO (blue). Symbols denote the trap DOS determined experimentally from noise measurements (Fig. 4). Black lines represent those computed from transfer characteristics (see Supplementary Note 6). The error bars represent compound errors that result from propagation of the uncertainties in \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) and transconductance
Discussion
We summarize our key findings in Table 1. \(S_{I_{\mathrm{D}}}{\mathrm{/}}I_{\mathrm{D}}^2\) obtained for the best quality of C8–DNBDT–NW FETs shows remarkably low noise level compared to other solution-processed semiconductors. The low-frequency noise essentially defines the sensitivity of amplifiers and transducers embedded in sensors43, where the amplitude of observable signal can be expressed as an integral of (1/f)2. Therefore, the observed low 1/f in organic single crystals would be highly advantageous for practical electronic sensors and amplifiers. In addition, the single crystal of C8–DNBDT–NW would provide an ideal platform for a high-speed operation of flexible organic electronics. The corner frequency is the characteristic frequency at which the 1/f approaches to that of thermal or shot noise (referred to as white noise). Because the 1/f noise level is the main contributor to phase noise in the oscillating system, lowering the 1/f noise at high frequency directly leads to improvement of stability and durability for communication applications. The observed corner frequency in C8–DNBDT–NW -FETs is ~ 50 kHz, which is significantly higher than that for any other organic semiconductor. Finally, we discuss how the noise level obtained for the present organic single-crystal semiconductors is comparable to that for other van der Waals semiconductors. Low-frequency 1/f noise has been extensively studied in van der Waals materials, such as graphene, and transition metal dichalcogenides. 1/f noise levels in these semiconductors are found to be superior by 2–3 orders of magnitude than that for organic single crystal semiconductors (see Supplementary Fig. 10 and Supplementary Note 7). A characteristic noise feature for van der Waals semiconductors follows the Hooge’s model, suggesting that the noise originates due to mobility fluctuations which are caused by scattering of carriers in bulk44. In contrast, we demonstrate here that noise for organic semiconductors is found to be McWhorter’s model, and can be suppressed by reducing interfacial trap DOS. Thus, it should be emphasized that reducing trap DOS will be a key engineering for further improving noise level in organic FETs.
In conclusion, we have successfully demonstrated the wide-band noise spectroscopy in a state-of-the-art organic single crystal. Comprehensive noise measurements presented in this work verified that the carrier trap/release is the source of noise. The McWhorter’s model is applicable to the organic single-crystal FETs. Given the low trap DOS in C8–DNBDT–NW, the single crystal form of organic semiconductors gives rise to remarkably low noise level compared to any other solution-processed semiconductors, including amorphous oxides. In practice, the demonstrated low noise feature will be highly advantageous for high-speed operation of organic integrated circuits.
Methods
Device fabrication
A 100 nm-thick Si substrate with a thermally grown SiO2 layer was precleaned by sonication with acetone and 2-propanol for 10 min each, and then treated with UV-O3 for 30 min. A self-assembled monolayer (SAM) of 2-(phenylhexyl)trimethoxysilane was formed on the surface by vapor deposition at 120 °C for 3 h. Organic crystalline films of C8–DNBDT–NW were then grown from a 0.025 wt% 3-chlorothiophene solution using the edge casting technique described. The solution was dropped to a preheated substrate (55 °C) and held with a small glass blade, such that upon evaporation of the solvent a crystal is grown towards the edge of the blade. Subsequently, the film was annealed at 55 °C in vacuum to remove residual solvent. The thickness of the crystalline films was measured to be 30 nm. Au was deposited through a metal mask to form the source/drain electrodes. Organic layers were patterned by dry-etching processes with an Yttrium Aluminum Garnet (YAG) laser (266 nm). To control the mobility of C8–DNBDT–NW, an imperfection of SAM was intentionally introduced by reducing the process temperature (~ 100 °C) during vapor deposition process, where the surface contact angle was measured to be 90 degree, (normally 78–82 degree for an ideal single crystal growth). PBTTT was deposited on SAM treated SiO2 via spin coating from 1.0 wt% of o-dichlorobenzene solution, and then annealed at 180 °C for 30 min45. IZO was deposited a precleaned SiO2 substrate via spin coating of a precursor solution, which consists of indium nitrate nonahydrate and zinc nitrate hexahydrate (In : Zn = 3 : 2) dissolved in 2-methoxyethernol. After spin coating, the resulting thin film was annealed at 350 °C for 4 h46. Thermally evaporated Al was used for source and drain electrodes.
Electronic noise model
It has been known that the low-frequency electronic noise commonly observed in OFETs is considered to be flicker noise (1/f noise). Among various models of 1/f noise, the most common manifestation is the McWhorter’s model23,24,25,26, that is also used to interpret 1/f noise in conventional Si metal-oxide-semiconductor (MOS) FETs35. McWhorter’s model takes the carrier capture/emission to the channel into account; the fluctuation of the number of carrier δn leads to current fluctuation, δI ∝ e(δn)μ. Because charge transport mechanism in disordered semiconductors is believed to be hopping transport, the carrier trapping/de-trapping process is likely to contribute to δn. The power spectral density in the current noise, \(S_{I_{\mathrm{D}}}\) specifically in FETs is described as;
where gm, kB, λ, N, f, and Ci are a transconductance, the Boltzmann constant, tunnel attenuation length, trap DOS, frequency, and capacitance of gate dielectric. It is more convenient to use current-normalized \(S_{I_{\mathrm{D}}}\) as;
where ID is the drain current. As clearly seen in both equations, the noise follows 1/f. To estimate trap DOS (N), we used the tunnel attenuation length λ = 4.2 nm, which is equivalent to the thickness of monolayer C8–DNBDT–NW25,26. It should be noted that, in OFETs, one has handled the alternative description of 1/f, namely Hooge’s model36. However, since the model describes electronic noise from a bulk of semiconductors, it is not acceptable to any FETs whose electrical conduction takes places at the interface. To avoid conceptional failure, we did not use the Hooge’s model. At a characteristic frequency, namely the corner frequency, 1/f noise upcoverts to high frequencies, and eventually approaches to f-insensitive thermal or shot noise (white noise).
Estimation of the Fermi energy relative to the transport level
To address the energy distribution of trap DOS, we estimated the effective Fermi energy relative to the transport level as follows41; Given the Debye length \(\left( {\lambda _{\mathrm{D}} = \sqrt {\epsilon k_{\mathrm{B}}T{\mathrm{/}}ne^2} } \right)\), where \(\epsilon\) is the permittivity of the organic semiconductor, the drain current (ID) can be written as:
The concentration of the mobile charges (n) should be given by Maxwell-Boltzmann statistics as:
where NBand is the number of states in the transport level and ΔE = EF − Ec is the Fermi energy relative to the transport level Ec. Combining Eqs. (3) and (4) yields:
Equation (5) allows the estimation of the Fermi energy and the energy of the deep trap states directly from macroscopic values.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author (Shun Watanabe; swatanabe@edu.k.u-tokyo.ac.jp) upon request.
References
Takeya, J. et al. Very high-mobility organic single-crystal transistors with in-crystal conduction channels. Appl. Phys. Lett. 90, 102120 (2007).
Minemawari, H. et al. Inkjet printing of single-crystal films. Nature 475, 364 (2011).
Mitsui, C. et al. High-performance solution-processable n-shaped organic semiconducting materials with stabilized crystal phase. Adv. Mater. 26, 4546–4551 (2014).
Uno, M. et al. High-yield, highly uniform solution-processed organic transistors integrated into flexible organic circuits. Adv. Electron. Mater. 3, 1600410 (2017).
Yamamura, A. et al. Painting integrated complementary logic circuits for single-crystal organic transistors: a demonstration of a digital wireless communication sensing tag. Adv. Electron. Mater. 3, 1600456 (2017).
Uno, M. et al. Short-channel solution-processed organic semiconductor transistors and their application in high-speed organic complementary circuits and organic rectifiers. Adv. Electron. Mater. 1, 1500178 (2015).
Steudel, S. et al. 50 mhz rectifier based on an organic diode. Nat. Mater. 4, 597–600 (2005).
Yamamura, A. et al. Wafer-scale, layer-controlled organic single crystals for high-speed circuit operation. Sci. Adv. 4, eaao5758 (2018).
Kjellander, B. C. et al. Optimized circuit design for flexible 8-bit rfid transponders with active layer of ink-jet printed small molecule semiconductors. Org. Electron. 14, 768–774 (2013).
Cantatore, E. et al. A 13.56-mhz rfid system based on organic transponders. IEEE J. Solid-State Circuits 42, 84–92 (2007).
Kogan, S. Electronic Noise and Fluctuations in Solids (Cambridge University Press, Cambridge, 2008).
Hooge, F., Kleinpenning, T. & Vandamme, L. Experimental studies on 1/f noise. Rep. Progress. Phys. 44, 479 (1981).
Balandin, A. A. Low-frequency 1/f noise in graphene devices. Nat. Nanotechnol. 8, 549–555 (2013).
Ante, F. et al. Contact resistance and megahertz operation of aggressively scaled organic transistors. Small 8, 73–79 (2012).
Moon, J. et al. Low-phase-noise graphene fets in ambipolar rf applications. IEEE Electron Device Lett. 32, 270–272 (2011).
Bid, A., Bora, A. & Raychaudhuri, A. 1/f noise in nanowires. Nanotechnology 17, 152 (2005).
Kang, H. & Subramanian, V. Measurement and analysis of 1/f noise under switched bias in organic thin film transistors. Appl. Phys. Lett. 104, 9_1 (2014).
Ke, L. et al. Low frequency noise analysis on organic thin film transistors. J. Appl. Phys. 104, 124502 (2008).
Ke, L. et al. Impact of self-assembled monolayer on low frequency noise of organic thin film transistors. Appl. Phys. Lett. 93, 153507 (2008).
Necliudov, P., Rumyantsev, S., Shur, M., Gundlach, D. & Jackson, T. 1/f noise in pentacene organic thin film transistors. J. Appl. Phys. 88, 5395–5399 (2000).
Martin, S. et al. Flicker noise properties of organic thin-film transistors. J. Appl. Phys. 87, 3381–3385 (2000).
Vandamme, L., Feyaerts, R., Trefán, G. & Detcheverry, C. 1/f noise in pentacene and poly-thienylene vinylene thin film transistors. J. Appl. Phys. 91, 719–723 (2002).
Jurchescu, O. D. et al. Correlation between microstructure, electronic properties and flicker noise in organic thin film transistors. Appl. Phys. Lett. 92, 132103 (2008).
Conrad, B. et al. Characterization of a soluble anthradithiophene derivative. Appl. Phys. Lett. 97, 213 (2010).
Xu, Y. et al. Origin of low-frequency noise in pentacene field-effect transistors. Solid State Electron. 61, 106–110 (2011).
Xu, Y. et al. Understanding thickness-dependent charge transport in pentacene transistors by low-frequency noise. IEEE Electron Device Lett. 34, 1298–1300 (2013).
Podzorov, V., Menard, E., Rogers, J. & Gershenson, M. Hall effect in the accumulation layers on the surface of organic semiconductors. Phys. Rev. Lett. 95, 226601 (2005).
Sakanoue, T. & Sirringhaus, H. Band-like temperature dependence of mobility in a solution-processed organic semiconductor. Nat. Mater. 9, 36–40 (2010).
Hasegawa, T. & Takeya, J. Organic field-effect transistors using single crystals. Sci. Technol. Adv. Mater. 10, 024314 (2009).
Miyata, K. et al. Coherent singlet fission activated by symmetry breaking. Nat. Chem. 9, 983 (2017).
Soeda, J. et al. Inch-size solution-processed single-crystalline films of high-mobility organic semiconductors. Appl. Phys. Express 6, 076503 (2013).
Choi, H. H., Cho, K., Frisbie, C. D., Sirringhaus, H. & Podzorov, V. Critical assessment of charge mobility extraction in fets. Nat. Mater. 17, 2 (2017).
Sakai, K. et al. The emergence of charge coherence in soft molecular organic semiconductors via the suppression of thermal fluctuations. NPG Asia Mater. 8, e252 (2016).
Tsurumi, J. et al. Coexistence of ultra-long spin relaxation time and coherent charge transport in organic single-crystal semiconductors. Nat. Phys. 13, 994 (2017).
McWhorter, A. L. in: Semiconductor Surface Physics (ed Kingston, R. H.) 207–228 (University of Pensylvania Press, Philadelphia,1957).
Hooge, F. 1/f noise. Phys. B+ C. 83, 14–23 (1976).
Kalb, W. L., Haas, S., Krellner, C., Mathis, T. & Batlogg, B. Trap density of states in small-molecule organic semiconductors: a quantitative comparison of thin-film transistors with single crystals. Phys. Rev. B 81, 155315 (2010).
Mei, Y. et al. Crossover from band-like to thermally activated charge transport in organic transistors due to strain-induced traps. Proc. Natl Acad. Sci. 114, E6739–E6748 (2017).
Oberhoff, D., Pernstich, K. P., Gundlach, D. J. & Batlogg, B. Arbitrary density of states in an organic thin-film field-effect transistor model and application to pentacene devices. IEEE Trans. Electron Devices 54, 17–25 (2007).
Häusermann, R. et al. Device performance and density of trap states of organic and inorganic field-effect transistors. Org. Electron. 28, 306–313 (2016).
Blülle, B., Häusermann, R. & Batlogg, B. Approaching the trap-free limit in organic single-crystal field-effect transistors. Phys. Rev. Appl. 1, 034006 (2014).
Nikolka, M. et al. High operational and environmental stability of high-mobility conjugated polymer field-effect transistors through the use of molecular additives. Nat. Mater. 16, 356 (2017).
Motchenbacher, C. D. & Connelly, J. A. Low Noise Electronic System Design (Wiley, New York,1993).
Karnatak, P., Paul, T., Islam, S. & Ghosh, A. 1/f noise in van der waals materials and hybrids. Adv. Phys.: X 2, 428–449 (2017).
Fujimoto, R. et al. Control of molecular doping in conjugated polymers by thermal annealing. Org. Electron. 47, 139–146 (2017).
Socratous, J. et al. Energy-dependent relaxation time in quaternary amorphous oxide semiconductors probed by gated hall effect measurements. Phys. Rev. B 95, 045208 (2017).
Conrad, B., Cullen, W., Yan, W. & Williams, E. Percolative effects on noise in pentacene transistors. Appl. Phys. Lett. 91, 242110 (2007).
Acknowledgements
S.W. thanks PRESTO-JST “Hyper-nano-space design toward Innovative Functionality” (grant no. JPMJPR151E) and Leading Initiative for Excellent Young Researchers of Japan Society of the Promotion of Science (JSPS). T.O. thanks PRESTO-JST “Molecular Technology and Creation of New Functions” (grant no. JPMJPR13K5) and “Scientific Innovation for Energy Harvesting Technology” (grant no. JPMJPR17R2) for financial support. This work was supported by JSPS KAKENHI grant nos. JP17H06123 and JP17H06200.
Author information
Authors and Affiliations
Contributions
R.H. and H.S. conceived, designed, and performed experiments. A.Y. helped device fabrications. B.B. and H.S. performed low-temperature noise measurements. S.W., H.S., R.H., and B.B. analyzed the data, and interpreted the results. S.W. wrote the manuscript with significant input from R.H., B.B., and J.T. T.O. synthesized and purified C8–DNBDT–NW. S.W. and J.T. supervised this work. All authors discussed the results and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Watanabe, S., Sugawara, H., Häusermann, R. et al. Remarkably low flicker noise in solution-processed organic single crystal transistors. Commun Phys 1, 37 (2018). https://doi.org/10.1038/s42005-018-0037-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0037-0
This article is cited by
-
Two-dimensional hole gas in organic semiconductors
Nature Materials (2021)
-
Charge transport in high-mobility conjugated polymers and molecular semiconductors
Nature Materials (2020)
-
Next-generation organic semiconductors driven by bent-shaped π-electron cores
Polymer Journal (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.