Introduction

Coordinated motion is crucial for the effective functioning of cilia and flagella, which are the elements of eukaryotic cells involved in generating fluid flow and motility1,2,3,4. Motile flagella and cilia also interact with the velocity field in the fluid, which is in the low Reynolds number (Re) regime5,6. These important organelles act simultaneously as mechanical actuators and mechanical sensors7. In arrays of cilia, the beating is known to be synchronized under normal conditions, and the synchrony helps to generate wave-like patterns called metachronal waves8,9,10. While this phenomenon could, in principle, result from contributions from a wide range of different mechanisms, such as excluded volume interactions or biochemical signaling, long-range hydrodynamic interactions provide a rich and versatile means of achieving coordination11,12,13,14. Synchronization is a general phenomenon15, and the class of driven microscopic mechanical actuators with hydrodynamic coupling offers a rich phenomenology16. We aim to understand how architectures leading to stable synchronized states of multiple cilia could have evolved, and this could be exploited in engineering artificial cilia systems17,18,19 and micro-swimmers20,21,22,23,24,25.

The bi-flagellated alga Chlamydomonas reinhardtii has been a test-bed for experiments exploring synchronization of flagella26. Direct hydrodynamic interaction can describe the phase-locked cilia dynamics when the alga is mechanically clamped27, in conjunction with elasticity-mediated coupling28, while for a freely swimming alga the hydrodynamic flows resulting from swimming are sufficient to keep the two cilia in synchrony29. While these studies have shed considerable light on the underlying mechanisms behind flagella synchronization, the complexities involved in working with biological systems (such as the possibility of inflicting several changes of different nature when using mutations) makes it desirable to have complementary studies on simpler and more controllable systems.

Particle-based conceptual models have been extremely helpful in understanding the underlying mechanisms behind the dynamic coordination16. Experimental and theoretical studies have identified the role that geometry9,30,31,32,33,34, type of drive or beat pattern35,36,37,38, variability of the intrinsic frequencies39, and details of the driving potential30,37,40,41,42 can have on the emerging dynamics of coupled arrays of driven colloidal phase oscillators. By enabling selective control of individual parameters, and providing analytical results in some limiting cases32,36,40, these models form a solid foundation to build our understanding of natural systems such as mucociliary tissues: they maintain the correct far-field form of the hydrodynamic flow caused by a cilium, they can describe the presence of a nearby solid surface, and most importantly, they can account for the physiological properties of the beating cilia (i.e., shape of the stroke, with power and recovery phases) by matching the properties of the cilia cycles in living systems as the driving rule. Since phase-dependent forces exerted by a flagellum on the fluid have been measured in living systems such as Chlamydomonas27,43, quantitative linking between the models and the living filaments has become more accurate27,37, and the models can be made more realistic.

A series of novel results has been obtained modeling cilia as rotors36,44,45, with recent work40 probing independently the flexibility of the orbit45,46 or the beat pattern36 in the force profile, and their corresponding contributions to determining the strength of synchronization. A combination of the two effects has been observed in ref. 41, but not described by a formal theory. Moreover, the experimentally observed run-and-tumble behavior of Chlamydomonas47, which is a priori not an expected behavior of the system due to the continuous nature of the configuration space of the beating cilia, can be understood in the context of a conceptual three-sphere model with intrinsic noise in the amplitude of the beat pattern48. It has also been demonstrated within the same model that modulating the beat pattern can lead to control over the state of synchronization49 as well as robust steering and phototactic response in the stochastic trajectory of freely swimming Chlamydomonas50.

The results discussed above hint at the fundamental notion that it might be possible to achieve control over the state of coordination between cilia by engineering the effective potential landscape so that more than one stable state of synchronization exists, and by precise tuning of the system near the boundaries between these states in the configuration space. Biological systems could achieve this by modulating the molecular motor activity or binding affinity, or by tuning the length and orientation of the cilia. This would provide a robust mechanism for controlling the system’s behavior through choosing the collective dynamical state.

Here, we combine experimental and theoretical investigations to demonstrate concretely how this scenario works using the rotor model of cilia. The theoretical work combines the two previously discovered contributions to synchronization (flexibility and beat pattern) and includes the effect of a nearby wall (as is relevant in many biological systems). It derives synchronization potentials not limited to phase differences close to the stable states as opposed to most studies on the “strength” of synchronization. Therefore, we provide the method for a full characterization of the synchronization properties in this system.

Results

Experimental realization of coupled “rotors”

The system is composed of two spherical beads moving on separate, almost circular, trajectories, both embedded in a plane at height h above a hard surface (Fig. 1a). The position of each bead i ∈ {1, 2} is described by a radius R i (which can deviate slightly from the predefined circle orbital radius R) and a phase angle ϕ i . The centers of the trajectories are separated by a distance d.

Fig. 1
figure 1

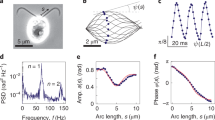
Complete control over the phase-locked state is demonstrated experimentally with colloidal rotors. a Schematic of optical tweezers “rotors” experiment: two rotors are made by driving colloidal particles along predefined closed circular trajectories of radius R, using a feedback-controlled optical trap to exert a force-clamp. The force magnitude depends on the angular position [F i  = F(ϕ i )] by maintaining the optical trap a distance ε(ϕ) ahead of the particle. In addition to the optical trap, the particles experience viscous friction, hydrodynamic interaction with each other, and thermal fluctuations. The confinement to the circular trajectory is soft, and the radius can deviate from R. This arrangement results in a pair of rotating particles for which the phase difference is not controlled externally; we show that control over the strength of coupling and the properties of the dynamical steady state can be achieved by tuning a set of parameters. b An example of temporal evolution of the phase difference Δ = Φ1 − Φ2 between rotors when varying the amplitude A of the modulation force over time as indicated (δ = 3π/4, R = 4.63 ± 0.03 μm, d = 15.60 ± 0.03 μm and h = 10 ± 1 μm). In these experiments, the imposed optical force F(ϕ) = 6πηav(ϕ) has an angular dependence; c shows for one condition the imposed (line) and actual (points) force over an experimental run

Full size image

In the absence of coupling (e.g., at far distances), two rotors will exhibit a random phase difference. We observe and study the phase locking that can occur due to the presence of hydrodynamic coupling, and demonstrate how it is possible to achieve full control over the state of synchronization by small adjustments of the system’s physical parameters (Fig. 1b). A necessary condition for synchronization is a breaking of the time reversal symmetry11. This model system breaks symmetry because: (i) the trajectory is not infinitely rigid, as there is a harmonic radial restoring force Fi,r = −k r (R i  − R), where k r is the radial stiffness; (ii) the tangential force is not constant, F i (t) = F(ϕ i ) = k t ε(ϕ i ) where k t is the tangential stiffness. These factors represent in a coarse grained fashion the elastic properties and the mechanical activity (due to the internal forces) of biological cilia, which are themselves an open area of study51,52,53,54,55; the parameters can be chosen so that the far-field fluid flow approximates well the field created by a biological cilium of a specific system. We have chosen the family of driving forces described by

$$F\left( \phi \right) = F_0\left[ {1 + A\,{\mathrm{sin}}\,\left( {\phi + \delta } \right)} \right],$$
(1)

and investigate the modulation parameter, A and the angle at which the particle speed will be maximum or minimum, δ together with the flexibility and radius of the orbits, and the distance between them. Figure 1c shows an example of the angular dependence of the driving force acting on a single particle. Since we want to model synchronization of identical motile cilia, we drive the two particles (with independent feedback) with the same parameters.

We explore different values of R, d, and h, in the far-field limit in which the distance between the rotors is much larger than the size of the trajectory \(\left( {R/d \ll 1} \right)\). In all the cases, we also have \(\left( {R/a \gg 1} \right)\). We also examine a range of behavior when approaching solid surfaces, with h > d and h > d, but maintaining h > a.

Phase locking and synchronization of colloidal rotors

Force modulation can affect the state of synchronization. Two particles driven along a circular orbit interact through the hydrodynamic flow induced in the viscous solvent. This hydrodynamic coupling is sufficient to induce the synchronization of the two rotors. The resulting motion is phase-locked, either in-phase (IP) or at any other phase difference (out-of-phase, OP). It is convenient to use a geometrical gauge to rescale the phase Φ = Φ(ϕ) in such a way that, in absence of hydrodynamic interactions, the intrinsic phase velocity is constant: \({\dot{\mathrm \Phi }} = 2\pi /T_0 = {\mathrm{\Omega }}\).

The modulation parameter A can even be changed during a continuous run (hence keeping identical experimental conditions otherwise): Figure 1b shows how the phase difference Δ = Φ1 − Φ2 equilibrates within a few periods, and depends strongly on the modulation amplitude A of the force profile. In these experimental conditions (k r  ≈ 3 pN/μm and F0 ≈ 3 pN), the particles rapidly converge to stable phase-locked states. When the amplitude of the force modulation is sufficiently high, the locked state can flip from IP to OP. As shown in Fig. 1b, Δ tends to 0 (or 2π) for values of A ≤ 0.5, while the system converges to an OP motion (Δ ≈ π or −π) if A ≥ 0.65, independently of the initial positions of the two rotors. When A = 0.6, the system undergoes stochastic transitions between IP and OP locked states due to Brownian noise (see Supplementary Note 1 and Supplementary Figure 4 for a detailed experiment).

As discussed in the theory section, force modulation tends to stabilize either IP or OP depending on the amplitude of the driving force and geometric considerations, whereas flexibility (as determined by k r ) always favors IP. Playing these terms together allows to control phase-locking arbitrarily, and biological systems could have evolved to exploit this physical mechanism.

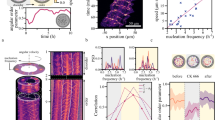
The orbit radius influences the phase locking. In addition to force modulation, geometric characteristics can be used to control the synchrony between two colloidal rotors. We focus here on how the radius of the orbit R influences the phase locking state of the rotors. Figure 2a, b shows the evolution of Δ with time for two different values of R. For every run, we explore different initial conditions. We observe a change from IP to OP phase locking upon increasing R. We rationalize this on the basis that increasing R (at fixed k r ) makes the trajectories effectively less deformable, so the force modulation will dominate over the orbit flexibility.

Fig. 2
figure 2

Tuning synchrony by modifying the radius of the orbit: Increasing R leads to out-of-phase (OP) as opposed to in-phase (IP) synchronization. a, b The corresponding Δ(t) in experiments (each trace a different initial condition) considering different R (increased from 3.17 to 4.6 ± 0.03 μm). Other parameters are fixed: A = 0.6, δ = 3π/4, d = 15.85 ± 0.03 μm, h = 10 ± 1 μm. In each run, k r fluctuates over ϕ, with an average value of 3 ± 1 pN/μm. c The corresponding rate of change of the phase difference\(\dot \Delta\) versus Δ, for the IP (a) and OP (b) cases; this data is used to calculate the effective potentials V(Δ) plotted in Fig. 3a, b. The rate distributions are represented as box plots, indicating the median (red markers), the first and third quartiles (blue boxes), and the maxima and minima (black bars)

Full size image

An effective potential can describe the stability of dynamical states. The observed dynamics of the two rotors can be used to construct an effective potential that “drives” the phase difference Δ. A complete range of initial conditions is covered for the different particle orbital radii explored in Fig. 2a, b. This procedure allows us to put together data from many experimental runs, to identify the stable and metastable synchronized states, and to compare with theory. The potential is calculated through the temporal evolution of the phase difference \(\dot \Delta (t)\). In experiments, \(\dot \Delta\) is calculated as

$${\dot{\mathrm \Delta }}\left( t \right) = \left({\mathrm{\Delta }}\left( {t + T_0} \right) - {\mathrm{\Delta }}\left( t \right)\right)/T_0,$$
(2)

where T0 = 2π/Ω. Each experimental set of runs in Fig. 2a, b gives a distribution of \(\dot \Delta\) for each value of Δ as shown in Fig. 2c. By first averaging over time, then the effective potential V(Δ) can be calculated as

$$V\left( \Delta \right) = - {\int}_{\hskip -1pt0}^\Delta {\dot{\mathrm \Delta }}\left( {\tilde \Delta } \right){\rm{d}}{\tilde{\mathrm \Delta }}.$$
(3)

This potential V(Δ) allows us to identify the stable and metastable locked states at a glance: by definition, the pair of rotors are phase-locked when there is a minimum in the potential, hence \({\dot{\mathrm \Delta }} = - {\rm{d}}V/{\rm{d}}{\mathrm{\Delta }} = 0\). Figure 3a, b shows the effect of the orbit radius and the amplitude A of the modulation of the driving force on V(Δ). While the IP state is usually dominant (because the orbit flexibility always favors IP), we find that an increase of either R or A can shift the synchronized state from Δ = 0 to about −π/2. Some combinations of parameters lead to two potential minima in V(Δ). Depending on the size of the potential barrier that separates them and the level of noise, the frequency of jumps from a minimum to the other can vary: at high noise level, the system can be considered as synchronized in a single global minimum, but with large fluctuations of Δ (see the steady states reached in Fig. 2); at moderate noise level, jumps can be distinguished (Supplementary Figure 4); and at low noise phase, jumps do not occur, and the system can remain trapped in a metastable state. Note that, except for A = 0, the potentials are tilted (despite that the oscillators are identical with the same intrinsic frequency, see the theoretical investigation below for the origin of this behavior). Such tilted potentials can induce biased phase slips between the oscillators (Supplementary Figure 5).

Fig. 3
figure 3

Experimental determination of an effective potential V(Δ) shows agreement with theory and simulation. a Influence of the orbit radius on the phase locked state; R = 3.17 and 4.6 μm, with d = 15.85 μm. Force profile parameters are A = 0.5 and δ = 3π/4. b Influence of the modulated driving force on the phase locked state: V versus Δ for a force modulation profile, varying A with δ = 3π/4. R = 3.17 μm and d = 15.85 μm are kept constant. Distance to the wall was fixed to h = 10 μm in all the cases. The reduced effective potential V, normalized by Ωa/d, versus Δ for an experiment with two rotors, with R = 3.17 μm, d = 15.85 μm, and h/d = 0.5: Two cases are addressed, A = 0.5 (c) converging to IP, and A = 0.7 (d) converging to OP. δ = 3π/4 in both cases. See Supplementary Note 2 for effects of varying h and δ

Full size image

Theoretical investigation of the model system

The experimental system can be described theoretically by a coupled-oscillator equation for the phases ϕ1(t), ϕ2(t)36,40, which is derived by balancing the force F i due to the optical tweezer and the viscous drag force g i . The viscous drag force is given by g i  = γ[v(r i ) − r i ], where r i is the particle velocity and v(r) is the flow velocity field. The latter is linearly related to the drag force on the particles as v(r1) = −G12 ⋅ g2 and v(r2) = − G21 ⋅ g1, where G ij  = G(r i , r j ) is the Green function of the Stokes equation with no-slip boundary condition at the substrate (Blake tensor)56. Solving the equation of force balance, F i  + g i  = 0, we obtain the coupled-oscillator equation in the form

$$\frac{{\dot \phi _i}}{{\omega _i}} = 1 + \mathop {\sum}\limits_{j \ne i} \left[ {\frac{{F\left( {\phi _j} \right)}}{{F\left( {\phi _i} \right)}}{\kern 1pt} {\mathbf{e}}_{t,i} \cdot \hat {\mathbf{G}}_{ij} \cdot {\mathbf{e}}_{t,j} - \frac{{F\left( {\phi _j} \right)}}{{k_rR}}{\kern 1pt} {\mathbf{e}}_{r,i} \cdot \hat {\mathbf{G}}_{ij} \cdot {\mathbf{e}}_{t,j}} \right].$$
(4)

Here, ω i  = F(ϕ i )/(γR) is the intrinsic phase velocity (i.e., the phase velocity in the absence of hydrodynamic coupling and for the unperturbed trajectory R i  = R), er,i = (cos ϕ i , sin ϕ i , 0) and et,i = (−sin ϕ i , cos ϕ i , 0) are the radial and tangential unit vectors, and \(\hat {\mathbf{G}}_{ij} = \gamma {\mathbf{G}}_{ij}\) is the normalized (dimensionless) Green function. The first term in the square bracket on the RHS describes the stiff limit as in ref. 40. We also include here in the second term a correction due to flexibility, for which we assume \(\lambda = F_0/k_rR \ll 1\) and only retain O(λ) terms in the equation (see Supplementary Note 3 for details of the derivation). Therefore, this theory includes the two main mechanisms for cilia synchronization.

Since we assume weak coupling, time evolution of the phase is dominated by the intrinsic phase velocity ω i  ∝ F(ϕ i ), the periodic modulation of which causes rapid oscillation of the phase difference ϕ1 − ϕ2. In order to extract the slow dynamics due to hydrodynamic coupling, we change the gauge of the phase variable from ϕ to Φ(ϕ) so that the latter has the constant intrinsic velocity Ω = 2π/T0. The intrinsic phase velocities \(\dot \phi = F\left( \phi \right)/\gamma R\) and \({\dot{\mathrm \Phi }} = {\mathrm{\Omega }}\) give \({\rm{d}}{\mathrm{\Phi }}/{\rm{d}}\phi = {\dot{\mathrm \Phi }}/\dot \phi \propto 1/F\left( \phi \right)\) and thus

$${\mathrm{\Phi }}\left( \phi \right) = 2\pi \cdot \frac{{K\left( \phi \right)}}{{K\left( {2\pi } \right)}},\quad K\left( \phi \right) = {\int}_0^\phi \frac{{{\rm{d}}\phi \prime }}{{F\left( {\phi \prime } \right)}}.$$
(5)

In the new gauge, the phase difference Δ = Φ1 − Φ2 becomes a slow variable as it is driven only by the hydrodynamic coupling. Using the mean phase \({\bar{\mathrm \Phi }} = \frac{1}{2}\left( {{\mathrm{\Phi }}_1 + {\mathrm{\Phi }}_2} \right)\) and substituting \({\mathrm{\Phi }}_{1,2} = {\bar{\mathrm \Phi }} \pm {\mathrm{\Delta }}/2\) into Eq. (4), we obtain the dynamical equation for Δ in the form \({\dot{\mathrm \Delta }} = W\left( {\bar \Phi ,{\mathrm{\Delta }}} \right)\). We can set \({\bar{\mathrm \Phi }} = {\mathrm{\Omega }}t\) up to the lowest order in the hydrodynamic coupling and coarse-grain the timescale by taking the period average as

$${\dot{\mathrm \Delta }} = \frac{1}{{2\pi }}{\int}_0^{2\pi } {\rm{d}}{\bar{\mathrm \Phi }}{\kern 1pt} {\kern 1pt} W\left( {{\bar{\mathrm \Phi }},{\mathrm{\Delta }}} \right) \equiv - \frac{{{\rm{d}}V\left( {\mathrm{\Delta }} \right)}}{{{\rm{d}}{\mathrm{\Delta }}}}.$$
(6)

This equation defines the effective potential V(Δ) up to a constant, which we fix by the condition V(0) = 0 as in Eq. (3). The integration has to be done numerically in general, but in some simplifying limits we can derive the expression of V(Δ) analytically. The Blake tensor G ij has the asymptotic form \(\hat {\mathbf{G}}_{ij} = G_I{\mathbf{I}} + G_D{\mathbf{e}}_x{\mathbf{e}}_x\) with the coefficients G I and G D given by G I  = G D  = 3a/4d when \(R \ll d \ll h\) (bulk, far-field limit), and G I  = 0, G D  = 9ah2/d3 for \(h,R \ll d\) (near substrate, far-field limit). In these cases, the sinusoidal force profile (Eq. (1)) yields

$$\begin{array}{*{20}{l}} {\frac{{V\left( {\mathrm{\Delta }} \right)}}{{\mathrm{\Omega }}}} \hfill & = \hfill & {\frac{{G_D}}{4}A^2{\mathrm{sin}}\left( {2\delta } \right)\left( {1 - {\mathrm{cos}}\,{\mathrm{\Delta }}} \right)} \hfill \\ {} \hfill & {} \hfill & { + \lambda \left( {2G_I + G_D} \right)\left[ {\left( {1 - A^2} \right)\left( {1 - {\mathrm{cos}}\,{\mathrm{\Delta }}} \right) + \frac{{A^2}}{4}\left( {1 - {\mathrm{cos}}\,2{\mathrm{\Delta }}} \right)} \right],} \hfill \end{array}$$
(7)

up to O(A2). The first term on the RHS arises solely from the force modulation, and leads to either in-phase (Δ = 0) or anti-phase (Δ = π) synchronization depending on the sign of sin(2δ). The second term describes the effect of flexibility and always favors in-phase synchronization. Thus we can control the dynamical equilibrium state by tuning the parameters A, δ, and λ. By taking into account near-field effects (i.e., keeping R/d finite), the effective potential takes an asymmetric shape (which is the case in Fig. 3), and its minimum can be tuned smoothly in the entire range −π < Δ < π. In general, we can decompose the effective potential into three parts as

$$V\left( {\mathrm{\Delta }} \right) = V_A\left( {\mathrm{\Delta }} \right) + V_\lambda \left( {\mathrm{\Delta }} \right) + V_{{\mathrm{cross}}}\left( {\mathrm{\Delta }} \right),$$
(8)

where V A (Δ) = V(Δ)|λ→0 is the contribution from force-modulation, V λ (Δ) = V(Δ)|A→0 is the flexibility-induced term, and Vcross(Δ) describes the cross-coupling effect. Two examples of the decomposed potential are shown in Supplementary Note 3 (Supplementary Figure 8).

To verify the theoretical description, we compare the experimentally constructed effective potentials with Eq. (7). Figure 3c, d shows such a comparison for two different values of A with the exact geometric characteristics (R, d, and h) and force parameters (k r and ε(ϕ)) extracted from the experiments. To account for the role of noise, we also performed stochastic Brownian Dynamics simulations using the method of Ermak and McCammon57, including hydrodynamic interactions through the Blake tensor (see for details Supplementary Note 4). We find a good agreement between the experimental potential, the analytical result of Eq. (7), and simulations, for both values of the force modulation parameter. In particular, both Eq. (7) and the simulations confirm the experimentally observed trend of the minimum of the potential shifting from IP (at Δ = 0) to OP (Δ = −π/2) upon increasing A.

This agreement helps us rationalize the parameters that are able to tune the shape of the potential, and hence the synchronized states. Firstly, in the particular example of Fig. 3, the two rotors lock into IP at a moderate value of the force modulation A = 0.5 because the potential is predominantly driven by the elastic component of V λ (Δ) (always locking into IP). When A is increased, the force modulation component V A (Δ) becomes more important, and for δ = 3π/4, the potential favors an OP synchronized state.

Stringent test: full control over phase locking

The synchronization of the two oscillators is summarized as a phase diagram in Fig. 4, obtained from simulations and experiments (a–c), and theory (d–f). In a large fraction of our parameter space the system synchronizes in phase, because the orbit flexibility favors this locked state. Strong deviations from IP can however be seen for various ranges of parameters, in particular at high modulation A, small h or small R, when δ = 3π/4. These parameters all increase the asymmetry of the geometric configuration of the system. Tuning them allows to control precisely the state of synchronization in a wide range of Δ. Simulations with thermal noise (Fig. 4a–c) show dependencies similar to the theory, although the average Δ state displays smoother variations with the parameters. Superimposed markers show experimental points classified as either IP (circles) or OP (squares) and are in good agreement with the simulations. To explain the discrepancy with the theory, we show in Fig. 4(g) (simulations) and Fig. 4(h) (theory) a cut of the phase diagram as indicated by the dashed lines in Fig. 4a, b. While in Fig. 4g, the graph still represents the same quantity \({\mathrm{arg}}\left( {\left\langle {{\sum} e^{i\Delta }} \right\rangle } \right)\), all local minima are indicated in the theory (Fig. 4h); the theory shows that a bifurcation occurs at about A = 0.7, with the appearance of a secondary stable minimum that becomes the global minimum. In the simulations, Fig. 4g, the transition is continuous. This is due to the fact that the barrier that separates the coexisting IP and OP minima for A > 0.4 is small and that switching between IP and OP is possible in the presence of noise. An example of such stochastic switching is explored in detail in Supplementary Figure 4. To further explore the role of the Brownian noise, we have also performed simulations at various noise strengths, see Supplementary Note 1.

Fig. 4
figure 4

Phase diagrams show control can be achieved to arbitrary phase locking Δ modulating rotor properties. a–c Simulations with thermal fluctuations (with experiments as markers), and d–f theory without noise. The average state in the simulations is the angle of the average direction, \({\mathrm{arg}}\left( {\left\langle {{\sum} e^{i{\mathrm{\Delta }}}} \right\rangle } \right)\), while it is simply the position of the global minimum of potential Δmin in the theory. The maps represent cuts of the phase diagram at h = 10 μm and δ = 3π/4 in a, d, R = 4.7 μm and δ = 3π/4 in b, e, and R = 4.7 μm and h = 10 μm in (c), f. The two types of markers in a–c show experiments with an average phase difference below () and above () Δ = 0.1 rad. The cut (line in a and d) is shown in detail in (g) and h for simulations and theory, respectively. Theory shows a first-order transition, which is smoothed out in the experiments and simulations. Error bars are standard deviation over all runs

Full size image

Discussion

This work provides a comprehensive description of the pair synchronization of a large class of oscillators: those described by a flexible fixed orbit, which is parameterized by (R(ϕ), F(ϕ), k r (ϕ)). While we have limited ourselves to constant R and k r , and to a given shape for F(ϕ), the extension of the theory to phase-dependent parameters with arbitrary shapes is straightforward. The theory therefore describes a model that is a good approximation of many systems of oscillators coupled by hydrodynamic interaction, as long as the oscillators can be coarse-grained. Our results illustrate the rich behavior of the system even with the limited set of parameters we have chosen. We showed that the pair of oscillators can synchronize in a variety of phase-locked states that can differ from the usual IP state, in particular when δ = 3π/4, at high modulation of the force A, close to the wall and for large orbits.

The results can help to understand synchronization of motile cilia. Depending on the biological system, different properties may be desired. In a carpet of many cilia with some fluctuations of the intrinsic properties from an oscillator to another, and of their geometric arrangement, it may be relevant to work in a region of the phase diagram for pair-oscillators that shows little variation of the locked state with respect to small variations of the control parameters.

On the contrary, a switch between two states with a small variation of a parameter may be relevant to other systems, and can be achieved by profiting from the bifurcation. The control mechanism underpinning large scale changes in cilia-driven flows in the brain during sleep is not known58, and it is tempting to speculate that this could be a manifestation of two quite different dynamical states that could be selected via small changes. The particular case of two cilia occurring in biflagellated organism, where the state of synchronization plays an important role in motility, has been addressed quantitatively in detail, and changes in the state of synchronization manifest as transitions between “run” and “tumble” phases47. The nature of the cilia coupling during the tumble phase is not fully understood: it could be either a “disordered beating”, which mathematically corresponds to one or more phase slips on an underlying tilted potential. However in a mutant of Chlamydomonas a stable anti-phase beating, corresponding to tumble motility, was observed59, indicating that perhaps a correct model description should be in terms of a stable phase-locked condition, with the possibility of tuning the locked phase. We cannot speculate here too much on how the underlying cilia drive parameters (hence orbits) would change in time during the tumble phase; changes could come from “biological modulations” internal to the cilium (calcium or motor activity), but also from the environment, since the cilium is coupled and subject to external forces. Conceptually our model would pick up variations of the cilia drive by modifying the shape of the potential (e.g., small changes in A, k r , or δ). At this level, the non-linearity of the cilium becomes itself important, and in future it might become possible to study the full intra/inter-cilium system. The concept of a potential that can be easily modulated by cilia beat properties is in contrast with the interpretation of the phenomenon where the tumble would be described by the system sliding down in a sine-like tilted potential (detuning leads to tilted potentials), with slips induced by fluctuations (thermal or biological noise).

Many biological systems must manage to balance robustness against noise (thermal, and from the “biological variations” such as detuning or biochemical noise) but also maintain the flexibility to display more than one state (e.g., tumble, which has a biological function).

We have shown that the complex shape of the phase diagram—that could be made even more diverse by including other parameters—, makes it in principle possible to manage both robustness against the fluctuations of some parameters and still retain possibility of a control of the state with other parameters. In this model, the hydrodynamic coupling is sufficient to provide such a fine control.

Methods

Building on our previous methods41,60, the displacement of the particles is captured at 230 frames/second and processed in real time, so that a feedback system can position an optical trap based on the current position of the particle, a distance ε tangentially ahead on the prescribed orbit. The trap is effectively a moving harmonic potential, and by prescribing a dependence of ε on the phase angle it is possible to modulate the tangential driving force around the orbit, whilst maintaining the radial stiffness constant (calibration is described in detail in Supplementary Information Methods and Supplementary Figure 1).

The trapping laser is time-shared by steering through an acoustic-optical deflector (AOD), updating the position of each optical trap based on the current position of the particle. Silica beads (Bangs Labs) with radius a = 1.75 μm are dispersed in a solution of water/glycerol with a viscosity η = 6 mPas. Images are taken through an AVT Marlin F-131B CMOS camera, and trap positions are updated at the same frequency, with a small delay (feedback time) of \(\tau _f \simeq 5\,{\mathrm{ms}}\); feedback thus occurs on a time scale much shorter than the relaxation time of the particle in the trap (\(\tau = \gamma /k \simeq 65{\kern 1pt} \,{\mathrm{ms}}\), where k is the trap stiffness and the harmonic traps have k r  = k t  = k, and γ = 6πηa is the Stokes drag). Videos are acquired for over 30 min and then analyzed using custom Matlab scripts.

Data availability

All relevant data are available from the authors.