Introduction

Quantum entanglement implies correlations beyond those allowed by classical models and plays a fundamental role in quantum metrology1. In optical metrology, photon pairs generated by spontaneous parametric downconversion (SPDC)2 are the most practical realization of correlated light beams. Because the process is coherent, the emitted photons are in essence entangled. However, it is of interest to experimentally be able to tune the correlations originating from quantum states, from purely quantum to classical; in particular, since it is not always obvious to distinguish between advantages in metrology originating from genuine entanglement and effects due to classical correlations3. We distinguish here effects due to the quantum nature of light, as sub-shot noise measurements4, from entanglement-induced processes. While some schemes where previously thought to be based on entanglement, they actually only rely on classical correlations. For instance in ghost imaging5, coincidence measurements from a thermal source allow one to reproduce the image of an object, without the need of nonclassical transverse correlations as originating from an SPDC source6. Another example can be found in photon number correlations. In SPDC, the downconverted photons are created pairwise, leading to a linear absorption rate for two-photon absorption processes7. However, classical thermal light also shows photon bunching, and thus, can be exploited to enhance two-photon absorption as well8. The quantum nature of dispersion cancellation was also subject to debate9, 10.

Energy entangled biphoton states are an essential tool in the prospect of experimentally realizing quantum spectroscopy experiments11, 12, and more generally for any energy-time two-photon metrology scheme, as for example quantum-optical coherence tomography13. Here the relevance of entanglement can also be misleading. For instance, in the case of two independent atoms, each of them excited by a single photon, a predicted enhanced absorption rate was first attributed to energy-time entanglement between the photons14. Yet it was later shown that only classical frequency anticorrelations are actually enhancing the absorption rate15. Similarly in ref. 16 a pump–probe scheme is proposed, where a sample is excited by a classical pulse and probed by a photon from an entangled pair. Again, such scheme rely fundamentally on classical energy correlations and not on genuine entanglement.

In this paper, we propose and experimentally realize a scheme to control the transition from quantum to classical correlations with energy correlated photons. A characteristic of entangled photon pairs is to show very strong energy correlations, together with strong temporal correlations. By introducing random phases on their spectral components and measuring the temporal shape of the two-photon wavefunction, we observe a decrease of the temporal correlations. The process is non-unitary and differs from interferometric schemes where a phase parameter control the degree of entanglement17. For polarization entangled photonic states, adding random phase has been shown to be a useful tool to generate, in a controlled way, the mixed states required to test quantum protocols18,19,20,21,22,23,24. We observe a decrease of the temporal correlations with increasing noise, that is well described by a model of the experiments. The possibility to control the amount of classical versus quantum energy correlations opens the way for practical demonstration of the genuine advantage of entanglement, for instance as in quantum spectroscopy schemes12.

Results

Theoretical model

Energy entangled photon pairs, as emitted by SPDC with a pump energy of ωp, are described by a two-photon join spectral amplitude (JSA) Λ(ωi, ωs) with ωi,s the energies of the idler and signal photons. One can define shifted energy variables with \({\Omega}_{\mathrm{i,s}}={\omega}_{{\mathrm{i,s}}} - \frac{{{\omega} _{\mathrm{p}}}}{2}\) such that the two photon states reads

$$\left| {\mathrm{\Psi }} \right\rangle = {\int} {\kern 1pt} {\mathrm{d}}{{\Omega }}_{\mathrm{i}} {\mathrm{d}}{{\Omega }}_{\mathrm{s}} {\mathrm{\Lambda }}\left( {{{\Omega }}_{\mathrm{i}},{{\Omega }}_{\mathrm{s}}} \right) \left| {{{\Omega }}_{\mathrm{i}}} \right\rangle _{\mathrm{i}}\left| {{{\Omega }}_{\mathrm{s}}} \right\rangle_{\mathrm{s}},$$
(1)

where \(| {{\it{\Omega }}_{{\mathrm{i,s}}}} \rangle _{{\mathrm{i,s}}}\) is the state of an idler, respectively signal, photon with energy Ωi,s. Equivalently the state can be written in the time basis

$$\left| {\mathrm{\Psi }} \right\rangle = {\int} {\kern 1pt} {\mathrm{d}}\tau _{\mathrm{i}}{\kern 1pt} {\mathrm{d}}\tau _{\mathrm{s}}{\kern 1pt} {\hat{\mathrm \Lambda }}\left( {\tau _{\mathrm{i}},\tau _{\mathrm{s}}} \right)\left| {\tau _{\mathrm{i}}} \right\rangle _{\mathrm{i}}\left| {\tau _{\mathrm{s}}} \right\rangle _{\mathrm{s}},$$
(2)

where the join temporal amplitude (JTA) \({\hat{\mathrm \Lambda }}\left( {\tau _{\mathrm{i}},\tau _{\mathrm{s}}} \right)\) is the 2D Fourier transform of Λ(Ωi, Ωs). Changing the variables to Ω± = (Ωi ± Ωs)/2 and τ± = τi ± τs we can write

$${\hat{\mathrm \Lambda }}\left( {\tau ^ + ,\tau ^ - } \right) = {\int} {\kern 1pt} {\mathrm{d}}{\it{\Omega }}^ + {\kern 1pt} {\mathrm{d}}{\it{\Omega }}^ - {\kern 1pt} {\mathrm{\Lambda }}\left( {{\it{\Omega }}^ + ,{\it{\Omega }}^ - } \right)e^{i{\it{\Omega }}^ + \tau ^ + }e^{i{\it{\Omega }}^ - \tau ^ - }$$
(3)

In the approximation of a monochromatic pump the JSA is fully defined by a one-photon spectrum λ(Ω)

$${\mathrm{\Lambda }}\left( {{\it{\Omega }}_{\mathrm{i}},{\it{\Omega }}_{\mathrm{s}}} \right) = \delta \left( \left( {{\it{\Omega }}_{\mathrm{i}} + {\it{\Omega }}_{\mathrm{s}}} \right)/2\right)\lambda \left( \left({{\it{\Omega }}_{\mathrm{i}} - {\it{\Omega }}_{\mathrm{s}}} \right) / 2\right) = \delta \left( {{\it{\Omega }}^ + } \right)\lambda \left( {{\it{\Omega }}^ - } \right),$$
(4)

with δ(x) being the Dirac delta function. The quantum state reduces then to

$$\left| {\mathrm{\Psi }} \right\rangle = {\int} {\kern 1pt} {\mathrm{d}}{{\Omega }} {\mathrm{\lambda }}({{\Omega }})\left| {{\Omega }} \right\rangle _{\mathrm{i}}\left| { - {{\Omega }}} \right\rangle _{\mathrm{s}}.$$
(5)

In this approximation, the SPDC process generates perfect energy anticorrelations in the continuous energy domain and therefore its entanglement content diverges to infinity. More generally, for quasi monochromatic pump, the entanglement of the state, as quantified by the entropy of entanglement, can be very high25.

In the time domain the JTA only depends on the time differences τ−.

$${\hat{\mathrm \Lambda }}\left( {\tau ^ + ,\tau ^ - } \right) = {\int} {\mathrm{d}}{{\Omega }}^ - \lambda \left( {{{\Omega }}^ - } \right)e^{i{{\Omega }}^ - \tau ^ - }$$
(6)

and

$$\left| {\mathrm{\Psi }} \right\rangle = {\int} {\mathrm{d}}\tau _{\mathrm{i}}{\mathrm{d}}\tau _{\mathrm{s}} \hat \lambda \left( {\tau _{\mathrm{i}} - \tau _{\mathrm{s}}} \right)\left| {\tau _{\mathrm{i}}} \right\rangle _{\mathrm{i}}\left| {\tau _{\mathrm{s}}} \right\rangle _{\mathrm{s}},$$
(7)

where \(\hat \lambda (\tau )\) is the Fourier transform of λ(Ω). It is related to the second-order correlation function defined by \({G}^{(2)} \left( {\tau _{\mathrm{i}}} , {\tau _{\mathrm{s}}}\right) = \left| {\left\langle {\tau _{\mathrm{i}}} \right|\left\langle {\tau _{\mathrm{s}}|{\mathrm{\Psi }}} \right\rangle } \right|^2\), such that \({G}^{(2)} (\tau ^ - ) \propto | {\hat \lambda (\tau ^ - )} |^2\). Separable states satisfy an inequality on the product of the variances V(τ−)V(Ω+) ≥ 1 which can be violated by entangled states26.

In order to demonstrate the real advantage of entanglement for quantum measurements, it is needed to be able to generate states of light where the energy correlations can be continuously tuned from purely quantum, as given by the state of Eq. (5) to fully classical, all other parameters of the state being egal. The classically correlated state is described by a mixed state

$$\hat \rho ^{{\mathrm{(c)}}} = {\int} {\mathrm{d}}{\it{\Omega }} p({{\Omega }})\left| {{\Omega }} \right\rangle _{\mathrm{i,i}}\left\langle {{\Omega }} \right|\left| { - {{\Omega }}} \right\rangle _{\mathrm{s,s}}\left\langle { - {{\Omega }}} \right|,$$
(8)

with \(p (\Omega) = \left| {{\mathrm{\Lambda }}({\it{\Omega }})} \right|^2\).

The main difference between \(\hat \rho ^{{\mathrm{(q)}}} = \left| {\mathrm{\Psi }} \right\rangle \left\langle {\mathrm{\Psi }} \right|\) and \(\hat \rho ^{{\mathrm{(c)}}}\) is the coherence terms between different frequencies. Assuming we can apply an arbitrary transfer function M j (Ω) on the photons, the entangled state \(\hat \rho ^{{\mathrm{(q)}}}\) transforms into \(\hat \rho _j = | {{\mathrm{\Psi }}_j} \rangle \langle {{\mathrm{\Psi }}_j} |\) with

$$\left| {{\mathrm{\Psi }}_j} \right\rangle = {\int} {\mathrm{d}}{{\Omega }} {\mathrm{\lambda }}({{\Omega }})M_j({{\Omega }})M_j( - {{\Omega }})\left| {{\Omega }} \right\rangle _{\mathrm{i}}\left| { - {{\Omega }}} \right\rangle_{\mathrm{s}} .$$
(9)

In order to generate an arbitrarily correlated state, we can induce phase decoherence on \(\hat \rho ^{{\mathrm{(q)}}}\). This is realized by applying random transfer functions M j (Ω) chosen from a set {M j (Ω)}, j ∈ {1, 2, …, N} with probabilities p j . The state then becomes

$$\hat \rho = \mathop {\sum}\limits_{j = 1}^N p_j\hat \rho _j.$$
(10)

We select the transfer functions to be dephasing operations M j (Ω) = exp(iϕ j (Ω)) with random phases

$$\phi _j({\it{\Omega }}) = \left\{ {\begin{array}{*{20}{l}} {0,} \hfill & {{\it{\Omega }} < 0,} \hfill \\ {X_{j,{\it{\Omega }}},} \hfill & {{\it{\Omega }} \ge 0.} \hfill \end{array}} \right.$$
(11)

The random variables Xj,Ω follow a Gaussian distribution with average 0 and variance σ2. They take not only a random value for different j but also for different Ω. The sum over all states in (10) can be evaluated as a sum over all transfer functions. For a sufficiently large mixture (N → ∞), it is given by the correlation function

$$\begin{array}{l}\hskip -117pt \left\langle {M_j({{\Omega }})M_j( - {{\Omega }})M_j^ \ast ({{\Omega }}\prime )M_j^ \ast ( - {{\Omega }}\prime )} \right\rangle \\ \hskip 18pt =\mathop {{{\mathrm{lim}}}}\limits_{N \to \infty } \mathop {\sum}\limits_{j = 1}^N p_j {\mathrm{exp}}\left\{ {i\left[ {\phi _j({{\Omega }}) + \phi _j( - {{\Omega }}) - \phi _j({{\Omega }}\prime ) - \phi _j( - {{\Omega }}\prime )} \right]} \right\}\\ \hskip -132pt = \left\{ {\begin{array}{*{20}{c}} {1,} & {\left| {{{\Omega }}\prime } \right| = \left| {{\Omega }} \right|} \\ {{\mathrm{e}}^{ - \sigma ^2},} & {\left| {{{\Omega }}\prime } \right| \ne \left| {{\Omega }} \right|.} \end{array}} \right.\end{array}$$
(12)

Making use of (12) in (10) leads to the final state

$$\hat \rho = {\mathrm{e}}^{ - \sigma ^2}\hat \rho ^{{\mathrm{(q)}}} + \left( {1 - {\mathrm{e}}^{ - \sigma ^2}} \right)\hat \rho ^{{\mathrm{(c)}}}.$$
(13)

By tuning the variance σ2 of the random phase distribution from zero to infinity, the final state undergoes a smooth transition from the entangled pure state \(\hat \rho ^{{\mathrm{(q)}}}\) to a classically frequency anti-correlated state \(\hat \rho ^{{\mathrm{(c)}}}\).

Experiment

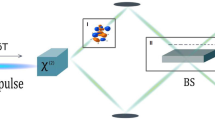
Figure 1 shows the experimental realization. A photon from a narrowband pump laser at 532 nm is downconverted into a pair of photons, idler and signal, each of them having a broad energy spectrum centered around 1064 nm with a width of about 40 nm, as measured by a spectrometer. The generated state is of the form of Eq. (5). In order to verify that the photons are also temporally correlated according to Eq. (7), the second-order correlation function G(2)(τ−) has to be measured by coincidence measurements with a time resolution shorter than its width. This is achieved by broadband up-conversion of both photons in a second nonlinear crystal27, 28, and by applying the required transfer functions on the photons spectrum with the help of a spectral shaper29. The later is inspired from ultrafast optics and combines dispersive elements in a prism compressor configuration with a spatial light modulator (SLM). The dispersion introduced by the compressor is tuned by changing the position of the prisms. It is set such that the total dispersion induced by the optical setup from the source to the detection crystal is compensated. The fine tuning is performed by introducing a quadratic phase on the SLM. The width of the measured G(2)(τ−) is minimal when the dispersion is fully compensated. The entanglement in this configuration has been demonstrated by observing nonlocal dispersion compensation29 and was used for quantum information protocols30. Explicitly, the second-order correlation function is given by

$$G^{(2)}(\tau ) = \left| {{\int} {\mathrm{d}}{\it{\Omega }} \lambda ({\it{\Omega }})e^{i\Omega \tau }} \right|^2.$$
(14)

However, as only the even component of the transfer functions is relevant as seen from (9), we have to express G(2)(τ) solely in terms of experimentally measurable quantities. Using the symmetry property λ(Ω) = λ(−Ω), we derive the identity29

$$G^{(2)}(\tau ) = \left| {{\int} {\mathrm{d}}{\it{\Omega }} \lambda ({\it{\Omega }})e^{i|{\it{\Omega }}|\tau }} \right|^2 - 4\left| {\mathop {\int}\limits_0^\infty {\mathrm{d}}{\it{\Omega }} \lambda ({\it{\Omega }}) {\mathrm{sin}}({\it{\Omega }}\tau )} \right|^2$$
(15)

The first term in the right-hand side can be implemented by a transfer function

$$M_{\mathrm{a}}({\it{\Omega }},\tau ) = \left\{ {\begin{array}{*{20}{c}} {e^{ - i{\it{\Omega }}\tau /2},} & {{\it{\Omega }} < 0} \\ {e^{i{\it{\Omega }}\tau /2},} & {{\it{\Omega }} \ge 0,} \end{array}} \right.$$
(16)

and the second term by a transfer function

$$M_{\mathrm{b}}({\it{\Omega }},\tau ) = \left\{ {\begin{array}{*{20}{l}} {1,} \hfill & {{\it{\Omega }} < 0} \hfill \\ {{\mathrm{\sin}}({\it{\Omega }}\tau ),} \hfill & {{\it{\Omega }} \ge 0.} \hfill \end{array}} \right.$$
(17)

Therefore, G(2)(τ) can be computed by taking the difference between two measured count rates G(2)(τ) ∝ S(τ) = Sa(τ) − Sb(τ). Here, \(S_{\mathrm{a}}(\tau ) \buildrel\textstyle.\over= S[M_j({\it{\Omega }})M_{\mathrm{a}}({\it{\Omega }},\tau )]\) is the signal measured with a total transfer function given by the product of the transfer function of Eq. (16) and the random function given by Eq. (11) inducing decoherence; similarly, \(S_{\mathrm{b}}(\tau ) \buildrel\textstyle.\over= 4S[M_j({\it{\Omega }})M_{\mathrm{b}}({\it{\Omega }},\tau )]\) with the transfer function of Eq. (17).

Fig. 1
figure 1

Schematic of the experimental setup. The pump laser is focused by lens L0 into a PPKTP (Potassium titanyl phosphate) crystal and generates energy-time entangled photons at plane Σ0. The photons propagate through a four-prism compressor (P1–P4) and are imaged (lenses L1 and L2) to Σ2. The spatially separated spectrum is shaped by an spatial light modulator (SLM) at the symmetry plane Σ1. The residual pump is blocked by a beam dump (BD). In a second PPKTP crystal, the photons are detected by means of upconversion and the resulting upconverted photons are imaged by lenses L3 and L4 to a single photon counting module (SPCM), while the residual downconverted light is blocked by filters (F)

Full size image

Each of the signals needed to measure the time difference between signal and idler are averaged over 100 acquisitions of one second each with different random transfer functions implemented on the SLM, such that for k ∈ {a, b}

$$\langle S_k(\tau ,\sigma )\rangle \propto \left\langle {\left| {{\int} {\mathrm{d}}\Omega \lambda ({\it{\Omega }})M_k( - {\it{\Omega }},\tau )M_k({\it{\Omega }},\tau ){\mathrm{e}}^{i\left( {\phi _j({\it{\Omega }}) + \phi _j( - {\it{\Omega }})} \right.}} \right|^2} \right\rangle$$
(18)

Because of the linearity of the trace, it is valid to evaluate the signal contribution of each transfer function setting separately, and average over all j afterwards. The procedure is repeated for different values of σ.

The transfer function of the SLM is linear and disentangles the state by introducing phase decoherence31. As a consequence, we are able to reduce the temporal correlations without changing the energy correlations.

Figure 2a shows the results of the measured two photon temporal correlation functions for various levels of noise σ, together with curves computed from a model of the density matrix of the state. The parameters of the theory are determined by fitting the measurement with σ = 0 rad according to a model of the signal given by \({S} (\tau , {\sigma = 0})= B {\mathrm{cos}}\left( {\mu \tau } \right){\mathrm{e}}^{ - \sigma \prime ^2\tau ^2/2}\), with the fitting parameters B, μ and σ′. This model is justified by the fact that the entangled photon spectrum for the chosen SPDC phase matching can be well approximated by a double Gaussian curve given by

$$S(\omega ,\sigma = 0) = \frac{B}{{2\sigma \prime }}\left( {\mathrm{e}}^{ - \frac{{(\omega - \mu )^2}}{{2\sigma {\prime ^2}}}} + {\mathrm{e}}^{ - \frac{{(\omega + \mu )^2}}{{2\sigma{\prime} ^2}}} \right).$$
(19)

We find B = 708.71 Hz, σ′ = 0.022 rad fs−1, and μ = 0.0275 rad fs−1. The corresponding spectral width given by \(\sqrt {\sigma'^2 + \mu ^2}\) is 21 nm. It is smaller than the width measured with a spectrometer, as only a part of the SPDC spectrum is contributing to the upconversion signal. In the present experimental configuration it is not possible to measure directly the width of the effectively upconverted spectrum, which therefore is taken as a fitting parameter of the temporal measurement.

Fig. 2
figure 2

Time of arrival difference between signal and idler \(\left\langle {S(\tau ,\sigma )} \right\rangle\) for increasing amount of phase noise σ. a Dark count subtracted measurements (blue dots) and model (red curve), from top to bottom: σ = 0, 0.5, 1, 2, 10 rad. The error bars are calculated under the assumptions of a Poisson distribution. The shaded gray region indicates the averaging region that is used to estimate the background level; b Theoretical values of \(\left\langle {S(\tau ,\sigma )} \right\rangle\). The white dotted lines, labeled with numbers 1 to 5, indicate the cross sections, where measurements are taken

Full size image

In order to compare the the measurements with the theoretical model we compute \(| {{\mathrm{\Psi }}_j} \rangle\) as given by Eq. (9) for 10,000 random SLM settings, and simulate the corresponding expected signals. They are then averaged in order to compute the correlation function for arbitrary noise σ, as shown in Fig. 2b. It should be noted that we do not observe a broadening of the correlation peak, as it would be expected simply from dispersion, but a mixture of two features in the temporal curves. Apart from a decreasing correlation peak whose shape remains constant, we observe an increasing constant background. This is the component leading to a diverging time-difference variance V(τ−), as pointed out in ref. 26. The measured standard deviation of τ− rises from 37 fs for σ = 0 to 106 fs for σ = 10 rad, being here only limited by the temporal observation window of [−200, 200] fs. The model allows to compute the fractions of entangled state and classically correlated state as seen in Fig. 3a. They are equal for \(\sigma = \sqrt {{\mathrm{ln}}(2)} \approx 0.833\) rad. In order to further estimate the relative contributions of those two components of the signal, we evaluate the mean of the signal \(\left\langle {S(\tau ,\sigma )} \right\rangle\) in the range of τ ∈ {[−200, −180], [180, 200]} fs, indicated in Fig. 2a by the gray shaded region. The rising background is proportional to the fraction of \(\hat \rho ^{{\mathrm{(c)}}}\) in (13) that contributes to the measured mixture. For σ = 2 rad the mixture consists of less than 2% entangled states, and thus the background reaches its asymptotic value as seen in Fig. 3b. Its is measured to be (28.8 ± 1.8) Hz, in good agreement with the value given by the simulations of (26.93 ± 0.03) Hz.

Fig. 3
figure 3

a Fraction of classically correlated \(\hat \rho ^{{\mathrm{(c)}}}\) (red) and purely entangled states \(\hat \rho ^{{\mathrm{(q)}}}\) (blue) in the mixture as a function of the noise level σ; b Rising constant background of the signal \(\left\langle {S(\tau ,\sigma )} \right\rangle\) as a function of the noise level σ. Measured values from Fig. 2a (blue) and calculated curve (red). The error bars are calculated under the assumptions of a Poisson distribution

Full size image

Discussion

In conclusion, we have demonstrated the full control on the degree of quantum versus classical energy correlations in photon pairs by adding random phase noise on the photons spectrum. We have observed a reduction of the strength of the temporal correlations and the divergence of their variance in agreement with the theory. Such a tunable entangled source will be an essential tool to experimentally verify the fundamental advantage of entangled states against classical correlations in any setup relying on time-energy measurements.

Data availability

The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.