Introduction

A collection of cold atoms in a periodic optical potential1,2 is a useful tool for metrological applications as well as fundamental studies. Atomic clocks using optical lattices are reported to have ultrahigh resolution3. Studies on nonlinear dynamics and chaotic motion due to photon recoil and lattice amplitude modulation4,5,6 have been proposed based on the atomic motion corresponding to classically well-understood harmonic oscillators in the optical lattice. Josephson junction array of cold atoms7 in optical lattice, Landau–Zener tunneling8 by lattice acceleration, and Mott insulator–metal transition9 by using periodic modulation of the lattice amplitude have been investigated. As seen in these examples, cold atom systems have experimental advantages in realizing ideal lattice models. They are much more controllable than real electron systems10.

Recently, non-equilibrium dynamics of cold atoms has become an active research topic11,12, expanding our understanding based on the existing equilibrium physics. In particular, non-equilibrium steady states (NESSs), the stationary states with continuous flows among them, have drawn much interest among various non-equilibrium phenomena. For example, biochemical reactions such as ATP hydrolysis and other biomolecular motors are described by a stochastic NESS theory13. In quantum physics, NESS is suggested as a possible pathway to entanglement at high temperature14 and generation of high-temperature Bose–Einstein condensates15. Associated with an array of particles, a particular interest lies in asymmetric simple exclusion process (ASEP)16, describing a driven diffusive system of one-dimensional lattice of particles hopping to other sites at a certain rate along the lattice. A model of ASEP with the Langmuir kinetics, which includes absorption and desorption of particles in a lattice connected to a reservoir, is suggested17 to describe the NESS system of mRNA translation18, for example. Related to cold atom systems, several theoretical investigation on NESS19,20,21 as well as ratchet effect closely related to the principle of NESS was investigated by cold atoms in optical lattices22. Recently, observation of bistability in a driven superfluid in the context of NESS of cold atoms has been reported23. However, experimental observation of NESS with ASEP characteristics in a cold atom system has not been reported yet.

A hybrid trap combining a magneto-optical trap (MOT) and an optical lattice potential24 is a possible approach to facilitate such studies. This hybrid trap can be generated by a passively phase-stabilized MOT25,26 in which time-dependent phase fluctuation is canceled out to produce a stable optical lattice. The atoms affected by sub-Doppler cooling are then strongly confined at the local minima of the lattice potential27. They are in the so-called Lamb–Dicke regime (LDR)28 and their spectrum exhibits a Rayleigh peak as well as Raman sidebands spaced by the vibrational frequency Δωosc of the optical lattice. Previously, matter–wave tunneling among the optical lattice sites was observed by measuring the resonance fluorescence spectrum of the trapped atoms29.

It is suggested that the atoms interacting with radiation fields under an external drive can be in a NESS30. Likewise, in the aforementioned hybrid trap, a non-equilibrium situation can be achieved if the optical lattice is made to move at a certain speed. In this case, the lattice motion introduces a potential modulation in time and thus acts as an external drive. Moreover, the photon recoils present in the system make the atomic motion stochastic. Because of these processes, two different atomic motional states, one localized in the optical lattice and the other trapped as a cold gas in the background MOT, can coexist31 in the steady state with continuous flows between them. The coexistence of such motional states in the steady state would then establish an NESS.

In this paper, we investigate the dynamics of cold atoms in an NESS with ASEP characteristics in a hybrid trap of an moving optical lattice and a background MOT. The optical lattice is made to move by introducing a frequency detuning between the counter-propagating trap lasers in a phase-stabilized MOT. Dynamics of the atoms are observed non-destructively by measuring the resonance fluorescence spectrum of atoms with a photon-counting-based heterodyne technique32 for various lattice speeds. The high-resolution fluorescence spectrum then reveals different atomic motional states. The observed atomic dynamics are analyzed with a deterministic rate equation model describing transitions among the vibrational states of the optical lattice and the MOT cold-gas state. As a result, we can show that the atoms are in an NESS. Atoms localized by the lattice potential can be nonlocalized via tunneling through the lattice potential barrier due to the lattice motion. On the other hand, the nonlocalized atoms can be localized again in the lattice via momentum diffusion due to photon recoils33 in the background MOT. These transitions occur simultaneously and continuously while the population of each motional states are stationary.

Results

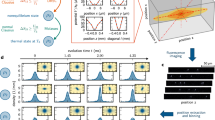
In our experiment, the details of which are described in Methods, the resonance fluorescence spectrum of atoms was measured for various trap-laser frequency difference Δω between 0 and 500 kHz, by which the speed of the moving optical lattice was determined to be between 0 and 0.34 m s−1. Five spectral peaks were observed in the spectrum when optical lattice was moving. We analyzed the spectra by fitting them with appropriate profiles as shown in Fig. 1a. The two broad peaks at both ends are made by the atoms that are not localized in the lattice but trapped as a cold gas in the MOT. We will call them “nonlocalized” in the optical lattice in short in the discussions below. These atoms scatter off the two different-frequency trap lasers, creating a peak around each trap-laser frequency. These atoms are also continuously subject to the sub-Doppler cooling by polarization gradient, which results in a non-Gaussian velocity distribution34. The distribution is well fit by a Voigt profile. A Gaussian profile does not fit the tail part of the distribution well. Root mean square error with the Gaussian fit outside the 1/e point of the distribution is five times larger than that with the Voigt profile. The middle three picks correspond to the atoms that are localized at the potential minima of the optical lattice and thus move along with the lattice. Let us call them “localized” in the optical lattice in short from now on. These atoms are in a state associated with the LDR. The atoms in LDR, confined in the optical lattice, exhibit three Lorentzian peaks: a Rayleigh peak in the center and Raman sidebands at both sides.

Fig. 1
figure 1

Observed resonance fluorescence spectrum of atoms. a Fitting the fluorescence spectrum. The broad peaks at both ends represent the atoms nonlocalized in the lattice but trapped in the background MOT. The narrow three peaks in the center represent the atoms localized in the lattice potential minima. The zero frequency corresponds to the atomic transition frequency minus 3Γ (red detuning). In the present frequency scale, the frequency of one trap laser is at +140 kHz and that of the other is at −140 kHz (Δω/2π = 280 kHz). b Fluorescence spectrum at various lattice speeds. The population of nonlocalized(localized) atoms increase(decrease) as the speed of the lattice increases

Full size image

By fitting the observed spectrum with the appropriate profiles, the proportions of the localized atoms as well as the nonlocalized atoms in the lattice is obtained, respectively. The number of the localized(nonlocalized) atoms in the optical lattice is proportional to the area under the inner three peaks(the outer two broad peaks). It is observed that as the lattice speed increases the peaks at both ends gets larger [Fig. 1b], which means the fraction of the atoms nonlocalized in the lattice increases.

Note that the peak heights of the nonlocalized atoms are different. This can be understood in the following way. As shown in Eq. (5) in Methods, the center of atomic cloud is shifted to a nonzero magnetic field region, where atoms experience the Zeeman shifts. As a result, the effective detunings of the σ+ and σ− trap beams experienced by the atoms in various ground-state magnetic sublevels are different, making the scattering rates of the σ+ and σ− polarization lasers differ significantly. Moreover, the scattered light by the σ+ and σ− trap beams are in different elliptical polarizations while the detectors are measuring only the polarization in a particular direction (horizontal polarization in the laboratory coordinates), further deepening the discrepancy. A detailed analysis on the asymmetric peak heights is given in ref. 35.

Signature of the localized atoms in the moving lattice

In our experiment, the optical lattice moves at the speed of vl = Δω/2k in the direction of the trap-laser beam with the higher frequency ω+Δω, where ω is the frequency of the lower-frequency trap-laser beam and k = ω/c with c the speed of light. If the atoms move along with the lattice while localized at the lattice potential minima, the higher(lower) frequency trap laser is Doppler shifted by −kvl = −Δω/2(+kvl = +Δω/2) in the rest frame of the moving atoms. The higher-frequency trap-laser beams propagate in x, y, and z directions, respectively, in the Cartesian coordinates, and therefore the resulting lattice velocity points to (1, 1, 1) direction, which is orthogonal to (−1, 1, 0) direction leading to our detector. Therefore, the light resonantly scattered from all six trap beams by these atoms into the detector direction would have the same frequency of ω+Δω/2. The Rayleigh peaks in the spectra shown in Fig. 2a occur at this frequency as confirmed in Fig. 2b and thus represent the atoms moving along with the lattice. The Rayleigh peak and two Raman sidebands on both sides are the signature of the atoms in LDR, confined in a space whose dimension is less than the wavelength λ, and therefore together they represent the atoms localized in the potential minima of the moving optical lattice.

Fig. 2
figure 2

Evolution of spectral peaks with the trap-laser frequency difference. a Evolution of the position of the Rayleigh peaks as the speed of the lattice increases. The frequency is measured with respect to the lower frequency ω of the trap lasers. b Rayleigh peaks occur at frequency ω+Δω/2, indicating that the contributing atoms move along with the lattice, i.e., localized at the potential minima of the lattice. Error bars are smaller than the symbol. c The center frequencies of the peaks corresponding to the nonlocalized atoms are slightly shifted away from the trap-laser frequencies. It is because the momentum distribution of the nonlocalized atoms are biased opposite to the lattice moving direction. The frequency is measured with respect to ω+Δω/2 and thus the trap-laser frequencies are at ±Δω/2. d Frequency difference (magnitude) between the peak position and the trap-laser frequency. The slower the lattice moves, the more biased is the momentum distribution of the nonlocalized atoms. e The velocity distributions of the nonlocalized atoms are illustrated at various lattice speeds. The black curve represents the atoms under momentum diffusion without being localized in the lattice potential minima. The red solid (dashed) curve represents the nonlocalized (localized) atoms in the lattice at an intermediate lattice speed. The blue solid (dashed) curve represents the nonlocalized (localized) atoms in the lattice at a slow lattice speed

Full size image

Biased momentum distribution of the nonlocalized atoms

The atoms nonlocalized in the lattice still undergo continuous scattering of the trap-laser beams, resulting in cooling of the atoms. In the steady state, therefore, these atoms acquire a certain momentum distribution36. Among these atoms, the atoms with their velocities close to the velocity of the lattice tend to be captured in the lattice and thus the distribution near the lattice velocity is decreased. As a result, the velocity distribution of the nonlocalized atoms is biased in the opposite direction to the traveling direction of the lattice. Figure 2c shows the experimental evidence of this bias. The broad peaks at both sides in the spectrum represents the resonance fluorescence of the nonlocalized atoms excited by the trap lasers with the frequencies ω and ω+Δω(Δω/2π = 280 kHz), respectively. The dashed red vertical line represents the frequency of trap beam at ω. If there is no bias in the atomic velocity distribution, the pick should be centered around this line. However, the peak is centered around the dashed blue line biased by about 47 kHz to the red. In addition, the peak on the right side is biased by about 51 kHz to the blue. Both observations indicate that the velocity distribution of the nonlocalized atoms is biased in the opposite direction to the lattice propagation direction.

As seen in Fig. 2d, the momentum bias is larger when the detuning of trap beam Δω, proportional to the speed of lattice, is smaller. We can explain this feature as follows. Suppose the optical lattice moves so fast that most of atoms are nonlocalized in the lattice while remaining as a cold gas in the background MOT. Their momentum distribution resulting from laser cooling would then be centered around v = 0, corresponding to a black curve in Fig. 2e. Now consider the case where the lattice moves at an intermediate speed corresponding to the red arrow in Fig. 2e. The atoms with a velocity similar to the lattice speed would then be localized in the lattice (red dashed curve). As a result, the distribution around that velocity is reduced (red solid curve), inducing the distribution to be biased to the opposite direction. If the speed of the lattice is further reduce close to zero, most of the atoms would be localized in the lattice (blue dashed curve), leaving only the atoms moving fast in the opposite direction to the lattice propagation direction. As a result, the distribution of the nonlocalized atoms is strongly biased to the opposite direction (blue solid curve).

Evolution of the nonlocalized state population with the lattice speed

The number of atoms localized in the lattice is proportional to the area under the Rayleigh peak and the Raman sidebands. Similarly, the number of nonlocalized atoms in the lattice is obtained from the area under the two Doppler-broadened peaks. The red open dots in Fig. 3a–c represent the relative population of the nonlocalized atoms as a function of the lattice speed. The relative population of the nonlocalized atoms increases with the lattice speed. Interestingly, the population increases with a small stepwise jump at a particular lattice speed indicated by arrows. This tendency can be observed more clearly when the trap depth is larger (with larger trap-laser intensity). This interesting feature is due to the transmittance of the first-excited vibration state of the atoms localized in one lattice node to neighboring ones as shown below.

Fig. 3
figure 3

Relative population of the nonlocalized atoms at various trap-laser intensity. Red open dots represent the populations from the experimental observation at various potential height U0 and the trap-laser intensity I0. a U0 = 840Er with I0 = 0.89 mW cm−2, b U0 = 1600Er with I0 = 1.8 mW cm−2, and c U0 = 2400Er with I0 = 2.7 mW cm−2, where Er is the photon-recoil energy with a value of Er/ħ = 3.86 kHz. Error bars are derived from the fitting errors as in Fig. 1a. Stepwise increase in population is observed in experiment. Red solid curves are the solutions of the rate equation, Eqs. (1), (2), and (3). The stepwise increase is shown to be due to the characteristic transmittance of the first-excited vibration state localized at a potential minimum of the moving lattice

Full size image

Discussion

Theoretical methods such as the quantum Bloch equation37 and the Monte-Carlo wave function method38 are usually employed in order to explain matter–wave effects in a modulated optical lattice. However, owing to the inherent complexity of MOT, it is difficult to apply those methods directly to the present problem. Moreover, even if we were able to do so, it would be difficult to obtain a clear physical picture. Instead, we take a different approach. First, we expect the present system to be describable in terms of a non-equilibrium steady state with continuous transitions among the localized vibrational states of the lattice and the nonlocalized state. We recall that the deterministic rate equation models—populations among states changing at deterministic rates—are applied when describing non-interacting driven dissipative bosonic systems30 and molecular motors39 in NESSs from a macroscopic point of view. Similarly, we adapt a rate equation model to explain the experimental results in Fig. 3a–c.

Our rate equation model describes the atomic transitions among the localized and nonlocalized motional states of atoms (Fig. 4). First, only the two lowest-bound states of a lattice node is considered in the model because the band structure of the three-dimensional optical lattice generated by the present passively stabilized MOT shows that only the ground and the first-excited vibrational states are tightly bound29,40. The atoms in the localized states are strongly confined in the lattice potential minima. On the other hand, the nonlocalized atoms are considered to be in a cold-gas state trapped in the background MOT. We consider the atomic motion in a one-dimensional lattice in the traveling direction of the optical lattice and neglect the atomic motion perpendicular to the lattice motion. It is because the motion to other directions in the rest frame of the moving optical lattice is suppressed by high potential barriers. In addition, the interstate transition rates in our rate equation are preaveraged over a time period T = lnode/vl, which is the time taken for the lattice to move one lattice period lnode. The reason for this averaging is because the lattice potential is periodic and thus the rapid atomic dynamics during the time period T is continuously repeated as the lattice moves. By such preaveraging, we can eliminate rapid changes occurring in the time scale of T in the rate equation and can deal with the slow evolution of the state populations. By the same reason, we only consider one lattice period denoted by lnode as shown in Fig. 4. The rate equation can then be written as

$$\dot a = - \frac{1}{T}\left[ {R(v_{\mathrm{l}}) + T_0(v_{\mathrm{l}})} \right]a + \frac{{R(v_{\mathrm{l}})}}{T}b + g(v_{\mathrm{l}})c$$
(1)
$$\dot b = \frac{{R(v_{\mathrm{l}})}}{T}a - \frac{1}{T}\left[ {T_1(v_{\mathrm{l}}) + R(v_{\mathrm{l}})} \right]b + f(v_{\mathrm{l}})c$$
(2)
$$\dot c = \frac{1}{T}\left[ {T_0(v_{\mathrm{l}})a + T_1(v_{\mathrm{l}})b} \right] - \left[ {f(v_{\mathrm{l}}) + g(v_{\mathrm{l}})} \right]c$$
(3)

where a and b are the populations of the ground and the first-excited bound states of the lattice potential as shown in Fig. 4, respectively, and c is the population in the nonlocalized state. We assume that nonlocalized atoms have a certain momentum distribution corresponding to the observed Doppler-broadened peaks in the spectrum. The quantities T0(vl) and T1(vl) are the transition amplitudes from the ground(the first excited) vibrational state to the nonlocalized state during the time period T. The rates f(vl) and g(vl) are the transition rates from the nonlocalized state to the ground and the first-excited vibrational states, respectively, whereas R(vl) is the transition amplitude between the two vibrational states during the time period T. Explicit formulae for these parameters are derived in Methods. Because what we observed in the experiment corresponds to a steady state, we solve the rate equation for the steady state by letting \(\dot a = \dot b = \dot c = 0\).

Fig. 4
figure 4

Schematics of the rate equation model. The lattice moves at a speed of vl. Because of the periodicity of the lattice potential, we only consider one lattice period denoted by lnode. By the same reason, we consider time evolution during T = lnode/vl. The populations in the ground(the first excited) vibration state is denoted by a(b) while the population in the nonlocalized state is expressed as c. The rates f(vl) and g(vl) and the transition amplitudes T0(vl), T1(vl), and R(vl) are defined in the text

Full size image

As explained in the previous section, the nonlocalized atoms have a biased momentum distribution due to the sub-Doppler cooling by the moving lattice. The atoms that have velocities around the moving lattice speed are cooled by the lattice and then become localized in the lattice. The probability of the atoms being cooled to the bound states of the lattice would decrease as the lattice speed increases. This trend is reflected in the transition rates f(vl) and g(vl) as shown in Fig. 5a. They were calculated by using Eqs. (8) and (9) in Methods, respectively.

Fig. 5
figure 5

Variation of the calculated transition rates and transition amplitudes with the lattice speed. a Transition rates f(vl) and g(vl) calculated by using Eqs. (8) and (9) in Methods, respectively. b Transition amplitude R(vl) between two bound states of the lattice during the time period T, calculated by using Eq. (12). Lattice potential height U0 = 1600Er corresponding to I0 = 1.8 mW cm−2 and the oscillation frequency ωosc/2π = 91 kHz are used with a free parameter η = 3 × 107 s−1 for numerical calculations. c–e Transition amplitude or transmittance of the atoms in the bound states during the time period T as the lattice speed increases in the case of three different potential heights. Parameters used in the calculations are as follows: c U0 = 840Er, d U0 = 1600Er, and e U0 = 2400Er. The black curve represents the transmittance of the ground state and the red curve corresponds to the first-excited state. Transmittance shape gets extended as the depth of the optical lattice potential increases

Full size image

The atoms in the bound states of the lattice would undergo mutual transitions between the bound states when the lattice is translated rapidly. We expect the transition amplitude R(vl) would increase as the lattice speed goes up and eventually reach 0.5 at very high lattice speeds. This is exactly what we observe in the numerically calculated R(vl) as shown in Fig. 5b.

When the lattice moves, some atoms localized in the lattice would tunnel through or go over the potential barrier to the neighboring lattice nodes. These atoms are no longer localized in the potential minima of the lattice and thus considered to be “nonlocalized.” They will end up in the cold gas in the background MOT. This transition to the nonlocalized state is closely related to the momentum distribution in the bound states. If the momentum distribution has a large component in the opposite direction to the lattice motion, the transition amplitude would be high. The probability amplitude of the ground state has a Gaussian distribution and thus its momentum distribution is also a Gaussian centered at zero momentum. The ground state is thus expected to show a smooth transition to the nonlocalized state as the lattice speed increases.

On the other hand, the probability amplitude of the first-excited state has a node in the center and its momentum distribution has two opposite momentum components (see Methods). As the lattice speed increases, the momentum component opposite to the lattice motion would undergo the transition to the nonlocalized state first. The momentum component in the same direction as the lattice motion would do so only when the lattice speed is larger enough. As a result, for the first-excited vibrational state we expect to see a stepwise transition to the nonlocalized state as the lattice speed increases. This trend is confirmed in the numerically calculated transition amplitudes T0(vl) and T1(vl) as shown in Fig. 5c–e.

The stepwise transmittance of the first-excited state is strongly reflected in the evolution of the nonlocalized state population as the lattice speed increases. Our rate equation model well reproduces the observed stepwise evolution of the nonlocalized state population as shown in Fig. 3 at three different potential heights. This agreement supports the validity of our rate equation model.

Based on the above analysis of the atomic dynamics, we conclude that our system is in an NESS. When a system is in an NESS, not only the system is in a steady state but also there must be non-vanishing currents among possible states. In our case, both conditions are satisfied. First, we know that the atoms are in a steady state because we can observe a stationary atom cloud as well as the spectrum of resonance fluorescence of atoms. We also know that the total number of atoms in the hybrid trap composed of the optical lattice and the background MOT is nearly unchanged when we vary Δω from 0 to 500 kHz as in Figs. 2, 3, and 5. It is because the trap-laser frequency is not changed much compared to the overall red detuning of 3Γ/2π = 18 MHz. The difference in the scattering rates of these frequency-detuned trap lasers is at most 0.9%.

Next, the biased momentum distribution of atoms in the nonlocalized state is a strong evidence that the unlocalized atoms are recaptured by stochastic momentum diffusion to the localized state in the optical lattice nodes. In other words, we have a continuous current of atoms from the unlocalized to the localized states. We also have a current in the opposite direction. Otherwise, all of the atoms localized in the moving lattice would move to the edge of the MOT and then escape from the MOT. This would result in a significant reduction of the total number of atoms in the hybrid trap when we move the optical lattice. Instead, we observed the total number of atoms almost unchanged. This indicates that the localized atoms in the lattice continuously undergo a transition to the nonlocalized state. The relative strength of these currents in opposite directions determine the relative populations in the localized and the unlocalized states as a function of the lattice speed. From these considerations, we conclude that our system is in an NESS41.

Generally, an NESS system is associated with a stochastic process for particles. In some cases, an additional external drive is present13. In our experiment, atomic momentum change due to light scattering of trap lasers can be considered as a stochastic process, and the moving lattice potential can be regarded as an external drive. Particularly, our system approximately suits the conditions of ASEP42. In ASEP, the particles in a lattice hop from one node to neighboring nodes asymmetrically, biased by an external drive. Moreover, hopping to a neighboring node already occupied by a particle is suppressed. In our case, tunneling or hopping rates to neighboring nodes are asymmetric because of the lattice motion. Moreover, only one atom can occupy a local minimum of the lattice potential because of the high light-assisted two-atom collision rate (~ 108/s at least)43 in each small volume of the local minima of the lattice potential.

When ASEP is combined with the Langmuir kinetics17, it can describe particle absorption from and emission to a reservoir of absorbates. In our system, the moving optical lattice plays a role of an external drive as well as absorbing sites and the nonlocalized atoms in the background MOT serve as absorbates. Under this setting, some atoms are localized at the potential minima of the optical lattice while some tunnel through the potential barrier to the adjacent potential minima. Moreover, some atoms in the nonlocalized state are captured to the optical lattice (absorption of absorbates), resulting in a biased momentum distribution of the atoms in the nonlocalized state. We also have some of the localized atoms undergo a transition to the nonlocalized state (emission to the reservoir). These considerations indicate that our system is in an NESS with characteristics of ASEP with Langmuir kinetics. Therefore, our system can be used to simulate the NESSs in various biochemical systems16,44. Interestingly, our system supports quantum-mechanical vibrational energy levels of atoms localized at the lattice nodes, which lacks in the standard ASEP model, and thus our system can be regarded as an extended model suitable for low temperature. More detailed analysis of our systems in the viewport of ASEP is beyond the scope of the present study but would be interesting to perform in the future.

Methods

Generation of a moving optical lattice in a hybrid trap

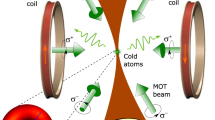
In a phase-stabilized MOT, two phase-related trap beams propagating in the opposite directions are folded to form three sets of counter-propagating laser beams as shown in Fig. 6a. In the case of a static optical lattice, the trap lasers have the same frequency detuning of −3Γ from the (F = 3) ↔ (F = 4) transition of 85Rb D2 line, where Γ/2π = 6 MHz is the decay rate of the transition. At the chosen trap-laser detuning, the atoms in the lattice are confined most tightly so that the dynamics of atoms (localized and unlocalized) are well distinguished40. The interference pattern forming the optical lattice is stable due to the time-phase relation of two trap beams29. In our experiments, the trap depth of the lattice potential can be adjusted by the laser intensity between 840Er and 2400Er, where Er is the recoil energy with a value of Er/ħ = 3.86 kHz. The atoms then experience the sub-Doppler cooling due to the polarization gradient of the trap beams45 and become localized at the potential minima of the optical lattice. In most of our experiments, the trap depth was 1600 Er and the oscillation frequency ω/2π of the generated lattice potential was 91 kHz.

Fig. 6
figure 6

Passively stabilized MOT with a moving optical lattice and a set-up for measuring resonance fluorescence spectrum. a Three-dimensional laser configuration for a moving optical lattice in a phase-stabilized MOT. The blue arrows represent the trap laser with frequency of ω+Δω while the green arrows indicate the trap laser with frequency of ω. The yellow arrow represents the direction of the moving optical lattice. In the coordinate system shown, it is in (1, 1, 1) direction. Fluorescence is collected in (−1, 1, 0) direction. b Configuration of laser beams for a one-dimensional static optical lattice. c The same for a one-dimensional moving optical lattice. d Experiment schematic for measuring resonance fluorescence spectrum of atoms. A hybrid of a moving optical lattice and a background MOT is generated in a phase-stabilized MOT with two bichromatic lasers whose frequencies are detuned by AOMs. Spectrum measurements are done by using PCSOCS on the fluorescence mixed with a local oscillator (LO). The diode laser frequency ω0 = ω + Δω/2 is detuned by −3Γ from the atomic resonance. The detuning for the local oscillator is ΔωLO = −10 MHz

Full size image

In our experiment, we achieved a stable atomic cloud as well as steady fluorescence spectrum by stabilizing the frequency and the power of the trap-laser beams actively, as discussed below. Furthermore, our trap is only 50 microns in diameter and the trap-laser intensity was at most twice of the saturation intensity, unlike the other studies employing hybrid traps24,26,31. Therefore, the perturbations by the inhomogeneous magnetic field as well as strong laser beams could be avoided in our experiment.

We can move the optical lattice by changing the frequency of one of the trap-laser beams. With a frequency difference Δω between them, the optical lattice moves in the direction of the higher-frequency trap laser with a speed of vl = Δω/2k, where k = 2π/λ is the wave number and λ is the trap-laser wavelength [see Fig. 6b, c]. We used acousto-optic modulators to shift the trap-laser frequencies. In the three-dimensional case of Fig. 6a, the optical lattice moves with an equal velocity component of vl along each axis, resulting in the lattice velocity in (1, 1, 1) direction in the Cartesian coordinate system.

The MOT force experienced by atoms in this trap is different from that of the conventional MOT. The force in the conventional one-dimensional model of MOT with the same trap-laser detunings can be described as46,

$$F_{{\mathrm{MOT}}} = - \alpha v - \frac{{\alpha \beta }}{k}z,$$
(4)

where v and z are the velocity and position of an atom, respectively, and α and β are the constants determined by the MOT parameters. If the frequencies of the trap beams are different by Δω, the force of MOT changes to

$$F_{{\mathrm{MOT}}}^\prime = - \alpha v - \frac{{\alpha \beta }}{k}\left( {z - z_0} \right),$$
(5)

where z0 ≡ Δω/2β. Owing to the modified restoring force given by the second term in Eq. (5), the near-Doppler-temperature atoms would then be trapped at a shifted trap center z0 while the sub-Doppler-cooled low-temperature atoms would be localized at the potential minima of the moving optical lattice.

Spectrum measurement

In our experiments, the MOT with the moving optical lattice was loaded and then the fluorescence spectrum of trapped atoms exited by the trap laser was measured. We used a ultrasensitive heterodyne spectroscopic technique called the photon-counting-based second-order correlation spectroscopy32. In this technique, the atomic fluorescence is mixed with a local oscillator laser and all of the arrival times of the photons of the combined light are recorded on two single-photon counting modules as shown in Fig. 6d.

The photon arrival time record is then used to obtain the second-order correlation function g(2)(τ), and the spectrum can then be obtained by Fourier transforming it. Typical photon count rate registered on each detector was about 106 cps and the fluorescence was measured for about an hour for enough signal-to-noise ratios. In order to make both the magnitude of the lattice potential and the lattice velocity well defined, it was essential to stabilize the frequency as well as the intensity of the trap laser. We employed a proportional-integral-derivative feedback control in stabilizing the intensity and frequency of the trap laser. The intensity of the laser was stabilized within 5% of its maximum, and the frequency of the laser was stabilized within 5 kHz, which mainly contributed to the resolution of the spectrum.

Formulae for the parameters used in the rate equation model

Transition amplitudes T0(vl) and T1(vl) from the ground and the excited vibrational states, respectively, to the nonlocalized state are obtained by calculating the transmittance of the corresponding vibrational state through the potential barrier as the lattice potential moves during time T = lnode/vl. We solve the time-dependent Schrödinger equation for time T with an initial wave function ψ0,1(x, t = 0) placed at a minimum of the lattice potential.

$$i\hbar \frac{{\partial \psi }}{{\partial t}} = - \frac{{\hbar ^2}}{{2m}}\frac{{\partial ^2\psi }}{{\partial x^2}} + V\left( {x - v_{\mathrm{l}}t} \right),\quad (0  <  t  <  T)$$
(6)

where V describes a one-dimensional lattice potential moving at a speed of vl with a lattice period of lnode = \(\sqrt 3 {\mathrm{/}}2\lambda\) and m is the atomic mass. For the initial wave functions, we use the ground and the first-excited states of a simple harmonic oscillator with the same oscillation frequency as our experiment.

Since we are interested in the change of the wave function in one lattice period, we approximate the periodic potential with a moving barrier corresponding to one period of the optical lattice potential as shown in Fig. 7a, b. At t = 0, the center of the potential barrier is located at x = 0 and the wave function is centered around x = lnode/2. Transmittance is obtained by integrating the absolute square of the wave function between x = 0 and x = lnode at time t = T.

$$T_{0,1}(v_{\mathrm{l}}) = {\int}_{\hskip -0pt 0}^{l_{node}} | {\psi _{0,1}(x,T)} |^2dx$$
(7)
Fig. 7
figure 7

Transmittance calculation example and momentum distributions of localized as well as unlocalized atoms. Calculating transmitted waves (red curves) through a moving potential barrier (black curve). a The initial wave function is the ground state. b The initial wave is the first-excited state of a harmonic oscillator. The probability amplitude in the region between x = 0 and lnode is considered being transmitted. In this example, the following parameters were used: V0 = 1600Er, vl = 0.086  m s−1, and ωosc/2π = 91 kHz. c The momentum distribution ρu(p) of the unlocalized atoms under momentum diffusion, compared with the momentum distributions \({|} {\phi _{0,1}\left( {p - mv_{\mathrm{l}}} \right)} {|}^2\) of the localized atoms in the ground and the first-excited states of a local potential minimum of the optical lattice. The distribution ρu(p) is estimated from the spectrum at a large trap-laser detuning of Δω/2π = 500 kHz, with most of the atoms in the background MOT. The distribution corresponds to the atomic temperature of about 35 μK. In this example, the lattice moves with a speed of vl = 0.067 m s−1 with the trap-laser detuning of Δω/2π = 100 kHz

Full size image

Calculation of transmittance was done numerically47. We set the “transmitted” atoms as the atoms to be found in the neighboring potential minimum corresponding to a region shaded in yellow in Fig. 7a, b. Because we are interested in the time evolution during T with a periodic potential moving by one lattice period, we consider only the transmitted wave in that region. Examples of calculated T0(vl) and T1(vl) are shown in Fig. 5a–c as a function of Δω (or vl = Δω/2k).

The rates f(vl) and g(vl) shown in Fig. 5a are the transition rates from the nonlocalized state to the localized states, i.e., the ground and the first-excited states of the potential minimum, respectively. The unlocalized atoms undergo momentum diffusion due to the continuous scattering of the trap-laser light, resulting in a certain momentum distribution ρu(p) affected by sub-Doppler cooling. The momentum distribution function ρu(p) can be estimated from the spectrum at high lattice speeds with most of the atoms in the background MOT. Momentum diffusion eventually drives atoms to be captured in the lattice. The transition rate to a localized state is proportional to the convolution of ρu(p) and the momentum distribution \({|} {\phi _{0,1}\left( {p - mv_{\mathrm{l}}} \right)} {|}^2\) of the localized states [Fig. 7c]. Thus, f(vl) and g(vl) can be expressed as

$$f(v_{\mathrm{l}}) = \eta {\int}_{\hskip -3pt - \infty }^\infty {\kern 1pt} \rho _{\mathrm{u}}(p)| {\phi _0\left( {p - mv_{\mathrm{l}}} \right)} |^2dp$$
(8)
$$g(v_{\mathrm{l}}) = \eta {\int}_{\hskip -3pt - \infty }^\infty {\kern 1pt} \rho _{\mathrm{u}}(p)\left| {\phi _1\left( {p - mv_{\mathrm{l}}} \right)} \right|^2dp$$
(9)

where η is a constant related to the momentum diffusion. The rates f(vl) and g(vl) decrease as the lattice speed increases, which means that the atoms tend to be nonlocalized as the lattice speed increases. The parameter η takes a role of a fitting parameter in the rate equation model, and its value is listed in Table 1.

Table 1 Experimental parameters used to determine the values of transition rates and amplitudes appearing in the rate equations, Eqs. (1), (2) and (3)
Full size table

The transition amplitude R(vl) between the ground and the first-excited vibrational states during the time period T is obtained by approximating a node of the moving optical lattice with a harmonic oscillator with the same oscillation frequency moving at the same speed. The equation of motion for the probability amplitudes in the case of a moving harmonic oscillator of an oscillation frequency ωosc is given by48,

$$\dot a_n = a_{n + 1}v\sqrt {\frac{{(n + 1)m\omega _{{\mathrm{osc}}}}}{{2\hbar }}} e^{ - i\omega _{{\mathrm{osc}}}t} - a_{n - 1}v\sqrt {\frac{{nm\omega _{{\mathrm{osc}}}}}{{2\hbar }}} e^{i\omega _{{\mathrm{osc}}}t}$$
(10)

where a n is the probability amplitude of the nth state. We consider the transition between the first two vibrational states. The result is

$$\left| {a_1(t)} \right|^2 = \frac{1}{{1 + \frac{{\hbar \omega _{{\mathrm{osc}}}}}{{2mv^2}}}}{\mathrm{sin}}^2\left( {\frac{t}{2}\sqrt {2m\omega _{{\mathrm{osc}}}v^2{\mathrm{/}}\hbar + \omega _{{\mathrm{osc}}}^{\mathrm{2}}} } \right)$$
(11)

for initial condition a0(0) = 1 and a1(0) = 0. The expression for |a0(t)|2 has the same form as \(\left| {a_1(t)} \right|^2\) in Eq. (11) for initial condition a0(0) = 0 and a1(0) = 1, and thus a single parameter R(vl) is sufficient. It is obtained by taking a time average of the transition probability,

$$R(v_{\mathrm{l}}) = \frac{1}{T}{\int}_{\hskip -0pt 0}^T \left| {a_1(t)} \right|^2dt \simeq \frac{1}{{2\left( {1 + \frac{{\hbar \omega _{{\mathrm{osc}}}}}{{2mv_{\mathrm{l}}^2}}} \right)}}.$$
(12)

Table 1 lists the values of several parameters obtained from experimental results at various trap-laser intensities. These parameter values are used to calculate all of the parameters appearing in the rate equation. The momentum distribution ρu(p) is specified by a Voigt profile with a Gaussian width ωG and a Lorentzian width ωL. The eigenstates of the harmonic oscillator is determined by the oscillation frequency ωosc. From the eigenstates, the momentum distribution ϕ0,1(p) can be obtained. The transition rates f(vl) and g(vl) are then given by Eqs. (8) and (9) with η to be determined by fitting the experimental results in Fig. 3. The transition amplitude R(vl) is given by Eq. (12) using ωosc. For the calculation of the transmittance T0,1(vl), the trap depth and the oscillation frequency values are used. The parameter vle in Table 1 is the lattice speed at which an atom initially stationary can go over the potential barrier classically. It is not needed to determine the parameters appearing in the rate equation, but its values are listed as a reference. It is noted that the transition from the localized to the unlocalized states occurs around vle or the corresponding detuning Δωle/2π in Figs. 3 and 5c–e.

Data availability

All data generated or analyzed during this study are included in this published article.