Abstract
The formation of an equilibrium state from an uncorrelated thermal one through the dynamical crossing of a phase transition is a central question of quantum many-body physics. During such crossing, the system breaks its symmetry by establishing numerous uncorrelated regions separated by spontaneously generated defects, whose emergence obeys a universal scaling law with quench duration. The ensuing re-equilibrating or “coarse-graining” stage is governed by the evolution and interactions of such defects under system-specific and external constraints. We perform a detailed numerical characterisation of the entire non-equilibrium process associated with the Bose–Einstein condensation phase transition in a three-dimensional gas of ultracold atoms, addressing subtle issues and demonstrating the quench-induced decoupling of condensate atom number and coherence growth during the re-equilibration process. Our findings agree, in a statistical sense, with experimental observations made at the later stages of the quench, and provide valuable information and useful dynamical visualisations in currently experimentally inaccessible regimes.
Similar content being viewed by others
Introduction
The quenched crossing of a continuous second-order phase transition has been investigated both theoretically and experimentally in many physical systems. The prevailing scenario to date, known as the Kibble–Zurek mechanism (KZM), describes the crossing under the assumption that, in the critical region, the dynamics of the system order parameter is frozen1,2 (see ref. 3 for a recent review). A common formulation of KZM relates the number of defects generated between regions of different (approximately constant) phases to the rate of external quenching. In condensed matter, such a mechanism has been experimentally studied in superfluid helium4,5, superconducting Josephson junctions6,7, liquid crystals8,9, multiferroic crystals10,11, ions12,13,14 and ultracold atoms15,16,17,18,19,20,21,22. Ultracold atoms facilitate a controlled study of the non-equilibrium processes and the Bose–Einstein condensation (BEC) phase transition, and recent experiments have already provided strong evidence for KZM through measurements of the number of spontaneously generated defects in three-dimensional (3D) harmonic traps15,17,21 or winding numbers in ring traps18,22, with correlation function measurements in a 3D box-like potential used to extract critical exponents19, building on an extensive body of literature for condensate growth dynamics23,24,25,26,27,28,29,30,31,32,33,34 (see refs. 35,36 for recent reviews). Related quenched studies include soliton generation37,38,39, ring-trap geometries40, spinor41,42,43, multi-component44,45 and Josephson-coupled46 gases and optical lattices16,47,48.
An emerging question is the extent to which the defect formation process described by KZM can be decoupled from the dissipative evolution expected to occur when defects co-exist within a finite region, which is crucial to the modelling of any experiment. Previous work on purely one-dimensional (1D) evaporatively cooled gases has indicated the spontaneous emergence of dark solitons, whose number gradually decreases during thermalisation, with the coherence length of the final post-quench thermal state being set by the average distance between defects39. Decoupling these two dynamical features is not a trivial task, as one does not a priori know exactly when to count the defects; moreover, at the time at which one is supposed to count them, the system is so disordered that it is not even clear whether any counting would be possible. Nonetheless, numerous experiments with ultracold atoms have provided evidences of the emergence of the predicted power-law scaling of defect number with respect to quench rate, raising the question of why this scaling should survive after such a prolonged dynamical evolution. The Cambridge group19 insightfully avoided such issues by looking instead at correlation functions, which enabled them to extract critical exponents, without the need for direct defect counting.
In this work, we offer a unified analysis of quenched growth dynamics in a finite elongated 3D inhomogeneous system, incorporating the dynamical evolution, for different induced quench rates, from an equilibrium thermal state above the BEC transition temperature to a near-equilibrated, low-temperature phase-coherent Bose–Einstein condensate. By demonstrating the emergence of symmetry breaking in our simulations, we perform a detailed analysis of both the spontaneous emergence and complex nonlinear dynamics of defects, and the related evolution of coherence. The defects are vortex filaments of different lengths and shapes: while their initial positions and orientations are random, and they can be highly “tangled”, they gradually relax, through nonlinear evolution, to the lowest-energy excitations in the given geometry. The insight provided by our numerical visualisations, which extend beyond experimentally accessible time intervals, provides a natural framework for addressing the still unresolved interplay between KZM and coarse-graining dynamics. We address subtle questions in the condensate formation process, and show that coherence and condensate atom number growth dynamics are in general decoupled, due to competing growth mechanisms following a quench, except for cases of adiabatically slow growth which exhibit broadly similar timescales. We further demonstrate that the KZM power-law scaling for the defect number is not significantly affected over a prolonged evolution time after the transition. These findings are consistent with previous simulations in homogeneous systems49,50,51,52, which revealed the gradual dissipation of small spatial scales in favour of longer defects, as well as with late-time experimental measurements performed within our group17,21,53.
Results
Quench protocol
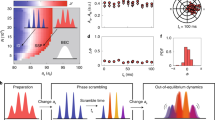
Our experiment is conducted in a cigar-shaped trap with ω x /2π = 13 Hz and ω⊥/2π = 131.4 Hz, where 23Na atoms in the \(\left| {F,m_F} \right\rangle = \left| {1, - 1} \right\rangle \) state are evaporatively cooled across the BEC phase transition at different rates17,21,53. The system has a finite size and is inhomogeneous and anisotropic; hence, the phase transition process is position dependent, with the condensate first emerging in the central trap regions, where the phase-space density is maximum. We also perform full 3D numerical simulations of the same system using the stochastic (projected) Gross–Pitaevskii equation15,29,45,46,54,55,56,57. To faithfully mimic both the changing temperature and the atom number observed in the experiments, our simulations are based on linear quenches (Fig. 1a) over a finite quench duration τR, both in temperature (T = 790 nK → 210 nK) and chemical potential (μ = −22ħω⊥ → μ = +22ħω⊥). Consistently, the atom number goes down from N = 22 × 106 to N = 6.6 × 106. Our parameters have been chosen such that t = 0 corresponds to the time when the system crosses the ideal gas critical temperature (μ = 0). Examples of simulations are given in Fig. 1. For each quench rate, the results are analysed over 3 to 7 individual realisations, which are sufficient for understanding the underlying physics. Our analysis is based on the characterisation of the emerging condensate, defined in our simulations as the mode with the largest eigenvalue of the one-body density matrix, based on the usual Penrose–Onsager definition54,58. We also note that at early evolution times there are a number of approximately equally largely populated modes, before one becomes randomly dynamically favoured by the system. Details of our experimental configuration have been reported elsewhere17,21, while the stochastic numerical method and data analysis scheme used to model such non-equilibrium dynamics are summarised in Methods.
Simulation of quench-induced dynamical equilibration. a Quench protocol: starting from a purely thermal state, with a given atom number, we linearly quench temperature to lower values and chemical potential to positive values over a ramp duration τR to mimic experimental conditions. b Dynamical response of an equilibrium thermal gas subjected to different cooling quench rates (τR = 1440, 144, 18 ms, from top to bottom), demonstrating the equilibration route towards a finite temperature phase-coherent condensate. The characteristic regions depicted here refer to density isosurfaces of the highest-populated mode, chosen such that n(t)/n(t → ∞) = 0.1% (yellow), or 3% (green), where n(t → ∞) describes the final equilibrated peak condensate density for N = 6.6 × 106 atoms. Different rows correspond to different durations of the constant applied external cooling ramps, from the very slow, quasi-adiabatic (top) to the very fast, nearly instantaneous ones (bottom), with the intermediate case representing typical quenches used in experimental studies of phase transitions. For rather slow ramps, most condensate formation happens during the external cooling. For shorter quench duration, the condensate appears around the end of the ramp, and there is a small number of spontaneously generated defects (vortex filaments), depicted in purple. In a fast quench, most condensate growth dynamics occurs after the end of the ramp, with the system at the end of the ramp being in a highly non-equilibrium state exhibiting large occupation of a handful of modes, and consisting of a dense random vortex tangle. Such a tangle unravels in time into a phase-fluctuating condensate, or quasi-condensate, with numerous well-formed interacting filaments, whose presence perturbs the phase and opposes the formation of long-range coherence; after further evolution, at most few long-living vortices may survive, and they are experimentally observed after expansion
Figure 1b shows that for a very slow quench (top), the system grows to its final equilibrium state remaining close to the corresponding equilibrium phase-coherent BEC during its evolution, except in a narrow time window within the region of critical fluctuations. Such slow evolution corresponds to the evaporatively cooled condensate growth scenario, in which both condensate atom number and correlation function grow gradually, on the ramp, with a small phase-coherent condensate present shortly after the phase transition. As the ramp speed is increased (middle and bottom images), we observe a rather violent falling out of equilibrium when crossing the phase transition, resulting in the spontaneous production of multiple defects in the form of a tangle of vortex filaments.
The underlying physical picture here is that coherence only forms in local patches of constant—but random—phase, and the defects separate such regions of different phases. Faster quenches (bottom) lead to a faster growth of quantum-degenerate states and to a larger number of defects than slower quenches (middle); for such rapid quenches, most of the condensate (and also coherence) growth occurs after the removal of the external ramp. As the system grows, the vortex filaments are stretched out while also undergoing complicated nonlinear dynamics in the inhomogeneous background. As a result, their number decreases gradually, allowing phase coherence to spread to the entire system. For the set of parameters considered here, the final equilibrated state—obtained asymptotically for the case of near-instantaneous ramps—consists of a fully phase-coherent defect-free finite-temperature BEC with condensate fraction N0/N ≈ 0.75 (characteristic single-realisation growth sequences are shown in Supplementary Figs. 1 and 2 and Supplementary Movies 1 and 2). In the following, we analyse in detail the distinct stages in the dynamical equilibration.
Dynamical crossing of the phase transition
The dynamics near the transition is naturally incorporated within our numerical approach. As the system is cooled at a finite rate, with its atom number decreasing (as in experiments), it cannot instantaneously acquire coherence across its entire spatial extent, and so a dynamical symmetry breaking occurs over a relatively short temporal range; this allows the system to become infilled by a densely packed random network of vortex filaments, signalling a stark deviation from equilibrium. An example is shown in Fig. 2 for a quench time τR = 84 ms. Consistent with experiments, our simulations clearly show the gradual emergence of a higher-density condensate region (green region, t ≥ 31 ms) which gradually grows towards the trap edges. The origin of this is associated with the lowering of the system temperature, the incorporated atom loss and the presence of the harmonic confinement, all of which lead to a centre-peaked position-dependent increase in local phase-space density. However, looking at the finer level during such evolution, we find the defects also interact, coalesce and decay. Such processes, which are not included in KZM, are crucial to the growth of the phase-coherent regions. In the early stages, while numerous defects are present, the system can be classed as a quasi-condensate23,59 in the sense that different regions of coherent density exhibit no common phase between them, such that the observed coherence length is considerably smaller than the system size, consistent with the large population of a number of modes.
Dynamical crossing of the BEC phase transition. We show here a 3D visualisation of characteristic density profiles of the highest-occupied (Penrose–Onsager) mode during the condensation process, for the case of quench time τR = 84 ms. Depicted images show respectively snapshots at times t corresponding to a the time t = 0 (when μ = 0), and b–f times t = 28, 29, 30, 31 and 32 ms, respectively. Above the transition temperature (a, b), we see low-amplitude random density fluctuations (yellow) within our entire simulation grid. As the density begins to condense in real space, reflecting the underlying elongated trap geometry, the system breaks its symmetry spontaneously (c, d), leading to the appearance of defects (purple), which evolve within a growing (green) high-density region (e,f), signalling the emergence of a highly fluctuating condensate. Such defects undergo their own evolution dynamics, violently perturbed by interactions with other defects (see Supplementary Fig. 3 and Supplementary Movie 3)
As the phase transition is crossed, the system enters into a rather complex dynamical regime, in which the physics is dominated by a combination of (i) defect stretching due to the growing condensate size; (ii) defect propagation in an inhomogeneous environment; (iii) occasional but rather violent defect interactions, including vortex reconnections, bouncing and “ejection” from the condensate60; and (iv) additional forced relaxation in cases of slow cooling. All of them lead to the gradual equilibration of the system, which evolves from a defect-filled condensate to a state at \(T \ll T_{\mathrm{c}}\) defined by the final quench parameters. Our numerical visualisation reveals the complexity of attempting to extract, whether numerically or in actual experiments, the early physics of defect formation. This is of particular relevance for addressing the interplay between the bare KZM and the “coarse-graining” dynamics governing the defect evolution and decay. Our analysis shows that one cannot decouple the two processes—at least not in the context of inhomogeneous systems.
Condensate growth dynamics
Early condensate growth experiments25,33,34 and their numerical modelling26,28,30 revealed a number evolution N0(t) well described by an S-shaped curve. However, slower quenches31 and elongated geometries61 were observed to feature a pronounced region of critical fluctuations, leading to a “time delay” or “onset time” for condensate growth and a slower initial growth rate31; although the presence of such features is well documented and broadly attributed to the initial emergence of the quasicondensate, there has been little quantitative discussion of this issue, which becomes particularly relevant for dynamically driven quenches.
To address this point, we firstly compare our numerical and experimental condensate growth curves for different characteristic temperature quench rates dT/dt, as shown in Fig. 3a, d. Consistent with earlier numerical studies of condensate growth (including KZM15,45), the constant γ appearing in our theoretical model (see Methods) is treated as a free parameter, choosing its value such that it reproduces the experimental growth rate for dT/dt = 5.6 μK s−1 (Fig. 3b). Although the maximum N0 in the experiments depends on quench rate21, our simulations are conducted for a fixed final N0—defined as the largest eigenvalue of the one-body density matrix—because such a choice minimises numerical uncertainties and allows for an unequivocal numerical demonstration of the decoupling of number and coherence growth (see later). With this in mind, our numerical results are shown to accurately reproduce experimental growth curves near the transition for the entire range of quenches probed.
Condensate growth dynamics. a–d Comparison of dynamical simulations (filled symbols, solid lines) and experimental data (open black circles, dashed lines) for different cooling rates, labelled here by the rate of change of temperature with time (dT/dt). Each subplot shows a complete averaged experimental sequence of condensate atom number N0 for a particular quench rate, with the depicted averaged numerical results corresponding to quench rates at either side of the experimental values. In the simulations we assume a fixed initial (T = 790 nK > Tc, N = 22 × 106 atoms) and final equilibrium (T = 210 nK < Tc, N = 6.6 × 106 atoms) states. We also fit the numerical data with an S-shaped function (see Methods) to extract the growth timescale τG. e Dependence of τG on the ramp duration τR in the simulations, with error bars representing the 95% confidence bounds of the fits. f Condensation onset time, tbec, as a function of τR, demonstrating that slower quenches feature a delayed onset. Error bars here represent the difference in time for the condensate atom number to reach 3% (lower bound) or 7% of the total final atom number
The precise determination of the phase-transition crossing and associated critical temperature is a rather challenging problem, both numerically and experimentally, particularly in the presence of inhomogeneous confinement. Experiments typically identify the critical region as the time at which a clearly detectable condensate emerges. As in the experiments, in our numerical simulations we identify a condensation “onset time”, tbec, as the time at which the condensate atom number, N0, reaches 5% of the total final atom number for our chosen final equilibrium parameters. Shifting our numerical growth curves by the “onset” time tbec enables a direct comparison to experimental growth curves, with the good agreement shown in Fig. 3a–d (see also Supplementary Fig. 4). All curves are well fitted by an S-shaped curve with a single free parameter, corresponding to the quenched growth timescale, τG (fits shown in Supplementary Fig. 5). The dependence of τG and condensate onset time tbec on ramp duration is shown in Fig. 3e, f. For \({\mathrm{\tau }}_{\mathrm{R}}\) ⪅ 300 ms, we find a practically constant growth timescale τG = 15.8 ± 0.7 ms, which is consistent with the finding of overlapping condensate growth curves once these are plotted against shifted time (t − tbec). Note that the condensate onset time tbec is a linear-like monotonically increasing function of τR. This behaviour is qualitatively robust to changes in the exact definition of the condensate number/fraction chosen to mark such transition, as demonstrated by the small error bars in Fig. 3f.
Defect number dynamics and visualisation
Next, we discuss the number (Fig. 4) and nature (Fig. 5) of the emerging defects restricting our analysis to times t ≥ tbec, with a qualitative analysis at earlier times prohibited by the densely packed defect configurations present at early post-quench evolution times.
Mean defect number dynamics and dependence on cooling ramp. a Evolution of mean defect (vortex) number, Nv, after the onset of condensation for different τR, highlighting the initial rapid defect decay regime (\(t - t_{{\mathrm{bec}}}\) ⪅ 30 ms) and the subsequent regime where few vortices prevail for an extended amount of time. b Dependence of mean defect number on inverse cooling rate (dT/dt)−1 for two different simulated evolution times t − tbec ≈ 50 ms (red diamonds) and ≈200 ms (blue squares) compared to corresponding experimental values after a free evolution time of 250 ms (black circles). The solid line is a linear fit to the experimental data in log–log scale in the slow quench region (last nine points). The emergence of a plateau-like region on the left (quenches with \({\mathrm{\tau }}_{\mathrm{R}}\) ⪅ 144 ms, or high dT/dt) is consistent with the saturation of the number of long-lived defects seen for long simulation times in (a). Error bars in vortex numbers represent statistical uncertainties (see Methods); horizontal error bars in (a) arise from the uncertainty in the determination of tbec
Defect visualisation at late evolution times. Shown here are representative density side views containing respectively (top to bottom) 1, 2 and 3 solitonic vortices in the condensate. a, b Experimental densities obtained after condensate free expansion, integrated along a transverse (a) or longitudinal (b) axis. c–e Numerical simulations showing corresponding characteristic in situ density and phase plots for (t − tbec) ≈ 250 ms and τR = 84 ms. Specifically: c condensate density isosurfaces from different viewing angles (set by z = 0, or y = 0). d Corresponding isosurfaces from the x = 0 viewing angle. e Planar phase profiles of two-dimensional cuts at z = 0 and y = 0: the latter, only pick up defects crossing the z = 0, or y = 0 lines (see also Supplementary Figs. 6 and 7, and Supplementary Movie 4, for further visualisations, including during the entire dynamical evolution). In comparing experimental and simulated images, we note that the long dark stripes, spanning the entire transverse direction, seen in the experimental images arise as a result of expansion, with such images only containing information about the axial positions of the defects, and not their orientation. This is in contrast to the simulated images, depicting in situ observations: in particular, the simulated phase profiles at such late evolution times reveal a non-uniform distribution of the 2π phase winding around the density minimum of the vortex filaments, which is direct evidence of their solitonic vortex nature. Expansion of such solitonic vortices is known65,66 to lead to dark vertical stripes, highlighting the consistency between experimental and simulated profiles
Focussing initially on defect generation and evolution, we note that the number of defects present at tbec varies significantly with ramp duration, being higher for faster ramps, as such ramps create more non-equilibrium initial configurations. Despite the difference in absolute numbers, all defect-number curves exhibit a similar time evolution, as evident in Fig. 4a. During the first ≈30 ms, they exhibit a rather rapid initial decrease associated with defect interactions, followed by a period of slower decrease with just a few defects present in the system. Such defects are vortex filaments which interact only occasionally, and mostly in pairs, because their average distance is relatively large; they can also produce sound waves, or be ejected from the condensate (details of such mechanisms are discussed in ref. 60). Consistent with previous observations53, for which the defect number could only be reliably measured after about a 100 ms of in-trap evolution, we find the decay in the number of defects to be significantly slower once only two defects are left in the system in any given individual run; in that case, their dynamics becomes largely decoupled, dominated by free propagation in the inhomogeneous condensate. This latter evolution stage is consistent with exponential decay, on a timescale of one hundred to few hundred ms.
Next, we address the relation of our findings to the KZM. Specifically, we investigate (Fig. 4b) the mean number of defects (vortices) as a function of ramp duration (top axis) or, equivalently, inverse temperature evolution (bottom axis). According to the idealised KZM for defect generation, one expects a power-law decay. However, such Kibble–Zurek predictions are specific for a relatively early evolution time within the critical region, whereas experiments typically count defects after a significant in-trap evolution time. Our simulations have already shown (Fig. 4a) that the defect number significantly changes during the in-trap evolution; nonetheless, the power-law scaling of the defect decay (i.e., the slope of the decaying region in Fig. 4b) appears to be roughly insensitive to the post-quench timing of the measurement. A detailed analysis of defect number vs. quench rate for two different evolution times (t − tbec) ~50 ms (red diamonds) and 200 ms (blue squares), reveals an evolution broadly consistent with the experimental measurements conducted at 250 ms, with a power-law exponent of the same order. Our simulations also recover the experimentally observed plateau region for fast quenches, a behaviour which we find to set in already at early post-quench times. This is attributed to a combination of the maximum defect counting resolution of a tangled configuration in a restricted (inhomogeneous) volume, and the quench rate exceeding internal system timescales, implying that the assumption of a well-defined local temperature starts to break down. The occurrence of a plateau for fast quenches has also been discussed in recent work in the context of (2 + 1)-dimensional holographic superfluids62.
Finally, we discuss the nature and visualisation of defects. Typical experimental measurements made after an evolution time of about 250 ms and based on integration over different (radial or axial) directions after time-of-flight (TOF) expansion are shown in Fig. 5a, b for cases corresponding to different defect numbers. The experimental images after TOF are in qualitative agreement with our numerically generated images of the in-situ condensate at the same evolution times (Fig. 5c, d); the simulations also enable direct visualisation of the condensate phase (Fig. 5e), which is crucial for probing the nature of the emerging defects. Numerical analysis of the phase evolution and corresponding density plots indicates a gradual evolution from the random distribution of tangled vortex filaments (already seen in Fig. 2), into few vortices preferentially stretched along the transverse directions. Such evolution is consistent with the accelerated decay of small-scale features in favour of longer, more relaxed, defects50,51,52. In an elongated geometry, the lowest-energy configuration of a quantised vortex corresponds to a vortex line lying in a transverse radial plane with squashed 2π phase winding, also known as a solitonic vortex63,64. In our simulations, we indeed find such structures appearing after a typical time (t − tbec) ~100 ms (Supplementary Fig. 6 and Supplementary Movie 4). This also agrees with the experiments, where the solitonic vortex nature of the defects has been checked with different techniques, including the characterisation of the free expansion of the condensate in TOF, which produces a peculiar twisted-stripe feature in transverse imaging65,66. It is also worth noticing that a comparable timescale was found in refs. 67,68 for the decay of phase-imprinted dark solitons into solitonic vortices in superfluid Fermi gases in a very similar elongated geometry.
Coherence and equilibration dynamics
Having demonstrated solid agreement with experimental observations in appropriate regimes, and the ability to further interpret those through our simulations, we now use our numerical scheme to provide a deeper insight into the complicated nonlinear dynamical evolution and equilibration of quenched systems, covering also regimes where no experimental measurements are available.
In our quenched evolution of an initially equilibrium thermal gas, we have seen the system falling out of equilibrium around the critical region, and identified a subsequent time, tbec, associated with the onset of condensation. Here we investigate the re-equilibration dynamics of such a system to a final state dictated uniquely by our final quench parameters (μfinal, Tfinal). We show that this relaxation process depends on τR in a nontrivial way: in particular, while the condensate-number growth dynamics depends solely on the growth timescale, τG (which is itself a function of τR, see Fig. 3e), the coherence growth is additionally sensitive to details of the defect-filled state of the system following the quench. This points directly to the link between relaxation of quench-induced defects on the one hand and coherence growth and final system equilibration on the other.
From the condensate-number growth fits, we have identified two distinct dynamical regimes: for slow enough quenches (τR ≳ 300 ms), the growth timescale is a monotonically increasing function of the quench duration, whereas faster quenches (τR ≲ 300 ms) all exhibit a similar number growth timescale (Fig. 3e). Nonetheless, such rapid quenches lead to a notable increase in the number of spontaneously generated defects, whose subsequent (“coarse-graining”) dynamics is crucial for the evolution of coherence.
To study the growth of coherence, we follow the procedure of the Cambridge group19 by numerically shifting the wavefunction by a fixed amount and autocorrelating this with the unshifted copy of itself. This method provides an estimate of the coherence length of the system, lcoh. Due to geometrical considerations, we focus here on the axial coherence length, obtained by transversal integration (see Methods). In all cases we find that the integrated coherence length only starts increasing noticeably about 30 ms after tbec, consistent with the end of the previously identified rapid defect decay stage (Fig. 4a). The amount of vorticity present in the system sets a maximum limit to the dynamical system coherence length. This is to be expected, and has already been noted, for example, in 1D39,69 and 2D70. Importantly, however, we see that for the slowest quenches, the coherence length grows much more rapidly (when normalised to the corresponding quenched growth timescale) than for faster ones, also saturating at higher values. This observation points to the importance of a system expelling practically all of its defects before it can acquire a coherence length comparable to the system size.
Starting from the same initial thermal condition, whose rapidly decaying correlation function is shown in Fig. 6a, the subsequent Fig. 6b, shows how the dynamical correlation functions (solid lines) evolve in cases of fast (left), intermediate (middle) and slow (right) ramps, comparing them to the corresponding equilibrium functions (dashed lines). Our analysis here focuses on the re-equilibration dynamics, and so all dynamical data presented here correspond to times t > 0 (with μ(t) > 0) after the system has crossed the ideal-gas transition temperature, with times scaled to the quenched growth timescale τG in order to suppress corresponding differences in condensate number growth dynamics. In the context of our adopted definition for the correlation function19, this implies that the correlation function approaches a diagonal straight line as the coherence length approaches/exceeds the system size, which is always the case for the equilibrium systems considered here, due to their large atom numbers: this is decoupled from the fact that the equilibrium coherence length is increasing in absolute terms as the condensate size grows. Looking at times 0 < t < tbec we see that although the corresponding equilibrium correlation functions already exhibit near-perfect coherence across the probed central region, the corresponding dynamical behaviour at (t − tbec)/τG ≈ −1.2 deviates noticeably: in the case of the faster ramp (left column of Fig. 6b), the dynamical correlation function has only mildly increased from its incoherent thermal state initial value, contrary to a much stronger increase for the slower (quasi-adiabatic) ramp, which nonetheless also exhibits a phase coherence length significantly smaller than the quantum-degenerate system size (right column of Fig. 6b). Figure 6c shows the dynamical coherence length as a function of the rescaled timescale (t − tbec)/τG. For all ramps, the coherence length increases with time, but it does so in a much slower manner for the faster quench. As a result, significant coherence has already built up for the slower ramp already at our identified condensation onset time, tbec, highlighting that such a system approaches the equilibrium state rapidly in the early stages after crossing the phase transition, even before significant number growth takes place; this is in stark contrast to the faster ramp, which still exhibits hardly any coherence. The images shown in Fig. 6b highlight the emerging difference in the dynamical phase correlation function, \(g_{\mathrm{1}}^{{\mathrm{int}}}\left( {d_x} \right)\) (defined, at a general time, t, in Methods), in a most pronounced way, with the slow ramp becoming phase coherent already for (t − tbec)/τG ≳ 1.5, when the system is still only at the initial part of its number growth curve, as opposed to the faster ramp whose coherence length remains smaller than the system size even at the much later time (t − tbec)/τG = 12.7.
Decoupling of number and coherence growth. a Integrated first-order correlation function, \(g_{\mathrm{1}}^{{\mathrm{int}}}\left( {d_x} \right)\) (defined, at a general time, t, in Methods), for the initial equilibrium thermal state. b Dynamical evolution of \(g_{\mathrm{1}}^{{\mathrm{int}}}\left( {d_x} \right)\) (solid lines/bands) for fast (τR = 84 ms, left), intermediate (τR = 300 ms, middle) and slow (τR = 1440 ms, right) quench rates, depicted in terms of scaled time (t − tbec)/τG. Images also show the corresponding equilibrium values for the same (μ(t), T(t)) combinations (dashed lines). For our chosen parameters, the equilibrium system is already in the phase-coherent condensate regime, for which \(g_{\mathrm{1}}^{{\mathrm{int}}}\left( {d_x} \right)\approx \left( {1 - \left| {d_x} \right|{\mathrm{/}}L} \right)\), for all times t ≳ tbec, with the correlation function for slower ramps approaching the corresponding equilibrium ones faster than for fast ramps. c Growth of the coherence length in time: systems with more than two vortices on average exhibit coherence smaller than the system size, indicating that for the fastest ramps the system is still in the phase-fluctuating regime. d Condensate growth curves collapsing onto a single curve when time from the condensate onset is scaled to the intrinsic system growth timescale τG. Inset shows corresponding ratio, rPO, of most-populated to next-most-populated eigenmode of the one-body density matrix. e Corresponding scaled deviation, δlcoh(t), of dynamical to equilibrium coherence length [based on Eq. (1)]. At t = tbec, the slower ramps (600 ms, 1440 ms) are closer to equilibrium than the faster ones. Slower ramps, scaled to their respective τG, re-equilibrate faster to a phase-coherent BEC (for which δlcoh = 0), with faster ramps only reaching full system coherence asymptotically. Statistical errors are shown by coloured bands in (b) and vertical error bars in (c, e). Horizontal error bars in (c–e) arise from the combination of the uncertainty in identifying tbec and the fitting error for τG
To quantify such re-equilibration dynamics further after the system has fallen out of equilibrium upon entering the critical phase-transition region, we introduce here the scaled deviation, δlcoh, of the dynamical correlation length, \(l_{{\mathrm{coh}}}^{{\mathrm{dyn}}}(t)\), from the corresponding equilibrium one, \(l\,_{{\mathrm{coh}}}^{{\mathrm{equil}}}(\mu (t),T(t))\), defined by
Despite similar condensate growth rates (Fig. 6d) the corresponding coherence growth dynamics shown in Fig. 6e exhibit starkly distinct features, remaining strongly dependent on the quench rate: in such relative timescales, slower ramps lead to much more rapid equilibration than the faster ramps; the latter are slowed down by the detrimental role of the defects persisting within the system. Contrary to this, slow ramps which perturb the system less lead to the emergence of a nearly defect-free and therefore phase-coherent condensate already around t ≈ tbec. The inset in Fig. 6d highlights the rapid emergence of a single macroscopically occupied mode for the slower ramps (600 and 1440 ms), consistent with the rapid monotonic decrease of δlcoh(t), indicating the rapid crossover to a phase-coherent condensate. The vertical error bars arising solely from our numerical averaging are significantly larger in the case of fast quenches, which is a measure of the deviation between different trajectories for the same ramp. This is easy to understand, since the more vortices there are in the system, the more likely their configuration is to be significantly different from shot to shot.
Discussion
Motivated by recent experiments with dilute ultracold atomic gases, we have investigated numerically the dynamics of an equilibrium thermal gas quenched over a finite timescale across the BEC phase transition to deep in the phase-coherent condensate regime. Monitoring the entire evolution, we have presented an insightful graphical representation of the critical region dynamics, during which the dynamical system falls out of equilibrium with the corresponding parameter equilibrium system, through the dynamical symmetry-breaking spontaneous emergence of defects. The emphasis of our analysis has been on the less-studied re-equilibration dynamics, addressing the interplay between defect emergence and dynamical evolution, and growth of coherence.
Depending on the quench duration we have identified different emerging dynamical regimes: for fast quenches, we observed a saturation in the number of detectable defects, associated with detrimental defect interactions and the inherent difficulty in counting randomly oriented defects within a very tight volume. Rescaling the condensate number growth for all quench rates by the characteristic growth timescale for each ramp, we demonstrated the decoupling of coherence and number growth dynamics arising from the detrimental effect of defect emergence and propagation on system coherence. Although the overall growth timescale might be longer for systems undergoing slower external cooling quenches, in such cases the dynamical system quickly re-approaches the corresponding equilibrium configuration, as the slow evolution enables it to mimic local equilibration during its growth, falling out of equilibrium only in a relatively small time window upon entering the region of critical fluctuations. In cases where the quench induces numerous defects, we have observed, as expected, enhanced shot-to-shot variability.
Our numerical analysis has also shed more light into the dynamical crossover from quasicondensation to true Bose–Einstein condensation, studied here in the context of an elongated geometry; such a geometry is known to lead to an enhanced decoupling of characteristic temperatures for the onset of density and phase fluctuations59,71; this, in turn, effectively translates into different growth rates for the phase-coherent and density-coherent parts of the system, and so different growth rates for coherence and quasicondensation. Quasicondensation here refers to a defect-filled phase-fluctuating state with a coherence length smaller than the quantum-degenerate system size exhibiting suppressed density fluctuations and spanning many largely populated modes; this is directly contrasted to “true” condensation, which refers to a phase-coherent condensate with little, or no, defects and a single emerging macroscopically occupied mode, a definition which holds even if the system is growing in time. Even though the quasicondensate stage in the critical region pre-empts all phase-coherent condensate growth due to the decoupling of the two corresponding characteristic temperatures, the dynamical quasicondensate regime is enhanced both in parameter space and in the temporal domain by the prolonged survival of the defects, thus being critically dependent on the quench rate responsible for their initial spontaneous generation. For slow quenches and large enough atom numbers considered here, the system may already be largely phase coherent, i.e., a “true” condensate, as soon as it has grown to a size which makes it experimentally detectable. We note however that such findings are sensitive to the details of the system, and specifically here to both the system geometry and the chosen final state of the system, with reduced dimensionality enhancing such a distinction by enhancing the role of phase fluctuations59,61,72.
Our findings are consistent with experimental measurements in the appropriate limits, and for the relevant quantities, where those exist. Moreover, the detailed numerical visualisation of the defect-filled quenched phase-transition dynamics allows access to a broad temporal range of dynamics not accessible in typical experiments. We expect our generic conclusions to persist across different geometries and dimensionalities, with precise details and the nature of the defects depending on system configuration. Our results can be of relevance to a broad range of future investigations with quantum-degenerate systems, and could also have technological implications for dynamical control and state-engineering of a quantum system. Given that our numerical scheme has demonstrated good qualitative description also of the much-harder-to-model approach to the phase transition, we believe that our method could in the future offer further insight into delicate features of non-equilibrium condensate dynamics, including a critical assessment and extension of the inhomogeneous Kibble–Zurek mechanism.
Methods
Experiments
We produce ultracold samples of sodium atoms in the internal state \(\left| {F,m_{\mathrm{F}}} \right\rangle = \left| {1, - 1} \right\rangle \) in a cigar-shaped harmonic magnetic trap with trap frequencies ω x /2π = 13 Hz and ω⊥/2π = 131.4 Hz. The thermal gas is cooled down via forced evaporative cooling and pure BECs of typically 107 atoms are produced. The part of the evaporation ramp in the vicinity of the transition is performed at different rates, from 50 kHz s−1 to 2 MHz s−1. The quench ramp is followed by a variable wait time, during which a radio frequency shield is kept on to prevent from heating. After that, the atoms are released from the trap and are observed in two possible ways: either we take simultaneous absorption images of the full atomic distribution along the radial and the axial directions21,65 or we extract, uniformly, a small amount of atoms from the trapped sample and image it after a short time of flight53,60. The protocol is such that images are taken, and vortices are counted, after a fixed overall time interval from the BEC transition point, which is clearly identifiable for each quench ramp. As discussed in detail in ref.21, we are also able to precisely identify the frequency ν of the RF field at the critical temperature Tc, which lies in the range 600–800 nK, as well as to control the temperature variation in time via the speed of the evaporation ramp (∂ν/∂t), with (∂T/∂t) found to vary, to good approximation, linearly with frequency. The defects that we observe at the time of imaging are quantised vortex lines which are seen as dark stripes when looking at the BEC from a radial direction after time-of-flight. The natural size of the defects in the trapped BEC, at the end of the cooling ramp, is of the order of the in situ healing length ξ, which is of the order of 200 nm. After a long TOF, the defect size becomes larger than our imaging resolution of 3 μm. The presence of a levitating magnetic field gradient makes it possible to achieve long TOF preventing the BEC from falling. The measured vortex number is averaged over many experimental realisations in order to get good statistical samples for each experimental condition.
Numerical model
Out study is performed by means of the (simple growth) stochastic projected Gross-Pitaevskii equation (SPGPE)54 (see also related model without projector29,55,56,57), already demonstrated as a useful tool for the quenched crossing of the BEC phase transition15,29,38,45,46,51,52. In brief we simulate the low-lying highly occupied modes of the system, denoted by the classical field (or c-field54) \({\mathrm{\Psi }}_{\cal C}({\bf{r}},t)\) through the dynamical equation
where \({\cal P}_{\cal C}\) is the projection operator truncating the modes above the c-field regime (so above an appropriately identified energy cutoff), γ is a constant determining the condensate growth timescale, μ(t) is the time-dependent chemical potential, and \({\cal L}\) = \( - \hbar ^2\nabla ^2{\mathrm{/}}2m + V({\bf{r}})\) + \(g\left| {{\mathrm{\Psi }}_{\cal C}({\bf{r}},t)} \right|^2\) with V(r) = (m/2) \(\left[ {\omega _x^2x^2 + \omega _ \bot ^2\left( {y^2 + z^2} \right)} \right]\). Fluctuations are included through the complex white noise, dW γ , defined by \(\left\langle {dW^ \ast ({\bf{r}},t)dW({\bf{r}}\prime ,t)} \right\rangle \) = \((2\gamma k_BT{\mathrm{/}}\hbar )\delta _{\cal C}({\bf{r}} - {\bf{r}}\prime )\) where \(\delta _{\cal C}({\bf{r}} - {\bf{r}}\prime )\) = \(\mathop {\sum}\nolimits_{n \in {\cal C}} {\kern 1pt} \psi _n^ \ast ({\bf{r}})\psi _n({\bf{r}}\prime )\) in the chosen orthogonal basis set, {ψ n (r)}. The constant γ can be analytically approximated (at least for near-equilibrium cases) as54,55,73
where g = 4πħ2a/m is the interaction strength, corresponding to the s-wave scattering length a. Although the above formula indicates the leading functional dependence of γ, the factor of “few” conceals within it the fact that this is an effective scaling, and so one should only rely on this for order-of-magnitude estimates. Consistent with earlier related analysis15, here we treat γ as a fitting parameter. Comparing to experimental condensate growth data for dT/dt = 5.6 μK s−1 (Fig. 3b), we identify an “optimal” value γ = 0.005, which is about 10 times the analytically predicted value for the initial temperature (the effect of changing γ on condensate growth dynamics can be seen in Supplementary Fig. 4). To mimic the experimental cooling process, the chemical potential μ(t) and temperature T(t) are quenched linearly within a ramp duration τR. The initial and final values of (μ,T) are set as (−22ħω⊥, 790 nK) and (22ħω⊥, 210 nK), corresponding to a change of total equilibrium atom number (when also including above cutoff atoms under the usual assumption that they are static) from 22 × 106 to 6.6 × 106 with a 75% final condensate fraction. In our simulations, which start from a highly incoherent equilibrium state well above Tc, the time t = 0 is chosen as the time when μ(t) = 0, since most interesting dynamics occurs after this time; this implies that, in any given simulation, the initial (equilibrium) configuration is at a time t = −τR/2.
We solve the SPGPE with 4th-order Runge–Kutta in a plane-wave basis using a grid size L x = 54aho,x along the x and L y = L z = 6aho,x along the transverse directions, where aho,x = \(\sqrt {\hbar {\mathrm{/}}m\omega _x} \approx 5.8\) μm is the characteristic harmonic oscillator length in the long direction (x-axis); we use a temporal discretisation dt = 10−3/ω x and an energy cutoff fixed at 2.5 times the value of the final chemical potential (22ħω⊥) in a grid consisting of N x = 1170 and N y = N z = 130 points. Simulations are run on Newcastle University’s High-Performance-Computing cluster, Topsy, using 20 to 24 nodes. A single dynamical run takes between 120 and 300 CPU hours with an additional ≈40 CPU hours for the Penrose–Onsager diagonalisation of the selected snapshots. We estimate the total amount of presented simulations to have taken over 10,000 CPU hours.
Identification of the condensate
The one-body density matrix is defined as
where Nsample is the number of samples for the short-time average number and δt is set as Δt/Nsample with an appropriately short time-interval Δt (so that the system dynamics is not masked). Such short-time averaging mimics the ensemble averaging based on the ergodicity hypothesis54. The notation \(\overline {\langle \ldots \rangle } \) used in this and the next subsections denotes short-time averaging. In our simulations, Nsample = 101, and the tests of probing Δt provide a value of around 8 ms for our simulations, which is smaller than the characteristic timescale of the harmonic trap τho = 1/ω x ≈ 12.2 ms. The condensate, or Penrose–Onsager (PO) mode58 at a given time t is identified as the eigenmode of the one-body density matrix \(\rho ({\bf{r}},{\bf{r}}\prime ;t)\) with the largest eigenvalue. To assess the degree of fragmentation of the condensate, in the sense of competition between different highly occupied modes, we evaluate the ratio, rPO, of the largest to the second largest eigenvalues of \(\rho ({\bf{r}},{\bf{r}}\prime ;t)\).
Correlation function analysis
We follow the procedure of the Cambridge quenched-dynamics experiment19, which measured the correlation function by interfering a displaced copy of the system with itself. Specifically we define the function
where L is a chosen length. In ref.19, the correlation length lcoh was extracted by fitting the experimentally-measured (integrated) correlation function with \(\left( {1 - \left| {d_x} \right|{\mathrm{/}}L} \right){\mathrm{exp}}\left( { - \left| {d_x} \right|{\mathrm{/}}l_{{\mathrm{coh}}}} \right)\), in which the triangular-shape function in the bracket arises from the integration. Here we probe the spatial coherence of our c-field wavefunction \({\mathrm{\Psi }}_{\cal C}\) within a region [−L/2, L/2] with L ~ 54 μm, and numerically evaluate this through the phase–phase correlation function by
where the operation H[f] is defined as
and ϕ(r, t) is the argument of \({\mathrm{\Psi }}_{\cal C}({\bf{r}},t)\). To obtain transversal averaging we use the integrated version,
where the prime integration is performed over the yellow region (i.e., density isosurface at values of 0.1% of the final peak condensate density). To take finite-size effects into account we have also introduced into the above definition a density-dependent weighting function wPO(d x , y, z;t) which assigns higher weighting to the large-density regions. This is defined here through wPO(d x , y, z;t) = \(H\left[ {n_{{\mathrm{PO}}}({\bf{r}}){\mathrm{/}}n_{{\mathrm{PO,peak}}}} \right]{\mathrm{/}}{\cal N}\), where \({\cal N}\) ensures the normalisation condition \({\int\ \!\!\!\!\!\int} ^\prime {\mathrm{d}}y{\kern 1pt} {\mathrm{d}}z{\kern 1pt} w_{{\mathrm{PO}}}\left( {d_x,y,z;t} \right) = 1\) is satisfied at any given d x (the second-order correlation function shown in Supplementary Figs. 6 and 7 and Supplementary Movie 4 is defined as the onsite correlation function g2(r) ≡ g2(r, r, r, r) = \(\overline {\left\langle {\left| {{\mathrm{\Psi }}_{\cal C}({\bf{r}})} \right|^4} \right\rangle } /\left[ {\overline {\left\langle {\left| {{\mathrm{\Psi }}_{\cal C}({\bf{r}})} \right|^2} \right\rangle } } \right]^2\)).
Dynamical timescales
Consistent with typical experimental measurements, in which Tc is identified as the time of emergence of an observable condensate, we define here the “onset” or “delay” time for condensate growth, tbec, as the moment that the number of atoms in the condensate, N0, reaches 5% of the final total particle number (including in our considerations the particle number above the c-field region, which is assumed to be static). We have a posteriori verified this to provide (when used with our value of γ) an excellent description of condensate growth across all experimentally probed regimes, and have also checked that the main findings presented in this paper are insensitive to the details of such definition.
In addition to tbec, we also define the condensate growth timescale, τG, which is extracted by fitting the condensate growth curve over the entire temporal range t with
where N0,i (N0,f) denote the initial (final) PO condensate atom numbers, \(\tilde t\) is the moment that \(N_0(\tilde t{\kern 1pt} )\) reaches the mid-value (N0,i + N0,f)/2, and τG is the single fitting parameter. We note here two things: firstly, that the mid-value is unique to all numerical growth curves, since we have a unique set of experimentally relevant initial and final parameters in our simulations; moreover, we have checked that the extracted τG values are largely insensitive to whether the fit is performed over the entire temporal range t, or whether it is constrained to values t ≥ tbec, suggesting the independence of the two timescales tbec and τG.
Defect identification
In our work we identify the location of vortices by the regions of high velocity, v(r) = (ħ/m) Im\(\left[ {{\mathrm{\Psi }}_{\cal C}^ \ast ({\bf{r}})\nabla {\mathrm{\Psi }}_{\cal C}({\bf{r}})} \right]{\mathrm{/}}\left| {{\mathrm{\Psi }}_{\cal C}({\bf{r}})} \right|^2\), characterising the region around the vortex core. By scanning the whole local maximum of the velocity field within the yellow region, we identify the positions of the vortex cores.
Statistical analysis and error bars
For each numerically simulated quench rate, we have analysed between \({\cal N}\) = 3 and 7 independent noise realisations. The statistical uncertainty in the vortex number, Nv, was estimated as
Determination of the most likely vortex number, Nv, in each independent noise realisation was performed manually by four independent (human) observers. Such a method is prone to systematic errors introduced by the use of subjective criteria in the identification of single vortices in situations where a vortex is at the boundary of the condensate or two vortex lines are very close to each other. However, we have checked that the corresponding uncertainty is significantly smaller than the statistical error defined above.
Our procedure for assigning errors to the determination of the characteristic timescales is as follows: firstly, we recall that the condensate onset time, tbec was defined as the time at which the condensate (Penrose–Onsager) atom number reaches 5% of the total final atom number. Error bars in our determination of tbec arise from shifting the (heuristic) value of 5% between 3% and 7%, values which are still consistent with the experimental growth curves reported in Fig. 3. Regarding the quenched growth timescales, τG, depicted errors arise from the 95% confidence bounds of the fit to our numerical growth curves: the quality of the fits can be seen in Supplementary Fig. 4. Those two errors are treated as independent in the determination of temporal error bars for the scaled time (t − tbec)/τG discussed in Fig. 6.
Data availability
Data supporting this publication is openly available under an “Open Data Commons Open Database License”. Additional metadata are available at: https://doi.org/10.17634/122626-7.
References
Kibble, T. Topology of cosmic domains and strings. J. Phys. A Math. Gen. 9, 1387 (1976).
Zurek, W. H. Cosmological experiments in superfluid liquid helium? Nature 317, 505–508 (1985).
del Campo, A., Kibble, T. & Zurek, W. Causality and non-equilibrium second-order phase transitions in inhomogeneous systems. J. Phys. Condens. Matter 25, 404210 (2013).
Bäuerle, C., Bunkov, Y. M., Fisher, S. N., Godfrin, H. & Pickett, G. R. Laboratory simulation of cosmic string formation in the early universe using superfluid 3He. Nature 382, 332–334 (1996).
Ruutu, V. M. H. et al. Vortex formation in neutron irradiated 3He as an analogue of cosmological defect formation. Nature 382, 334–336 (1996).
Carmi, R., Polturak, E. & Koren, G. Observation of spontaneous flux generation in a multi-Josephson-junction loop. Phys. Rev. Lett. 84, 4966–4969 (2000).
Monaco, R., Mygind, J., Aaroe, M., Rivers, R. J. & Koshelets, V. P. Zurek-kibble mechanism for the spontaneous vortex formation in Nb–Al/Alox/Nb josephson tunnel junctions: new theory and experiment. Phys. Rev. Lett. 96, 180604 (2006).
Chuang, I., Durrer, R., Turok, N. & Yurke, B. Cosmology in the laboratory: defect dynamics in liquid crystals. Science 251, 1336–1342 (1991).
Fowler, N. & Dierking, I. Kibble-Zurek scaling during defect formation in a nematic liquid crystal. Chemphyschem 18, 812–816 (2017).
Chae, S. C. et al. Direct observation of the proliferation of ferroelectric loop domains and vortex-antivortex pairs. Phys. Rev. Lett. 108, 167603 (2012).
Lin, S.-Z. et al. Topological defects as relics of emergent continuous symmetry and Higgs condensation of disorder in ferroelectrics. Nat. Phys. 10, 970–977 (2014).
Ulm, S. et al. Observation of the Kibble-Zurek scaling law for defect formation in ion crystals. Nat. Commun. 4, 2290 (2013).
Pyka, K. et al. Topological defect formation and spontaneous symmetry breaking in ion coulomb crystals. Nat. Commun. 4, 2291 (2013).
Ejtemaee, S. & Haljan, P. C. Spontaneous nucleation and dynamics of kink defects in zigzag arrays of trapped ions. Phys. Rev. A 87, 051401 (2013).
Weiler, C. N. et al. Spontaneous vortices in the formation of Bose-Einstein condensates. Nature 455, 948–952 (2008).
Chen, D., White, M., Borries, C. & DeMarco, B. Quantum quench of an atomic Mott insulator. Phys. Rev. Lett. 106, 235304 (2011).
Lamporesi, G., Donadello, S., Serafini, S., Dalfovo, F. & Ferrari, G. Spontaneous creation of Kibble-Zurek solitons in a Bose-Einstein condensate. Nat. Phys. 9, 656–660 (2013).
Corman, L. et al. Quench-induced supercurrents in an annular Bose gas. Phys. Rev. Lett. 113, 135302 (2014).
Navon, N., Gaunt, A. L., Smith, R. P. & Hadzibabic, Z. Critical dynamics of spontaneous symmetry breaking in a homogeneous Bose gas. Science 347, 167–170 (2015).
Chomaz, L. et al. Emergence of coherence via transverse condensation in a uniform quasi-two-dimensional Bose gas. Nat. Commun. 6, 6162 (2015).
Donadello, S. et al. Creation and counting of defects in a temperature-quenched Bose-Einstein condensate. Phys. Rev. A 94, 023628 (2016).
Aidelsburger, M. et al. Relaxation dynamics in the merging of n independent condensates. Phys. Rev. Lett. 119, 190403 (2017).
Kagan, Y. M., Svistunov, B. & Shylapnikov, G. Kinetics of Bose condensation in an interacting Bose gas. Sov. Phys. JETP 74, 279–285 (1992).
Stoof, H. T. C. Initial stages of Bose-Einstein condensation. Phys. Rev. Lett. 78, 768 (1997).
Miesner, H.-J. et al. Bosonic stimulation in the formation of a Bose-Einstein condensate. Science 279, 1005 (1998).
Gardiner, C. W., Lee, M. D., Ballagh, R. J., Davis, M. J. & Zoller, P. Quantum kinetic theory of condensate growth: Comparison of experiment and theory. Phys. Rev. Lett. 81, 5266 (1998).
Stamper-Kurn, D. M. et al. Reversible formation of a Bose-Einstein condensate. Phys. Rev. Lett. 81, 2194 (1998).
Bijlsma, M. J., Zaremba, E. & Stoof, H. T. C. Condensate growth in trapped Bose gases. Phys. Rev. A 62, 063609 (2000).
Stoof, H. T. C. & Bijlsma, M. J. Dynamics of fluctuating Bose-Einstein condensates. J. Low Temp. Phys. 124, 431–442 (2001).
Davis, M. J. & Gardiner, C. W. Growth of a Bose-Einstein condensate: a detailed comparison of theory and experiment. J. Phys. B At., Mol. Opt. Phys. 35, 733–742 (2002).
Köhl, M., Davis, M. J., Gardiner, C. W., Hänsch, T. W. & Esslinger, T. Growth of Bose-Einstein condensates from thermal vapor. Phys. Rev. Lett. 88, 080402 (2002).
Shvarchuck, I. et al. Bose-Einstein condensation into nonequilibrium states studied by condensate focusing. Phys. Rev. Lett. 89, 270404 (2002).
Hugbart, M. et al. Population and phase coherence during the growth of an elongated Bose-Einstein condensate. Phys. Rev. A 75, 011602 (2007).
Ritter, S. et al. Observing the formation of long-range order during Bose-Einstein condensation. Phys. Rev. Lett. 98, 090402 (2007).
Davis, M. J., Wright, T. M., Gasenzer, T., Gardiner, S. A. & Proukakis, N. P. in Universal Themes of Bose-Einstein Condensation (eds Proukakis, N. P., Snoke, D. W. & Littlewood, P. B.) (Cambridge University Press, Cambridge, 117–150. 2017).
Beugnon, J. & Navon, N. Exploring the Kibble-Zurek mechanism with homogeneous Bose gases. J. Phys. B At., Mol. Opt. Phys. 50, 022002 (2017).
Zurek, W. H. Causality in condensates: gray solitons as relics of BEC formation. Phys. Rev. Lett. 102, 105702 (2009).
Damski, B. & Zurek, W. H. Soliton creation during a Bose-Einstein condensation. Phys. Rev. Lett. 104, 160404 (2010).
Witkowska, E., Deuar, P., Gajda, M. & Rzażewski, K. Solitons as the early stage of quasicondensate formation during evaporative cooling. Phys. Rev. Lett. 106, 135301 (2011).
Das, A., Sabbatini, J. & Zurek, W. H. Winding up superfluid in a torus via Bose Einstein condensation. Sci. Rep. 2, 352 (2013).
Sadler, L. E., Higbie, J. M., Leslie, S. R., Vengalattore, M. & Stamper-Kurn, D. M. Spontaneous symmetry breaking in a quenched ferromagnetic spinor Bose-Einstein condensate. Nature 443, 312 (2006).
Świsłocki, T., Witkowska, E., Dziarmaga, J. & Matuszewski, M. Double universality of a quantum phase transition in spinor condensates: Modification of the Kibble-Zurek mechanism by a conservation law. Phys. Rev. Lett. 110, 045303 (2013).
Saito, H., Kawaguchi, Y. & Ueda, M. Kibble-Zurek mechanism in a trapped ferromagnetic Bose-Einstein condensate. J. Phys. Condens. Matter 25, 404212 (2013).
Sabbatini, J., Zurek, W. H. & Davis, M. J. Phase separation and pattern formation in a binary Bose-Einstein condensate. Phys. Rev. Lett. 107, 230402 (2011).
Liu, I.-K. et al. Stochastic growth dynamics and composite defects in quenched immiscible binary condensates. Phys. Rev. A 93, 023628 (2016).
Su, S.-W., Gou, S.-C., Bradley, A., Fialko, O. & Brand, J. Kibble-Zurek scaling and its breakdown for spontaneous generation of Josephson vortices in Bose-Einstein condensates. Phys. Rev. Lett. 110, 215302 (2013).
Dziarmaga, J., Tylutki, M. & Zurek, W. H. Quench from Mott insulator to superfluid. Phys. Rev. B 86, 144521 (2012).
Braun, S. et al. Emergence of coherence and the dynamics of quantum phase transitions. Proc. Natl. Acad. Sci. USA 112, 3641–6 (2015).
Mondello, M. & Goldenfeld, N. Scaling and vortex-string dynamics in a three-dimensional system with a continuous symmetry. Phys. Rev. A 45, 657–664 (1992).
Antunes, N. D., Bettencourt, L. M. A. & Zurek, W. H. Vortex string formation in a 3d u(1) temperature quench. Phys. Rev. Lett. 82, 2824–2827 (1999).
Kobayashi, M. & Cugliandolo, L. F. Thermal quenches in the stochastic gross-pitaevskii equation: morphology of the vortex network. EPL 115, 20007 (2016).
Kobayashi, M. & Cugliandolo, L. F. Quench dynamics of the three-dimensional u(1) complex field theory: geometric and scaling characterizations of the vortex tangle. Phys. Rev. E 94, 062146 (2016).
Serafini, S. et al. Dynamics and interaction of vortex lines in an elongated Bose-Einstein condensate. Phys. Rev. Lett. 115, 170402 (2015).
Blakie, P., Bradley, A., Davis, M., Ballagh, R. & Gardiner, C. Dynamics and statistical mechanics of ultra-cold Bose gases using c-field techniques. Adv. Phys. 57, 363–455 (2008).
Proukakis, N. P. & Jackson, B. Finite-temperature models of Bose-Einstein condensation. J. Phys. B At. Mol. Opt. Phys. 41, 203002 (2008).
Proukakis, N. P., Gardiner, S. A., Davis, M. J. & Szymaska, M. H. (eds) Quantum Gases: Finite Temperature and Non-Equilibrium Dynamics: 1 (Cold Atoms) (Imperial College Press, London, 2013).
Cockburn, S. P. et al. Matter-wave dark solitons: stochastic versus analytical results. Phys. Rev. Lett. 104, 174101 (2010).
Penrose, O. & Onsager, L. Bose-Einstein condensation and liquid helium. Phys. Rev. 104, 576–584 (1956).
Petrov, D. S., Shlyapnikov, G. V. & Walraven, J. T. M. Phase-fluctuating 3D Bose-Einstein condensates in elongated traps. Phys. Rev. Lett. 87, 050404 (2001).
Serafini, S. et al. Vortex reconnections and rebounds in trapped atomic Bose-Einstein condensates. Phys. Rev. X 7, 021031 (2017).
Dettmer, S. et al. Observation of phase fluctuations in elongated Bose-Einstein condensates. Phys. Rev. Lett. 87, 160406 (2001).
Chesler, P. M., Garcia-Garcia, A. M. & Liu, H. Defect Formation beyond Kibble-Zurek Mechanism and Holography. Phys. Rev. X 5, 021015 (2015).
Brand, J. & Reinhardt, W. P. Solitonic vortices and the fundamental modes of the “snake instability”: possibility of observation in the gaseous Bose-Einstein condensate. Phys. Rev. A. 65, 043612 (2002).
Komineas, S. & Papanicolaou, N. Solitons, solitonic vortices, and vortex rings in a confined Bose-Einstein condensate. Phys. Rev. A 68, 043617 (2003).
Donadello, S. et al. Observation of solitonic vortices in Bose-Einstein condensates. Phys. Rev. Lett. 113, 065302 (2014).
Tylutki, M. et al. Solitonic vortices in Bose-Einstein condensates. Eur. Phys. J. Spec. Top. 224, 577–583 (2015).
Ku, M. J. H. et al. Motion of a solitonic vortex in the BEC-BCS crossover. Phys. Rev. Lett. 113, 065301 (2014).
Ku, M. J. H., Mukherjee, B., Yefsah, T. & Zwierlein, M. W. Cascade of solitonic excitations in a superfluid fermi gas: from planar solitons to vortex rings and lines. Phys. Rev. Lett. 116, 045304 (2016).
Karpiuk, T. et al. Spontaneous solitons in the thermal equilibrium of a quasi-1D Bose gas. Phys. Rev. Lett. 109, 205302 (2012).
Jelić, A. & Cugliandolo, L. F. Quench dynamics of the 2d XY model. J. Stat. Mech. Theory Exp. 2011, P02032 (2011).
Proukakis, N. P. Interplay of density and phase fluctuations in ultracold one-dimensional Bose gases. Phys. Rev. A 73, 023605 (2006).
Richard, S. et al. Momentum spectroscopy of 1D phase fluctuations in Bose-Einstein condensates. Phys. Rev. Lett. 91, 010405 (2003).
Penckwitt, A. A., Ballagh, R. J. & Gardiner, C. W. Nucleation, growth, and stabilization of Bose-Einstein condensate vortex lattices. Phys. Rev. Lett. 89, 260402 (2002).
Acknowledgements
N.P.P. and I.-K.L. acknowledge discussions with Jérôme Beugnon, Paolo Comaron, Leticia Cugliandolo, Jean Dalibard, Zoran Hadzibabic, Fabrizio Larcher, Nir Navon and Rob Smith during the course of the project, computational assistance by Kean Loon Lee and George Stagg and help with diagonalising huge matrices from T.-M. Huang and W.-W. Lin. This work was supported by the Taiwan MOST 103-2112-M-018-002-MY3 grant, the UK EPSRC Grant No. EP/K03250X/1, the QUIC grant of the Horizon 2020 FET program, Provincia Autonoma di Trento, the National Center of Theoretical Sciences, Taiwan and the QuantERA ERA-NET cofund project NAQUAS.
Author information
Authors and Affiliations
Contributions
I.-K.L. undertook all the numerical simulations and analyses, in direct consultation with N.P.P. who coordinated the research, led the interpretations and produced the first draft. S.D., G.L. and G.F. designed and conducted the experiments, which were analysed jointly with F.D. Theoretical aspects were discussed by I.-K.L, S.-C.G., F.D. and N.P.P. All authors contributed to discussions, final data analysis and interpretations, and the final form of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, IK., Donadello, S., Lamporesi, G. et al. Dynamical equilibration across a quenched phase transition in a trapped quantum gas. Commun Phys 1, 24 (2018). https://doi.org/10.1038/s42005-018-0023-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0023-6
This article is cited by
-
Anomalous correlation-induced dynamical phase transitions
Scientific Reports (2023)
-
Observation of vortices and vortex stripes in a dipolar condensate
Nature Physics (2022)
-
Kibble–Zurek universality in a strongly interacting Fermi superfluid
Nature Physics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.