Introduction

Over the past 30 years, frequency combs have been of significant interest for their use in diverse areas of physics such as metrology or spectroscopy1,2,3,4,5,6. In particular, dual-comb spectroscopy (DCS), based on the interference of two mutually coherent frequency combs with slightly different repetition rates (dual comb), has been investigated in depth for its high-resolution, sensitivity and short data acquisition time7, 8. However, most of DCS setups need the two combs to be locked, which requires state-of-the-art stabilization or complex synchronization9,10,11. Even so, when the combs are generated from an intensity-modulated single continuous wave (CW) laser with two fast electro-optic modulators (EOM) and spectrally broadened in a single optical fiber, the mutual coherence requirement between the combs is thus naturally satisfied12,13,14. Nevertheless, the spectral region probed by such EOM-based setups is generally limited to a few THz in the near-infrared (NIR) at telecommunication wavelengths (C/L bands, 1.53–1.61 μm)12,13,14, where molecular absorption is at least thousand times weaker than in the mid-infrared (MIR) range, thus implying long absorption cells12. Therefore, previous works have already shown the possibility of DCS in the MIR region15,16,17,18,19,20 but none has directly used the EOM-based method, probably due to the smaller bandwidth and extinction ratio of the modulators in the MIR. So far, the best solution for exploiting EOMs in the MIR region is opting for NIR to MIR conversion techniques. Recently, such a conversion has been demonstrated in the 3.4 μm region: each NIR signal comb was converted to the MIR by difference frequency generation between the signal comb and a several watts CW laser at 1.06 μm in a temperature-controlled periodically poled lithium niobate crystal21. However, this kind of approach is limited by its significant size, free-space requirement and the need for a costly powerful laser.

In this article, we experimentally demonstrate an alternative way of frequency down converting an EOM-based dual comb from the C/L telecommunication bands to 2 μm using fourth-order modulation instability (4MI)22,23,24. More precisely, two pump combs with slightly different repetition frequencies counter-propagate into a normally dispersive highly nonlinear silica fiber with a low power idler CW laser frequency agile in the O telecommunication band (1.29–1.31 μm). This way, a 4MI frequency conversion is seeded and results with the generation of two signal combs around 2 μm. By studying the interference between the two signal combs, we found that their mutual coherence is preserved through the nonlinear frequency conversion process. With a judicious choice of fiber parameters and by tuning the wavelength of the idler wave, the dual comb is converted in the 2 μm region and tunable over 3 THz (37 nm). DCS performed on the CO2 molecule reveals a good sensitivity of our setup and an excellent agreement with the HITRAN molecular spectroscopic database.

Results

A highly nonlinear fiber for conversion

An optical frequency comb usually corresponds to the spectrum of a femtosecond mode-locked laser3,4,5,6. Such spectrum possesses very interesting characteristics since it is composed of n equally spaced lines of frequencies f n expressed as f n  = nfrep + fc, where frep is the comb line spacing given by the repetition frequency of the laser and fc is an offset frequency due to the difference of velocity between the carrier and the envelope. When generated with an EOM, the comb is generally made in the NIR at telecommunication wavelengths (1.53–1.61 μm).

In this work, our main objective is the wavelength conversion of a dual comb generated with EOMs from 1.57 μm to near 2 μm, i.e., with a frequency shift around 40 THz. To keep an all-fibered and compact setup, this conversion can be achieved using 4MI taking place in the normal dispersion regime of highly nonlinear fiber (HNLF). This phenomenon is highlighted when a weak perturbation associated with a pump is considered in the nonlinear Schrödinger equation, which is the equation governing the propagation of a pulse in an optical fiber (see “Methods”). Figure 1a, b, respectively, represents the principle of 4MI when the pump is a CW or a spectrally wide pump. Under particular conditions, new spectral components can be created within a bandwidth Δf centered at two optimum frequencies ±fopt defined by the dispersive coefficients of the n-th order β n with n = 2 and n = 4, the nonlinear coefficient γ and the pump power P. Thus, we have selected an optical fiber whose dispersion parameters lead to fopt ≈ 40 THz and an idler wave detuned from the pump by fopt will be converted by the 4MI process into a signal wave detuned by −fopt.

Fig. 1
figure 1

Principle of the 4MI phenomenon in the frequency domain. a Electrical field \(\tilde E(f)\) of a CW pump at frequency fpump when the 4MI phenomenon used for converting frequency combs occurs. The dashed lines represent the two amplification bands of bandwidth Δf and centered at a frequency detuning ±fopt from the pump. b 4MI phenomenon associated with a spectrally wide pump showing the broadening of the amplification bands compared to CW case (see also “Methods”)

Full size image

Since our setup is developed with frequency agile EOM-based combs12 and a wavelength tunable idler wave in the telecommunication O band around 1.3 μm, the frequency difference between the pump and the idler waves is easy to set to fopt. Moreover, Δf is in first approximation γP linearly dependent, thus the use of an HNLF will lead to a wider MI gain. Therefore, the HNLF under study, delivered by Sumitomo Electrics, has the following parameters at 1.5686 μm: β2 = 1.93 × 10−1 ps2 km−1, β3 = 3.89 × 10−2 ps3 km−1, β4 = −4 × 10−5 ps4 km−1, α = 0.8 dB km−1 (linear loss coefficient) and γ = 20 W−1 km−1, which lead to fopt = 38.6 THz and Δf = 0.76 THz for a pump power Ppump = 5.5 W. The signal will thus be centered at 1.96 μm with these parameters.

Two-micron dual-comb generation

To observe the signal generated by 4MI, we first consider the conversion of a single EOM-based comb generated at a repetition frequency of frep = 300 MHz. Figure 2 shows the optical spectrum recorded by an optical spectrum analyzer (OSA) placed at the output of a 60 m long HNLF when a single comb at 1.5686 μm with a peak power of Ppump = 5.5 W copropagates through the HNLF with a CW idler at 1.3049 μm with a power of Pidler = 100 mW. This spectrum clearly shows the generation of a signal centered at 1.966 μm with a spectral width of 0.78 THz (10 nm). We can notice that the comb lines separated by frep = 300 MHz cannot be resolved due to the finite resolution of the OSA (≈4 GHz). We also observe that the conversion efficiency (CE) is as low as −40 dB. A characterization of the HNLF using a scanning electron microscope has revealed a core diameter as small as 2.8 μm. With such a small core, the relative fluctuations of the core diameter along the fiber can therefore be quite important resulting in longitudinal fluctuations of the dispersion parameters of the fiber, which lead to a lower CE compared to the case of using an ideal fiber with no dispersion fluctuations24,25,26,27. Note that several works27,28,29 have demonstrated the design of such ideal fibers thus achieving a CE of −15 dB29. Since the fiber used in our experiments does not allow such a high CE, a thulium-doped fiber amplifier (TDFA) has been used to compensate for the low power of the signals at 2 μm.

Fig. 2
figure 2

Optical spectrum recorded with an OSA at the output of a 60 m long HNLF with Ppump = 5.5 W and Pidler = 100 mW. The inset shows a zoom of the signal around 2 μm resulting from the conversion of the pump by stimulated 4MI. ASE amplified spontaneous emission

Full size image

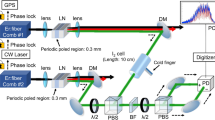
After demonstrating 4MI conversion of a single comb we now aim to extend the method to a dual comb while preserving the mutual coherence between the combs. Thus, the DCS setup presented in Fig. 3 (see “Methods” for details) was used with a 5 m long HNLF and with Ppump = 5.5 W and Pidler = 25 mW for each comb. Briefly, the EOM-based dual comb generated at 1.57 μm with a repetition frequency of frep = 300 MHz and frep + Δfrep = 300.057 MHz is coupled with a 1.3 μm CW idler and the set is counter-propagatively launched in the HNLF. At the output, the 2 μm signals are separated, amplified with a TDFA, sent in an absorption cell, and directed toward a photodetector.

Fig. 3
figure 3

Experimental all-fibered setup for DCS around 2 μm. A dual comb at 1.57 μm (Comb 1 and Comb 2) is generated with EOMs and converted around 2 μm by stimulated 4MI taking place in an HNLF using a CW laser at 1.31 μm. After conversion, the 2 μm dual comb is amplified in a TDFA and filtered. At the output of the filter, 10% of the dual-comb beam serves as a reference channel, whereas the rest is directed toward a cell for spectroscopic applications. The signal is then electronically acquired by a detector to reveal a comb in the radio frequency domain. WDM wavelength division multiplexer

Full size image

Figure 4a shows a typical example of the Fourier transform of an interferogram (RF spectrum) recorded before the absorption cell. Note that the RF spectrum has a very smooth envelope unlike the optical spectrum of Fig. 2 (inset) obtained with a longer fiber (60 m), which exhibits oscillations. Such a smooth envelope is only possible with a small length of HNLF. Indeed, due to the large pump-signal frequency detuning (38.6 THz), the signal and the pump do not propagate at the same velocity along the fiber. This phenomenon known as walk-off effect has to be taken into account in the 4MI-based conversion process and we checked from numerical integration of the nonlinear Schrödinger equation that this effect leads to the generation of spectral oscillations as those observed in the optical spectrum of Fig. 2 (inset). However, by designing a fiber with a convenient β3 parameter to limit this undesired walk-off effect, oscillations should be avoided. From numerical integration of the nonlinear Schrödinger equation, we can estimate that a reduction of the β3 parameter by about one order of magnitude would be sufficient to highly reduce the walk-off effect and thus obtain a flat spectrum when using tens of meters long HNLFs. With the fiber under study, the only way to avoid such deleterious oscillations was to limit the fiber length to just a few meters, 5 m here. The cost of such reduction is a weaker 4MI conversion leading to an optical power as low as 150 nW before the TDFA. Note that by increasing the power of the idler wave and of the pump, one could obtain a more powerful signal but this would require costly equipment that is then less accessible. Moreover, short fiber lengths have the double advantage of suppressing Raman scattering, which appears at longer distances as already visible in Fig. 2 and also of decreasing the important linear losses around 2 μm that we measured at 20 dB km−1. A zoom of the RF spectrum (Fig. 4b) shows that the comb lines are clearly resolved with an expected spacing of Δfrep = 57 kHz and with a transformed-limited linewidth of 3.3 Hz measured with a time-scale of 0.5 s (Fig. 4c). In the optical domain, such measurements correspond to a comb linewidth of 18 kHz. This value is a maximum value since the obtained RF comb linewidth of 3.3 Hz was limited by the recording time of the interferogram (0.5 s) but an optical comb linewidth of 18 kHz still surpasses usual dual-comb setups by one order of magnitude9, 18. The RF comb, whose width is limited by the optical filter used to avoid aliasing, is composed of more than 500 resolved lines. In the optical domain, the power per line is 2.5 µW. Although not essential for further applications, the power per line could easily be increased by stepping the gain supplied by the TDFA up. The obtained results show that the 4MI-based conversion possesses important features: the initial mutual coherence between the two combs is preserved; the residual continuous background coming from the EOMs and the oscillations resulting from the spectral broadening at 1.57 μm by dispersive shock waves are no more detrimental12, 30, 31; the signal-to-noise ratio of the RF spectrum exceeds 20 dB with an acquisition time of 33 ms.

Fig. 4
figure 4

Experimental RF spectrum obtained with our 2 μm dual-comb spectrometer. a RF spectrum recorded with a 5 m long HNLF with Ppump = 5.5 W and Pidler = 25 mW in each arms. When zoomed in, this spectrum reveals b the Δfrep = 57 kHz line spacing and c the 3.3 Hz half-width at half-maximum of one line of the RF comb

Full size image

Spectroscopic applications

We tested the potential of the setup described in Fig. 3 to perform DCS of CO2 molecules in the 1.96 μm region. First, we recorded a CO2 absorption spectrum over a few tens of nanometers, allowing us to investigate the P and R branches of the 2ν1 + ν3 band. For this, we take benefit of the spectral width of the pump responsible for the broadening of the 4MI amplification band (see “Methods” and Fig. 1b). Therefore, by tuning the wavelength of the idler wave in the O band around 1.3 μm, the converted signals can be tuned over ≈3 THz covering the spectral range 1.9435–1.9803 μm. Figure 5a shows a CO2 absorption spectrum obtained by concatenation of several spectra with an overlap of at least one molecular line between each individual spectrum. The total recorded time needed to collect all data was only 0.8 s, whereas the total time required to interrogate the spectrum was less than 3 s and mainly limited by the tuning speed of the laser source that generates the idler wave which is of 1.77 THz s−1. A comparison with a calculated spectrum from the HITRAN database32 was made by calibrating the frequency of only one absorption line on the value given by the database. The “observed-HITRAN” residuals with a standard deviation of 2.3% shows an excellent agreement between the two sets of data, with no ad-hoc fitting parameters. The spectrum also reveals lines that are tens of times less intense than the P(10), such as the ones associated to the 21111–01101 transition with a minimum detectable intensity of 10−23 cm per molecule. The noise-equivalent absorption coefficient at 1 s time-averaging per comb line was found to be 7.4 × 10−7 cm−1 \({\mathrm{Hz}}^{ - {\textstyle{1 \over 2}}}\). The potential applications of such a sensibility could be real-time sensing of CO2 mixed with other gases. For example, Fig. 5b shows the absorption spectrum of the P and R branches of the 2ν1 + ν3 band with a gas mixture of 15% of CO2 and 85% of O2. A superposition of Lorentzian profiles was fitted to the experimental spectrum and the “observed-fit” residuals with a standard deviation of 1.24% shows an excellent agreement between the two sets of data with any systematic deviation.

Fig. 5
figure 5

Experimental absorption spectra and comparisons. a Absorption spectrum of the CO2 molecule at 0.582 atm (top) compared with the HITRAN database (middle) and difference between the two (bottom). b Absorption spectrum at 1.283 atm of a gas mixture of 15% CO2 + 85% O2 (top) compared with a fit of a superposition of Lorentzian profiles (middle) and difference between the two (bottom)

Full size image

Regarding the stability over time of the setup, we did not observe any modification or deviation of the RF signal during the measurements and for several hours following them. Even more we observed that when the setup is turned off after being optimized, restarting it after several days only requires slight adjustment of the polarization controllers for optimal operation.

Finally, we focused our attention on the P(10) and P(44) rotational–vibrational transitions of the spectrum and we measured their collisional self-broadening coefficients Γ at a temperature of T = 295 K. We recorded several spectra at different pressures and a least-square Voigt profile fit to the experimental spectrum at each pressure leads to the collisional self-broadening half-width Δν of the spectral lines. Figure 6 shows the collisional half-width Δν of the P(10) and P(44) lines versus pressure. The slopes of the least-square straight lines correspond to the collisional self-broadening coefficients, namely ΓP(10) = (0.1097 ± 0.0011) cm−1 atm−1 and ΓP(44) = (0.0761 ± 0.0017) cm−1 atm−1, which are in very good agreement with the values given by the HITRAN database32 \({\mathrm{\Gamma }}_{{\mathrm{P(10)}}}^{{\mathrm{Hit}}}\) = 0.109 cm−1 atm−1 and \({\mathrm{\Gamma }}_{{\mathrm{P(44)}}}^{{\mathrm{Hit}}}\) = 0.078 cm−1 atm−1.

Fig. 6
figure 6

Measured collisional half-width of the P(10) and P(44) lines of CO2 gas versus pressure at T = 295 K. The slope of the least-squares straight line gives the collisional self-broadening coefficient

Full size image

Discussion

In this article, we experimentally demonstrated a straightforward novel technique to convert an EOM-based dual comb from the C/L bands to the 2 μm region by fourth-order modulation instability in the normal dispersion regime of a highly nonlinear optical fiber. With a single idler continuous wave laser of only a few tens of milliwatts and since the nonlinear optical fiber used for wavelength conversion is common to the two combs, we showed that two pump combs can be converted while preserving their mutual coherence with no active stabilization, which significantly reduces the experimental complexity compared to systems based on mode-locked femtosecond lasers. The converted dual comb was suitable to carry out DCS in the 2 μm region with good sensitivity and high reliability, thanks to the all-fibered components available in the different telecommunication bands O, C/L and 2 μm. The spectral resolution that is given by the line spacing of the two combs can be adjusted very easily with the electro-optic modulators and does not depend on any resonant optical elements. Thanks to frequency agility of the idler wave in the O band, the all-fibered dual-comb spectrometer is wavelength tunable around 2 μm, allowing the observation of an absorption spectrum of the CO2 molecule over 3 THz (37 nm). The DCS device was also used successfully for measuring the collisional self-broadening coefficients of some rotational–vibrational lines. The results were found to be in a very good agreement with the HITRAN molecular spectroscopic database. Other gases are investigable in the same spectral region probed here, such as N2O, H2O, or NH3. Using another silica HNLF with suitable parameters, this all-fibered conversion technique might be used in the whole NIR. On the other hand, since modulation instability has already been observed in other materials, one could replace the nonlinear silica fiber with dispersion-engineered tellurite or chalcogenide infrared glass fibers, which could extend the technique further into the MIR33. Once again, the fluctuation of the dispersion parameters would drastically affect the conversion efficiency except if the fiber is carefully engineered34 similarly to silica-based fibers27,28,29. To the same aim, the HNLF could also be replaced by waveguides which could open up new opportunities in generating MIR frequency combs19, 35,36,37. Possible utilities might be trace-gas detection38 or real-time spectroscopy diagnostics, such as in medical applications for the monitoring of isotopic ratios of CO2 in the exhaled air of human breath39.

Methods

Modulation instability-based conversion

The propagation of a slowly varying pulse envelope ψ in an optical fiber is ruled by the scalar nonlinear Schrödinger equation, which can be written in the retarded time frame (z, t) as40:

$$i\partial _z\psi + \gamma \left| \psi \right|^2\psi + i\frac{\alpha }{2}\psi + \mathop {\sum}\limits_{n = 2}^\infty {\kern 1pt} i^n\frac{{\beta _n}}{{n!}}\partial _t^n\psi = 0$$
(1)

where γ is the nonlinear Kerr coefficient, \(\left| \psi \right|^2\) the wave power, α the linear loss coefficient, and β n the n-th order chromatic dispersion coefficient. The MI phenomenon shows that weak periodic perturbations of an intense carrier pump wave can grow exponentially along the fiber, leading to energy shedding of the pump wave into new frequencies within a certain spectral bandwidth Δf and symmetrically situated with respect to the pump at optimum frequency detunings of ±fopt for which the MI gain is maximum (see Fig. 1a). When dispersion is taken into account up to the fourth order, a standard linear stability analysis applied to Eq. (1) shows that 4MI can exist with β2 > 0 and β4 < 022,23,24. In that case the optimum frequency fopt is given by22:

$$\left( {2\pi f_{{\mathrm{opt}}}} \right)^2 = \frac{{ - 2}}{{\beta _4}}\sqrt {9\beta _2^2 - 6\beta _4\gamma P} - 6\frac{{\beta _2}}{{\beta _4}}$$
(2)

where \(P = \left| {\psi (z = 0,t)} \right|^2\). Moreover, from the cutoff frequencies of the 4MI gain given in ref. 22 we found that, when \(\frac{{ - \beta _4}}{{\beta _2^2}}\gamma P \ll 1\), the gain width is given by \({\mathrm{\Delta }}f \cong \frac{{\gamma P}}{{2\pi }}\left( {\frac{{ - \beta _4}}{{3\beta _2^3}}} \right)^{{\textstyle{1 \over 2}}}\) and linearly depends on nonlinearity γP.

Note that the nonlinear fiber used in our experiment has a negligible birefringence. However, the modulation instability linear stability analysis could easily be extended to the case of a birefringent nonlinear fiber41.

Detailed setup for 2 μm DCS

We describe the experimental technique used here to perform DCS around 2 μm. The setup is all-fibered and presented in Fig. 3. In a first stage two EOM-based combs are generated at 1.57 μm with slightly different repetition frequencies, frep = 300 MHz and frep + Δfrep = 300.057 MHz. Both combs are spectrally broadened by dispersive shock waves in a 222 m long normally dispersive optical fiber12, 14, 31. The combs consist of 60 ps pulses with 0.2 THz spectral width. The principle of this first stage is fully described in ref. 12.

The two pump combs at 1.57 μm are coupled with an idler CW laser tunable in the telecommunication O band (1.29–1.31 μm) for seeding the 4MI frequency conversion. Note that for efficient common-noise rejection and for maintaining the mutual coherence between the two combs while converted, a single HNLF was used, in which the two pump combs with their associated idler wave counter-propagate and are separated with a 1.5/2 μm wavelength division multiplexer (WDM) at each fiber end. Polarization controllers are placed on each input branch of the WDMs. The two 1.96 μm signal beams are then combined and their interference leads to a comb in the radio frequency (RF) region. Note also that each idler wave undergoes an attenuation of 3 dB through the 1.5/2 μm WDM leading to a less intense 4MI conversion in the HNLF, which is compensated by amplifying the 1.96 μm signal with a TDFA. Moreover, using a TDFA permits us to compensate the low CE originating from the fluctuations of the dispersion parameters24,25,26,27. At the amplifier output, a filter is used to select half of the optical spectrum for avoiding any aliasing in the RF domain and to remove the amplified spontaneous emission coming from the TDFA. Once filtered, the converted dual comb at 1.96 μm is launched into a 78.1 cm long fibered cell and then directed toward a photodetector before digitalization and spectral analysis in the RF domain.

Broadening of the 4MI band

According to a linear stability analysis applied to Eq. (1), the 4MI amplification bands are centered at two frequencies ±fopt given by Eq. (2)22. However, when dealing with a chirped pump, each of its spectral components will generate its own 4MI amplification band since the second-order dispersion coefficient β2 is frequency dependent42. The 4MI amplification band is thus broadened relatively to a variation of β2 within a range Δβ2≈Δw p β3, where Δw p is the spectral width of the pump (see Fig. 1b). This broadening gives us a tunability of our signals of ≈3 THz, which has to be compared to Δf = 0.76 THz with a continuous wave.

Data availability

The data that support the work presented in this paper are available from the corresponding author on reasonable request.