Understanding the interactions between the bis(trifluoromethylsulfonyl)imide anion and absorbed CO₂ using X-ray diffraction analysis of a soft crystal surrogate

Abstract

The selective carbon dioxide (CO₂) absorption properties of ionic liquids (ILs) are highly pertinent to the development of methods to capture CO₂. Although it has been reported that fluorinated components give ILs enhanced CO₂ solubilities, it has been challenging to gain a deep understanding of the interactions occurring between ILs and CO₂. In this investigation, we have utilized the soft crystalline material [Cu(NTf₂)₂(bpp)₂] (NTf₂^‒ = bis(trifluoromethylsulfonyl)imide, bpp = 1,3-bis-(4-pyridyl)propane) as a surrogate for single-crystal X-ray diffraction analysis to visualize interactions occurring between CO₂ and NTf₂^‒, the fluorinated IL component that is responsible for high CO₂ solubility. Analysis of the structure of a CO₂-loaded crystal reveals that CO₂ interacts with both fluorine and oxygen atoms of NTf₂^‒ anions in a trans rather than cis conformation about the S–N bond. Theoretical analysis of the structure of the CO₂-loaded crystal indicates that dispersion and electrostatic interactions exist between CO₂ and the framework. The overall results provide important insight into understanding and improving the CO₂ absorption properties of ILs.

Introduction

Ionic liquids (ILs) have received increasing attention in the past several decades owing to their wide variety of potential industrial applications^1,2,3. This is especially true for ILs that have selective carbon dioxide (CO₂) absorption properties as a result of the tremendous interest in and urgency for stemming global warming by removal of green house gases from the atmosphere⁴. It is known that anion components of ILs significantly influence CO₂ absorption capacities and that fluorine containing anions are superior CO₂ absorbers as compared to those that lack this halogen⁵. This phenomenon is exemplified by the bis(trifluoromethylsulfonyl)imide (NTf₂^‒) anion, which is one of the most interesting building blocks for the construction of ILs with high CO₂ absorption propensities⁶. Although several theories have been advanced to explain the physical interactions that take place between NTf₂^‒-containing ILs and CO₂, some of which have been tested experimentally and by using simulations^{7,8,9,10,11,12}, a full understanding of the interactions has not yet been gained. In particular, based on the current state of knowledge, it is still not possible to ascertain whether oxygen or fluorine is the key CO₂ absorption site in NTf₂^‒, and to determine the nature of primary interactions occurring between this anion and this gas. The main hurdle to obtaining this information is associated with difficulties with determining the structures of ILs owing to their non-crystalline nature. In addition, the conformationally flexible structure of the NTf₂^‒ anion, originating from reasonably rapid rotation (barrier of 25.1 kJ mol⁻¹) of the CF₃SO₂ substituent around the S–N bond (Supplementary Fig. 13), complicates elucidation of the IL-CO₂ interactions.

Recently, a new class of materials, referred to as soft crystals, has attracted great attention. These materials can exist in both a highly crystalline and soft states, which can be reversibly interconverted in response to external chemical and physical stimuli^13,14. Interestingly, some of the soft materials retain their single crystalline nature upon being treated with external stimuli. We envisaged that it might be possible to design and fabricate soft crystals, which contain components that are the same as or similar to those present in ILs, and that might possess the ability to absorb CO₂ in synchrony with stimuli promoted structural changes. In this way, it would be possible to utilize these substances as surrogates to determine the structures of and elucidate important interactions in ILs containing absorbed CO₂ using standard single-crystal X-ray diffraction techniques.

To explore this proposal, we prepared a new soft crystal [Cu(NTf₂)₂(bpp)₂] (1), which is composed of an NTf₂^‒ anion and the flexible 1,3-bis(4-pyridyl)propane (bpp) ligand and Cu²⁺ (Fig. 1) that possess an alkyl chain and positively charged Cu²⁺ coordinated nitrogen centers that are typical of those present in a ILs (e.g., the alkylimidazolium and NTf₂^‒ containing IL in Fig. 1). In the effort described below, we demonstrated that the soft crystal 1 displays reversible absorption of CO₂ associated with a stimulus-induced structural transformation, while retaining its permanent single-crystalline nature. Moreover, by using standard single-crystal X-ray diffraction techniques, we elucidated the nature of interactions with the NTf₂^‒ anion that are responsible for CO₂ absorption.

Fig. 1: Molecular structures.

Structures of the components of soft crystal 1 (left) and a typical IL [1-n-butyl-3-methylimidazolium][NTf₂^‒] containing NTf₂^‒ (right)⁶.

Results

Crystal structure of as-synthesized soft crystal

A single-crystal of 1 was prepared by using the diffusion method and a three-phase system, including a 0.1 M aqueous Cu(NTf₂)₂ bottom layer, a 1:1 water and MeOH, middle layer, and 0.2 M bpp in MeOH top layer. Upon standing, this system generated transparent and rod-like purple single crystals, which were shown by using the elemental analysis to have the desired atomic composition and purity. The soft crystal 1 crystallized in the monoclinic space group P2/n, containing crystallographically independent one copper ion, two NTf₂^‒ anions and two bpp ligands. The copper ion, surrounded by two NTf₂^‒ anions and four bpp ligands, exists in a distorted octahedral environment (Fig. 2a). The distance between the copper ion and NTf₂^‒ anions (Cu1-O1 = 2.801(2) Å) is much longer than that between the copper ion and the bpp ligands (Cu1–N1 = 2.002(2) Å, Cu1–N2 = 2.013(3) Å) as a consequence of Jahn-Teller distortion and the weak coordination ability of NTf₂^‒. The NTf₂^‒ anions exist in a trans conformation (Fig. 2b and Supplementary Fig. 1), which is known to be thermodynamically more stable than the cis conformation¹⁵. The bpp ligands bridge the copper ion to form one-dimensional (1D) chains oriented along the b-axis with a toroidal space of 6.4 Å × 12.2 Å (Fig. 2c and Supplementary Fig. 2). The 1D chains aggregate through weak CH/π interactions to form quasi two-dimensional (2D) layers with an interchain distance of 9.9 Å (Supplementary Fig. 3). In addition, NTf₂^‒ anions are sandwiched between the 2D layers through weak coordinative interactions, in which the distance between two neighboring layers is 8.0 Å (Supplementary Fig. 3). The 2D layers and NTf₂^‒ anions are densely packed through the above-mentioned weak coordinative interactions and weak hydrogen bonding interactions between the trifluoromethylsulfonyl groups of NTf₂^‒ and pyridyl groups of the bpp ligands (Supplementary Fig. 4). As a result, almost no pores exist in the crystal structure of 1, and the pore space calculated by using MERCURY software (probe radius: 1.2 Å, approximately grid spacing: 0.7 Å) is only 0.7%.

Fig. 2: Crystal structures.

Views of the crystal structures of a–c 1 and d–f 1·2CO₂. Coordination environment around the Cu center in a 1 and d 1·2CO₂. Conformation of NTf₂^‒ in b 1 and e 1·2CO₂. 1D chain structures in c 1 and f 1·2CO₂.

CO₂ absorption properties and stability for water

Inspection of absorption/desorption isotherms of 1 displayed in Fig. 3a shows that almost no absorption of N₂ and Ar occurs at 77 K proving that this soft crystal has a densely assembled structure. In contrast, 1 exhibits a steep increase and decrease in the amount of absorbed CO₂ at P/P₀ = 0.21 and 0.09, respectively, and 195 K, while N₂ and Ar are not absorbed even at 195 K (Supplementary Fig. 9), which suggests that absorption of this gas takes place in association with a change between a closed and an open structure¹⁶. The saturated absorption amount of CO₂ was found to be 2.03 mol mol⁻¹ at P/P₀ = 0.98 (P ≅ fugacity = 0.99 bar), which corresponds to 1.02 mol per mol of NTf₂^‒. This value is close to those of NTf₂^‒-containing CO₂ absorbing ILs at 313 K and 40 bar (fugacity = 34 bar) (under this condition, absorption by NTf₂^‒-containing ILs is ca. 0.5 CO₂ mole fraction, corresponding to 1 mol per one mol of NTf₂^‒)¹⁷. In order to elucidate the role of fluorinated moieties in governing CO₂ absorption, we synthesized the nonfluorinated analog of [Cu(NMes₂)₂(bpp)₂] (2), in which NMes₂^‒ is bis(methylsulfonyl)imide, which has a one-dimensional structure that is similar to that of 1 (Supplementary Fig. 6) and measured its absorption properties. As shown in Fig. 3a and Supplementary Fig. 10, CO₂ is selectively absorbed to 2 but the threshold pressure in the absorption isotherm (P/P₀ = 0.32) is higher than that of 1 (P/P₀ = 0.21), indicating that the fluorinated component facilitates the CO₂ absorption. A similar observation has been made in studies of the ILs with NTf₂^‒ and NMes₂^‒ anions⁵. The integer number (2 mol mol⁻¹) of the amount of CO₂ absorbed at saturation may be related to the free volume and/or specific absorption sites in the soft crystal 1.

Fig. 3: Absorption/desorption properties and PXRD patterns.

a Absorption (closed symbols)/desorption (open symbols) isotherms of CO₂ (black circle), N₂ (blue square), Ar (green pentagon), and H₂O (red rhombus) at 195 K (CO₂), 77 K (N₂ and Ar), and 298 K (H₂O), respectively, for 1 and of CO₂ (gray triangle) at 195 K for 2. b Calculated PXRD pattern of 1 from its single-crystal X-ray structure (black) and observed PXRD patterns of as-synthesized 1 (red), 1 soaked in H₂O (purple) and 0.1 M HCl (blue) for 2 days.

The results of investigation of the variable-temperature CO₂ absorption of 1 reveal that similar behavior is followed but that different threshold pressures exist in the absorption and desorption isotherms (Supplementary Fig. 11). Because the threshold positions are related to equilibrium pressures for the CO₂ absorption reaction, their temperature dependence enables an evaluation of the enthalpy of CO₂ absorption (Q_st) by using the Clausius-Clapeyron equation. A plot of the natural logarithm of the threshold positions vs 1/T was found to be linear (Supplementary Fig. 12), and analysis of the slope yields a Q_st value of ‒29.1 kJ mol⁻¹. This enthalpy value is only moderate when compared with those of other CO₂ absorption/adsorption materials, including a 30 wt% monoethanolamine solution (‒72 to ‒79 kJ mol⁻¹)¹⁸, amine-functionalized porous organic polymer (‒61 kJ/mol)¹⁹ and zeolites (‒49.1, ‒50.0, and −38.0 kJ mol⁻¹ for NaX, Na-ZSM-5 and H-ZSM-5, respectively)²⁰. [1-n-Alkyl-3-methylimidazolium][NTf₂^‒] (alkyl = ethyl, butyl, and hexyl) ILs have smaller Q_st values ranging from ‒11 to ‒14 kJ mol⁻¹ because of more limited physisorption between dynamic liquid and a gas phase²¹. The only moderate Q_st value among those of other solid adsorbents suggests that the interaction between NTf₂^‒ in 1 and CO₂ and/or that between bpp and CO₂ is not strong.

The stability and absorbability of 1 for water, which are important issues when contemplating practical uses, were also investigated. NTf₂^‒ anion is hydrophobic as reflected by the fact that the IL [1-n-butyl-3-methylimidazolium][NTf₂^‒] (Fig. 1) has a low absorbability for water and a CO₂ absorption capacity that is not affected by water absorption¹⁷. The soft crystal 1 also has negligible H₂O absorbability (Fig. 3a). Furthermore, soaking in neutral and acidic (0.1 M HCl) H₂O for 2 d does not affect the powder X-ray diffraction (PXRD) patterns of 1 (Fig. 3b). These results show that 1 has outstanding stability and low water absorbability.

Crystal structure of CO₂-loaded soft crystal

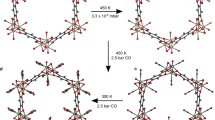
Because soft crystal 1 retains its single crystalline nature after absorption of CO₂, we were able to determine the structure of the CO₂-loaded crystal 1·2CO₂ by using standard single-crystal X-ray diffraction analysis. The space group of 1·2CO₂ was found to be C2/c, which can be considered as being a transform to a C-centered lattice with space group P2/n. The coordination environments of the copper ion in 1 and 1·2CO₂ are similar (Figs. 2a and 2d), while the distance between the copper center and NTf₂^‒ anion is 7% shorter (Cu1′-O1′ = 2.600(2) Å) and that between the copper center and bpp ligands is slightly longer (Cu1′–N1′ = 2.015(3) Å, Cu1′–N2′ = 2.018(3) Å) in 1·2CO₂ compared to 1. The toroidal shape of 1D chains in 1·2CO₂ are almost unchanged (6.3 Å × 12.3 Å, Fig. 2f and Supplementary Fig. 2) in comparison with 1, and the dihedral angles of neighboring pyridine rings coordinated to the same copper ions decrease from 69°/68° in 1 to 59°/64° in 1·2CO₂. Moreover, 1·2CO₂ contains slightly different quasi 2D layers in comparison to 1. Specifically, each 1D chain in 1·2CO₂ is inclined against the plane composed of copper ions, resulting in a slightly larger interchain distance (10.3 Å) (Supplementary Fig. 3). The interlayer space is occupied by both NTf₂^‒ anions and CO₂ molecules, and the presence of absorbed CO₂ causes a significant expansion of the interlayer distance from 8.0 to 8.6 Å (Supplementary Fig. 3). Consequently, the cell volume of 1·2CO₂ is 8.5 % larger than that of 1 largely because of a 7.5% expansion of the interlayer.

As mentioned above, all NTf₂^‒ anions in 1 are arranged in a parallel manner in the trans conformation. However, after CO₂ absorption, six NTf₂^‒ anions exist in a cis conformation (Supplementary Fig. 1) and are positioned at corners of hexagonal vertexes (Supplementary Fig. 5) to form a cavity which encloses two CO₂ molecules (Fig. 2e). The significant changes taking place in the interlayer distance and conformation of NTf₂^‒ anions, along with other slight structural changes suggest that the soft crystal 1 undergoes an induced-fit type change to accommodate CO₂.

Interactions that exists between the 1D chains and CO₂ in 1·2CO₂ are shown in Fig. 4. CO₂ molecules in 1·2CO₂ are disordered over two sites with occupancies of 0.66 (molecule A) and 0.34 (molecule B). The shortest contact exists between a fluorine of one NTf₂^‒ anion and the carbon of CO₂ with F•••C distances of 2.95(2) (molecule A) and 2.68(5) Å (molecule B), which are shorter than the sums of their van der Waals radii (3.05–3.23 Å)²². On the other hand, the distances between oxygen of another NTf₂^‒ anion and the carbon of CO₂ in molecule A (O•••C = 3.02(2) Å) and molecule B (O•••C = 3.28(5) Å) are comparable with the sums of their van der Waals radii (3.00–3.35 Å)²². Considering that molecule A has a larger occupancy, it is expected that both fluorine and oxygen in the NTf₂^‒ anion should play prominent roles in governing CO₂ absorption. Weak hydrogen bonding interactions also exist between the bpp ligand and CO₂ (H•••O and C•••O = 2.52(2) and 3.30(2) Å & 2.91(4) and 3.42(4) Å in molecule A and 2.58(4) and 3.34(4) Å & 2.83(6) and 3.34(6) Å in molecule B, Fig. 4).

Fig. 4: CO₂-Absorbed structure.

View of the intermolecular contacts between the CO₂ molecule (blue: molecule A, red: molecule B) and structural components in 1·2CO₂.

The degree of quadrupole-quadrupole interactions between CO₂ molecules is related to the distances between the carbons of two neighboring CO₂ molecules. In 1·2CO₂, the respective distances between CO₂ carbons in molecules A and A, molecules A and B, and molecules B and B are 3.82(3) Å, 4.03(6) Å and 4.28(8) Å. Although the crystal structure of 1·2CO₂ was determined at a temperature below the sublimation point of CO₂, the intermolecular C–C distances are longer than the intermolecular distance (3.58 Å) in solid CO₂²³. Moreover, the C–C distance between CO₂ molecules in molecules B and B is greater than 4.1 Å, which is the intermolecular C–C distance in gaseous CO₂²⁴. The differences in the intermolecular CO₂•••CO₂ distances show that a quadrupole-quadrupole interaction contributes little to stabilization of absorbed CO₂ in 1·2CO₂ and, consequently, demonstrate that interactions with both a fluorine and oxygen atom in the NTf₂^‒ anion are the most influential in governing absorption of CO₂ gas by 1.

Theoretical calculations

A density functional theory calculation was performed under periodic boundary conditions to gain more information about interactions occurring between NTf₂^‒ anions and CO₂ in 1·2CO₂. The binding energy (E_b) was determined by using the equation E_b = E_{Framework+gas} ‒ (E_Framework + E_Gas), where E_{Framework + gas} and E_Framework are the respective energies of the complete complex 1·2CO₂ and only the framework of 1·2CO₂, and E_Gas is the energy of CO₂ in a sufficiently large super cell. The calculated E_b value was found to be ‒31.3 kJ mol⁻¹, which is consistent with the experimentally determined enthalpy of CO₂ absorption. Next, an analysis of the interaction of 1·2CO₂ was performed, utilizing a cluster model and an energy decomposition analysis with the natural orbitals from chemical valence theory, in order to elucidate the nature and trend of the interaction that most strongly contributes to CO₂ absorption. The results (Supplementary Table 4) show that large contributors to the stabilization of the structure of 1·2CO₂ are a dispersion force (‒28.7 kJ mol⁻¹) and an electrostatic interaction (‒25.0 kJ mol⁻¹), and that orbital interaction energy (‒13.3 kJ mol⁻¹) is a minor contributor. This result is consistent with previous findings, which suggest that calculated Lewis acid-base binding energies between CO₂ and naked anions are inversely proportional to the solubility of CO₂ in ILs. Thus, Lewis acid-base interactions are not important contributors to solubilities of CO₂ in ILs²⁵.

Discussion

In Fig. 5 are displayed schematic views of the structures of soft crystal 1 formed during the CO₂ absorption process. Analysis of the structures before and after CO₂ absorption shows that the CO₂ absorption process by 1 has features that are similar to those of ILs. Firstly, 1 preferably absorbed CO₂ over other gases such as N₂ and Ar. Secondly, during absorption, the lattice of 1 expands to create an interstitial space for CO₂²⁶, while the distance between the cation (in this case, copper) and anion (in this case, NTf₂^‒) changes only slightly²⁷. In addition, our studies have uncovered a unique feature not observed previously in studies of CO₂ absorption by ILs. Specifically, we obtained direct evidence showing that the NTf₂^‒ anion undergoes a conformational change from the trans to cis upon CO₂ binding. In ILs, the NTf₂^‒ anion can exist in two possible conformations (trans and cis) at room temperature with the trans form being thermodynamically more stable^15,28. The reason why the conformation of the NTf₂^‒ anion changes when 1 absorbs CO₂ is that cohesion energy is enhanced owing to the larger dipole moment of the cis form (dipole moments for trans and cis forms are 0.2–0.4 and 4.4–5.4, respectively)²⁹. This enables the absorbed CO₂ molecule interact more strongly and cooperatively with the fluorine and oxygen atoms of the two neighboring cis- NTf₂^‒ anions by taking full advantage of delocalized negative charges (Supplementary Table 3), in the 1D alternate arrangement of •••NTf₂^‒•••CO₂•••NTf₂^‒•••CO₂•••.

Fig. 5: Schematic representation of CO₂ absorption process.

Schematic views of structural changes occurring in the CO₂ absorption process by soft crystal 1. The upper figures show packing structures viewed along the b-axis and bottom figures show arrangements of NTf₂^‒ anions in the presence and absence of CO₂. The 1D [Cu(bpp)₂] chains are oriented along the b-axis. The dotted lines indicate intermolecular interactions between the NTf₂^‒ anion and CO₂. The yellow meandering line shows the 1D alternate arrangement of •••NTf₂^‒•••CO₂•••NTf₂^‒•••CO₂•••.

Gas absorption taking place in association with a change between a closed structure and an open structure of an absorbent is dominated by a balance between the energy barrier for the structural transition of the absorbent and the enthalpy change associated with the open form absorbing the gas^30,31. The fluorinated moieties contribute to decreasing the energy barrier for the structural transition because they have an ability to delocalize charge (Supplementary Table 3) and low electronic polarizability that leads to weakening intermolecular interactions³². The effect of the fluorinated groups on the gas absorption enthalpy change is likely not related to Lewis basicity because the result of this study reveal that Lewis acid-base interactions are not important contributors to solubilities of CO₂. Indeed, the most basic sites in anions are close to the most acidic sites in cations, which prevents the occurrence of Lewis acid-base interactions between CO₂ and the most basic sites. Although the issue requires more detailed studies, it appears that charge delocalization and low electric polarizability promoted by fluorination have respective impacts on electrostatic interactions and dispersion forces that influence CO₂ absorption.

Prior to the study described above, numerous experiments have been conducted to elucidate the CO₂ absorption states in ILs^{7,8,9,10,11,12}. In this effort, using the soft crystal 1 as a surrogate, we were able to visualize interactions that occur between the NTf₂^‒ anion component of ILs and CO₂. The pyridine rings in bpp ligands and NTf₂^‒ anions in 1 synergistically constrain CO₂ molecules in the crystal. The NTf₂^‒ anion contains the primary absorption sites for CO₂ comprised of a trifluoromethyl fluorine and sulfonyl oxygen atom. The bpp ligand supports the NTf₂^‒-CO₂ interaction through the formation of a weak phenyl hydrogen-CO₂ interaction. As a result, a dispersion force and electrostatic interaction are the main contributors to stabilization of the CO₂-absorbed complex. Furthermore, a conformational change of the NTf₂^‒ anions from trans to cis occurring upon CO₂ capture by 1 also contributes to the absorption capacity. Of course, we understand that the observations made in this investigation have been made using a surrogate and not under real IL conditions especially because of differences in temperature and fluidity of the system. In addition, ILs with the NTf₂^‒ anion are not practical for CO₂ separation because the perfluorinated groups containing NTf₂^‒ anion is not an environment-friendly. Nevertheless, the findings should not only increase the level of understanding of CO₂ absorption by ILs but also provide new approaches to probe interactions between ILs and CO₂ and to design new systems for CO₂ separation applications.

Methods

Synthesis

Commercially available reagents were used as received without further purification. Cu(NTf₂)₂ and Cu(NMes₂)₂ were synthesized using previously described procedures^28,33.

A single-crystal of [Cu(NTf₂)₂(bpp)₂] (1) was prepared by using a diffusion method in the straight glass tube containing a bottom layer of 0.1 M aqueous Cu(NTf₂)₂, a middle layer of 1:1 water and MeOH, and a top layer of 0.2 M bpp in MeOH. After 1 week, the formed transparent and rod like purple single crystals were separated by filtration, washed with water, and dried in the atmosphere. Elemental analysis was used to confirm the atomic composition and purity of the as-synthesized single crystals. Elemental analysis (%) calcd for C₃₀H₂₈Cu₁F₁₂N₆O₈S₄: C 35.31, H 2.77, N 8.24, F 22.34, S 12.57. Found: C 34.86, H 2.57, N 8.04, F 22.77, S 12.69. The thermogravimetric curve and Fourier transform infrared spectrum of 1 are shown in Supplementary Figs. 7 and 8.

A single-crystal of {[Cu(NMes₂)₂(bpp)₂]·3H₂O} (2·3H₂O) was prepared by using a solvent evaporation method in the beaker containing 0.1 M aqueous Cu(NMes₂)₂ and 0.2 M bpp in MeOH. After 1 week, the formed transparent and plate like blue single crystals were separated by filtration, washed with MeOH, and dried in the atmosphere. This crystal lost a part of hydrated water during drying, which was confirmed using elemental analysis. Elemental analysis (%) calcd for C₃₀H_44.4Cu₁N₆O_10.2S₄ (2·2.2H₂O): C 42.69, H 5.30, N 9.96. Found: C 42.20, H 4.98, N 9.76. A single-crystal of [Cu(NMes₂)₂(bpp)₂] (2) was prepared by drying 2·3H₂O under N₂ flow at 373 K for 30 min.

Single-crystal X-ray diffraction analysis of 1, 1·2CO₂, and 2

Crystal data for 1 were collected at 173 K on a RIGAKU RAXIS-RAPID imaging-plate diffractometer with a graphite-monochromated Mo-Kα radiation (λ = 0.71075 Å). Crystal data for 2 were collected at 293 K on a RIGAKU XtaLab Synergy-R with a multi-mirror monochromated Mo-Kα radiation (λ = 0.71075 Å). The structures were solved by using direct method (SHELXT)³⁴ and refined by using full-matrix least-squares techniques on F² using SHELXL-2018³⁵. All non-hydrogen atoms were refined anisotropically. Hydrogen atoms were located at geometrically calculated positions and refined using a riding model. Olex2 was used as a graphical user interface³⁶. Crystallographic data are shown in Supplementary Tables 1 and 2 and Supplementary Data 1 and 3.

The structural determination of 1·2CO₂ was carried out using the following procedure. A single crystal of 1 was placed at the bottom of a glass capillary, which was then adhered to the base using glue. The base was installed on the absorption equipment (BELSORP-mini, MicrotracBEL Corp.) and the crystal was heated at 373 K for 30 min under a vacuum as the pre-treatment. After pre-treatment, CO₂ gas at 40 kPa was added and the capillary was cut and sealed quickly. The capillary containing single crystal sample and CO₂ gas was placed in the single-crystal X-ray diffractometer with a cryogenic unit, and cooled at a rate of 1 K min⁻¹ from 293 K to 173 K, and then held at 173 K for 4 h. X-ray diffraction measurements were then made at 173 K on a RIGAKU XtaLAB P200 with a multi-mirror monochromated Cu-Kα radiation (λ = 1.5418 Å). Data analysis was performed in the manner described for 1. Crystallographic data are shown in Supplementary Table 1 and Supplementary Data 2.

Gas absorption isotherm experiments

CO₂ (195 K), N₂ (77 K and 195 K) and Ar (77 K and 195 K) absorption/desorption isotherms were measured by using a BELSORP-max (MicrotracBEL Corp.). Water absorption/desorption isotherms were measured at 298 K by using a BELSORP-aqua (MicrotracBEL Corp.). Before the measurement, the sample was heated at 373 K in a vacuum overnight for activation by BELPREP-vac (MicrotracBEL Corp.). High-pressure CO₂ absorption/desorption isotherms were measured by using a BELSORP-HP (MicrotracBEL Corp.). Activation of the sample was performed on a BELSORP-HP at 373 K in a vacuum.

Theoretical calculations

For determining the S–N bond rotational barrier in NTf₂^‒, relax scan calculations were performed using gaussian 09 Rev. E.01 software at the B3LYP/aug-cc-pVDZ level of theory³⁷. A PBE functional³⁸, with projector augmented wave potentials and van der Waals interaction corrected by using a D3 scheme³⁹ to optimize the atomic positions of 1, CO₂ and 1·2CO₂, was used to obtain an estimate of the binding energy of CO₂ (Supplementary Fig. 14). In all cases, spin polarized calculations were employed under periodic boundary condition and Γ-point approximation using the Vienna Ab initio Simulation Package (VASP)^40,41,42,43 with the cut-off energy of 400 eV. The atomic charges were evaluated based on Bader analysis (Supplementary Table 3)^44,45,46,47. In a manner that is similar to other reported approaches^48,49,50, after optimization of 1·2CO₂, a model consisting of one CO₂, three NTf₂⁻ and three (4-pyridyl)butane, which are protonated instead of bonded to Cu²⁺ (Supplementary Fig. 15), was employed to investigate the nature of the interaction between CO₂ and 1. The positions of added H atoms were optimized with a PBE functional using Amsterdam Density Functional 2018 program⁵¹. A standard triple-ζ STO basis set with two sets of polarization functions (TZ2P)⁵² and a Grimme D3 type dispersion correction were applied to all atoms in the model. The model structure was optimized and analyzed by using the energy decomposition method⁵³ combined with the natural orbitals for chemical valence theory^54,55 with the same level of theory as that used for optimization of H atoms.