Abstract
Helium, ammonia and ice are among the major components of giant gas planets, and predictions of their chemical structures are therefore crucial in predicting planetary dynamics. Here we demonstrate a strong driving force originating from the alternation of the electrostatic interactions for helium to react with crystals of polar molecules such as ammonia and ice. We show that ammonia and helium can form thermodynamically stable compounds above 45 GPa, while ice and helium can form thermodynamically stable compounds above 300 GPa. The changes in the electrostatic interactions provide the driving force for helium insertion under high pressure, but the mechanism is very different to those that occur in ammonia and ice. This work extends the reactivity of helium into new types of compounds and demonstrates the richness of the chemistry of this most stable element in the periodic table.
Similar content being viewed by others
Introduction
The noble gas (NG)1 elements are usually quite inert to chemical reactions due to their closed shell configurations. Among all NG elements, He is the most stable one since its ionization energy is almost twice that of Xe. Although hundreds of NG compounds2,3 have been synthesized, stable solid compounds of He have been discovered only very recently4. Application of high pressure is one of the effective methods for preparing NG compounds3,5,6,7,8. High pressures can change the relative energy ordering of atomic orbitals and can promote new oxidation states of elements. Xe can adopt +2, +4, and +6 oxidation states with O or F under high pressures. In these compounds, Xe forms covalent bonds with O or F by sharing its 5p electrons5,9,10,11,12. Xe can also be oxidized by Fe under high pressure13. Under high pressure, Xe can also gain electrons from Mg or Li14,15. The lighter NG elements such as Kr and Ar can also form compounds under high pressure via electron transfer16,17,18. As the radii of the NG elements become smaller, their ionization potential become higher and the electron affinity lower. Up till very recently, no solid compound with strong binding has been found for He and Ne. The known compounds consisting of He are either charged molecular species such as helium hydride ion (HeH+)19,20, or the pressure stabilized van der Waals compounds, such as Ne(He)221,22 and He(N2)1123. Interestingly, He was also shown to form HeN4 in a pressure range from 8.5 to 69 GPa24.
In a recent work, Dong et al. 25 showed that He could react with Na to form a thermodynamically stable Na2He structure under high pressure26. In their work, interstitial quasi-atoms27 appear in the chemical product Na2He, which can be regarded as Na+2E2-He, where E2− represents the interstitial site occupied by two valence electrons. The oxides and sulfides of alkali metals28 can also form compounds with formulae A2OHe or A2SHe. In these He compounds there is no charge transfer or electron sharing between He and other elements. In our previous work29, we demonstrated that the change in the Madelung energy is the driving force which stabilizes the He insertion compounds. He insertion into A2B or AB2 type ionic compounds decreases the Madelung energy, while in AB type compounds He insertion increases the Madelung energy. The stability of He insertion into ionic compounds is a consequence of the competition between the Madelung energy and other opposing factors. This driving force is so strong that He insertion could also occur in highly polarized covalent compounds such as SiO230,31. Similar mechanism might also promote the insertion of He into FeO2, a recently identified important mineral in the Earth’s lower mantle that plays important role for the cycle of oxygen and water in Earth32. This rapid discovery of new He compounds inspires a new question: can He react with crystals of highly polarized molecules under pressure? Liu et al.33 have already shown that H2O and He can form stable compounds above around 300 GPa. However, under that pressure, H2O has already become A2B type ionic compound via hydrogen-bond symmetrization.
In this work, we study the reactivity of He with two representative molecular crystals, ammonia and ice. These molecules and He are among the major components of giant gas planets. Therefore, the understanding of their reactivity with He is important for studying the evolution and dynamics of these planets. Both H2O and NH3 are non-linear polarized molecules with unequal numbers of positively and negatively charged atoms. Based on recent work, this feature of the composition induces changes in the electrostatic energy that favor He insertion. Indeed, our calculations show that both ammonia and ice can react with He and form stable ternary compounds at pressures above 45 and 300 GPa, respectively. However, analysis of the geometries and the electronic structures show that the mechanism is quite different in the two molecular crystals. In ammonia the insertion of He leads to rearrangement of the molecules and the reorientation of their dipoles. The corresponding gain in the Madelung energy and the PV term is the major driving force. The insertion of He in ice occurs only at pressures above the ionization of water molecules. Therefore, the insertion of He in ice is similar to the insertion of He in an A2B crystal ionic type.
Results
Stability and structure
The reaction enthalpy is commonly used to analyze the thermal stability of compounds. It is formulated as the sum of the enthalpies of the molecular crystals of interest, minus the sum of the enthalpies of the He insertion compounds:
where, X stands for the covalent compound of interest, and ΔHr stands for relative enthalpy. As shown in Fig. 1, we calculate the reaction enthalpy of NH3+He and 2H2O+He. The solid lines with symbols show the reaction enthalpies calculated for different molecular structures. He inserted compounds become stable when the reaction enthalpy is above zero.
Figure 1a shows results for He insertion in an ammonia crystal. The resulting NH3He compound becomes thermodynamically stable against decomposition into molecular NH3 and elemental He above 45 GPa. Increasing the pressure stabilizes the He inserted compound, and the relative enthalpy difference increases to 0.38 eV/f.u. at 600 GPa. In order to calculate the stability of NH3He we must calculate the enthalpy of formation of NH3 as a function of pressure. Structural phase transitions in ammonia34 at high pressure have been well studied. We have investigated the stability of five NH3 structures at high pressures with space groups P213, P212121, Pma2, P21/m, and Pnma, and the stability of NH3He compounds. Figure 1a shows the reaction enthalpy and also reveals the ordering of the thermodynamically stable structures at various pressures, which agrees well with the previous study34. NH3 adopts space group P213 at ambient pressure, which has an intermolecular distance (N–N) larger than 3.29 Å. Between 31 and 98 GPa the NH3 structure adopts space group P212121. This structure is well-packed due to the high pressure and the decrease in intermolecular distances. For instance, at 50 GPa, the N–N distance is 2.71 Å. Above 98 GPa, NH3 adopts the space group Pma2 up to 297 GPa. In this structure self-ionization occurs as shown by the reaction \(2{\mathrm{NH}}_3 \to {\mathrm{NH}}_4^ + + {\mathrm{NH}}_2^ -\) (Fig. 2a). Between 297 and 430 GPa, the NH3 structure adopts the space group P21/m. The \({\mathrm{NH}}_4^ +\) unit and N–H chain exist in this structure, which is also the result of self-ionization35. At pressures above 430 GPa, NH3 transforms into a Pnma structure that shows no self-ionization.
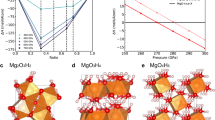
Structures of corresponding compounds under high pressure. NH3 structures in space group of a Pma2 under 150 GPa, b P21/m under 350 GPa, c Pnma at 600 GPa. d NH3He structure in space group of P212121 under 600 GPa. e H2O structure in space group of Pbcm under 400 GPa. f (H2O)2He structure in space group of Ibam under 400 GPa. The blue and red balls represent N and O atoms; the small and large white balls represent the H and the He atoms
The structure parameters, including the space groups, the lattice parameters, and the atom positions, are shown in Supplementary Table 1–4. The structure of NH3He has space group P212121, as shown in Fig. 2d. At 50 GPa, the lattice constants are a = 4.168 Å, b = 3.356 Å, and c = 5.406 Å. The NH3 molecules remain in this compound. The insertion of He actually keeps the NH3 molecular lattice from self-ionization when pressure increases. However, these NH3 molecules are lower in symmetry compared with free molecules due to the intermolecular interactions. There are two different N–H bond lengths of lengths 1.021 and 1.017 Å at 50 GPa. At the same pressure, the nearest He–H, He–N, and N–N distances are 1.789, 2.158, and 2.756 Å, and the next-nearest N–H distance is 1.781 Å. It is interesting that the unreacted NH3 crystal has the same P212121 space group. At 50 GPa, its lattice parameters are a = 2.740 Å, b = 4.522 Å, and c = 4.757 Å. The N–H bond lengths are 1.026 and 1.014 Å, and the next-nearest and third-nearest N–H distances are 1.709 and 1.814 Å.
He insertion into H2O has been demonstrated in the work33 of Liu et al. H2O forms a compound with He at a ratio of 2:1. We chose three structures of H2O for the stability analysis, which have space groups Cmc21 (ice XI), Pn\(\bar 3\) m (ice X), and Pbcm. The structures with space group Cmc21 (ice XI) are stable at a pressure range below 100 GPa. When the pressure is higher than 100 GPa, the three structures become very close in energy up to 309 GPa. Above 309 GPa, Pbcm becomes the distinct thermodynamically stable structure. Figure 1b shows the reaction enthalpies of He insertion into H2O molecular crystals. Our calculations show that at pressures above 300 GPa, H2O and He can react to form a stable (H2O)2He compound. This compound adopts a structure with space group Ibam. The driving force for forming such compounds is quite large since the reaction enthalpy reaches 0.95 eV/f.u. when the pressure is 600 GPa. This result agrees well with previous work33. For the three phases of H2O at around 300 GPa, the pressure at which He insertion become stable, share very similar structural features. The three phases lose the features of the H2O molecule and become A2B type ionic crystals. The energies of the three structures are also very similar since the structural differences between them do not contribute significantly to the energy. This is the major difference between the behavior of H2O and NH3. As shown earlier, NH3 remains a molecular crystal at the pressures of interest above 430 GPa while He insertion is energetically favored.
Electronic structure
In order to analyze the bonding features of He inserted H2O and NH3 we calculated the electron localization function (ELF). In Fig. 3a and b, the ELFs of NH3 in the Pma2 structure below 250 GPa and P21/m structure below 400 GPa are shown, respectively. The electrons are found to be strongly localized between H and N, which is typical for the strong covalent N–H bonds. The electrons are also largely localized in the inter-molecule space due to the hydrogen bonding effect. The most important features of the electronic structure are shown in Fig. 3c, i.e., there is hardly any ELF in the regions between the He atoms and the H2O or NH3 molecules. This strongly suggests that He atoms do not form any type of chemical bond with neighboring atoms. Figure 3d shows the ELF of H2O in the Pbcm structure below 600 GPa projected onto the (001) plane. It clearly shows a chain structure formed by connecting O atoms with shared H atoms. The ELF of (H2O)2He compound (Fig. 3e) again shows no bond formation between He and the neighboring atoms.
The absence of chemical bond connecting He and its neighboring atoms is also indicated by other electronic structure methods. Interestingly, the electronic density of states (DOS) and electronic projected DOS (PDOS) of He inserted compounds resemble very similar features as in those without He insertion (Supplementary Fig. 1), which strongly suggests the lack of strong chemical bonding between He and the neighboring molecules. The insertion of He does noticeably change the band gap (Supplementary Note 1), which is due to the fact that the insertion increases the distances between the neighboring molecules. After forming compounds with He, the band gap of H2O increases from 9.25 to 10.06 eV; and the band gap of NH3 increases from 3.01 to 4.06 eV. We also calculated the integrated crystal orbital Hamilton population36 that can show the bond strength (Supplementary Note 2, Supplementary Tables 5 and 6). The values are generally small, consistent with the ELF and PDOS results. However, some values are not negligible. This is due to the fact that COHP are calculated by projecting crystal orbitals to atomic orbitals, which might erroneously lead to finite contributions of He atomic orbitals.
Madelung energy analysis
We analyze the mechanism that stabilizes the He insertion into NH3 and H2O. Regardless whether the molecules are maintained or not under high pressure, the atoms (H, N, O) are highly charged, and the change of the electrostatic energy (Madelung energy) upon the insertion of He atoms is the major driving force of the reactions. Similar to ionic compounds such as MgF2, the charges of the atoms change only slightly with increasing pressure (Supplementary Fig. 2), therefore the change of the Madelung energy is mainly caused by the displacement of the molecules or atoms.
First, we decompose the reaction enthalpy ΔH into the change in internal energy ΔE and the compression work ΔPV. The results are shown in Fig. 4a. for NH3 and in Fig. 4b for H2O. NH3He becomes stable at around 45 GPa, which is due to the contributions from the decrease in both ΔPV and ΔE, although the former term is negative whereas the latter term is positive. Due to the complex phase transitions of the NH3 crystal, ΔPV and ΔE do not change monotonically, although their sum ΔH does. Roughly speaking, the stabilization of NH3He is due to the decrease in ΔPV energy pressures below 400 GPa, whereas due to the decrease in ΔE when the pressure is above 400 GPa.
For He insertion in H2O, the internal energy change ΔE is 1.05 eV at ambient pressure, which does not favor He insertion. While the pressure increases, ΔE decreases somewhat up to 50 GPa and then increases significantly up to 250 GPa. In contrast, the ΔPV term decreases by about 1.25 eV from 100 GPa to 300 GPa, which greatly favors He insertion under high pressure. However, the He inserted compounds only become thermodynamically stable at pressures >309 GPa at which the change in internal energy ΔE significantly decreases from its peak value at 250 GPa. Therefore, the stabilization of He insertion results from both the changes in the internal energy and the reduction in the volume.
We calculated the change in the Madelung energy ΔEM for both of the He inserted molecular crystals and compared them with the change in the internal energy ΔE in Fig. 4c, d. In both cases the ΔEM and ΔE changes are almost parallel with increasing pressure, indicating that the major part of the change in ΔE arises from the change in the Madelung energy. The kinks in ΔEM and ΔE originate from the structural transitions that occur in NH3 under pressure. The value of ΔEM for He insertion in H2O increases up to about 250 GPa, and then decreases in a similar way to ΔE.
Interestingly, although methane (CH4) is not a polar molecule, it still presents the above driving force for the He insertion (Supplementary Fig. 3). This is due to the fact that both C and H atoms are still highly charged, despite that the molecules are non-polar due to their highly symmetric geometry. The large number of positively charged H atoms causes strong repulsive interactions among the molecules under high pressure, which will be lessened by the insertion of He atoms. Our calculations clearly reveal a strong driving force for the insertion of He into CH4 lattice (Supplementary Fig. 3).
The large difference between the He insertion pressures for NH3 and H2O is originated from their structure features. Although both molecules are strongly polarized, NH3 consists of three N–H bonds forming a rigid pyramid structure. Furthermore, the cation/anion ratio is 3:1 that is higher than the 2:1 of H2O. Comparing to H2O, it is harder to reduce the volume and the strong H–H repulsive electrostatic interactions in NH3 molecular crystal under high pressure. Therefore, the energy gain by inserting He in the crystal is more significant for NH3 than H2O.
Besides reaction pressure, another major difference between NH3 and H2O is that the former remains a molecular crystal while He insertion occurs above 50 GPa; whereas H2O has already lost its molecule features and becomes an A2B type ionic compound at the pressure of insertion. Therefore, the He insertion in H2O is very similar to that in an A2B ionic compound, which has been discussed in detail in our previous work29. In contrast to H2O, NH3 molecules remain in the He inserted compound. The reduction of the volume (correspondingly the PV term) and the Madelung energy during He insertion in NH3 is achieved by reorienting the NH3 molecules. Such reorientations can increase the size of the intermolecular space, which can accommodate inserted He atoms. He insertion actually prevent the ionization and hydrogen-bond symmetrization for both H2O and NH3. In NH3He compound, NH3 keeps a molecular form from 0 to 600 GPa. Also, from the comparison of intermolecular and intramolecular H–O distance (Supplementary Notes 3 and 4, and Supplementary Figs. 4 and 5), we can also see the hydrogen-bond symmetrization happens at a higher pressure in He inserted H2O. The ionization in the compressed ice decreases the internal energy. This is why the Madelung (and the internal) energy actually increases upon He insertion in the pressure range from 100 to 250 GPa (Fig. 4b). Only while the H2O phase becomes totally ionized, the insertion of He will lower the Madelung energy (and the internal energy) and make (H2O)2He stable. This is another reason that the reaction pressure of forming (H2O)2He is much higher than that of forming NH3He.
In summary, we demonstrate that He can be inserted into both NH3 and H2O, which can form stable compounds under high pressure. Although the driving force of such an insertion reaction are the reduction of the Madelung energies in both cases, the reaction mechanisms are quite different in the two molecular crystals. He insertion into H2O only happens at very high pressures, while the H2O molecules have dissociated and become an ionic compound. The insertion of He is similar to the reaction of He with Na2O or MgF2. In contrast, the NH3 molecules remain in the He inserted compounds, and the mechanism of the insertion including the reduction of the volume and the Madelung energy are achieved by reorientation of the NH3 molecules. Our work further extends the reactivity of He to crystals of highly polarized molecules.
Methods
Structure search
In order to find the structures of He inserted NH3 and H2O, we employed the particle swarm optimization (PSO) algorithm as implemented in the CALYPSO code (Crystal structure AnaLYsis by PSO)37,38,39,40. The structures of NH3He and (H2O)2He as well as the pure NH3 and H2O are searched under 100, 200, 400, and 600 GPa. In all, 2, 3, and 4 formula units are used for the searches. For each composition and pressure, the structure search are carried out for 30 generations and in some cases for multiple times. In each generation, 60% new randomly created structures are added and 40 percent of the structures are generated using the PSO method. Besides using the PSO algorithm41,42 the CALYPSO code also employs techniques such as application of symmetry constraints, a bond characterization matrix, and coordinate characterization functions to improve the search efficiency. Its accuracy has been proven in numerous previous works. The stable structures are further optimized using density-functional theory (DFT) total energy calculations.
Electronic structure and total energy calculations
The formation enthalpies and electronic properties are calculated using DFT implemented in VASP43. The DFT calculations were performed using a generalized gradient approximation exchange-correlation functional using the Perdew–Burke–Ernzerhof density functional)44. A hybrid functional based on the framework of Heyd–Scusera–Ernzerhof was tested (Supplementary Note 5 and Supplementary Fig. 6). The projector augmented wave (PAW)45,46 method was used to describe electron-ion interactions. The validity of PAW potentials under extremely high pressures are tested by comparing the calculated equation of states of NH3He and (H2O)2He with those calculated by a full potential linear augmented plane wave47 method (Supplementary Note 6 and Supplementary Fig. 7). For the plane-wave DFT calculations, we set the cut-off energy as 1400 eV, which guarantees that the enthalpy is converged to within 0.01 meV. Also, the Monkhorst-Pack k-mesh has an interval smaller than 2π × 0.05−1. The employed k-mesh is shown in Supplementary Table 7. The structures are optimized till the total energies converge to 0.1 meV. The self-consistent calculations of the electronic structures converge with a criterion of 0.01 meV for the energy. The effects of dispersion forces48 (van der Waals interactions) and zero-point energy49 are also tested. Their influences to the reaction enthalpies for the He insertion into NH3He and (H2O)2He are quite small (Supplementary Notes 7 and 8, and Supplementary Figs. 8 and 9) and will not change the major conclusions of the current work.
Madelung energy calculation
The Madelung energy calculations are performed by a method implemented in VESTA50. A Fourier Transform method is used in this code. There are two parameters; the ionic radius and the cut-off frequency, which are mentioned in the VESTA manual. The charge distribution ρ(r) is defined inside the ionic sphere. The charge distribution can be described by ρ(r) = ρ0[1 − 6(r/s)2 + 8(r/s)3 − 3(r/s)4] for r < s else ρ(r) = 0. Here, s is the sphere radius. The radius s is no larger than one-half of the interatomic distance and can readily be determined by a convergent procedure. The cut-off frequency is set at the recommended value of 2.0−1 as given in the VESTA manual.
Data availability
The data supporting this publication are available from the authors on request.
References
Pauling, L. The formulas of antimonic acid and the antimonates. J. Am. Chem. Soc. 55, 1895–1900 (1933).
Bartlett, N. Xenon hexafluoroplatinate(V) Xe+ [PtF6]−. Proc. Chem. Soc. Lond. 6, 197–236 (1962).
Loubeyre, P., Letoullec, R. & Pinceaux, J. P. Compression of Ar(H2)2 up to 175 GPa: a new path for the dissociation of molecular hydrogen? Phys. Rev. Lett. 72, 1360–1363 (1994).
Li, T. H., Mou, C. H., Chen, H. R. & Hu, W. P. Theoretical prediction of noble gas containing anions FNgO− (Ng = He, Ar, and Kr). J. Am. Chem. Soc. 127, 9241–9245 (2005).
Kurzydlowski, D. et al. Freezing in resonance structures for better packing: XeF2 becomes (XeF+)(F−) at large compression. Inorg. Chem. 50, 3832–3840 (2011).
Kleppe, A. K., Amboage, M. & Jephcoat, A. P. New high-pressure van der Waals compound Kr(H2)4 discovered in the krypton-hydrogen binary system. Sci. Rep. 4, 4989 (2014).
Howie, R. T. et al. Formation of xenon-nitrogen compounds at high pressure. Sci. Rep. 6, 34896 (2016).
Hermann, A. & Schwerdtfeger, P. Xenon suboxides stable under pressure. J. Phys. Chem. Lett. 5, 4336–4342 (2014).
Zhu, Q. et al. Stability of xenon oxides at high pressures. Nat. Chem. 5, 61–65 (2013).
Peng, F., Botana, J., Wang, Y. C., Ma, Y. M. & Miao, M. S. Unexpected trend in stability of Xe-F compounds under pressure driven by Xe-Xe covalent bonds. J. Phys. Chem. Lett. 7, 4562–4567 (2016).
Dewaele, A. et al. Synthesis and stability of xenon oxides Xe2O5 and Xe3O2 under pressure. Nat. Chem. 8, 784–790 (2016).
Brock, D. S. & Schrobilgen, G. Synthesis of the missing oxide of xenon, XeO2, and its implications for earth’s missing xenon. J. Am. Chem. Soc. 133, 6265–6269 (2011).
Zhu, L., Liu, H. Y., Pickard, C. J., Zou, G. T. & Ma, Y. M. Reactions of xenon with iron and nickel are predicted in the Earth’s inner core. Nat. Chem. 6, 644–648 (2014).
Miao, M. S. et al. Anionic chemistry of noble gases: formation of Mg-NG (NG = Xe, Kr, Ar) compounds under pressure. J. Am. Chem. Soc. 137, 14122–14128 (2015).
Liu, Z., Botana, J., Miao, M. S. & Yan, D. D. Unexpected Xe anions in XeLin intermetallic compounds. Europhys. Lett. 117, 26002 (2017).
Zaleski-Ejgierd, P. & Lata, P. M. Krypton oxides under pressure. Sci. Rep. 6, 18938 (2016).
Kurzydlowski, D., Soltysiak, M., Dzoleva, A. & Zaleski-Ejgierd, P. High-pressure reactivity of Kr and F2-stabilization of krypton in the +4 oxidation state. Crystals 7, 329 (2017).
Li, X. et al. Stable lithium argon compounds under high pressure. Sci. Rep. 5, 16675 (2015).
Glockler, G. & Fuller, D. L. Helium hydride ion. J. Chem. Phys. 1, 886–887 (1933).
Beach, J. Y. Quantum-mechanical treatment of helium hydride molecule-ion HeH+. J. Chem. Phys. 4, 353–357 (1936).
Loubeyre, P., Jean-Louis, M., LeToullec, R. & Charon-Gerard, L. High pressure measurements of the He-Ne binary phase diagram at 296 K: evidence for the stability of a stoichiometric Ne(He)2 solid. Phys. Rev. Lett. 70, 178–181 (1993).
Cazorla, C., Errandonea, D. & Sola, E. High-pressure phases, vibrational properties, and electronic structure of Ne(He)2 and Ar(He)2: a first-principles study. Phys. Rev. B 80, 064105 (2009).
Vos, W. L. et al. A high-pressure van der Waals compound in solid nitrogen-helium mixtures. Nature 358, 46–48 (1992).
Li, Y. W. et al. Route to high- energy density polymeric nitrogen t-N via He-N compounds. Nat. Commun. 9, 722 (2018).
Dong, X. et al. A stable compound of helium and sodium at high pressure. Nat. Chem. 9, 440–445 (2017).
Miao, M. S. Helium chemistry: react with nobility. Nat. Chem. 9, 409–410 (2017).
Miao, M. S. & Hoffmann, R. High pressure electrides: a predictive chemical and physical theory. Acc. Chem. Res. 47, 1311–1317 (2014).
Sun, J., Pickard, C. J. & Needs, R. J. Prediction of pressure-induced stabilization of noble-gas-atom compounds with alkali oxides and alkali sulfides. Phys. Rev. Mater. 3, 015002 (2019).
Liu, Z. et al. Reactivity of He with ionic compounds under high pressure. Nat. Commun. 9, 951 (2018).
Matsui, M., Sato, T. & Funamori, N. Crystal structures and stabilities of cristobalite-helium phases at high pressures. Am. Mineral. 99, 184–189 (2014).
Sato, T., Funamori, N. & Yagi, T. Helium penetrates into silica glass and reduces its compressibility. Nat. Commun. 2, 345 (2011).
Zhang, J. et al. Rare helium-bearing compound FeO2He stabilized at deep-earth conditions. Phys. Rev. Lett. 121, 255703 (2018).
Liu, H. Y., Yao, Y. S. & Klug, D. D. Stable structures of He and H2O at high pressure. Phys. Rev. B 91, 014102 (2015).
Griffiths, G. I. G., Needs, R. J. & Pickard, C. J. High-pressure ionic and molecular phases of ammonia within density functional theory. Phys. Rev. B 86, 144102 (2012).
Palasyuk, T. et al. Ammonia as a case study for the spontaneous ionization of a simple hydrogen-bonded compound. Nat. Commun. 5, 3460 (2014).
Dronskowski, R. & Bloechl, P. E. Crystal orbital Hamilton populations (COHP): energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 97, 8617–8624 (1993).
Luo, X. Y. et al. Predicting two-dimensional boron-carbon compounds by the global optimization method. J. Am. Chem. Soc. 133, 16285–16290 (2011).
Wang, Y. C., Lv, J., Zhu, L. & Ma, Y. M. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Lv, J., Wang, Y., Zhu, L. & Ma, Y. Particle-swarm structure prediction on clusters. J. Chem. Phys. 137, 084104 (2012).
Kennedy, J. & Eberhart, R. C. A discrete binary version of the particle swarm algorithm. in 1997 IEEE International Conference on Systems, Man, And Cybernetics 5, 4104–4108, (IEEE, New York, 1997).
Eberhart, R. C. & Shi, Y. H. Particle swarm optimization: developments, applications and resources. in Proc 2001 Congress on Evolutionary Computation 1, 81–86, (IEEE, Seoul, South Korea, 2001).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Blaha, P., Schwarz, K., Sorantin, P. & Trickey, S. B. Full-potential, linearized augmented plane-wave programs for crystalline systems. Comput. Phys. Commun. 59, 399–415 (1990).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006).
Gonze, X. Adiabatic density-functional perturbation theory. Phys. Rev. A 52, 1096–1114 (1995).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Acknowledgements
M.M. acknowledges the support of NSF CAREER award 1848141 and ACS PRF 50249-UN16. D.Y. acknowledges the National Natural Science Foundation of China (NSFC) for the grants under Nos. 21434001 and 21374011. Z.L. acknowledges the China Postdoctoral Science Foundation (No. 2018M630064). R.J.N. and C.J.P. acknowledge funding from EPSRC under Grants EP/P034616/1 and EP/P022596/1. We acknowledge the use of computational resources from the Beijing Computational Science Research Center to compete the most calculation of this work. Part of the calculations are performed on NSF-funded XSEDE resources (TG-DMR130005) especially on the Stampede cluster run by Texas Advanced Computing Center.
Author information
Authors and Affiliations
Contributions
Y.B. and Z.L. contribute equally on this project. M.S.M. proposed the mechanism and designed the study. Y.B. and Z.L. conducted most calculations. M.S.M., D.Y., and H.L. guided and advised the research. All the authors were involved in the analysis of the results. M.S.M., Z.L., J.B., Y.B., J.S., C.J.P., and R.J.N. wrote and revised the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bai, Y., Liu, Z., Botana, J. et al. Electrostatic force driven helium insertion into ammonia and water crystals under pressure. Commun Chem 2, 102 (2019). https://doi.org/10.1038/s42004-019-0204-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-019-0204-6
This article is cited by
-
Helium incorporation induced direct-gap silicides
npj Computational Materials (2021)
-
Chemistry under high pressure
Nature Reviews Chemistry (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.