Abstract
Carbon-bearing compounds display intriguing structural diversity, due to variations in hybrid bonding of carbon. Here, first-principles calculations and unbiased structure searches on yttrium dicarbide at pressure reveal four new structures with varying carbon polymerisation, in addition to the experimentally observed high-temperature low-pressure I4/mmm dimer phase. At low pressures, a metallic C2/m phase (four-member single-chain carbide) is stable, which transforms into a Pnma phase (single-chain carbide) upon increasing pressure, with further transformation to an Immm structure (double-chain carbide) at 54 GPa and then to a P6/mmm phase (sheet carbide) at 267 GPa. Yttrium dicarbide is structurally diverse, with carbon bonded as dimers (at lowest pressure), four-member single chains, infinite single chains, double chains and eventually sheet structures on compression. Electron–phonon coupling calculations indicate that the high-pressure phases are superconducting. Our results aid the understanding and design of new superconductors and illuminate pressure-induced carbon polymerisation in carbides.
Similar content being viewed by others
Introduction
Structural variation of the atomic arrangements in crystalline solids is the typical response to changes in chemical composition, temperature or pressure1,2,3. The application of varying external hydrostatic pressure can have significant impact on the structural stability of solids as their structures adapt to denser configuration on increasing pressure. In particular, pressure can induce rather surprising changes that runs counter to expectations based on traditional understandings of the chemical bond. Structures and chemical compositions may be controlled by packing considerations and optimisation of density, rather than the disposition of outer electrons that describe chemistry as it is usually understood. Hence, pressure-dependent structural variations provide a powerful method to probe the physical and chemical characteristics of materials, and especially give a route to understand in the behaviour of solids in a wide range of applications, from understanding the nature of deep planetary interiors to developing novel materials with designer properties such as super-hardness and superconductivity.
In carbon-bearing solids, the ability of carbon to form both sp2− and sp3− bonding states leads to exceptional structural diversity and chemical variation, especially under non-ambient conditions. There has, for example, been long-standing interest in graphitisation of low-density arrangements, the formation of graphite-related crystal structures, and their ultimate transformation to super-hard materials based on network polymerised structures akin to diamond4. Among the wide variety of such carbon-bearing materials, the properties of mixed yttrium–carbon-bearing solids has attracted attention in view of its possible relationship to CaC2-type solids. The peculiar physical properties of compressed yttrium carbides, especially the Y-based dicarbide YC2, is the focus of our attention here. YC2, experimentally synthesised at ambient conditions, is found to be metallic and adopts a tetragonal CaC2-type structure (space group I4/mmm, Z = 2)5. The structure of YC2 comprises strong covalently-bonded C2 units bound together via dominantly ionic interactions to yttrium. The formal valence state of yttrium in YC2 is of particular interest in this structure. The fact that it forms as a phase isostructural with CaC26 might suggest that it is present as in YC2 as Y2+, in contrast with the expected Y3+ valence state. Indeed, within the range of organo-yttrium compounds Y has previously been observed to show variable formal oxidation state, from 0 to +3, with a variety of yttrium carbides previously recorded, including Y3C7, Y2C8, Y2C39, and even endohedral fullerenes10, as well as YC2. No experimental investigations have been undertaken on YC2 at high pressure but, by analogy with other carbon-bearing structures, one anticipates that changes in the carbon-bonding network may occur.
Yttrium carbides have previously been demonstrated to be superconducting. As long ago as 1968, Giogri et al. determined a Tc of 3.88 K in yttrium dicarbide, and indeed this was the first πreported occurrence of superconductivity in a CaC2-type structure11. Subsequently, other rare-earth-containing carbides, including Y2C3, La2C3, Y1-xThxC2, Y1-xCaxC2, and LaC2 have been found to be superconductors at ambient pressure12,13,14. This family of rare-earth carbides have, however, recently attracted renewed interest owing to the discovery of superconductivity in the layered yttrium carbide halides Y2C2I2 (Tc = 9.97 K) and Y2C2Br2 (Tc = 5.04 K)15. Though known to be good superconductors at ambient pressure, the superconducting properties of yttrium dicarbides under pressure remain unexplored. The role of pressure is of particular interest in view of the recent discoveries of high Tc superconductivity at high pressure among the rare-earth hydrides. For example, yttrium’s hydrides are even predicted to be room-temperature superconductors, with a predicted Tc in YH6 of 264 K at 120 GPa and for YH10 a Tc of 305–326 K at 250 GPa16,17,18. This leads to the obvious need to explore potential superconductivity in compounds of yttrium with other light elements.
More generally, then, many open questions remain regarding the behaviour of compressed rare-earth metal dicarbides. Among the most pressing are: (1) How do C2 dimers evolve upon the application of increased pressure? (2) Do any new high-pressure phases display metallic properties? And finally, (3) do any new metallic high-pressure phases show superconductivity? The approach that we have adopted to investigate the structural properties of YC2 at high pressure exploit developments in global structural searching schemes, combined with first-principles total energy calculations.
Here we show that, on increasing pressure, the dimer-based YC2 low-pressure structure, transforms to intermediate four-member chain structures, transforms into layered structures. Thus carbon atoms first form one-dimensional (1D) chains and then double chains, and finally two-dimensional (2D) graphene sheets separated by Y atomic layers. Of the four new high-pressure phases that we find, one has monoclinic symmetry, two have orthorhombic symmetry (Pnma and Immm) and the fourth is a MgB2 structure-type with P6/mmm symmetry. Our electronic structure calculations demonstrate that all of these new high-pressure phases are metallic in character. Finally, these high-pressure phases of YC2 show phonon-mediated superconductivity, as demonstrated by our exploration of electron–phonon coupling in these structures.
Results
Structure search
Structure search calculations on stoichiometric YC2 performed at ambient pressure readily reproduced the experimentally-observed CaC2-type phase of YC211. This confirmed the reliability of our method and its application to this system (see Supplementary Table 1). Structure predictions of the most stable phases of compressed YC2 were obtained from simulations with one to four YC2 formula units per cell at 10, 50, 100, 200, 250, and 300 GPa. Analysis of the predicted structures provided a shortlist of candidate structures with space groups C2/m (Z = 2), Pnma (Z = 4), Immm (Z = 4) and P6/mmm (Z = 1). Further optimisation of these structures over a pressure range of −15 to 300 GPa revealed the sequence of pressure-induced phase transitions that occur for this material (Fig. 1). Enthalpies of YC2 for each of these structure types are also shown as a function of pressure in Fig. 1.
Phase stabilities with pressure. The calculated enthalpy per atom of YC2 is shown as a function of pressure up to 300 GPa relative to the Immm structure, and (insert) around ambient pressure relative to the Pnma structure. Arrows indicate the phase transition pressures. The pressure-induced phase transition sequence at 0 K is indicated by the coloured bars
We found that the C2/m phase, Pnma phase and previously-reported I4/mmm phase have very similar enthalpy at ambient pressure, and for this reason their enthalpies vs. pressure curves around ambient pressure are better depicted in the insert in Fig. 1. One can see that, for YC2, in addition to the previously-reported I4/mmm phase (referred as YC2-I), a previously-unreported C2/m structure, comprising four carbons in a kinked-linear arrangement, is stable at low pressure (YC2-II). On increasing pressure, a new orthorhombic Pnma phase (referred as YC2-III) is stable up to 54 GPa. At higher pressure, a further orthorhombic Immm phase (referred as YC2-IV) becomes stable and remains so over the wide pressure interval of 54–267 GPa. At the highest pressures of our simulations of 267 GPa and above, a MgB2-type structure with space group of P6/mmm (referred as YC2-V) is stable. The dynamical stability of each of the four new phases of YC2 was confirmed by calculation of their phonon dispersion relations, and verification of the absence of imaginary frequencies, across the pressure ranges of their thermodynamic stability (Supplementary Figure 1). Furthermore, we find that (at 0 GPa and 10 GPa) YC2 is stable against decomposition into a mixture of adjoining or end-member compositions, lying as it does on the convex hull of the Y-C system (Supplementary Figure 3).
Temperature effects
Two energetically competitive structures (C2/m and Pnma) are predicted at 0 GPa, at which pressure the I4/mmm phase, which has the higher enthalpy, was reported from experiment11. In view of the fact that synthesis was carried out from the melt by arc-melting followed by quenching, we further included temperature effects via quasi-harmonic Gibbs free energy calculations with phonon spectra obtained from the finite-displacement method, for all these three phases between −12 and 15 GPa. The contribution of vibrational effects, depicted in Fig. 2, stabilises the experimentally-observed YC2-I phase over the C2/m phase at temperatures greater than 1500 K. This is in good agreement with the experimental results, since the melting point of I4/mmm YC2 is reported to be 2415 °C at ambient pressure19 and the I4/mmm phase crystallises from this melt.
Incorporation of the effect of temperature does not change the sequence of expected phase transitions. It shifts the pressures of the phase transitions slightly, according to the Clapeyron equation. We note that the Clapeyron slope of the I–II transition is quite different from that of the II-III transition, which may be understood in terms of the structural control on ΔV at each transition: YC2-II and YC2-III are structurally similar (as chain structures) while YC2-I is structurally distinct. We focus on 0 K high-P calculations in the following discussions. Each of the P-induced phase transition in YC2 is first-order in thermodynamic character, although relationships between the structures can be deduced. The volume compressibility (Supplementary Figure 4) shows significant breaks at each phase transition, with successive high-P phases adopting increasingly dense structures.
Discussion
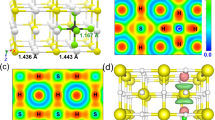
It is instructive to consider how the carbon-carbon-bonding changes between each of the structures with increasing P, as this yields insight into phase transformation mechanisms. The optimised structural parameters of each predicted stable phase are listed in Supplementary Table 1 and further illustrated in Fig. 3. From the low-P phase to highest-P structure, the C-C bonding shows changes due to the influence both of external P and internal chemical pre-compression associated with changes in the yttrium connectivity. In YC2-I, our calculations show that isolated carbon dimers are orientated along the crystallographic z axis (Fig. 3a), with (at 0 GPa) a C-C bond length of 1.303 Å. The lattice parameters match available experimental observations well, validating the structural results that we have obtained.
With increasing P, the distance between individual carbon dimers in YC2-I decreases, transforming to four-member carbon chains in YC2-II (Fig. 3b). In this structure, all yttrium atoms lie at the Wyckoff 4i site and carbon atoms occupy another two different 4i sites. Increasing P further results YC2-III, in which structure carbon atoms rearrange into single chains (Fig. 3c). Four yttrium atoms lie at the Wyckoff 4c site and eight carbon atoms occupy the 8 f site. As such, the carbon atoms form a one-dimensional chain parallel to the y-axis.
Upon further increase in P, each carbon chain in YC2-III moves closer to its neighbours until carbons come together to form six-membered rings in the double chains of YC2-IV (Fig. 3d), akin to quasi-1D carbon ribbons, each of which lies in the centre of a ‘cylinder’ composed of yttrium ions. In this structure, there are four-molecules in the unit cell with all four yttrium atoms on the Wyckoff 4i site. There are two crystallographically distinct types of carbon: four lie on the Wyckoff 4 h site while the other four carbon atoms occupy Wyckoff 4 g sites.
In the double-chain YC2-IV phase there are two different C-C bond lengths (referred as d1 and d2) in the double chain. At 200 GPa, for example, two among the six C-C bonds (d1) have a bond length of 1.418 Å, and four of them (d2) have a length of 1.409 Å. Upon further compression, the difference (∆d) between d1 and d2 decreases smoothly (Fig. 4) up to the transition point, when d1 and d2 suddenly become identical at the first-order transition at 267 GPa. The double chains link up to form a hexagonal graphene-like sheet, the YC2-V phase (Fig. 3e). Simultaneously, the yttrium atoms become confined to the interlayer regions between the graphene sheets, and this highest-pressure structure is a layered carbide. Structurally, YC2-V comprises hexagonal ‘honeycomb’ layers (i.e. graphene sheets) of carbon atoms linked by planes of yttrium ions, with the yttrium atoms positioned above and below the centres of the carbon hexagons. Thus, the pressure-induced structural modification is akin to graphitisation of compressed YC2, as is observed in YC2-V. In YC2-V, there is one formula unit per unit cell and the carbon sheet is perfectly planar. Our optimisation gives equilibrium lattice parameters, at 300 GPa, of the hexagonal unit cell as a = 2.483 Å and c = 3.414 Å. In each unit cell, one yttrium atom sits at the Wyckoff 1b position and two carbon atoms lie on the 2c site.
Pressure dependence of the structural order parameter in high-pressure phases of YC2. Through the Immm (YC2-IV) - P6/mmm (YC2-V) phase transition, upon compression, the lengths of two kinds of C-C bonds in the double chain of the YC2-IV phase gradually approach one another before a first-order transition to the sheet structure of YC2-V
The relationship between P6/mmm YC2-V and Immm YC2-IV is supergroup-subgroup in nature, with a symmetry-breaking transition pathway from P6/mmm to Immm possible via a Cmmm intermediate. We find no evidence for the Cmmm intermediate in our calculations, but note that the behaviour of the interatomic spacings for carbon atoms (Fig. 4) is consistent with such a symmetry-breaking behaviour, with a strongly first-order phase transition character.
Increasing polymerisation of the carbon sub-structure in YC2 is associated with gradual changes in the nature of the Y-C bond. Our electron localisation function (ELF) calculations (Fig. 5) show that density is well-localised around carbon atoms, with doubly-bonded carbon dimers in the lowest pressure structure. In the single-chain structure, lone pair electrons are seen at every carbon, and in the double-chain structure they are seen on the ‘outer’ carbons, demonstrating the sp2− like nature of bonding in these chain structures, which becomes complete in the YC2-V carbon planar structure. The carbon atoms accept electrons from yttrium as they populate sp2− orbitals. We have carried out a Bader charge analysis (Supplementary Figure 5) of our structures as a function of pressure20. At ambient pressure, each C atom accepts 0.9 electrons from Y, with an electron loss of 1.8 electrons from each Y. This shows that carbon is isoelectronic to nitrogen in the YC2 structure, and the polymerisation of C in the structure could, superficially, be considered relevant to polymerisation of nitrogen, a topic of significant current interest21. On increasing pressure, YC2 displays gradual reduction of charge transfer between yttrium and carbon as increasingly dense structural arrangements are adopted. This is indicative of the increasing dominance of density in controlling chemical structure at high pressure.
Before calculating possible superconducting properties, we analyse the electronic structures of predicted YC2 phases (Supplementary Figure 2). The metallic nature of all the predicted phases is apparent. The projected density of states show that the Y-d orbital plays an important role in the metallisation. The YC2-V phase is an especially good metal with multiple bands crossing the Fermi level along several directions. It has been observed experimentally that YC2-I is a superconductor with a transition temperature of 3.9 K at ambient pressure [11], in good agreement with our theoretical calculation of ~4.5 K based on the linear response theory. The same method was applied to explore the possible superconductivity of newly-proposed high pressure phases of YC2, apart from YC2-II, whose density of states at Fermi level of is too small for a good superconductor. The obtained electron–phonon coupling parameter (λ), logarithmic average of phonon frequency ωlog and Tc are given in Supplementary Table 2. The Tc of YC2 varies in the pressure range of 0 to 300 GPa, as shown in Supplementary Figure 6. The Tc is strongly structure-dependent: we found a Tc of 2.9 K for YC2-V at 300 GPa, while the electron-coupling calculations for YC2-III and YC2-IV give relatively small Tc, no greater than 2 K. The YC2-V structure is similar to graphene and we find that, in this system, the carbon has a significant contribution to the superconductivity.
In conclusion, we have studied the structures and properties of YC2 as a function of pressure using first-principles electronic structure predictions and calculations. YC2 is found to form a series of stable compounds with varying structures under pressure up to 300 GPa, on the basis of the formation enthalpies of the predicted structures relative to elemental yttrium and carbon: dimer-type carbon found in the ambient pressure structure is polymerised first into ordered arm-chair chains which polymerise further into quasi-1D well-ordered double chains and eventually form 2D graphite sheets. Our phonon calculations suggest that these YC2 structures are also dynamically stable. Furthermore, our electron–phonon coupling calculation demonstrate that YC2 is a good electron–phonon superconductor with a superconducting critical temperature of 2.9 K at 300 GPa. Our results reveal the role of pressure on modifying the carbon polymerization within this carbide, in particular in the gradual increase of C-C connectivity with pressure. The YC2 system provides an unusual example of superconductivity in graphite/graphene C intercalated with metals.
Methods
Structure search
The search for low-energy high-pressure crystalline YC2 phases was first performed using the swarm-intelligence based CALYPSO method22,23,24 and then confirmed using the ab initio random structure searching approach (AIRSS)25, 26. Recent successful applications of these two methods include several examples of structure predictions for various crystalline systems, ranging from elemental solids to binary and ternary compounds27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45. Structural optimisations, enthalpies, electronic structures, and phonons were calculated using a first-principles implementation of density-functional theory.
Castep46, 47 was used for the AIRSS searches. The plane wave basis set was constructed using an energy cut-off of 500 eV in all CASTEP calculations, and the Brillouin zone was sampled with a k-point resolution of 2π x 0.03 Å−1. On The Fly (OTH) potentials are adopted for both Y and C. The exchange-correlation functional was described using the Perdew-Buike-Ernzerhof form of the generalized gradient approximation, as was done for VASP calculations.
Structure optimisation
The underlying optimisations were performed using the Vienna ab initio simulation (VASP) program48 and projector-augmented plane wave potentials49 with an energy cut-off of 600 eV. The Y and C potentials have 4s24p65s24d1 and 2s22p2 as valence states, respectively, employing the PBE functional50. Other density functionals, including LDA51 and PBEsol52, 53, were also tested for comparison (see Supplementary Figure 7). Dense k-point meshes (2π X 0.03 Å−1) were employed to sample the first Brillion Zone for candidate structures and ensure the energies converged well.
Phonon calculations
We explored the effects of temperature using the quasi-harmonic approximation. The phonon calculations were performed using the PHONOPY code54. Electron–phonon coupling was performed using the pseudopotential plane wave method and density-functional perturbation theory as implemented in the QUANTUM ESPRESSO package55. The technique for the calculation of electron–phonon coupling has been described in detail previously18. Convergence tests led us to determine and set the most appropriate kinetic energy cut off at 60 Ry.
Data availability
The datasets generated during the current study are available in the figshare repository at https://doi.org/10.6084/m9.figshare.7038659.v1
References
Zhang, L., Wang, Y., Lv, J. & Ma, Y. Materials discovery at high pressures. Nat. Rev. Mat. 2, 17005 (2017).
Needs, R. J. & Pickard, C. J. Perspective: role of structure prediction in materials discovery and design. APL Mater. 4, 053210 (2016).
Wang, Y. & Ma, Y. Perspective: crystal structure prediction at high pressures. J. Chem. Phys. 140, 040901 (2014).
Liu, H., Li, Q., Zhu, L. & Ma, Y. Superhard and superconductive polymorphs of diamond-like BC3. Phys. Lett. A 375, 771–774 (2011).
Spedding, F. H., Gschneidner, K. & Daane, A. H. The crystal structures of some of the rare earth carbides. J. Am. Chem. Soc. 80, 4499–4503 (1958).
Li, Y.-L. et al. Pressure-induced superconductivity in CaC2. Proc. Natl Acad. Sci. USA 110, 9289–9294 (2013).
Gschneidner, K. A. & Calderwood, F. W. The C-Y (Carbon-Yttrium) system. Bull. Alloy Phase Diagr. 7, 564–568 (1986).
Feng, C. et al. First-principle study of pressure-induced phase transitions and electronic properties of electride Y2C. Solid State Commun. 266, 34–38 (2017).
Zhong, X. et al. Pressure stabilization of long-missing bare C 6 hexagonal rings in binary sesquicarbides. Chem. Sci. 5, 3936–3940 (2014).
Zhang, J. et al. Nanoscale fullerene compression of an yttrium carbide cluster. J. Am. Chem. Soc. 134, 8487–8493 (2012).
Giorgi, A. L., Szklarz, E. G., Krupka, M. C., Wallace, T. C. & Krikorian, N. H. Occurrence of superconductivity in yttrium dicarbide. J. Less Common Met. 14, 247 (1968).
Krupka, M. C., Giorgi, A. L., Krikorian, N. H. & Szklarz, E. G. High pressure synthesis and superconducting properties of yttrium sesquicarbide. J. Less Common Met. 17, 91–98 (1969).
Giorgi, A. L., Hill, H. H., Szklarz, E. G. & White, R. W. Pressure dependence of T/sub c/ for carbides of thorium, yttrium, and scandium. Int. Nucl. Inf. Syst. 8, 8281000 (1976).
Krupka, M. C., Giorgi, A. L., Krikorian, N. H. & Szklarz, E. G. High-pressure synthesis of yttrium-thorium sesquicarbide: a new high-temperature superconductor. J. Less Common Met. 19, 113–119 (1969).
Henn, R. W., Schnelle, W., Kremer, R. K. & Simon, A. Bulk superconductivity at 10 K in the layered compounds Y2C2I2 and Y2C2Br2. Phys. Rev. Lett. 77, 374–377 (1996).
Li, Y. et al. Pressure-stabilized superconductive yttrium hydrides. Sci. Rep. 5, 9948 (2015).
Peng, F. et al. Hydrogen clathrate structures in rare earth hydrides at high pressures: possible route to room-temperature superconductivity. Phys. Rev. Lett. 119, 107001 (2017).
Liu, H., Naumov, I. I., Hoffmann, R., Ashcroft, N. W. & Hemley, R. J. Potential high- T c superconducting lanthanum and yttrium hydrides at high pressure. Proc. Natl. Acad. Sci. 114, 6990–6995 (2017).
Feng, X. et al. Low-density superhard materials: computational study of Li-inserted B-substituted closo-carboranes LiBC11 and Li2B2C10. RSC Adv. 6, 52695–52699 (2016).
Feng, X. & Redfern, S. A. T. Iodate in calcite, aragonite and vaterite CaCO3: Insights from first-principles calculations and implications for the I/Ca geochemical proxy. Geochim. Cosmochim. Acta 236, 351–360 (2018).
Li, Y. et al. Route to high-energy density polymeric nitrogen t-N via He-N compounds. Nat. Commun. 9, 722 (2018).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. CALYPSO: a method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012).
Wang, H. et al. CALYPSO structure prediction method and its wide application. Comput. Mater. Sci. 112, 406–415 (2016).
Pickard, C. J. & Needs, R. J. High-pressure phases of silane. Phys. Rev. Lett. 97, 045504 (2006).
Pickard, C. J. & Needs, R. J. Ab initio random structure searching. J. Phys. Condens. Matter 23, 053201 (2011).
Zhu, L. et al. Substitutional alloy of Bi and Te at high pressure. Phys Rev Lett 106, 145501 (2011).
Liu, H., Naumov, I. I. & Hemley, R. J. Dense hydrocarbon structures at megabar pressures. J. Phys. Chem. Lett. 7, 4218–4222 (2016).
Peng, F., Yao, Y., Liu, H. & Ma, Y. Crystalline LiN5 predicted from first-principles as a possible high-energy material. J. Phys. Chem. Lett. 6, 2363–2366 (2015).
Miao, M. S. et al. Anionic chemistry of noble gases: formation of Mg-NG (NG = Xe, Kr, Ar) compounds under pressure. J. Am. Chem. Soc. 137, 14122–14128 (2015).
Zhang, S., Wang, Y., Zhang, J., Liu, H. & Zhong, X. Phase diagram and high- temperature superconductivity of compressed selenium hydrides. Sci. Rep. 5, 15433 (2015).
Zhang, M. et al. Two-dimensional boron–nitrogen–carbon monolayers with tunable direct band gaps. Nanoscale 7, 12023–12029 (2015).
Yan, Y., Zhang, Y., Wang, Y. & Yang, G. Pressure-induced reappearance of superconductivity in the oC24 phase of lithium. Solid State Commun. 225, 7–11 (2016).
Pickard, C. J. & Needs, R. J. Aluminium at terapascal pressures. Nat. Mater. 9, 624–627 (2010).
Pickard, C. C. J. & Needs, R. R. J. Structure of phase III of solid hydrogen. Nat. Phys. 3, 473–476 (2007).
Pickard, C. J. & Needs, R. J. Highly compressed ammonia forms an ionic crystal. Nat. Mater. 7, 775–779 (2008).
Yong, X. et al. Crystal structures and dynamical properties of dense CO2. Proc. Natl. Acad. Sci. USA 113, 11110–11115 (2016).
Liu, Z. et al. Reactivity of He with ionic compounds under high pressure. Nat. Commun. 9, 951 (2018).
Lv, J., Wang, Y., Zhu, L. & Ma, Y. B38: an all-boron fullerene analogue. Nanoscale 6, 11692–11696 (2014).
Li, Y., Hao, J., Liu, H., Li, Y. & Ma, Y. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 140, 174712 (2014).
Lu, S., Wang, Y., Liu, H., Miao, M. S. & Ma, Y. Self-assembled ultrathin nanotubes on diamond (100) surface. Nat. Commun. 5, 3666 (2014).
Zhu, L., Liu, H., Pickard, C. J., Zou, G. & Ma, Y. Reactions of xenon with iron and nickel are predicted in the Earth’s inner core. Nat. Chem. 6, 644–648 (2014).
Wang, H., Tse, J. S., Tanaka, K., Iitaka, T. & Ma, Y. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. 109, 6463–6466 (2012).
Liu, H., Wang, H. & Ma, Y. Quasi-molecular and atomic phases of dense solid hydrogen. J. Phys. Chem. C. 116, 9221–9226 (2012).
Miao, M. S. Caesium in high oxidation states and as a p-block element. Nat. Chem. 5, 846–852 (2013).
Clark, S. J. et al. First principles methods using CASTEP. Z. für Krist. 220, 567–570 (2005).
Segall, M. D. et al. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 14, 2717 (2002).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B - Condens. Matter Mater. Phys. 54, 11169 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Perdew, J., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133 (1965).
Perdew, J. P. et al. Erratum: restoring the density-gradient expansion for exchange in solids and surfaces (Physical Review Letters (2008) 100 (136406)). Phys. Rev. Lett. 102, 039902 (2009).
Perdew, J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Giannozzi, P. et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Acknowledgements
X.F. is grateful for China Scholarship Council. C.J.P. is supported by the Royal Society through a Royal Society Wolfson Research Merit award and the EPSRC through EP/P022596/1. S.A.T.R is grateful for support from NERC (NE/P012167/1). Y.M. acknowledge funding from the Science Challenge Project at Grant No. TZ2016001, the National Natural Science Foundation of China under Grant No. 11534003 and the National Key Research and Development Program of China under Grant No. 2016YFB0201200.
Author information
Authors and Affiliations
Contributions
X.F. and S.L. made equal contributions to this work. X.F., S.L., H.L. and C.J.P. conceived the methods and carried out calculations, Y.M., S.A.T.R. and C.J.P. directed the research. X.F. and S.A.T.R. wrote the manuscript which subsequently underwent revision with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Feng, X., Lu, S., Pickard, C.J. et al. Carbon network evolution from dimers to sheets in superconducting ytrrium dicarbide under pressure. Commun Chem 1, 85 (2018). https://doi.org/10.1038/s42004-018-0085-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-018-0085-0
This article is cited by
-
Chemistry under high pressure
Nature Reviews Chemistry (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.