Abstract
Comparative analysis of high throughput sequencing data between multiple conditions often involves mapping of sequencing reads to a reference and downstream bioinformatics analyses. Both of these steps may introduce heavy bias and potential data loss. This is especially true in studies where patient transcriptomes or genomes may vary from their references, such as in cancer. Here we describe a novel approach and associated software that makes use of advances in genetic algorithms and feature selection to comprehensively explore massive volumes of sequencing data to classify and discover new sequences of interest without a mapping step and without intensive use of specialized bioinformatics pipelines. We demonstrate that our approach called GECKO for GEnetic Classification using k-mer Optimization is effective at classifying and extracting meaningful sequences from multiple types of sequencing approaches including mRNA, microRNA, and DNA methylome data.
Similar content being viewed by others
Introduction
Studies of variation in gene expression, initially through probe-based technology and more recently high throughput sequencing (HTS), have considerably advanced knowledge of disease etiology and classification1,2,3. The recent promotion of HTS across a wide spectrum of diseases has generated a wealth of data that measure gene expression and transcript diversity but also explore its putative genetic and epigenetic regulators. Still, despite more than a decade of development, computational analysis and integration of these data presents a major challenge. Each type of HTS experiment is compartmentalized to a set of computational pipelines and statistical approaches that often require a full-time bioinformatics specialist. In addition, most of these pipelines rely on a reference genome or transcriptome and thus cannot inherently account for the diversity in non-reference transcripts or individual variations4. To remove the requirement of a reference, recent methodologies use k-mer representation; they directly compare the counts of nucleotide sequences of length k between samples5. These approaches have been successful at detecting novel transcripts but only on a very small subset of RNA sequencing data4 and would be impossible to implement for the classification of large patient cohorts using the entire transcriptome. In the field of metagenomics, numerous algorithms have been developed to discover unique k-mers or k-mer signatures to classify organisms6,7. However, these were developed for organisms with smaller genomes that do not have billions of different k-mers. In addition, they were designed for inter-species studies where unique k-mers can be attributed to the genomes of different taxonomic identities.
Exploring a large set of k-mers to classify samples can be framed as a global optimization problem for which many recent approaches have been published and compared8. Amongst these is a class of nature-inspired algorithms termed Genetic Algorithm which are based on the processes of mutation, crossing over and natural selection. These have appealing properties that could apply to the exploration of a large set of k-mers. They have low memory requirements because they explore only part of the data at each stage and they can produce multiple solutions that fit well with biological interpretation of data. However, despite these properties, genetic algorithms are rarely used to optimize problems with relatively small sample sizes and such a large number of parameters, in this case billions of k-mers.
We have created a novel approach and associated software called GECKO for genetic classification using k-mer optimization that is especially designed for HTS data. GECKO is based on k-mer decomposition coupled with an adaptive genetic algorithm that explores HTS data from two or more input conditions. This algorithm searches for groups of k-mers that, combined together are highly informative; they are able to classify the input categories with high accuracy. Because GECKO uses k-mer counts, it can theoretically be applied to any type of HTS experiment and does not rely on a reference genome or transcriptome. Here, we successfully apply GECKO to a variety of biological problems and sequencing data. These include microRNA (miRNA) sequencing to classify normal blood cells, mRNA sequencing to classify subtypes of breast cancer and to predict response to chemotherapy, and bisulfite sequencing (BS-seq) on normal versus chronic lymphocytic leukemia (CLL) samples. Regardless of the type of data, GECKO finds small, accurate signatures that classify these samples and could thus be used as diagnostic and prognostic markers. In addition, by visualizing how the genetic algorithm evolves to find solutions, GECKO can be used to explore novel sequences or groups of functionally related sequences associated with normal biology and disease.
Results
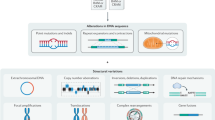
GECKO is designed around two main steps; these are a k-mer matrix preparation step and an adaptive genetic algorithm (Fig. 1).
Overview of the GECKO algorithm. Input fastq or bam files from two or more conditions are transformed into a matrix of k-mer counts across all samples. The k-mers for which the counts are below a noise threshold or that do not vary across samples are removed (red dots on the right of the k-mer matrix). The adaptive genetic algorithm randomly selects groups of k-mers from the k-mer matrix to form individuals. These individuals will go through rounds of mutation, crossing-over and selection to discover individuals capable of classifying the input samples with high accuracy
The k-mer matrix preparation, uses an input sequencing file (.bam or .fastq) to create a matrix of k-mer counts; that is the number of times a sequence of length k appears in each sample (k = 30 by default). This matrix is filtered for k-mers with low counts and non-informative or redundant k-mers (see the section “Methods”). Then, during the second step an adaptive genetic algorithm will explore the matrix to discover combinations of k-mers that can accurately classify input samples. The adaptive genetic algorithm starts by creating thousands of digital individuals; these are groups of randomly selected k-mers. The set of individuals is called a population. This population will then go through phases of mutation, where individuals replace one of their k-mers with another randomly selected k-mer; a phase of crossing-over where individuals exchange a portion of their k-mers with each other and selection, where individuals that do not classify the input samples well enough will be removed from the population and replaced. Mutation allows GECKO to explore local solutions similar to the individual to be mutated; crossing-over, allows GECKO to explore a broader set of solutions and reduces the chances of getting stuck in a local minimum (see the section “Methods”). Each cycle of mutation, crossing-over, and selection is called a generation. By default, GECKO will iterate through 20,000 generations or stop when the number of new solutions discovered throughout generations slows down (see stopping criteria in the section “Methods”). This algorithm is called adaptive because the mutation and crossing-over rates depend on how well individuals in the population perform. Individuals that perform well have lower rates to prevent them from changing drastically and thus enabling them to converge faster to a solution; individuals that do not perform well will have higher rates to enable wider exploration of solutions.
In the analyses presented in this study and by default in the software, GECKO’s performance is systematically tested on 1/6th of the data that is randomly selected and set aside before running the algorithm (see the section “Methods”). This test set allows us to evaluate the accuracy and overfitting for each run; it measures whether the algorithm fits too closely to the training set and thus will not correctly predict future input samples. GECKO is thus run on the remaining 5/6th of the data with cross-validation at each generation of the algorithm.
Classifying miRNA sequencing data of blood cells
We first tested GECKO’s performance on a miRNA expression data of seven types of blood cells sorted from 43 healthy patients for a total of 413 samples9. We ran GECKO on this dataset using 20-mers (k-mer size of 20; miRNAs generally vary in size from 20 to 23) to find a set of k-mers that could correctly classify the seven blood-cell types.
After 6000 generations (15 h on 15 cores; see Supplementary Table 1 for parameters and Supplementary Fig. 1 for runtimes and memory usage) GECKO discovered an individual composed of only three k-mers (ACCCGTAGAACCGACCTTGC, CCCCAGGTGTGATTCTGATA, AGTGCATGACAGAACTTGGG) that could distinguish the groups with 0.96 accuracy (Fig. 2a, b and Supplementary Data 1 and 2).
GECKO can accurately classify miRNA data from seven types of blood cells using three k-mers. a GECKO output showing the separation of the seven blood-cell types at each generation (G) of GECKO analysis using t-SNE visualization applied to k-mer counts. b GECKO output showing the accuracy of separation for the training and test set across 6000 generations. c variance stabilized counts of the three miRNAs that correspond to the three k-mers discovered by GECKO across the seven blood-cell types (n = 43 biologically independent donors)
In the initial study, the authors described a signature of 136 cell-type-specific miRNAs. These 136 miRNAs could classify the groups with 0.97 accuracy. Thus, we found a much smaller signature that could classify the seven blood-cell types with similar accuracy without the use of a miRNA-dedicated bioinformatics pipeline.
We then aligned the three k-mers discovered by GECKO to a database of known miRNAs10. Two of these mapped perfectly to miRNAs 152-3p and 99b-5p, which were annotated in the original study as specific to NK cells and T helper cells, respectively. The third mapped to miRNA 361-3p which was not found to be specific to any of the seven cell types and was thus ignored in the initial study. Separately, the first two k-mers could classify one cell-type each and the third would have been overlooked. Together these three k-mers classify all seven groups with high accuracy because of their contrasting expression between each cell types (Fig. 2c).
Classifying breast cancer subtypes using mRNA sequencing data
Breast cancer is a heterogeneous disease in regards to response to treatment and its transcriptional background. Defining the subtypes luminal A (LumA), luminal B (LumB), HER2-enriched (HER2) and basal-like are crucial for prognosis and predicting outcome of breast cancer. These subtypes were initially defined through unsupervised clustering of gene expression and are currently identified using a standard qPCR assay of 50 genes called the PAM5011,12. To assess whether GECKO could identify k-mers that classify breast cancer subtypes, we used a dataset of 1087 mRNA-Seq breast cancer samples from the Cancer Genome Atlas Pan-Gyn cohort13 (patients per class: Basal 175, Her2 73, LumA 513, LumB 185). We ran GECKO for 20,000 generations (75 h on 15 cores; see Supplementary Table 1 for parameters and Supplementary Fig. 1 for runtimes and memory usage) and extracted the highest scoring individual at its term (Supplementary Table 2). We then tested how well these k-mers classified the four cancer subtypes compared to PAM50 expression values calculated as transcript per million (TPM). Both the k-mer counts and PAM50 TPMs were trained using a linear support vector machine (see the section “Methods”) with identical training data and evaluated on the same test set. The 10 k-mers had higher accuracy rates compared to the PAM50 on all four classes (Fig. 3 and Table 1).
We then further inspected the 10 k-mers discovered by GECKO by mapping them to the human genome. We found that four of the k-mers mapped to genes from the PAM50 list (FOXC1, ESR1, KRT14, KRT17). Three others mapped to genes NISCH, TPX2, and ATF3, the first of which is linked to breast cancer aggressiveness13 and the two latter both affect cell viability in breast cancer cells14,15. The three last k-mers mapped to three genes KLHL6, KANSL2, and PHF10 shown to be involved in tumorigenesis but not in breast cancer16,17,18. Of the 10 k-mers, 3 map to coding regions and 7 map to 3′ untranslated regions for which multiple isoforms exist. k-mer counting can thus integrate alternative transcription to classify mRNA-Seq samples.
Classifying response to chemotherapy of triple negative breast cancer on small sample sizes of mRNA-Seq
We then tested GECKO on a dataset with more heterogeneous cell populations and smaller sample sizes. We used a cohort of triple-negative breast cancer patients, an aggressive, heterogeneous subtype of breast cancer with poor outcomes. This cohort taken from the Breast Cancer Genome Guided Therapy (BEAUTY) study19,20 was divided into 19 patients that had a complete response to chemotherapy and 20 patients that did not. In such cases of small sample size and high heterogeneity, we recommend using GECKO’s voting mode (Fig. 4a).
GECKO voting mode for small sample sizes. a GECKO’s voting mode will run 10 separate genetic algorithms with added Gaussian noise. The best solutions of these runs will be fed into a final genetic algorithm to produce a final solution. b GECKO output showing the t-SNE separation of patients with complete response to chemotherapy from those that did not using five k-mers from the winning individual. Triangles correspond to the test dataset that was excluded from GECKO training can thus be used to estimate overfitting
This mode compensates for bias that may be introduced when splitting a small number of samples between training and test datasets and may thus accentuate batch effects. The voting mode will run 10 instances of the genetic algorithm for 10,000 generations. At their term, it will select k-mers from the top individuals across the 10 instances and run a final genetic algorithm on this subset of k-mers for another 10,000 generations. Running multiple genetic algorithms and aggregating their results prevents overfitting on a specific split of the data between the training and test set. In addition, the voting mode introduces Gaussian noise by default into the data to further prevent overfitting. This option is recommended for experiments with <30 samples per condition.
Using the voting mode (83 h using 15 cores; see Supplementary Table 1 for parameters and Supplementary Fig. 1 for runtimes and memory usage), we found an individual that was able to classify patients with 0.93 accuracy (Fig. 4b) with only five k-mers of length 30 (Supplementary Table 3). As expected three of these k-mers mapped to genes that had clear roles in resistance to chemotherapy; JAK3 is involved in chemotherapy resistance in triple-negative breast cancer8, BOP1 reduces chemotherapy resistance21 and VTCN1 is associated with poor clinical outcomes in numerous cancers including breast cancer22.
Classifying BS-seq data
We then wanted to see if GECKO could accurately classify samples using epigenetic sequencing data, such as BS-seq generated to investigate DNA methylation. BS-seq requires extensive bioinformatics processing to discover changes in methylation and thus, a method that could directly classify BS-seq samples could be of great interest. To test GECKO on BS-seq we downloaded raw sequencing files from a study on methylome diversity in 104 primary CLLs samples compared with 26 normal B cell samples23. Although global hypomethylation has been well described in cancer, these alterations are highly variable between CLL samples23 and thus present a challenge for classification.
We ran GECKO for 20,000 generations (39 h; see Supplementary Table 1 for parameters and Supplementary Fig. 1 for runtimes and memory usage) and found a winning individual that was able to classify normal from CLL samples with an accuracy of 1 using 20 k-mers (Fig. 5a; Supplementary Table 4). In addition to this final classification, GECKO plots the evolution of winning organisms across the 20,000 generations (Fig. 5b). This graph can be used to identify individual k-mers that are essential for classification and thus worth investigating. Here we found three k-mers that were most frequently used by winning individuals for classification (Supplementary Table 5).
GECKO can accurately classify normal and CLL patients using k-mers from bisulfite sequencing data. a GECKO output showing the t-SNE separation of CLL and normal samples using 20 k-mers from the winning individual. b GECKO output of K-mer exploration across 20,000 generations; k-mers that are frequently found in winning organisms are displayed as horizontal lines across generations; dots represent k-mers that were selected in one generation but eliminated in the following generation often due to a decrease in fitness of the model. c IGV screenshots showing the methylation status of normal and CLL samples of regions corresponding to three most frequently used k-mers in winning organisms determined by the Bismark software
We verified the methylation status of the loci where these k-mer sequences were mapped using the Bismark software24 and found that all three of them displayed dramatic changes in DNA methylation between normal and CLL samples (Fig. 5c). Interestingly the two k-mers that were finally selected after 20,000 generations, K107977 and K90528 overlapped binding sites for CTCF and GATA3, both of which are affected by DNA methylation status25,26. K107977 overlaps a CTCF-binding site for the ATP6V1G1 gene27, which codes for a proton pump responsible for acidification of the cell, a hallmark of cancer promotion. K90528 overlaps a GATA3-binding site for the SULF2 gene that has already been identified as a diagnostic and prognostic marker in multiple cancers28,29,30.
Discussion
HTS data analysis often requires extensive data transformations through tailored bioinformatics pipelines to organize the sequences in a manner that is coherent with our understanding of biology. Mapping to a reference, using ad hoc statistical thresholds and grouping sequences by functional elements, such as transcripts are common steps in most bioinformatics pipelines.
We designed GECKO with the aim of creating a classifier that could explore HTS data without a reference genome or transcriptome and without the need of bioinformatics pipelines dedicated to a specific library preparation or technology. The approach we describe here can in theory explore any type of sequencing data. Because GECKO considers groups of k-mers for classification, it can make use of co-dependencies between sequences to find smaller and more accurate classifiers. Thus, GECKO is capable of better classification than the commonly used approach that consists of selecting genes for which the expression is statistically significant between conditions to build a classifier (Supplementary Fig. 2). In the miRNA analysis of blood cells for example, one of the k-mers that participated in making an excellent classifier was not statistically significant by itself and would have been overlooked.
Using k-mer counts removes the requirement of a mapping step and makes GECKO applicable to numerous types of sequencing experiments. In addition, we found that using k-mers instead of other metrics, such as fragments per kilobase million (FPKM) or read counts resulted in higher predictive power even when run with the same genetic algorithm (Supplementary Fig. 3). This can be explained by the fact that k-mers can measure changes in transcription, isoform abundance, and sequence simultaneously. When applied to bisulfite converted data, each epigenetic change can potentially lead to the appearance of a novel k-mer in samples where the modification is present. These sample-specific k-mers allow GECKO to make very efficient classifications and to pinpoint the exact location of the modification.
Unlike regression analysis our approach provides multiple solutions (Supplementary Fig. 4). For research purposes this allows us to investigate why different groups of solutions work well together, explore co-dependencies between sequences and functional pathways that allow a good separation of input samples. In a clinical setting, providing multiple good solutions allows more flexibility for selecting diagnostic or prognostic targets. Importantly, the k-mers used for classification are not biased towards higher expressed genes (Supplementary Fig. 5) and mostly map to unique locations in the genome or transcriptome (Supplementary Fig. 6). Thus, GECKO can make use of unique transcriptional elements across a large spectrum of expression.
GECKO’s ability to work across multiple types of data without the need of dedicated bioinformatics tools could make it invaluable for cross-platform large-scale analyses but also for individual researchers and clinicians who would be able to compare HTS data between cohorts of patients with no bioinformatics training. It is worth noting that the longest and computationally intensive part of our procedure is obtaining the k-mer matrix. This step need be performed only once per dataset however and providing a k-mer matrix for online datasets along with sequencing files could result in widespread use of non-biased approaches such as GECKO. In addition, k-mer-based approaches, such as GECKO have the advantage of being portable; k-mer sequences will not change with new versions of the genome.
Methods
Data preparation
The k-mer decomposition into a matrix of k-mer counts is performed using Jellyfish 231. This step can be preceded by a filtering of sequencing adaptors by Trim Galore (bioinformatics.babraham.ac.uk/projects/trim_galore/) if the user selects this option in GECKO. GECKO will then eliminate k-mers for which the count is below a noise threshold, k-mers that are uninformative for the given study and k-mers that are redundant (i.e. that share the same information as another k-mer).
The noise threshold is determined empirically from the input samples and is calculated for each separate run of GECKO. To do this, we count the number of times a k-mer count appears in one sample with null values in all other samples from the same group for the same k-mer. Starting at a k-mer count of 1, we search how many times the value 1 appears for a k-mer in one sample with 0 in every other sample for the same k-mer. We then iterate this process for k-mer counts 2, 3, etc. When this frequency drops dramatically as determined by the slope of frequency counts (determined by calculating the derivative at each point), we consider that we are above background and set the threshold as the k-mer count just before the greatest inflection of the slope (Supplementary Fig. 7).
To determine uninformative k-mers, that is k-mers that do not vary across input samples, we first discretize the k-mer counts using a chi-square statistic that determines the minimum number of discrete intervals with minimum loss of class attribute interdependence32. This algorithm is unsupervised and determines the existence and number of separate levels in continuous data. If there are no clear categories, the discretization will output a vector of 1’s. Following this discretization, if there is not a minimum of 10% of samples with a different level, then this k-mer is considered uninformative. By default, this minimum number is set at 10% of the size of the input condition with the least replicates. For example, if the condition with the least replicates has 30 samples, then at least three samples must have a different discretized level to the other samples.
To eliminate redundant k-mers we use symmetric uncertainty (SU) between pairs of k-mers. Instead of comparing each k-mer to all other k-mers, we first split the k-mers into buckets of equal size and perform pairwise comparisons within a bucket. To determine which k-mers will be bucketed together, we calculate the sum of their counts across samples. k-mers with a similar sum across samples are put together; k-mers within a bucket have a higher chance of being redundant than if they were randomly bucketed. When all k-mers within buckets have been compared and redundant k-mers filtered, this process of bucketing by sum and filtering is repeated. This process of bucketing the k-mers by sum lead to 10 times faster filtering process on smaller samples and larger gains with larger matrices.
The SU between two k-mers A and B is given by the formula:
where H(A) and H(B) are the entropies of the two k- mers along the samples and H(A, B) is the entropy of the combined k-mer counts A and B along the samples.
The Entropy is given by the formula:
where G is the total number of k-mer frequencies given by the discretization step, Mi is the number of samples at the given discretization level N is the total number of samples. In our analysis, we empirically set the limit of SU at 0.7, above which two k-mers were considered as redundant.
GECKO keeps a record of all k-mers eliminated due to redundancy along with the ID of the k-mer that caused it to be eliminated. Thus, when the genetic algorithm finds a solution, GECKO can provide all the redundant k-mers that would have provided a similar solution.
All code for the data preparation was implemented in C++.
The adaptive genetic algorithm
The algorithm begins by splitting the input data into a training and test set. The test set is created by randomly selecting a number of samples from each input category. By default the number of samples selected is 1/6th of the category with the smallest amount of samples. The test set is used to establish a final test score that will have no impact on the genetic algorithm’s evolution but allows us to estimate how well GECKO performs on a given dataset.
Training: At each generation of the AG, all individuals are scored based on their ability to classify the input samples using a machine learning algorithm. In this study, the algorithm used was a Linear Support Vector Classification (LinSVC). This method combines excellent results on smalls datasets and unbalanced groups with a good generalization potential, for a small computational resource cost. LinSVC is implemented in GECKO via the Scikit-learn package33. GECKO can also be used with a random forest model or neural networks, however these have higher computational costs and require dedicated hardware to be implemented within reasonable time-frames.
To calculate the fitness score of an individual at each generation we randomly split up the training set into two. 2/3 of the training set becomes the inner training set and the remaining 1/3 becomes the inner test set. We contrast the inner test set, which is used to score individuals at each generation of the adaptive genetic algorithm with the test set which is not used to train the adaptive genetic algorithm but instead is used to estimate the performance of our model. The inner split on the training data is random and is performed five times. The score of each individual is an average of these five iterations trained on the inner training sets and tested on the inner test sets. This rotation of the training data avoids sample batch effect biases at each generation.
Natural selection: After testing the fitness of each individual of our population we delete individuals with lower fitness scores. By default, this is 30% of the population. We call this process natural selection.
We sort the individuals by ascending rank and then apply the following probabilistic rule:
where X is the individual rank and the following conditions are satisfied:
where α, β are scalar values, N is the size of the population, and \(\begin{array}{*{20}{c}} N \\ {P-{\mathrm{{value}}}} \end{array}{\mathrm{{and}}} \begin{array}{*{20}{c}} {N/2} \\ {P-{\mathrm{{value}}}} \end{array}\) are, respectively, the probability for the individual rank N and rank N/2 to be deleted.
Mutation and crossing over rates: GECKO makes use of three different types of Genetic Algorithm. These adapt the mutation and cross-over probabilities depending on the homogeneity and the performances of the population in order to converge faster and more accurately.
The three algorithms are:
-
A simple adaptative genetic algorithm34. This algorithm has a fixed factor for individuals for which the fitness is inferior to the average and a decreasing linear function for the better performing half of individuals.
-
Another improved adaptive genetic algorithm35 that, similar to the simple adaptive genetic algorithm, has a crossover probability fixed above the average fitness, but uses exponential instead of the linear function for fitness values below the average.
-
An improved adaptive genetic algorithm36 that models the probabilities with two linear functions, with a breakpoint for the individuals that have a fitness equal to the average fitness.
We recommend using the last model as it shows better exploration and higher convergence rates for the kind of data used for GECKO. This approach aims to maintain the population’s diversity while protecting good individuals from modifications. The mutation and cross-over probabilities are decreased when the individual’s fitness is high compared to the average and increased if it is low. Similarly, the probabilities are decreased when the population is heterogeneous and increased when the population is homogeneous to favor exploration of novel solutions. These probabilities are modeled by two linear functions depending on whether the individual is above the average fitness of the population or below it and is given by the formula below.
Here f is the individual’s fitness, fmin is the fitness of the population’s worst individual, favg is the population’s average fitness and fmax is the fitness of the population’s best individual. k1 is the rate applied when f = fmin, k2 when f = favg, and k3 when f = fmax.
Stopping criteria: By default, GECKO will run for an input number of generations. The user may however choose to make use of a stopping criteria that will stop the algorithm prematurely. The stopping criteria is checked after at least 5000 generations of the genetic algorithm. At this moment, the number of occurrences of each k-mer in the population is calculated across bins of 500 generations from the start of the algorithm to the current generation. The top 1% of most frequent k-mers in each bin are selected. We then estimate the difference in k-mer composition between the current bin and all previous ones using a Hamming distance. This distance measures the quantity of highest scoring k-mers that are changing across generations. When the slope of Hamming distance across generations drops below 1%, the stopping criteria is triggered.
Adding Gaussian noise: The user may add Gaussian noise to the model to prevent overfitting. The characteristics of this noise are determined for each k-mer separately. They are a mean of 0 and a standard deviation equal to the standard deviation of the k-mer in the training set. The user can modify the level of noise by changing noisefactor which multiplies the standard deviation by the input value. This noise is generated at each training of machine-learning model and for each individual.
tSNE visualization: t-SNE plots are generated using scikit-learn with the default parameters but initialization with PCA. This initialization option allows for better reproducibility of t-SNE graphs. Below is the corresponding command-line: manifold.TSNE (n_components = 2, init = ‘pca’, random_state = 0, perplexity = 30.0, early_exaggeration = 12.0, learning_rate = 200.0, n_iter = 1000, n_iter_without_progress = 300).
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data that support the findings of this study are available from NCBI Gene Expression Omnibus under the accession numbers GSE100467 and GSE58889; the Cancer Genome Atlas under the Pan-Gyn cohort name; the database of Genotypes and Phenotypes under the accession numbers phs000435.v2.p1 and phs001050.v1.p1 but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available. Data are however available by submitting a request to these repositories.
Code availability
GECKO is available at https://github.com/RitchieLabIGH/GECKO under the CeCILL license.
References
Learn, C. A. et al. Resistance to tyrosine kinase inhibition by mutant epidermal growth factor receptor variant III contributes to the neoplastic phenotype of glioblastoma multiforme. Clin. Cancer Res. 10, 3216–3224 (2004).
Zhang, Z.-M. et al. Pygo2 activates MDR1 expression and mediates chemoresistance in breast cancer via the Wnt/β-catenin pathway. Oncogene 35, 4787–4797 (2016).
Martín-Martín, N. et al. Stratification and therapeutic potential of PML in metastatic breast cancer. Nat. Commun. 7, 12595 (2016).
Audoux, J. et al. DE-kupl: exhaustive capture of biological variation in RNA-seq data through k-mer decomposition. Genome Biol. 18, 243 (2017).
Kirk, J. M. et al. Functional classification of long non-coding RNAs by k-mer content. Nat. Genet. 1, https://doi.org/10.1038/s41588-018-0207-8 (2018).
Ounit, R., Wanamaker, S., Close, T. J. & Lonardi, S. CLARK: fast and accurate classification of metagenomic and genomic sequences using discriminative k-mer0s. BMC Genom. 16, 236 (2015).
Breitwieser, F. P., Baker, D. N. & Salzberg, S. L. KrakenUniq: confident and fast metagenomics classification using unique k-mer counts. Genome Biol. 19, 198 (2018).
Sergeyev, Y. D., Kvasov, D. E. & Mukhametzhanov, M. S. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci. Rep. 8, 453 (2018).
Juzenas, S. et al. A comprehensive, cell specific microRNA catalogue of human peripheral blood. Nucleic Acids Res. 45, 9290–9301 (2017).
Kozomara, A. & Griffiths-Jones, S. miRBase: annotating high confidence microRNAs using deep sequencing data. Nucleic Acids Res. 42, D68–D73 (2014).
Perou, C. M. et al. Molecular portraits of human breast tumours. Nature 406, 747–752 (2000).
Hoadley, K. A. et al. Cell-of-origin patterns dominate the molecular classification of 10,000 tumors from 33 types of cancer. Cell 173, 291–304. e6 (2018).
Maziveyi, M. & Alahari, S. K. Breast cancer tumor suppressors: a special emphasis on novel protein nischarin. Cancer Res. 75, 4252–4259 (2015).
Hasim, M. S., Nessim, C., Villeneuve, P. J., Vanderhyden, B. C. & Dimitroulakos, J. Activating transcription factor 3 as a novel regulator of chemotherapy response in breast cancer. Transl. Oncol. 11, 988–998 (2018).
Gijn, S. E. van et al. TPX2/Aurora kinase A signaling as a potential therapeutic target in genomically unstable cancer cells. Oncogene 1, https://doi.org/10.1038/s41388-018-0470-2 (2018).
Choi, J. et al. Loss of KLHL6 promotes diffuse large B-cell lymphoma growth and survival by stabilizing the mRNA decay factor roquin2. Nat. Cell Biol. 20, 586–596 (2018).
Solari, N. E. F. et al. The NSL chromatin-modifying complex subunit KANSL2 regulates cancer stem-like properties in glioblastoma that contribute to tumorigenesis. Cancer Res. 76, 5383–5394 (2016).
Tatarskiy, V. V. et al. Stability of the PHF10 subunit of PBAF signature module is regulated by phosphorylation: role of β-TrCP. Sci. Rep. 7, 5645 (2017).
Goetz, M. P. et al. Tumor sequencing and patient-derived xenografts in the neoadjuvant treatment of breast cancer. J. Natl. Cancer Inst. 109, 7 (2017).
Thomas, S. J., Snowden, J. A., Zeidler, M. P. & Danson, S. J. The role of JAK/STAT signalling in the pathogenesis, prognosis and treatment of solid tumours. Br. J. Cancer 113, 365–371 (2015).
Sapio, R. T. et al. Inhibition of post-transcriptional steps in ribosome biogenesis confers cytoprotection against chemotherapeutic agents in a p53-dependent manner. Sci. Rep. 7, 9041 (2017).
Podojil, J. R. & Miller, S. D. Potential targeting of B7-H4 for the treatment of cancer. Immunol. Rev. 276, 40–51 (2017).
Landau, D. A. et al. Locally disordered methylation forms the basis of intratumor methylome variation in chronic lymphocytic leukemia. Cancer Cell 26, 813–825 (2014).
Krueger, F. & Andrews, S. R. Bismark: a flexible aligner and methylation caller for Bisulfite-Seq applications. Bioinformatics 27, 1571–1572 (2011).
Wang, H. et al. Widespread plasticity in CTCF occupancy linked to DNA methylation. Genome Res. 22, 1680–1688 (2012).
Fleischer, T. et al. DNA methylation at enhancers identifies distinct breast cancer lineages. Nat. Commun. 8, 1379 (2017).
Lesurf, R. et al. ORegAnno 3.0: a community-driven resource for curated regulatory annotation. Nucleic Acids Res. 44, D126–D132 (2016).
Alhasan, S. F. et al. Sulfatase-2: a prognostic biomarker and candidate therapeutic target in patients with pancreatic ductal adenocarcinoma. Br. J. Cancer 115, 797–804 (2016).
Rosen, S. D. & Lemjabbar-Alaoui, H. Sulf-2: an extracellular modulator of cell signaling and a cancer target candidate. Expert Opin. Ther. Targets 14, 935–949 (2010).
Lui, N. S. et al. SULF2 expression is a potential diagnostic and prognostic marker in lung cancer. PLoS ONE 11, e0148911 (2016).
Marçais, G. & Kingsford, C. A fast, lock-free approach for efficient parallel counting of occurrences of k-mers. Bioinformatics 27, 764–770 (2011).
Gonzalez-Abril, L., Cuberos, F. J., Velasco, F. & Ortega, J. A. Ameva: an autonomous discretization algorithm. Expert Syst. Appl. 36, 5327–5332 (2009).
Pedregosa, F. et al. Scikit-learn: machine learning in python. ArXiv12010490 Cs (2012).
Zhang, J., Chung, H. S. H. & Hu, B. J. Adaptive probabilities of crossover and mutation in genetic algorithms based on clustering technique. In Proc. 2004 Congress on Evolutionary Computation (ed Greenwood, G. W.) (IEEE Cat. No. 04TH8753), Vol. 2, 2280–2287 (IEEE Portland, OR, USA, USA, 2004).
Ravindran, S., Jambek, A. B., Muthusamy, H. & Neoh, S.-C. A novel clinical decision support system using improved adaptive genetic algorithm for the assessment of fetal well-being. Comput. Math. Methods Med. 2015, 283532 (2015). https://doi.org/10.1155/2015/283532.
Yan, M. et al. Improved adaptive genetic algorithm with sparsity constraint applied to thermal neutron CT reconstruction of two-phase flow. Meas. Sci. Technol. 29, 55404 (2018).
Acknowledgements
We wish to acknowledge the Genotoul platform (genotoul.fr) for providing us with calculation time on their servers. We thank Jerome Audoux, Jean-Philippe Villemin and Giacomo Cavalli for their advice. We wish to acknowledge the Agence Nationale de la Recherche (ANRJCJC-WIRED), the Labex EpiGenMed and the MUSE initiative for their financial support.
Author information
Authors and Affiliations
Contributions
W.R., A.T., S.B., J.B., C.R., R.S., G.B., L.B. designed the algorithm; A.M., C.L. designed part of the k-mer filtering step; A.T. and S.B. coded the software; W.R., A.T., S.B., J.-P.V. designed the experiments. W.R., A.T., S.B. wrote the article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thomas, A., Barriere, S., Broseus, L. et al. GECKO is a genetic algorithm to classify and explore high throughput sequencing data. Commun Biol 2, 222 (2019). https://doi.org/10.1038/s42003-019-0456-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42003-019-0456-9
This article is cited by
-
Reference-free transcriptome signatures for prostate cancer prognosis
BMC Cancer (2021)
-
In silico design of novel aptamers utilizing a hybrid method of machine learning and genetic algorithm
Molecular Diversity (2021)
-
iMOKA: k-mer based software to analyze large collections of sequencing data
Genome Biology (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.