Abstract
Proton-exchange membrane fuel cells demand efficient electrode–electrolyte interfaces to catalyse the oxygen reduction reaction (ORR), the kinetics of which depends on the energetics of surface adsorption and on electrolyte environment. Here we show an unanticipated effect of non-specifically adsorbed anions on the ORR kinetics on a Pt(111) electrode; these trends do not follow the usual ORR descriptor, that is *OH binding energy. We propose a voltammetry-accessible descriptor, namely reversibility of the *O ↔ *OH transition. This descriptor tracks the dependence of ORR rates on electrolyte, including the concentration/identity of anions in acidic media, cations in alkaline media and the effect of ionomers. We propose a model that relates the ORR rate on Pt(111) to the rate of the *O to *OH transition, in addition to the thermodynamic *OH binding energy descriptor. Our model also rationalizes different trends for the ORR rate on stepped Pt surfaces in acidic versus alkaline media.

Similar content being viewed by others
Main
The operating energy efficiency of proton-exchange membrane fuel cells (PEMFCs), an appealing power source for transportation, remains well below the thermodynamic value of 83%, primarily because of the high overpotential of the cathodic oxygen reduction reaction (ORR)1,2,3,4,5. Because of the high cost and low abundance of platinum—currently an indispensable catalytic element for ORR in PEMFCs—substantial efforts have been devoted to deliberately structuring Pt-based nanocatalysts in terms of composition6,7, architecture8,9,10 and geometry11,12, having realized substantial enhancements in both fundamentally intrinsic activity and industry-relevant mass activity in acidic environments13.
Part of this progress was guided by a descriptor-based approach, in which the activity of the catalyst is related to the binding energy of the key adsorbed intermediates. A widely adopted ORR descriptor is the oxygen or hydroxyl adsorption energy. Using such a descriptor as the key catalyst property, catalyst-dependent ORR activities are arranged in a so-called volcano plot, with the best catalyst possessing the most optimal oxygen binding energy located at the top of the volcano14,15,16. However, the ORR has multiple oxygen-containing intermediates, and they cannot all be optimized independently because their binding energies exhibit a scaling relation: if one binding energy changes, the others change as well, often in a very predictable way. Such scaling relations eliminate the possibility of independent tuning of each intermediate, and yield a minimum thermodynamic overpotential that cannot be overcome by solely engineering the solid surface for optimum adsorption17,18. Thus, a formidable challenge is to break the scaling relation, with limited experimental success achieved to date19.
One important (often tacit) assumption in the volcano approach is that a catalytic reaction has a single descriptor. However, it is well known that (electro)catalytic reactions may have multiple descriptors; hydrogen evolution/oxidation in alkaline media is a good example, the multiple descriptors of which are currently much discussed in the literature20,21. For the ORR, it appears that oxygen binding energy is a good descriptor when it comes to the properties of the catalyst. However, as we will show here, there is also a significant effect of the electrolyte on ORR activity, which does not follow the predictions of this descriptor. ORR activities are routinely evaluated in 0.1 M HClO4 environments, because of the quantitative agreement between activities of a benchmark nanoparticulate Pt catalyst measured in a half-cell and in a membrane electrode assembly22. Hydrated non-specifically adsorbed anions, located at the outer Helmholtz plane (OHP), are generally considered to be innocent to the intrinsic ORR activity, although hydrated cations have been reported to regulate ORR kinetics in alkaline media23.
We show here that non-specifically adsorbed (NSA) anions are in fact not innocent to the ORR activity, and that the ORR activity trend with anion concentration on Pt(111) cannot be rationalized on the basis of the thermodynamic oxygen binding energy descriptor. We therefore introduce a kinetic descriptor, related to the kinetics of the *O to *OH transition on Pt(111), which correlates well with the electrolyte-induced activity trends in both acidic and alkaline media. The kinetic descriptor also explains the effect of the perfluorosulfonic acid (PFSA) ionomer on ORR activity. We will then discuss how a combination of the traditional thermodynamic descriptor with our kinetic descriptor can rationalize the different ORR activity trends for stepped Pt surfaces in acidic and alkaline media. We believe that our enhanced model for what determines the ORR activity, including both thermodynamic and kinetic factors, pays more credit to the intrinsic complexity of the reaction compared to the traditional volcano model, and provides an avenue towards a more complete understanding of the various factors that determine the ORR rate on Pt surfaces.
Results
CVs and ORR activities of Pt(111) in 0.1 and 0.02 M HClO4
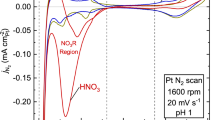
We first investigated how NSA anions affect the chemisorption of oxygen-containing species on Pt(111), which is relevant to the electrocatalytic performance for ORR. Figure 1a compares the blank cyclic voltammograms (CVs) of Pt(111) in HClO4 for two concentrations, that is, the customary 0.1 M and a more diluted 0.02 M solution, both showing the typical voltammetric characteristics of a Pt(111) surface. Negligible differences in the hydrogen underpotential desorption (Hupd, between 0.07 and 0.35 V) or double-layer charging (DL, between 0.35 and 0.55 V) regions were observed between the two electrolytes, indicating the absence of surface reconstruction or specific adsorption. On the other hand, a small but significant difference in the reversible OH adsorption (OHad, between 0.55 and 0.85 V) region is observed, with an overall higher charge of OHad in 0.02 M compared with 0.1 M HClO4 (Fig. 1b). The similar OHad profiles between 0.1 M HClO4 and a control electrolyte (0.02 M HClO4 + 0.08 M KClO4) suggest that OHad formation is more sensitive to the anion concentration than to the electrolyte pH (see the corresponding curve in Fig.1b). This indicates that the saturation coverage of OHad is electrolyte dependent (as it is known that perchlorate interacts with OHad (refs. 24,25), it presumably interferes with the lateral interactions between adsorbed OH).
a, Typical blank CVs recorded at a scan rate of 50 mV s−1. b, Charge density of adsorbed OH (*OH, after the correction of double-layer charging current) as a function of applied potential. c, ORR polarization curves recorded at a scan rate of 20 mV s−1. d, Tafel plots of Pt(111) in 0.02 M HClO4, 0.1 M HClO4 and a mixed solution of 0.02 M HClO4 and 0.08 M KClO4.
The OHad adsorption energy of a Pt surface has been widely used to predict the corresponding ORR activity, on the basis of two proposed mechanisms. The first mechanism suggests that OHad serves as a non-reactive spectator and blocks surface active sites for the adsorption of molecular O2 (refs. 6,26,27). As a result, a lower OHad coverage (Θ*OH) at the potential of interest (ORR activity is customarily evaluated at 0.9 V versus Reversible Hydrogen Electrode (RHE)) results in a higher ORR activity because of a higher pre-exponential factor (1 − Θ*OH) in the rate expression. Here, it is important to note the distinction between NSA (for example, ClO4− and methanesulfonate) and specifically adsorbed anions (for example, HSO4−, Cl− and Br−); the latter (located in the inner Helmholtz plane) directly impact the ORR rate by contributing to the (1 − Θad) term (where Θad includes both *OH and specifically adsorbed anions) of the rate expression given by Marković et al.26,27. The second mechanism is based on the notion that OHad, as an intermediate, binds too strongly on Pt(111), and needs to be weakened by ~0.1 eV to reach the top of the volcano28,29. It has been proposed that an experimental measure of the OHad adsorption strength can be indicated by the electrode potential required for a Θ*OH of 1/6 monolayer, that is, 40 μC cm−2 for Pt(111) (dashed line in Fig. 1b)30. A more negative (positive) potential then means stronger (weaker) OHad adsorption strength. Both mechanisms predict a lower ORR activity for Pt(111) in 0.02 M HClO4 compared with 0.1 M HClO4 because of a higher Θ*OH and a more negative potential for 1/6 of Θ*OH.
Strikingly, we find the opposite trend experimentally. Figure 1c compares the ORR polarization curves of Pt(111) in different electrolytes (see Methods and Supplementary Fig. 1 for ORR test and data processing), all of which show three distinguishable regions: a mixed kinetic-diffusion control region (0.8 < E < 1.0 V), followed by a well-defined diffusion-limiting current region (0.3 < E < 0.7 V) and a region where Hupd interferes with ORR (0.1 < E < 0.3 V). The half-wave potential (E1/2, the potential at half of the diffusion-limiting current density) of Pt(111) in 0.1 M HClO4 is around 0.86 V, in agreement with the literature31. Pt(111) in 0.02 M HClO4 shows higher ORR activity than in 0.1 M HClO4, as evidenced by a positive shift of E1/2 by 25 mV. The mixed-region curve (where the ORR kinetic parameters were derived and compared) of Pt(111) in the control 0.02 M HClO4 + 0.08 M KClO4 electrolyte overlaps with that in 0.1 M HClO4, showing that the ORR activity depends on anion concentration but not on electrolyte pH (see the corresponding curve in Fig. 1c). We find that the Tafel slope increases slightly with the HClO4 concentration, but is close to 60 mV dec−1 in all cases (Fig. 1d and Supplementary Table 1), which agrees well with the literature and suggests that the ORR mechanism is independent of electrolyte32. We note here that, for ORR on Pt surfaces, derivation of the rate-determining step (RDS) from the measured Tafel slope is not straightforward and remains disputed33. At a constant overpotential of 0.3 V, a lower activation energy of 20.5 kJ mol−1 was obtained in 0.02 M HClO4 than in 0.1 HClO4 (31.1 kJ mol−1, see Methods for testing and processing details for activation energy and Supplementary Fig. 2 for corresponding Arrhenius plots), underscoring the negative impact of ClO4− on the ORR kinetics.
The above observations suggest that ORR rate on a Pt surface cannot be solely described by the thermodynamic binding energy descriptor, and imply the existence of another factor that accounts for the above-observed electrolyte effect. To pursue the origin of this effect, we revisit the ORR mechanism on Pt surfaces, which can be simplified as follows34,35:
where * represents an adsorption site on the surface. This mechanism involves three adsorbed reaction intermediates, that is, *OOH, *O and *OH. Probing these intermediates under reaction dynamics remains a huge challenge. However, existing experimental evidence from both ex situ and in situ ambient-pressure X-ray photoelectron spectroscopy (XPS) suggests that, within the mixed kinetic-diffusion potential region, the dominant surface species gradually change from *O to *OH with increasing ORR overpotential36,37. This highlights the role of *O as a key surface adsorbate for ORR proceeding at the potential of interest, that is 0.9 V, and thus motivates us to investigate the voltammetry of *O and to further probe its functional link with the ORR kinetics on Pt surfaces.
A descriptor for electrolyte effect on ORR
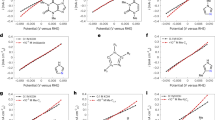
To study the kinetics of the *O to *OH transition, we recorded CVs of Pt(111) in an extended potential window (between 0.07 and 1.15 V) in HClO4 of four concentrations (Fig. 2a). The upper potential limit of 1.15 V was chosen to avoid irreversible surface reconstruction of Pt(111)38. Following the traditional interpretation, we assigned the anodic peak located between 0.95 and 1.1 V as the oxidation of *OH to *O38. A typical characteristic of high-quality Pt(111) surface is the plateau between 0.85 and 1 V, which was previously interpreted as a high kinetic barrier to oxidize Pt(111) with a 1/3 monolayer of Θ*OH, based on density functional theory (DFT) calculations and electrochemical impedance spectroscopy (EIS) studies39. The most pronounced trend from Fig. 2a is that the *O peak shifts positively with the HClO4 concentration, which suggests that *OH → *O conversion is easier in an electrolyte with a lower ClO4− concentration. The reverse reduction of *O to*OH (step 3 of ORR) is then expected to show the same electrolyte dependence. However, the kinetically slow *O → *OH reduction peak overlaps with the fast *OH desorption peak, giving rise to a broad reduction peak between 0.55 and 1 V in the CV (Fig. 2a), comprising both processes. Such a convolution poses experimental difficulties to probe the electrolyte-dependent kinetics of *O to *OH transition on Pt(111). To deconvolute these two processes, we performed experiments at different scan rates and different temperatures.
a, Extended cyclic voltammograms of Pt(111) in HClO4 solutions of different concentrations from 0.02 to 0.2 M, recorded at a scan rate of 50 mV s−1. b, Extended CVs of Pt(111) in 0.02 and 0.1 M HClO4 electrolytes recorded at different scan rates from 10 to 200 mV s−1. c, Specific activities of Pt(111) in HClO4 and methanesulfonic acid (MSA) as a function of electrolyte concentration. The specific activity is the kinetic current density calculated at 0.9 V versus RHE (jk at 0.9 V). Error bars represent the standard deviations of at least three independent measurements.
Leveraging the kinetic difference of *O to *OH transition and *OH desorption on Pt(111), we can manipulate their respective positions by recording CVs at different scan rates from 200 to 10 mV s−1 (Fig. 2b). The two reductive processes were gradually deconvoluted with decreasing scan rate, and became fully separated at 10 mV s−1. The forward and backward peaks corresponding to the *O ↔ *OH redox have a smaller peak-to-peak potential difference at a slower scan rate, proving that there is a kinetic barrier associated with this reaction. Another way to deconvolute the peak is to accelerate the sluggish *O ↔ *OH rate by increasing temperature. Recording CVs of Pt(111) as a function of temperature, we observe a gradual separation of the reduction peaks with increasing temperature (Supplementary Fig. 3). Notably, both scan-rate- and temperature-controlled experiments suggest an electrolyte dependence of the *O ↔ *OH kinetics, namely that it proceeds faster in more diluted HClO4.
In another typical NSA electrolyte, that is methanesulfonic acid (MSA), we observed the same concentration dependence of the ORR activity on Pt(111), suggesting generality of the suppression effect of NSA anions towards ORR (Fig. 2c). Figure 2c plots the specific activity of ORR on Pt(111), denoted by the kinetic current density at 0.9 V (jk, see Methods for calculation details), which decreases with HClO4 and MSA concentration (Fig. 2c), or more specifically, with lower perchlorate and methanesulfonate concentration. The measured jk of Pt(111) in 0.1 M HClO4 is 1.93 mA cm−2, in good agreement with the literature6. The effect of the methanesulfonate concentration on the kinetics of the *O ↔ *OH process is also identical to the effect of the perchlorate concentration (Supplementary Fig. 4).
The observation that the rate of both *O ↔ *OH and ORR depend on the concentration of NSA anions in the same way, suggests that they are related; or more specifically, the rate of the *O ↔ *OH process may act as a descriptor of the ORR rate. To provide quantitative support for this relation, we plot the kinetic current at 0.9 V of ORR versus peak-to-peak separation (ΔEpeak) of the *O ↔ *OH process in Fig. 3a,b. Increasing from 0.02 to 0.1 M HClO4, the anodic and cathodic peak shifts positively and negatively, respectively, by ~25 mV, very close to the E1/2 change of ORR (Fig. 1c). The smaller the ΔEpeak, the more reversible the *O ↔ *OH process, and the faster the ORR rate. We will discuss possible interpretations of this relation in the Discussion section.
a, Redox *O ↔ *OH region of Pt(111) cyclic voltammograms (CVs) recorded in various HClO4 concentrations at a scan rate of 10 mV s−1. b, Peak-to-peak potential difference between the anodic and cathodic peak from a (ΔEpeak, black), the specific activities (red) and peak potential of *O from CVs of 50 mV s−1 from Fig. 2a (E*O, blue) as a function of HClO4 concentration. The smaller the ΔEpeak, the more reversible the *O ↔ *OH process, and the faster the ORR rate.
Effects of alkaline cations and ionomers
Having introduced a kinetic descriptor for the electrolyte effect on Pt(111) in acid solution, we now show its applicability in alkaline media, in which hydrated cations are the main electrolyte players. We recorded CVs of Pt(111) in 0.1 M and 0.02 M NaOH using a slow scan rate of 10 mV s−1, to deconvolute the two cathodic processes (Supplementary Fig. 5a). At a lower NaOH concentration of 0.02 M, the peaks related to *O ↔ *OH redox are more reversible. According to the proposed descriptor, Pt(111) would show a higher ORR activity in 0.02 M than in 0.1 M NaOH, which was verified experimentally by a positive shift of E1/2 by 12 mV (Supplementary Fig. 5b). The kinetic descriptor also tracks the ORR dependence of monovalent cation identity in alkaline electrolytes. On Pt(111), the reversibility of *O ↔ *OH redox and ORR activity follow the same trend of LiOH < NaOH < KOH < CsOH (refs. 23,40). Our kinetic descriptor is also valid for the effect of bivalent cations, such as Ba2+, on the ORR kinetics of Pt(111) in alkaline solutions41.
In real fuel cells, Pt catalysts are generally surrounded with hydrated PFSA-based ionomer instead of anions or cations42,43. We investigated the effect of ionomers on CVs and ORR activities of Pt(111) by depositing a thin layer of the widely adopted Nafion ionomer (see Methods for details). The orientation of Pt(111) was well preserved after the deposition, as evidenced from the negligible change in Hupd profile (Fig. 4a). We observed a higher peak potential for the *OH to *O transition, and a lower ORR activity on Nafion-covered Pt(111) relative to the unmodified Pt(111), validating our kinetic descriptor (Fig. 4b). Further experimental support can be found in the work from Kodama et al., who showed that the ORR activity decreases as bare Pt(111) > perfluorosulfonimide-coated Pt(111) > Nafion-coated Pt(111), while the peak potential for the *OH to *O transition follows the opposite trend44, in agreement with our kinetic descriptor. Our finding offers a plausible explanation for the counterintuitive observation that the addition of ionomers negligibly impacts the electrochemical surface area of nanoparticulate Pt catalyst, yet deteriorates its intrinsic activity45. This provides an important insight into the challenge of the performance transfer of advanced nanocatalysts from half-cell measurements to membrane electrode assembly (MEA) systems46,47.
Electrolyte effect on stepped surfaces and an enhanced model
Finally, we want to show how our kinetic descriptor can be used to offer an explanation for an unsolved puzzle in understanding ORR activity trends on stepped Pt surfaces in acidic and alkaline media. To show the relation between our kinetic descriptor and ORR activity on stepped Pt, we employed a series of Pt(111) vicinal surfaces with (110) steps, denoted as [n(111)×(110)], including Pt(151514) [30(111)×(110)], Pt(554) [10(111)×(110)] and Pt(553) [5(111)×(110)]. We verified the absence of surface faceting on our stepped Pt electrodes by integrating the charge densities of step-related Hupd peaks and comparing them with those predicted from a hard-sphere model48. By comparing their CV profiles with that of Pt(111), we assigned the oxidation peak between 1 and 1.15 V to the formation of *O on (111) terrace (*O(terrace)), the intensity of which decreases with increasing step density (Supplementary Fig. 6). The *O(terrace) peak of all stepped Pt surfaces shifts positively with the HClO4 concentration (Supplementary Fig. 7), in line with the trend of Pt(111). From 0.02 to 0.2 M, the peak potential of *O(terrace) on Pt(111) increased by 30 mV, followed by Pt(151514) of 25 mV, Pt(554) of 19 mV and Pt(553) of 14 mV (Fig. 5a). Following the voltammetry results and the kinetic descriptor, ORR activities on all Pt surfaces are expected to decrease with the HClO4 concentration, in the sequence of Pt(111) > Pt(151514) > Pt(554) > Pt(553). This was experimentally verified by normalizing jk of other concentrations to that of 0.1 M HClO4, as displayed in Fig. 5b, which suggests that a single-crystal Pt surface with a higher step density is less sensitive to the electrolyte effect. We therefore deduce that the electrolyte effect mainly applies to the (111) terraces of Pt surfaces, but also that terraces still make a significant contribution to the overall ORR activity of stepped Pt surfaces.
a, Peak potential of *O on terrace (E*O(terrace)) from cyclic voltammograms of 50 mV s−1 (E*O(terrace)). b, Normalized ORR activities (to that of 0.1 M HClO4). c, Illustration of different active sites, proposed ORR scenario in acidic and alkaline media on stepped surfaces, exemplified using Pt(554). Site A has a higher generalized coordination number and lower oxygen binding energy than site B. Site A serves as the dominant reactive site in acid, in which case the ORR activity follows the thermodynamic descriptor; in alkaline media, site B serves as the dominant reactive site because of the blockage of site A by cations, and the ORR activity follows the kinetic descriptor. d, Specific activities of Pt(111) and stepped surfaces as a function of HClO4 concentration. Activities were compared at 0.93 V because 0.9 V is too close to the diffusion-limiting region for Pt(553). Step density increases in a sequence of Pt(111) < Pt(151514) < Pt(554) < Pt(553); while the changes in E*O(terrace) and ORR activity follow the opposite sequence. Error bars represent the standard deviations of at least three independent measurements.
Stepped Pt surfaces are known to show higher ORR activities than Pt(111) in 0.1 M HClO4 (refs. 31,49). Previous studies have explained this phenomenon based on the oxygen binding energy descriptor. Two types of active sites, categorized by the so-called generalized coordination number, were proposed on stepped surfaces as illustrated in Fig. 5c. Site A (terrace atoms adjacent to steps) has a higher generalized coordination number than site B (basically equal to the terrace atom of Pt(111) electrode). This endows stepped Pt surfaces with lower oxygen binding energy and thus higher ORR activity than Pt(111) following the traditional thermodynamic descriptor, as supported by voltammetry and DFT calculation results12,50. However, previous studies rarely discussed the fact that sites of type B (less energetically favourable sites) also contribute to the ORR rate of stepped surfaces, which show a strong electrolyte effect as demonstrated above. Therefore, we propose an enhanced model for ORR electrocatalysis on Pt surfaces: the ORR rate is jointly governed by the electrode and electrolyte effect, which can be modelled by the traditional thermodynamic oxygen binding energy descriptor and our proposed kinetic descriptor of the *O to *OH transition rate, respectively (Fig. 5c). While the thermodynamic descriptor ascribed higher activities of stepped Pt surfaces to the presence of site A; the kinetic descriptor predicts higher ORR activities on site B of all Pt surfaces with a lower concentration of NSA anions, with Pt(111) being the most sensitive (Fig. 5d and Supplementary Table 2).
With this model, we can understand the longstanding puzzle of the different structure sensitivity of ORR on Pt surfaces in acid versus alkaline media—compared with stepped surfaces, the ORR rate of Pt(111) is lower in acid, but higher in alkaline media51. In acid, site A serves as the dominant reactive site according to the thermodynamic descriptor, which explains the higher ORR rate of stepped surfaces. In alkaline media, previous studies found that alkali metal cations are preferentially located at the step sites21,52. This results in the blockage of site A and as a result site B provides the main contribution to the ORR activity on stepped Pt surfaces (Fig. 5c). In this scenario, the ORR rate is solely governed by the kinetic descriptor according to the above proposed model. Using E*O (Fig. 5a) as a kinetic descriptor, Pt(111) is then predicted to have a higher ORR activity than stepped Pt surfaces because of a faster *O to *OH transition on Pt(111) compared with stepped surfaces, in agreement with the experimental trend.
Discussion
The ORR is a complex multi-proton multi-electron transfer reaction. In the traditional approach for modelling the ORR activities of various electrocatalysts, this complexity is mapped onto a single thermodynamic descriptor, namely the binding energy of *OH or *O on the catalyst. This descriptor has a proven ability to predict and/or reproduce many experimental trends14, but there remain experimental observations for which this descriptor has no explanative or predictive power. In this paper, we have shown that one such experimental observation is the effect of the electrolyte composition on the ORR rate. Specifically, in acidic media the concentration of non-specifically adsorbed anions (such as perchlorate and methanesulfonate), and in alkaline media the concentration of non-specifically adsorbed cations (such as the alkali cations), have a significant effect on the ORR rate on Pt(111), which does not follow the traditional thermodynamic descriptor. To this end, we have introduced a kinetic descriptor, namely the kinetic rate of the *O to *OH transition, which can be estimated from the reversibility of the *O ↔ *OH transition on the (111) terrace. This kinetic descriptor tracks well the observed changes in the ORR rate with the concentration/identity of anions, cations and ionomers on Pt(111) surfaces (Supplementary Fig. 8). We also measured a higher ORR activity on polycrystalline Pt electrodes in a lower concentration of HClO4 (Supplementary Fig. 9), showing that the effect also transfers to more practical surfaces.
This observation requires a discussion of the molecular basis for this kinetic descriptor. In the classical mechanism of ORR on Pt surfaces, equations 1–4, the transition from *O to *OH is the penultimate reaction step. In the prevalent thermodynamic model, the parameter that determines the rate of ORR is the thermodynamics of the last step, namely the conversion of *OH to water, that is the binding energy of *OH. The weaker this binding, the more free Pt sites will be available for the ORR reaction at a given potential. As mentioned, this descriptor works well when changes in the electronic structure, for instance by alloying, lead to changes in the potential of the *OH ↔ H2O transition28. However, it is important to note that the onset of ORR, say 0.95 VRHE, is in the potential window where the Pt(111) surface is still almost completely covered with the *O adsorbate. One may wonder what exactly this free site is on which ORR should take place, when this *O adsorbate just starts to be reduced to *OH. Also, as the onset of ORR is in the potential window where *O covers the surface, it becomes logical to expect that the rate at which this adsorbate is converted to *OH co-determines the ORR rate. Indeed, DFT calculations by Sakong et al. suggest that there is a competition between step 3 and step 4 for the RDS of ORR, and the energetics of step 3 is sensitive to electrochemical environment53. One could argue that although the final step may be the (main) potential-determining step of the overall reaction, the preceding step can still be partially rate-determining. In general, it is unlikely that only one step in a mechanism fully controls the overall rate54. If we accept that the rate of this step co-determines the overall rate, then it is reasonable that it is related to the rate of the *O ↔ *OH transition observed in the blank voltammetry, in the absence of oxygen. An important assumption here is that the *O ↔ *OH transition observed in the blank voltammetry is the same as the reaction in equation 3 in the ORR mechanism, or at least that these reactions have similar kinetic pathways. It is to be expected that under ORR conditions, the actual *O coverage is higher than in the absence of oxygen in solution, and it may therefore be that the *O intermediate formed during ORR is not exactly the same as the *O formed during the blank voltammetry.
A second important question is why this *O ↔ *OH transition is slow or kinetically irreversible, and why this rate is influenced by the concentration of non-specifically adsorbed anions or cations? First of all, it is important to nuance the term non-specifically adsorbed. We generally consider anions such as perchlorate and methanesulfonate as non-specifically adsorbed because they do not chemically interact with the platinum metal surface. However, there are several reports that have shown that once an *OH adlayer is formed on Pt(111), this induces a weak but distinguishable interaction with perchlorate24,25. A similar statement holds for the effect of cations and their interaction with the *OH layer. Marković et al. have termed this latter interaction non-covalent23. In recent DFT calculations, we have shown that *OH and near-surface cations compete for water solvation, and hence exhibit an indirect (non-covalent) interaction mediated through the interfacial water52. From the results shown in Figs. 2a and 3a, we must conclude that a stronger interaction of the anions or cations with the *OH layer leads to a slower kinetics of the *O ↔ *OH transition. The exact reason for this influence of the anions or cations is not yet clear. Gómez-Marín et al. have performed some limited kinetic measurements of the *OH → *O reaction and provided evidence for nucleation-and-growth type kinetics38. Drnec et al. have provided X-ray-based evidence that the peak at 1.05–1.1 V, that we associate with the formation of *O, involves buckling of the surface to the extent that it may correspond to the onset of (reversible) place exchange, which would then suggest that the *O species may actually be a subsurface species55. Their result implies that subsurface *O (*Osubsurface) might be involved in the ORR mechanism, at least close to the onset potential. In this scenario, step 3 of the ORR mechanism becomes *Osubsurface → *OH, which presumably involves a place exchange process (*Osubsurface → *Osurface) followed by a surface reduction reaction (*Osurface → *OH). If this step becomes (partially) rate-limiting, the rate of ORR can be also indicated by our descriptor. Potentiodynamic impedance spectroscopy results by Bondarenko et al. showed that the structures of the Pt(111)/electrolyte interface in the *O potential region in the absence and presence of ORR, are very similar39. This hypothesis of the involvement of subsurface *Osubsurface in the ORR mechanism, at least at the onset potential, of course requires more direct experimental evidence, in relation to the exact reason for the slow kinetics of the *O/*Osubsurface → *OH transition, including the role of anions. Anions are known to change the interfacial water configuration. Computational work by Eikerling et al. with an explicit water model has shown a strong impact of interfacial water on the energetics of adsorbed oxygen species on Pt(111) surface56,57. Clearly a more detailed study of the kinetics of the *O ↔ *OH transition will be needed to further elucidate the true nature of its slow kinetics. For the purpose of this paper, it suffices to reiterate our key assumption that its kinetics reflects the rate of equation 3 in the ORR mechanism, and this step is at least partially rate-determining in the overall ORR rate. Further microscopic understanding of ORR on Pt is limited by the lack of knowledge on the exact structure of *O reactant in step 3. DFT studies found there co-exists three different *O species on Pt(111) at the on-set potential58. It, however, remains unknown which of these O species is (directly or indirectly) involved in the ORR. Future experimental and computational clarification of this aspect would permit more realistic modelling for this reaction. Finally, our results on the stepped Pt surfaces show that the ORR rates on these surfaces can be understood as the sum or combination of the ORR rates on two different sites: A-type step-related sites and B-type terrace-related (111) sites. The ORR rate on the A sites is dominated by the traditional thermodynamic descriptor, and under acidic conditions, these sites are more active than B sites, and hence the thermodynamic descriptor works well in explaining the activity trends in acid. However, in alkaline solution, cations block the A sites, and render them less active than the B sites. The ORR rate on the B-type (111) sites are dictated by the kinetic descriptor as introduced here. As a result, in alkaline media, Pt(111) is more active than stepped Pt surfaces. This simple model of two different descriptors for the A and B sites solves the paradox of the different ORR activity trends on stepped Pt electrodes in acidic and alkaline conditions.
In conclusion, we have reported here the role of non-specifically adsorbing anions in suppressing the kinetics of ORR on Pt surfaces in acid. This anion effect is rationalized by the proposed descriptor – the reversibility of the *O ↔ *OH transition on the (111) terrace, which is accessible from voltammetry. This descriptor tracks the ORR activity dependences on the concentration/identity of anions, cations and ionomers on Pt surfaces. We have proposed an enhanced model for ORR on the basis of the traditional thermodynamic descriptor and a kinetic descriptor, which rationalizes the different structure sensitivity of ORR activity on Pt surfaces in acid versus alkaline media. Our findings provide a more comprehensive model for ORR on Pt catalysts, which could potentially aid closure of the performance gap between half-cell and MEA measurements by considering the electrolyte effect and improvement of ORR activity using the upgraded ORR model.
Methods
Electrochemical cells and electrolytes
Electrochemical measurements were performed in a glass cell (for all acidic electrolytes) and a fluorinated ethylene propylene electrochemical cell (for all alkaline electrolytes). Prior to each measurement, all cell parts were cleaned by first immersing in a mix solution of H2SO4 (Sigma-Aldrich, 95.0–97.0%) and KMnO4 (Sigma-Aldrich, ≥ 99.0%) overnight, then storing in a mixed solution of H2SO4 and H2O2 (Merck KGaA, 35%) for at least 2 hours, and finally boiling in ultra-high purity water (Merck Milli-Q® IQ 7000, 18.2 MΩ·cm at 298 K) at least five times. Electrolytes were prepared with ultra-high purity water and concentrated perchloric acid (traceSELECT, Fluka), concentrated methanesulfonic acid (Merck KGaA) or concentrated sodium hydroxide (Suprapur, Merck). Either disk- or bead-type platinum single-crystal electrodes were used as working electrodes in the hanging meniscus configuration. A flame-annealed platinum wire and a reversible hydrogen electrode were used as counter and reference electrode, respectively.
Single-crystal electrodes
Single-crystal Pt(111) and stepped electrodes, including Pt(151514), Pt(554) and Pt(553) were prepared by first flame-annealing with butane torches for 2 minutes, then quickly transferring to a cooling cell in an Ar/H2 atmosphere of 3/1 (for Pt(111)) and 1/1 (for stepped Pt surfaces). After cooling to room temperature, the electrodes were dipped and covered with a droplet of ultra-high pure water for protection, before being transferred into the electrochemical cell for measurements. The Nafion coating solution was prepared by diluting commercial Nafion solution (Sigma-Aldrich, 5%) by 1,000 times. The coating solution (10 μl) was then added to the protective water droplet of Pt(111), and subsequently dried in a flow of Ar gas before electrochemistry tests.
Electrochemical measurements
Electrochemical tests were performed on a Biologic VSP-300 potentiostat using a three-electrode system. All potentials are reported against the RHE. The CVs were recorded in Ar-saturated electrolytes between 0.07 V and 0.9 V or between 0.07 V and 1.15 V (for extended CVs) at various scan rates, and reported after iR correction. A minimum scan rate of 10 mV s−1 was chosen to avoid interference from trace amounts of contaminants. A blank CV of Pt(111) was always pre-recorded to assure the cleanliness and reproducibility of testing set-ups. We plotted the charge profile of *OH peak by integrating blank CVs, after double-layer correction. Specifically, we subtracted the lowest current density located at ~0.55 V (chosen as double-layer charging current). For ORR experiments, the single-crystal electrodes were mounted on a commercial rotator (Pine Instruments) as the working electrode. The ORR performances were assessed by recording CVs from 0.1 V to 1 V at 20 mV s−1 in O2-saturated electrolytes at a rotating rate of 1600 rpm, with the positive-going curves being used for activity determination (Supplementary Fig. 1). Kinetic currents were calculated via the Koutecky–Levich equation: Ik = (Ilim × I)/(Ilim − I), where Ilim is the limiting current and I is the measured current at a given potential (either 0.9 or 0.93 V were used in this study). Only polarization curves with Ilim approaching the theoretical value (variation < 5%) were considered to be valid. The specific activity was obtained by normalizing the calculated kinetic current to the corresponding geometric surface area, assuming a roughness factor of 1 for all single-crystal electrodes.
The temperature-dependent measurements were performed by placing the electrochemical cell in a temperature-controlled water bath. A leak-free Ag/AgCl electrode was used as the reference electrode, which was calibrated with hydrogen evolution/oxidation polarization curve of a Pt electrode for each temperature. The calculation method for activation energy follows the work by Paulus et al.59. The ORR overpotential of each temperature was determined from the corresponding measured potential in RHE scale and the reversible H2:O2 cell potential.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Gröger, O., Gasteiger, H. A. & Suchsland, J. P. Review—electromobility: batteries or fuel cells? J. Electrochem. Soc. 162, A2605–A2622 (2015).
Kodama, K., Nagai, T., Kuwaki, A., Jinnouchi, R. & Morimoto, Y. Challenges in applying highly active Pt-based nanostructured catalysts for oxygen reduction reactions to fuel cell vehicles. Nat. Nanotechnol. 16, 140–147 (2021).
Wang, X. X., Swihart, M. T. & Wu, G. Achievements, challenges and perspectives on cathode catalysts in proton exchange membrane fuel cells for transportation. Nat. Catal. 2, 578–589 (2019).
Debe, M. K. Electrocatalyst approaches and challenges for automotive fuel cells. Nature 486, 43–51 (2012).
Fan, J. et al. Bridging the gap between highly active oxygen reduction reaction catalysts and effective catalyst layers for proton exchange membrane fuel cells. Nat. Energy 6, 475–486 (2021).
Stamenkovic, V. R. et al. Improved oxygen reduction activity on Pt3Ni(111) via increased surface site availability. Science 315, 493–497 (2007).
Escudero-Escribano, M. et al. Tuning the activity of Pt alloy electrocatalysts by means of the lanthanide contraction. Science 352, 73–76 (2016).
Strasser, P. et al. Lattice-strain control of the activity in dealloyed core-shell fuel cell catalysts. Nat. Chem. 2, 454–460 (2010).
Bu, L. et al. Biaxially strained PtPb/Pt core/shell nanoplate boosts oxygen reduction catalysis. Science 354, 1410–1414 (2016).
Chen, C. et al. Highly crystalline multimetallic nanoframes with three-dimensional electrocatalytic surfaces. Science 343, 1339–1343 (2014).
Li, M. et al. Ultrafine jagged platinum nanowires enable ultrahigh mass activity for the oxygen reduction reaction. Science 354, 1414–1419 (2016).
Calle-Vallejo, F. et al. Finding optimal surface sites on heterogeneous catalysts by counting nearest neighbors. Science 350, 185–189 (2015).
Stephens, I. E., Rossmeisl, J. & Chorkendorff, I. Toward sustainable fuel cells. Science 354, 1378–1379 (2016).
Kulkarni, A., Siahrostami, S., Patel, A. & Norskov, J. K. Understanding catalytic activity trends in the oxygen reduction reaction. Chem. Rev. 118, 2302–2312 (2018).
Stamenkovic, V. R. et al. Changing the activity of electrocatalysts for oxygen reduction by tuning the surface electronic structure. Angew. Chem. Int. Ed. 45, 2897–2901 (2006).
Nørskov, J. K. et al. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 108, 17886–17892 (2004).
Sakong, S. et al. Influence of local inhomogeneities and the electrochemical environment on the oxygen reduction reaction on Pt-based electrodes: a DFT study. J. Phys. Chem. C. 124, 27604–27613 (2020).
Koper, M. T. M. Theory of multiple proton–electron transfer reactions and its implications for electrocatalysis. Chem. Sci. 4, 2710 (2013).
Pérez-Ramírez, J. & López, N. Strategies to break linear scaling relationships. Nat. Catal. 2, 971–976 (2019).
Strmcnik, D. et al. Improving the hydrogen oxidation reaction rate by promotion of hydroxyl adsorption. Nat. Chem. 5, 300–306 (2013).
McCrum, I. T. & Koper, M. T. M. The role of adsorbed hydroxide in hydrogen evolution reaction kinetics on modified platinum. Nat. Energy 5, 891–899 (2020).
Gasteiger, H. A., Kocha, S. S., Sompalli, B. & Wagner, F. T. Activity benchmarks and requirements for Pt, Pt-alloy, and non-Pt oxygen reduction catalysts for PEMFCs. Appl. Catal. B Environ. 56, 9–35 (2005).
Strmcnik, D. et al. The role of non-covalent interactions in electrocatalytic fuel-cell reactions on platinum. Nat. Chem. 1, 466–472 (2009).
Huang, Y. F., Kooyman, P. J. & Koper, M. T. M. Intermediate stages of electrochemical oxidation of single-crystalline platinum revealed by in situ Raman spectroscopy. Nat. Commun. 7, 12440 (2016).
Attard, G. A., Brew, A., Hunter, K., Sharman, J. & Wright, E. Specific adsorption of perchlorate anions on Pt{hkl} single crystal electrodes. Phys. Chem. Chem. Phys. 16, 13689–13698 (2014).
Marković, N. M., Schmidt, T. J., Stamenkovic, V. & Ross, P. N. Oxygen reduction reaction on Pt and Pt bimetallic surfaces: a selective review. Fuel Cells 1, 105–116 (2001).
Marković, N. M., Gasteiger, H. A., Grgur, B. N. & Ross, P. N. Oxygen reduction reaction on Pt(111): effects of bromide. J. Electroanal. Chem. 467, 157–163 (1999).
Stephens, I. E. L., Bondarenko, A. S., Grønbjerg, U., Rossmeisl, J. & Chorkendorff, I. Understanding the electrocatalysis of oxygen reduction on platinum and its alloys. Energy Environ. Sci. 5, 6744–6762 (2012).
Greeley, J. et al. Alloys of platinum and early transition metals as oxygen reduction electrocatalysts. Nat. Chem. 1, 552–556 (2009).
Bandarenka, A. S., Hansen, H. A., Rossmeisl, J. & Stephens, I. E. Elucidating the activity of stepped Pt single crystals for oxygen reduction. Phys. Chem. Chem. Phys. 16, 13625–13629 (2014).
Gómez-Marín, A. M. & Feliu, J. M. Oxygen reduction on nanostructured platinum surfaces in acidic media: promoting effect of surface steps and ideal response of Pt(111). Catal. Today 244, 172–176 (2015).
Wang, J. X., Markovic, N. M. & Adzic, R. R. Kinetic analysis of oxygen reduction on Pt(111) in acid solutions: intrinsic kinetic parameters and anion adsorption effects. J. Phys. Chem. B 108, 4127–4133 (2004).
Shinagawa, T., Garcia-Esparza, A. T. & Takanabe, K. Insight on Tafel slopes from a microkinetic analysis of aqueous electrocatalysis for energy conversion. Sci. Rep. 5, 13801 (2015).
Koper, M. T. M. Thermodynamic theory of multi-electron transfer reactions: Implications for electrocatalysis. J. Electroanal. Chem. 660, 254–260 (2011).
Gómez–Marín, A. M. & Ticianelli, E. A. A reviewed vision of the oxygen reduction reaction mechanism on Pt-based catalysts. Curr. Opin. Electrochem. 9, 129–136 (2018).
Wakisaka, M., Suzuki, H., Mitsui, S., Uchida, H. & Watanabe, M. Identification and quantification of oxygen species adsorbed on Pt(111) single-crystal and polycrystalline Pt electrodes by photoelectron spectroscopy. Langmuir 25, 1897–1900 (2009).
Casalongue, H. S. et al. Direct observation of the oxygenated species during oxygen reduction on a platinum fuel cell cathode. Nat. Commun. 4, 2817 (2013).
Gómez-Marín, A. M., Clavilier, J. & Feliu, J. M. Sequential Pt(111) oxide formation in perchloric acid: an electrochemical study of surface species inter-conversion. J. Electroanal. Chem. 688, 360–370 (2013).
Bondarenko, A. S. et al. The Pt(111)/electrolyte interface under oxygen reduction reaction conditions: an electrochemical impedance spectroscopy study. Langmuir 27, 2058–2066 (2011).
Stoffelsma, C. et al. Promotion of the oxidation of carbon monoxide at stepped platinum single-crystal electrodes in alkaline media by lithium and beryllium cations. J. Am. Chem. Soc. 132, 16127–16133 (2010).
Strmcnik, D. et al. Effects of Li+, K+, and Ba2+ cations on the ORR at model and high surface area Pt and Au surfaces in alkaline solutions. J. Phys. Chem. Lett. 2, 2733–2736 (2011).
Orfanidi, A., Rheinländer, P. J., Schulte, N. & Gasteiger, H. A. Ink solvent dependence of the ionomer distribution in the catalyst layer of a PEMFC. J. Electrochem. Soc. 165, F1254–F1263 (2018).
Ott, S. et al. Ionomer distribution control in porous carbon-supported catalyst layers for high-power and low Pt-loaded proton exchange membrane fuel cells. Nat. Mater. 19, 77–85 (2020).
Kodama, K. et al. Catalyst poisoning property of sulfonimide acid ionomer on Pt (111) surface. J. Electrochem. Soc. 161, F649–F652 (2014).
Liu, C. et al. Operando X-ray absorption spectroscopic study on the influence of specific adsorption of the sulfo group in the perfluorosulfonic acid ionomer on the oxygen reduction reaction activity of the Pt/C catalyst. ACS Appl. Energy Mater. 4, 1143–1149 (2021).
Banham, D. & Ye, S. Current status and future development of catalyst materials and catalyst layers for proton exchange membrane fuel cells: an industrial perspective. ACS Energy Lett. 2, 629–638 (2017).
Pan, L., Ott, S., Dionigi, F. & Strasser, P. Current challenges related to the deployment of shape-controlled Pt alloy oxygen reduction reaction nanocatalysts into low Pt-loaded cathode layers of proton exchange membrane fuel cells. Curr. Opin. Electrochem. 18, 61–71 (2019).
Climent, V. & Feliu, J. M. in Nanopatterned and Nanoparticle-Modified Electrodes, Advances in Electrochemical Science and Engineering. (eds R.C. Alkire, P.N. Bartlett, J. Lipkowski) 1–49 (John Wiley & Sons, 2017).
Hoshi, N., Nakamura, M. & Hitotsuyanagi, A. Active sites for the oxygen reduction reaction on the high index planes of Pt. Electrochim. Acta 112, 899–904 (2013).
Calle-Vallejo, F. et al. Why conclusions from platinum model surfaces do not necessarily lead to enhanced nanoparticle catalysts for the oxygen reduction reaction. Chem. Sci. 8, 2283–2289 (2017).
Rizo, R., Herrero, E. & Feliu, J. M. Oxygen reduction reaction on stepped platinum surfaces in alkaline media. Phys. Chem. Chem. Phys. 15, 15416–15425 (2013).
McCrum, I. T., Chen, X., Schwarz, K. A., Janik, M. J. & Koper, M. T. M. Effect of step density and orientation on the apparent pH dependence of hydrogen and hydroxide adsorption on stepped platinum surfaces. J. Phys. Chem. C. 122, 16756–16764 (2018).
Sakong, S. et al. Influence of local inhomogeneities and the electrochemical environment on the oxygen reduction reaction on Pt-based electrodes: a DFT study. J. Phys. Chem. C. 124, 27604–27613 (2020).
Campbell, C. T. The degree of rate control: a powerful tool for catalysis research. ACS Catal. 7, 2770–2779 (2017).
Drnec, J. et al. Initial stages of Pt(111) electrooxidation: dynamic and structural studies by surface X-ray diffraction. Electrochim. Acta 224, 220–227 (2017).
Malek, A. & Eikerling, M. H. Chemisorbed oxygen at Pt(111): a DFT study of structural and electronic surface properties. Electrocatalysis 9, 370–379 (2018).
Eslamibidgoli, M. & Eikerling, M. H. Electrochemical formation of reactive oxygen species at Pt (111)—a density functional theory study. ACS Catal. 5, 6090–6098 (2015).
Eslamibidgoli, M. J. & Eikerling, M. H. Atomistic mechanism of Pt extraction at oxidized surfaces: insights from DFT. Electrocatalysis 7, 345–354 (2016).
Paulus, U. A., Schmidt, T. J., Gasteiger, H. A. & Behm, R. J. Oxygen reduction on a high-surface area Pt/Vulcan carbon catalyst: a thin-film rotating ring-disk electrode study. J. Electroanal. Chem. 495, 134–145 (2001).
Acknowledgements
This project received funding from the European Commission Horizon 2020—Research and Innovation Framework Programme (Marie Skłodowska-Curie actions Individual Fellowship awarded to M.L., No. 897818).
Author information
Authors and Affiliations
Contributions
M.L. and M.T.M.K. designed the experimental plan. M.L. carried out the experiments and data analysis. M.L. and M.T.M.K. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Catalysis thanks Olaf Magnussen and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–9, and Tables 1 and 2.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Luo, M., Koper, M.T.M. A kinetic descriptor for the electrolyte effect on the oxygen reduction kinetics on Pt(111). Nat Catal 5, 615–623 (2022). https://doi.org/10.1038/s41929-022-00810-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41929-022-00810-6
This article is cited by
-
Materials descriptors of machine learning to boost development of lithium-ion batteries
Nano Convergence (2024)
-
Direct measurement of the oxygen reduction reaction kinetics on iron phthalocyanine using advanced transient voltammetry
Nature Catalysis (2024)
-
Exploring the Cation Regulation Mechanism for Interfacial Water Involved in the Hydrogen Evolution Reaction by In Situ Raman Spectroscopy
Nano-Micro Letters (2024)
-
Key role of electron accessibility at the noble metal-free catalytic interface in hydrogen evolution reaction
Nano Research (2024)
-
Precise synthetic control of exclusive ligand effect boosts oxygen reduction catalysis
Nature Communications (2023)