Abstract
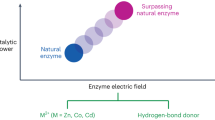
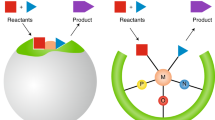
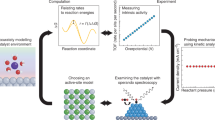
Although the ubiquitous role that long-ranged electric fields play in catalysis has been recognized, it is seldom used as a primary design parameter in the discovery of new catalytic materials. Here we illustrate how electric fields have been used to computationally optimize biocatalytic performance of a synthetic enzyme, and how they could be used as a unifying descriptor for catalytic design across a range of homogeneous and heterogeneous catalysts. Although focusing on electrostatic environmental effects may open new routes toward the rational optimization of efficient catalysts, much more predictive capacity is required of theoretical methods to have a transformative impact in their computational design — and thus experimental relevance — when using electric field alignments in the reactive centres of complex catalytic systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
27 September 2018
In the version of this Perspective originally published, there were errors in equation (1) and the sentence immediately following it, as well as in Fig. 1; the details are shown in the correction notice. These errors have now been corrected.
References
Calabrese Barton, S., Gallaway, J. & Atanassov, P. Enzymatic biofuel cells for implantable and microscale devices. Chem. Rev. 104, 4867–4886 (2004).
Wei, H. & Wang, E. Nanomaterials with enzyme-like characteristics (nanozymes): next-generation artificial enzymes. Chem. Soc. Rev. 42, 6060–6093 (2013).
Kandemir, T., Schuster, M. E., Senyshyn, A., Behrens, M. & Schlogl, R. The Haber–Bosch process revisited: on the real structure and stability of “ammonia iron” under working conditions. Angew. Chem. 52, 12723–12726 (2013).
Parida, B., Iniyan, S. & Goic, R. A review of solar photovoltaic technologies. Renew. Sust. Ener. Rev 15, 1625–1636 (2011).
Warshel, A. Energetics of enzyme catalysis. Proc. Natl Acad. Sci. USA 75, 5250–5254 (1978).
Jindal, G. & Warshel, A. Misunderstanding the preorganization concept can lead to confusions about the origin of enzyme catalysis. Proteins 85, 2157–2161 (2017).
Shaik, S., Mandal, D. & Ramanan, R. Oriented electric fields as future smart reagents in chemistry. Nat. Chem 8, 1091–1098 (2016).
Bhowmick, A., Sharma, S. C. & Head-Gordon, T. The importance of the scaffold for de novo enzymes: a case study with kemp eliminase. J. Am. Chem. Soc. 139, 5793–5800 (2017).
Liu, C. T. et al. Probing the electrostatics of active site microenvironments along the catalytic cycle for Escherichia coli dihydrofolate reductase. J. Am. Chem. Soc. 136, 10349–10360 (2014).
Reppert, M. & Tokmakoff, A. Computational amide I 2D IR spectroscopy as a probe of protein structure and dynamics. Ann. Rev. Phys. Chem 67, 359–386 (2016).
Pollack, R. M. Enzymatic mechanisms for catalysis of enolization: ketosteroid isomerase. Bioorg. Chem. 32, 341–353 (2004).
Kamerlin, S. C., Sharma, P. K., Chu, Z. T. & Warshel, A. Ketosteroid isomerase provides further support for the idea that enzymes work by electrostatic preorganization. Proc. Natl Acad. Sci. USA 107, 4075–4080 (2010).
Fried, S. D., Bagchi, S. & Boxer, S. G. Extreme electric fields power catalysis in the active site of ketosteroid isomerase. Science 346, 1510–1514 (2014).
Chen, D. & Savidge, T. BIOPHYSICS. Comment on “Extreme electric fields power catalysis in the active site of ketosteroid isomerase”. Science 349, 936 (2015).
Natarajan, A. et al. BIOPHYSICS. Comment on “Extreme electric fields power catalysis in the active site of ketosteroid isomerase”. Science 349, 936 (2015).
Wang, L., Fried, S. D. & Markland, T. E. Proton network flexibility enables robustness and large electric fields in the ketosteroid isomerase active site. J. Phys. Chem. B 121, 9807–9815 (2017).
Baker, D. An exciting but challenging road ahead for computational enzyme design. Protein Sci. 19, 1817–1819 (2010).
Korendovych, I. V. & DeGrado, W. F. Catalytic efficiency of designed catalytic proteins. Curr. Opin. Struct. Bio 27, 113–121 (2014).
Jindal, G., Ramachandran, B., Bora, R. P. & Warshel, A. Exploring the development of ground-state destabilization and transition-state stabilization in two directed evolution paths of kemp eliminases. ACS Catal 7, 3301–3305 (2017).
Frushicheva, M. P., Cao, J., Chu, Z. T. & Warshel, A. Exploring challenges in rational enzyme design by simulating the catalysis in artificial kemp eliminase. Proc. Natl Acad. Sci. USA 107, 16869–16874 (2010).
Labas, A., Szabo, E., Mones, L. & Fuxreiter, M. Optimization of reorganization energy drives evolution of the designed Kemp eliminase KE07. Biochim. Biophys. Acta 1834, 908–917 (2013).
Vaissier, V., Sharma, S. C., Schaettle, K., Zhang, T. & Head-Gordon, T. Computational optimization of electric fields for improving catalysis of a designed kemp eliminase. ACS Catal 8, 219–227 (2017).
Breiner, B., Clegg, J. K. & Nitschke, J. R. Reactivity modulation in container molecules. Chem. Sci 2, 51–56 (2011).
Mansoor, E., Mynsbrugge, J. Vd, Head-Gordon, M. & Bell, A. T. Impact of long-range electrostatic and dispersive interactions on theoretical predictions of adsorption and catalysis in zeolites. Catal. Today 312, 51–65 (2018).
Csicsery, S. M. Shape-selective catalysis in zeolites. Zeolites 4, 202–213 (1984).
Deshlahra, P. & Iglesia, E. Toward more complete descriptors of reactivity in catalysis by solid acids. ACS Catal 6, 5386–5392 (2016).
Dusselier, M., Van Wouwe, P., Dewaele, A., Jacobs, P. A. & Sels, B. F. GREEN CHEMISTRY. Shape-selective zeolite catalysis for bioplastics production. Science 349, 78–80 (2015).
Gorin, C. F., Beh, E. S. & Kanan, M. W. An electric field-induced change in the selectivity of a metal oxide-catalyzed epoxide rearrangement. J. Am. Chem. Soc. 134, 186–189 (2012).
Kaphan, D. M., Toste, F. D., Bergman, R. G. & Raymond, K. N. enabling new modes of reactivity via constrictive binding in a supramolecular-assembly-catalyzed aza-prins cyclization. J. Am. Chem. Soc. 137, 9202–9205 (2015).
Levin, M. D. et al. Scope and mechanism of cooperativity at the intersection of organometallic and supramolecular catalysis. J. Am. Chem. Soc. 138, 9682–9693 (2016).
Frushicheva, M. P., Mukherjee, S. & Warshel, A. Electrostatic origin of the catalytic effect of a supramolecular host catalyst. J. Phys. Chem. B 116, 13353–13360 (2012).
Mardirossian, N. & Head-Gordon, M. Mapping the genome of meta-generalized gradient approximation density functionals: The search for B97M.-V. J. Chem. Phys. 142, 074111 (2015).
Mardirossian, N. et al. Use of the rVV10 nonlocal correlation functional in the B97M-V density functional: defining B97M-rV and related functionals. J. Phys. Chem. Lett. 8, 35–40 (2017).
Pacchioni, G., Lomas, J. R. & Illas, F. Electric field effects in heterogeneous catalysis. J. Mol. Catal. A 119, 263–273 (1997).
Lee, V. J. Heterogeneous catalysis: effect of an alternating electric field. Science 152, 514 (1966).
Simons, R. Strong electric field effects on proton transfer between membrane-bound amines and water. Nature 280, 824–826 (1979).
Chen, L. D., Urushihara, M., Chan, K. & Nørskov, J. K. Electric field effects in electrochemical CO2 Reduction. ACS Catal 6, 7133–7139 (2016).
Liu, M. et al. Enhanced electrocatalytic CO2 reduction via field-induced reagent concentration. Nature 537, 382–386 (2016).
Sorenson, S. A., Patrow, J. G. & Dawlaty, J. M. Solvation reaction field at the interface measured by vibrational sum frequency generation spectroscopy. J. Am. Chem. Soc. 139, 2369–2378 (2017).
Patrow, J. G., Sorenson, S. A. & Dawlaty, J. M. Direct spectroscopic measurement of interfacial electric fields near an electrode under polarizing or current-carrying conditions. J. Phys. Chem. C 121, 11585–11592 (2017).
Aragones, A. C. et al. Electrostatic catalysis of a Diels–Alder reaction. Nature 531, 88–91 (2016).
Akamatsu, M., Sakai, N. & Matile, S. Electric-field-assisted anion–π catalysis. J. Am. Chem. Soc. 139, 6558–6561 (2017).
Copéret, C., Chabanas, M., Saint‐Arroman, R. P. & Basset, J. M. Homogeneous and heterogeneous catalysis: bridging the gap through surface organometallic chemistry. Angew. Chem. Int. Ed. 42, 156–181 (2003).
Alemani, M. et al. Electric field-induced isomerization of azobenzene by STM. J. Am. Chem. Soc. 128, 14446–14447 (2006).
Rideout, D. C. & Breslow, R. Hydrophobic acceleration of Diels–Alder reactions. J. Am. Chem. Soc. 102, 7816–7817 (1980).
Korzenski, M. B. & Kolis, J. W. Diels–Alder reactions using supercritical water as an aqueous solvent medium. Tetrahedron Lett. 38, 5611–5614 (1997).
Acevedo, O., Jorgensen, W. L. & Evanseck, J. D. Elucidation of rate variations for a Diels–Alder reaction in ionic liquids from QM/MM simulations. J. Chem. Theory Comput. 3, 132–138 (2007).
Harano, Y., Sato, H. & Hirata, F. Solvent effects on a Diels−Alder reaction in supercritical water: RISM-SCF Study. J. Am. Chem. Soc. 122, 2289–2293 (2000).
Dinpajooh, M. & Matyushov, D. V. Dielectric constant of water in the interface. J. Chem. Phys. 145, 014504 (2016).
Zhang, C., Gygi, F. & Galli, G. Strongly anisotropic dielectric relaxation of water at the nanoscale. J. Phys. Chem. Lett. 4, 2477–2481 (2013).
Sobrino Fernández, M., Peeters, F. M. & Neek-Amal, M. Electric-field-induced structural changes in water confined between two graphene layers. Phys. Rev. B 94, 045436 (2016).
Muñoz-Santiburcio, D. & Marx, D. Nanoconfinement in slit pores enhances water self-dissociation. Phys. Rev. Lett. 119, 056002 (2017).
Ruiz Pestana, L., Felberg, L. E. & Head-Gordon, T. Coexistence of multilayered phases of confined water: the importance of flexible confining surfaces. ACS Nano 12, 448–454 (2018).
Sundararaman, R. & Schwarz, K. Evaluating continuum solvation models for the electrode–electrolyte interface: challenges and strategies for improvement. J. Chem. Phys. 146, 084111 (2017).
Hansen, H. A., Viswanathan, V. & Nørskov, J. K. Unifying kinetic and thermodynamic analysis of 2e– and 4e– reduction of oxygen on metal surfaces. J. Phys. Chem. C 118, 6706–6718 (2014).
Sundararaman, R., Schwarz, K. A., Letchworth-Weaver, K. & Arias, T. A. Spicing up continuum solvation models with SaLSA: the spherically averaged liquid susceptibility ansatz. J. Chem. Phys. 142, 054102 (2015).
Cox, S. J. & Geissler, P. L. Interfacial ion solvation: obtaining the thermodynamic limit from molecular simulations. Preprint at https://arxiv.org/abs/1801.00810 (2018).
Jinnouchi, R. & Anderson, A. B. Electronic structure calculations of liquid–solid interfaces: combination of density functional theory and modified Poisson–Boltzmann theory. Phys. Rev. B 77, 245417 (2008).
Fried, S. D. & Boxer, S. G. Electric fields and enzyme catalysis. Ann. Rev. Biochem 86, 387–415 (2017).
Ruiz Pestana, L., Mardirossian, N., Head-Gordon, M. & Head-Gordon, T. Ab initio molecular dynamics simulations of liquid water using high quality meta-GGA functionals. Chem. Sci 8, 3554–3565 (2017).
Mardirossian, N. & Head-Gordon, M. Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals. Mol. Phys. 115, 2315–2372 (2017).
Dziedzic, J. et al. TINKTEP: a fully self-consistent, mutually polarizable QM/MM approach based on the AMOEBA force field. J. Chem. Phys. 145, 124106 (2016).
Mao, Y. et al. Performance of the AMOEBA water model in the vicinity of QM solutes: a diagnosis using energy decomposition analysis. J. Chem. Theory Comput. 13, 1963–1979 (2017).
Sauer, J. & Freund, H.-J. Models in catalysis. Catal. Lett. 145, 109–125 (2014).
Piccini, G., Alessio, M. & Sauer, J. Ab Initio calculation of rate constants for molecule–surface reactions with chemical accuracy. Angew. Chem. 55, 5235–5237 (2016).
Vaissier, V. & Van Voorhis, T. Quantum chemical approaches to [NiFe] hydrogenase. Essays Biochem. 61, 293–303 (2017).
Dong, G. & Ryde, U. Protonation states of intermediates in the reaction mechanism of [NiFe] hydrogenase studied by computational methods. J. Biolog. Inorg. Chem. 21, 383–394 (2016).
Ghosh, S., Castillo-Lora, J., Soudackov, A. V., Mayer, J. M. & Hammes-Schiffer, S. Theoretical insights into proton-coupled electron transfer from a photoreduced ZnO nanocrystal to an organic radical. Nano Lett. 17, 5762–5767 (2017).
Olsson, M. H. M., Siegbahn, P. E. M. & Warshel, A. Simulations of the large kinetic isotope effect and the temperature dependence of the hydrogen atom transfer in lipoxygenase. J. Am. Chem. Soc. 126, 2820–2828 (2004).
Marsalek, O. & Markland, T. E. Ab initio molecular dynamics with nuclear quantum effects at classical cost: ring polymer contraction for density functional theory. J. Chem. Phys. 144, 054112 (2016).
Ghosh, S., Soudackov, A. V. & Hammes-Schiffer, S. Role of Proton Diffusion in the nonexponential kinetics of proton-coupled electron transfer from photoreduced ZnO nanocrystals. ACS Nano 11, 10295–10302 (2017).
Ribeiro, A. J. M., Santos-Martins, D., Russo, N., Ramos, M. J. & Fernandes, P. A. Enzymatic flexibility and reaction rate: a QM/MM study of HIV-1 protease. ACS Catal 5, 5617–5626 (2015).
Limmer, D. T. & Willard, A. P. Nanoscale heterogeneity at the aqueous electrolyte–electrode interface. Chem. Phys. Lett. 620, 144–150 (2015).
Albaugh, A., Niklasson, A. M. N. & Head-Gordon, T. Accurate classical polarization solution with no self-consistent field iterations. J. Phys. Chem. Lett. 8, 1714–1723 (2017).
Margul, D. T. & Tuckerman, M. E. A stochastic, resonance-free multiple time-step algorithm for polarizable models that permits very large time steps. J. Chem. Theory Comput. 12, 2170–2180 (2016).
Vitale, V. et al. Performance of extended Lagrangian schemes for molecular dynamics simulations with classical polarizable force fields and density functional theory. J. Chem. Phys. 146, 124115 (2017).
Frenzel, J., Meyer, B. & Marx, D. Bicanonical ab initio molecular dynamics for open systems. J. Chem. Theory Comput. 13, 3455–3469 (2017).
Cheng, T., Xiao, H. & Goddard, W. A. Full atomistic reaction mechanism with kinetics for CO reduction on Cu(100) from ab initio molecular dynamics free-energy calculations at 298 K. Proc. Natl Acad. Sci. USA 114, 1795 (2017).
Bhowmick, A., Sharma, S. C., Honma, H. & Head-Gordon, T. The role of side chain entropy and mutual information for improving the de novo design of Kemp eliminases KE07 and KE70. Phys. Chem. Chem. Phys. 18, 19386–19396 (2016).
Chen, X. et al. The formation time of Ti–O• and Ti–O•–Ti radicals at the n-SrTiO3/aqueous interface during photocatalytic water oxidation. J. Am. Chem. Soc. 139, 1830–1841 (2017).
Acknowledgements
The catalysis application supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division under Contract no. DE-AC02-05CH11231. The material on theory and methods is based upon work supported by the US Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Scientific Discovery through Advanced Computing (SciDAC) program. This research received a 2017 ASCR Leadership Computing Challenge (ALCC) allocation at the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the US Department of Energy under Contract no. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
T.H.G. conceived the theme, V.V. and T.H.G. wrote the manuscript, and V.V. and L.R.P. designed the figures and the graphical abstract image. All authors contributed data and insights, discussed the Perspective and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Welborn, V.V., Ruiz Pestana, L. & Head-Gordon, T. Computational optimization of electric fields for better catalysis design. Nat Catal 1, 649–655 (2018). https://doi.org/10.1038/s41929-018-0109-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41929-018-0109-2
This article is cited by
-
Nanocurvature-induced field effects enable control over the activity of single-atom electrocatalysts
Nature Communications (2024)
-
Enhanced active-site electric field accelerates enzyme catalysis
Nature Chemistry (2023)
-
Positive direction of polarization-induced electric field improves formic acid electrooxidation on Pd
Nano Research (2023)
-
Electrostatics advancing green catalysis events
Science China Chemistry (2023)
-
A catastrophe theory-based model for optimal control of chemical reactions by means of oriented electric fields
Theoretical Chemistry Accounts (2023)