Main

Acoustoelectric interactions of propagating phonons and electrons lead to the non-reciprocal amplification of radio-frequency (RF) acoustic waves1,2,3. This has the potential to allow the piezoelectric acoustic wave devices that are currently used as filters in radios to also be used as amplifiers, as well as enable important functionalities, such as isolation and circulation, to be achieved on the same chip. Current technology typically co-packages piezoelectric acoustic filters with semiconductor-based amplifiers and, less frequently, gyromagnetic non-reciprocal devices. Therefore, combining the filtering, amplifying, and non-reciprocal functions into a single device architecture could provide considerable miniaturization, given the small feature sizes of acoustic wavelength-scale structures at microwave frequencies. However, creating a non-reciprocal acoustoelectric amplifier that continuously operates at gigahertz frequencies and produces a net (terminal) gain—that is, more gain than insertion loss—remains a challenge. This is due to a range of issues, including weak interactions between the piezoelectric acoustic wave and semiconductor carriers4,5,6, poor thermal conductivity causing deleterious heating effects,7,8,9,10,11 and the difficulty of integrating high-quality semiconductor materials with strongly piezoelectric materials such as lithium niobate (LiNbO3) (refs. 12,13,14).

In this Article, we report an amplifier architecture that is based on an acoustoelectric heterostructure consisting of an ultrathin compound semiconductor (indium gallium arsenide (In0.53Ga0.47As)) with low electrical conductivity (σ) and high mobility (μ), a strongly piezoelectric thin film (LiNbO3) directly underneath the semiconductor, and a substrate (silicon) chosen to have multiple beneficial properties. The substrate enhances the confinement of phonons in the thin piezoelectric film, provides a high-thermal-conductance medium for the removal of dissipated heat, and offers low dielectric RF loss. We use this approach to create a 500-µm-long, non-reciprocal acoustoelectric delay line amplifier with 28.0 dB of acoustic gain (4.0 dB net RF gain) for 1 GHz phonons, continuously operating while dissipating 40.5 mW of d.c. power. Moreover, the acoustic noise figure at 1 GHz is 2.8 dB, and the non-reciprocal transmission is 41.0 dB. At a different operating point of the same device, an acoustic gain of 30.5 dB is achieved (6.5 dB net gain) with a d.c. power dissipation of 65 mW, an acoustic noise figure of 4.0 dB, and a non-reciprocal transmission of more than 44 dB.

Additional devices are characterized with subsets of performance characteristics that exceed this device, including one with an acoustic gain of 37.0 dB (net gain of 11.3 dB) for 1 GHz phonons with 19.6 mW of d.c. power dissipation and non-reciprocal transmission of more than 55 dB. We also use several devices with non-overlapping transducer bandwidths to show that our heterostructure, with a single-film stack, supports a maximum gain slope that peaks at 1.3 dB V–1 at approximately 1 GHz, and maintains a value of 0.5 dB V–1 or greater over a bandwidth that exceeds 3 GHz. Together with the recent development of acoustoelectric circulators and switches9,15,16, our devices provide a route to all-acoustic RF signal processing front ends that can be fabricated on a single chip, which could lead to higher performance and miniaturization of RF systems.

Acoustoelectric heterostructure

A schematic of a general three-layer heterostructure that provides high-performance acoustic wave amplification is shown in Fig. 1a. We focus on a specific implementation with an In0.53Ga0.47As semiconducting layer, a LiNbO3 piezoelectric film, and a silicon substrate. An illustration of the acoustoelectric effect, which occurs when semiconductor charge carriers interact with a piezoelectric acoustic wave, is shown in Fig. 1b. In the heterostructure reported here, the interaction occurs between the evanescent longitudinal electric field of the piezoelectric acoustic wave that penetrates the semiconducting film and the charge carriers therein. A finite element method model of the longitudinal electric field of the guided piezoelectric acoustic wave with primarily shear-horizontal (SH) acoustic polarization in the In0.53Ga0.47As–LiNbO3–silicon heterostructure is shown in Fig. 1c. As shown by the modelled displacement in Supplementary Note 1, this is a guided SH0-like mode17. The evanescent overlap between the longitudinal electric field in LiNbO3 and 50-nm-thick In0.53Ga0.47As semiconductor layer enables the acoustoelectric effect in this material stack.

Fig. 1: Material platform overview.
figure 1

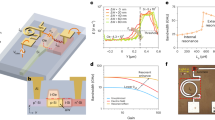
a,b, Schematic of a three-layer heterostructure supporting high-performance active acoustic wave devices based on the acoustoelectric effect (a) and schematic of the interaction between the semiconductor charge carriers and piezoelectric acoustic wave (b). c, Longitudinal electric field (Ex) model in our material stack of an In0.53Ga0.47As semiconducting film on a Y-cut LiNbO3 piezoelectric film on bulk silicon. The black arrows indicate material displacement. The acoustic wavelength (Λ) is 3.75 μm, the LiNbO3 thickness is 5 μm, and the In0.53Ga0.47As thickness is 50 nm. d, Camera image of the heterostructure wafer after processing. e, Optical micrograph of a fabricated acoustic wave amplifier. f, Scanning electron micrograph showing additional details of the IDT, amplifier layer, and mesa contact structure.

Full size image

An image of the fabricated heterostructure wafer with acoustic wave amplifiers and delay lines is shown in Fig. 1d. These devices are fabricated using a microfabrication process that is described in detail in the Methods. Wafer bonding provides an intimate contact between LiNbO3 and In0.53Ga0.47As. The interdigital transducer (IDT) launches and receives acoustic waves, whereas a quasi-ohmic electrical contact is made to the In0.53Ga0.47As amplifier layer via a mesa contact structure. The mesa contact comprises a silver/gold electrode layer on an epitaxial contact heterostructure that provides vertically graded doping from the highly insulating amplifier layer to the metal. An optical micrograph of an acoustic wave amplifier is shown in Fig. 1e, and a scanning electron micrograph showing the IDT, mesa contact structure, and amplifier layer is shown in Fig. 1f.

With this heterostructure approach, there is increased flexibility to tailor the material parameters of each layer, which allows us to realize large gain in a small device footprint and simultaneously achieve low dissipated power and noise figure. We select In0.53Ga0.47As for the semiconductor layer because it has a high bulk μ of 10,000 cm2 V–1 s–1 and can be grown by metal–organic chemical vapour deposition within an In0.53Ga0.47As/indium phosphide (InP) lattice-matched stack with controllable thickness and doping as well as with low defectivity18. We show here that even for a thin layer (~50 nm) in an acoustoelectric heterostructure, the μ value of In0.53Ga0.47As can exceed 4,000 cm2 V–1 s–1. This semiconducting material is also able to bond to LiNbO3 using a 5 nm InP non-intentionally doped intermediary layer, which prevents any degradation of device performance on account of being highly insulating and 1/1,000th the acoustic wavelength. We select LiNbO3 as the piezoelectric layer because, as we report here, electromechanical coupling coefficients (k2) exceeding 10% and low acoustic loss can be achieved in Y-cut LiNbO3 films on silicon for a specially chosen acoustic mode with primarily SH polarization. Silicon is used as the substrate material due to its more than 30 times larger thermal conductivity compared with bulk LiNbO3 (refs. 19, 20). The higher thermal conductivity greatly contributes to our acoustic wave amplifier’s ability to run with a continuously applied drift field and achieving terminal gain. In addition, the high acoustic velocity in silicon supports a guided acoustic wave in the LiNbO3 film and silicon substrates can be made with high resistivity (>10 kΩ), which enables low RF dielectric loss that can cause excess loss for piezoelectric acoustic waves propagating in LiNbO3.

Gain and noise figure of acoustic wave amplifier

A three-layer acoustoelectric heterostructure can be used to develop high-performance acoustic wave amplifiers by optimizing the most critical material parameters for device operation. We characterize acoustic wave amplifiers in terms of their gain, noise figure, and other performance characteristics. Using an amplifier with the lowest possible metal–semiconductor contact resistance (which gives the most accurate measurements), we explore how improving individual critical performance characteristics affects the device properties and discuss how to approach the heterostructure design to achieve an even larger gain with a smaller footprint, power dissipation, and noise figure in a single device. Figure 2 shows the characterization of gain, isolation, and noise figure for an amplifying delay line, analogous to that shown in Fig. 1e, with a length of 500 μm, an IDT resonance frequency of approximately 1 GHz, and an IDT aperture of 56 μm.

Fig. 2: Characterization of acoustic wave amplifier.
figure 2

a, Terminal gain as a function of frequency for increasing drift field values with an RF input power of −30 dBm. A terminal gain of 6.5 dB is achieved at 1.01 GHz. For this device, the length is 500 μm, the acoustic wavelength is 3.75 μm, the IDT aperture is 56 μm, and each IDT has ten electrode pairs. b, Values of S21 and S12 plotted as a function of drift field. A non-reciprocal transmission of >44 dB is achieved at a drift field of 1 kV cm–1. The modelled transmission is shown with the dashed red (S21) and black (S12) lines. c, Acoustic output power as a function of acoustic input power. The inset shows the power efficiency η as a function of acoustic input power. The measured noise figure is shown in d as a function of acoustic and terminal gain. We demonstrate a minimum acoustic noise figure of 2.8 ± 0.5 dB at 28.0 dB of acoustic gain in this device. Data are presented as mean values ± one standard deviation for the acoustic noise figure. These values are determined via the propagation of measurement error from three consecutive measurements for a single device (Supplementary Note 4).

Full size image

A plot of the measured terminal gain as a function of frequency for increasing drift fields is shown in Fig. 2a. A terminal gain of 6.5 dB is achieved at a frequency of 1.01 GHz and a drift field of 1 kV cm–1 (50 V applied across 500 μm). The technique and experimental setup for the gain measurements are described in the Methods. Terminal gain is achieved only when the gain exceeds the total end-to-end losses across the device, including the losses from the IDTs, propagation losses, and losses due to acoustoelectric effect in the unbiased case. The semiconductor and electromechanical properties of the heterostructure are as follows: a semiconductor thickness of 58 nm, µ of 4,220 cm2 V–1 s–1, and k2 of 14% (Methods). Potential physical mechanisms leading to gain ripples, which become more evident at higher gain, as well as the apparent frequency shift in the off-resonance gain at a drift field of 1 kV cm–1, are discussed in Supplementary Note 1.

Figure 2b shows a plot of the measured S21 and S12 values as a function of the drift field for charge carriers. The transmission difference exceeds 44 dB between the forward- and backward-propagating acoustic waves at a drift field of 1 kV cm–1, demonstrating an extremely high degree of non-reciprocity for transmission. This device was not measured past a drift field of 1 kV cm–1, as the S21 plateau (Fig. 2b) indicates an onset of thermal effects that can cause measurement instabilities, and ultimately, thermal runaway that leads to device destruction. Figure 2b also shows the modelled transmission based on an acoustoelectric equivalent circuit model (Supplementary Note 2)21. The model accurately predicts the measured terminal gain (S21) below a drift field of 1 kV cm–1; the onset of substantial self-heating ultimately causes the gain to deviate from theoretical predictions and prohibits operating at the maximum gain. As shown in Fig. 2b, if the measured gain followed the predicted behaviour, then >15 dB of terminal gain would be achieved at a drift field of 1 kV cm–1 in this device. The measured isolation (S12) deviates substantially from the modelled values. At a drift field of 1 kV cm–1, the measured isolation is 37.9 dB, whereas the predicted value is >70 dB. The experimentally achieved isolation for the backward-propagating acoustic wave is likely to be limited due to the excitation of additional acoustic modes with lower k2 values (Supplementary Note 1), which will only be weakly amplified or attenuated with an applied bias and lead to a constant background. Additional optimization of the material stack and device layout is likely to reduce the effect of these modes and therefore lead to even larger non-reciprocal transmission.

Figure 2c shows a plot of the acoustic output power as a function of acoustic input power (Methods shows the experimental details). The measured gain is approximately independent of the acoustic input power up to an acoustic input power of −30 dBm, where it reaches a compression of approximately 1 dB. As described in Supplementary Note 3, we also evaluate the gain compression for an acoustoelectric amplifier operating at 250 MHz. A gain compression of 1.0 dB is observed at an acoustic input power of 1 dBm when operating at the maximum bias, corresponding to an acoustic gain of 12.5 dB. As with all amplifiers, a tradeoff is expected between the saturation output power and maximum gain; in the case of acoustoelectric amplifiers, the physical mechanism is related to the total number of carriers that can participate in the amplification process, and higher carrier concentrations are expected to increase the saturation output power and reduce the maximum gain for a given applied electric field. Future work will explore this tradeoff and attempt to find device characteristics that allow for the creation of high saturation output powers with lower gain (that is, a power amplifier). Additional improvements to thermal management could also allow these devices to operate with higher saturation output power. We also consider the d.c.-to-acoustic power conversion efficiency. Figure 2c (inset) shows a plot of power efficiency η as a function of acoustic input power. Here the power efficiency (in percent) is defined as η = 100 × (PA,OUT)/(Pd.c.,IN), where PA,OUT is the acoustic output power and Pd.c.,IN is the input d.c. power. At an acoustic input power of −1 dBm, we achieve an acoustic output power of 9.6 dBm and efficiency of 14%. One way to further improve η would be to utilize acoustic waveguiding to reduce the semiconductor width, which would lower d.c. power dissipation without reducing gain. This approach requires acoustic focusing22,23 and will be explored in future work. Reducing acoustic propagation losses will also result in a larger acoustic output power and therefore increased η.

A plot of the acoustic noise figure as a function of acoustic and terminal gain is shown in Fig. 2d. Also, the corresponding RF terminal noise figure is shown, including the impact of IDTs that are lossy and thus substantially increase the noise figure of the system. The noise figure was measured by turning a calibrated noise source on and off and assessing the change in the measured noise power on a spectrum analyser. This approach is commonly known as the Y-factor method and is described in more detail in the Methods. An acoustic noise figure of 2.8 ± 0.5 dB is achieved at 1.01 GHz with an acoustic gain of 28.0 dB. We determined the standard deviation for the acoustic noise figure by assessing error propagation in our measurement (Supplementary Note 4). The corresponding RF terminal noise figure is 13.75 dB and is limited by the IDT losses. A comparison of our measured noise figure with an acoustoelectric noise model based on isothermal diffusive processes7 indicates that our minimum noise figure deviates from the isothermal model. This is attributable to Joule heating and the resulting thermal instabilities, as further evidenced by the sudden increase in noise figure at high drift field (Fig. 2d) that also corresponds to the drift field at which the gain becomes unstable. There are several paths forward to mitigate this effect, as discussed in the following section. However, one simple approach is to reduce the semiconductor conductivity σ by lowering the amplifier-layer doping concentration, which will lower the dissipated power required to achieve terminal gain. We anticipate that if thermal effects are mitigated, the next dominant source of noise will be diffusion effects from semiconductor traps. As mentioned above, a theoretical treatment for the noise figure for an acoustoelectric amplifier including the impact of semiconductor traps has already been developed7 based on the impedance field method together with normal mode theory24 (Supplementary Note 5). This theoretical model suggests that it is possible to reduce our acoustic noise figure in this heterostructure to below 1 dB. Lower IDT loss would also substantially reduce our terminal noise figure and should be achievable25,26,27. The IDTs in this work were far from ideal, being bidirectional and having a non-ideal duty cycle on account of being close to the resolution limit of the optical lithography system used to pattern them. However, in high-k2 systems such as this one, it is possible to optimize the insertion loss of an IDT to less than 1 dB (refs. 25,26,27). Regardless, the noise figure we report here is the smallest acoustic and RF terminal noise figure ever achieved for an acoustoelectric amplifier. While this device architecture is already enabling for phonon amplification, optimization of materials and IDTs should result in devices with a terminal noise figure less than 3 dB, making them directly competitive for integration into RF electronic systems.

A second wafer was fabricated with smaller acoustic apertures to reduce the dissipated d.c. power and resulting self-heating effects9, as well as modified IDT processing steps to reduce IDT insertion loss (Methods). While this particular wafer had an increased metal–semiconductor contact resistance, which prohibits a complete characterization of the semiconductor and electromechanical properties, these devices do show the potential to achieve larger terminal gain at lower d.c. power dissipation and higher operating frequencies. A plot of terminal gain as a function of frequency for acoustic wave amplifiers with three different lengths is shown in Fig. 3a, and Fig. 3b plots the terminal gain at 1.04 GHz as a function of device length. A terminal gain of 11.3 dB is achieved at 1.04 GHz with a device length of 500 μm and dissipated power of 19.6 mW (additional performance characteristics, including a plot of the acoustic output power as a function of acoustic input power, are given in Supplementary Note 6). In Fig. 3c, the free spectral range for the gain ripples is plotted as a function of device length. The trend follows that expected for the formation of an acoustic cavity, where the depth of the ripples increases with the amplifier gain (Supplementary Note 1).

Fig. 3: Towards larger terminal gain and higher operating frequency.
figure 3

a, Measured terminal gain as a function of frequency for three different devices with lengths of 150, 250, and 500 μm. For these devices, the acoustic wavelength is 3.75 µm, the IDT aperture is 35 µm, and each IDT has 12 electrode pairs. The RF input power is −30 dBm. b, Terminal gain at 1.04 GHz as a function of device length. For the 500-μm-long device, a terminal gain of 11.3 dB is achieved at 1.04 GHz with a dissipated power of 19.6 mW. c, Free spectral range (FSR) of the gain ripple as a function of device length. The linear decrease in the free spectral range of the ripples with amplifier length shows that these ripples are due to multiple reflections. d, Measured transmission increase at the third harmonic of an IDT designed to operate at approximately 1 GHz as a function of frequency with and without the application of 45 V. e, Measured gain slope as a function of frequency. Data are presented as mean values ± one standard deviation based on measurements from five devices. The three different marker colours correspond to the data taken from three different wafers.

Full size image

A plot of transmission as a function of frequency around the 3.4 GHz resonance, with and without an applied bias of 45 V, for the 250-μm-long amplifying delay line is shown in Fig. 3d. This frequency corresponds to the third harmonic of the IDT designed for operation around 1 GHz. Although terminal gain is not achieved, there is a transmission increase of 40 dB at 3.4 GHz with the applied bias. These results suggest that terminal gain is achievable at higher frequencies contingent on IDT optimization to minimize excess insertion losses. Figure 3e shows the measured gain slope as a function of operating frequency from devices measured across three different wafers. Broadband gain from 0.25 to 3.40 GHz with a gain slope exceeding 0.5 dB V–1 is achieved in this material platform. This shows that these types of amplifiers can achieve gain across a very large bandwidth, demonstrating the feasibility of ultrabroadband acoustoelectric amplifiers in a heterostructure with fixed film thickness.

The maximum operating frequency for an acoustoelectric amplifier in our heterostructure is determined by diffusion effects from charge carriers24 and the minimum feature size with which an IDT can be patterned. For the particular guided wave mode used and modelled in this work, k2 decreased with increasing frequency; however, at very high frequencies, Rayleigh and SH-surface acoustic wave quasi-surface modes can be utilized and have higher k2 than the guided wave mode in this regime. Also, as described in Supplementary Note 7, with increasing frequency, the InP adhesion layer can become an appreciable fraction of the acoustic wavelength (thickness/wavelength > 0.01), thereby reducing the evanescent overlap of the longitudinal field with the carriers (reducing the effective k2) and, in turn, reducing the gain. Although we generally seek to maximize the achievable gain, the variation in gain with adhesion-layer thickness potentially allows a tailorable frequency-dependent gain, such as a flat broadband gain response, given that gain typically increases with frequency.

Heterostructure design and optimization

For a delay line amplifier built in the In0.53Ga0.47As–LiNbO3–silicon heterostructure, a plot of the theoretical acoustic gain as a function of drift field is shown in Fig. 4a. Details on modelling of the acoustic gain and a complete discussion of all the material and device parameters are given in Supplementary Note 2. The maximum gain is set by k2, but in practise, the ability to achieve this maximum is hindered by thermal effects. We then seek to optimize the maximum gain slope (gain per volt), which occurs around the drift field where the charge-carrier drift velocity (vd) is equal to the acoustic-wave phase velocity (va), to achieve large gain with minimal power dissipation. This requires maximizing k2 and optimizing σt, which in this case corresponds to minimizing σt. As thermal effects have been an outstanding issue for the successful operation of active acoustic wave devices7,8,9,10, any practical design of these devices must also seek to minimize the temperature rise from power dissipation (ΔT).

Fig. 4: Heterostructure optimization.
figure 4

a, Theoretical acoustic gain as a function of drift field for an acoustoelectric equivalent circuit model. The red dashed line indicates the synchronous point where vd = va, the dashed blue line indicates the maximum gain value, and the green line indicates the maximum gain slope. b, Contour plot of the modelled k2 value as a function of LiNbO3 film thickness and acoustic wavelength. c, Theoretical maximum gain slope and modelled k2 value as a function of acoustic wavelength for a LiNbO3 film thickness of 5 μm. The inset shows a plot of the theoretical gain slope as a function of σt. d, Plot of the theoretical Rth as a function of substrate thermal conductivity. The inset shows the computed Rth for a heat-transfer finite element method model of the In0.53Ga0.47As–LiNbO3–silicon heterostructure as a function of LiNbO3 thickness. In these models, the In0.53Ga0.47As layer serves as the heat source, with a thickness of 50 nm, length of 500 µm, and width of 50 µm.

Full size image

Maximizing k2 is achieved first and foremost with the choice of piezoelectric material, propagation direction, and polarization of acoustic waves in that material, as well as the frequency of operation relative to the thickness. Here we choose a SH-like guided mode propagating in the X material direction of Y-cut LiNbO3 with particle motion primarily in the Z material direction, as this is analogous to YX SH-SAW modes in bulk LiNbO3 that achieve the highest k2 for bulk material but have high propagation losses due to coupling to bulk modes10. As the bulk modes are forbidden in this vertical guided wave system, we use this mode to find a simultaneously low-loss and high-k2 mode. Figure 4b shows a contour plot extracted from a finite element method model of k2 for the guided acoustic mode with primarily SH polarization in a film of YX LiNbO3 on silicon, as a function of LiNbO3 thickness and acoustic wavelength. A large k2 can be achieved for a notable range of acoustic wavelengths and LiNbO3 thicknesses. At high operating frequencies, which correspond to small acoustic wavelengths, a high k2 (>5%) can be achieved in this heterostructure with a 5-μm-thick LiNbO3 film by transitioning to a Rayleigh or SH-SAW quasi-surface mode as opposed to the guided acoustic mode used in this work. This can be used, for example, to achieve large, broadband gain using a single choice of film thickness.

Figure 4c shows the theoretical maximum gain slope and modelled k2 value as a function of acoustic wavelength for a fixed thickness of 5 μm, which is a common commercially available thickness for LiNbO3–silicon wafers. Figure 4c (inset) shows that the theoretical gain slope can reach exceptionally high values (>3,500 dB V–1) by modifying σt. The discrepancy between the optimal gain slope and the gain slope observed here is due to challenges that limit semiconductor mobility, doping concentration and thickness (Supplementary Note 3). However, not all the uses of acoustoelectric amplifiers favour the absolute maximum gain slope; for example, the saturation output power for an acoustoelectric amplifier is fundamentally limited by the capture of all the available charge carriers in the acoustic wave potential and therefore is increased with a higher Nd (ref. 24), showing that the optimization of materials is actually application dependent.

As discussed above, it is critical to minimize the temperature rise from power dissipation, ΔT, which is generally minimized by decreasing the heterostructure thermal resistance (Rth) and dissipated power. Figure 4d shows a plot of Rth as a function of substrate thermal conductivity and Fig. 4d (inset) shows a plot of Rth as a function of LiNbO3 film thickness. Details on the thermal modelling are given in Supplementary Note 8. With 5 µm of LiNbO3, we achieve an almost ten times improvement in Rth compared with bulk LiNbO3, and this can be further improved another three times by reducing the LiNbO3 thickness to 1 μm. Increasing the film resistivity or reducing the amplifier width (that is, the width of the semiconductor amplifier region) also leads to a lower ΔT via reduced power dissipation that does not compromise gain (Supplementary Note 8). However, these cannot necessarily be independently optimized in every case, as increasing the semiconductor resistivity is limited by the material platform and a narrow acoustic wave device can result in substantial diffraction losses; for this reason, it is universally desirable to use a substrate with high thermal conductivity for long delay lines.

Conclusions

We have reported an In0.53Ga0.47As–LiNbO3–silicon heterostructure that provides a monolithic acoustoelectric amplifier that operates continuously and achieves terminal gain. We demonstrated 28.0 dB of acoustic gain (4.0 dB net RF gain) for 1 GHz phonons in a 500-µm-long amplifying delay line with 40.5 mW of dissipated power and an acoustic noise figure of 2.8 dB. At a different operating point of the same device, a larger acoustic gain of 30.5 dB (6.5 dB net gain) was demonstrated with 65 mW of dissipated power and an acoustic noise figure of 4.0 dB. We also have shown performance characteristics that exceed this device, including 11.3 dB of terminal gain with a d.c. power dissipation of 19.6 mW and non-reciprocal transmission greater than 55 dB. The maximum gain slope was shown to have a peak value of 1.3 dB V–1 at approximately 1 GHz and maintain a value of 0.5 dB V–1 or greater over a bandwidth exceeding 3 GHz.

Together with our experimental results, we have reported modelling that suggests that there is potential for improved performance: that is, a single device could achieve higher gain in a shorter length with reduced dissipated power and lower noise figure. Thinning the LiNbO3 layer will reduce Rth and increase thermal stability without compromising gain. Decreasing the semiconductor conductivity, thickness or both will also lead to reduced power dissipation, improved thermal properties, and increased gain slope. For example, reducing the doping concentration to Nd = 5 × 1015 cm−3 could increase the demonstrated gain slope by sixfold. Further reduction in the semiconductor amplifier width, especially when combined with acoustic guiding28,29,30,31 or focusing23,32,33 methods, could also reduce the dissipated power and improve the overall device thermal stability. These developments should also improve the noise figure, as our acoustic noise figure is currently limited by the onset of thermal instability. Our terminal noise figure is currently limited by input losses and should improve with the development of low-loss IDTs for LiNbO3 films on silicon.

Our heterostructure approach can easily accommodate other material stacks. For example, lithium tantalate could be used as the piezoelectric film, which could potentially provide reduced variability in performance as a function of temperature34. Another option is aluminium nitride doped with scandium (ScxAl1–xN), which is still a highly piezoelectric material but is available as a physical-vapour-deposited film, making it easier to achieve very thin films as well as being easier and cheaper to manufacture. Moreover, ScxAl1–xN has a large acoustic velocity, which makes operating at gigahertz frequencies less constrained by IDT patterning capabilities35,36. A substrate such as silicon carbide could provide as much as a twofold increase in thermal conductivity over silicon, improving the d.c. and RF power handling and providing even stronger waveguiding effects, as its acoustic velocity is of the order of 13 km s–1. The continued development of piezoelectric thin films, wafer bonding, and low-defectivity material deposition and growth should continue to expand the possible material combinations to achieve high-performing active acoustic wave device architectures like the ones demonstrated here.

Comparing acoustoelectric amplification technology with current state-of-the-art low-noise amplifiers for RF signal processing, it is important to consider fundamental limitations to the gain, noise figure and operating bandwidth. The gain is fundamentally limited by the electromechanical coupling k2 and can be exceptionally high; for example, in our 500-µm-long 1 GHz amplifier, the maximum acoustic gain would be >150 dB if self-heating could be suppressed enough to achieve the maximum. Moreover, theoretical predictions7 and computational modelling for these systems suggest than an acoustic noise figure less than 1 dB is achievable in our heterostructure. Although the bandwidth of a single amplifier that uses IDTs is tied to the current state-of-the-art electromechanical transducer technology, there are multiple ways in which the full bandwidth of the acoustoelectric amplifier could be employed. One way to harness the entirety of the acoustoelectric amplifier bandwidth is to avoid IDTs for the generation and measurement of acoustic waves, such as in Brillouin optomechanical phonon transduction on a chip37. Another route is to use a bank of IDTs connected by acoustoelectric switches16. Finally, the largest benefits of this technology may come in the context of entirely acoustic systems, rather than RF systems that use acoustic elements. In particular, we have demonstrated a large acoustic gain of 28.0 dB, with an acoustic noise figure of 2.8 dB; this is a performance for the amplification of phonons comparable with state-of-the-art low-noise RF amplifiers in the electronic domain38,39.

Although acoustic non-reciprocity can be achieved using acoustic nonlinearities40,41,42, the acoustic Zeeman effect43, non-reciprocal bianisotropy44,45 or spatiotemporal modulation of acoustic resonators46,47, we have shown here that large non-reciprocal transmission (>55 dB) can be achieved at gigahertz frequencies using the acoustoelectric effect. This non-reciprocity is also tunable, broadband, only requires an applied d.c. bias, and occurs in an on-chip device with a small footprint. Building on the non-reciprocal directional amplifier presented here, this work could lead to novel approaches to non-Hermetian phononics, such as acoustic wave isolation and routing, in compact and continuously operating devices at microwave frequencies with low noise.

Piezoelectric acoustic wave devices also allow coupling between electrical circuits and optomechanical devices, and recent experimental demonstrations have shown the potential advantage of implementing additional functionalities in the acoustic domain for classical and quantum information processing48,49,50. The acoustoelectric effect using our heterostructure approach could, thus, enable tunable acoustic loss (or gain) and tunable non-reciprocity in these hybrid electrical and piezo-optomechanical circuits. The acoustoelectric effect has also been directly proposed for novel quantum information processing architectures using piezoelectric semiconductors51,52,53. Our heterostructure approach to acoustoelectric devices could provide enhanced performance and new applications in these quantum systems. There is also the potential to achieve net round-trip gain in a resonator using our material platform, which could lead to on-chip frequency-selective resonant amplifiers and oscillators54. Together with other passive acoustic, active (nonlinear) and non-reciprocal acoustoelectric components9,16, these devices provide a library for integration in the front end of RF electronic systems and miniaturized RF systems that use all-acoustic RF signal processing.

Methods

Device fabrication

A lattice-matched epitaxial semiconductor In0.53Ga0.47As–InP layered structure is first grown by metal–organic chemical vapour deposition on a two-inch InP substrate. The structure consists of a 500 nm non-intentionally doped InP buffer, a 3 µm non-intentionally doped In0.53Ga0.47As etch stop, a 100 nm InP etch stop doped with silicon at Nd = 1 × 1018 cm−3, a two-layer epitaxial contact (100-nm-thick In0.53Ga0.47As and 30-nm-thick InP contact layers doped with silicon at Nd = 2 × 1019 cm−3 and Nd = 1 × 1018 cm−3, respectively), an In0.53Ga0.47As amplifier layer with a target silicon doping level of Nd = 1 × 1016 cm−3 and a target thickness of 50 nm, and a final 5-nm-thick non-intentionally doped InP adhesion layer. The InP substrate is then bonded, at the wafer scale, to a four-inch substrate consisting of a 5-µm-thick LiNbO3 film on bulk silicon. The LiNbO3 layer on the silicon substrate is commercially available and prepared by bonding a LiNbO3 wafer to a silicon wafer followed by thinning and polishing LiNbO3 down to a 5 μm film. The bonding between the InP and LiNbO3–silicon substrates occurs via manual initiation followed by annealing at 100 °C in vacuum. The InP substrate and buffer layer are then etched away in a hydrochloric acid solution followed by the removal of the In0.53Ga0.47As etch-stop layer in a solution of sulfuric acid, hydrogen peroxide and water. The InP etch-stop layer is then removed in a solution of hydrochloric acid and phosphoric acid. The epitaxial contact is then patterned, and the wafer is placed in a sulfuric acid, hydrogen peroxide and water solution to first etch the In0.53Ga0.47As layer followed by a hydrochloric acid and phosphoric acid solution to etch the InP contact layer. Following patterning and etching of the epitaxial contact, the In0.53Ga0.47As amplifier layer is patterned and etched in a sulfuric acid, hydrogen peroxide and water solution, landing on LiNbO3. The IDTs are fabricated using a metal liftoff process where the pattern is made by photolithography or electron-beam lithography. With electron-beam lithography, the pattern quality is improved, which leads to reduced IDT insertion loss and improved generation of acoustic modes at higher harmonics of the IDT resonance frequency. The IDT metal is 150 nm aluminium with a 10 nm chrome adhesion layer. A second liftoff step of a stack of 10 nm titanium, 500 nm gold, 500 nm silver and 100 nm gold forms the metal contact. The metal contact stack is chosen based on previous work where the contact resistance was optimized for extremely thin n-type InGaAs contact layers55. This contact type is suitable for our acoustoelectric heterostructure such that the epitaxial contact layers can be acoustically thin to prevent acoustic reflections and annealing is not required, which could cause the semiconductor films to delaminate. In this structure, the metal contact is fabricated so that it is not in the acoustic wave’s path, which allows us to apply a drift field for the charge carriers and minimize the acoustic reflection loss.

Passive delay line and gain measurements

The delay line and acoustic amplifier devices are evaluated on a custom RF–d.c. probe station with separate ground–signal–ground RF probes and d.c. probes. Scattering (S) parameters are measured using a Keysight E5071c network analyser. A two-port short–load–open–through calibration is performed using an impedance standard substrate before device measurements. To evaluate the acoustic amplifier performance, a continuous drift field is applied using a d.c. power supply and the S parameters are measured as a function of frequency. For each measurement, the voltage value is set on the d.c. power supply and the continuous drift field is left on for several seconds. A frequency sweep is then acquired using the network analyser with the RF input power set to −30 dBm. For the case of acoustoelectric amplifiers operating near 1 GHz, both centre frequency and span are set to 1 GHz. The continuous RF source is swept across the frequency span for each measurement as the terminal gain is simultaneously measured. The transient response of the acoustoelectric amplifier itself is governed by three timescales. The first is given by the RC response time of the semiconductor–piezoelectric system, which is related to the conductivity of the semiconductor in addition to the dielectric constants and geometry of the system (Supplementary Note 2). This timescale is given by 2π/ωc, where ωc is the dielectric relaxation frequency and is approximately 14 ps (ref. 21). The second timescale is the acoustic propagation time across the semiconductor region, which is determined by the speed of sound and amplifier length; this sets a timescale for transient dynamics of approximately 100 ns. The third timescale is set by the thermal time constant of the structure. Utilizing a finite element method model for heat transfer in solids, we determined the maximum thermal time constant in the amplifying delay line to be approximately 6 μs (Supplementary Note 8). For the frequency sweep parameters used in this work, the dwell time spent in each frequency bin is more than ten times longer than the timescale of transient dynamics of the amplifying delay line. We, therefore, do not expect that it would make any difference to use a continuous RF signal generator instead of a network analyser operating in the frequency sweep mode for these measurements. It is important to note that the terminal gain is also measured using a calibrated noise source during the noise figure measurement, as described below, and the same peak terminal gain is achieved within ±0.1 dB, although the measurement conditions differ substantially. The current is simultaneously measured with a source meter. The dissipated power is evaluated as the applied bias multiplied by the measured current. Terminal gain is the measured and calibrated S21 value on the network analyser, meaning that for terminal gain to be achieved, acoustic wave amplification must overcome all the device losses including input/output losses at the IDTs. Acoustic gain on a log scale (GAE,dB) is given by GAE,dB = ILOFF − ILON − αAE, where ILOFF is the measured insertion loss on the network analyser with no charge-carrier drift field applied, ILON is the measured insertion loss with the applied drift field and αAE is the loss due to the acoustoelectric effect with no applied drift field. The value for αAE is determined by the drift field required to achieve the synchronous velocity condition vd = va, which is specified by the measured Hall mobility and device length. In contrast to terminal gain, which only occurs when the gain is large enough to overcome end-to-end device losses, acoustic gain is achieved when the drift velocity is large enough to overcome the synchronous condition of vd = va. To determine the acoustic output power as a function of acoustic input power, the terminal gain was measured with increasing RF input power. The acoustic input power was determined from subtracting the input IDT loss from the RF input power. From the measured terminal gain, the acoustic gain was determined as described above. The acoustic output power is then the acoustic input power with the added acoustic gain and the subtracted propagation losses.

Determination of semiconductor and electromechanical properties

The thickness of the patterned In0.53Ga0.47As amplifier layer was measured by a profilometer after device fabrication at three different places on the wafer and the thickness was determined to be 58 ± 3 nm. The Hall coefficient of the In0.53Ga0.47As amplifier layer was measured by the van der Pauw method using Hall structures patterned on the wafer such that they go through the exact same fabrication process flow as the amplifier devices. Measurements were made on two separate Hall structures using a Bio-Rad fixed-magnetic-field Hall effect measurement system. The average values for the Hall coefficient and Hall mobility were –(3.5 ± 0.1) × 103 m2 C–1 and 4,220 ± 40 cm2 V–1 s–1, respectively. The experimental data near the synchronous point were fit to the theoretical gain slope with k2 as a fitting parameter to determine k2 = 14 ± 1%.

Noise figure measurement

The noise figure was determined by measuring the noise temperature of the acoustic wave amplifier by the Y-factor method on a Rohde & Schwarz FPL1007 spectrum analyser with an internal preamp using a calibrated noise source with an excess noise ratio of 26 dB. The spectrum analyser is specifically designed to measure the noise figure and can perform a second-order calibration to remove the effect of noise temperature for the spectrum analyser itself, which we have done in all the measurements presented here. We then directly measured the terminal noise temperature for our acoustic wave amplifier, which includes the impact of IDT input and output to the acoustoelectric interaction region. The noise factor F can be calculated from the noise temperature of a system Tsys according to F = (T0 + Tsys)/T0, where T0 is the input noise temperature. We refer our noise to a room temperature of T0 = 290 K. The noise figure NF is F expressed in dB (instead of on a linear scale), such that NF = 10log10(F) = 10log10(1 + Tsys/290 K). The Y-factor method determines the noise temperature and gain of a system by measuring the linear noise power on a spectrum analyser for a low-temperature noise source (\(T_{\mathrm{source}}^{\mathrm{OFF}}\)), which corresponds to when the calibrated noise source is off, and a high-temperature noise source (\(T_{\mathrm{source}}^{\mathrm{ON}}\)), which corresponds to when the calibrated noise source is on. The Y-factor term, Y, is given by the ratio of the linear noise power with the noise source on (Non) and noise source off (Noff) such that Y = Non/Noff and the noise temperature is given by \(T_{{{{\mathrm{sys}}}}} = \frac{{T_{\mathrm{source}}^{\mathrm{ON}} - Y \times T_{\mathrm{source}}^{\mathrm{OFF}}}}{{Y - 1}}\). To ensure device stability, each measurement was taken three times and the reported values are the average from these three measurements. From these measured values, we can determine the acoustic noise figure by considering the losses present in our system. In particular, we need to determine the loss from the input and output IDTs. To do this, we first determine the total loss with no applied drift field as measured on the spectrum analyser and confirmed with measurements from a network analyser. From this total loss, we then subtract the loss due to the acoustoelectric effect with no applied drift field and the acoustic propagation loss, including the impact of the semiconductor film. The resulting value is the combined loss from the input and output. We split these remaining losses in half and assign one half to the input loss and the other half to the output loss. This approach was confirmed by (1) comparing the S11 and S22 values on the network analyser and (2) measuring the noise figure with the input and output ports switched. To evaluate the acoustic noise figure, which corresponds to the noise figure of the acoustoelectric interaction region, we use Friis’s formula for the noise temperature of a system \(T_{{{{\mathrm{sys}}}}} = T_1 + \frac{{T_2}}{{G_1}} + \frac{{T_3}}{{G_1G_2}} = T_{{{{\mathrm{IDT}}}},{{{\mathrm{in}}}}} + \frac{{T_{\mathrm{AE}}}}{{G_{{{{\mathrm{IDT}}}},{{{\mathrm{in}}}}}}} + \frac{{T_{{{{\mathrm{IDT}}}},{{{\mathrm{out}}}}}}}{{G_{{{{\mathrm{IDT}}}},{{{\mathrm{in}}}}}G_{\mathrm{AE}}}}\), where T1 = TIDT,in and G1 = GIDT,in are the noise temperature and linear power gain, respectively, associated with the lossy input IDT; T2 = TAE and G2 = GAE are the noise temperature and linear power gain, respectively, associated with the acoustoelectric amplification region; and T3 = TIDT,out is the noise temperature of the lossy output IDT56. The acoustic noise figure is then NFacoustic = 10log10(1 + TAE/290 K).